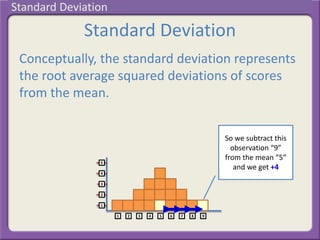
The document discusses the conceptual definition of standard deviation. Standard deviation represents the root average of the squared deviations of scores from the mean. It explains that to calculate standard deviation, each score's deviation from the mean is squared, those squared deviations are averaged, and then the square root of the average is taken to determine the standard deviation in the original units of measurement.

1. Standard Deviation
Conceptual Explanation
Standard Deviation

2. Standard Deviation
Conceptually, the standard deviation represents
the root average squared deviations of scores
from the mean.
Standard Deviation

3. Standard Deviation
Conceptually, the standard deviation represents
the root average squared deviations of scores
from the mean.
So, what does this
mean?
Standard Deviation

4. Standard Deviation
Conceptually, the standard deviation represents
the root average squared deviations of scores
from the mean.
Let’s see an
example:
Standard Deviation

5. Standard Deviation
Conceptually, the standard deviation represents
the root average squared deviations of scores
from the mean.
1 2 3 4 5 6 7 8 9
1
2
3
4
5
Here is a
distribution of
scores
Standard Deviation

6. Standard Deviation
Conceptually, the standard deviation represents
the root average squared deviations of scores
from the mean.
1 2 3 4 5 6 7 8 9
1
2
3
4
5
The mean of this
distribution is 5
Standard Deviation

7. Standard Deviation
Conceptually, the standard deviation represents
the root average squared deviations of scores
from the mean.
1 2 3 4 5 6 7 8 9
1
2
3
4
5
And this
observation is
9
Standard Deviation

8. Standard Deviation
Conceptually, the standard deviation represents
the root average squared deviations of scores
from the mean.
1 2 3 4 5 6 7 8 9
1
2
3
4
5
So we subtract this
observation “9”
from the mean “5”
and we get +4
Standard Deviation

9. Standard Deviation
Conceptually, the standard deviation represents
the root average squared deviations of scores
from the mean.
1 2 3 4 5 6 7 8 9
1
2
3
4
5
This means that this
observation is +4
units from the
mean.
Standard Deviation

10. Standard Deviation
Conceptually, the standard deviation represents
the root average squared deviations of scores
from the mean.
1 2 3 4 5 6 7 8 9
1
2
3
4
5
And this observation
is +3 units from the
mean.
Standard Deviation

11. Standard Deviation
Conceptually, the standard deviation represents
the root average squared deviations of scores
from the mean.
1 2 3 4 5 6 7 8 9
1
2
3
4
5
And this observation
is +2 units from the
mean.
Standard Deviation

12. Standard Deviation
Conceptually, the standard deviation represents
the root average squared deviations of scores
from the mean.
1 2 3 4 5 6 7 8 9
1
2
3
4
5
And this observation
is +1 unit from the
mean.
Standard Deviation

13. Standard Deviation
Conceptually, the standard deviation represents
the root average squared deviations of scores
from the mean.
1 2 3 4 5 6 7 8 9
1
2
3
4
5
This observation is
+1 unit from the
mean.
Standard Deviation

14. Standard Deviation
Conceptually, the standard deviation represents
the root average squared deviations of scores
from the mean.
1 2 3 4 5 6 7 8 9
1
2
3
4
5
And this observation
is +2 units from the
mean.
Standard Deviation

15. Standard Deviation
Conceptually, the standard deviation represents
the root average squared deviations of scores
from the mean.
1 2 3 4 5 6 7 8 9
1
2
3
4
5
And this observation
is +1 unit from the
mean.
Standard Deviation

16. Standard Deviation
Conceptually, the standard deviation represents
the root average squared deviations of scores
from the mean.
1 2 3 4 5 6 7 8 9
1
2
3
4
5
These values are all
0 units from the
mean
Standard Deviation

17. Standard Deviation
Conceptually, the standard deviation represents
the root average squared deviations of scores
from the mean.
1 2 3 4 5 6 7 8 9
1
2
3
4
5
This observation is
-1 unit from the
mean.
Standard Deviation`

18. Standard Deviation
Conceptually, the standard deviation represents
the root average squared deviations of scores
from the mean.
1 2 3 4 5 6 7 8 9
1
2
3
4
5
This observation is
-1 unit from the
mean.
Standard Deviation

19. Standard Deviation
Conceptually, the standard deviation represents
the root average squared deviations of scores
from the mean.
1 2 3 4 5 6 7 8 9
1
2
3
4
5
This observation is
-1 unit from the
mean.
Standard Deviation

20. Standard Deviation
Conceptually, the standard deviation represents
the root average squared deviations of scores
from the mean.
1 2 3 4 5 6 7 8 9
1
2
3
4
5
This observation is
-2 units from the
mean.
Standard Deviation

21. Standard Deviation
Conceptually, the standard deviation represents
the root average squared deviations of scores
from the mean.
1 2 3 4 5 6 7 8 9
1
2
3
4
5
This observation is
-2 units from the
mean.
Standard Deviation

22. Standard Deviation
Conceptually, the standard deviation represents
the root average squared deviations of scores
from the mean.
1 2 3 4 5 6 7 8 9
1
2
3
4
5
This observation is
-3 units from the
mean.
Standard Deviation

23. Standard Deviation
Conceptually, the standard deviation represents
the root average squared deviations of scores
from the mean.
1 2 3 4 5 6 7 8 9
1
2
3
4
5
This observation is
-4 units from the
mean.
Standard Deviation

24. Standard Deviation
Conceptually, the standard deviation represents
the root average squared deviations of scores
from the mean.
1 2 3 4 5 6 7 8 9
1
2
3
4
5
Some might think all we
need to do now is take the
average of all of these
values and we’ll get the
average deviation.
Standard Deviation

25. Standard Deviation
Conceptually, the standard deviation represents
the root average squared deviations of scores
from the mean.
1 2 3 4 5 6 7 8 9
1
2
3
4
5
Some might think all we
need to do now is take the
average of all of these
values and we’ll get the
average deviation.
Standard Deviation

26. Standard Deviation
Conceptually, the standard deviation represents
the root average squared deviations of scores
from the mean.
1 2 3 4 5 6 7 8 9
1
2
3
4
5
But, because half of the
deviations are positive and
the other half are negative,
if you take the average it
will come to zero
Standard Deviation

27. So to avoid this happening, we square each deviation
(-42 = 16, -12 = 1, 22 = 4, 42 = 16).
Then we add up all of the squared deviations and divide
that number by the number of observations
Standard Deviation
Conceptually, the standard deviation represents
the root average squared deviations of scores
from the mean.
1 2 3 4 5 6 7 8 9
1
2
3
4
5
Standard Deviation

28. So to avoid this happening, we square each deviation
(-42 = 16, -12 = 1, 22 = 4, 42 = 16).
Then we add up all of the squared deviations and divide
that number by the number of observations
Standard Deviation
Conceptually, the standard deviation represents
the root average squared deviations of scores
from the mean.
1 2 3 4 5 6 7 8 9
1
2
3
4
5
Standard Deviation

29. So to avoid this happening, we square each deviation
(-42 = 16, -12 = 1, 22 = 4, 42 = 16).
Then we add up all of the squared deviations and divide
that number by the number of observations
Standard Deviation
Conceptually, the standard deviation represents
the root average squared deviations of scores
from the mean.
1 2 3 4 5 6 7 8 9
1
2
3
4
5
So to avoid this happening, we square each deviation
(-42 = 16, -12 = 1, 22 = 4, 42 = 16).
Then we add up all of the squared deviations and divide
that number by the number of observations
2 134
So to avoid this happening, we square each deviation
(-42 = 16, -12 = 1, 22 = 4, 42 = 16).
Then we add up all of the squared deviations and divide
that number by the number of observations
So to avoid this happening, we square each deviation
(-42 = 16, -12 = 1, 22 = 4, 42 = 16).
Then we add up all of the squared deviations and divide
that number by the number of observations
So to avoid this happening, we square each deviation
(-42 = 16, -12 = 1, 22 = 4, 42 = 16).
Then we add up all of the squared deviations and divide
that number by the number of observations
4 units below
the mean
Standard Deviation

30. So to avoid this happening, we square each deviation
(-42 = 16, -12 = 1, 22 = 4, 42 = 16).
Then we add up all of the squared deviations and divide
that number by the number of observations
Standard Deviation
Conceptually, the standard deviation represents
the root average squared deviations of scores
from the mean.
1 2 3 4 5 6 7 8 9
1
2
3
4
5
So to avoid this happening, we square each deviation
(-42 = 16, -12 = 1, 22 = 4, 42 = 16).
Then we add up all of the squared deviations and divide
that number by the number of observations
1
So to avoid this happening, we square each deviation
(-42 = 16, -12 = 1, 22 = 4, 42 = 16).
Then we add up all of the squared deviations and divide
that number by the number of observations
So to avoid this happening, we square each deviation
(-42 = 16, -12 = 1, 22 = 4, 42 = 16).
Then we add up all of the squared deviations and divide
that number by the number of observations
So to avoid this happening, we square each deviation
(-42 = 16, -12 = 1, 22 = 4, 42 = 16).
Then we add up all of the squared deviations and divide
that number by the number of observations
1 unit below the
mean
Standard Deviation

31. So to avoid this happening, we square each deviation
(-42 = 16, -12 = 1, 22 = 4, 42 = 16).
Then we add up all of the squared deviations and divide
that number by the number of observations
Standard Deviation
Conceptually, the standard deviation represents
the root average squared deviations of scores
from the mean.
1 2 3 4 5 6 7 8 9
1
2
3
4
5
So to avoid this happening, we square each deviation
(-42 = 16, -12 = 1, 22 = 4, 42 = 16).
Then we add up all of the squared deviations and divide
that number by the number of observations
1 2
So to avoid this happening, we square each deviation
(-42 = 16, -12 = 1, 22 = 4, 42 = 16).
Then we add up all of the squared deviations and divide
that number by the number of observations
So to avoid this happening, we square each deviation
(-42 = 16, -12 = 1, 22 = 4, 42 = 16).
Then we add up all of the squared deviations and divide
that number by the number of observations
So to avoid this happening, we square each deviation
(-42 = 16, -12 = 1, 22 = 4, 42 = 16).
Then we add up all of the squared deviations and divide
that number by the number of observations
2 units above
the mean
Standard Deviation

32. So to avoid this happening, we square each deviation
(-42 = 16, -12 = 1, 22 = 4, 42 = 16).
Then we add up all of the squared deviations and divide
that number by the number of observations
Standard Deviation
Conceptually, the standard deviation represents
the root average squared deviations of scores
from the mean.
1 2 3 4 5 6 7 8 9
1
2
3
4
5
So to avoid this happening, we square each deviation
(-42 = 16, -12 = 1, 22 = 4, 42 = 16).
Then we add up all of the squared deviations and divide
that number by the number of observations
1 2 3 4
So to avoid this happening, we square each deviation
(-42 = 16, -12 = 1, 22 = 4, 42 = 16).
Then we add up all of the squared deviations and divide
that number by the number of observations
So to avoid this happening, we square each deviation
(-42 = 16, -12 = 1, 22 = 4, 42 = 16).
Then we add up all of the squared deviations and divide
that number by the number of observations
So to avoid this happening, we square each deviation
(-42 = 16, -12 = 1, 22 = 4, 42 = 16).
Then we add up all of the squared deviations and divide
that number by the number of observations
4 units above
the mean
Standard Deviation

33. Standard Deviation
Conceptually, the standard deviation represents
the root average squared deviations of scores
from the mean.
1 2 3 4 5 6 7 8 9
1
2
3
4
5
This gives us the average squared deviation (or
distance) of all the scores from the mean, which in this
case let’s say is 9. This is called the variance and will be
discussed later.
Standard Deviation

34. Standard Deviation
Conceptually, the standard deviation represents
the root average squared deviations of scores
from the mean.
1 2 3 4 5 6 7 8 9
1
2
3
4
5
This gives us the average squared deviation (or
distance) of all the scores from the mean, which in this
case let’s say is 9. This is called the variance and will be
discussed later.
Standard Deviation

35. Standard Deviation
Conceptually, the standard deviation represents
the root average squared deviations of scores
from the mean.
1 2 3 4 5 6 7 8 9
1
2
3
4
5
To get the average deviation (or distance) from the
mean we just take the square root of the average
squared deviation from the mean. The square root of 9
would be 3.
Standard Deviation

36. Standard Deviation
Conceptually, the standard deviation represents
the root average squared deviations of scores
from the mean.
1 2 3 4 5 6 7 8 9
1
2
3
4
5
To get the average deviation (or distance) from the
mean we just take the square root of the average
squared deviation from the mean. The square root of 9
would be 3.
Standard Deviation

37. Standard Deviation
Conceptually, the standard deviation represents
the root average squared deviations of scores
from the mean.
1 2 3 4 5 6 7 8 9
1
2
3
4
5
By taking the square root of the variance we are putting
the value back into the original unit of measurement.
If the original unit of measurement were INCHES then
the standard deviation would be 3 INCHES
Standard Deviation

38. Standard Deviation
Conceptually, the standard deviation represents
the root average squared deviations of scores
from the mean.
1 2 3 4 5 6 7 8 9
1
2
3
4
5
By taking the square root of the variance we are putting
the value back into the original unit of measurement.
If the original unit of measurement were INCHES then
the standard deviation would be 3 INCHES
Standard Deviation

39. Standard Deviation
Conceptually, the standard deviation represents
the root average squared deviations of scores
from the mean.
1 2 3 4 5 6 7 8 9
1
2
3
4
5
By taking the square root of the variance we are putting
the value back into the original unit of measurement.
If the original unit of measurement were DECIBELS then
the standard deviation would be 3 DECIBELS

40. Standard Deviation
Conceptually, the standard deviation represents
the root average squared deviations of scores
from the mean.
1 2 3 4 5 6 7 8 9
1
2
3
4
5
By taking the square root of the variance we are putting
the value back into the original unit of measurement.
If the original unit of measurement were DECIBELS then
the standard deviation would be 3 DECIBELS
Standard Deviation

41. Standard Deviation
Conceptually, the standard deviation represents
the root average squared deviations of scores
from the mean.
1 2 3 4 5 6 7 8 9
1
2
3
4
5
By taking the square root of the variance we are putting the
value back into the original unit of measurement.
If the original unit of measurement were HOCKEY STICKS
then the standard deviation would be 3 HOCKEY STICKS

42. Standard Deviation
Conceptually, the standard deviation represents
the root average squared deviations of scores
from the mean.
1 2 3 4 5 6 7 8 9
1
2
3
4
5
By taking the square root of the variance we are putting the
value back into the original unit of measurement.
If the original unit of measurement were HOCKEY STICKS
then the standard deviation would be 3 HOCKEY STICKS
Standard Deviation

43. Standard Deviation
The standard Deviation is used in many
statistical formulas and analyses.

44. Standard Deviation
The standard Deviation is used in many
statistical formulas and analyses.
Here is the formula:
Standard Deviation

45. Standard Deviation
The standard Deviation is used in many
statistical formulas and analyses.
Here is the formula:
Standard Deviation

46. Standard Deviation
Standard Deviation

47. Standard Deviation
Person Score
A 1
B 4
C 7
Standard Deviation

48. Standard Deviation
Person Score
A 1
B 4
C 7
Standard Deviation

49. Standard Deviation
Person Score
A 1
B 4
C 7
Standard Deviation

50. Standard Deviation
Person Score
A 1
B 4
C 7
Mean 4
Standard Deviation

51. Standard Deviation
Person Score
A 1
B 4
C 7
Mean 4
Standard Deviation

52. Standard Deviation
Person Score
A 1
B 4
C 7
Mean 4
Score - Mean
1 – 4
4 – 4
7 – 4
Standard Deviation

53. Standard Deviation
Person Score
A 1
B 4
C 7
Mean 4
Score - Mean
1 – 4
4 – 4
7 – 4
Deviation
= -3
= 0
= +3
Standard Deviation

54. Standard Deviation
Person Score
A 1
B 4
C 7
Mean 4
Score - Mean
1 – 4
4 – 4
7 – 4
Deviation
= -3
= 0
= +3
Squared
-32 = 9
02 = 0
+32 = 9

55. Standard Deviation
Person Score
A 1
B 4
C 7
Mean 4
Score - Mean
1 – 4
4 – 4
7 – 4
Deviation
= -3
= 0
= +3
Squared
-32 = 9
02 = 0
+32 = 9
Sum 18
Standard Deviation

56. Standard Deviation
Person Score
A 1
B 4
C 7
Mean 4
Score - Mean
1 – 4
4 – 4
7 – 4
Deviation
= -3
= 0
= +3
Squared
-32 = 9
02 = 0
+32 = 9
Sum 18
Standard Deviation

57. Standard Deviation
Person Score
A 1
B 4
C 7
Mean 4
Score - Mean
1 – 4
4 – 4
7 – 4
Deviation
= -3
= 0
= +3
Squared
-32 = 9
02 = 0
+32 = 9
Sum 18
Average 6
Standard Deviation

58. Standard Deviation
Person Score
A 1
B 4
C 7
Mean 4
Score - Mean
1 – 4
4 – 4
7 – 4
Deviation
= -3
= 0
= +3
Squared
-32 = 9
02 = 0
+32 = 9
Sum 18
Average 6
Standard Deviation

59. Standard Deviation
Person Score
A 1
B 4
C 7
Mean 4
Score - Mean
1 – 4
4 – 4
7 – 4
Deviation
= -3
= 0
= +3
Squared
-32 = 9
02 = 0
+32 = 9
Sum 18
Average 6
Square
Root
2.4
Standard Deviation

60. Standard Deviation
Person Score
A 1
B 4
C 7
Mean 4
Score - Mean
1 – 4
4 – 4
7 – 4
Deviation
= -3
= 0
= +3
Squared
-32 = 9
02 = 0
+32 = 9
Sum 18
Average 6
Square
Root
2.4
Standard Deviation

61. Standard Deviation
Person Score
A 1
B 4
C 7
Mean 4
Score - Mean
1 – 4
4 – 4
7 – 4
Deviation
= -3
= 0
= +3
Squared
-32 = 9
02 = 0
+32 = 9
Sum 18
Average 6
Square
Root
2.4
This is the Standard Deviation
Standard Deviation

62. Standard Deviation
Person Score
A 1
B 4
C 7
Mean 4
Score - Mean
1 – 4
4 – 4
7 – 4
Deviation
= -3
= 0
= +3
Squared
-32 = 9
02 = 0
+32 = 9
Sum 18
Average 6
Square
Root
2.4
So, technically, the standard deviation is the
root average squared deviation from the
mean.
Standard Deviation

63. Standard Deviation
Person Score
A 1
B 4
C 7
Mean 4
Score - Mean
1 – 4
4 – 4
7 – 4
Deviation
= -3
= 0
= +3
Squared
-32 = 9
02 = 0
+32 = 9
Sum 18
Average 6
Square
Root
2.4
So, technically, the standard deviation is the
root average squared deviation from the
mean.
Standard Deviation

64. Standard Deviation
Person Score
A 1
B 4
C 7
Mean 4
Score - Mean
1 – 4
4 – 4
7 – 4
Deviation
= -3
= 0
= +3
Squared
-32 = 9
02 = 0
+32 = 9
Sum 18
Average 6
Square
Root
2.4
So, technically, the standard deviation is the
root average squared deviation from the
mean.
Standard Deviation

65. Standard Deviation
Person Score
A 1
B 4
C 7
Mean 4
Score - Mean
1 – 4
4 – 4
7 – 4
Deviation
= -3
= 0
= +3
Squared
-32 = 9
02 = 0
+32 = 9
Sum 18
Average 6
Square
Root
2.4
So, technically, the standard deviation is the
root average squared deviation from the
mean.
Standard Deviation

66. Standard Deviation
Person Score
A 1
B 4
C 7
Mean 4
Score - Mean
1 – 4
4 – 4
7 – 4
Deviation
= -3
= 0
= +3
Squared
-32 = 9
02 = 0
+32 = 9
Sum 18
Average 6
Square
Root
2.4
So, technically, the standard deviation is the
root average squared deviation from the
mean.
Standard Deviation

67. Standard Deviation
Person Score
A 1
B 4
C 7
Mean 4
Score - Mean
1 – 4
4 – 4
7 – 4
Deviation
= -3
= 0
= +3
Squared
-32 = 9
02 = 0
+32 = 9
Sum 18
Average 6
Square
Root
2.4
So, technically, the standard deviation is the
root average squared deviation from the
mean.
Standard Deviation

68. Standard Deviation
The standard deviation has many uses.
Standard Deviation

69. Standard Deviation
The standard deviation has many uses.
First and foremost it is a number that describes how
scores in a distribution are spread out from one
another.
Standard Deviation

70. Standard Deviation
The standard deviation has many uses.
First and foremost it is a number that describes how
scores in a distribution are spread out from one
another.
Standard Deviation = 2
Standard Deviation

71. Standard Deviation
The standard deviation has many uses.
First and foremost it is a number that describes how
scores in a distribution are spread out from one
another.
Standard Deviation = 2 Standard Deviation = 18
Standard Deviation

72. Standard Deviation
The standard deviation has many uses.
First and foremost it is a number that describes how
scores in a distribution are spread out from one
another.
Standard Deviation = 2 Standard Deviation = 18
What do you think a distribution with a standard deviation of 1 might look like?
Standard Deviation

73. Standard Deviation
The standard deviation has many uses.
First and foremost it is a number that describes how
scores in a distribution are spread out from one
another.
Standard Deviation = 2 Standard Deviation = 18
What about standard deviations of 10 or 20?
Standard Deviation

74. The End
Standard Deviation