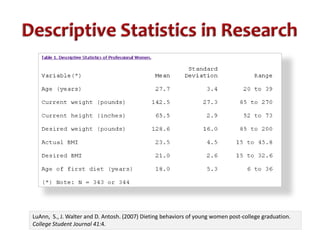
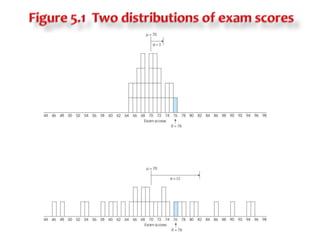
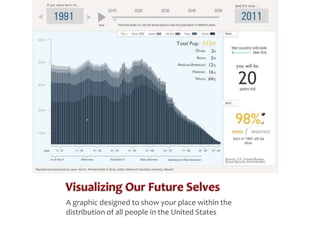
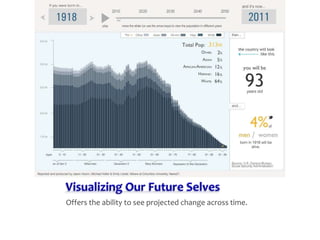
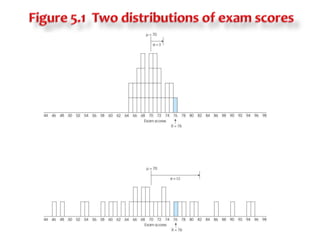
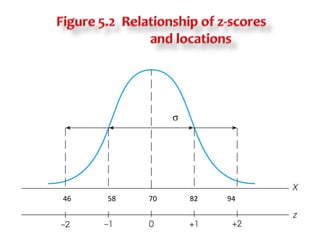
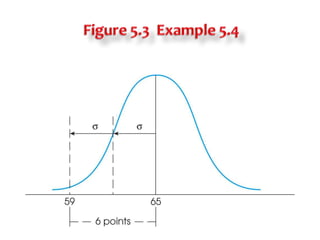
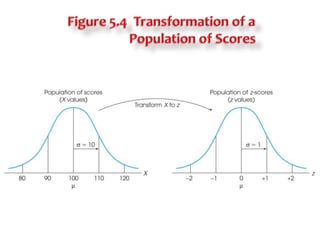
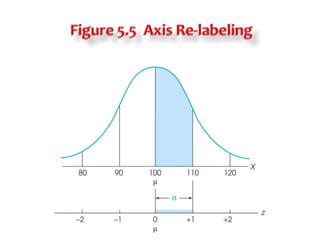
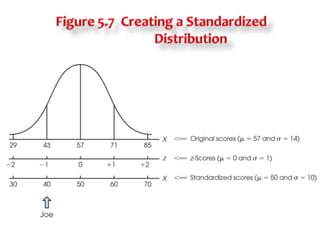
1) Z-scores describe the exact location of a score within a distribution by indicating how many standard deviations the score is above or below the mean, with the sign indicating direction and the number indicating distance. 2) Transforming scores to z-scores standardizes distributions so they have a mean of 0 and standard deviation of 1, allowing direct comparison of scores from different distributions. 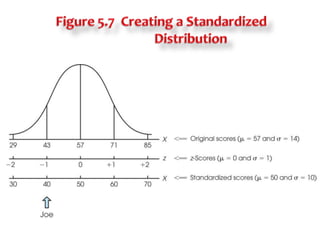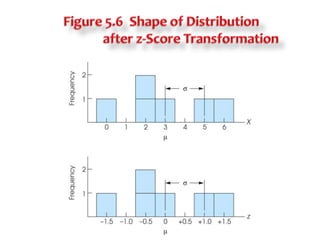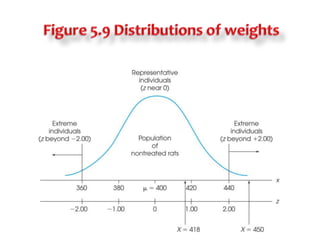3) Standardizing a distribution transforms all original scores to z-scores, preserving the shape of the distribution but setting it to have a mean of 0 and standard deviation of 1 for comparative purposes.

1. z-Scores: Location in DistributionsChapter 5 in Essentials ofStatistics for the Behavioral Sciences, by Gravetter & Wallnau

2. Statistics is a class about thinking.Numbers are the material we work with.Statistical techniques are tools that help us think.

3. History of the termStandard DeviationThe concept of “root-mean-square-error” (RMSE) was used by physical scientists in the late 18th century.Karl Pearson was the first to use “standard deviation” as a shorthand phrase for RMSE in a lecture in 1893, then in a book in 1894.Through Pearson, it came to be a central concept in most forms of modern statistics.Standard deviation is the accepted term in most social, behavioral, and medical sciences.Karl Pearson (1857-1936) established the discipline of mathematical statistics. In 1911 he founded the world's first statistics department at University College London. He was a controversial proponent of eugenics, and a protégé and biographer of Sir Francis Galton.

4. CNN-Money uses Standard DeviationMake fear and greed work for youWall Street constantly swings between these two emotions. You can either get caught in the frenzy - or profit from it.By Janice Revell, Money Magazine senior writerLast Updated: July 21, 2009: 10:56 AM ET“Making matters worse, the big stock bet would be far riskier on a year-to-year basis than other strategies. The most common measure of portfolio risk is standard deviation, which tells you how much an investment's short-term returns bounce around its long-term average. Since 1926 stocks have returned average gains of 9.6% a year, with a standard deviation of 21.5 percentage points, according to Ibbotson Associates. That means that about two-thirds of the time, the annual return on stocks landed 21.5 percentage points below or above the average - that is, in any given year, your results would range from a 12% loss to a 31% gain. You'd need either an iron stomach or a steady supply of Zantac to stay the course. And if you happened to be at or near retirement when one of those really bad years hit, you might have to rethink your plans.”http://money.cnn.com/2009/07/20/pf/funds/fear_greed.moneymag/

5. Descriptive Statistics in ResearchLuAnn, S., J. Walter and D. Antosh. (2007) Dieting behaviors of young women post-college graduation. College Student Journal41:4.

6. When you finish studying Chapter 5 you should be able to …Explain how a z-score provides a precise description of a location in a distribution, including information provided by the sign (+ or -) and the numerical value.Transform an X score into a z-score, and transform z-scores back into X scores, when the mean and standard deviation are given.Use z-scores to make comparisons across variables and individuals.Describe the effects when an entire data set is standardized by transforming all the scores to z-scores, including the impact on the shape, mean and standard deviation, and its comparability to other standardized distributions.Use z-scores to transform a distribution into a standardized distribution.Use SPSS to create standardized scores for a distribution.

7. Concepts to reviewThe mean (Chapter 3)The standard deviation (Chapter 4)Basic algebra (math review, Appendix A)

8. Figure 5.1 Two distributions of exam scores

9. Visualizing Our Future SelvesA graphic designed to show your place within the distribution of all people in the United States

10. Visualizing Our Future SelvesOffers the ability to see projected change across time.

11. 5.2 Locations and DistributionsExact location is described by z-scoreSign tells whether score is located above or below the meanNumber tells distance between score and mean in standard deviation units

12. Figure 5.1 Two distributions of exam scores

13. Figure 5.2 Relationship of z-scores and locations 64 67 70 73 7646 58 70 82 94

14. Equation for z-scoreNumerator is a deviation scoreDenominator expresses deviation in standard deviation units

15. Determining raw score from z-scoreNumerator is a deviation scoreDenominator expresses deviation in standard deviation units

16. Figure 5.3 Example 5.4

17. z-Scores for ComparisonsAll z-scores are comparable to each otherScores from different distributions can be converted to z-scoresThe z-scores (standardized scores) allow the comparison of scores from two different distributions along

18. Figure 5.7 Creating a Standardized Distribution

19. Practice Problems

20. What are your Questions?

21. 5.3 Standardizing a DistributionEvery X value can be transformed to a z-score

22. Characteristics of z-score transformation

23. Same shape as original distribution

24. Mean of z-score distribution is always 0.

25. Standard deviation is always 1.00

26. A z-score distribution is called a standardized distributionFigure 5.4 Transformation of a Population of Scores

27. Figure 5.5 Axis Re-labeling

28. Figure 5.6 Shape of Distribution after z-Score Transformation

29. z-Scores for ComparisonsAll z-scores are comparable to each otherScores from different distributions can be converted to z-scoresThe z-scores (standardized scores) allow the comparison of scores from two different distributions along

30. 5.4 Other Standardized DistributionsProcess of standardization is widely used AT has μ = 500 and σ = 100IQ has μ = 100 and σ = 15 PointStandardizing a distribution has two stepsOriginal raw scores transformed to z-scoresThe z-scores are transformed to new X values so that the specific μ and σ are attained.

31. Figure 5.7 Creating a Standardized Distribution

32. 5.6 Looking to Inferential StatisticsInterpretation of research results depends on determining if (treated) sample is noticeably different from the populationOne technique for defining noticeably different uses z-scores.