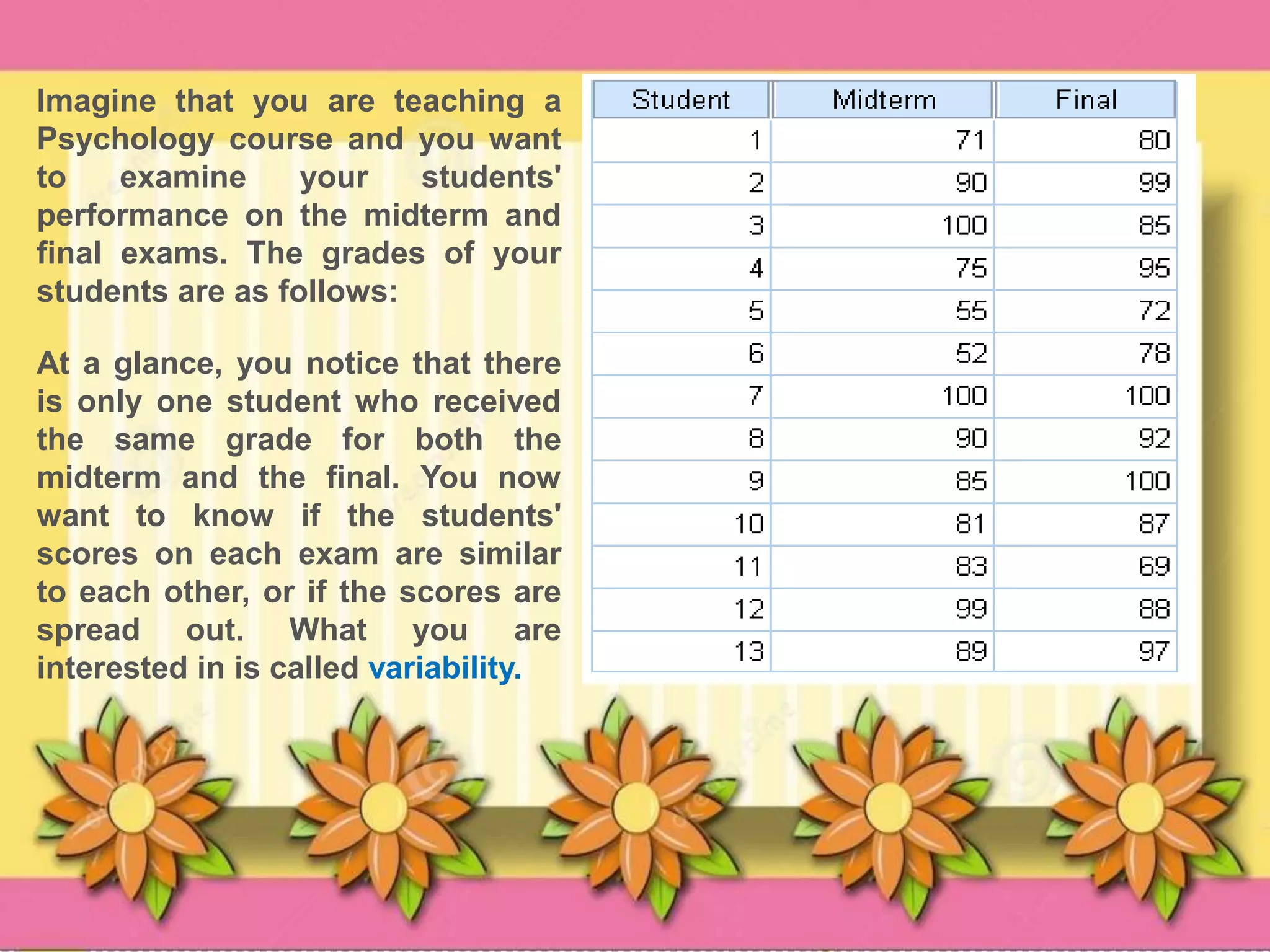
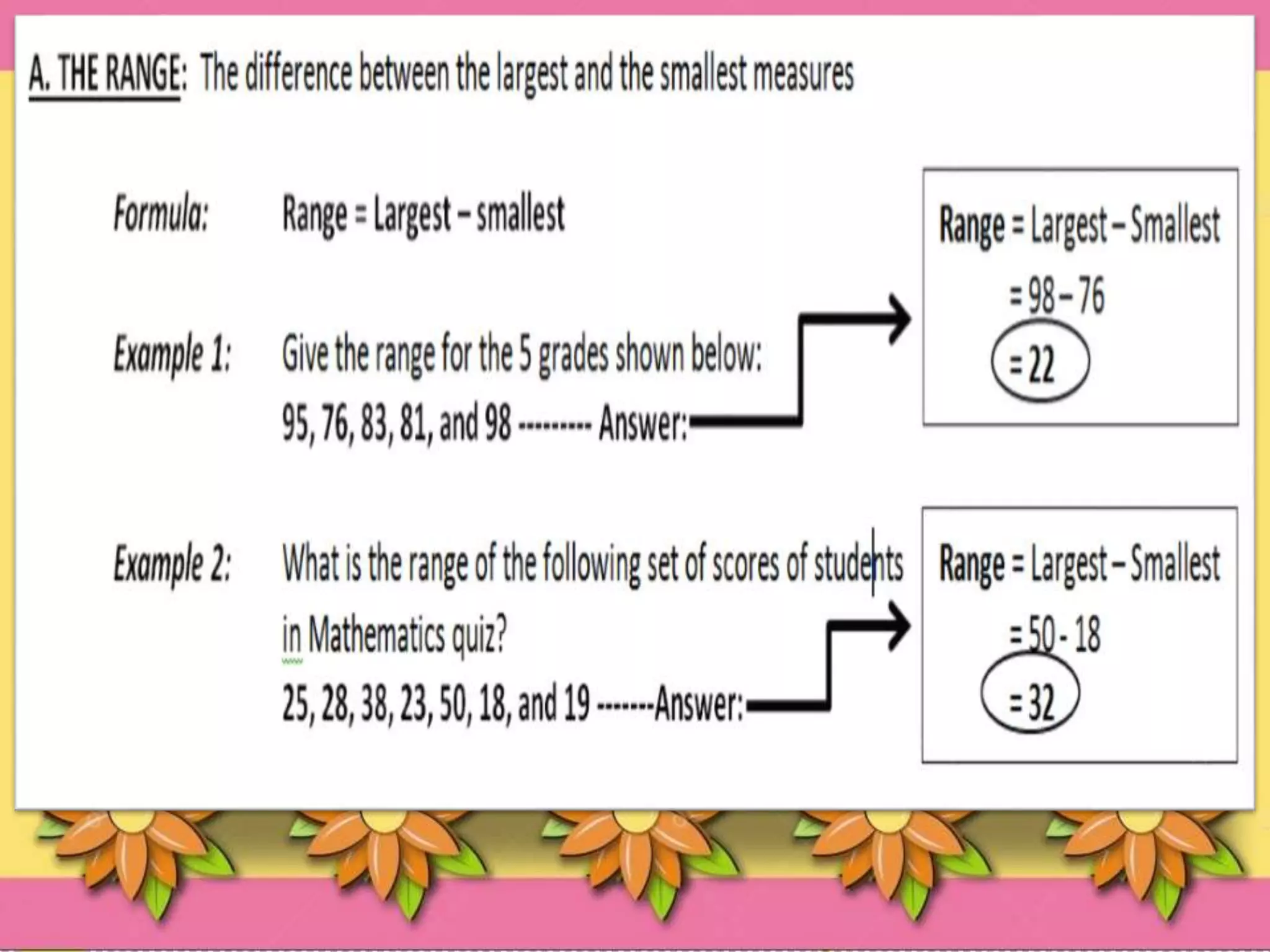
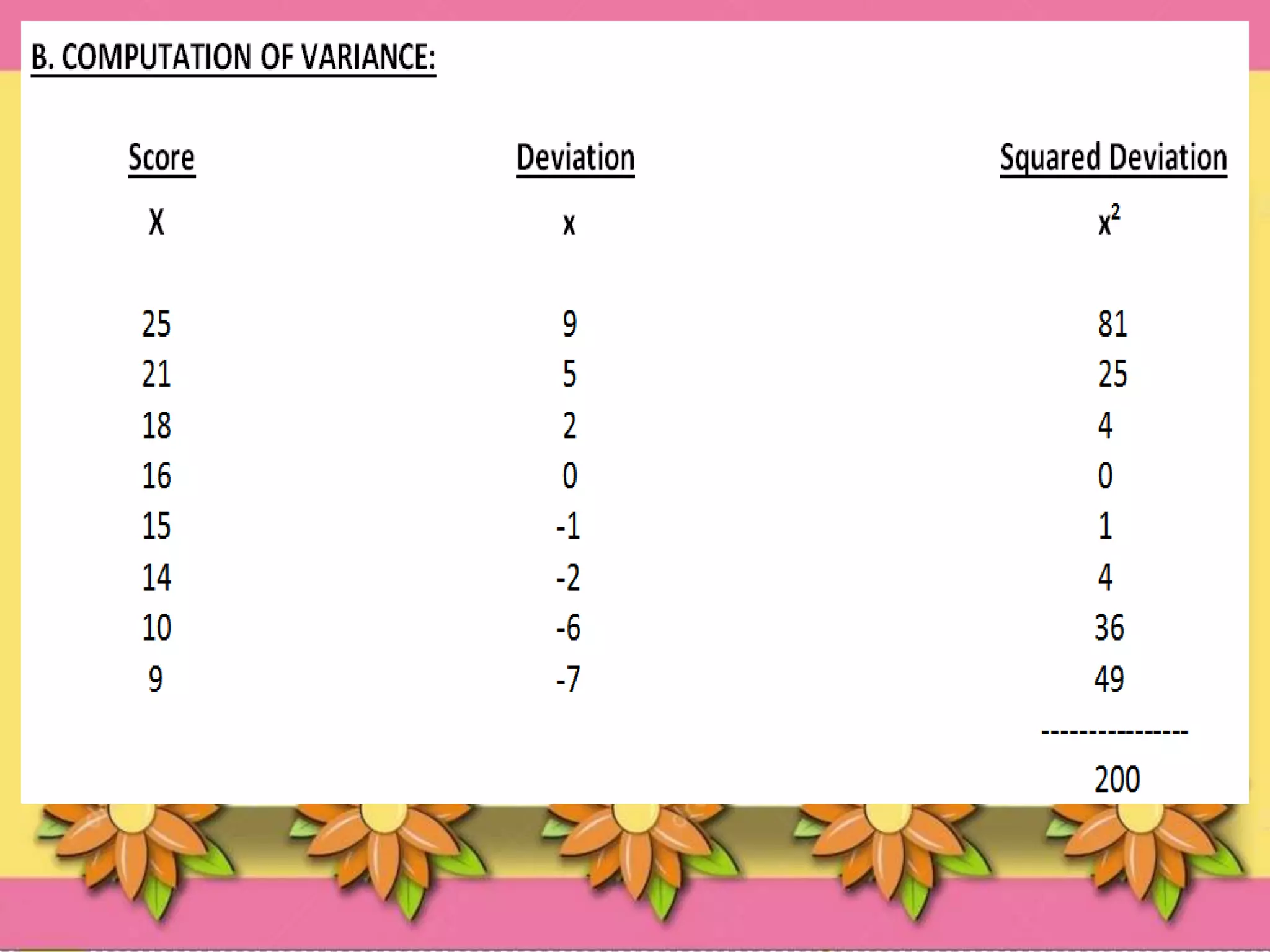
This document discusses measures of variability, which refer to how spread out a set of data is. Variability is measured using the standard deviation and variance. The standard deviation measures how far data points are from the mean, while the variance is the average of the squared deviations from the mean. To calculate the standard deviation, you take the square root of the variance. This provides a measure of variability that is on the same scale as the original data. The standard deviation and variance are widely used statistical measures for quantifying the spread of a data set.

1. Measures
of Variability
MARY KRYSTLE DAWN D. SULLEZA
Reporter
CHAPTER FOUR:

2. VARIABILITY: the “spread” in a set of measurement.
-it refers to how spread out a group of data is.
In other words, variability measures how much your
scores differ from each other. Variability is also
referred to as dispersion or spread. Data sets with
similar values are said to have little variability, while
data sets that have values that are spread out have
high variability.

3. Imagine that you are teaching a
Psychology course and you want
to examine your students'
performance on the midterm and
final exams. The grades of your
students are as follows:
At a glance, you notice that there
is only one student who received
the same grade for both the
midterm and the final. You now
want to know if the students'
scores on each exam are similar
to each other, or if the scores are
spread out. What you are
interested in is called variability.

8. D. THE STANDARD DEVIATION AND VARIANCE:
The most widely used measure for showing the
variability of a set of scores are the Standard
Deviation (s) and the Variance (s2). Some writers
used σ rather than s. The s as used here will apply to
statistic derived from a sample of scores drawn from a
population.
VARIANCE: is the mean or average of the squares of
the deviation of each measurement from the mean.

13. The variance cannot easily be related to the original
measures from which it was obtained because all the
differences from the mean were squared. A measure
of variability that is compatible to the original
measure is obtained by taking the square root of the
variance. The result is called the Standard Deviation.

14. The above method of solving for the standard
deviation is known as the “ deviation-score” method
for ungrouped data. Another frequently used
method for finding s is the “raw-score” method for
ungrouped data. The formula is given below;

16. THE END!!!
  
Thank You for
Listening.