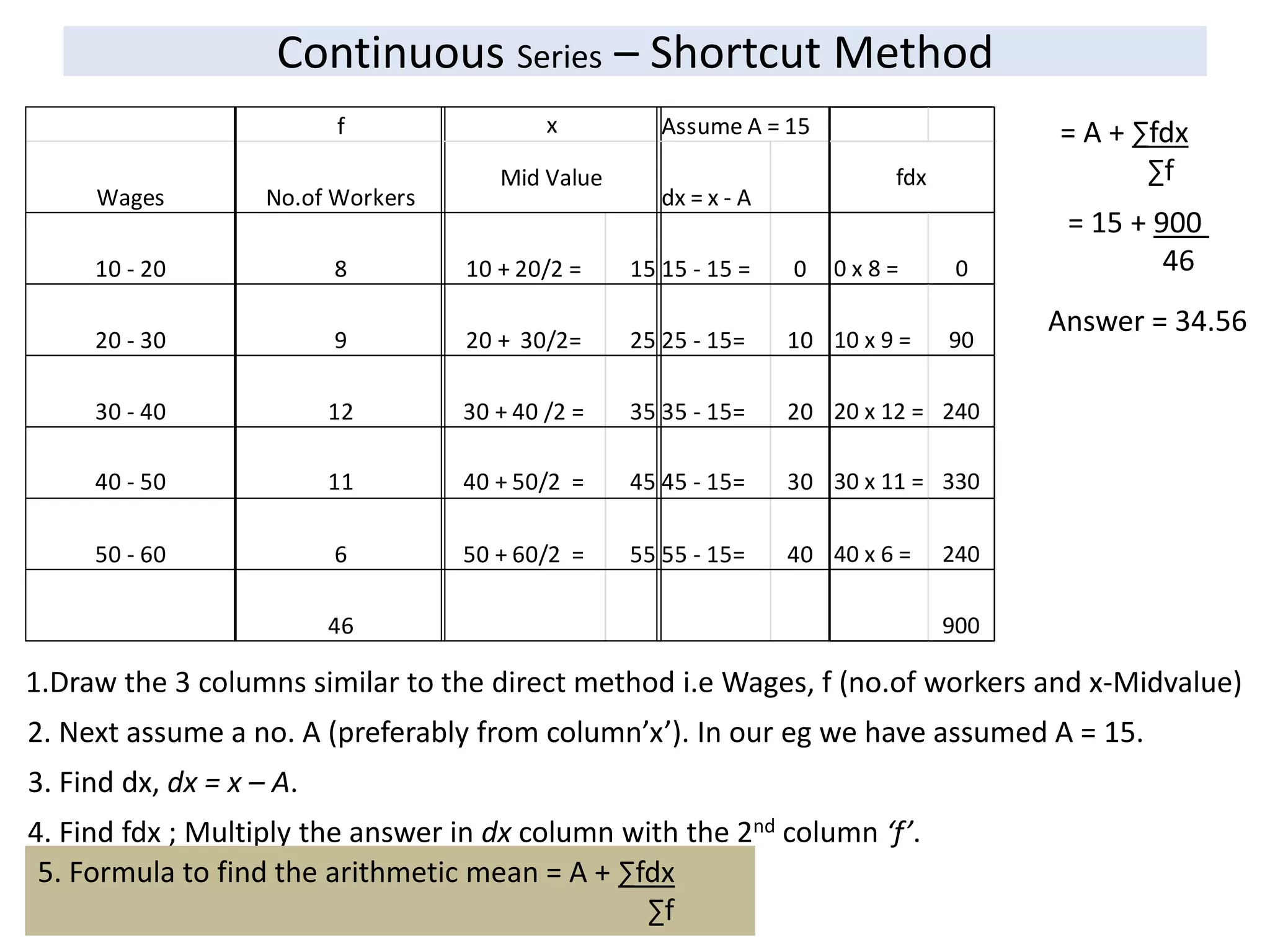
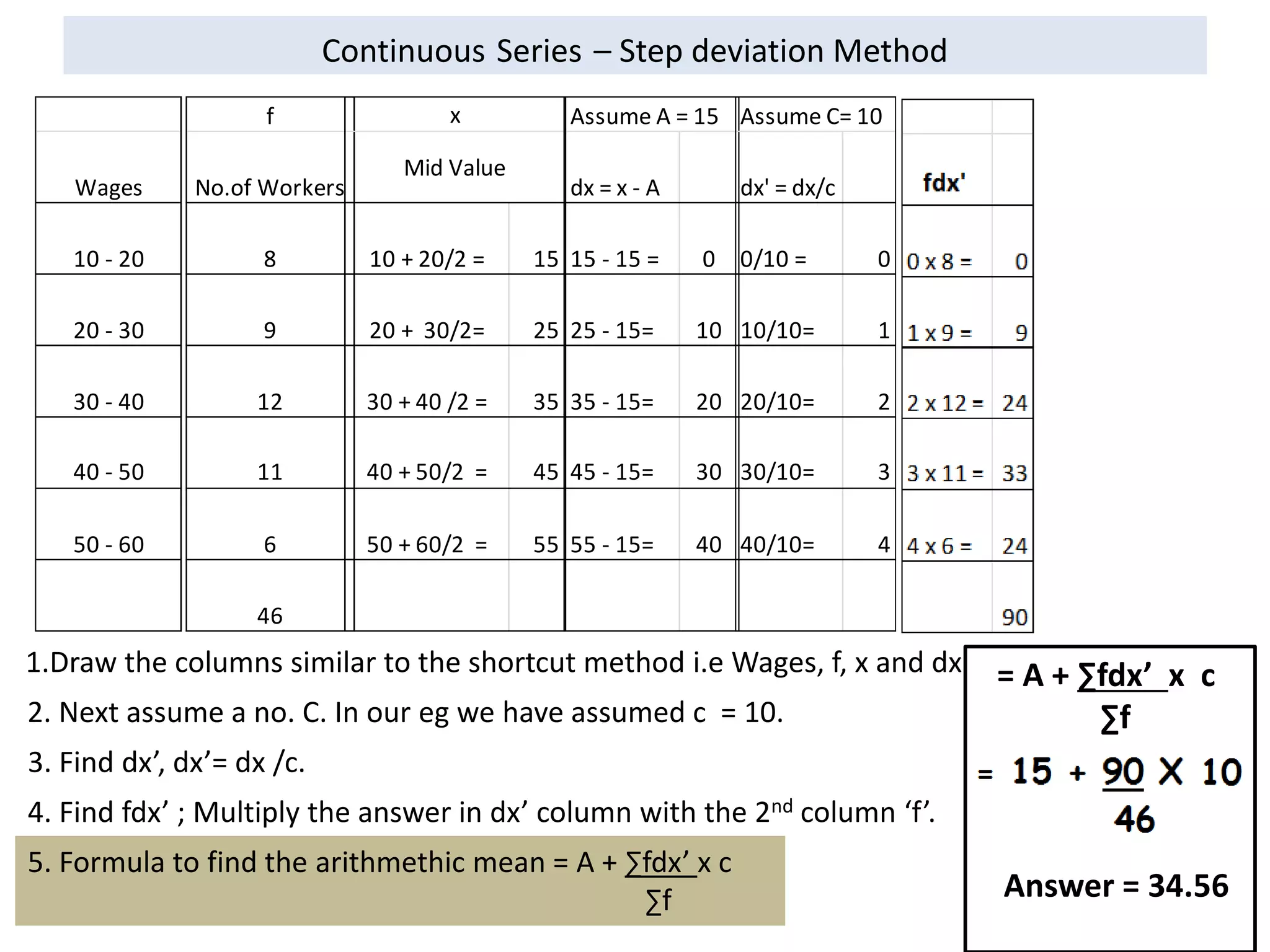
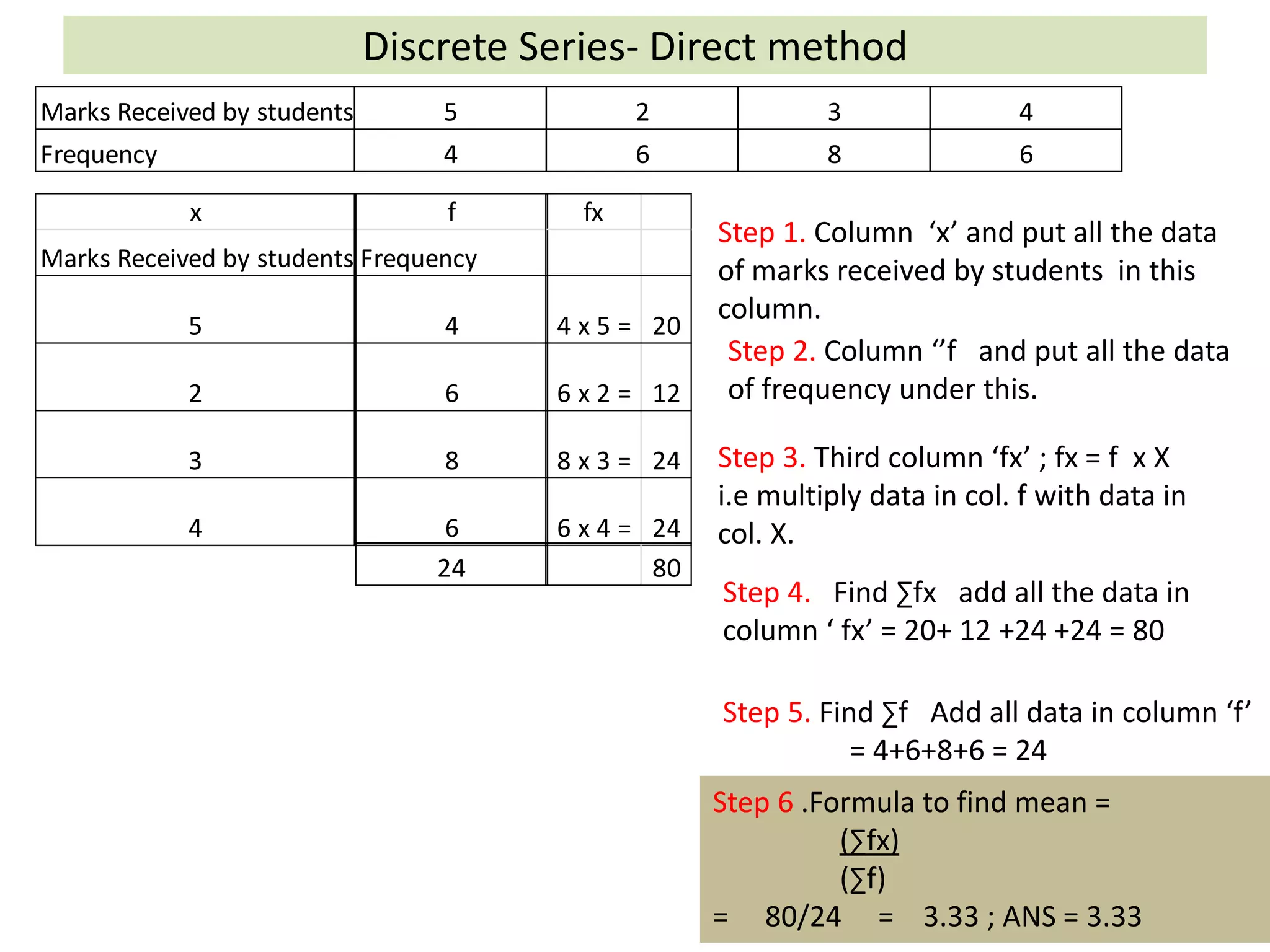
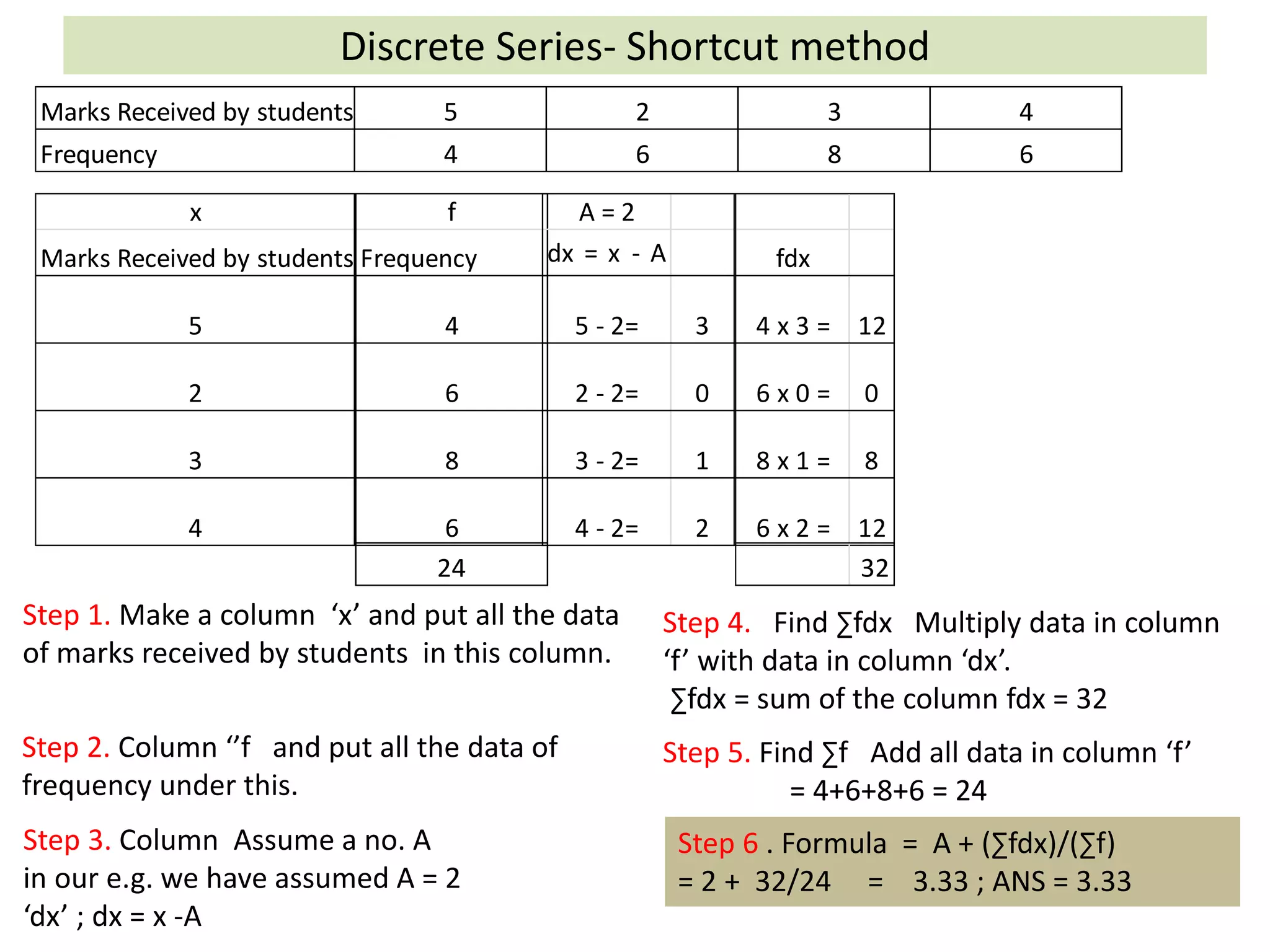
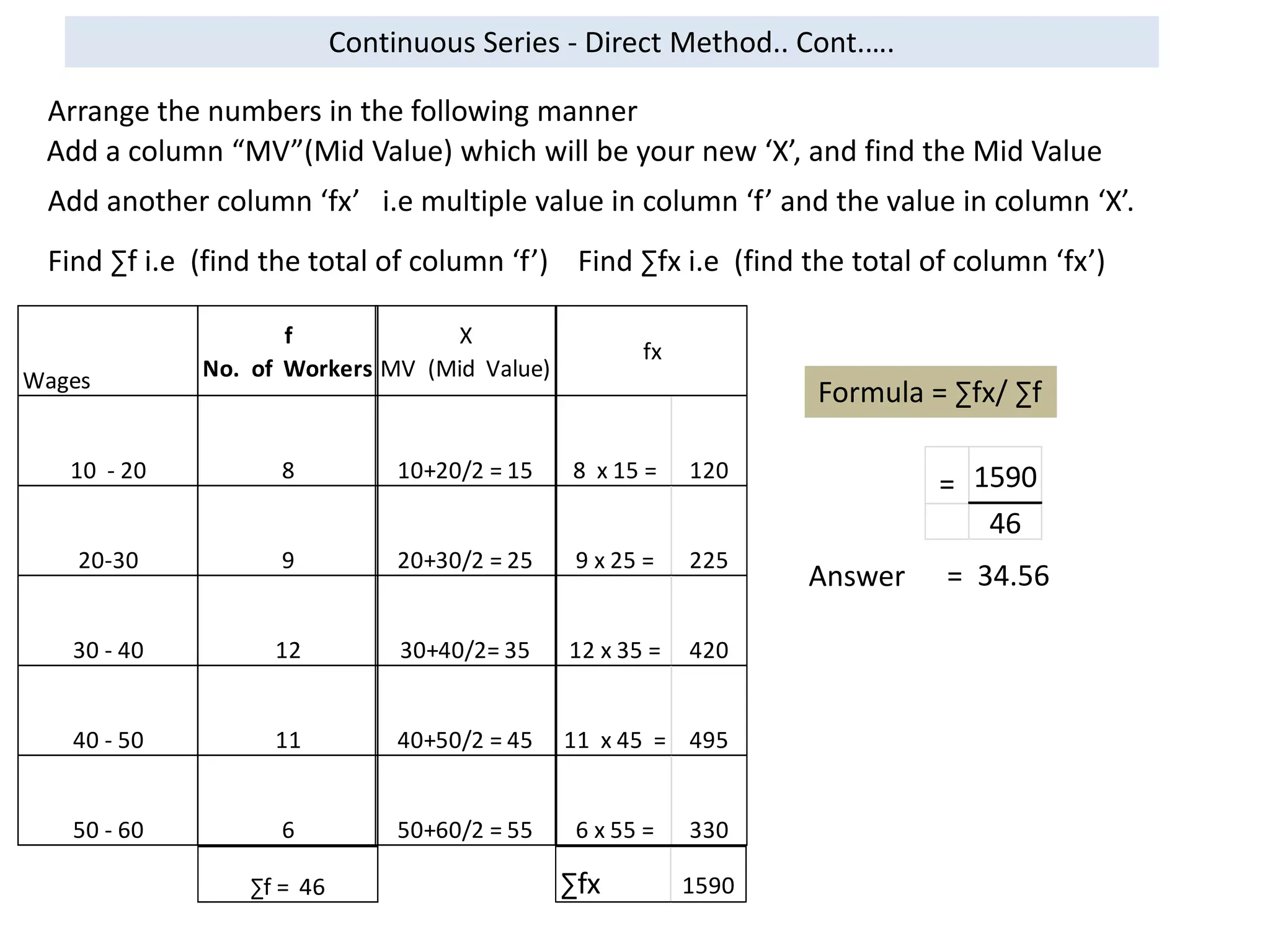
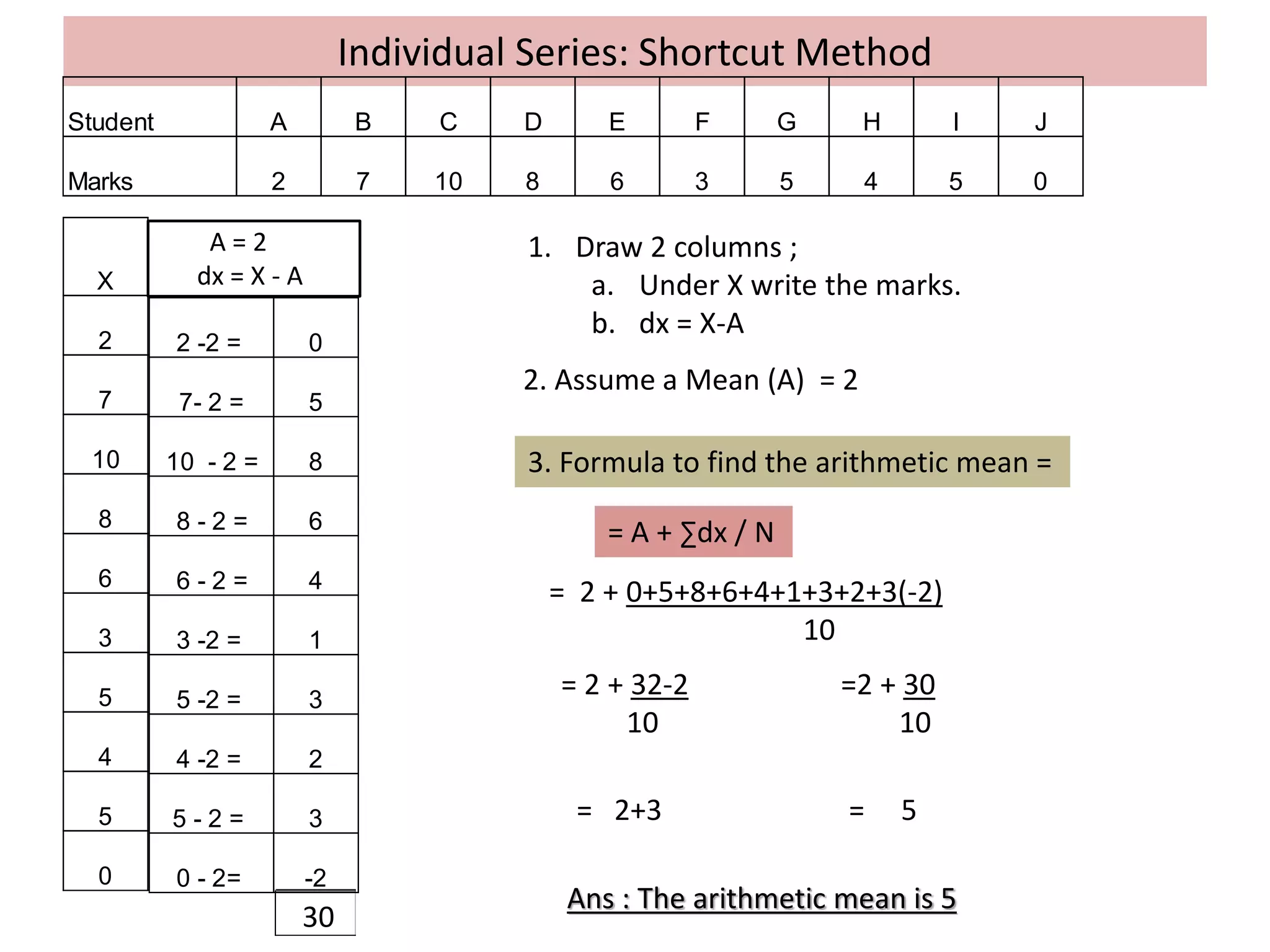
The document discusses different methods to calculate arithmetic mean from various types of data series. It explains the direct and shortcut methods to find the arithmetic mean for individual, discrete and continuous data series. For individual series, the direct method sums all data points and divides by the total number of data points. The shortcut method assumes a mean, calculates the differences from the assumed mean, and finds the mean as the assumed mean plus the sum of the differences divided by the total number of data points.

1. Calculation of Arithmetic Mean

2. Arithmetic Mean
• Arithmetic mean is one of the methods of calculating central
tendency.
• It is an average.
• It is calculated to reach a single value which represents the entire
data.
• Calculating an Average
• For example (1, 2, 2, 2, 3, 9). The arithmetic mean is
1 + 2 + 2 + 2 + 3 + 9
6
= 19/6 = 3.17
Arithmetic means are used in situations such as working out cricket
averages.
• Arithmetic means are used in calculating average incomes.

3. Different Series and different methods
• Individual Series
» Direct Method
» Shortcut Method
• Discrete Series
» Direct Method
» Shortcut Method
• Continuous Series
» Direct Method
» Shortcut Method
» Step Deviation Method

4. Individual Series - Direct Method
Student A B C D E F G H I J
Marks 2 7 10 8 6 3 5 4 5 0
The Problem – Calculate the arithmetic mean for the data given below
1. Write the sum in rows and column format.Student X
A 2
B 7
C 10
D 8
E 6
F 3
G 5
H 4
I 5
J 0
2. Formula to find the arithmetic mean=
= 2+7+10+8+6+3+5+4+5+0
10
= 50
10
= 5
Ans : The arithmetic mean is 5
50
∑x Nis the number of
observations
N is the number of
observations in our
e.g. there are 10
students so N =10

5. Individual Series: Shortcut Method
Student A B C D E F G H I J
Marks 2 7 10 8 6 3 5 4 5 0
2. Assume a Mean (A) = 2
1. Draw 2 columns ;
a. Under X write the marks.
b. dx = X-A
3. Formula to find the arithmetic mean =
= 2 + 0+5+8+6+4+1+3+2+3(-2)
10
= 2 + 32-2
10
= 2+3 = 5
Ans : The arithmetic mean is 5
=2 + 30
10
X
2
7
10
8
6
3
5
4
5
0
A = 2
dx = X - A
2 -2 = 0
7- 2 = 5
10 - 2 = 8
8 - 2 = 6
6 - 2 = 4
3 -2 = 1
5 -2 = 3
4 -2 = 2
5 - 2 = 3
0 - 2= -2
30
= A + ∑dx / N

6. Discrete Series- Direct method
Marks Received by students 5 2 3 4
Frequency 4 6 8 6
Step 1. Column ‘x’ and put all the data
of marks received by students in this
column.
Step 2. Column ‘’f and put all the data
of frequency under this.
Step 3. Third column ‘fx’ ; fx = f x X
i.e multiply data in col. f with data in
col. X.
Step 4. Find ∑fx add all the data in
column ‘ fx’ = 20+ 12 +24 +24 = 80
Step 5. Find ∑f Add all data in column ‘f’
= 4+6+8+6 = 24
Step 6 .Formula to find mean =
(∑fx)
(∑f)
= 80/24 = 3.33 ; ANS = 3.33
x
Marks Received by students
5
2
3
4
f
Frequency
4
6
8
6
24
fx
4 x 5 = 20
6 x 2 = 12
8 x 3 = 24
6 x 4 = 24
80

7. Discrete Series- Shortcut method
Marks Received by students 5 2 3 4
Frequency 4 6 8 6
Step 1. Make a column ‘x’ and put all the data
of marks received by students in this column.
Step 2. Column ‘’f and put all the data of
frequency under this.
Step 3. Column Assume a no. A
in our e.g. we have assumed A = 2
‘dx’ ; dx = x -A
Step 4. Find ∑fdx Multiply data in column
‘f’ with data in column ‘dx’.
∑fdx = sum of the column fdx = 32
Step 5. Find ∑f Add all data in column ‘f’
= 4+6+8+6 = 24
Step 6 . Formula = A + (∑fdx)/(∑f)
= 2 + 32/24 = 3.33 ; ANS = 3.33
x
Marks Received by students
5
2
3
4
f
Frequency
4
6
8
6
A = 2
dx = x - A
5 - 2= 3
2 - 2= 0
3 - 2= 1
4 - 2= 2
fdx
4 x 3 = 12
6 x 0 = 0
8 x 1 = 8
6 x 2 = 12
24 32

8. Continuous Series - Direct Method
The following table shows wages of workers. Calculate the arithmetic mean.
Wages 10 - 20 20-30 30 - 40 40 - 50 50 - 60
No. of Workers 8 9 12 11 6
The wages are given in a group series
e.g. how many workers get wages between 10 to 20 Ans. 8.
How many workers get wages between 20 and 30 Ans. 9.
Here ‘X’ is the wages, but we cannot identify one number for ‘X’.
So we need to find the ‘Mid Value’ of each group.
e.g. To find the Mid value of the first group ‘10 – 20’
Formula to find the Mid Value
L1 + L2/ 2
L1 = the first number in the group in our example it is ‘10’
L2 = the second number in the group, in our example it is ‘20 ‘
Divide by 2, because we need to divide into two halves
so we know which number is in the middle.
So the mid value (M.V) for the first group ‘10 – 20’ =
10 + 20 / 2 = 30 /2 = 15

9. Arrange the numbers in the following manner
Add a column “MV”(Mid Value) which will be your new ‘X’, and find the Mid Value
X
MV (Mid Value)
10+20/2 = 15
20+30/2 = 25
30+40/2= 35
40+50/2 = 45
50+60/2 = 55
Formula = ∑fx/ ∑fWages
f
No. of Workers
10 - 20 8
20-30 9
30 - 40 12
40 - 50 11
50 - 60 6
Add another column ‘fx’ i.e multiple value in column ‘f’ and the value in column ‘X’.
fx
8 x 15 = 120
9 x 25 = 225
12 x 35 = 420
11 x 45 = 495
6 x 55 = 330
Find ∑f i.e (find the total of column ‘f’) Find ∑fx i.e (find the total of column ‘fx’)
∑f = 46 ∑fx 1590
= 1590
46
Answer = 34.56
Continuous Series - Direct Method.. Cont.….

10. Continuous Series – Shortcut Method
Wages
10 - 20
20 - 30
30 - 40
40 - 50
50 - 60
f
No.of Workers
8
9
12
11
6
46
x
Mid Value
10 + 20/2 = 15
20 + 30/2= 25
30 + 40 /2 = 35
40 + 50/2 = 45
50 + 60/2 = 55
Assume A = 15
dx = x - A
dxf
15 - 15 = 0
25 - 15= 10
35 - 15= 20
45 - 15= 30
55 - 15= 40
1.Draw the 3 columns similar to the direct method i.e Wages, f (no.of workers and x-Midvalue)
2. Next assume a no. A (preferably from column’x’). In our eg we have assumed A = 15.
3. Find dx, dx = x – A.
4. Find fdx ; Multiply the answer in dx column with the 2nd column ‘f’.
5. Formula to find the arithmetic mean = A + ∑fdx
∑f
= A + ∑fdx
∑f
= 15 + 900
46
Answer = 34.56
fdx
0 x 8 = 0
10 x 9 = 90
20 x 12 = 240
30 x 11 = 330
40 x 6 = 240
900

11. Continuous Series – Step deviation Method
1.Draw the columns similar to the shortcut method i.e Wages, f, x and dx
2. Next assume a no. C. In our eg we have assumed c = 10.
3. Find dx’, dx’= dx /c.
4. Find fdx’ ; Multiply the answer in dx’ column with the 2nd column ‘f’.
5. Formula to find the arithmethic mean = A + ∑fdx’ x c
∑f
= A + ∑fdx’ x c
∑f
Answer = 34.56
Wages
10 - 20
20 - 30
30 - 40
40 - 50
50 - 60
f
No.of Workers
8
9
12
11
6
46
x
Mid Value
10 + 20/2 = 15
20 + 30/2= 25
30 + 40 /2 = 35
40 + 50/2 = 45
50 + 60/2 = 55
Assume A = 15
dx = x - A
dxf
15 - 15 = 0
25 - 15= 10
35 - 15= 20
45 - 15= 30
55 - 15= 40
Assume C= 10
dx' = dx/c
0/10 = 0
10/10= 1
20/10= 2
30/10= 3
40/10= 4

12. Individual Series
Direct Method :
Shortcut Method :
Discrete Series
Direct Method : = ∑fx
∑f
Shortcut Method : = A + ∑fdx
∑f
Continuous Series
Direct Method
Shortcut Method
Step Deviation
X
X dx
X f dx fdx
X f fx
X f x(M.V) fx
No. of Boxes
x f x (M.V) dx fdx
x f x (M.V) dx dx' fdx'