الكتاب هو منهج دراسي للمادة الرياضيات للصف الثالث المتوسط في العراق، يهدف لتطوير قدرات الطلاب في الرياضيات من خلال دراسات نظرية وتطبيقية. يتضمن الكتاب عدة موضوعات مثل الأعداد الحقيقية، الهندسة، والحدوديات، ويعتمد أسلوب تدريجي لتسهيل الفهم. تم تأليفه بواسطة لجنة مختصة تابعة لوزارة التربية العراقية، ويُتوقع أن يسهم في تحسين مستوى التعليم في هذا المجال.

1. ‫العراق‬ ‫جمهورية‬
‫التربية‬ ‫وزارة‬
‫للمناهج‬ ‫العامة‬ ‫املديرية‬
‫املتوسط‬ ‫الثالث‬ ‫للصف‬
‫اجلواهري‬ ‫الغفور‬ ‫عبد‬ ‫محمد‬ ‫احلديثي‬ ‫شعبان‬ ‫طارق‬ ‫الدكتور‬
‫علوان‬ ‫حـــسيــــن‬ ‫منـــــــــعم‬ ‫مـــكـــي‬ ‫اهلل‬ ‫مــــال‬ ‫مــهـــــدي‬
‫5102م‬ - ‫6341هـ‬ ‫اخلامسة‬ ‫الطبعة‬
‫الرياضيات‬
‫املؤلفون‬

2. : ‫الطبع‬ ‫على‬ ‫العلمي‬ ‫املشرف‬
‫رجب‬ ‫شعبان‬ ‫طارق‬ .‫د‬
: ‫الطبع‬ ‫على‬ ‫الفني‬ ‫املشرف‬
‫جواد‬ ‫غازي‬ ‫علي‬

3. ُ‫ة‬‫م‬ّ‫املقد‬
‫باعادة‬ ‫التربية‬ ‫وزارة‬ ‫تعنى‬ ‫خاصة‬ ‫والرياضيات‬ ‫كافة‬ ‫الدراسية‬ ‫المواد‬ ‫في‬ ‫الحاصل‬ ‫الكبير‬ ‫للتطور‬ ً‫ا‬‫نظر‬
‫كتب‬ ‫وتلقى‬ ‫الغرض‬ ‫لهذا‬ ‫تؤلف‬ ‫مختصة‬ ‫لجان‬ ‫وفق‬ ‫تأليفه‬ ‫اعادة‬ ‫او‬ ‫وتنقيحه‬ ‫المدرسي‬ ‫الكتاب‬ ‫في‬ ‫النظر‬
.‫العناية‬ ‫هذه‬ ‫من‬ ‫الوافي‬ ‫نصيبها‬ ‫الرياضيات‬
‫بعشرة‬ ‫الكتاب‬ ‫هذا‬ ‫رتبنا‬ ‫وقد‬ ، ‫المتوسطة‬ ‫للمرحلة‬ ‫الرياضيات‬ ‫كتب‬ ‫سلسلة‬ ‫من‬ ‫الثالث‬ ‫الكتاب‬ ‫وهذا‬
‫الثالث‬ ‫الفصل‬ ‫اما‬ ، ‫الحقيقية‬ ‫االعداد‬ ‫الثاني‬ ‫والفصل‬ ‫التطبيقات‬ ‫بموضوع‬ ‫االول‬ ‫الفصل‬ ‫يبدأ‬ ،‫فصول‬
‫الدائرة‬ ‫موضوع‬ ‫اما‬ ‫المثلثات‬ ‫الخامس‬ ‫الفصل‬ ‫في‬ ‫يتبعه‬ ‫المتباينات‬ ‫الرابع‬ ‫الفصل‬ ‫ويتضمن‬ ‫الحدوديات‬
‫التحويالت‬ ‫هندسة‬ ‫الثامن‬ ‫الفصل‬ ‫اما‬ ‫االحداثية‬ ‫الهندسة‬ ‫السابع‬ ‫الفصل‬ ‫وعند‬ ‫السادس‬ ‫الفصل‬ ‫في‬ ‫فهو‬
‫موضوع‬ ‫بدراسة‬ ‫اختص‬ ‫الذي‬ ‫العاشر‬ ‫بالفصل‬ ‫الكتاب‬ ‫وينتهي‬ ‫المثلثات‬ ‫حساب‬ ‫التاسع‬ ‫الفصل‬ ‫يتضمن‬
. ‫االحصاء‬
‫الحديثة‬ ‫التربوية‬ ‫الطرق‬ ‫نستخدم‬ ‫ان‬ ‫وحاولنا‬ ‫المقرر‬ ‫الدراسي‬ ‫للمنهج‬ ً‫ا‬‫وفق‬ ‫الكتاب‬ ‫هذا‬ ‫وضع‬ ‫تم‬ ‫لقد‬
‫االكثار‬‫وتوخينا‬‫االفهام‬‫بقصد‬ ً‫ا‬‫شرح‬‫العلمية‬‫المادة‬‫توضيح‬‫اعيننا‬‫نصب‬‫واضعين‬‫المجهود‬‫بهذا‬‫فقمنا‬
‫الصعب‬‫الى‬‫السهل‬‫من‬‫ومتدرجة‬‫حياته‬‫في‬‫الطالب‬‫يصادفها‬‫التي‬‫العملية‬‫والتمارين‬‫المحلولة‬‫االمثلة‬‫من‬
: ‫وهم‬ ‫الكتاب‬ ‫هذا‬ ‫بانجاز‬ ‫ساهما‬ ‫الذين‬ ‫العلميين‬ ‫الخبيرين‬ ‫جهود‬ ‫نثمن‬ ‫ان‬ ‫اال‬ ‫يسعنا‬ ‫وال‬
‫نجم‬ ‫محمد‬ .‫د‬ ‫حسن‬ ‫كامل‬ ‫ماجد‬
‫يوافونا‬ ‫ان‬ ‫المدرسين‬ ‫اخواننا‬ ‫من‬ ‫نرجو‬ ‫و‬ ‫الطلبة‬ ‫ابنائنا‬ ‫لخدمة‬ ‫وفقنا‬ ‫قد‬ ‫نكون‬ ‫ان‬ ‫نرجو‬ ً‫ا‬‫وختام‬
..‫وحده‬ ‫هلل‬ ‫والكمال‬ ، ‫فيه‬ ‫النقص‬ ‫نتالفى‬ ‫لكي‬ ‫الكتاب‬ ‫هذا‬ ‫حول‬ ‫بمالحظاتهم‬
‫التوفيق‬ ‫ولي‬ ‫واهلل‬
‫المؤلفون‬

4. Mappings ‫التطبيقات‬
f:AB
AB
f
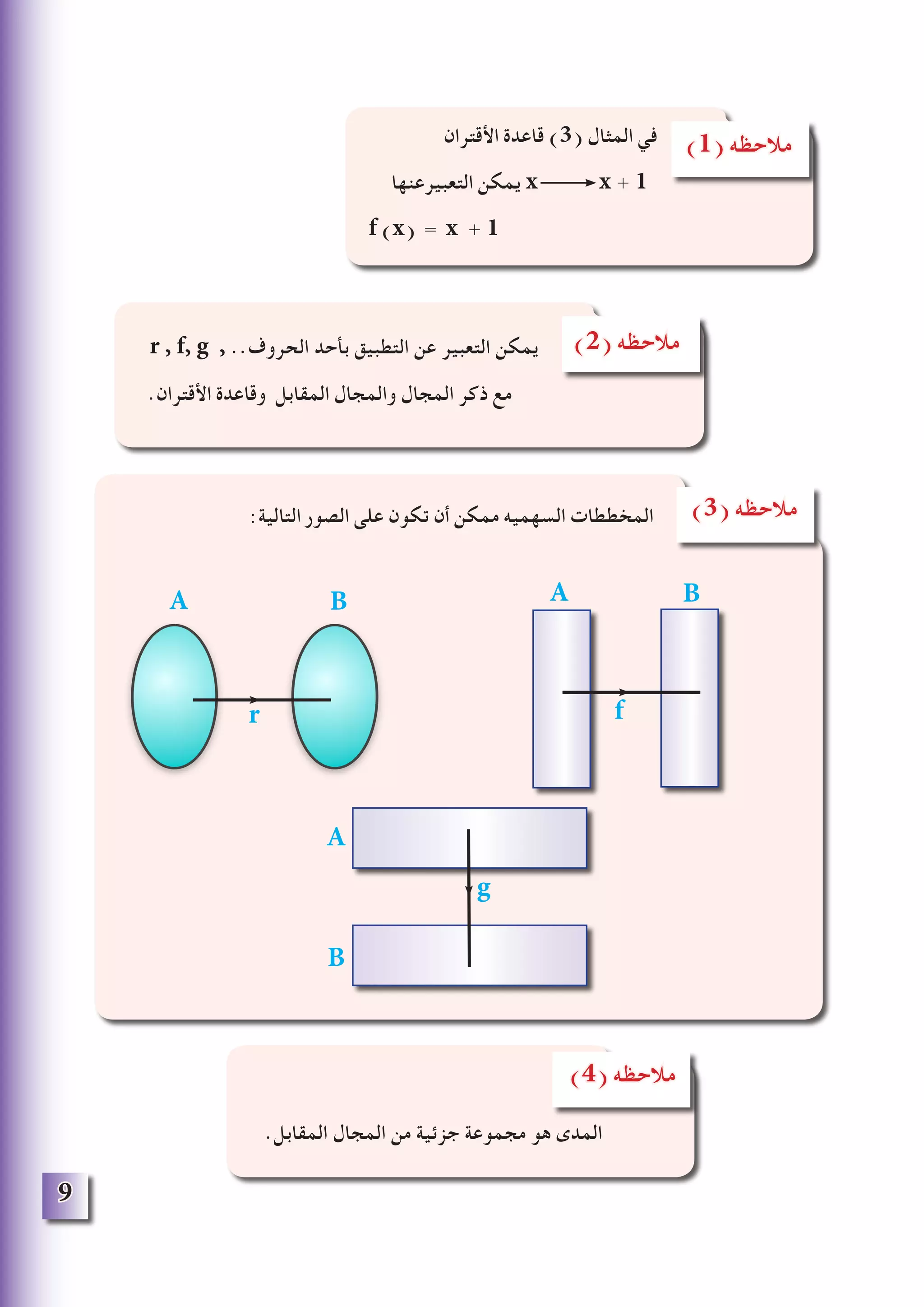
. ‫التطبيق‬ ]1-1[
. ‫التطبيق‬ ‫نوع‬ ]1-2[
. ‫للتطبيق‬ ‫البياني‬ ‫املخطط‬ ]1-3[
. ‫التطبيقات‬ ‫تركيب‬ ]1-4[
1‫االول‬ ‫الفصل‬
‫الرياضية‬ ‫العالقة‬ ‫أو‬ ‫الرمز‬ ‫المصطلح‬
N ‫الطبيعية‬ ‫األعداد‬
Z ‫الصحيحة‬ ‫األعداد‬
Q ‫النسبية‬ ‫األعداد‬
fog ‫أو‬ gof ‫التطبيقين‬ ‫تركيب‬
f , g

5. Mappings ‫التطبيقات‬
‫مقدمة‬
A ‫املجموعة‬ ‫من‬ ‫العالقة‬ ً‫ا‬‫أيض‬ ‫وتعلمت‬ ‫عليها‬ ‫والعمليات‬ ‫املجموعات‬ ‫موضوع‬ ‫درست‬ ‫وأن‬ ‫سبق‬
.B ‫الى‬ A ‫من‬ ‫للعالقة‬ ‫رمز‬ r ‫أن‬ ‫حيث‬ .‫املرتبة‬ ‫األزواج‬ ‫من‬ ‫مجموعة‬ ‫هي‬ B ‫املجموعة‬ ‫الى‬
A × B ‫الديكارتي‬ ‫الضرب‬ ‫حاصل‬ ‫من‬ ‫جزئية‬ ‫مجموعة‬ r ‫وأن‬
: ‫مثل‬ ‫املجموعة‬ ‫على‬ ‫العالقة‬ ‫خواص‬ ‫أيضا‬ ‫ودرست‬
.)Reflexive( ‫األنعكاسية‬‫اخلاصية‬ -
. )Symmetric( ‫املتناظرة‬ ‫واخلاصية‬-
. )Transitive(‫املتعدية‬ ‫واخلاصية‬-
. ‫السابقة‬ ‫الثالث‬ ‫اخلواص‬ ‫حققت‬ ‫اذا‬ )Equivalence( ‫التكافؤ‬ ‫خاصية‬ ‫وكذلك‬-
.)‫متعدية‬ ،‫متناظرة‬ ،‫(أنعكاسية‬
)Mapping( ‫التطبيق‬ ‫هو‬ ‫أخر‬ ‫مفهوم‬ ‫على‬ ‫سنتعرف‬ ،‫الدراسية‬ ‫املرحلة‬ ‫هذه‬ ‫في‬
‫الفصل‬
r A×B
1
⊆

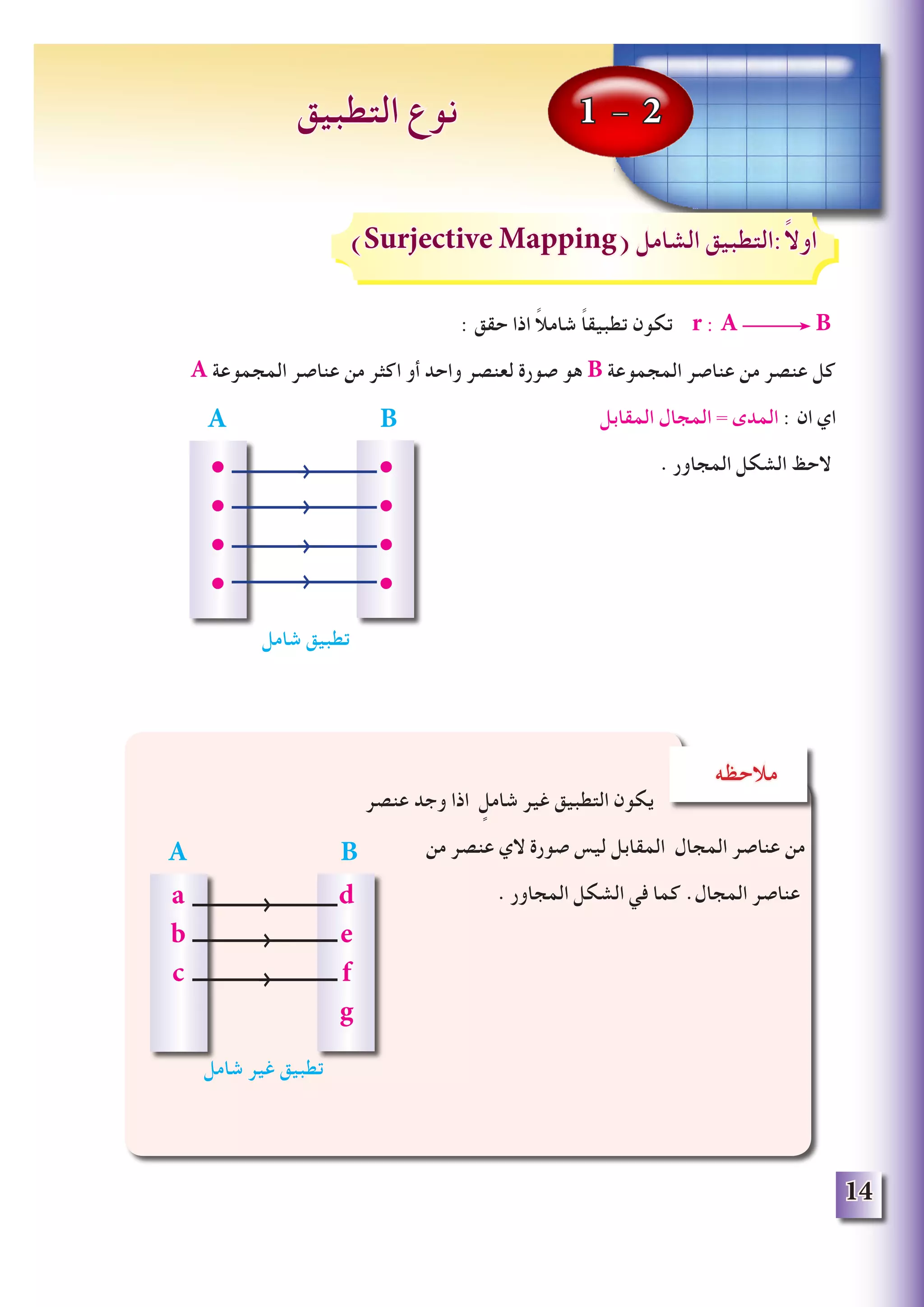
6. ( ‫وتقرأ‬ r : A B ‫لتكن‬
= } a , b , c , d { ‫و‬ A = } 1 , 2 , 3 , 4 { ‫ولتكن‬
r = { ( 1 , a ) , ( 2 , b ) , ( 3 , c ) , ( 4 , d ) }
‫التي‬ B ‫المجموعة‬ ‫في‬ ‫وحيد‬ ‫بعنصر‬ ‫يقترن‬ ‫بالمجال‬ ‫تسمى‬ ‫التي‬ A ‫المجموعة‬ ‫في‬ ‫عنصر‬ ‫كل‬ ‫أن‬ ‫الحظ‬
. r ‫للعالقة‬ ‫السهمي‬ ‫المخطط‬ ‫يمثل‬ ‫الذي‬ ]1-1[ ‫الشكل‬ ‫في‬ ‫كما‬ ‫المقابل‬ ‫بالمجال‬ ‫تسمى‬
‫من‬ ‫واحد‬ ‫عنصر‬ ‫مع‬ ‫ليرتبط‬ A ‫المجموعة‬ ‫في‬ ‫عنصر‬ ‫كل‬ ‫من‬ ‫ينطلق‬ ‫فقط‬ ‫واحد‬ ‫سهم‬ ‫هناك‬ ‫الشكل‬ ‫خالل‬ ‫ومن‬
‫يسمى‬ ) ‫(التطبيق‬ ‫تأثير‬ ‫تحت‬ A ‫المجموعة‬ ‫عناصر‬ ‫صور‬ ‫وأن‬ ‫تطبيق‬ ‫العالقة‬ ‫لهذه‬ ‫يقال‬ . B ‫المجموعة‬
.‫التطبيق‬ )Range( ‫مدى‬
1 - 1)Mapping( ‫التطبيق‬
B
]1-1[ ‫عامة‬ ‫بصورة‬
‫بحيث‬ B ≠ ∅‫حيث‬ B ‫املجموعة‬ ‫الى‬ A ≠ ∅ ‫حيث‬ A ‫املجموعة‬ ‫من‬ ‫عالقة‬ : r ‫التطبيق‬
‫املقابل‬ ‫املجال‬ ‫عناصر‬ ‫من‬ ‫فقط‬ ‫واحد‬ ‫بعنصر‬ ‫يرتبط‬ ‫أو‬ ‫يقترن‬ ‫املجال‬ ‫عناصر‬ ‫عنصرمن‬ ‫كل‬ ‫أن‬
:‫أي‬ ‫األقتران‬ ‫قاعدة‬ ‫ضمن‬
) x , y ) ∈ r ‫بحيث‬ y ∈ B ‫وحيد‬ ‫عنصر‬ ‫يوجد‬ x ∈ A ‫لكل‬
A
a
b
c
d
1
2
3
4
B
]1-1[ ‫الشكل‬
r
) B ‫الى‬ A ‫من‬ ‫عالقة‬ r

7. ‫بالل‬
‫اهلل‬ ‫عبد‬
‫مثنى‬
‫أنكليزي‬
‫فرنسي‬
A
B
a b c d
e f g
B ‫الى‬ A ‫من‬ ‫معرفه‬ r ‫والعالقة‬ .‫لغات‬ ‫مجموعة‬B ‫ولتكن‬ . ‫طالب‬ ‫مجموعة‬ A ‫لتكن‬ -: ‫الشكل‬ ‫الحظ‬
:‫كانت‬ ‫فاذا‬ .»
‫يدرس‬ «
‫عالقة‬ ‫هي‬
A = } ‫مثنى‬ , ‫اهلل‬ ‫عبد‬ , ‫بالل‬ {
B = } ‫فرنسية‬ , ‫انكليزية‬ {
.‫السبب‬ ‫ذكر‬ ‫مع‬ ‫؟‬ ً‫ا‬‫تطبيق‬ ‫تمثل‬ r ‫هل‬ ، r : A B ‫وأن‬
.ً‫ا‬‫تطبيق‬ ‫التمثل‬ r /‫احلل‬
‫المقابل‬ ‫المجال‬ ‫في‬ ‫بلغتين‬ ‫أرتبط‬ ‫وقد‬ ‫المجال‬ ‫الى‬ ‫ينتمي‬ ‫بالل‬ ‫ألن‬
r : A B ‫لتكن‬
A = { a , b , c , d }
B = { e , f , g }
r = { ( a , e ) , ( b , f ) , ( d , g ) }
.‫السبب‬ ‫ذكر‬ ‫مع‬ ‫ً؟‬‫ا‬‫تطبيق‬ ‫تمثل‬ r ‫هل‬ )1
.‫سهمي‬ ‫بمخطط‬ ‫مثله‬ )2
.ً‫ا‬‫تطبيق‬ ‫التمثل‬ )1 /‫احلل‬
B ‫المقابل‬ ‫المجال‬ ‫في‬ ‫عنصر‬ ‫بأي‬ ‫يرتبط‬ ‫لم‬ c ∈ A ‫ألن‬
)2
( 1 ) ‫مثال‬
) 2 ( ‫مثال‬
A B

8. A = { 1 , 2 , -3 { ‫كانت‬ ‫اذا‬
B = { 2 , 3 , - 2 , -4 }
f : A B -:‫كاآلتي‬ ‫معرف‬ ‫تطبيق‬ f
x x + 1 ‫ حيث‬
‫المرتبة‬ ‫األزواج‬ ‫من‬ ‫مجموعة‬ ‫شكل‬ ‫على‬ f ‫التطبيق‬ ‫أكتب‬ :ً‫ال‬‫أو‬
‫سهمي‬ ‫بمخطط‬ ‫مثله‬ :ً‫ا‬‫ثاني‬
f ‫التطبيق‬ ‫مدى‬ ‫أوجد‬ :ً‫ا‬‫ثالث‬
/‫احلل‬
x x + 1
1 1 + 1 = 2
2 2 + 1 = 3
-3 -3 + 1 = -2
∴ f = { ( 1 , 2 ) , ( 2 , 3 ) , ( -3 , -2 ) }
‫السهمي‬ ‫-المخطط‬ :ً‫ا‬‫ثاني‬
} 2 , 3 ,-2{= ‫التطبيق‬ ‫مدى‬ -:ً‫ا‬‫ثالث‬
A
2
3
-2
-4
1
2
-3
B
) 3 ( ‫مثال‬
-:ً‫ال‬‫او‬

9. ‫األقتران‬ ‫قاعدة‬ )3( ‫المثال‬ ‫في‬
‫التعبيرعنها‬ ‫يمكن‬ x x + 1
f (x) = x + 1
)1( ‫مالحظه‬
)2( ‫مالحظه‬r , f, g , ..‫الحروف‬ ‫بأحد‬ ‫التطبيق‬ ‫عن‬ ‫التعبير‬ ‫يمكن‬
.‫األقتران‬ ‫وقاعدة‬ ‫المقابل‬ ‫والمجال‬ ‫المجال‬ ‫ذكر‬ ‫مع‬
)3( ‫مالحظه‬:‫التالية‬ ‫الصور‬ ‫على‬ ‫تكون‬ ‫أن‬ ‫ممكن‬ ‫السهميه‬ ‫المخططات‬
A B
A
B
)4( ‫مالحظه‬
.‫المقابل‬ ‫المجال‬ ‫من‬ ‫جزئية‬ ‫مجموعة‬ ‫هو‬ ‫المدى‬
BA
r f
g

10. 10
‫النسبية‬ ‫االعداد‬ ‫مجموعة‬ Q ‫حيث‬ g : A Q ‫كانت‬ ‫اذا‬
A = { -1 , 1 , 2 , -3 }
g (x) = x2
- 4
‫التطبيق‬ ‫مدى‬ ‫أوجد‬ )1
‫للتطبيق‬ ‫السهمي‬ ‫المخطط‬ ‫أرسم‬ )2
‫عناصره‬ ‫بذكر‬ ‫التطبيق‬ ‫3)أكتب‬
/ ‫احلل‬
1) g (x) = x2
- 4
g (-1) = (-1)2
- 4 = 1- 4 = -3
g (1) = (1)2
- 4 =1- 4 = -3
g (2) = (2)2
- 4 = 4 - 4 = 0
g (-3)=(-3)2
- 4 = 9 - 4 = 5
∴ Range = {-3,0,5} ‫المدى‬
2)
3) g = {(-1,-3), (1,-3),(2,0),(-3,5)}
( 4 ) ‫مثال‬
-3
0
5
-1
1
2
-3
A
g
..
.....
......
..Q

11. 11
5 ‫من‬ ‫األصغر‬ ‫الموجبة‬ ‫الطبيعية‬ ‫األعداد‬ ‫مجموعة‬ A ‫كانت‬ ‫اذا‬
‫الصحيحة‬ ‫االعداد‬ ‫مجموعة‬ Z ‫حيث‬ ، f : A Z ‫وكانت‬
f (x) = 2x - 3 ‫كان‬ ‫اذا‬ ‫التطبيق‬ ‫مدى‬ ‫جد‬
/‫احلل‬
f (x) = 2 x- 3
f (1) = (2)(1) - 3 = -1
f (2) = (2)(2) - 3 = 1
f (3) = (2)(3)- 3 = 3
f (4 ) = (2)( 4 ) - 3 = 5
∴ Range = {-1 , 1 , 3 , 5 } ‫المدى‬
g : Q Q ‫ان‬ ‫العلم‬ ‫مع‬ g (x) = 10 ‫عندما‬ x ‫قيمة‬ ‫فجد‬ g (x) = 4x - 7 ‫كان‬ ‫اذا‬
. ‫النسبية‬ ‫االعداد‬ ‫مجموعة‬ Q ‫حيث‬
∵ g (x) = 4 x- 7 /‫احلل‬
g (x) = 10
∴10 = 4x - 7
⇒ 4x = 10 + 7
⇒ 4x = 17 (4( ‫على‬ ‫المعادلة‬ ‫طرفي‬ ‫بقسمة‬
⇒ x = ∈ Q
( 5 ) ‫مثال‬
( 6 ) ‫مثال‬
Qg(x) = 4x − 7
g(x) =10
∴10 = 4x − 7
⇒ 4x =10+ 7
⇒ 4x = 17
⇒ x =
17
4
∈ Q
17
4
A = { 1 , 2 , 3 , 4 }

12. 12
1 1
، A = { a , b , c { ‫وكانت‬ r : A B ‫كان‬ ‫اذا‬ /1‫س‬
r = { ( a , 4 ) , ( b , 7 ) , ( c , 3 ) }
r = { ( a , 3 ) , ( b , 3 ) , ( c , 3 ) }
‫السهمي‬ ‫المخطط‬ ‫ارسم‬ :ً‫ا‬‫ثاني‬ ‫ولماذا؟‬ ً‫ا‬‫تطبيق‬ r ‫هل‬ :ً‫ال‬‫او‬
A ‫كانت‬ ‫اذا‬ /2‫س‬
B ‫وكانت‬
f(x) = x + 1 ‫حيث‬ B ‫الى‬ A ‫من‬ ‫عالقة‬ f
‫؟‬ ‫لماذا‬ ، ً‫ا‬‫تطبيق‬ ‫يمثل‬ f :ً‫ا‬‫ثاني‬ ‫السهمي‬ ‫المخطط‬ ‫ارسم‬ :ً‫ال‬‫أو‬
g : A Z ‫وكان‬ A = { 1 , 2 , -2 , -3 { ‫كانت‬ ‫س3/اذا‬
. g (x) = 5x - 3 ‫كان‬ ‫اذا‬ ‫التطبيق‬ ‫مدى‬ ‫جد‬
‫ولتكن‬ A = }‫الملوية‬ ، ‫الحضر‬ ، ‫عشتار‬ ‫{باب‬ ‫حيث‬ .‫العراق‬ ‫في‬ ‫االثرية‬ ‫المناطق‬ ‫مجموعة‬ A ‫لتكن‬ /4‫س‬
. B = } ‫بغداد‬ ، ‫بابل‬ ، ‫الدين‬ ‫صالح‬ ، ‫قار‬ ‫ذي‬ ، ‫البصرة‬ ، ‫الموصل‬ ، ‫كركوك‬ {
.‫تختاره‬ ‫سهمي‬ ‫بمخطط‬ ‫عراقية‬ ‫محافظة‬ ‫لكل‬ ‫االثرية‬ ‫المناطق‬ ‫انسب‬ r : A B ‫وان‬
B = { 3 , 4 , 5 , 6 , 7{
7 ‫من‬ ‫األصغر‬ ‫الزوجية‬ ‫الطبيعية‬ ‫األعداد‬ ‫مجموعة‬
8 ‫من‬ ‫األصغر‬ ‫الفردية‬ ‫الطبيعية‬ ‫األعداد‬ ‫مجموعة‬
1)
2)

13. 13
f (x ) = 2 x + 8 ‫حيث‬ f : N Q ‫كان‬ ‫اذا‬ /5‫س‬
. ‫التطبيق‬ ‫مدى‬ ‫اكتب‬ :ً‫ال‬‫او‬
. x ‫قيمة‬ ‫فجد‬ f ( x ) = 16 ‫كان‬ ‫اذا‬ :ً‫ا‬‫ثاني‬
.‫التطبيق‬ ‫تمثل‬ ‫التي‬ ‫المرتبة‬ ‫االزواج‬ ‫مجموعة‬ ‫اكتب‬ :ً‫ا‬‫ثالث‬
r = { ( 1 , a ) , ( 2 , b ) , (3 , c) , ( 4 , d ) , ( 5 , a ({ ‫كانت‬ ‫/اذا‬ 6‫س‬
r : A B ‫حيث‬
. B , A ‫من‬ ً‫ال‬‫ك‬ ‫جد‬ )1
.‫التطبيق‬ ‫مدى‬ ‫أكتب‬ )2
.‫السهمي‬ ‫المخطط‬ ‫ارسم‬ )3
f ( x ) = 2x 2
- x + 3 ‫حيث‬ f : A Q ‫كان‬ ‫اذا‬ / 7‫س‬
A = { 1 , -1 , 0 { ‫وإن‬
.‫المدى‬ ‫اكتب‬ )1
.‫التطبيق‬ ‫تمثل‬ ‫التي‬ ‫المرتبة‬ ‫األزواج‬ ‫مجموعة‬ ‫اكتب‬ )2
.‫السهمي‬ ‫المخطط‬ ‫ارسم‬ )3

14. 14
1 - 2‫التطبيق‬ ‫نوع‬
: ‫حقق‬ ‫اذا‬ ً‫ال‬‫شام‬ ً‫ا‬‫تطبيق‬ ‫تكون‬ r : A B
A ‫المجموعة‬ ‫عناصر‬ ‫من‬ ‫اكثر‬ ‫أو‬ ‫واحد‬ ‫لعنصر‬ ‫صورة‬ ‫هو‬ B ‫المجموعة‬ ‫عناصر‬ ‫من‬ ‫عنصر‬ ‫كل‬
‫المقابل‬ ‫المجال‬ = ‫المدى‬ : ‫ان‬ ‫اي‬
. ‫المجاور‬ ‫الشكل‬ ‫الحظ‬
‫شامل‬ ‫تطبيق‬
)Surjective Mapping( ‫الشامل‬ ‫ً:التطبيق‬‫ال‬‫او‬
A
•
•
•
•
•
•
•
•
B
‫عنصر‬ ‫وجد‬ ‫اذا‬ ٍ‫شامل‬ ‫غير‬ ‫التطبيق‬ ‫يكون‬
‫من‬ ‫عنصر‬ ‫الي‬ ‫صورة‬ ‫ليس‬ ‫المقابل‬ ‫المجال‬ ‫عناصر‬ ‫من‬
. ‫المجاور‬ ‫الشكل‬ ‫في‬ ‫كما‬ .‫المجال‬ ‫عناصر‬
‫شامل‬ ‫غير‬ ‫تطبيق‬
A
d
e
f
g
a
b
c
B
‫مالحظه‬

15. 15
( 1 ) ‫مثال‬
‫ً؟‬‫ال‬‫شام‬ ً‫ا‬‫تطبيق‬ ‫تمثل‬ ‫االتية‬ ‫السهمية‬ ‫المخططات‬ ‫من‬ ً‫ا‬‫اي‬ ‫حدد‬
B = { 4 , 6 , 8 , 10 } , A = { 3 , 5 , 7 , 9 , 11 { ‫حيث‬ f : A B ‫ليكن‬
‫ً؟‬‫ال‬‫شام‬ ً‫ا‬‫تطبيق‬ f ‫هل‬ ، f = { ( 3 , 4 ) , ( 5 , 6 ) , ( 7 , 8 ) , ( 9 , 10 ) , ( 11 , 4 ( { ‫وان‬
}4 , 6 , 8 , 10 { ‫المدى‬ /‫احلل‬
B ‫المقابل‬ ‫المجال‬ = ‫المدى‬ ‫ان‬ ‫بما‬
. ً‫ال‬‫شام‬ ً‫ا‬‫تطبيق‬ ‫يمثل‬ f ∴
A B
-1
2
5
-3
0
3
4
) 2(
‫ليست‬ 4 ‫الن‬ ً‫ال‬‫شام‬ ً‫ا‬‫تطبيق‬ ‫يمثل‬ ‫ال‬
‫المجال‬ ‫في‬ ‫لعنصر‬ ‫صورة‬
A
B
1 2 3
2 3 4
)3(
ً‫ال‬‫شام‬ ‫ليس‬ ً‫ا‬‫تطبيق‬
( 2 ) ‫مثال‬
A
e
f
g
h
a
b
c
d
B
)1(
ً‫ال‬‫شام‬ ً‫ا‬‫تطبيق‬
F G
H

16. 16
‫شامل؟‬ ‫تطبيق‬ f ‫هل‬ ، x x2
+ 1 , A = { -1 , -2 , 1 , 2 {‫حيث‬ f : A N
/‫احلل‬
f(-1) = (-1) 2
+ 1 = 2
f (-2) = (-2) 2
+ 1 = 5
f (1) = (1) 2
+ 1 =2
f(2) = (2)2
+ 1 = 5
Range = { 2 , 5 } ‫المدى‬
N ‫المقابل‬ ‫المجال‬ ≠ ‫المدى‬
‫شامل‬ ‫غير‬ ‫تطبيق‬ f
‫شامل؟‬ f ‫التطبيق‬ ‫هل‬ ‫بين‬ f : N N , f (x) = 3x + 2
/‫احلل‬
f(0) =3 (0) + 2 = 2
f (1) = 3(1) + 2 = 5
f (2) = 3(2) + 2 = 8
f(3) = 3(3) + 2 = 11
Range = { 2 , 5 , 8 , 11 , ....} ‫المدى‬
ً‫ال‬‫شام‬ ‫ليس‬ f
N ‫المقابل‬ ‫المجال‬ ≠ ‫المدى‬ ‫الن‬
( 4 ) ‫مثال‬
( 3 ) ‫مثال‬
∴
∴
∴
f (x) = 3x + 2

17. 17
‫عواصم‬ ‫مجموعة‬ B ‫ولتكن‬} ‫االردن‬ ، ‫مصر‬ ، ‫سوريا‬ ، ‫العراق‬{ ‫بـ‬ ‫المتمثلة‬ ‫العربية‬ ‫الدول‬ ‫مجموعة‬ A ‫لتكن‬
: ‫السهمي‬ ‫المخطط‬ ‫في‬ ‫كما‬ ‫مبينة‬ ‫والعالقة‬ } ‫عمان‬ ، ‫القاهرة‬ ، ‫دمشق‬ ، ‫بغداد‬ { ‫بـ‬ ‫المتمثلة‬ ‫الدول‬ ‫هذه‬
‫عاصمتها‬ ‫تمثل‬ ‫والتي‬ B ‫المجموعة‬ ‫في‬ ‫واحدة‬ ‫بمدينة‬ ‫أرتبطت‬ A ‫المجموعة‬ ‫في‬ ‫عربية‬ ‫دولة‬ ‫كل‬ ‫ان‬ ‫الحظ‬
:‫تحقق‬ ‫اذا‬ ً‫ا‬‫متباين‬ ‫التطبيق‬ ‫يكون‬ ‫اذن‬ ، ً‫ا‬‫متباين‬ ً‫ا‬‫تطبيق‬ ‫يسمى‬ ‫التطبيق‬ ‫هذا‬ ‫مثل‬ ‫ان‬ ‫اعاله‬ ‫الشكل‬ ‫في‬ ‫كما‬
:‫أن‬ ‫أي‬
. ‫المقابل‬ ‫المجال‬ ‫في‬ ‫مختلفتان‬ ‫صورتان‬ ‫لهما‬ ‫المجال‬ ‫في‬ ‫مختلفين‬ ‫عنصرين‬ ‫ألي‬
:‫أن‬ ‫أي‬
Injective Mapping ‫المتباين‬ ‫التطبيق‬ : ً‫ا‬‫ثاني‬
1) ∀x1 ,x2 ∈ A , x1 ≠ x2 ⇒ R x1( ) ≠ R x2( )
2) ∀x1, x2 ∈ A , R x1( ) = R x2( ) ⇒ x1 = x2
ff,
‫المجال‬ ‫عناصر‬ ‫من‬ ‫مختلفان‬ ‫عنصران‬ ‫وجد‬ ‫اذا‬ ‫متباين‬ ‫غير‬ ‫التطبيق‬ ‫يكون‬
. ‫المقابل‬ ‫المجال‬ ‫في‬ ‫الصورة‬ ‫نفس‬ ‫لهما‬
‫مالحظه‬
‫العراق‬
‫سوريا‬
‫مصر‬
‫االردن‬
A
‫بغداد‬
‫دمشق‬
‫القاهرة‬
‫عمان‬
B
1) ∀x1 ,x2 ∈ A , x1 ≠ x2 ⇒ R x1( ) ≠ R x2( )
2) ∀x1, x2 ∈ A , R x1( ) = R x2( ) ⇒ x1 = x2
ff, =

18. 18
. ‫لها‬ ‫السهمي‬ ‫المخطط‬ ‫ارسم‬ ‫ثم‬ ‫متباينة‬ ‫االتية‬ ‫التطبيقات‬ ‫أي‬ ‫بين‬
f : A B ‫كان‬ ‫واذا‬ B = } 1 , 4 , 9 , 16 { ‫و‬ A= } 1 , 2 , 3 , 4 { ‫كانت‬ ‫اذا‬ )1
. f(x) = x2
‫حيث‬
/‫احلل‬
f(x) = x 2
f (1) = (1) 2
= 1
f (2) = (2) 2
= 4
f(3) = (3)2
= 9
f(4) = (4)2
= 16
∴ f = { ( 1 , 1 ) , ( 2 , 4 ) , ( 3 , 9 ) , ( 4 , 16 ) }
.‫المقابل‬ ‫المجال‬ ‫في‬ ‫مختلفتان‬ ‫صورتان‬ ‫لهما‬ ‫المجال‬ ‫من‬ ‫مختلفين‬ ‫عنصرين‬ ‫لكل‬ ‫النه‬ ‫متباين‬ f ∴
‫كاالتي‬ ً‫ا‬‫معرف‬ ً‫ا‬‫تطبيق‬ g : A A ‫وكان‬ A = } 1 , 2 , 3 , 4 , 5 { ‫كانت‬ ‫اذا‬ )2
g = { ( 1 , 4 ) , ( 2 , 2 ) , ( 3 , 1 ) , ( 4 , 2 ) , ( 5 , 4 ) }
/‫احلل‬
‫وكذلك‬ g (2) = g (4) = 2 ‫بينما‬ 2 ≠ 4 ‫الن‬ ‫متباين‬ ‫غير‬ ‫التطبيق‬
g (1) = g (5) = 4 ‫بينما‬ 1 ≠ 5
f(x) = 3x ‫ان‬ ‫حيث‬ f : N
+
N ‫كان‬ ‫اذا‬ )3
/‫احلل‬
( 5 ) ‫مثال‬
1
4
9
16
1
2
3
4
A B
1
2
3
4
5
1
2
3
4
5
A A
f(x) = 3x
f (1) = 3
f (2) = 6
f(3) = 9
1 , 2 , 3 , 4 .....
0 , 1 , 2 , 3 , 4 , 5 , 6 , 7 , 8 , 9 , ....
‫املجال‬
‫املجال‬
‫املقابل‬
N
+
N

19. 19
( 6 ) ‫مثال‬
Bijective Mapping ‫تقابل‬ ‫التطبيق‬ : ً‫ا‬‫ثالث‬
( 7 ) ‫مثال‬
.‫المقابل‬ ‫المجال‬ ‫في‬ ‫مختلفتان‬ ‫صورتان‬ ‫لهما‬ ‫المجال‬ ‫في‬ ‫مختلفين‬ ‫عنصرين‬ ‫كل‬ ‫الن‬ ‫متباين‬ ‫التطبيق‬
. ‫منتهيتين‬ ‫غير‬ ‫مجموعتان‬ ‫المقابل‬ ‫والمجال‬ ‫المجال‬ ‫ان‬ ‫الحظ‬
f : A B ‫وكان‬ B = }2 , 5 , 10 { ‫و‬ A = } -1 , 2 , 3 , 1 { ‫كانت‬ ‫اذا‬
‫متباين؟‬ ‫هل‬ . f(x) = x 2
+ 1
f (1) = f ( -1 ) = 2 ‫بينما‬ 1 ≠ -1 ‫ألن‬ ‫متباين‬ ‫غير‬ ‫التطبيق‬ / ‫احلل‬
-: ‫اآلتيين‬ ‫الشرطين‬ ‫حقق‬ ‫اذا‬ ً‫ال‬‫تقاب‬ ‫التطبيق‬ ‫يكون‬
. ً‫ال‬‫شام‬ ‫التطبيق‬ )1
. ً‫ا‬‫متباين‬ ‫التطبيق‬ )2
B = { 0 , 2 , 3 , 8 } , A = { 1 , 2 , 3 { ‫كانت‬ ‫اذا‬
f ‫التطبيق‬ ‫نوع‬ ‫اذكر‬ )2 , ‫المدى‬ )1 ‫جد‬ f (x) = x 2
- 1 ‫بحيث‬ f : A B
‫للتطبيق‬ ‫السهمي‬ ‫المخطط‬ ‫ارسم‬ )3
f(x) = x 2
- 1 )1 /‫احلل‬
f (1) = (1)2
- 1 = 0
f (2) = (2)2
- 1 = 3
f(3) = (3)2
- 1 = 8
∴ Range = { 0 , 3 , 8 } ‫المدى‬
‫المقابل‬ ‫المجال‬ ≠ ‫المدى‬ ‫او‬ ‫المجال‬ ‫في‬ ‫لعنصر‬ ‫صورة‬ ‫ليس‬ 2 ‫الن‬ ٍ‫شامل‬ ‫غير‬ ‫التطبيق‬ )2
. ً‫ال‬‫شام‬ ‫ليس‬ ‫النه‬ ً‫ال‬‫تقاب‬ ‫ليس‬ ، ً‫ا‬‫متباين‬ ‫التطبيق‬
f(x)

20. 20
‫السهمي‬ ‫المخطط‬ )3
‫االعداد‬ ‫مجموعة‬ Z ‫حيث‬ f ‫التطبيق‬ ‫نوع‬ ‫بين‬ f (x) = 2 x2
- 3 ‫حيث‬ ، f : Z Z ‫كانت‬ ‫اذا‬
. ‫الصحيحة‬
f(x) =2 x 2
-3 /‫احلل‬
f (-2) = 2 (-2) 2
-3 = 8 - 3 = 5
f (-1) = 2 (-1) 2
-3 = 2 - 3 = -1
f(0) = 2(0)2
- 3 = -3
f(1) = 2(1)2
- 3 = 2 -3 = -1
f(2) = 2(2)2
- 3 = 8 -3 = 5
‫المقابل‬ ‫المجال‬ ≠ ‫المدى‬ ‫الن‬ ً‫ال‬‫شام‬ ‫ليس‬ ‫التطبيق‬ : ً‫ال‬‫او‬
-1 ≠1 ‫بينما‬ f (-1) = f (1) = -1 ‫الن‬ ً‫ا‬‫متباين‬ ‫ليس‬ ‫التطبيق‬ : ً‫ا‬‫ثاني‬
.ً‫ال‬‫تقاب‬ ‫ليس‬ ‫التطبيق‬ :ً‫ا‬‫ثالث‬
( 8 ) ‫مثال‬
0
2
3
8
1
2
3
A B
∴
‫مالحظة‬‫مجموعة‬ Z ‫الن‬ ‫التطبيق‬ ‫لهذا‬ ‫كامل‬ ‫مخطط‬ ‫رسم‬ ‫اليمكن‬
‫منتهية‬ ‫غير‬
Z
Z... , -3 , -2 , -1 , 0 ,1 , 2 , 3 , 4 , 5 , ....
... , -2 , -1 , 0 , 1 , 2 , .....

21. 21
1 - 3‫للتطبيق‬ ‫البياني‬ ‫املخطط‬
. ‫سهمية‬ ‫مخططات‬ ‫شكل‬ ‫على‬ ‫التطبيقات‬ ‫مثلنا‬ ‫السابقة‬ ‫االمثلة‬ ‫في‬
ً‫ا‬‫تطبيق‬ r : A B ‫كان‬ ‫عندما‬ ً‫ال‬‫مث‬
A = { 1, 2 , 3 , 4 {
B = { 2 , 3 4 , 5 {
r = { ( 1 , 2 ) , ( 2 , 3 ) , ( 3 , 4 ) , ( 4 , 5 ) } ‫حيث‬
‫هو‬ r ‫للعالقة‬ ‫السهمي‬ ‫المخطط‬ ‫فأن‬
. ‫الشكل‬ ‫في‬ ‫كما‬ ‫بياني‬ ‫بمخطط‬ ‫المرتبة‬ ‫االزواج‬ ‫خالل‬ ‫من‬ r ‫العالقة‬ ‫تمثيل‬ ً‫ا‬‫ايض‬ ‫ويمكن‬
2
3
4
5
1
2
3
4
A B
y
1
2
3
4
5
1 2 3 4 5 60
x

22. 22
A = { 1, 2 , 3 { ‫كان‬ ‫اذا‬
B = { 3 , 5 , 2 {
r : A B
r = { ( 1 , 3 ) , ( 2 , 5 ) , ( 3 , 2 ( { ‫حيث‬
.‫للتطبيق‬ ‫السهمي‬ ‫المخطط‬ ‫إرسم‬ )1
. ‫للتطبيق‬ ‫البياني‬ ‫المخطط‬ ‫إرسم‬ )2
. ‫التطبيق‬ ‫نوع‬ ‫بين‬ )3
‫سهمي‬ ‫بمخطط‬ )1( /‫احلل‬
‫البياني‬ ‫المخطط‬ )2(
) ‫تقابل‬ ، ‫متباين‬ ،‫(شامل‬ ‫التطبيق‬ )3(
( 1 ) ‫مثال‬
2
3
5
1
2
3
A B
y
1
2
3
4
5
1 2 3 4 5 60
X

23. 23
f : A B ‫كان‬ ‫اذا‬
A = { -1 , 2 , -2 {
B = { 1 , 4 {
f ( x ) = x 2
‫وكانت‬
‫نوعه‬ ‫وبين‬ ‫للتطبيق‬ ‫البياني‬ ‫المخطط‬ ‫أرسم‬
/ ‫احلل‬
f(x) = x 2
∴ f (-1) = (-1) 2
= 1
f (2) = (2) 2
= 4
f(-2) = (-2)2
= 4
f = {(-1 , 1) , ( 2 , 4 ) , ( -2 , 4 ) }
} 1 , 4 { = ‫المدى‬
‫المقابل‬ ‫المجال‬ = ‫المدى‬ ‫الن‬ ‫شامل‬ ‫التطبيق‬
‫ألن‬ ‫متباينا‬ ‫ليس‬ ‫التطبيق‬
2 ≠ -2 ⇒ f(2) = f(-2)
ً‫ا‬‫متباين‬ ‫ليس‬ ‫النه‬ ً‫ال‬‫تقاب‬ ‫ليس‬ ‫التطبيق‬
y
X
1
2
3
4
5
1 2 3 4 5 60-1-2
( 2 ) ‫مثال‬

24. 24
:‫البياني‬ ‫بالمخطط‬ ‫ممثلة‬ r : A { 2 , 5 , 8 , 11{ ‫كان‬ ‫اذا‬
. ‫التطبيق‬ ‫نوع‬ ‫بين‬ )3 ‫المدى‬ )2 r , A )1
)1( / ‫احلل‬
r ‫العالقة‬ ‫نجد‬ ‫البياني‬ ‫المخطط‬ ‫من‬
)2(
‫المقابل‬ ‫المجال‬ ≠ ‫المدى‬ ‫الن‬ ً‫ال‬‫شام‬ ‫ليس‬ ‫التطبيق‬ )3(
‫متباين‬ ‫التطبيق‬
ً‫ال‬‫شام‬ ‫ليس‬ ‫النه‬ ً‫ال‬‫تقاب‬ ‫ليس‬ ‫التطبيق‬
( 3 ) ‫مثال‬
y
X
1
2
3
4
5
6
7
8
1 2 3 40
9
10
11
}8 , 5 , 11 { = ‫المدى‬
A = 1,2,3{ }
r = 1,5( ), 2,8( ) , 3,11( ){ }
:‫جد‬

25. 25
/‫تعريف‬
:‫التطبيقات‬ ‫تركيب‬
‫قاعدة‬ ‫بتأثير‬ ‫المجال‬ ‫عناصر‬ ‫صور‬ ‫إيجاد‬ ‫وكيفية‬ ‫وانواعه‬ ‫التطبيق‬ ‫تعريف‬ ‫على‬ ‫الفصل‬ ‫هذا‬ ‫في‬ ‫تعرفنا‬
. ‫فأن‬ f x( ) = x2
+1 ‫حيث‬ f:Q → Q ‫كانت‬ ‫إذا‬ : ً‫ال‬‫مث‬ ،‫اإلقتران‬
‫نوضحه‬ g ، f ،‫معلومين‬ ‫تطبيقين‬ ‫تركيب‬ ‫من‬ ‫ناتج‬ ‫التطبيقات‬ ‫من‬ ‫آخر‬ ‫نوع‬ ‫على‬ ‫نتعرف‬ ‫سوف‬ ‫واآلن‬
:‫اآلتي‬ ‫بالتعريف‬
‫صورة‬ ‫وأن‬ g x( )‫هي‬ g ‫التطبيق‬ ‫بتأثير‬ x ‫صورة‬ ‫فأن‬ g ‫مجال‬ ‫في‬ ً‫ا‬‫عنصر‬ x ، ً‫ا‬‫تطبيق‬ g ، f ‫من‬ ‫كل‬ ‫ليكن‬
‫تركيب‬ (( ‫الجديد‬ ‫التطبيق‬ ‫هذا‬ ‫يسمى‬ f g x( )( ) ‫هي‬ f ‫التطبيق‬ ‫بتأثير‬ g x( ) ‫الجديد‬ ‫االعنصر‬
: ‫التالي‬ ‫المخطط‬ ‫ويوضحه‬ )) f ، g ‫االتطبيقين‬
)fog( ‫بالرمز‬ f g x( )( ) ‫لـ‬ ‫نرمز‬ ‫سوف‬
. g ‫تركيب‬ f ‫هي‬ )fog( ‫قراءة‬ ‫وأن‬ fog( ) x( ) = f g x( )( ) :‫أن‬ ‫أي‬
: f ‫تركيب‬ g ‫يقرأ‬ ‫فأنه‬ )gof( ‫اآلخر‬ ‫التركيب‬ ‫إيجاد‬ ‫عند‬
: ‫ان‬ ‫اي‬
1 - 4‫التطبيقات‬ ‫تركيب‬
Composition of Mappings
fog
x g(x( f(g(x((
fg
gof( ) x( ) = g f x( )( )
f
1
2
⎛
⎝
⎜
⎞
⎠
⎟ =
1
4
+ 1 =
5
4

26. 26
f g x( )( ) ‫نجد‬ ‫كيف‬
. g x( ) ‫أي‬ g ‫التطبيق‬ ‫إقتران‬ ‫قاعدة‬ ‫في‬ x ‫صورة‬ ً‫ال‬‫أو‬ ‫نجد‬ *
. f g x( )( ) ‫أي‬ f ‫التطبيق‬ ‫إقتران‬ ‫قاعدة‬ ‫في‬ g x( ) ‫صورة‬ ‫نجد‬ ‫ثم‬ *
:‫محلولة‬ ‫أمثلة‬
g : N N ‫وان‬ f (x) = 4 x + 3 ‫حيث‬ f : { 1 , 2 , 3 } N ‫ليكن‬
. gof ‫مدى‬ ‫ايجاد‬ ‫والمطلوب‬ g(x) = x + 1 ‫حيث‬
: ‫المخطط‬ ‫الحظ‬
{ 8 , 12 , 16 } = ( gof ) ‫مدى‬ ∴
( 1 ) ‫مثال‬
f (3) = 4 (3) + 3 = 15x = 3 g (15) = 15 + 1 =16 g(f(3(( = 16
f (2) = 4 (2) + 3 = 11x = 2 g (11) = 11 + 1 =12 g(f(2(( = 12
f (1) = 4 (1) + 3 = 7x = 1 f(1)=7
g (7) = 7 + 1 = 8 g(f(1(( = 8
f(2)=11
f(3)=15

27. 27
f : N N , f (x) = 2x + 1 ‫كان‬ ‫اذا‬
g : N N , g (x) = x 2
f(1) , g (1( :ً‫ال‬‫او‬ ‫جد‬
‫؟‬ ‫تالحظ‬ ‫ماذا‬ )gof)(3) , (fog) (3( : ً‫ا‬‫ثاني‬
/‫احلل‬
f (x) = 2 x + 1 ⇒ f(1) = 2(1) +1 : ً‫ال‬‫او‬
f(1) = 3
g (x) = x 2
⇒ g(1) = (1)2
g(1) = 1
‫لنجد‬ : ً‫ا‬‫ثاني‬
A = { 1 , 2 , 3 { ‫كانت‬ ‫اذا‬
f : A A ‫وكان‬
f = {( 1 , 3 ) , ( 3 , 3 ) , ( 2 , 3 ( {
g = { ( 3 , 1 ) , ( 1 , 2 ) , ( 2 , 3 ( {
gof , fog ‫جد‬
( 3 ) ‫مثال‬
( 2 ) ‫مثال‬
(gof) (3)
(gof) (3) = g ( f (3))
= g (2(3)+1)
= g(7 )
=(7)2
= 49
(fog) (3)
(fog) (3) = f (g (3))
= f (32
)
= f(9 )
=2(9) + 1
=19
(fog) (3) ≠ (gof) (3) ‫ان‬ ‫الحظ‬
g : A A

28. 28
/‫احلل‬
fog ‫نجد‬ / ً‫ال‬‫او‬
) fog) (1) = f(g(1)) = f (2) = 3
) fog) (2) = f(g(2)) = f (3) = 3
) fog) (3) = f(g(3)) = f (1) = 3
∴ fog = } )1 , 3 ( , ) 2 , 3 ( , ) 3 , 3({
gof ‫نجد‬ / ً‫ا‬‫ثاني‬
) gof) (1) = g(f(1)) = g (3) = 1
) gof) (2) = g(f(2)) = g (3) = 1
) gof) (3) = g(f(3)) = g (3) = 1
∴ gof = } ) 1 , 1 ( , ) 2 , 1 ( , ) 3 , 1({
‫؟‬ ‫تالحظ‬ ‫ماذا‬
f : Z Z , x ∈ Z , x 3x + 1
g :Z Z , x ∈ Z , x 2x+ 5
) fog ) (x) = 28 ‫كان‬ ‫اذا‬ x ‫قيمة‬ ‫جد‬
) fog) (x) = f(g(x)) = f (2x + 5( /‫احلل‬
= 3 ( 2x + 5 ) + 1
= 6x + 15 + 1
= 6x + 16
∵ )fog) (x) = 28
∴ 6x + 16 = 28
6x = 28 -16
6x = 12 ⇒ x = 2
( 4 ) ‫مثال‬

29. 29
g (x) = x2
+ 3 ‫حيث‬ g : Z N ‫كان‬ ‫اذا‬ /1‫س‬
. ‫مرتبة‬ ‫ازواج‬ ‫شكل‬ ‫على‬ ‫عناصرها‬ ‫بذكر‬ g ‫اكتب‬ *
.‫المدى‬ ‫اكتب‬ *
.‫التطبيق‬ ‫نوع‬ ‫بين‬ *
f (x) = 5x + 2 ‫حيث‬ f : N N ‫كان‬ ‫اذا‬ /2‫س‬
g (x) = x + 3 ‫حيث‬ g : N N
. ‫المرتبة‬ ‫االزواج‬ ‫بذكر‬ fog ‫اكتب‬ *
. fog ‫مدى‬ *
.fog ‫التطبيق‬ ‫نوع‬ ‫بين‬ *
f (x) = 6x - 1 ‫حيث‬ f : Q Q ‫كان‬ ‫س3/اذا‬
g (x) = x2
+ 1 ‫حيث‬ g : Q Q
. ) fog ) (x) = 17 ‫ان‬ ‫علمت‬ ‫اذا‬ x ‫قيمة‬ ‫جد‬
1 2
1
2

30. 30
f (x) = x 3
‫حيث‬ f : Z Z ‫كان‬ ‫اذا‬ /4 ‫س‬
g (x) = 7 ‫حيث‬ g : Z Z
-49 ، 343 ، -7 ، 7 : ‫يساوي‬ )fog)(-1( ∗ :‫فأن‬
1 ، -1 ، -7 ، 7 : ‫يساوي‬ ∗
f (x) = 3x + 4 ‫حيث‬ f : Q Q ‫كان‬ ‫اذا‬ /5 ‫س‬
g (x) = 1-2 x ‫حيث‬ g : Q Q
, )fog( )3( ‫جد‬ ∗
. x ‫قيمة‬ ‫فجد‬ ‫كان‬ ‫اذا‬ ∗
f (x) = 4 x -3 ‫حيث‬ f : { 1 , 2 , 3 ,.... } Z ‫كان‬ ‫اذا‬ /6 ‫س‬
. ‫التطبيق‬ ‫مدى‬ ‫اكتب‬ )1
. ‫عناصره‬ ‫بذكر‬ f ‫التطبيق‬ ‫بيان‬ )2
.‫التطبيق‬ ‫نوع‬ )3
. x ‫قيمة‬ ‫جد‬ f(x) = 53 ‫كان‬ ‫اذا‬ )4
. x ‫قيمة‬ ‫)جد‬f of) (x) = 1 ‫كان‬ ‫اذا‬ )5
(gog)(x)
(gof)(-1)
(gof)(x)=-43

31. 31
.‫االعداد‬ ‫من‬ ‫املزيد‬ ‫الى‬ ‫احلاجة‬ ] 2 - 1[
. ‫احلقيقية‬ ‫االعداد‬ ‫خواص‬ ] 2 - 2[
. ‫التربيعية‬ ‫اجلذور‬ ] 2 - 3[
. ‫التكعيبية‬ ‫اجلذور‬ ] 2 - 4[
‫احلقيقية‬ ‫األعداد‬
Real Numbers
3
a.b3
=a3
.b3a
b
3=
a3
b3
‫الرياضية‬ ‫العالقة‬ ‫او‬ ‫الرمز‬ ‫املصطلح‬
R ‫احلقيقية‬ ‫االعداد‬
Q ‫النسبية‬ ‫االعداد‬
H ‫النسبية‬ ‫غير‬ ‫االعداد‬
‫التربيعي‬ ‫اجلذر‬
‫التكعيبي‬ ‫اجلذر‬
2‫الثاني‬ ‫الفصل‬

32. : ‫هي‬ ‫اساسية‬ ‫مجموعات‬ ‫على‬ ‫دراستنا‬ ‫من‬ ‫سابقة‬ ‫مراحل‬ ‫في‬ ‫تعرفنا‬
. N = { 0 , 1 , 2 , 3 , 4 , ....} (Natural Numbers ( ‫الطبيعية‬ ‫االعداد‬ ‫مجموعة‬ . 1
}... , -3 , -2 , -1 , 0 , +1 , +2 , +3 , ...{ ) (‫الصحيحة‬ ‫االعداد‬ ‫مجموعة‬ .2
Q = { a
b
: a , b ∈ Z , b ≠ 0 { ) ( ‫النسبية‬ ‫االعداد‬ ‫مجموعة‬ . 3
‫المعادالت‬ ‫بعض‬ ‫حل‬ ‫من‬ ‫ذلك‬ ‫مكننا‬ ‫وقد‬ ‫قبلها‬ ‫التي‬ ‫المجموعة‬ ‫تحوي‬ ‫منها‬ ‫مجموعة‬ ‫كل‬ ‫ان‬ ‫والحظنا‬
‫)حيث‬x=-2( ‫قيمة‬ ‫الن‬ )N( ‫في‬ ‫حل‬ ‫لها‬ ‫ليست‬ ) x + 2 = 0 ( ‫المعادلة‬ ً‫ال‬‫فمث‬ ‫والمسائل‬
. ‫سالبة‬ ً‫ا‬‫اعداد‬ ‫تحوي‬ ‫النها‬ ‫وامثالها‬ ‫المعادلة‬ ‫هذه‬ ‫حل‬ ‫على‬ ‫قادرة‬ Z ‫لتصبح‬ )N( ‫وسعت‬ ‫لذلك‬
‫هكذا‬
3
2
∌ Z ، y = 3
2
‫قيمة‬ ‫الن‬ Z ‫في‬ ‫حل‬ ‫لها‬ ‫ليست‬ ) 2y - 3 = 0 ( ‫المعادلة‬ ‫كذلك‬
‫مجموعة‬ ‫حيث‬ ) ax + b = 0 , a ≠ 0 ( ‫بالصورة‬ ‫معادلة‬ ‫الية‬ ً‫ال‬‫ح‬ ‫لتوفر‬ )Q( ‫المجموعة‬ ‫اوجدت‬
.} -
b
a
{‫الحل‬
‫النه‬ ) x2
= 3 ( ‫المعادلة‬ ً‫ال‬‫مث‬ Q ‫في‬ ‫حلها‬ ‫تستطيع‬ ‫ال‬ ‫والمسائل‬ ‫المعادالت‬ ‫من‬ ‫العديد‬ ‫هناك‬ ‫لكن‬
‫(مجموعة‬ ‫ميت‬ ُ‫س‬ ‫االعداد‬ ‫من‬ ‫جديدة‬ ‫مجموعة‬ ‫الى‬ ‫الحاجة‬ ‫دعت‬ ‫لذلك‬ . )3( ‫مربعه‬ ‫نسبي‬ ‫عدد‬ ‫اليوجد‬
‫المعادالت‬ ‫من‬ ‫الكثير‬ ‫حل‬ ‫خاللها‬ ‫من‬ ‫لنستطيع‬ )R( ‫لها‬ ‫ويرمز‬ )Real Numbers ‫الحقيقية‬ ‫االعداد‬
.‫والمسائل‬
: ‫ان‬ ‫واضح‬
Ingteres
Rational Numbers
-2 ∉ N
N ⊂ Z ⊂ Q ⊂ R
N
Z
Q
R
Z =
‫االعداد‬ ‫من‬ ‫مزيد‬ ‫الى‬ ‫احلاجة‬
‫الفصل‬
2 2 - 1
H

33. 33
)H) Irrational Numbers ‫النسبية‬ ‫غير‬ ‫االعداد‬ .4
}- , , 7 , 4 . 14{ ‫الشكل‬ ‫على‬ ‫ليست‬ ‫اعداد‬ ‫الى‬ ‫الحاجة‬ ‫توضحت‬ ‫سبق‬ ‫ما‬ ‫كل‬ ‫من‬
. ) b ≠ 0 ، ‫صحيحة‬ ‫اعداد‬ a , b ‫حيث‬ ‫بالصورة‬ ‫وضعها‬ ‫يمكن‬ ‫ال‬ ‫(اي‬
‫االعداد‬ ‫مربعات‬ ‫انها‬ ‫اي‬ ( ‫كاملة‬ ‫مربعات‬ ‫سميت‬ ‫نسبية‬ ‫اعداد‬ ‫على‬ ً‫ال‬‫مفص‬ ‫تعرفنا‬ ‫السابقة‬ ‫المرحلة‬ ‫وفي‬
. B ∈ Q ‫حيث‬ ) B 2
( ‫وصورتها‬ )‫نسبية‬
. 25 = 52
, 4 = 22
ً:‫مثال‬
.‫الخ‬ ..
49
64
=
7
8
, 25 = 5, 4 = 2 ‫نسبية‬ ‫اعداد‬ ‫هي‬ ‫االعداد‬ ‫لهذه‬ ‫التربيعية‬ ‫والجذور‬
‫ليست‬ ً‫ا‬‫اعداد‬ ‫التربيعية‬ ‫جذورها‬ ‫تكون‬ 5 ، 3 ، 2 ً‫ال‬‫مث‬ ‫كاملة‬ ‫مربعات‬ ‫ليست‬ ‫التي‬ ‫النسبية‬ ‫االعداد‬ ‫اما‬
1000 ، 27 ، 8 ‫كاالعداد‬ ) ‫الكاملة‬ ‫(المكعبات‬ ‫النسبية‬ ‫االعداد‬ ‫كذلك‬(... 5, 3, 2) ‫نسبية‬
. ‫نسبية‬ ‫اعداد‬ ‫التكعيبية‬ ‫جذورها‬ ‫تكون‬
‫اتحاد‬ ‫وان‬ ‫نسبية‬ ‫ليست‬ ‫التكعيبية‬ ‫جذورها‬ ‫تكون‬ : ً‫ال‬‫مث‬ ‫االخرى‬ ‫واالعداد‬
. R ‫الحقيقية‬ ‫األعداد‬ ‫مجموعة‬ ‫يمثل‬ ” H ‫النسبية‬ ‫غير‬ ‫واالعداد‬ Q ‫النسبية‬ ‫“االعداد‬ ‫المجموعتين‬
‫االعداد‬ ‫مستقيم‬
‫سالبة‬ ‫اعداد‬ ‫موجبة‬ ‫اعداد‬
1
5
2
3
a
b
R = Q ∪ H
10003
= 10 , 273
= 3 , 83
= 2
53
, 33
, 23
-3 -2 -1 1 2 3
(... 5, 3, 2)
1
2
-
O

34. 34
2 - 2‫احلقيقية‬ ‫االعداد‬ ‫خواص‬
ً‫ال‬‫او‬
: ‫يلي‬ ‫ما‬ ‫وتتضمن‬ ‫الحقيقية‬ ‫االعداد‬ ‫لمجموعة‬ ‫المهمة‬ ‫الخواص‬ ‫من‬ ‫الخاصية‬ ‫هذه‬ ‫عتبر‬ُ‫ت‬
: ‫صائبة‬ ‫االتية‬ ‫الحاالت‬ ‫من‬ ‫فقط‬ ‫واحدة‬ ‫فان‬ a ∈ R ‫كان‬ ‫اذا‬ .1
‫االعداد‬ ‫خط‬ ‫على‬ ‫الصفر‬ ‫يمين‬ ‫على‬ ‫يقع‬ )‫موجب‬ ‫(عدد‬ a 0 , a = 0
‫االعداد‬ ‫خط‬ ‫على‬ ‫الصفر‬ ‫يسار‬ ‫على‬ ‫يقع‬ )‫سالب‬ ‫(عدد‬ a 0
: ‫تتحقق‬ ‫العالقات‬ ‫هذه‬ ‫من‬ ‫فقط‬ ‫واحدة‬ ‫فان‬ a , b ∈ R ‫كان‬ ‫اذا‬ .2
a = b , a b , a b
a , b , c ∈ R ‫لكل‬ ‫والضرب‬ ‫الجمع‬
0 ‫موجب‬‫سالب‬
a=0 a0a0
Property ‫اخلاصية‬Addition ‫اجلمع‬Multiplication ‫الضرب‬
clousre ‫االنغالق‬a +b ∈ Ra . b ∈ R
Commutativity ‫االبدالية‬a + b = b + aa. b = b . a
Associativity ‫التجميعية‬) a +b ) + c = a +( b + c() a . b ).c = a . (b . c(
‫احملايد‬ ‫العنصر‬
Idetity Element
a + 0 = 0 + a = a
0 ‫هو‬ ‫احملايد‬ ‫العنصر‬
a.1 = 1.a =a
1 ‫هو‬ ‫احملايد‬ ‫العنصر‬
Inverse ‫النظير‬‫اجلمعي‬ ‫النظير‬
Additive Inverse
a + (-a ) = ( -a) +a =0
‫الضربي‬ ‫النظير‬
Multiplicative
Inverse
a ‫للعدد‬ ‫الضربي‬ ‫النظير‬
, a ≠ 0
‫حيث‬ ‫هو‬1
a
1
a
a . ( ) = ( ). a = 11
a
Order Property ‫الترتيب‬ ‫خاصية‬ ]2 - 2 - 1[
‫الحقيقية‬ ‫االعداد‬ ‫على‬ ‫العمليات‬ ‫بعض‬ ‫خواص‬ ]2 - 2 - 2[

35. 35
‫والقسمة‬ ‫الطرح‬
‫النظير‬ ‫مع‬ a ‫جمع‬ . ‫يعني‬ a ‫من‬ b ‫طرح‬ ‫اي‬ a - b = a + (-b ( : ‫االتي‬ ‫بالشكل‬ ‫يعرف‬ :‫الطرح‬
.b ‫للعدد‬ ‫الجمعي‬
‫ضرب‬ ‫حاصل‬ ‫تعني‬ b ‫على‬ a ‫قسمة‬ ‫اي‬ a ÷ b = a . , b ≠ 0 : ‫االتي‬ ‫بالشكل‬ ‫تعرف‬ :‫القسمة‬
b ≠ 0 ‫ان‬ ‫شرط‬ b ‫للعدد‬ ‫الضربي‬ ‫النظير‬ ‫في‬ a ‫العدد‬
‫والطرح‬ ‫الجمع‬ ‫على‬ ‫الضرب‬ ‫عملية‬ ‫توزيع‬
a , b , c ∈ R ‫لكل‬
a . ( b + c ) = ( a . b ) + ( a . c )
a . ( b - c ) = ( a . b ) - ( a . c )
:‫اي‬ ً‫ا‬‫سابق‬ ‫درستها‬ ‫كما‬ ‫نفسها‬ ‫االشارات‬ ‫ضرب‬ ‫قواعد‬ ‫تطبيق‬
1) - ( - a ) = a
2) a ( - b ) = - ( ab)
3 ) ( -a ) ( -b ) = ab
= , = , a , b , c ∈ R
b ≠ 0 , c ≠ 0
:‫كان‬ ‫اذا‬
ً‫ا‬‫ثاني‬
1
b
ً‫ا‬‫ثالث‬
ً‫ا‬‫رابع‬
ً‫ا‬‫خامس‬
a
b
a . c
b . c
a
b
a ÷ c
b ÷ c
ً‫ا‬‫سادس‬
Distributive property
‫كالهما‬ ‫او‬ b = 0 ‫او‬ a = 0 ‫فان‬ a . b = 0)‫الصفري‬ ‫العامل‬ ‫(خاصية‬Zero Factor Property
‫لكل‬

36. 36
ً‫ا‬‫جذر‬ ‫يسمى‬ )a( ‫مربعه‬ ‫عدد‬ ‫فاي‬ ) a ≥ 0 ( ً‫ا‬‫سالب‬ ‫ليس‬ ً‫ا‬‫حقيقي‬ ً‫ا‬‫عدد‬ )a( ‫كانت‬ ‫اذا‬ ‫بانه‬ ‫تعلمت‬ ‫ان‬ ‫سبق‬
. a ‫له‬ ‫ويرمز‬ )a( ‫للعدد‬ ً‫ا‬‫تربيعي‬
،
3
4
,22
= 4 ‫الن‬ ( 4 = 2)4 ‫للعدد‬ ً‫ا‬‫تربيعي‬ ً‫ا‬‫جذر‬ 2 ‫/العدد‬ ً‫ال‬‫مث‬
. ‫حيث‬
)2-1( ‫تعريف‬
.b2
= a ‫ان‬ ‫أي‬ a ‫مربعه‬ ً‫ا‬‫سالب‬ ‫ليس‬ ً‫ا‬‫حقيقي‬ ً‫ا‬‫عدد‬ b ‫حيث‬ a = b ‫فان‬ a ≥ 0 , a ∈ R ‫لتكن‬
a ‫فان‬ a : ‫كذلك‬ ، a = 32
= 9 ‫فان‬ a ‫كانت‬ ‫اذا‬ : ً‫ال‬‫مث‬
: ‫الجذور‬ ‫خواص‬ ‫ومن‬
b ≥ 0 , a ≥ 0 ‫حيث‬ ‫صحيح‬ ‫والعكس‬ ab = a . b : ‫فان‬ a , b ∈ R ‫كانت‬ ‫اذا‬ - 1
: ‫كذلك‬ / ً‫ال‬‫مث‬
ً‫ال‬‫مث‬ ‫صحيح‬ ‫والعكس‬ ‫و‬ b 0 , a ≥ 0 - 2
10 = 10. 10 , 8. 8 = 8 ‫صحيح‬ ‫والعكس‬ a ≥ 0 , a . a = a - 3
2 - 3‫التربيعية‬ ‫اجلذور‬
9
16
=
3
4
⎛
⎝
⎜
⎞
⎠
⎟
9
16
= 3=
3
4
3 . 5 = 1521 = 7. 3
=
9
25
=
9
25
=
3
5
a
b
a
b
3
4
‫للعدد‬ ً‫ا‬‫تربيعي‬ ً‫ا‬‫جذر‬
=
3
4
⎛
⎝
⎜
⎞
⎠
⎟
2
=
9
16
‫وكذلك‬
4
9
=
4
9
=
2
3
4
9
=
4
9
=
2
3
=
2
3

37. 37
: ‫صورة‬ ‫ابسط‬ ‫في‬ ‫ضع‬
a)
b)
c)
d)
e)
f)
)c( ‫الفرع‬ ‫في‬ ‫كما‬ ً‫ة‬‫مباشر‬ )f( ‫حل‬ ‫ميكن‬
( 1 ) ‫مثال‬
3 5 +2 5 −6 5 = 5 3+ 2 − 6( ) = 5 −1( ) = − 5
4 3 +1( )+ 3 3 −1( )
= 4 3 + 4 + 3 3 − 3 = 7 3 +1
+( ), ≥ 0 , ≥ 0a b a b
2 2 +5( )−2 1− 3 2( )
= 2. 2 +5 2 −2+6 2
= 2+5 2 −2+6 2
= 2 −2( )+ 5+ 6( ) 2 = 0+11 2
=11 2
7 +2( ) 3+ 7( )
= 3 7 + 7. 7 +6+2 7
= 3 7 + 7+ 6+2 7
= 3+2( ) 7 +13 = 5 7 +13
5 − 2( )
2
= 5 − 2( ) 5 − 2( )
= 5. 5( )− 5. 2( )− 2. 5( )+ 2. 2( )
= 5 − 5×2 − 2×5 +2
= 5 − 10 − 10 +2 = 7 −2 10
2
= ( )
2
+ 2 +( )
2
= + 2 +a a b b a ab b.

38. 38
( 2 ) ‫مثال‬
( 3 ) ‫مثال‬
: ‫مماياتي‬ ً‫ال‬‫ك‬ ‫صورة‬ ‫ابسط‬ ‫في‬ ‫ضع‬
a) 3 8 +2 50 − 32
b) 125 − 20 − 4 45
)a(/‫احلل‬
)b(/ ‫احلل‬
. ً‫ا‬‫نسبي‬ ً‫ا‬‫عدد‬ ‫المقام‬ ‫يكون‬ ‫بحيث‬ −
4
5
,
2
3
,
1
2
‫االعداد‬ ‫اكتب‬
‫في‬ ‫والمقام‬ ‫البسط‬ ‫بضرب‬
‫في‬ ‫والمقام‬ ‫البسط‬ ‫بضرب‬
‫في‬ ‫والمقام‬ ‫البسط‬ ‫بضرب‬
3 8 +2 50 − 32
= 3 4 ×2 +2 25× 2 − 16×2
= 3 4. 2 +2 25. 2 − 16. 2
= 3×2 2 +2×5 2 − 4 2
= 6 2 +10 2 − 4 2 =12 2
125 − 20 − 4 45
= 25( ) 5( ) − 4( ) 5( ) − 4 9( ) 5( )
= 25. 5 − 4. 5 − 4 9. 5
= 5 5 −2 5 −12 5
= −9 5
1
2
=
1
2
.
2
2
=
2
2
2
3
=
2
3
.
3
3
=
2 3
3
−4
5
=
−4
5
.
5
5
=
−4 5
5
2
3
5

39. 39
( 5 ) ‫مثال‬
( 4 ) ‫مثال‬
‫صورة‬ ‫ابسط‬ ‫في‬ ‫اختصر‬
:B ‫في‬ ‫الزاوية‬ ‫قائم‬ ‫مثلث‬ A B C :‫المجاور‬ ‫الشكل‬ ‫في‬
. AC ‫طول‬ ‫جد‬ BC = cm , AB = cm
‫؟‬ ‫المثلث‬ ‫مساحة‬ ‫وما‬
/ ‫احلل‬
‫فيثاغورس‬ ‫مبرهنة‬
‫المثلث‬ ‫مساحة‬ )AC)2
= ( AB )2
+ ( BC(2
)AC)2
∴)AC(2
A =
1
2
× AB × BC
A =
1
2
× 3 2 × 6
A =
3
2
2×6
A =
3
2
4 × 3
A = 3 3
A =
1
2
× AB × BC
A =
1
2
× 3 2 × 6
A =
3
2
2×6
A =
3
2
4 × 3
A = 3 3
AC( )
2
= AB( )
2
+ BC( )
2
= 3 2( )
2
+ 6( )
2
= 9×2+6
AC( )
2
= 24
∴ AC = 24 = 2 6AC
3
4
+
1
3
−
25
12
=
3
4
+
1
3
−
25
12
=
3
2
+
1
3
−
5
4( ) 3( )
=
3
2
+
1
3
.
1
3
−
5
2 3
.
3
3
=
3
2
+
1
3
−
5 3
6
=
3 3 +2 − 5 3
6
=
2 − 2 3
6
=
1− 3
3
3
3 3 − 5 3
=
5 3 − 5 3
6
=
0
6
= 0
2
= ‫المساحة‬∴3 3
A =
1
2
× AB × BC
A =
1
2
× 3 2 × 6
A =
3
2
2×6
A =
3
2
4 × 3
A = 3 3
(AB)(BC)
3 2( ) 6( )
A
B C
3 2cmcm
6 cm
cm
cm

40. 40
2 1
a( :‫صورة‬ ‫ابسط‬ ‫في‬ ‫يأتي‬ ‫مما‬ ً‫ال‬‫ك‬ ‫ضع‬ / 1‫س‬
b)
:‫صورة‬ ‫ابسط‬ ‫في‬ ‫يأتي‬ ‫مما‬ ً‫ال‬‫ك‬ ‫/ضع‬ 2‫س‬
a)
b)
c)
d)
e)
:‫االتية‬ ‫العبارات‬ ‫خطأ‬ ‫او‬ ‫صحة‬ ‫بين‬ / 3‫س‬
a)
b)
c)
d)
: ً‫ا‬‫نسبي‬ ً‫ا‬‫عدد‬ ‫المقام‬ ‫يكون‬ ‫بحيث‬ ‫يأتي‬ ‫مما‬ ‫كل‬ ‫في‬ b ≠ 0 , ‫حيث‬ , a2
‫جد‬ / 4‫س‬
a) a
b) a
c) a
1
4
7 -
3
2
5 +
3
4
7
2 3 −5 2 + 3 − 4 2
3 2(4 2 − 3)
(2 3 + 5)(3 3 −2 5)
(4 6 − 3)2
, (1− 2)3
, ( 3 + 2)2
( 3 − 2)
(1− 2)3
, ( 3 + 2)2
( 3 − 2)
1- 2( )
3
a2
b
= 2 2 , = 3
= 2 - 2 , = 3
= - 4 3 , = - 2
b
b
b
+
−
3 + 3 = 6
8 + 2 = 3 2
12 = 2 6
2 3 × 3 3 = 6 33 3( )2 3( )
a2
b ,

41. 41
a( -: ‫االتية‬ ‫المقادير‬ ‫اختصر‬ / 5‫س‬
b)
c)
d)
: ‫هي‬ x ‫قيمة‬ ‫كانت‬ ‫اذا‬ 4x2
- 2x + 5 : ‫االتي‬ ‫المقدار‬ ‫قيمة‬ ‫جد‬ ) a/ 6‫س‬
14 cm2
‫تساوي‬ ABCD ‫المستطيل‬ ‫مساحة‬ ‫كانت‬ ‫اذا‬ ‫المجاور‬ ‫الشكل‬ ‫في‬ x ‫قيمة‬ ‫جد‬ )b
ABC ‫المثلث‬ ‫مساحة‬ ‫جد‬ )c
48 - 3 75 - 2 12
20 - 12 5 - 5
1
5
5
3
10
- 2
5
6
-
15
32
5 , 1 - 2 ,
1
2
( 2 - 3 )
A
D C
B
- 2( )
+ 2( )x
x
+
+
A
5 + 2
5 - 2
CB
3
3
‫حيث‬ x 2
2 63 - 7
2
7
- 3 282
1
7
2 63 - 7
2
7
- 3 28

42. 42
. a ‫للعدد‬ ً‫ا‬‫تكعيبي‬ ً‫ا‬‫جذر‬ ‫يسمى‬ )a( ‫العدد‬ ‫مكعبه‬ ‫عدد‬ ‫اي‬ ‫فان‬ aa ∈ RR ‫كان‬ ‫اذا‬
)2-2( ‫تعريف‬
a ‫مكعبه‬ ‫الذي‬ ‫الوحيد‬ ‫الحقيقي‬ ‫العدد‬ ‫هو‬ b ‫حيث‬ a = b ‫فان‬ a R ‫كان‬ ‫اذا‬
b3
= a : ‫ان‬ ‫اي‬
: ً‫ال‬‫فمث‬ ‫وحيد‬ ‫تكعيبي‬ ‫جذر‬ ‫حقيقي‬ ‫عدد‬ ‫لكل‬ ‫ان‬ ‫يالحظ‬
( 273
= 3) ‫ان‬ ‫(72)اي‬ ‫للعدد‬ ‫التكعيبي‬ ‫الجذر‬ ‫هو‬ )3(
( −643
= −4) ‫ان‬ ‫اي‬ )-64( ‫للعدد‬ ‫التكعيبي‬ ‫الجذر‬ ‫هو‬ )-4(
‫ان‬ ‫اي‬8
125
3 =
2
5
,
8
125
‫للعدد‬ ‫التكعيبي‬ ‫الجذر‬ ‫هو‬ ) 2
5
(
2 - 4
‫التكعيبية‬ ‫اجلذور‬
a ∈ R
8
125
3 =
2
5
,
8
125
( )
33
: ‫انه‬ ‫سبق‬ ‫مما‬ ‫نستنتج‬
)‫(سالب‬ b 0 ‫فان‬ a 0 ‫كان‬ ‫اذا‬ )*(
)‫(موجب‬b 0 ‫فان‬ a 0 ‫كان‬ ‫اذا‬ )*(
b = 0 ‫فان‬ a = 0 ‫كان‬ ‫اذا‬ )*(
a 0a 0
a 0 a 0
‫مالحظة‬

43. 43
: ‫فان‬ a , ba,b ∈ RR ‫كان‬ ‫اذا‬
a . b = a . b
a . a = a3
= a
a . a = a2
≠ a
543
− 3 163
− 4 1283 : ‫التالي‬ ‫المقدار‬ ‫بسط‬
/ ‫احلل‬
‫االقل‬ ‫على‬ ‫كامل‬ ‫مكعب‬ ‫احدهما‬ ‫عاملين‬ ‫الى‬ 128 ، 16 ، 54 ‫االعداد‬ ‫نحلل‬
( 1 ) ‫مثال‬
3 3 3
3
= , b ≠ 0
a
b
3
3
a
b
3 3 3
3
3
3
1) ‫صحيح‬ ‫والعكس‬
2)
3)
‫صحيح‬ ‫والعكس‬
‫صحيح‬ ‫والعكس‬3 3 33 3 32
4) 3 3 33 3 3
‫ان‬ ‫الحظ‬
: ‫التكعيبية‬ ‫الجذور‬ ‫خواص‬ ‫من‬
= 33
2 − 3 × 23
2 - 4 × 43
2
3
54 =3
27 . 2 = 3
27 . 3
2 = 33
2
163
= 83
. 23
= 2 23
1283
= 643
. 23
= 4 23
= −19 23
∴ 543
− 3 163
− 4 1283 3 3

44. 44
3
-a = 3
a
5
1
16
3 − 323
− 3
−1
2
3 : ‫التالي‬ ‫المقدار‬ ‫بسط‬
/ ‫احلل‬
: ‫مالحظة‬
: ‫فان‬ aa 00 ‫كانت‬ ‫اذا‬
= 5
1
16
×
4
4
3 − 8× 43
+ 3
1
2
×
4
4
3
= 5
4
64
3 −2 43
+ 3
4
8
3
=
5 43
4
−2 43
+
3 43
2
=
5 43
−8 43
+6 43
4
.‫اجلانبية‬ ‫ومساحته‬ ‫حجمه‬ ‫جد‬ ‫ضلعه‬ ‫طول‬ ‫مكعب‬
.A ‫الجانبية‬ ‫ومساحته‬ v ‫المكعب‬ ‫حجم‬ ‫نفرض‬ / ‫احلل‬
‫واحد‬ ‫وجه‬ ‫مساحة‬ × 4 = ‫للمكعب‬ ‫اجلانبية‬ ‫املساحة‬ )‫الضلع‬ ‫(طول‬3
= ‫املكعب‬ ‫حجم‬
( 2 ) ‫مثال‬
33
−
=
3
4
43
( 3) ‫مثال‬
= 3 43
( )
2
× 4
= 43
. 43
( )× 4
= 163
( )× 4
= 23
. 83
( )× 4
= 23
× 2 × 4
=8 23
cm2
= 3 43
.3 43
( )×4
= 9 163
( )×4
= 9 23
. 83
( )×4
= 9 23
×2×4
= 72 23
cm2
= 3 43
( )
3
=33
. 43
. 43
. 43
=27. 643
= 27( ). 4( )
=108 cm3
‫املكعب‬ ‫حجم‬
v
3 43
3 23
cm
A
‫مربع‬
‫مربع‬
‫مربع‬
‫مربع‬
= 3 43
( )
3
=33
. 43
. 43
. 43
=27. 643
= 27( ). 4( )
=108 cm3

45. 45
:‫التالية‬ ‫املقادير‬ ‫اختصر‬ / 1‫س‬
a)
b)
c)
23
+1( ) 43
- 23
+1( ) ‫ناجت‬ ‫جد‬ / 2‫س‬
. ‫الكلية‬ ‫ومساحته‬ ‫حجمه‬ ‫جد‬ cm ‫ضلعه‬ ‫طول‬ ‫مكعب‬ : ‫املجاور‬ ‫الشكل‬ ‫في‬ / 3‫س‬
‫طول‬ ‫وحدة‬ 6
33
,
5
43
,
3
23
: ‫ابعاده‬ ‫مستطيلة‬ ‫سطوح‬ ‫متوازي‬ / 4‫س‬
.‫صورة‬ ‫ابسط‬ ‫في‬ ‫حجمه‬ ‫جد‬
2 2
7 543
− −163
+ 4 −1283
2 33
2
33
813
− −243
− 3 =
−1
9
3813
− −243
− 3 =
−1
9
3
323
+ 2
1
2
3 − (-2)23

46. ‫احلدوديات‬
Polynomials
‫مراجعة‬ ]3-1[
‫مكعبني‬ ‫بني‬ ‫الفرق‬ ‫حتليل‬ ]3-2[
‫مكعبني‬ ‫مجموع‬ ‫حتليل‬ ]3-3[
‫الثالثية‬ ‫احلدوديات‬ ‫حتليل‬ ]3-4[
‫الكامل‬ ‫املربع‬ ‫حتليل‬ ]3-5[
‫األصغر‬ ‫املشترك‬ ‫واملضاعف‬ ‫األكبر‬ ‫املشترك‬ ‫العامل‬ ]3-6[
‫اجلبرية‬ ‫املقادير‬ ‫تبسيط‬ ‫في‬ ‫التحليل‬ ‫إستخدام‬ ]3-7[
‫الرياضية‬ ‫العالقة‬ ‫او‬ ‫الرمز‬ ‫املصطلح‬
‫األكبر‬ ‫املشترك‬ ‫العامل‬
‫األصغر‬ ‫املشترك‬ ‫املضاعف‬
a+b()
2
=a2
+2ab+b2−−
LCM
GCF
3‫الثالث‬ ‫الفصل‬

47. ً‫ال‬‫او‬
:‫بين‬ ‫الفرق‬ ‫نوضح‬ ‫سوف‬ ‫ذلك‬ ‫وقبل‬ .‫الحدوديات‬ ‫موضوع‬ ‫في‬ ً‫ا‬‫سابق‬ ‫درست‬ ‫ما‬ ‫مراجعة‬ ‫المفيد‬ ‫من‬
. ) x2
)3
, 4x , x4
x4
= x . x . x. x ‫مرات‬ 4 ‫نفسه‬ ‫في‬ x ‫ضرب‬ ‫أي‬
4x = x + x + x +x ‫مرات‬ ‫اربعة‬ x ‫جمع‬ ‫أي‬
)x2
(3
= )x2
( )x2
( )x2
(
∴ )x2
(3
= )x( )x( )x( )x( )x( )x( = x6
= x)2()3(
:‫أخرى‬ ‫حدانية‬ ‫في‬ ‫حدانية‬ ‫ضرب‬
) 2x - 1( ) x + 3( ‫ناتج‬ ‫إيجاد‬ ‫كيفية‬ ‫نتذكر‬ ‫ان‬ ‫نحاول‬
) 2x - 1 ( ) x + 3 ( = 2x )x(+ 2x )3( - 1 )x( - 1 )3(
= 2x2
+ 6x - x - 3
= 2x2
+ 5x - 3
2x2
+ 5x-3 ‫هو‬ ) 2x - 1 ( ) x + 3( ‫ضرب‬ ‫حاصل‬ ‫ناتج‬ ‫أن‬ ‫أي‬
‫حدانية‬ ‫مربع‬
) x + 5(2
‫ناتج‬ ‫إيجاد‬ ‫خطوات‬ ‫تأمل‬
) ً‫ا‬‫جبري‬ ( ) ً‫ا‬‫هندسي‬ (
x + 5
)x + 5 (2
= ) x + 5 ( ) x + 5(
= x)x( + x )5( + 5 )x( + 5 ) 5(
= x2
+ 10x + 25
ً‫ا‬‫ثاني‬
x
+
5
x2
5x
5x 25
3 - 1‫مراجعة‬
‫الفصل‬
3

48. 48
‫األكبر‬ ‫املشترك‬ ‫العامل‬ ‫بإيجاد‬ ‫حدودية‬ ‫حتليل‬
)G.C.F( ‫اآلكبر‬ ‫المشترك‬ ‫العامل‬ ‫بإستخراج‬ ‫اآلتية‬ ‫الحدودية‬ ‫نحلل‬ ‫ان‬ ‫لنحاول‬
6x3
y2
+ 12 x y3
6x3
y2
= )2( )3( )x( )x( )x( )y( ) y(
12x y3
= )2( )2( )3( )x( )y( )y( )y(
)2( )3( )x( )y( )y(
‫التحليل‬‫سيكون‬‫لذا‬ 6x y2
:‫هو‬ ‫األكبر‬ ‫المشترك‬ ‫العامل‬ ً‫ا‬‫اذ‬
6x3
y2
+ 12x y3
=)6x y2
( ] x2
+ 2y[
‫مربعين‬ ‫بين‬ ‫الفرق‬ ‫تحليل‬
9x2
- 16 = )3x( 2
- )4(2
9 x 2
- 16 ‫حلل‬ :ً‫ال‬‫فمث‬
= ) 3x - 4 ( ) 3x +4(
.‫األخرى‬ ‫التحليل‬ ‫طرق‬ ‫ألكمال‬ ‫الالحقة‬ ‫البنود‬ ‫في‬ ‫سنتطرق‬ ‫المختصرة‬ ‫المراجعة‬ ‫هذه‬ ‫بعد‬
‫عامة‬ ‫وبصورة‬
) a + b ) 2
= a 2
+ 2ab + b2--
ً‫ا‬‫ثالث‬
ًً‫ا‬‫رابع‬
∗ ∗
∗
∗ ∗∗ ∗
‫عامة‬ ‫وبصورة‬
a2
- b2
= (a - b)(a + b(

49. 49
.‫التوزيع‬ ‫بطريقة‬ ‫األقواس‬ ‫فك‬ ‫كيفية‬ ً‫ا‬‫سابق‬ ‫تعلمت‬
‫ينتج؟‬ ‫ماذا‬ ) a2
+ ab + b2
( ‫في‬ )a -b( ‫ضربنا‬ ‫لو‬ ً‫ال‬‫فمث‬
) a - b ) (a 2
+ ab + b2
(
= a ( a2
) + a(ab) + a(b2
) - b(a2
) - b(ab) - b(b2
(
= a 3
+ a2
b + ab2
- b a2
- ab2
- b3
= a 3
- b3
‫مكعبني‬ ‫بني‬ ‫الفرق‬ ‫تسمى‬ a3
-b3
:‫الصورة‬ ‫ان‬
3 - 2‫مكعبني‬ ‫بني‬ ‫الفرق‬ ‫حتليل‬
)‫تكعيب‬ a ‫تقرأ‬ a3
(
‫عامة‬ ‫وبصورة‬
) a3
- b3
) = ( a - b )(a2
+ab +b2
(
/ ‫ويالحظ‬
a3
‫لـ‬ ‫التكعيبي‬ ‫اجلذر‬ ‫هو‬ a
b3
‫لـ‬ ‫التكعيبي‬ ‫هواجلذر‬ b
/ ‫مالحظة‬. R ‫في‬ ‫يتحلل‬ ‫ال‬ )a2
+ab+b2
( ‫العامل‬

50. 50
‫م‬
:‫يأتي‬ ‫مما‬ ً‫ال‬‫ك‬ ‫حلل‬
1) x3
-27 2) 8x3
-125y3
3) -
4) a6
-b6
/‫احلل‬
1) x3
- 27= (x-3)(x2
+3x+9)
(x)3
(3)3
2) 8x3
- 125y3
= (2x-5y)((2x)2
+(2x)(5y)+(5y)2
)
(2x)3
(5y)3
3)
4) a6
- b6
= (a2
-b2
)((a2
)2
+(a2
)(b2
)+(b2
)2
)
(a2
)3
(b2
)3
= (a2
-b2
)(a4
+a2
b2
+b4
)
‫مثال‬
Qg(x) = 4x − 7
g(x) =10
∴10 = 4x − 7
⇒ 4x =10+ 7
⇒ 4x = 17
⇒ x =
17
4
∈ Q
1
a3
Qg(x) = 4x − 7
g(x) =10
∴10 = 4x − 7
⇒ 4x =10+ 7
⇒ 4x = 17
⇒ x =
17
4
∈ Q
64
b3
1
a3
-
64
b3
=
1
a
-
4
b
⎛
⎝
⎜
⎞
⎠
⎟
1
a
⎛
⎝
⎜
⎞
⎠
⎟
2
+
1
a
⎛
⎝
⎜
⎞
⎠
⎟
4
b
⎛
⎝
⎜
⎞
⎠
⎟+
4
b
⎛
⎝
⎜
⎞
⎠
⎟
2⎛
⎝
⎜⎜
⎞
⎠
⎟⎟
1
a
⎛
⎝
⎜
⎞
⎠
⎟
3
64
b3
⎛
⎝
⎜
⎞
⎠
⎟ =
1
a
-
4
b
⎛
⎝
⎜
⎞
⎠
⎟
1
a2
+
4
ab
+
16
b2
⎛
⎝
⎜
⎞
⎠
⎟
)a-b)(a+b( ‫هو‬ ‫وتحليله‬ ‫مربعين‬ ‫بين‬ ‫فرق‬ ‫هو‬ a2
- b2
‫بأن‬ ً‫ا‬‫سابق‬ ‫تعلمته‬ ‫ومما‬ ‫تالحظ‬ ‫وكما‬
:‫اآلتي‬ ‫بالشكل‬ ‫التحليل‬ ‫سيكون‬ ‫الحالة‬ ‫هذه‬ ‫في‬
a6
-b6
=(a-b)(a+b)(a4
+a2
b2
+b4
)
‫التحليل‬ ‫ونكمل‬ a6
- b6
= ( a3)2
- ( b3)2
: ‫اآلتية‬ ‫بالطريقة‬ ‫أو‬
= 2x-5y( ) 4x2
+10xy+25y2
( )= (2x-5y)
( )
4
b
3

51. 51
a3
+b3
‫لتحليل‬ ‫العامة‬ ‫الصورة‬ ‫وضع‬ ‫يمكن‬ ‫مكعبين‬ ‫بين‬ ‫فرق‬ ‫تحليل‬ ‫في‬ ‫المتبع‬ ‫واالسلوب‬ ‫السياق‬ ‫بنفس‬
:‫حيث‬
:‫يأتي‬ ‫مما‬ ً‫ال‬‫ك‬ ‫حلل‬
1) 64x3
+1 2) 27
a3
+8b3
3) 0.125x3
+y6
4) x2
y5
+y2
x5
5) 1
2
h3
+4
/‫احلل‬
1) 64x3
+ 1 = (4x + 1)((4x)2
- 4x(1) + (1)2
)
(4x)3
(1)3
= (4x+1)(16x2
-4x+1)
2) 27
a3
+8b3
=
3
a
+2b
⎛
⎝
⎜
⎞
⎠
⎟
3
a
⎛
⎝
⎜
⎞
⎠
⎟
2
-
3
a
⎛
⎝
⎜
⎞
⎠
⎟ 2b( )+(2b)2
⎛
⎝
⎜⎜
⎞
⎠
⎟⎟
3
a
⎛
⎝
⎜
⎞
⎠
⎟
3
2b( )
3
=
3
a
+2b
⎛
⎝
⎜
⎞
⎠
⎟
9
a2
-
6b
a
+4b2⎛
⎝
⎜
⎞
⎠
⎟
3 - 3‫مكعبني‬ ‫مجموع‬ ‫حتليل‬
a3
+b3
=(a+b)(a2
-ab+b2
(
‫مثال‬

52. 52
3) 0.125x3
+ y6
= (0.5x+y2
)((0.5x)2
-(0.5x)(y2
)+(y2
)2
)
(0.5x)3
(y2
)3
= (0.5x+y2
)(0.25x2
- 0.5xy2
+y4
)
4) x2
y5
+y2
x5
x2
y2
(y3
+x3
)
= x2
y2
(y+x)(y2
-xy+x2
)
5) 1
2
h3
+4=
1
2
h3
+8( )
‫نستخرج‬
‫مشترك‬ ‫عامل‬
=
1
2
h+2( ) h2
-2h+4( )
1
2
h3+4=
h3+8
2
=
1
2
(h3+8)3
3
3
=
1
2
h+2( ) h2
-2h+4( )
x2
y2
‫املشترك‬ ‫العامل‬ ‫بإستخراج‬
‫املقامات‬ ‫بتوحيد‬ ‫أو‬

53. 53
: ‫صورة‬ ‫ابسط‬ ‫في‬ ‫يأتي‬ ‫مما‬ ً‫ال‬‫ك‬ ‫حلل‬ /1‫س‬
1) x3
- 125 2) 8 + 27y3
3) a3
- 64b3
4) 3x3
+ 81y3
5) 2xy4
+ 16x4
y 6)
7) 8) 1000a3
-b3
9) x6
+ y6
10) 11) x9
+ x3
12)
13) x4
- x 14) 0.064 x3
- 0.027y3
:‫صحيحة‬ ‫فقط‬ ‫واحدة‬ ‫إجابات‬ ‫أربع‬ ‫يأتي‬ ‫مما‬ ‫سؤال‬ ‫لكل‬ /2‫س‬
1) :‫هو‬ x3
+ 8 ‫المقدار‬ ‫عوامل‬ ‫احد‬
a) x - 2 b) x2
- 4 x + 4 c) x2
- 2x + 4 d) x2
+ 2x + 4
2) ( x - y ) ( x2
+ xy + y 2
) - ( x + y ) ( x2
- xy + y2
) =
a) -2y3
b) 2y3
c) -2x3
d) 2x3
3)
a) 12 b) -2 c) 35 d) 2
4) 1 - x3
=
a) ( 1 - x )( 1 + x + x2
) b) ( 1 - x ) ( 1 - x - x 2
)
c) ( 1 + x ) (1 - x + x2
) d) ( x + 1 ) ( 1 + x + x2
)
3 1
8
27
a3
- 1
1
5
+ 25z3
32 -
1
2
a3
3x3
+
1
9
y3
x3
+y3
= ‫فأن‬ x2
- xy + y2
= 7 ‫وان‬ ) x + y ) = 5 ‫كان‬ ‫اذا‬

54. 54
:‫اآلتية‬ ‫الحدوديات‬ ‫تحليل‬ ‫لنحاول‬
a) x2
+ 8x + 12
-: ‫بالتجربة‬ ‫التحليل‬ ‫في‬
‫والوسطين‬ ‫الطرفين‬ ‫ضرب‬ ‫اوجدناحاصل‬ ‫اننا‬ ‫الحظ‬
‫الحد‬ ‫يمثل‬ ‫والذي‬ ‫لهما‬ ‫الجبري‬ ‫المجموع‬ ‫بايجاد‬ ‫وقمنا‬
. ‫الثالثية‬ ‫الحدودية‬ ‫في‬ ‫االوسط‬
. ‫الطرفين‬ ‫ضرب‬ ‫حاصل‬ +6x
. ‫الوسطين‬ ‫ضرب‬ ‫حاصل‬ +2x
. ‫االوسط‬ ‫الحد‬ +8x
x2
+ 8x + 12 = ( x + 2 ) ( x + 6 (
b) x2
- 9x + 18
. ‫الوسطين‬ ‫ضرب‬ ‫حاصل‬ -3x
.‫الطرفين‬ ‫ضرب‬ ‫حاصل‬ -6x
. ‫االوسط‬ ‫الحد‬ -9x
x2
- 9x +18 = ( x - 3 ) ( x - 6 (
3 - 4‫الثالثية‬ ‫احلدوديات‬ ‫حتليل‬
ً‫ال‬‫او‬x2
+ bx + c ‫نوع‬ ‫من‬
( 1 ) ‫مثال‬
12 ‫العدد‬ ‫عوامل‬‫العوامل‬ ‫جمع‬
(1) (12)1+12 = 13
(2)(6)2+6=8
(3)(4)3+4=7
✓
‫العوامل‬ ‫جمع‬ 18 ‫العدد‬ ‫عوامل‬ ‫من‬
1+ 18 = 19 (1) (18)
2 + 9 = 11 (2)(9)
3 + 6 = 9 (3)(6)
-
3 + -
6 = -
9 (-3)(-6) ✓

55. 55
c) x2
+ 6x - 27
‫العوامل‬ ‫جمع‬ -27 ‫العدد‬ ‫عوامل‬
1-27=-26 (1)(-27)
27-1=26 (27)(-1)
3-9=-6 (3)(-9)
9-3=6 (9)(-3)
x2
+ 6x -27 = ( x + 9 ) ( x - 3 (
d) x2
- 3x -18
‫العوامل‬ ‫جمع‬ -18 ‫العدد‬ ‫عوامل‬
1-18=-17 (1)(-18)
18-1=17 (18)(-1)
2-9=-7 (2)(-9)
9-2=7 (9)(-2)
3-6=-3 (3)(-6)
6-3=3 (-3)(6)
x2
- 3x -18 = ( x -6 ) ( x + 3 (
✓
✓

56. 56
e) x2
- 4xy - 77y2
‫العوامل‬ ‫جمع‬ -77 ‫العدد‬ ‫عوامل‬
1-77=-76 (1)(-77)
77-1=76 (-1)(77)
11-7=4 (-7)(11)
7-11=-4 (7)(-11)
x2
- 4xy - 77y2
= ( x - 11y ) ( x + 7y (
‫الحدودية‬ ‫تحليل‬ ‫لنحاول‬
a) 6x2
+ 17x + 7
(1)(7) = 7 (1)(6)
= 6 ‫العدد‬
(2) (3)
(1)(6) (1)(7) ⇒ (1)(1) + (6)(7) = 43
(1)(6) + (7)(1) = 13
(2) (3) (1)(7) (2)(1) + (3)(7) = 23
(2)(7) + (3)(1) = 17
∴ 6x2
+ 17x + 7 = ( 2x + 1) ( 3x + 7 )
ً‫ا‬‫ثاني‬ax2
+ bx + c ، ‫نوع‬ ‫من‬
( 2 ) ‫مثال‬
⎤
⎦
3
14
‫العدد‬
✓
✓
a ≠ 0

57. 57
b) 7x2
- 26x - 8
(1)(8)
= 8 (1)(7) = 7
(2) (4)
(1)(1) - (8)(7) = -55
(1)(7) - (8)(1) = -1
(2)(1) - (4)(7) = -26
(2)(7) - (4)(1) = 10
∴ 7x2
- 26x - 8 = ( 7x + 2) ( x- 4 )
c) 3x2
- 17x + 10
(1)(10)
= 10 (1)(3) = 3
(2) (5)
(1)(1) + (10)(3) = 31
(1)(3) + (10)(1) = 13
(2)(1) + (5)(3) = 17
(2)(3) + (5)(1) = 11
∴ 3x2
- 17x + 10 = ( 3x - 2) ( x- 5)
⎤
⎦
2
-28
-2
-15 ‫عامة‬ ‫وبصورة‬
ax2
+ bx + c
( + ) ( + )
. = a . = c
. + . = b
⎤
⎦
‫العدد‬ ‫العدد‬
‫العدد‬ ‫العدد‬
✓
✓

58. 58
:‫نحلل‬ ‫ان‬ ‫نحاول‬
a) x2
- 8x + 16
(x)2
(4) 2
‫كامل‬ ‫مربع‬ ‫اي‬
∴ x2
- 8x + 16 = (x - 4)2
b) 9x2
+ 12x + 4
(3x)2
(2) 2
‫كامل‬ ‫مربع‬ ‫اي‬
∴ 9x2
+ 12x + 4 = (3x + 2)2
c) 25 - 25x + 4x2
(5)2
(2x) 2
ً‫ال‬‫كام‬ ً‫ا‬‫مربع‬ ‫ليس‬
‫الكامل‬ ‫املربع‬ ‫حتليل‬ 3 - 5
( 1 ) ‫مثال‬
-2 (x) (4) = -8x
2 (3x) (2) = 12x
-2 (2x) (5) = -20x ≠ -25x-2 (2x) (5) = -20x ≠ -25x-2 (2x) (5) = -20x ≠ -25x-2 (2x) (5) = -20x ≠ -25x

59. 59
‫عامة‬ ‫وبصورة‬
ً‫ال‬‫كام‬ ً‫ا‬‫مربع‬ ax2
+ bx + c ‫الحدودية‬ ‫تكون‬
‫كان‬+
_
2 (ax2
) (c) = bx
+ 2 (ax2
) (c) = +2 (x2
)(25) = 10x = bx
- 2 (ax2
) (c) = -2 (9x2
)(4) = -12x = bx
- 2 (ax2
) (c) = -2 (16x2
)(1) = -8x = bx
‫اذا‬
≠
‫؟‬ ً‫ال‬‫كام‬ ً‫ا‬‫مربع‬ ‫تمثل‬ ‫الحدوديات‬ ‫اي‬
a) x2
+ 10x + 25
b) 9x2
- 37x + 4
c) 16x2
- 8x + 1
d) 3x2
- 20x - 9
e) 25x2
+ 76x + 3
/ ‫احلل‬
a) ً‫ال‬‫كام‬ ً‫ا‬‫مربع‬
b) ً‫ال‬‫كام‬ ً‫ا‬‫مربع‬ ‫ليس‬
c) ً‫ال‬‫كام‬ ‫مربعا‬
d) 3x2
- 20x - 9 ً‫ا‬‫سالب‬ ‫االخير‬ ‫الحد‬ ‫ألن‬ ً‫ال‬‫كام‬ ً‫ا‬‫مربع‬ ‫ليس‬
e) 25x2
+ 76x + 3 ً‫ال‬‫كام‬ ً‫ا‬‫مربع‬ ‫ليست‬ 3 ‫ألن‬ ً‫ال‬‫كام‬ ً‫ا‬‫مربع‬ ‫ليس‬
( 2 ) ‫مثال‬
+
_
2 (ax2
) (c) = bx+
_
2 (ax2
) (c) = bx

60. 60
‫باستخدام‬ ‫المفقود‬ ‫الحد‬ ‫ايجاد‬ ‫ويمكن‬ ax2
+ bx + c ‫بصورة‬ ‫هي‬ ‫عام‬ ‫بشكل‬ ‫الثالثية‬ ‫الحدودية‬
: ‫االتي‬ ‫القانون‬
25x2
- ...... + 49 ‫الحدودية‬ ‫في‬ ‫المفقود‬ ‫الحد‬ ‫جد‬
ً‫ال‬‫كام‬ ً‫ا‬‫مربع‬ ‫لتصبح‬
/‫احلل‬
x2
+ ...... + 100y2
‫الحدودية‬ ‫في‬ ‫المفقود‬ ‫الحد‬ ‫جد‬
ً‫ال‬‫كام‬ ً‫ا‬‫مربع‬ ‫لتصبح‬
/‫احلل‬
ً‫ال‬‫كام‬ ً‫ا‬‫مربع‬ ‫لتصبح‬ ....+ 8x +16 ‫الحدودية‬ ‫في‬ ‫المفقود‬ ‫الحد‬ ‫جد‬
/‫احلل‬
- : ً‫ال‬‫كام‬ ً‫ا‬‫مربع‬ ‫لتصبح‬ ‫الثالثية‬ ‫الحدودية‬ ‫في‬ ‫المفقود‬ ‫الحد‬ ‫ايجاد‬ ]3 - 5 - 1[
bx =
_
+ 2 (ax2
)(c)
( 3 ) ‫مثال‬
bx = 2 (ax2
)(c) = 2 (ax2
)(100y2
) = 2x(10y)
= 20xy
∴ x2
+20xy +100y2
= (x +10y)2
( 4 ) ‫مثال‬
bx = 2 (ax2
)(c)
bx = 2 (25x2
)(49) = 2(5x)(7) = 70x
25x2
- 70x + 49 = (5x -7 )2
( 5 ) ‫مثال‬
∓
(
bx = 2 (ax2
) (c)
8x = 2 (ax2
) (16)
64x2
= 4 × 16 × ax2
64x2
64
= ax2
⇒ ax2
= x2
∴ x2
+ 8x + 16 = ( x + 4 )2

61. 61
ً‫ال‬‫كام‬ ً‫ا‬‫مربع‬ ‫لتصبح‬ .... -20x + 25 ‫الحدودية‬ ‫في‬ ‫المفقود‬ ‫جدالحد‬
/‫احلل‬
ً‫ال‬‫كام‬ ً‫ا‬‫مربع‬ ‫لتصبح‬ x2
+ 14x + .... ‫الحدودية‬ ‫في‬ ‫المفقود‬ ‫جدالحد‬
/‫احلل‬
9x2
- 60x + .... ‫الحدودية‬ ‫في‬ ‫المفقود‬ ‫الحد‬ ‫جد‬
ً‫ال‬‫كام‬ ً‫ا‬‫مربع‬ ‫لتصبح‬
/‫احلل‬
( 6 ) ‫مثال‬
( 7 ) ‫مثال‬
(8 ) ‫مثال‬
bx = 2 (ax2
) (c)
14x = 2 (x2
) (c)
196x2
= 4 × x2
× c
196x2
4x2
= c ⇒ c = 49
∴ x2
+ 14x + 49 = ( x + 7 )2
bx = 2 (ax2
) (c)
20x = 2 (ax2
) (25)
400x2
= 4 × 25 × ax2
ax2
=
400x2
100
⇒ ax2
= 4x2
∴ 4x2
- 20x + 25 = ( 2x - 5 )2
bx = 2 (ax2
) (c)
20x = 2 (ax2
) (25)
400x2
= 4 × 25 × ax2
ax2
=
400x2
100
⇒ ax2
= 4x2
∴ 4x2
- 20x + 25 = ( 2x - 5 )2
bx = 2 (ax2
) (c)
20x = 2 (ax2
) (25)
400x2
= 4 × 25 × ax2
ax2
=
400x2
100
⇒ ax2
= 4x2
∴ 4x2
- 20x + 25 = ( 2x - 5 )2
bx = 2 (ax2
) (c)
20x = 2 (ax2
) (25)
400x2
= 4 × 25 × ax2
ax2
=
400x2
100
⇒ ax2
= 4x2
∴ 4x2
- 20x + 25 = ( 2x - 5 )2
bx = 2 (ax2
) (c)
20x = 2 (ax2
) (25)
400x2
= 4 × 25 × ax2
ax2
=
400x2
100
⇒ ax2
= 4x2
∴ 4x2
- 20x + 25 = ( 2x - 5 )2
bx = 2 (ax2
) (c)
60x = 2 (9x2
) (c)
3600x2
= 4 × 9x2
× c
3600x2
= 36 x2
× c
c =
3600x2
36x2
⇒ c = 100
∴ 9x2
- 60x + 100 = ( 3x - 10 )2

62. 62
)LCM(‫االصغر‬‫المشترك‬‫والمضاعف‬)GCF(‫االكبر‬‫المشترك‬‫العامل‬‫ايجاد‬‫طريقة‬‫تعلمت‬‫وان‬‫سبق‬
‫الحدوديات‬ ‫تحليل‬ ‫طرق‬ ‫على‬ ‫المتوسط‬ ‫الثاني‬ ‫الصف‬ ‫وفي‬ ‫السابقة‬ ‫البنود‬ ‫في‬ ‫تعرفت‬ ‫وكذلك‬ ‫اكثر‬ ‫او‬ ‫لعددين‬
: ‫للحدوديات‬ ) LCM)،(GCF( ‫من‬ ‫كل‬ ‫ايجاد‬ ‫طريقة‬ ‫على‬ ‫سنتعرف‬ ‫البند‬ ‫هذا‬ ‫في‬
x3
- xy2
, 4x2
- 4xy , 6x2
y - 6xy2
‫االتية‬ ‫للحدوديات‬ ) LCM)،(GCF( ‫جد‬
/‫احلل‬
‫السابقة‬ ‫التحليل‬ ‫طرق‬ ‫وحسب‬ ‫حدة‬ ‫على‬ ‫حدودية‬ ‫كل‬ ‫نحلل‬
: ‫للحدوديات‬ ) LCM)،(GCF( ‫جد‬
a2
- 9 , a2
- 6a +9 , a2
- 8a + 15
/ ‫احلل‬
‫الحدوديات‬ ‫نحلل‬
3 - 6‫االكبر‬ ‫املشترك‬ ‫العامل‬
‫االصغر‬ ‫املشترك‬ ‫واملضاعف‬
)LCM( ‫االصغر‬ ‫المشترك‬ ‫والمضاعف‬ ) GCF( ‫االكبر‬ ‫المشترك‬ ‫العامل‬ ‫أيجاد‬ *
(1 ) ‫مثال‬
x3
- xy2
= x ( x2
-y2
)
= x(x -y)(x + y) ....* GCF = x( x - y )
4x2
- 4xy = (2)(2)x(x - y)....*
6x2
y - 6xy2
= (2)(2)x(x - y)....* LCM = 12xy( x - y )( x + y )
(2 ) ‫مثال‬
a2
- 9 = ( a - 3 ) ( a + 3 ) ....* GCF =( a -3 )
a2
- 6a + 9 = ( a - 3 )2
....*
a2
- 8a + 15 = ( a - 3 )( a - 5 ) ....* LCM = ( a - 3 )2 (a + 3)( a + 5)( a - 5 )
3 y x-y( ).. *
a-5( )
2

63. 63
: ‫االتية‬ ‫للحدوديات‬ ) LCM)،(GCF( ‫جد‬
2 a3
b - 2ab3
, a4
- 2a3
b +b2
a2
, 3a4
b - 3ab4
/ ‫الحل‬
) LCM)،(GCF( ‫اليجاد‬ ‫الخالصة‬
.‫الحدوديات‬ ‫نحلل‬ *
. ‫أس‬ ‫وباصغر‬ ‫فقط‬ ‫المشتركة‬ ‫العوامل‬ ‫ضرب‬ ‫حاصل‬ ‫يمثل‬ : GCF *
. ‫المشتركة‬ ‫وغير‬ ‫أس‬ ‫باكبر‬ ‫المشتركة‬ ‫العوامل‬ ‫ضرب‬ ‫حاصل‬ ‫يمثل‬ : LCM *
(3 ) ‫مثال‬
2a2
b - 2ab3
= 2ab ( a2
- b2
)
= 2ab ( a - b )( a + b ) ....*
a4
- 2a3
b + b2
a2
= a2
( a2
- 2ab + b2
)
= a2
( a - b )2
....*
a2
+ ab + b2
a2
= ( a - b )( a + 2b ) ....*
3a4
b - 3ab4
= 3ab ( a3
- b3
)
= 3ab ( a - b )( a2
+ 2ab + b2
) ....*
∴ GCF = ( a - b )
LCM = 6a2
b(a - b)2
(a + b)(a2
+ ab + b2
)
ab
3
2a2
b - 2ab3
= 2ab ( a2
- b2
)
= 2ab ( a - b )( a + b ) ....*
a4
- 2a3
b + b2
a2
= a2
( a2
- 2ab + b2
)
= a2
( a - b )2
....*
a2
+ ab + b2
a2
= ( a - b )( a + 2b ) ....*
3a4
b - 3ab4
= 3ab ( a3
- b3
)
= 3ab ( a - b )( a2
+ 2ab + b2
) ....*
∴ GCF = ( a - b )
LCM = 6a2
b(a - b)2
(a + b)(a2
+ ab + b2
)
2a2
b - 2ab3
= 2ab ( a2
- b2
)
= 2ab ( a - b )( a + b ) ....*
a4
- 2a3
b + b2
a2
= a2
( a2
- 2ab + b2
)
= a2
( a - b )2
....*
a2
+ ab + b2
a2
= ( a - b )( a + 2b ) ....*
3a4
b - 3ab4
= 3ab ( a3
- b3
)
= 3ab ( a - b )( a2
+ 2ab + b2
) ....*
∴ GCF = ( a - b )
LCM = 6a2
b(a - b)2
(a + b)(a2
+ ab + b2
)
2a2
b - 2ab3
= 2ab ( a2
- b2
)
= 2ab ( a - b )( a + b ) ....*
a4
- 2a3
b + b2
a2
= a2
( a2
- 2ab + b2
)
= a2
( a - b )2
....*
a2
+ ab + b2
a2
= ( a - b )( a + 2b ) ....*
3a4
b - 3ab4
= 3ab ( a3
- b3
)
= 3ab ( a - b )( a2
+ 2ab + b2
) ....*
∴ GCF = ( a - b )
LCM = 6a2
b(a - b)2
(a + b)(a2
+ ab + b2
)
2a2
b - 2ab3
= 2ab ( a2
- b2
)
= 2ab ( a - b )( a + b ) ....*
a4
- 2a3
b + b2
a2
= a2
( a2
- 2ab + b2
)
= a2
( a - b )2
....*
a2
+ ab + b2
a2
= ( a - b )( a + 2b ) ....*
3a4
b - 3ab4
= 3ab ( a3
- b3
)
= 3ab ( a - b )( a2
+ 2ab + b2
) ....*
∴ GCF = ( a - b )
LCM = 6a2
b(a - b)2
(a + b)(a2
+ ab + b2
)

64. 64
3 2
:‫ياتي‬ ‫مما‬ ‫كل‬ ‫حلل‬ /1 ‫س‬
. ً‫ال‬‫كام‬ ً‫ا‬‫مربع‬ ‫تمثل‬ ‫االتية‬ ‫الحدوديات‬ ‫اي‬ ‫بين‬ /2 ‫س‬
: ً‫ال‬‫كام‬ ً‫ا‬‫مربع‬ ‫لتصبح‬ ‫االتية‬ ‫الحدوديات‬ ‫اكمل‬ /3‫س‬
1) x2
+ 6x + 8
2) x2
- 2x - 15
3) x2
+ 3x + 2
4) 4x2
+ 21x + 27
5) x2
+ 11x - 80
6) 4x2
- 4x - 15
7) 6x2
- 7x - 20
8) x2
+ 20x + 100
9) 16x2
+ 8x + 1
10) 4x2
- 12x + 9
1) x2
- 18x + 81
2) x2
- 7xy + 49y2
3) 4x2
+ 25 - 12x
4) 4x2
+ 25 - 20x
5) 8x2
- 40x + 50
6) -x2
- 2xy - y2
1) ...... - 32x + 64
2) x2
- 12x + .....
3) 25x2
- ....... + 9y2
4) ...... + 24ab + 36b2
10) 4x2
- 12xy + 9y2
-

65. 65
: ‫يأتي‬ ‫مما‬ ‫لكل‬ ‫الصحيحة‬ ‫االجابة‬ ‫حدد‬ /4‫س‬
‫تساوي‬ ً‫ال‬‫كام‬ ً‫ا‬‫مربع‬ 25x2
- mx + 4 ‫الحدودية‬ ‫تجعل‬ ‫التي‬ m ‫قيمة‬ )1
a) 30 b) 20 c) 10 d) -10
: ‫هي‬ ً‫ال‬‫كام‬ ً‫ا‬‫مربع‬ y2
+ 12y - n ‫الحدودية‬ ‫تجعل‬ ‫التي‬ n ‫قيمة‬ ‫ان‬ )2
a) 36 b) -36 c) 144 ‫ذلك‬ ‫غير‬
:‫األتية‬ ‫للحدوديات‬ )GCF) , (LCM( ‫جد‬ / 5‫س‬
1)
2)
3)
4)
5)
6)
d(
5x2
-3x( )
3
, 5x2
+7x-6 , 10x2
-6x
x3
+y3
, x2
+4xy , x3
-xy2
x4
-16 , x4
+8x2
+16 , x6
+64
3x2
-3x2
y2
, 5x+5xy , x-xy-2xy2
1
2
x2
-2 , 2x2
-16 , 3x2
-x-10
x2
-y2
, x3
-y3
, x-y( )
4
7x-7y
xy, x3
-xy2
3
,

66. 66
:‫بشكل‬ ‫تكتب‬ Q ‫النسبية‬ ‫االعداد‬ ‫مجموعة‬ ‫ان‬
: ‫ان‬ ‫تعلم‬ ‫كما‬
:‫باألمثلة‬
3 - 7‫في‬ ‫التحليل‬ ‫استخدام‬
‫اجلبرية‬ ‫املقادير‬ ‫تبسيط‬
ً‫ال‬‫او‬‫النسبية‬ ‫احلدوديات‬ ‫اختصار‬
Q =
a
b
,a,b ∈ R,b ≠ 0
⎧
⎨
⎩
⎫
⎬
⎭
3
5
=
2( ) 3( )
2( ) 5( )
=
6
10
,
3
5
=
5( ) 3( )
5( ) 5( )
=
15
25
‫عامة‬ ‫وبصورة‬
‫فان‬ ً‫ا‬‫صفر‬ ‫اليساوي‬ ‫حقيقي‬ ‫عدد‬ ‫في‬ ‫والمقام‬ ‫البسط‬ ‫من‬ ‫كل‬ ‫ضرب‬ ‫اذا‬
‫التتغير‬ ‫الكسر‬ ‫قيمة‬
a
b
=
ac
bc
c ≠ 0
30
40
=
20
2
40
2
=
15
20
30
40
=
30
10
40
10
=
3
4
30
40
=
30
a
40
a
, a≠0
‫عامة‬ ‫وبصورة‬
‫قيمة‬ ‫فان‬ ً‫ا‬‫صفر‬ ‫اليساوي‬ ‫حقيقي‬ ‫عدد‬ ‫على‬ ‫والمقام‬ ‫البسط‬ ‫من‬ ‫كل‬ ‫قسم‬ ‫اذا‬
. ‫التتغير‬ ‫الكسر‬
3
5
=
a( ) 3( )
a( ) 5( )
=
3a
5a
, a≠0
30
a
b
=
a÷c
b÷c
,b,c ≠ 0
Z

67. 67
: ‫ياتي‬ ‫مما‬ ‫كال‬ ‫بسط‬
1) 6x+12
x2
-4
2) x3
-27
x3
+3x2
+ 9x
3) 2x2
-4x+2
x2
-7x+ 6
4) 2x2
- 2
3 - 3x3
/‫احلل‬
1)
2)
3)
4)
: ‫النسبية‬ ‫الحدوديات‬ ‫تبسيط‬ ‫توضح‬ ‫األتية‬ ‫االمثلة‬
(1 ) ‫مثال‬
6x+12
x2
-4
=
6 x+2( )
x+2( ) x-2( )
=
6
x-2( )
x3
-27
x3
+3x2
+ 9x
=
x-3( ) x2
+3x+9( )
x x2
+3x+9( )
=
x-3( )
x
2x2
-4x+2
x2
-7x+ 6
=
2 x2
-2x+1( )
x-6( ) x-1( )
=
2 x-1( )
2
x-6( ) x-1( )
=
2 x-1( )
x-6( )
=
2 x2
-1( )
3 1-x3
( )
=
2 x-1( ) x+1( )
-3 x3
-1( )
=
2 x-1( ) x+1( )
-3 x-1( ) x2
+x+1( )
=
2 x+1( )
-3 x2
+x+1( )
2x2
- 2
3 + 3x3
-

68. 68
. ‫النسبية‬ ‫الحدوديات‬ ‫ضرب‬
: ‫ان‬ ‫تعلم‬
: ‫ان‬ ‫اي‬
: ‫صورة‬ ‫ابسط‬ ‫في‬ ‫ضع‬
/ ‫احلل‬
: ‫صورة‬ ‫ابسط‬ ‫في‬ ‫ضع‬
/ ‫احلل‬
(2 ) ‫مثال‬
ً‫ا‬‫ثاني‬. ‫النسبية‬ ‫احلدوديات‬ ‫وقسمة‬ ‫ضرب‬
a
b
.
c
d
=
a( ) c( )
b( ) d( )
=
ac
bd
, b,d≠0
a
b
÷
c
d
=
a
b
c
d
= , b,c,d≠0
3x+2
2x+4
.
x2
+5x+6
9x2
-4
3x+2( )
2 x+2( )
.
x+3( ) x+2( )
3x+2( ) 3x-2( )
=
x+3( )
2 3x-2( )
3x+2
2x+4
.
x2
+5x+6
9x2
-4
(3 ) ‫مثال‬
x2
+3x+2
x2
+4x+4
÷
5x2
+5x
x2
-4
x2
+3x+2
x2
+4x+4
÷
5x2
+5x
x2
-4
x+2( ) x+1( )
x+2( )
2
÷
5x x+1( )
x-2( ) x+2( )
a
b
÷
c
d
=
a
b
.
d
c
=
=

69. 69
: ‫صورة‬ ‫ابسط‬ ‫في‬ ‫ضع‬
/ ‫احلل‬
: ‫صورة‬ ‫ابسط‬ ‫في‬ ‫ضع‬
/ ‫احلل‬
( 4 ) ‫مثال‬
x2
-25
x3
-125
÷
x2
+10x+25
x2
+x-20
( 5 ) ‫مثال‬
x2
+2x+1( )÷
x+1( )
3
x3
+1
x2
-25
x3
-125
÷
x2
+10x+25
x2
+x-20
x+5( ) x-5( )
x-5( ) x2
+5x+25( )
÷
x+5( )
2
x+5( ) x-4( )
x+5( ) x-5( )
x-5( ) x2
+5x+25( )
.
x+5( ) x-4( )
x+5( )
2
=
x-4( )
x2
+5x+25( )
x+2( ) x+1( )
x+2( )
2
.
x-2( ) x+2( )
5x x+1( )
=
x-2( )
5x
=
=
=
x2
+2x+1( )÷
x+1( )
3
x3
+1
x+1( )
2
1
÷
x+1( )
3
x+1( ) x2
-x+1( )
x+1( )
2
1
.
x+1( ) x2
-x+1( )
x+1( )
3
= x2
-x+1( )
=
=

70. 70
) LCM( ‫االصغر‬ ‫المشترك‬ ‫المضاعف‬ ‫نجد‬ ‫ان‬ ‫يجب‬ ، ‫النسبية‬ ‫الحدوديات‬ ‫طرح‬ ‫او‬ ‫جمع‬ ‫ناتج‬ ‫اليجاد‬
‫ذلك‬ ‫توضح‬ ‫اآلتية‬ ‫واالمثلة‬ ‫السابقة‬ ‫الطرائق‬ ‫وحسب‬ ‫بالتحليل‬ ‫وذلك‬ ‫الحدوديات‬ ‫لمقامات‬
: ‫صورة‬ ‫ابسط‬ ‫في‬ ‫ضع‬
/‫احلل‬
: ‫صورة‬ ‫ابسط‬ ‫في‬ ‫ضع‬
/‫احلل‬
ً‫ا‬‫ثالث‬. ‫النسبية‬ ‫احلدوديات‬ ‫وطرح‬ ‫جمع‬
( 6 ) ‫مثال‬
2
x2
-9
+
3
x2
-4x+3
2
x2
-9
+
3
x2
-4x+3
2
x-3( ) x+3( )
+
3
x-1( ) x-3( )
, LCM= x-3( ) x+3( ) x-1( )
2 x-1( )
x-3( ) x+3( ) x-1( )
+
3 x+3( )
x-3( ) x+3( ) x-1( )
2x-2+3x+9
x-3( ) x+3( ) x-1( )
5x+7
x-3( ) x+3( ) x-1( )
( 7 ) ‫مثال‬
2 x3
-64( )
x x2
+4x+16( )
-
x-1
x
2 x-4( ) x2
+4x+16( )
x x2
+4x+16( )
-
x-1( )
x
2 x-4( )
x
-
x-1( )
x
⇒
2 x-4( )- x-1( )
x
2x-8-x+1
x
⇒
x-7
x
⇒
2x3
-128
x3
+4x2
+16x
-
x-1
x
2x3
-128
x3
+4x2
+16x
-
x-1
x
=
=
=

71. 71
3 3
: ‫ياتي‬ ‫مما‬ ‫كال‬ ‫بسط‬ /1‫س‬
1) 2) x2
-y2
x2
-xy-2y2
3) 4)
: ‫صورة‬ ‫ابسط‬ ‫في‬ ‫ياتي‬ ‫مما‬ ‫كل‬ ‫ناجت‬ ‫جد‬ /2‫س‬
1) 2)
3) 4)
5) 6)
7) 8)
9) 10)
x3
+8
x3
-2x2
+4x
12-4x
x2
-2x-3
x 2x-1( )-1
x x-1( )
x2
+7x-8
x-1
.
x2
-4
x2
+6x-16
x2
+9x+20
x2
+5x-24
÷
x2
+15x+56
x2
+x-12
x2
+x+1
x4
-x
-
x+3
x2
+2x-3
x2
+4x-21
x2
+14x+49
÷
x-7
2x2
-98
x2
-2xy+y2
x-y
.
x+y
x-y
⎛
⎝
⎜
⎞
⎠
⎟÷
x2
-y2
x2
⎛
⎝
⎜
⎞
⎠
⎟x2
-xy-2y2
( )÷
x2
-y2
x2
-2xy+y2
. x3
-8y3
( )
⎛
⎝
⎜
⎞
⎠
⎟
3
x-1
+
2
x+1
+
4
x2
+2x-3
x-3
x-1
+
5x-15
x-3( )
2
-
3x+1
x2
-4x+3
x3
+27
x+3
÷
x3
-3x2
+9x
x2
⎛
⎝
⎜
⎞
⎠
⎟÷x
4x2
-1
4x2
-4x+1
+1
8
3

72. ‫املتباينات‬
Inequalities
‫الرياضية‬ ‫اجلمل‬ ]4-1[
‫اخلطية‬ ‫املتباينة‬ ]4-2[
‫مبتغيرين‬ ‫األولى‬ ‫الدرجة‬ ‫من‬ ‫املعادلة‬ ]4-3[
‫آنيا‬ ‫مبتغيرين‬ ‫األولى‬ ‫الدرجة‬ ‫من‬ ‫معادلتني‬ ‫حل‬ ]4-4[
‫واحد‬ ‫مبتغير‬ ‫الثانية‬ ‫الدرجة‬ ‫من‬ ‫املعادلة‬ ]4-5[
‫الكسرية‬ ‫املعادالت‬ ]4-6[
g
x()
a
b≤
f
x()≤
a
f
x()
d
‫الرياضية‬ ‫العالقة‬ ‫او‬ ‫الرمز‬ ‫المصطلح‬
‫متباينة‬
‫مزدوجة‬ ‫متباينة‬
T ‫صائبة‬
F ‫خاطئة‬
a,b ∈ R a b،
d f x( ) c
4‫الرابع‬ ‫الفصل‬

73. ‫المقدمة‬
‫لغوي‬ ‫منطق‬ ‫بالحقيقة‬ ‫هو‬ ‫والذي‬ ‫الرياضي‬ ‫المنطق‬ ‫موضوع‬ ‫في‬ ‫معرفة‬ ‫يتطلب‬ ‫الرياضية‬ ‫الجمل‬ ‫دراسة‬ ‫إن‬
:‫اآلتية‬ ‫الجمل‬ ‫في‬ ‫النظر‬ ‫أمعنا‬ ‫لو‬ ،‫الرياضيات‬ ‫لعلوم‬
. 5= 25 )4( ‫سالب‬ ‫صحيح‬ ‫عدد‬ ‫أكبر‬ -1 )3( 3 4 )2( ‫العراق‬ ‫عاصمة‬ ‫بغداد‬ )1(
‫أن‬ ‫يمكن‬ ‫وال‬ ،‫فقط‬ ‫خاطئة‬ ‫أو‬ ‫صائبة‬ ‫إما‬ ‫منها‬ ً‫ال‬‫ك‬ ‫أن‬ ‫وهو‬ ‫محدد‬ ‫معنى‬ ‫لها‬ ‫خبرية‬ ‫جملة‬ ‫منها‬ ً‫ال‬‫ك‬ ‫أن‬ ‫نالحظ‬
‫أخرى‬ ‫لقيم‬ ‫وخاطئة‬ ‫قيم‬ ‫لمجموعة‬ ‫صائبة‬ ‫فهي‬ ) 2x-1 = 0 ( ‫في‬ ‫كما‬ ً‫ا‬‫مع‬ ‫والخطأ‬ ‫الصواب‬ ‫تقبل‬
. ‫المعادالت‬ ‫موضوع‬ ‫في‬ ‫تعلمنا‬ ‫كما‬ ‫التعويض‬ ‫مجموعة‬ ‫على‬ ً‫ا‬‫إعتماد‬
‫وخاطئة‬ ‫صائبة‬ ‫تكون‬ ‫أن‬ ‫يمكن‬ ‫وال‬ ‫خاطئة‬ ‫أو‬ ‫صائبة‬ ‫إما‬ ‫محدد‬ ‫معنى‬ ‫ذات‬ ‫خبرية‬ ‫جملة‬ ‫هي‬ ‫العبارة‬
.‫واحد‬ ‫آن‬ ‫في‬
‫العبارة‬ ً‫ال‬‫مث‬ » ‫ليس‬ « ‫النفي‬ ‫أداة‬ ‫نستخدم‬ ‫اللغة‬ ‫في‬ :‫العبارات‬ ‫نفي‬
‫فاذا‬ 4 5 ‫بالرموز‬ ‫أو‬ 4 ‫من‬ ‫أكبر‬ ‫ليس‬ 5 ‫نفيها‬ ‫يكون‬ 4 5
‫صائبة‬ P ‫كانت‬ ‫وإذا‬ ، P ‫نفي‬ ‫هو‬ P( ) ‫فأن‬ ‫عبارة‬ P ‫كانت‬
. ‫الجدول‬ ‫في‬ ‫كما‬ ‫صحيح‬ ‫والعكس‬ ‫خاطئة‬ ‫نفيها‬ ‫فأن‬
∼
‫أمثلة‬
P∼ P
(1)
(2)
(3)
(4)
‫أولي‬ ً‫ا‬‫عدد‬ 2ً‫ا‬‫أولي‬ ‫ليس‬ ً‫ا‬‫عدد‬ 2
-3 ∈ N-3 ∉ N
5 ∉ Q5 ∈ Q
1
2
1
4
1
2
1
4
‫الفصل‬
4
4 - 1 ‫الرياضية‬ ‫الجمل‬
Statement ‫العبارة‬
P P
F T
T F
F T
F T
∼
P P
T F
F T
∼
: ]4-1[ ‫تعريف‬
1
2
⎧
⎨
⎩
⎫
⎬
⎭

74. ‫المركبة‬ ‫والعبارات‬ ‫الربط‬ ‫أدوات‬
) ∧ “ ‫و‬ ( ، ) ∨ “ ‫أو‬ ( : ‫الربط‬ ‫ألداتي‬ ‫المرحلة‬ ‫هذه‬ ‫في‬ ‫نتطرق‬ ‫سوف‬
.‫أولي‬ ‫غير‬ ‫عدد‬ 9 ‫أو‬ ‫نسبي‬ ‫غير‬ ‫عدد‬ 2 1
.‫مستطيل‬ ‫المربع‬ ‫و‬
180o
‫المثلث‬ ‫زوايا‬ ‫مجموع‬ 2
27 = −3( )
3
‫و‬ ‫متناصفان‬ ‫المعين‬ ‫قطرا‬ 3
.‫مركبة‬ ‫جملة‬ ‫تسمى‬ ‫جديدة‬ ‫جملة‬ ‫على‬ ‫للحصول‬ ‫و‬ ‫واألداة‬ ‫أو‬ ‫األداة‬ ‫أستخدمنا‬ ‫أننا‬ ‫الحظ‬
.‫خاطئة‬ ‫العبارتين‬ ‫كلتا‬ ‫تكون‬ ‫عندما‬ ‫فقط‬ ‫خاطئة‬ ‫أو‬ ‫باألداة‬ ‫جملتين‬ ‫ربط‬ ‫من‬ ‫الناتجة‬ ‫المركبة‬ ‫الجملة‬ ‫*تكون‬
،‫صائبة‬ ‫العبارتين‬ ‫كلتا‬ ‫تكون‬ ‫عندما‬ ‫فقط‬ ‫صائبة‬ ‫و‬ ‫باألداة‬ ‫جملتين‬ ‫ربط‬ ‫من‬ ‫الناتجة‬ ‫المركبة‬ ‫الجملة‬ ‫تكون‬ *
:‫اآلتية‬ ‫الجداول‬ ‫في‬ ‫كما‬
P1 ∨ P2
P2
P1P1 ∧ P2
P2
P1
TTTTTT
TFTFFT
TTFFTF
FFFFFF
. ‫صائبة‬ ‫عبارة‬ 1 :‫المثال‬ ‫ففي‬
. ‫صائبة‬ ‫عبارة‬ 2
. ‫خاطئة‬ ‫عبارة‬ 3
““
‫أمثلة‬
.‫جبريين‬ ‫تعبيرين‬ ‫بين‬ ‫التباين‬ ‫رموز‬ ‫أحد‬ ‫وضع‬ ‫من‬ ‫تتكون‬ ‫خبرية‬ ‫جملة‬ :‫المتباينة‬
: ]4-2[ ‫تعريف‬
T T = T
T T = T
T F = F
∧
∧
∨

75. 75
‫املعنى‬ ‫الرمز‬
‫من‬ ‫أكبر‬
‫من‬ ‫أصغر‬
‫يساوي‬ ‫أو‬ ‫أصغر‬ ≤
‫يساوي‬ ‫أو‬ ‫أكبر‬ ≥
‫يساوي‬ ‫ال‬ ≠
:ً‫ال‬‫فمث‬
2x - 1 5 , x + 3 ≤ 2 , 2 ≤ 3x - 4 5 , x2
- x 0
. 5x2
- 3x +1 ≤ 6 , 15 8 , 3 ≠ 5
‫فصل‬ ‫في‬ ‫درسنا‬ ‫وكما‬ .‫واحد‬ ‫متغير‬ ‫في‬ ‫األولى‬ ‫الدرجة‬ ‫من‬ ‫المتباينة‬ ‫المرحلةعلى‬ ‫هذه‬ ‫في‬ ‫دراستنا‬ ‫وستقتصر‬
. a - b 0 ‫أنه‬ ‫أي‬ ‫األعداد‬ ‫مستقيم‬ ‫على‬ b ‫يمين‬ ‫يقع‬ a ‫فأن‬ ) a b( ‫أن‬ ‫الحقيقية‬ ‫األعداد‬
ً‫ال‬‫فمث‬
:‫بشكل‬ ‫األعداد‬ ‫مستقيم‬ ‫على‬ ‫تمثل‬ )‫نفسه‬ 3 ‫(عدا‬ )3( ‫العدد‬ ‫يسار‬ ‫األعداد‬ )1(
. 3 ‫من‬ ‫أصغر‬ x ‫وتقرأ‬ ) x 3( ‫وتكتب‬
:‫بشكل‬ ‫األعداد‬ ‫مستقيم‬ ‫على‬ ‫تمثل‬ ‫نفسه‬ 1 ‫العدد‬ ‫عدا‬ )1( ‫العدد‬ ‫يمين‬ ‫األعداد‬ )2(
. 1 ‫من‬ ‫أكبر‬ x ‫وتقرأ‬ ) x 1( ‫وتكتب‬
:‫بشكل‬ ‫األعداد‬ ‫مستقيم‬ ‫على‬ ‫تمثل‬ )-3( ‫ضمنها‬ ‫ومن‬ )-3( ‫العدد‬ ‫يمين‬ ‫األعداد‬ )3(
. -3 ‫تساوي‬ ‫أو‬ ‫من‬ ‫أكبر‬ x ‫وتقرأ‬ ) x ≥ -3( ‫وتكتب‬
:‫بشكل‬ ‫تمثل‬ )2( ‫ضمنها‬ ‫ومن‬ )2( ‫يسار‬ ‫على‬ ‫األعداد‬ )4(
. 2 ‫يساوي‬ ‫أو‬ ‫من‬ ‫أصغر‬ x ‫وتقرأ‬ ) x ≤ 2( ‫وتكتب‬
3
1
-3
2

76. 76
)‫األولى‬ ‫الدرجة‬ ‫(من‬ ‫اخلطية‬ ‫املتباينة‬
‫الواحد‬ ‫املتغير‬ ‫ذات‬
4 - 2
ax + b 0
a , b , c ∈ R
a+c b+c
:‫اآلتية‬ ‫األشكال‬ ‫أحد‬ ‫تأخذ‬ ‫عالقة‬ ‫هي‬
. a ≠ 0 ‫حيث‬ ، ax + b 0 ، ax + b ≤ 0 ‫أو‬ ax + b ≥ 0
)16 5 ‫و‬ -3 4 ( ‫كذلك‬ ‫صائبة‬ ‫رياضية‬ ‫جمل‬ ‫هي‬ )2 ≠ 4 ‫أو‬ 7 3 ً‫ال‬‫(مث‬ ‫المتباينات‬ ‫بعض‬
. ‫معلومة‬ ‫تعويض‬ ‫مجموعة‬ ‫ضمن‬ ‫فيها‬ ‫المتغير‬ ‫لقيم‬ ‫صائبة‬ ‫تكون‬ ‫قد‬ ‫األولى‬ ‫المتباينات‬ ‫لكن‬ ، ‫خاطئة‬
ً‫ال‬‫مث‬
‫مجموعة‬ ‫فأن‬ ‫لذا‬ I = { 0 , 1 , 2 , 3 {‫هي‬ ‫التعويض‬ ‫مجموعة‬ ‫وكانت‬ 2x + 3 ≤ 8 :‫المتباينة‬ ‫أخذنا‬ ‫لو‬
. ‫صائبة‬ ‫العبارة‬ ‫تجعل‬ ‫التي‬ x ‫قيم‬ ‫اي‬ s = { 0 , 1 , 2 { ‫الحل‬
x ∈ I 2x + 3 ≤8 ‫املتباينة‬ ‫الصواب‬ ‫قيمة‬
0 0 + 3 ≤ 8 T
1 (2) (1) + 3 ≤ 8 T
2 (2)(2) + 3 ≤ 8 T
3 (2)(3) + 3 ≤ 8 F
: ‫فأن‬ ‫كانت‬ ‫إذا‬
‫التعدي‬ ‫خاصية‬ ........ a c ‫فأن‬ a b ‫و‬ b c ‫كانت‬ ‫اذا‬ )1(
‫الجمع‬ ‫خاصية‬ ........ ‫فأن‬ a b ‫كانت‬ ‫اذا‬ )2(
3 + 2 4 + 2 ‫فأن‬ c = 2 ، 3 4 ‫كان‬ ‫اذا‬
. ‫يتغير‬ ‫ال‬ ‫الترتيب‬ ‫فأن‬ ‫المتباينة‬ ‫طرفي‬ ‫الى‬ ‫متساوية‬ ‫اعداد‬ ‫إضافة‬ ‫عند‬ ‫أن‬ ‫أي‬
‫المتباينة‬ ‫حل‬ ‫مجموعة‬ ]4 - 2 - 1[
‫المتباينات‬ ‫خواص‬ ]4 - 2 - 2[

77. 77
2 -3 4 - 3
4
2
6
2
a
b
b
cc
a
c
b
c
8
-2
10
-2
‫الطرح‬ ‫خاصية‬ ....... a - c b - c : ‫فأن‬ a b ‫كانت‬ ‫اذا‬ )3(
، c = 3 ، 2 4 ‫كان‬ ‫اذا‬
:‫فأن‬ ‫موجب‬ ‫عدد‬ c , a b ‫كانت‬ ‫اذا‬ )4(
a c b c
.‫الترتيب‬ ‫بنفس‬ ‫صائبة‬ ‫تبقى‬ ‫فأنها‬ ‫موجب‬ ‫بعدد‬ ‫متباينة‬ ‫طرفي‬ ‫ضرب‬ ‫عند‬ ‫انه‬ ‫أي‬
)3()-3( )3( )2( ‫فأن‬ ، c = 3 ، -3 2
-9 6 ‫اي‬
:‫فأن‬ ‫سالب‬ ‫عدد‬ c , a b ‫كانت‬ ‫اذا‬ )5(
a c b c
:‫فأن‬ c = -2 , -2 5 ‫كان‬ ‫اذا‬
)-2( )-2( )-2( )5(
4 -10 ‫اي‬
.‫الترتيب‬ ‫بعكس‬ ‫صائبة‬ ‫المتباينة‬ ‫فأن‬ ‫سالب‬ ‫بعدد‬ ‫متباينة‬ ‫طرفي‬ ‫ضرب‬ ‫عند‬
:‫فأن‬ ‫موجب‬ ‫عدد‬ c ، a b ‫كانت‬ ‫اذا‬ )6(
2 3 ‫اي‬ ‫فأن‬ c = 2 ، 4 6 ‫كان‬ ‫اذا‬
‫الترتيب‬ ‫بنفس‬ ‫صائبة‬ ‫فأنها‬ ‫موجب‬ ‫عدد‬ ‫على‬ ‫متباينة‬ ‫طرفي‬ ‫قسمة‬ ‫عند‬
:‫فأن‬ ‫سالب‬ ‫عدد‬ c ، a b ‫كانت‬ ‫اذا‬ )7(
-4 -5 ‫اي‬ ‫فأن‬ c = -2 ، 8 10 ‫كان‬ ‫اذا‬ ،
. ‫الترتيب‬ ‫بعكس‬ ‫صائبة‬ ‫فأنها‬ ‫سالب‬ ‫عدد‬ ‫على‬ ‫متباينة‬ ‫طرفي‬ ‫قسمة‬ ‫عند‬
.) , , ≥ , ≤ , ≠( ‫التباين‬ ‫رموز‬ ‫لكل‬ ‫صحيحة‬ ‫المتباينات‬ ‫خواص‬ ‫بأن‬ ‫نذكر‬

78. 78
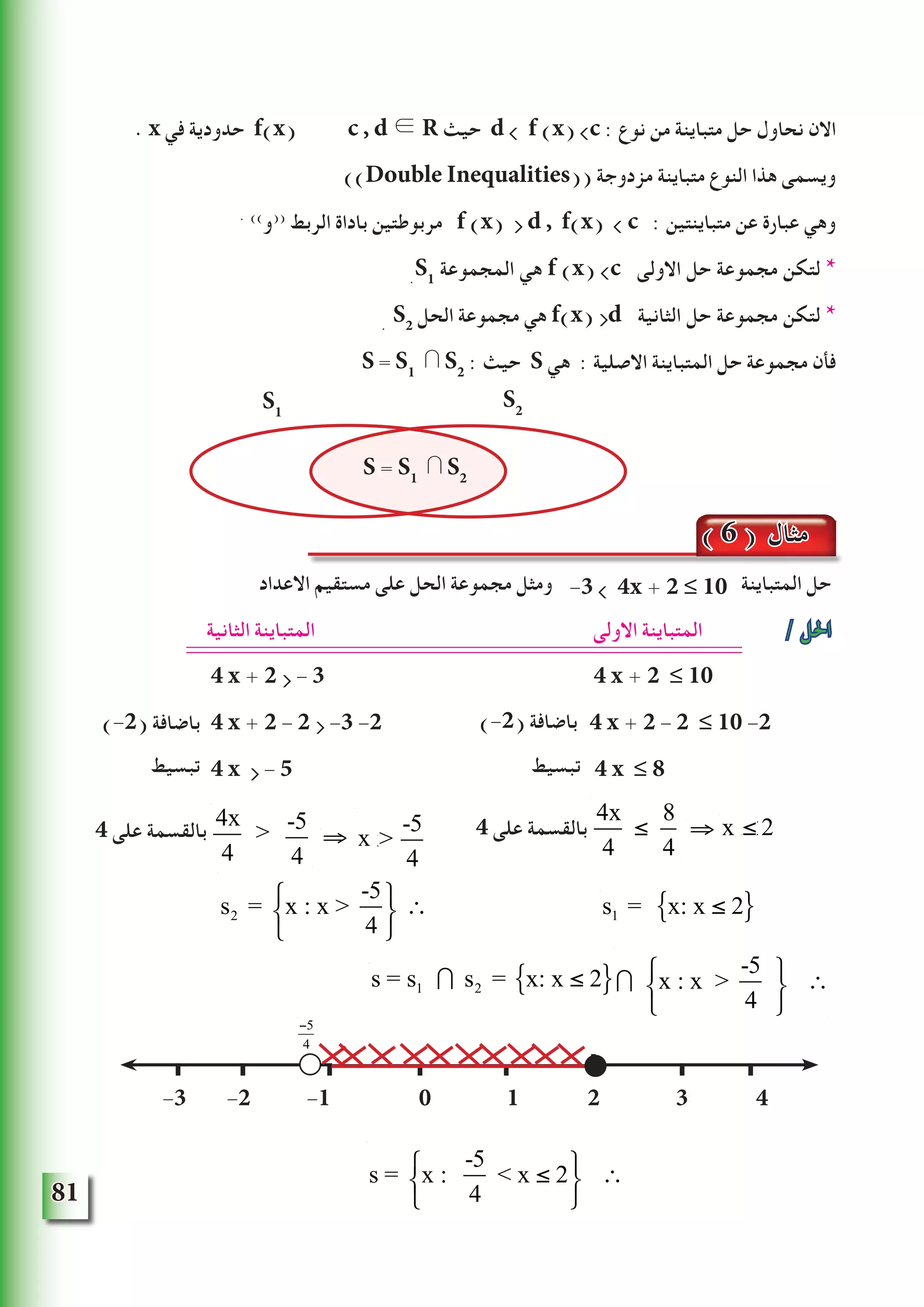
4x - 5 3 ( x - 2 ) - 1 ‫األعداد‬ ‫مستقيم‬ ‫على‬ ‫الحل‬ ‫مجموعة‬ ‫ومثل‬ ‫اآلتية‬ ‫المتباينة‬ ‫حل‬
/‫الحل‬
4x - 5 3 ( x - 2 ) - 1 ‫المتباينة‬
4x - 5 3 x - 7 ‫توزيع‬
4x - 5 -3x 3 x - 7 - 3x ‫للطرفين‬ ‫اضافة‬
x - 5 - 7
x - 5 + 5 - 7 + 5 ‫للطرفين‬ )5( ‫اضافة‬
∴ x -2
{x : x -2 } = ‫الحل‬ ‫مجموعة‬ ∴
-4(x - 2) 5 - 5 ( x - 1 ) ‫االعداد‬ ‫مستقيم‬ ‫على‬ ‫الحل‬ ‫مجموعة‬ ‫ومثل‬ ‫المتباينة‬ ‫حل‬
/‫الحل‬
-4(x - 2) 5 - 5 ( x - 1 ) ‫المتباينة‬
-4x + 8 5 - 5 x + 5 ‫االقواس‬ ‫ازالة‬
-4x + 8 10 - 5 x
-4x + 5x + 8 10 - 5 x + 5x ‫للطرفين‬ ‫اضافة‬
‫قيم‬ ‫مجموعة‬ ‫هي‬ x ‫في‬ ‫حدودية‬ ، m ∈ R ‫حيث‬ f(x) m : ‫المتباينة‬ ‫حل‬ ‫مجموعة‬
. ‫صائبة‬ ‫المتباينة‬ ‫تجعل‬ ‫التي‬ x ‫المتغير‬
f (x)
( 1 ) ‫مثال‬
-2-3-4-5 -1 0 1
( 2 ) ‫مثال‬
: ]4-3[ ‫تعريف‬
(-3x)
(5x)

79. 79
x + 8 10
x + 8 -8 10 - 8 ‫للطرفين‬ )-8(‫اضافة‬
∴ x 2
{x : x 2 } = ‫الحل‬ ‫مجموعة‬ ∴
‫االعداد‬ ‫مستقيم‬ ‫على‬ ‫ومثل‬ ‫المتباينة‬ ‫حل‬
/‫الحل‬
‫المتباينة‬
-5 ‫في‬ ‫المتباينة‬ ‫طرفي‬ ‫بضرب‬ )) ‫المتباينة‬ ‫اتجاه‬ ‫تغير‬ ‫((الحظ‬
. ‫للطرفين‬ )5x( ‫اضافة‬
‫للطرفين‬ )-3( ‫باضافة‬
3 ‫على‬ ‫بالقسمة‬
‫الحل‬ ‫مجموعة‬
2 3 4 5-1 0 1
( 3 ) ‫مثال‬
-2x + 3
-5
≤ x +1
-5
-2x + 3
-5
⎛
⎝
⎜
⎞
⎠
⎟ ≥ -5(x + 1 )
-2x + 3 ≥ -5x -5
3x + 3 - 3 ≥ -5 -3
3x ≥ -8
3x
3
≥
-8
3
∴ x ≥
-8
3
∴ s = x : x ≥ -2
2
3
⎧
⎨
⎩
⎫
⎬
⎭
-2x + 3
-5
≤ x +1
-2-3 2 3-1 0 1
-2
2
3
≥-5x-5
-5
-2x + 3
-5
⎛
⎝
⎜
⎞
⎠
⎟ ≥ -5(x + 1 )
-2x + 3 ≥ -5x -5
3x + 3 - 3 ≥ -5 -3
3x ≥ -8
3x
3
≥
-8
3
∴ x ≥
-8
3
∴ s = x : x ≥ -2
2
3
⎧
⎨
⎩
⎫
⎬
⎭
−2x + 3+ 5x ≥ −5x − 5 + 5x

80. 80
‫االعداد‬ ‫مستقيم‬ ‫على‬ ‫الحل‬ ‫مجموعة‬ ‫ومثل‬ ‫المتباينة‬ ‫حل‬
/‫الحل‬
‫المتباينة‬
4 ‫في‬ ‫المتباينة‬ ‫طرفي‬ ‫بضرب‬
‫الطرفين‬ ‫تبسيط‬
‫للطرفين‬ )-y( ‫باضافة‬
. } y : y -7 { = ‫الحل‬ ‫مجموعة‬ ∴
‫االعداد‬ ‫مستقيم‬ ‫على‬ ‫الحل‬ ‫مجموعة‬ ‫ومثل‬ ) -u ≠ -7 ( ‫المتباينة‬ ‫حل‬
-u ≠ -7 ‫المتباينة‬ /‫الحل‬
)-1( ‫على‬ ‫القسمة‬ ‫ويمكن‬ ..... )-1( ‫في‬ ‫الطرفين‬ ‫نضرب‬
‫الطرفين‬ ‫تبسيط‬
R-{7} = { u : u ≠ 7 { = ‫الحل‬ ‫مجموعة‬ ∴
( 4 ) ‫مثال‬
y - 3
4
-
y
2
y - 3
4
- 1
y
2
4
y - 3
4
⎛
⎝
⎜
⎞
⎠
⎟ - 4 (1) 4
y
2
⎛
⎝
⎜
⎞
⎠
⎟
y - 3 - 4 2y
y - 7 2y
y - 7 - y 2y - y
- 7 y
y -7
-2-3-4-5 -1 0-6-7-8-9
( 5 ) ‫مثال‬
(-1)(-u) ≠ (-1)(-7)
u ≠ 7
-1
-2-3 4 5-1 0 6 7 8 91 2 3

81. 81
. x ‫في‬ ‫حدودية‬ f(x) c , d ∈ R ‫حيث‬ d f (x) c : ‫نوع‬ ‫من‬ ‫متباينة‬ ‫حل‬ ‫نحاول‬ ‫االن‬
))Double Inequalities(( ‫مزدوجة‬ ‫متباينة‬ ‫النوع‬ ‫هذا‬ ‫ويسمى‬
. ))
‫و‬((
‫الربط‬ ‫باداة‬ ‫مربوطتين‬ f (x) d , f(x) c : ‫متباينتين‬ ‫عن‬ ‫عبارة‬ ‫وهي‬
.
S1
‫المجموعة‬ ‫هي‬ f (x) c ‫االولى‬ ‫حل‬ ‫مجموعة‬ ‫لتكن‬ *
.
S2
‫الحل‬ ‫مجموعة‬ ‫هي‬ f(x) d ‫الثانية‬ ‫حل‬ ‫مجموعة‬ ‫لتكن‬ *
S = S1
∩S2
: ‫حيث‬ S ‫هي‬ : ‫االصلية‬ ‫المتباينة‬ ‫حل‬ ‫مجموعة‬ ‫فأن‬
‫االعداد‬ ‫مستقيم‬ ‫على‬ ‫الحل‬ ‫مجموعة‬ ‫ومثل‬ ‫المتباينة‬ ‫حل‬
‫الثانية‬ ‫المتباينة‬ ‫االولى‬ ‫المتباينة‬ / ‫احلل‬
4 x + 2 - 3 4 x + 2 ≤ 10
4 x + 2 - 2 -3 -2 4 x + 2 - 2 ≤ 10 -2
4 x - 5 4 x ≤ 8
S = S1
∩S2
S1
S2
( 6 ) ‫مثال‬
-3 4x + 2 ≤ 10
10-1-2 2 3-3 4
−5
4
)-2( ‫باضافة‬ )-2( ‫باضافة‬
‫تبسيط‬ ‫تبسيط‬
⇒
4x
4
-5
4
4x
4
-5
4
4x
4
-5
4
x
-5
4
x
-5
4
x
-5
4
⇒
4x
4
≤
8
4
4x
4
≤
8
4
4x
4
≤
8
4
x≤2x≤2x≤24 ‫على‬ ‫بالقسمة‬4 ‫على‬ ‫بالقسمة‬
s2 = x : x
-5
4
⎧
⎨
⎩
⎫
⎬
⎭
∴ s1 = x: x ≤ 2{ }
s = x :
-5
4
x ≤ 2
⎧
⎨
⎩
⎫
⎬
⎭
∴
s = s1 I s2 = x: x ≤ 2{ }
I x : x
-5
4
⎧
⎨
⎩
⎫
⎬
⎭
∴

82. 82
. ‫االعداد‬ ‫مستقيم‬ ‫على‬ ‫الحل‬ ‫مجموعة‬ ‫ومثل‬ ‫المتباينة‬ ‫حل‬
/‫احلل‬
:‫السابق‬ ‫المثال‬ ‫في‬ ‫كما‬ ‫التجزئة‬ ‫الى‬ ‫الحاجة‬ ‫دون‬ ‫المتباينة‬ ‫حل‬ ‫يمكن‬
‫االصلية‬ ‫المتباينة‬
‫المتباينة‬ ‫طرفي‬ ‫الى‬ )-1( ‫باضافة‬
‫تبسيط‬
‫الترتيب‬ ‫تغير‬ ‫مراعاة‬ ‫مع‬ )-2( ‫على‬ ‫بالقسمة‬
‫ذلك‬ ‫ليكون‬ ‫اليسار‬ ‫الى‬ ‫االصغر‬ ‫العدد‬ ‫يكون‬ ‫ان‬ ‫المزدوجة‬ ‫المتباينة‬ ‫حلول‬ ‫مجموعة‬ ‫كتابة‬ ‫في‬ ‫يفضل‬
: ‫ان‬ ‫اي‬ ‫االعداد‬ ‫مستقيم‬ ‫على‬ ‫الترتيب‬ ‫خاصية‬ ‫مع‬ ً‫ا‬‫متناسق‬
35 ، 17 ‫بين‬ ‫يقع‬ ‫الناتج‬ ‫فان‬ )5( ‫امثالها‬ ‫ثالثة‬ ‫الى‬ ‫اضيفت‬ ‫اذا‬ ‫التي‬ ‫الصحيحة‬ ‫االعداد‬ ‫هي‬ ‫ما‬
/ ‫احلل‬
y = ‫الصحيحة‬ ‫االعداد‬ ‫احد‬ ‫نفرض‬
‫الجبرية‬ ‫بالصورة‬ ‫المسألة‬ ‫تصبح‬ ً‫ا‬‫اذ‬
(-5(‫باضافة‬
‫التباين‬ ‫ترتيب‬ ‫على‬ ‫المحافظة‬ ‫(3)مع‬ ‫على‬ ‫بالقسمة‬
5 , 6 , 7 , 8 , 9 ‫هي‬ ‫المسألة‬ ‫تحقق‬ ‫التي‬ ‫الصحيحة‬ ‫االعداد‬ ∴
( 7 ) ‫مثال‬
( 8 ) ‫مثال‬
31-2y≤10
31-2y≤10
3-11-2y-1≤10-1
2-2y≤9
2
-2
-2y
-2
≥
9
-2
-1y≥
-9
2
s = y :
−9
2
≤ y −1
⎧
⎨
⎩
⎫
⎬
⎭
17 3y+5 35
17 - 5 3y+5 - 5 35 - 5
12 3y 30
12
3
3y
3
30
3
4 y 10
. ‫الطريقة‬ ‫هذه‬ ‫بنفس‬ )6( ‫مثال‬ ‫حل‬ ‫تدريب‬
-2-3-4-5 -1 0
-9
2

83. 83
: ‫اآلتية‬ ‫العبارات‬ ‫من‬ ‫كل‬ ‫صحة‬ ‫في‬ ‫أبحث‬ /1‫س‬
.‫أولي‬ ‫عدد‬ 7 ‫و‬ −2( )
3
= −8 )1
.‫األعداد‬ ‫خط‬ ‫على‬ -2 ‫يمين‬ ‫على‬ ‫يقع‬ −3( ) ‫أو‬ 15 = 5. 3 )2
.‫مربع‬ ‫مستطيل‬ ‫كل‬ ‫و‬
60o
‫األضالع‬ ‫المتساوي‬ ‫المثلث‬ ‫في‬ ‫زاوية‬ ‫كل‬ ‫قياس‬ )3
. 6 = 2 + 3 ‫أو‬ ‫نسبي‬ ‫غير‬ ‫عدد‬ ‫الصفر‬ )4
.
6
6
= 6 ‫و‬ −643
= −4 )5
. ‫االعداد‬ ‫مستقيم‬ ‫على‬ ‫الحل‬ ‫مجموعة‬ ‫ومثل‬ ‫االتية‬ ‫المتباينات‬ ‫من‬ ‫كال‬ ‫حل‬ /2‫س‬
(1) 2x+3≤9 (2) 5-2y4 (3) 3Z+517 (4) 9≤5-3t
(5) 3k+5
2
4 (6) 2p-5
-3
≤2
(7) 2 2p-1( )≤6- p+8( )
(8) 1
3
t+
7
12
1
2
t+
3
4
(9) -10≤2b-3≤9 (10) -4
3m+2
2
5
(11) -1
3
y≠
1
2
(12) 2 p-1( )-32p+3 (13)
/ 3‫س‬
‫معدل‬ ‫على‬ ‫الحصول‬ ‫يريد‬ ‫وكان‬ )66( ‫االول‬ ‫الشهر‬ ‫في‬ ‫الرياضيات‬ ‫امتحان‬ ‫في‬ ‫زيد‬ ‫درجة‬ ‫كانت‬ ‫اذا‬ )a
‫في‬ ‫عليها‬ ‫يحصل‬ ‫ان‬ ‫يجب‬ ‫التي‬ ‫الدرجة‬ ‫تتراوح‬ ‫فكم‬ ‫درجة‬ 80 ، 70 ‫بين‬ ‫يتراوح‬ ‫الرياضيات‬ ‫في‬
‫الثاني؟‬ ‫االمتحان‬
. 7 ، -3 ‫بين‬ ‫الناتج‬ ‫كان‬ 6 ‫اليها‬ ‫اضيفت‬ ‫اذا‬ ‫التي‬ ‫الصحيحة‬ ‫االعداد‬ ‫مجموعة‬ ‫جد‬ )b
. ‫او‬ ‫الرمزين‬ ‫باحد‬ ‫يلي‬ ‫فيما‬ ‫االستفهام‬ ‫عالمة‬ ‫استبدل‬ / 4‫س‬
.a ? b ‫فان‬ a - b = -2 ‫كانت‬ ‫اذا‬ . a ? b ‫فان‬ a - b = 1 ‫كانت‬ ‫اذا‬ )a
4 1
10 p - 8 8 + 7p
)b

84. 84
‫االعداد‬ ‫من‬ ‫مرتب‬ ‫بزوج‬ ‫مثل‬ُ‫ت‬ ‫االحداثي‬ ‫المستوي‬ ‫في‬ ‫نقطة‬ ‫اية‬ ‫ان‬ ‫السابقة‬ ‫دراستك‬ ‫من‬ ‫تعلمت‬
. )x , y( ‫الحقيقية‬
‫تسمى‬ ‫و‬ ً‫ا‬‫مع‬ ‫و‬ ‫حيث‬ ً‫ا‬‫مع‬ : ‫صورتها‬ ‫التي‬ ‫فالمعادلة‬
.x , y ‫بمتغيرين‬ ‫خطية‬ ‫معادلة‬
: ‫المعادلة‬ ‫حلول‬ ‫مجموعة‬ ‫جد‬
: ‫للنظام‬ ‫الحل‬ ‫مجموعة‬ ‫او‬
/ ‫احلل‬
‫الجدول‬ ‫في‬ ‫كما‬ ‫المعادلة‬ ‫تحقق‬ ‫والتي‬ x , y ‫قيم‬ ‫مجموعة‬ ‫بايجاد‬ ‫الحل‬ ‫مجموعة‬ ‫ايجاد‬ ‫نحاول‬
)x, y(yx+y=3x
)-1 , 4(4-1+y = 3-1
) 0 , 3(30 +y = 30
)1 , 2(21 +y = 31
) 2, 1(12 + y = 32
. ‫ان‬ ‫بحيث‬ )x, y( ‫المرتبة‬ ‫االزواج‬ ‫من‬ ‫محددة‬ ‫غير‬ ‫مجموعة‬ ‫هناك‬ ‫ان‬ ‫واضح‬ ‫الجدول‬ ‫من‬
. ‫الحل‬ ‫مجموعة‬ ‫وتكون‬
4 - 3‫االولى‬ ‫الدرجة‬ ‫من‬ ‫املعادلة‬
‫مبتغيرين‬
ax+by+c=0a,b,c ∈ Ra≠0b≠0
‫متغيرين‬ ‫في‬ ‫االولى‬ ‫الدرجة‬ ‫من‬ ‫المعادلة‬ ‫حل‬ ‫مجموعة‬ ]4 - 3 - 1[
( 1 ) ‫مثال‬
x+y=3
x+y=3
x+y=3
s= 0,3( ), 1,2( ), 2,1( ), -1,4( )...{ }
.....
.....
.....
.....
A= x,y( ):x,y ∈ R, x+y=3{ }Z

85. 85
. . ‫حيث‬ 2x + 3y = 6 : ‫للمعادلة‬ ‫البياني‬ ‫المخطط‬ ‫ارسم‬
x ‫قيم‬ ‫مجموعة‬ / ‫احلل‬
. x = 3 , x = -1 ‫من‬ ‫الناتجتين‬ ‫بالنقطتين‬ ‫محددة‬ ‫مستقيم‬ ‫قطعة‬ ‫يمثل‬ ‫للمعادلة‬ ‫البياني‬ ‫المخطط‬ ‫ان‬ ‫واضح‬
: ]4-4[ ‫تعريف‬
‫المرتبة‬ ‫االزواج‬ ‫جميع‬ ‫مجموعة‬ ‫هي‬ x , y ‫بمتغيرين‬ ‫االولى‬ ‫الدرجة‬ ‫من‬ ‫المعادلة‬ ‫حل‬ ‫مجموعة‬
. ‫صائبة‬ ‫تجعلها‬ ‫التي‬ ‫اي‬ ax + by + c = 0 ‫المفتوحة‬ ‫الجملة‬ ‫تحقق‬ ‫التي‬ )x , y(
(2 ) ‫مثال‬
)x, y(y2x+3y=6x
(−1,
8
3
)
8
3
-2+3y=6-1
)0,2(
2
0+3y=60
(1,
4
3
)
4
3
2+3y=61
(2,
2
3
)
2
3
4+3y=62
)3,0(
0
6+3y=63
‫باخذ‬ ‫نكتفي‬ x , y ‫في‬ ‫بمتغيرين‬ ‫الخطية‬ ‫المعادلة‬ ‫لتمثيل‬ )1(
. ‫للدقة‬ ‫نقاط‬ ‫ثالث‬ ‫ويفضل‬ ‫المعادلة‬ ‫تحققان‬ ‫نقطتين‬
‫جزئية‬ ‫مجموعة‬ ‫او‬ ‫مستقيم‬ ax +by +c = 0 ‫للمعادلة‬ ‫البياني‬ ‫المخطط‬ )2(
. x ‫المتغير‬ ‫تعريف‬ ‫مجموعة‬ ‫على‬ ‫معتمد‬ )‫اوشعاع‬ ‫مستقيم‬ ‫(قطعة‬
‫مالحظة‬
• •• ••
-
1 0 1 2 3
[ ]
1-
1 2 3
3,0( )
y
x
•
•
(-1 ,
8
3
)
-1 ≤ x ≤ 3

86. 86
‫االولى‬ ‫الدرجة‬ ‫من‬ ‫معادلتني‬ ‫حل‬
ً‫ا‬‫اني‬ ‫مبتغيرين‬
‫لحل‬ x , y ‫بمتغيرين‬ ‫االولى‬ ‫الدرجة‬ ‫من‬ ‫معادلتين‬ L2 :a2x+b2y=c2
, L1:a1x+b1y=c1
‫لتكن‬
. ‫والمحددات‬ ‫المصفوفات‬ ‫وبطريقة‬ )‫الحذف‬ ، ‫(التعويض‬ ‫وتحليلية‬ ‫بيانية‬ : ‫طرق‬ ‫عدة‬ ‫هناك‬ ‫النظام‬ ‫هذا‬
. ‫فقط‬ ‫والحذف‬ ‫التعويض‬ ‫وطريقتي‬ ‫البيانية‬ ‫الطريقة‬ ‫سندرس‬ ‫المرحلة‬ ‫هذه‬ ‫في‬
. L1
‫معادلة‬ ‫حل‬ ‫مجموعة‬ ‫هي‬ S1
‫كانت‬ ‫اذا‬ ‫عام‬ ‫وبشكل‬
s1 = x,y( ):a1x+b1y=c1{ }
. L2
‫معادلة‬ ‫حل‬ ‫مجموعة‬ ‫هي‬ S2
. S2
, S1
‫المجموعتين‬ ‫تقاطع‬ ‫هي‬ ‫النظام‬ ‫حل‬ ‫مجموعة‬ ‫فتكون‬
. R ‫في‬ x - y = 1 , x + y = 3 : ‫النظام‬ ‫حل‬ ‫مجموعة‬ ‫جد‬
/ ‫احلل‬
: R ‫التعويض‬ ‫مجموعة‬ ‫من‬ ‫نقاط‬ ‫بثالث‬ ‫الجدول‬ ‫نعمل‬
4 - 4
s2 = x,y( ):a2x+b2y=c2{ }
s=s1 ∩ s2
ً‫ال‬‫او‬-: ‫البيانية‬ ‫الطريقة‬
(1 ) ‫مثال‬
L1:x+y=3
)x, y(yx
)0,3(30
)1,2(21
)2,1(12
)x, y(yx
(0,-1)-10
)1,0(01
)2,1(12
L2 :x-y=1
: ‫اي‬

87. 87
})2 , 1({ = ‫الحل‬ ‫مجموعة‬
*
‫أحدى‬ ‫من‬ y ، x ‫بين‬ ‫عالقة‬ ‫بإيجاد‬ ‫وذلك‬ ‫فقط‬ ‫واحد‬ ‫بمتغير‬ ‫معادلة‬ ‫الى‬ ‫المعادلتين‬ ‫أحدى‬ ‫بتحويل‬ ‫ويتلخص‬
:‫االتي‬ ‫المثال‬ ‫في‬ ‫كما‬ ‫االخرى‬ ‫المعادلة‬ ‫في‬ ‫وتعويضها‬ ‫المعادلتين‬
‫النظام‬ ‫حل‬ ‫مجموعة‬ ‫جد‬
: y ‫بداللة‬ x ‫نجد‬ )1( ‫المعادلة‬ ‫من‬ / ‫احلل‬
:‫ان‬ ‫اي‬
: ‫على‬ ‫لنحصل‬ )2( ‫المعادلة‬ ‫في‬ )3( ‫من‬ x ‫قيمة‬ ‫االن‬ ‫نعوض‬
ً‫ا‬‫ثاني‬-: ‫التعويض‬ ‫طريقة‬
( 2 ) ‫مثال‬
x-y=1.......... 1( )
x+y=3......... 2( )
x=1+y......... 3( )
1+y( )+y=3
1+2y=3
2y=2
∴ y=1
X
1
2
3
4
5
6
7
1 2 3 40
-1
-2
L2
L1
y
•
2,1( )
: ‫باالتي‬ ‫البياني‬ ‫الحل‬ ‫طريقة‬ ‫تتلخص‬
.‫االحداثي‬ ‫المستوي‬ ‫في‬ ‫والثاني‬ ‫االول‬ ‫المستقيمين‬ ‫من‬ ‫كل‬ ‫تمثيل‬ *
‫المحورين‬ ‫على‬ ‫النقطة‬ ‫من‬ ‫عمودين‬ ‫برسم‬ ‫المستقيمين‬ ‫تقاطع‬ ‫نقطة‬ ‫احداثي‬ ‫نجد‬ *
. ‫النظام‬ ‫حل‬ ‫مجموعة‬ ‫تمثل‬ ‫التقاطع‬ ‫نقطة‬ ‫فتكون‬ ‫والسيني‬ ‫الصادي‬

88. 88
:‫فتكون‬ )3( ‫في‬ ) y =1 ( ‫قيمة‬ ‫نعوض‬
‫الن‬ ‫احداهما‬ ‫في‬ ‫وليس‬ ‫المعادلتين‬ ‫كلتا‬ ‫في‬ ) y = 1 ) ( x = 2 ( ‫عن‬ ‫نعوض‬ ‫الحل‬ ‫صحة‬ ‫من‬ ‫وللتحقق‬
.‫صائبتين‬ ‫عبارتين‬ ‫على‬ ‫للحصول‬ ‫كلتيهما‬ ‫تحقق‬ ‫ان‬ ‫يجب‬ ‫الحل‬ ‫مجموعة‬
: ‫االولى‬ ‫المعادلة‬
: ‫الثانية‬ ‫المعادلة‬
‫المعادلتين‬ ‫لحل‬ ‫التعويض‬ ‫طريقة‬ ‫استخدم‬
‫و‬
/ ‫احلل‬
:)2( ‫المعادلة‬ ‫من‬
: y ‫هو‬ ‫واحد‬ ‫بمتغير‬ ‫جديدة‬ ‫معادلة‬ ‫على‬ ‫لنحصل‬ )1( ‫المعادلة‬ ‫في‬ ‫قيمة‬ ‫نعوض‬
2 ‫في‬ ‫الطرفين‬ ‫بضرب‬
‫االقواس‬ ‫فك‬
‫بالتبسيط‬
x=1+y
x=1+1
∴ x=2
s= 2,1( ){ }
x-y=1 ⇒ 2-1=1
1=1
x+y=3 ⇒ 2+1=3
3=3
( 3 ) ‫مثال‬
3x+2y=12..... 1( )2x+3y=13..... 2( )
2x=13-3y ⇒ x=
13-3y
2
x=
13-3y
2
3
13-3y
2
⎛
⎝
⎜
⎞
⎠
⎟ +2y=12
3 13-3y( )+4y=24
39-9y+4y=24
39-5y=24
∴ -5y=-15
-5y
-5
=
-15
-5
∴ y=3
✓

89. 89
‫في‬ y =3 ‫قيمته‬ ‫نعوض‬
‫على‬ ‫نحصل‬
{(2,3)} : ‫الحل‬ ‫مجموعة‬
.‫الحذف‬ ‫بطريقة‬ ‫االتيتين‬ ‫المعادلتين‬ ‫حل‬
x+2y=5..... 1( ) ,
3x-y=1..... 2( )
/ ‫احلل‬
‫بالقيمة‬ ً‫ا‬‫متساوي‬ ‫المتغيرين‬ ‫أحد‬ ‫معامل‬ ‫نجعل‬ y ‫أو‬ x ‫المتغيرين‬ ‫أحد‬ ‫لحذف‬
.‫المعادلتين‬ ‫كلتا‬ ‫في‬ ‫باالشارة‬ ً‫ا‬‫ومختلف‬
2 ‫العدد‬ ‫في‬ )2( ‫المعادلة‬ ‫ضرب‬ ‫بعد‬
: ‫على‬ ‫نحصل‬ 2 ‫مع‬ 1 ‫بجمع‬
0 = (-2y) + (2y) : ‫ألن‬
. ) ‫المعادلتين‬ ‫من‬ ‫معادلة‬ ‫بابسط‬ ‫(يفضل‬ ‫المعادلتين‬ ‫أحدى‬ ‫في‬ x = 1 ‫قيمة‬ ‫نعوض‬
‫الحل‬ ‫مجموعة‬
‫المعادلتين‬ ‫كلتا‬ ‫في‬ ‫نعوض‬ x=1 , y=2 : ‫للتحقق‬
x=
13-3y
2
x=2
ً‫ا‬‫ثالث‬-: ‫احلذف‬ ‫طريقة‬
( 4 ) ‫مثال‬
x+2y=5..... 1( )
6x-2y=2..... 2( )
7x=7
∴ x=1
1+2y=5
2y=4 ⇒ y=2
s= 1,2( ){ }
‫بالجمع‬

90. 90
)‫وجدت‬ ‫ان‬ ، ‫والكسور‬ ‫االقواس‬ ‫من‬ ‫(التخلص‬ ‫المعادلتين‬ ‫نبسط‬ -1
:‫القياسية‬ ‫بالصورة‬ ‫لوضعها‬
.‫العددية‬ ‫بالقيمة‬ ‫المعادلتين‬ ‫في‬ ً‫ا‬‫متساوي‬ ‫المتغيرين‬ ‫احد‬ ‫معامل‬ ‫نجعل‬ -2
.)‫المعامل‬ ‫الشارة‬ ً‫ا‬‫(وفق‬ ‫المعادلتين‬ ‫نطرح‬ ‫او‬ ‫نجمع‬ -3
‫احدى‬ ‫في‬ ‫نعوض‬ ‫ثم‬ ‫االخر‬ ‫المتغير‬ ‫قيمة‬ ‫على‬ ‫نحصل‬ )3( ‫الخطوة‬ ‫من‬ -4
.)‫(المحذوف‬ ‫المتغير‬ ‫قيمة‬ ‫على‬ ‫للحصول‬ ‫المعادلتين‬
.‫الحذف‬ ‫بطريقة‬ ‫االتيتين‬ ‫المعادلتين‬ ‫حل‬
3x+4y=10..... 2( ) ,
2x+3y=7..... 1( )
/ ‫احلل‬
:‫يلي‬ ‫كما‬ ‫المعادلتين‬ ‫من‬ x ‫حذف‬ ‫نحاول‬
.‫لهما‬ ‫مكافئتين‬ ‫جديدتين‬ ‫معادلتين‬ ‫على‬ ‫لنحصل‬ 2 ‫بالعدد‬ )2( ‫والمعادلة‬ 3 ‫بالعدد‬ )1( ‫بضرب‬
‫بالطرح‬
: y = 1 ‫قيمة‬ ‫عن‬ ) )1( ‫في‬ ‫اي‬ ( )‫االشارة‬ ‫تغيير‬ ‫(قبل‬ ‫احدهما‬ ‫في‬ ‫نعوض‬
.‫الناتج‬ ‫صحة‬ ‫من‬ ‫التحقق‬ ‫للطالب‬ ‫يمكن‬
: ‫الطريقة‬ ‫ملخص‬
( 5 ) ‫مثال‬
ax+by=c
2x+ 3 × 1( )=7
2x=4 ⇒ x=2
s= 2,1( ){ }
6x + 9y= 21..... 1( )
+ 6x + 8y= + 20..... 2( )
-
⇒ y=1
- -

91. 91
: ً‫ا‬‫ثاني‬ ً‫ا‬‫بياني‬ ‫ثم‬ ً‫ال‬‫او‬ ‫الحذف‬ ‫بطريقة‬ ‫االتيتين‬ ‫المعادلتين‬ ‫حل‬
3x-y=12......... 1( )6 , x-y=4......... 2( )
: ً‫ال‬‫او‬
: y ‫المتغير‬ ‫حذف‬ ‫من‬ ‫لنتمكن‬ )-1( ‫بالعدد‬ )2( ‫المعادلة‬ ‫طرفي‬ ‫نضرب‬ :‫الحذف‬ ‫بطريقة‬
‫بالجمع‬
:)1( ‫في‬ ‫او‬ : ً‫ال‬‫أص‬ )2( ‫في‬ ‫نعوض‬
: ً‫ا‬‫بياني‬ ‫احلل‬
( 6 ) ‫مثال‬
-x +y =-4....... 2( )
x y (x,y)
0
4
-4
0
(0,-4)
(4,0)
x y (x,y)
0
2
-6
0
(0,-6)
(2 , 0)
L2 :x-y=4L1:3x-y=12
3x -y =12....... 1( )6
2x=8 ⇒ x=42 1
4-y=4 ⇒ y=0−3
s = 1,−3( ){ }
3x-y=12......... 1( )6 x-y=4......... 2( )
L2
X
L1
y
‫التقاطع‬ ‫نقطة‬
)1 , -3(
1

92. 92
: ‫الحذف‬ ‫بطريقة‬ ‫اآلتيتين‬ ‫المعادلتين‬ ‫حل‬1
2
x+2( )-
1
3
y-2( )=3 ........1
1
4
x +
1
2
y = 0 ........2
) LCM( 6 ‫بالعدد‬ )1( ‫المعادلة‬ ‫طرفي‬ ‫بضرب‬ ‫وذلك‬ ‫المعادلتين‬ ‫كلتا‬ ‫في‬ ‫الكسور‬ ‫من‬ ‫نتخلص‬ /‫احلل‬
:‫ونبسط‬ . 4 ‫بالعدد‬ )2( ‫والمعادلة‬
⇒ 6( ) ×
1
2
x+2( )- 6( ) ×
1
3
y-2( )=6 × 3
⇒ 3 x+2( ) − 2 y-2( ) = 18
3x-2y+10=18
3x-2y=8 ........1
4( ) ×
1
4
x + 4( ) ×
1
2
y=0
⇒ x+2y=0 ........2
3x-2y=8 ........1‫بالجمع‬
4x=8 ⇒ x=2
)2( ‫بالمعادلة‬ ‫نعوض‬
1
4
⎛
⎝
⎜
⎞
⎠
⎟ × 2+
1
2
y=0
1
2
+
1
2
y=0
‫على‬ ‫نجصل‬ 2 ‫في‬ ‫بالضرب‬
1 + y=0 ⇒ y=-1
ss= 2,-1( ){ } ∴= 2,-1( ){ } ∴
( 7 ) ‫مثال‬

93. 93
4 2
:‫التعويض‬ ‫بطريقة‬ ‫اآلتيتين‬ ‫المعادلتين‬ ‫من‬ ً‫ال‬‫ك‬ ‫حل‬ / 1‫س‬
:‫الحذف‬ ‫بطريقة‬ ‫اآلتيتين‬ ‫المعادلتين‬ ‫من‬ ً‫ال‬‫ك‬ ‫حل‬ / 2‫س‬
.‫الحل‬ ‫صحة‬ ‫من‬ ‫تحقق‬ ‫ثم‬
: ‫أخرى‬ ‫بطريقة‬ ‫الناتج‬ ‫وحقق‬ ً‫ا‬‫بياني‬ ‫يأتي‬ ‫مما‬ ‫معادلتين‬ ً‫ال‬‫ك‬ ‫/حل‬ 3‫س‬
: ‫ذلك‬ ‫بين‬ ‫االنيتين‬ ‫المعادلتين‬ ‫حل‬ ‫مجموعة‬ } ) 3 , 2 ( { ‫ان‬ ‫هل‬ / 4‫س‬
, :‫املعادلتني‬ ‫حل‬ ‫مجموعة‬ ‫هي‬ {(2,−1)} ‫كانت‬ ‫اذا‬ / 5‫س‬
‫حقيقية‬ ‫ثوابت‬ a , b ‫حيث‬ a , b ‫جد‬
bx-2y=-2
2x+3y=13
3x-2y= 0
b-m
1-a
,
b − am
1-a
⎛
⎝
⎜
⎞
⎠
⎟
⎧
⎨
⎩
⎫
⎬
⎭
a)
x-2y= 11
2x-3y=18
b-m
1-a
,
b − am
1-a
⎛
⎝
⎜
⎞
⎠
⎟
⎧
⎨
⎩
⎫
⎬
⎭
b)
3x-4y-12=0
5x+2y+6=0
b-m
1-a
,
b − am
1-a
⎛
⎝
⎜
⎞
⎠
⎟
⎧
⎨
⎩
⎫
⎬
⎭
a)
3x+2y=12
x + y = 5
a)
1
2
x +
1
3
y =2
2 x+1( )+3 y-3( )=2
b)
0.1x-3y=12
0.2x-4y = 24
b) b-m
1-a
,
b − am
1-a
⎛
⎝
⎜
⎞
⎠
⎟
⎧
⎨
⎩
⎫
⎬
⎭
2x-ay=3
2x
3
-
y
2
= 1
3y
2
+
x
3
= 4

94. 94
, ‫حيث‬ : ‫هي‬ x ‫واحد‬ ‫بمتغير‬ ‫الثانية‬ ‫الدرجة‬ ‫لمعادلة‬ ‫العامة‬ ‫الصورة‬
. a,b,c ∈ R
m2
-m=0 ، y2
- 2y-1=0 ، ax2
-3x+1=0 : ً‫ال‬‫مث‬
‫المعادلة‬ ‫وحل‬ ‫الترتيب‬ ‫على‬ m , y , x ‫واحد‬ ‫لمتغير‬ ‫الثانية‬ ‫الدرجة‬ ‫من‬ ‫لمعادلة‬ ‫أمثلة‬ ‫هي‬
‫مجموعة‬ ‫ضمن‬ )‫صائبة‬ ‫(تجعلها‬ ‫المعادلة‬ ‫تحقق‬ ‫التي‬ x ‫قيم‬ ‫مجموعة‬ ‫ايجاد‬ ‫يعني‬
: ‫ومنها‬ ‫واحد‬ ‫بمتغير‬ ‫التربيعية‬ ‫المعادلة‬ ‫لحل‬ ‫مختلفة‬ ‫طرق‬ ‫وهناك‬ ‫معلومة‬ ‫تعويض‬
‫الدرجة‬ ‫من‬ ‫منهما‬ ‫كل‬ ‫عاملين‬ ‫ضرب‬ ‫حاصل‬ ‫صورة‬ ‫على‬ ‫امكن‬ ‫ان‬ ‫المقدار‬ ‫بوضع‬ ‫وذلك‬
: ‫ان‬ ‫اي‬ ‫االولى‬
:‫أن‬ ‫على‬ ‫تنص‬ ‫والتي‬ ‫الصفري‬ ‫العامل‬ ‫خاصية‬ ‫نستخدم‬ ‫ثم‬
: ‫كان‬ ‫اذا‬
‫اما‬
‫او‬
‫الحل‬ ‫مجموعة‬ ‫وتكون‬
‫الثالثية‬ ‫الحدوديات‬ ‫تحليل‬ ، ‫مربعين‬ ‫بين‬ ‫الفرق‬ : ‫الثنائية‬ ‫الحدوديات‬ ‫لتحليل‬ ‫المختلفة‬ ‫الطرق‬ ‫درسنا‬ ‫وكما‬
. ) ‫التجزئة‬ ( ‫الرباعية‬ ‫الحدوديات‬ ، ) ‫الكامل‬ ‫المربع‬ ، ‫(التجربة‬
4 - 5‫الثانية‬ ‫الدرجة‬ ‫من‬ ‫املعادلة‬
‫مبتغيرواحد‬
ax2
+bx+c=0a≠0( )
ax2
+bx+c=0
ً‫ال‬‫او‬-: ‫التحليل‬ ‫طريقة‬
ax2
+bx+c( )
ax2
+bx+c= a1x+c1( ) a2x+c2( )=0
ab=0
a=0
b=0
a1x+c1 =0 ⇒ x=
-c1
a1
a2x+c2 =0 ⇒ x=
-c2
a2
S=
-c1
a1
,
-c2
a1
⎧
⎨
⎩
⎫
⎬
⎭2

95. 95
‫مالحظة‬
: ‫التحليل‬ ‫بطريقة‬ ‫االتية‬ ‫المعادالت‬ ‫حل‬
a) x2
-25=0 b) 2x2
-3x=0
/‫الحل‬
a) x2
-25=0 ⇒ x-5( ) x+5( ) = 0
‫اما‬ :x-5=0 ⇒ x=5
‫او‬ :x+5=0 ⇒ x=-5
‫الحل‬ ‫مجموعة‬ ∴
b) 2x2
-3x=0
x 2x+3( )=0 ‫مشترك‬ ‫عامل‬ ‫باخراج‬ ‫تحليل‬
‫اما‬ : x=0
‫او‬ :
= ‫الحل‬ ‫مجموعة‬ ∴
( 1 ) ‫مثال‬
5,-5{ }
. ‫مربعين‬ ‫بين‬ ‫الفرق‬ ‫تحليل‬ ‫نذكر‬
) 1
: ‫وهي‬ ‫التربيعي‬ ‫الجذر‬ ‫بطريقة‬ 1 ‫المثال‬ ‫حل‬ ‫يمكن‬ ) 2
‫وكانت‬ ، ‫كانت‬ ‫اذا‬
‫او‬ : ‫فان‬
: ‫كان‬ ‫اذا‬ ‫اي‬
x2
-a2
= x-a( ) x+a( )
k ∈ Rk 0x2
=k
x= kx=- k
x2
=25
∴ x=+ 25
x=+5
∴ S= 5,-5{ }
2x-3=0 ⇒ x=
3
2
0,
3
2
⎧
⎨
⎩
⎫
⎬
⎭
-
-
-

96. 96
: ‫االتيه‬ ‫المعادالت‬ ‫حل‬
a) x-2( )
2
− 9=0
b) 1-2y( )
2
− 4=0
c) 2w+a( )
2
-4a2
=0
d) 1
y+1
⎛
⎝
⎜
⎞
⎠
⎟
2
-
1
4
=0
/‫احلل‬
a) x-2( )
2
− 9=0 ( ‫المعادلة‬ )
)‫االقواس‬ ‫(فك‬
)‫تبسيط‬ (
)‫تجربة‬ ‫(تحليل‬
‫اما‬ :
‫او‬ :
= ‫الحل‬ ‫مجموعة‬ ∴
( 2 ) ‫مثال‬
x2
-4x+4-9=0
x2
-4x-5=0
x-5( ) x+1( ) = 0
x-5=0 ⇒ x=5
x+1=0 ⇒ x=-1
-1,5{ }
‫للطالب‬ ‫تدريب‬
. x = 5 , x = - 1 ‫عن‬ ‫بالتعويض‬ ‫االجابة‬ ‫صحة‬ ‫حقق‬

97. 97
b) 1-2y( )
2
− 4=0 ( ‫المعادلة‬ )
( ‫االقواس‬ ‫فك‬ )
( ‫تبسيط‬ )
) ‫تجربة‬ ‫تحليل‬ (
: ‫اما‬
: ‫او‬
c) 2w+a( )
2
-4a2
=0 ( ‫المعادلة‬ )
( ‫مربيعين‬ ‫بين‬ ‫الفرق‬ ‫تحليل‬ )
( ‫تبسيط‬ )
: ‫اما‬
: ‫او‬
= ‫الحل‬ ‫مجموعة‬
d) 1
y+1
⎛
⎝
⎜
⎞
⎠
⎟
2
-
1
4
=0 ( ‫المعادلة‬ )
( ‫مربيعين‬ ‫بين‬ ‫الفرق‬ ‫تحليل‬ )
: ‫اما‬
1-4y+4y2
-4=0
4y2
-4y-3=0
2y+1( ) 2y-3( )=0
y =
-1
2
y =
3
2
a
2
,
-3a
2
⎧
⎨
⎩
⎫
⎬
⎭
∴ w=
-3a
2
2w+3a = 0
∴ w=
a
2
2w-a=0
2w-a( ) 2w+3a( ) = 0
2w+a( )-2a⎡⎣ ⎤⎦ 2w+a( )+2a⎡⎣ ⎤⎦=0
1
y+1
−
1
2
⎡
⎣
⎢
⎤
⎦
⎥
1
y+1
+
1
2
⎡
⎣
⎢
⎤
⎦
⎥=0
1
y+1
−
1
2
-1
2
,
3
2
⎧
⎨
⎩
⎫
⎬
⎭
= ‫احلل‬ ‫∴مجموعة‬
=0

98. 98
‫الوسطين‬ ‫ضرب‬ ‫حاصل‬ = ‫الطرفين‬ ‫ضرب‬ ‫حاصل‬
= ‫الحل‬ ‫مجموعة‬
: ‫بالتحليل‬ ‫االتية‬ ‫المعادالت‬ ‫حل‬
a) x x-2( )=35
b) 2x2
-12=5x
c) 1
3
x2
=
3
4
x
d) 2x2 -3+x( )=5x+9
e)
f) 3x+1( )
2
= 3x+1( )
/‫الحل‬
a) x x-2( )=35
x2
-2x-35=0
: ‫او‬ : ‫اما‬
= ‫احلل‬ ‫مجموعة‬ ∴
1
y+1
=
1
2
y+1=2
y=1
1
y+1
+
1
2
= 0
1
y+1
=
−1
2
-y-1=2
∴ y=3
-3,1{ }
( 3 ) ‫مثال‬
7, −5{ }
x+5=0 ⇒ x=-5 x-7=0 ⇒ x=7
x-7( ) x+5( ) = 0
−3
-
0.1x2
- 0.4x + 0.4 = 0
: ‫او‬

99. 99
‫مالحظة‬
b) 2x2
-12=5x
: ‫اما‬
: ‫او‬
= ‫الحل‬ ‫مجموعة‬ ∴
c) x
12 = LCM ‫في‬ ‫المعادلة‬ ‫طرفي‬ ‫بضرب‬ ‫الكسور‬ ‫من‬ ‫نتخلص‬
( ‫الطرفين‬ ‫تبسيط‬ )
: ‫اما‬
:‫او‬
= ‫الحل‬ ‫مجموعة‬
‫صحة‬ ‫من‬ ‫التحقق‬ ‫يمكن‬
. ‫االصلية‬ ‫بالمعادلة‬ ‫بالتعويض‬ ‫الناتج‬
2x2
-5x-12=0
2x+3( ) x-4( ) = 0
2x+3=0 ⇒ x=
-3
2
x-4=0 ⇒ x=4
-3
2
, 4
⎧
⎨
⎩
⎫
⎬
⎭
12
1
3
x2⎛
⎝
⎜
⎞
⎠
⎟ =12
3
4
x
⎛
⎝
⎜
⎞
⎠
⎟
1
3
x2
=
3
4
4x2
=9x
⇒ 4x2
-9x=0
⇒ 4x-9=0 ⇒ x=
9
4
0,
9
4
⎧
⎨
⎩
⎫
⎬
⎭
x=0
x ( 4x - 9 ) = 0
-6x+2x2
-5x+9=0
2x2
-11x+9=0
2x-9( ) x-1( ) = 9-6x+2x2
-5x+9=0
2 -3+x( )=5x+9d) 2x -
( ‫الطرفين‬ ‫تبسيط‬ )

100. 100
: ‫اما‬
: ‫او‬
= ‫الحل‬ ‫مجموعة‬ ∴
e)
‫الكسور‬ ‫من‬ ‫للتخلص‬ 10 ‫قي‬ ‫المعادلة‬ ‫طرفي‬ ‫بضرب‬
= ‫الحل‬ ‫مجموعة‬ ∴
f)
: ‫اما‬
: ‫او‬
= ‫الحل‬ ‫مجموعة‬ ∴
2x-9=0 ⇒ x =
9
2
x-1=0 ⇒ x=1
9
2
,1
⎧
⎨
⎩
⎫
⎬
⎭
3x+1( )
2
= 3x+1( )
3x+1( )
2
- 3x+1( )=0
3x+1( ) 3x+1( )-1⎡⎣ ⎤⎦=0
3x+1=0 ⇒ x=
-1
3
3x=0 ⇒ x=0
-1
3
, 0
⎧
⎨
⎩
⎫
⎬
⎭
.‫الحل‬ ‫واكمال‬ ‫االقواس‬ ‫فك‬ : ‫اخرى‬ ‫بطريقة‬ ‫حاول‬
‫المعادلة‬ ‫لتصبح‬ ) 3x + 1) = y : ‫ان‬ ‫بفرض‬ ‫المعادلة‬ ‫حل‬ ‫كذلك‬ ‫ويمكن‬
.‫الحل‬ ‫نكمل‬ ‫ثم‬ y2
= y : ‫بالشكل‬ ‫االصلية‬
‫للطالب‬ ‫تمرين‬
0.1x2
- 0.4x + 0.4 = 0
x2
- 4x + 4 = 0
(x - 2 )2
= 0
x - 2 = 0 ⇒ x = 2
s = 2{ }

101. 101
:‫اآلتية‬ ‫الخطوات‬ ‫نتبع‬ ‫الطريقة‬ ‫بهذه‬ ‫الحل‬ ‫مجموعة‬ ‫إليجاد‬
a≠0 ‫حيث‬ . ‫بالصورة‬ ‫التربيعية‬ ‫المعادلة‬ ‫نضع‬ - 1
. a ‫على‬ ‫المعادلة‬ ‫طرفي‬ ‫نقسم‬ ، ‫كان‬ ‫اذا‬ - 2
. ‫المقدار‬ ‫المعادلة‬ ‫طرفي‬ ‫الى‬ ‫نضيف‬ - 3
. ‫االيمن‬ ‫الطرف‬ ‫ونبسط‬ 3 ‫الخطوة‬ ‫بعد‬ ً‫ال‬‫كام‬ ً‫ا‬‫مربع‬ ‫اصبح‬ ‫والذي‬ ‫االيسر‬ ‫الطرف‬ ‫نحلل‬ - 4
. x ‫قيم‬ ‫ونجد‬ ‫للطرفين‬ ‫التربيعي‬ ‫الجذر‬ ‫نأخذ‬ - 5
. ‫المربع‬ ‫اكمال‬ ‫بطريقة‬ ‫المعادلة‬ ‫حل‬
/‫احلل‬
) ‫المعادلة‬ (
)‫المطلوبة‬ ‫بالصورة‬ ‫المعادلة‬ ‫(وضع‬
)2‫على‬ ‫الطرفين‬ ‫بقسمة‬ (
=
9
16
= ‫المضاف‬ ‫الحد‬
‫للطرفين‬ ‫باضافة‬
‫االيمن‬ ‫ونبسط‬ ‫االيسر‬ ‫الطرف‬ ‫تحليل‬
‫التربيعي‬ ‫الجذر‬ ‫خاصة‬
: ‫اما‬
ً‫ا‬‫ثاني‬
To Solve a Quadratic Equation by Completing the Square
ax2
+bx=-c
a≠1
x
⎛
⎝
⎜ ‫معامل‬ 1
2
⎞
⎠
⎟
2
( 4 ) ‫مثال‬
2x2
-3=3x
2x2
-3=3x
2x2
-3x=3
x2
-
3
2
x=
3
2
9
16
=
−3
2
×
1
2
⎛
⎝
⎜
⎞
⎠
⎟
2
9
16
∴ x2
-
3
2
x+
9
16
=
3
2
+
9
16
x-
3
4
⎛
⎝
⎜
⎞
⎠
⎟
2
=
33
16
∴ x-
3
4
=+
33
4
x=
3
4
+
33
4
=
3+ 33
4
-
‫املربع‬ ‫اكمال‬ ‫طريقة‬ :

102. 102
: ‫أو‬
= ‫الحل‬ ‫مجموعة‬ ∴
‫التربيعية‬ ‫للمعادلة‬ ‫العامة‬ ‫الصورة‬
‫القياسية‬ ‫الصورة‬ ً‫ا‬‫ايض‬ ‫تسمى‬
a ‫على‬ ‫بالقسمة‬
‫نصف‬ ‫مربع‬ ‫باضافة‬
‫للطرفين‬ x ‫معامل‬
‫االيمن‬ ‫الطرف‬ ‫ونبسط‬ ‫االيسر‬ ‫الطرف‬ ‫تحليل‬
: ‫اما‬
: ‫او‬
= ‫الحل‬ ‫مجموعة‬ ∴
:x ‫في‬ ‫التربيعية‬ ‫المعادلة‬ ‫حل‬ ‫مجموعة‬ ‫تكون‬ ‫وبذلك‬
‫التربيعية‬ ‫المعادلة‬ ‫قانون‬
= :‫المقدار‬ ‫يسمى‬
x=
3
4
−
33
4
=
3- 33
4
3+ 33
4
,
3- 33
4
⎧
⎨
⎩⎪
⎫
⎬
⎭⎪
: ً‫ا‬‫ثالث‬)‫فقط‬ ‫لالطالع‬ ‫(االشتقاق‬ ) ‫(الدستور‬ ‫القانون‬ ‫طريقة‬
ax2
+bx+c=0 , a≠0
ax2
+bx=-c
x2
+
b
a
x=
-c
a
ax2
+
b
a
x+
1
2
×
b
a
⎛
⎝
⎜
⎞
⎠
⎟
2
=
-c
a
+
1
2
×
b
a
⎛
⎝
⎜
⎞
⎠
⎟
2
x2
+
b
a
x+
b2
4a2
=
-c
a
+
b2
4a2
x+
b
2a
⎛
⎝
⎜
⎞
⎠
⎟
2
=
b2
-4ac
4a2
x+
b
2a
=+
b2
-4ac
2a
x=+
-b+ b2
-4ac
2a
x=+
-b- b2
-4ac
2a
-b- b2
-4ac
2a
,
-b+ b2
-4ac
2a
⎧
⎨
⎪
⎩⎪
⎫
⎬
⎪
⎭⎪
x=
-b+ b2
-4ac
2a
b2
-4ac( )∆( )b2
-4ac∆
x=
x=
-
‫بالرمز‬ ‫له‬ ‫ويرمز‬ ‫المميز‬ ‫بالمقدار‬Delta )‫(دلتا‬
-

103. 103
)‫الدستور‬ ( ‫بالقانون‬ ‫االتية‬ ‫المعادلة‬ ‫حل‬
/‫احلل‬
. ‫العامة‬ ‫بالصورة‬ ‫المعادلة‬ ‫وضع‬ )1
‫حيث‬ c , b , a ‫المعامالت‬ ‫تعيين‬ )2
: ‫بالقانون‬ c , b , a ‫عن‬ ‫نعوض‬ )3
: ‫اما‬
: ‫او‬
= ‫الحل‬ ‫مجموعة‬ ∴
‫جذري‬ ‫نوع‬ ‫فان‬ , ‫هو‬ ax2
+ bx + c = 0 ‫التربيعية‬ ‫للمعادلة‬ ‫المميز‬ ‫المقدار‬ ‫ان‬ ‫عرفنا‬
:‫يلي‬ ‫كما‬ ‫تتعين‬ ‫المعادلة‬
‫ن‬‫الجذري‬ ‫نوع‬
ً‫ال‬‫كام‬ ً‫ا‬‫ومربع‬ ‫موجب‬ ‫نسبيان‬ ‫حقيقيان‬ ‫جذران‬
ً‫ال‬‫كام‬ ً‫ا‬‫مربع‬ ‫ليس‬ ‫موجب‬ ‫ن‬‫نسبيي‬ ‫غير‬ ‫حقيقيان‬ ‫جذران‬
‫صفر‬ ‫واحد‬ ‫حقيقي‬ ‫جذر‬
‫سالب‬ )‫(تخيليان‬ ‫حقيقيين‬ ‫غير‬ ‫جذران‬
∅ = R ‫في‬ ‫الحل‬ ‫مجموعة‬ ∴
( 5 ) ‫مثال‬
x2
-3x=5
x2
-3x-5=0
a=1 ( x2
‫)معامل‬ , b=-3 (x‫)معامل‬
x=
-b+ b2
-4ac
2a
∴ x=
- -3( )+ -3( )
2
- 4 × 1 × 5( )
2 × 1
=
3+ 29
2
x=
3+ 29
2
x=
3- 29
2
3+ 29
2
,
3- 29
2
⎧
⎨
⎩⎪
⎫
⎬
⎭⎪
ً‫ا‬‫رابع‬The Discriminant ∆ ‫املميز‬ ‫املقدار‬
∆ = b2
-4ac( )
-b
2a
⎛
⎝
⎜
⎞
⎠
⎟
-
-
-
× -
c = -5 (‫المطلق‬ ‫)الحد‬
b2
-4ac∆ = b2
-4ac( )

104. 104
‫مالحظة‬
:‫املعادلة‬ : ً‫ال‬‫مث‬
52
= ً‫ال‬‫كام‬ ً‫ا‬‫مربع‬ 25 ‫والعدد‬
‫املقدار‬
‫حتليله‬ ‫ميكن‬
‫؟‬ ‫متساويني‬ ‫املعادلة‬ ‫جذري‬ ‫جتعل‬ ‫التي‬ m ‫الثابت‬ ‫قيمة‬ ‫ما‬
/‫احلل‬
0 = )‫املميز‬ ( ∆ ‫عندما‬ ‫متساويني‬ ‫املعادلة‬ ‫جذري‬ ‫يكون‬
: ‫اما‬
: ‫او‬
‫فان‬ ‫صحيحة‬ ً‫ا‬‫اعداد‬ c , b , a ‫كانت‬ ‫اذا‬ ‫انه‬ ‫مالحظة‬ ‫مع‬
. ً‫ال‬‫كام‬ ً‫ا‬‫مربع‬ ‫المميز‬ ‫كان‬ ‫اذا‬ ‫تحليله‬ ‫يمكن‬ ‫المقدار‬ax2
+bx+c( )
2x2
+3x-2=0
a=2, b=3, c=-2
∆ = b2
-4ac
=9- 4 × 2 × -2( )=25
2x2
+3x-2
= 2x-1( ) x+2( )
( 6 ) ‫مثال‬
x2
- m+1( )x+4=0
a=1, b=- m+1( ), c=4
∆= - m+1( )⎡⎣ ⎤⎦
2
-4 × 1 × 4= m+1( )
2
-16
∆=0 ⇒ m+1( )
2
− 16 = 0
∴ m+1( )
2
= 16 ⇒ m+1=+4
m=3
m=-5
2
-
‫مالحظة‬‫ان‬ ‫لتجد‬ ‫االصلية‬ ‫باملعادلة‬ m ‫قيمة‬ ‫عن‬ ‫بالتعويض‬ ‫حتقق‬
. m ‫قيم‬ ‫من‬ ‫قيمة‬ ‫لكل‬ ‫واحد‬ ‫حل‬ ‫للمعادلة‬

105. 105
. R ‫في‬ ‫حل‬ ‫لها‬ ‫ليس‬ ‫المعادلة‬ ‫ان‬ ‫بين‬
/‫احلل‬
. ً‫ا‬‫سالب‬ ً‫ا‬‫عدد‬ ‫يساوي‬ )‫المميز‬ (∆ ‫عندما‬ R ‫في‬ ‫حل‬ ‫لها‬ ‫ليس‬ ‫التربيعية‬ ‫المعادلة‬
: ‫العامة‬ ‫بالصورة‬ ‫المعادلة‬ ‫نضع‬
:‫حيث‬
)‫(سالب‬
. R ‫في‬ ‫حل‬ ‫لها‬ ‫ليس‬ ‫المعادلة‬
‫؟‬ ‫متساويان‬ ‫املعادلة‬ ‫جذري‬ ‫جتعل‬ ‫التي‬ m ‫الثابت‬ ‫قيمة‬ ‫ما‬
/‫احلل‬
. ‫كان‬ ‫اذا‬ ‫متساويان‬ ‫التربيعية‬ ‫املعادلة‬ ‫جذرا‬ ‫يكون‬
‫العامة‬ ‫بالصورة‬ ‫املعادلة‬
‫نجعل‬
( 7 ) ‫مثال‬
x2
+10=2x
∆0( )
x2
-2x+10=10
c=10, b=-2, a=1
∆=b2
-4ac
= -2( )
2
-4 × 1 × 10
=-36
∆=-360
∴
( 8 ) ‫مثال‬
y2
-16=m y+4( )
∆ = 0
y2
-16=my+4m
y2
-my-16-4m=0
a=1 , b=-m, c=-16-4m
∆=b2
-4ac
=m2
+16m+64
∆ = 0
⇒ m2
+16m+64=0
m+8( )
2
=0
∴ m=-8
0
= -m( )
2
-4 -16-4m( )= -m( )
2
-4 -16-4m( )× 1 ×

106. 106
) 480m2
( ‫مساحته‬ ‫وكانت‬ ‫عرضه‬ ‫ضعف‬ ‫على‬ )2m( ‫بمقدار‬ ‫يزيد‬ ‫السلة‬ ‫كرة‬ ‫ملعب‬ ‫طول‬ ‫كان‬ ‫اذا‬
. ‫الملعب‬ ‫بعدي‬ ‫جد‬
/‫احلل‬
y = ‫الملعب‬ ‫عرض‬ ‫نفرض‬
2y+2 = ‫الملعب‬ ‫طول‬
‫العرض‬ × ‫الطول‬ = )‫الشكل‬ ‫(مستطيلة‬ ‫الملعب‬ ‫مساحة‬
2‫على‬ ‫بالقسمة‬
‫يهمل‬ : ‫اما‬
: ‫او‬
= ‫العرض‬
= ‫الطول‬
2 × 15+2==
32m = ‫الطول‬ ∴
- : ‫واحد‬ ‫متغير‬ ‫في‬ ‫الثانية‬ ‫الدرجة‬ ‫من‬ ‫معادالت‬ ‫الى‬ ‫حلها‬ ‫يؤدي‬ ‫مسائل‬
(9 ) ‫مثال‬
y 2y+2( )=480
2y2
+ 2y=480
y2
+y-240=0
y+16( ) y-15( )=0
y=-16
y=15
15m
2y+2

107. 107
. )12( ‫بمقدار‬ ‫عليه‬ ‫يزيد‬ ‫مربعه‬ ‫الذي‬ ‫العدد‬ ‫جد‬
/‫احلل‬
x2
= ‫مربعه‬ ، x ‫العدد‬ ‫نفرض‬
: ‫اما‬
: ‫او‬
‫بمقدار‬ ‫سرعته‬ ‫زادت‬ ‫ولو‬ ‫معينة‬ ‫بسرعة‬ A , B ‫مدينتين‬ ‫بين‬ )60km( ‫مسافة‬ ‫قطع‬ ‫دراجة‬ ‫راكب‬ ‫اراد‬ ‫أذا‬
.ً‫ال‬‫او‬ ‫سرعته‬ ‫جد‬ .‫االول‬ ‫الزمن‬ ‫عن‬ ‫واحدة‬ ‫ساعة‬ ‫يقل‬ ‫بزمن‬ ‫المسافة‬ ‫هذه‬ ‫قطع‬ ‫من‬ ‫لتمكن‬
/ ‫احلل‬
V = ‫االولى‬ ‫سرعته‬ ‫نفرض‬
V + 10 = ‫الثانية‬ ‫سرعته‬ ∴
= ‫االول‬ ‫الزمن‬
= ‫الثاني‬ ‫الزمن‬
1 = ‫الثاني‬ ‫الزمن‬ - ‫األول‬ ‫الزمن‬ ∴
:LCM ‫في‬ ‫الطرفين‬ ‫بضرب‬
∴ V=-30 ‫تهمل‬ , V=20
(10 ) ‫مثال‬
∴ x2
-x=12
x2
-x-12=0
x-4( ) x+3( )=0
x=4
x=-3
(11 ) ‫مثال‬
(10 km/ h)
60
V
60
V
-
60
V +10
= 1
60
V +10
‫مالحظة‬
= ‫الزمن‬
‫املسافة‬
‫السرعة‬
V V+10( )
60 V+10( )-60V=V V+10( )
60V+600-60V=V2
+10V
⇒ V2
+10V-600=0 ⇒ V+34( ) V-20( )=0
km/h ً‫ال‬‫أو‬ ‫سرعته‬
30

108. 108
‫مربع‬ ‫كل‬ ‫ضلع‬ ‫طول‬ ‫زواياها‬ ‫من‬ ‫متساوية‬ ‫مربعات‬ ‫أربعة‬ ‫قطعت‬ )x cm(‫ضلعها‬ ‫طول‬ ‫الشكل‬ ‫مربعة‬ ‫قطعة‬
)16cm3
( ‫حجمه‬ ‫مستطيلة‬ ‫سطوح‬ ‫متوازي‬ ‫شكل‬ ‫على‬ ‫غطاء‬ ‫بدون‬ ‫صندوق‬ ‫فتكون‬ ‫بعدها‬ ‫4)وثنيت‬cm(
. ‫االصلية‬ ‫مساحةالقطعة‬ ‫جد‬
/ ‫احلل‬
. ‫القاعدة‬ ‫بعدي‬ )x - 8( ، ‫االرتفاع‬ 4 : ‫الصندوق‬ ‫ابعاد‬ ‫ان‬ ‫الشكل‬ ‫من‬ ‫واضح‬
. ‫االرتفاع‬ × ‫العرض‬ × ‫الطول‬ = ‫المستطيلة‬ ‫السطوح‬ ‫متوازي‬ ‫حجم‬
4 ‫على‬ ‫بالقسمه‬
‫التربيعي‬ ‫الجذر‬ ‫باخذ‬
: ‫اما‬
: ‫او‬
‫ضلع‬ ‫طول‬ ‫تعطي‬ ‫النها‬ ‫اهمالها‬ ‫يجب‬ x = 6 ‫ان‬ ‫نالحظ‬ ‫المسأله‬ ‫معطيات‬ ‫تطابق‬ ‫االجابتين‬ ‫من‬ ‫أي‬ ‫وللتحقق‬
. ‫ممكن‬ ‫غير‬ ‫وهو‬ ) - 2( ً‫ا‬‫سالب‬ ‫عددا‬ ) x-8( ‫القاعدة‬
) ‫أخرى‬ ‫بطريقه‬ x = 6 ‫اهمال‬ ‫تفسير‬ ‫(حاول‬
) x = 10 ( ‫االصليه‬ ‫القطعه‬ ‫ضلع‬ ‫طول‬ ∴
100 cm2
= 102
= ‫مساحتها‬ ‫وتكون‬
(12 ) ‫مثال‬
∴ 4 x-8( ) x-8( ) = 16
∴ x-8( )
2
= 4
∴ x-8 = +2
x=10
x=6
-
x - 8
4 4
4 4

109. 109
‫الخ‬ .... x2
- 4 = 0 ، x2
- x - 2 = 0 ً‫ال‬‫مث‬ ) ‫االساس‬ ‫في‬ ‫المتغير‬ ( ‫الحدودية‬ ‫المعادالت‬ ً‫ا‬‫سابق‬ ‫درسنا‬
. ) ‫الكسر‬ ‫مقام‬ ‫في‬ ‫متغيرها‬ ‫معادالت‬ ( ‫الكسرية‬ ‫المعادالت‬ ‫االن‬ ‫ندرس‬ ‫سوف‬
: ‫الحل‬ ‫صحة‬ ‫وحقق‬ ‫االتيه‬ ‫المعادالت‬ ‫من‬ ‫كال‬ ‫حل‬
a)
b)
c)
/ ‫احلل‬
: ‫الكسور‬ ‫من‬ ‫للتخلص‬ )3x( ‫للمقامات‬ LCM ‫في‬ ‫المعادلة‬ ‫طرفي‬ ‫نضرب‬
a)
‫تبسيط‬
‫بالتجربة‬ ‫تحليل‬
: ‫اما‬
: ‫او‬
‫عن‬ ‫بالمعادلة‬ ‫نعوض‬ : ‫التحقيق‬
‫االيسر‬ ‫الطرف‬
4 - 6
‫الكسرية‬ ‫املعادالت‬
5x+
x-2
3x
=
2
3
3x 5x( )+3x
x-2
3x
⎛
⎝
⎜
⎞
⎠
⎟ =3x
2
3
⎛
⎝
⎜
⎞
⎠
⎟
15x2
+x-2=2x
15x2
-x-2=0
5x-2( ) 3x+1( ) = 0
5x-2=0 ⇒ x=
2
5
3x+1=0 ⇒ x=
-1
3
x=
2
5
, x=
-1
3
x=
-1
3
L.H.S = 5 ×
-1
3
⎛
⎝
⎜
⎞
⎠
⎟ +
-1
3
-2
3 ×
-1
3
5x+
x-2
3x
=
2
3
2
y+2
-
2
2-y
=
y2
+4
y2
-4
6
x-2
+
x
2-x
=3
y
⇐

110. 110
=
−5
3
+
−7
3
−1
=
−5
3
+
7
3
=
2
3
‫للمعادلة‬ ‫جذر‬
‫عندما‬ ‫بسهولة‬ ‫التحقق‬ ‫يمكن‬ ‫كذلك‬
= ‫الحل‬ ‫مجموعة‬ ∴
b ( : ‫تغييرالمقام‬ ‫نحاول‬ ‫للمقامات‬ LCM ‫في‬ ‫المعادلة‬ ‫طرفي‬ ‫ضرب‬ ‫قبل‬
‫حيث‬ 2-y
‫معلومة‬
: ‫الحظ‬
y-2( ) y+2( )( ) LCM ‫في‬ ‫المعادلة‬ ‫طرفي‬ ‫بضرب‬
‫الطرفين‬ ‫تبسيط‬
−1
3
,
2
5
⎧
⎨
⎩
⎫
⎬
⎭
∴ x=
-1
3
x=
2
5
2
y+2
-
2
2-y
=
y2
+4
y2
-4
a-b=- b-a( )
2
y+2
-
2
− y-2( )
=
y2
+4
y2
-4
2
y+2
+
2
y-2
=
y2
+4
y-2( ) y+2( )
2 y-2( ) + y y+2( ) = y2
+4
2y-4+y2
+2y-y2
-4=0
4y-8=0 ⇒ y=2
: ‫االتي‬ ‫بالشكل‬ ‫تصبح‬ ‫المعادلة‬ ∴
y2
-4= y-2( ) y+2( )
2-y=- 2-y( )(y-2)
y
y
y
= ‫االيمن‬ ‫الطرف‬

111. 111
‫لذلك‬ ‫جائز‬ ‫غير‬ ‫وهذا‬ ‫الصفر‬ ‫على‬ ‫قسمة‬ ‫عملية‬ ‫على‬ ‫تحصل‬ ‫االصلية‬ ‫بالمعادلة‬ y = 2 ‫عن‬ ‫التعويض‬ ‫عند‬
. R ‫في‬ ‫حل‬ ‫لها‬ ‫ليس‬ ‫فالمعادلة‬
c (
) L . C . M ( ‫في‬ ‫المعادلة‬ ‫طرفي‬ ‫بضرب‬ : ) Correct Method ( ‫الصحيحة‬ ‫الطريقة‬ / ‫احلل‬
: ‫االتية‬ ‫المكافئة‬ ‫المعادلة‬ ‫على‬ ‫نحصل‬ ) X - 2 ( ‫وهو‬ ‫للمقامات‬
. S = {3 { : ‫للمعادلة‬ ً‫ا‬‫جذر‬ 3 ‫ان‬ ‫نالحظ‬ ً‫ال‬‫اص‬ ‫المعادلة‬ ‫في‬ ‫وبالتعويض‬
‫ميثل‬ ‫ال‬ ‫والذي‬ ) x - 2 ) ( 2 - x ( ‫باملقدار‬ ‫املعادلة‬ ‫طرفي‬ ‫نضرب‬ ‫أن‬ ‫هي‬ ‫الصحيحة‬ ‫غير‬ ‫الطريقة‬ ‫أما‬
‫ولذلك‬ ‫االصلية‬ ‫املعادلة‬ ‫حتقق‬ ‫ال‬ x = 2 ‫وقيمة‬ x= 2 , x = 3 ‫على‬ ‫نحصل‬ ‫سوف‬ ‫الننا‬ ‫الصحيح‬ ‫املضاعف‬
. ‫استبعادها‬ ‫يجب‬
∴ S = {3 {
2
0
=
y
2-y
⎛
⎝
⎜
⎞
⎠
⎟
‫مالحظة‬ ‫يجب‬ ‫متغيرها‬ ‫على‬ ‫يحتوي‬ ‫بمقدار‬ ‫معادلة‬ ‫طرفي‬ ‫ضرب‬ ‫عند‬
‫الى‬ ‫بالضرورة‬ ‫تؤدي‬ ‫ال‬ ‫الضرب‬ ‫عملية‬ ‫الن‬ ‫صحته‬ ‫من‬ ‫التحقق‬
. ‫القوى‬ ‫الى‬ ‫المعادلة‬ ‫طرفي‬ ‫رفع‬ ‫عملية‬ ‫كذلك‬ . ‫لالصل‬ ‫مكافئة‬ ‫معادلة‬
6
x-2
+
x
2-x
=3
x-2( )
6
x-2
+ x-2( )
x
2-x
=3 x-2( )
6-x=3x-6
4x=12
∴ x=3
∅ = ‫الحل‬ ‫مجموعة‬
‫مالحظة‬‫عزيزي‬ ‫الحظ‬
x - a = -( a- x ( : ‫أن‬ ‫الطالب‬
- (x-2)
-1

112. 112
: ‫االتية‬ ‫املعادالت‬ ‫من‬ ‫كال‬ ‫/حل‬ 1‫س‬
1 -
2 -
3 -
4 - ‫طريقة‬ ‫من‬ ‫باكثر‬
5 -
6 -
7- ‫بالدستور‬
) 44m2
( ‫المستطيل‬ ‫مساحة‬ ‫كانت‬ ‫فاذا‬ ) 1m( ‫بمقدار‬ ‫عرضه‬ ‫أمثال‬ ‫ثالثة‬ ‫عن‬ ‫يقل‬ ‫مستطيل‬ ‫س2/طول‬
. ‫المستطيل‬ ‫ابعاد‬ ‫جد‬
. ) 149( ‫يساوي‬ ‫مربعاتها‬ ‫مجموع‬ x-1( ) ، x ، x+1( ) ‫موجبة‬ ‫أعداد‬ ‫ثالثة‬ /3‫س‬
. ‫االعداد‬ ‫هذه‬ ‫جد‬
‫(03)؟‬ ‫الناتج‬ ‫كان‬ ‫مربعه‬ ‫الى‬ ) 5( ‫اضيف‬ ‫اذا‬ ‫الذي‬ ‫العدد‬ ‫ما‬ / 4 ‫س‬
4 3
x+1( ) x-3( ) = 12
y2
=7y
3t2
-4=-11t
2x-1( )
2
= 2x-1( )........
x2
-5=3x
4x2
+9=12x.......
1
3
x2
=
1
2
x-
5
6
........
‫بالدستور‬

113. 113
‫بمقدار‬ ُ‫ه‬‫وقاعدت‬ ُ‫ه‬‫أرتفاع‬ ‫من‬ ‫كل‬ ‫زاد‬ ‫فاذا‬ ) 1cm( ‫بمقدار‬ ‫ارتفاعه‬ ‫عن‬ ‫يزيد‬ ‫قاعدته‬ ‫طول‬ ‫مثلث‬ /5‫س‬
. ‫واالرتفاع‬ ‫القاعدة‬ ‫)جدطول‬21cm2
( ‫مساحته‬ ‫)أصبحت‬ 2cm(
‫ضلع‬ ‫طول‬ ‫متساوية‬ ‫مربعات‬ ‫اربعة‬ ‫زواياها‬ ‫من‬ ‫قطعت‬ ) y cm( ‫ضلعها‬ ‫طول‬ ‫الشكل‬ ‫مربعة‬ ‫/قطعة‬ 6‫س‬
‫غطاء‬ ‫بدون‬ ‫مستطيله‬ ‫سطوح‬ ‫متوازي‬ ‫شكل‬ ‫على‬ ‫صندوق‬ ‫فتكون‬ ‫بعدها‬ ‫وثنيت‬ ) 2cm( ‫منها‬ ‫كل‬
. ‫المربعة‬ ‫القطعة‬ ‫طول‬ ‫جد‬ .) 242 cm3
( ‫حجمه‬
‫وتره‬ ‫وطول‬ ‫االخر‬ ‫القائم‬ ‫الضلع‬ ‫عن‬ ) 2cm( ‫يزيد‬ ‫القائمين‬ ‫ضلعيه‬ ‫أحد‬ ‫طول‬ ‫الزاويه‬ ‫قائم‬ ‫مثلث‬ / 7‫س‬
. ‫مساحته‬ ‫وما‬ ‫المثلث‬ ‫اضالع‬ ‫أطوال‬ ‫جد‬ . ‫الصغير‬ ‫القائم‬ ‫الضلع‬ ‫طول‬ ‫ضعف‬ ‫)عن‬ 2cm( ‫يقل‬
/ 8‫س‬
‫؟‬ ‫متساويين‬ ‫جذرين‬ ‫للمعادلة‬ ‫تجعل‬ ‫التي‬ ) m( ‫الثابت‬ ‫قيمة‬ ‫ما‬ -a
‫؟‬ ‫متساويين‬ ‫المعادلة‬ ‫جذري‬ ‫تجعل‬ ‫التي‬ ) n( ‫الثابت‬ ‫ماقيمة‬ -b
: ‫منها‬ ‫كل‬ ‫في‬ ‫االجابة‬ ‫صحة‬ ‫وحقق‬ ‫االتية‬ ‫المعادالت‬ ‫/حل‬ 9‫س‬
a) 3y+5
2y-1
=
6y+2
5y-4
b) 5
x+2
+
3
2-x
=
2
x2
-4
c) y-7
y2
-2y
=
y
y-2
-
y+4
y
d) 2y
1-3y
=
5
3y-1
m y2
+y+1( )=y+1
w2
-16=n w+4( )

114. ‫الهندسة‬
Triangle ‫املثلث‬
‫الرياضية‬ ‫العالقة‬ ‫او‬ ‫الرمز‬ ‫املصطلح‬
‫الزاوية‬
Side S ‫الضلع‬
‫التطابق‬ ‫عالقة‬
m∠A A ‫الزاوية‬ ‫قياس‬
Angle ∠
≅
. ‫مراجعة‬ ]5-1[
. ‫املثلث‬ ‫زوايا‬ ‫منصفات‬ ]5-2[
. ‫للمثلث‬ ‫املتوسطة‬ ‫القطع‬ ]5-3[
A
B
C
5‫اخلامس‬ ‫الفصل‬

115. ‫االشكال‬ ‫بعض‬ ‫التفصيل‬ ‫من‬ ‫بشئ‬ ‫ودرسنا‬ ‫أساسية‬ ‫هندسية‬ ‫مفاهيم‬ ‫على‬ ‫تعرفنا‬ ‫سابقة‬ ‫دراسية‬ ‫مراحل‬ ‫في‬
،‫الدائرة‬ :‫األشكال‬ ‫هذه‬ ‫ومن‬ ‫المختلفة‬ ‫الحياتية‬ ‫المسائل‬ ‫في‬ ‫وتطبيقاتها‬ ‫وخواصها‬ ‫المعروفة‬ ‫الهندسية‬
.‫الخ‬ . . ‫والمثلث‬ ‫المربع‬
.‫مختلفة‬ ‫زوايا‬ ‫من‬ ‫والدائرة‬ ‫المثلث‬ ‫الى‬ ‫المرحلة‬ ‫هذه‬ ‫في‬ ‫نتطرق‬ ‫وسوف‬
:‫الضالعه‬ ‫بالنسبة‬ ‫نوعه‬ a
» ‫منتظم‬ « ‫االضالع‬ ‫متساوي‬ ‫االضالع‬ ‫مختلف‬
60° ‫فيه‬ ‫زاوية‬ ‫كل‬ ‫قياس‬
‫الساقين‬ ‫متساوي‬
AC = AB
:‫الساقين‬ ‫المتساوي‬ ‫المثلث‬ ‫خواص‬ ‫ومن‬
. )m ∠ C = m ∠ B( ‫متطابقتان‬ ‫القاعدة‬ ‫زاويتي‬ )1
.‫وينصفها‬ BC ‫القاعدة‬ ‫على‬ ‫عمودي‬ A ‫الرأس‬ ‫زاويه‬ ‫منصف‬ )2
NB = CN , AN BC , CB AN
‫ينصف‬
B
A
N
C
5 - 1‫مراجعة‬
‫املثلث‬
‫الفصل‬
5
A
BC
A
BC
AC = AB = BC
AC≠AB≠BC
‫عليه‬ ‫وعمودي‬

116. 116
:‫لزواياه‬ ‫بالنسبة‬ ‫نوعه‬ b
‫الزاوية‬ ‫قائم‬ ‫الزاوية‬ ‫منفرج‬ ‫الزوايا‬ ‫حاد‬
. S : side ، (S S S ( :‫الثالثة‬ ‫باالضالع‬ ‫تطابق‬ )1
∆ ABC ≅ ∆DFE
S.A.S . )‫بينهما‬ ‫(محصورة‬ ‫بهما‬ ‫المحددة‬ ‫والزاوية‬ ‫بضلعين‬ ‫تطابق‬ )2
∆ ABC ≅ ∆DEF
:‫املثلثني‬ ‫تطابق‬ ‫حاالت‬
D
E F
A
C B
A
B C
F
D
E

117. 117
)A.A.S( ‫مناظر‬ ‫وضلع‬ ‫بزاويتين‬ ‫تطابق‬ )3
∆ DEF ≅ ∆ ABC
.‫قائم‬ ‫وضلع‬ ‫بوتر‬ ‫الزاوية‬ ‫القائما‬ ‫املثلثان‬ ‫يتطابق‬ )4
∆ ABC ≅ ∆ DEF
:‫فيه‬ ‫رباعي‬ ‫شكل‬ PQRN:‫املجاور‬ ‫الشكل‬ ‫في‬
QR = QN = PQ , RQ NP
m ∠ 3, m ∠ 2, m ∠ 1 : ‫جد‬ m ∠ R = 70°
‫معطى‬ QR = QN ∵ /‫احلل‬
‫الساقني‬ ‫متساوي‬ ∆ ‫خواص‬ m ∠ R = m ∠ 4∴
∴ m ∠ 4 = 70°
‫املثلث‬ ‫زوايا‬ ‫مجموع‬ m∠1=180°-(70°×2(
∴ m 1 = 40°
‫معطى‬ RQ NP
)‫(متبادلة‬ ∴m ∠ 2 = m ∠ 1
∴ m ∠ 2 = 40°
A
B C
E
D
F
C
B
AD
E
F
(1) ‫مثال‬
P
R
N
Q
1 2
4
3
70ْ

118. 118
:‫المجاور‬ ‫الشكل‬ ‫في‬
AB = AC ‫فيه‬ ‫الساقين‬ ‫متساوي‬ ‫مثلث‬ ABC
AD = AE ‫ان‬ ‫بحيث‬ E ∈AC , D ∈ AB
∆ AEB ≅ ∆ ADC :‫ان‬ ‫أثبت‬
/ ‫المعطيات‬
‫للطالب‬ ‫تترك‬
/ ‫أثباته‬ .‫م‬
:‫فيهما‬ AEB , ADC ∆ ∆/ ‫البرهان‬
‫معطى‬ ... AE = AD
‫معطى‬ ... AC = AB
‫بينهما‬ ‫مشتركة‬ A ‫الزاوية‬
.‫بهما‬ ‫المحددة‬ ‫والزاوية‬ ‫بضلعين‬ ∆∆ ‫يتطابق‬ ∴
)‫(و.هـ.م‬
( 2 ) ‫مثال‬
C
A
B
DE
{
m p = m 2 = 40o
m 3 = 180o
− (40o
× 2)
∴m 3 = 100o
‫الساقين‬ ‫متساوي‬ ‫مثلث‬
‫المثلث‬ ‫زوايا‬ ‫مجموع‬

119. 119
/‫المعطيات‬
DO = AD , EB = AE , ∆ABO
/‫م.ث‬
DE = OB (2 , OB DE )1
/‫والبرهان‬ ‫العمل‬
. ON ‫فيكون‬ N ‫في‬ ED ‫امتداد‬ ‫فيالقي‬ BE ‫يوازي‬ ً‫ا‬‫مستقيم‬ ‫نرسم‬ O ‫نقطة‬ ‫من‬
AAS ‫مناظر‬ ‫وضلع‬ ‫بزاويتين‬ ∆ ODN ≅ ∆ ADE
‫معطى‬ . AD = OD )1 :‫حيث‬
.‫بالرأس‬ ‫متقابلة‬ . . . m ∠ ODN= m ∠ ADE )2
.ON BA ‫الن‬ ‫متبادلة‬ ... m ∠ 2 = m ∠ 1 )3
‫المتطابقة‬ ‫االشكال‬ ‫في‬ ‫المتناظرة‬ ‫االجزاء‬ ‫تتساوى‬ , DN=DE :‫التطابق‬ ‫من‬
...ON = AE
...EB = AE
ON= BE :‫على‬ ‫نحصل‬ )2( ، )1( ‫من‬
‫بالعمل‬ ON BE ‫الن‬ ‫أضالع‬ ‫متوازي‬ EBON ‫الشكل‬ ∴
‫االضالع‬ ‫متوازي‬ ‫خواص‬ ... BO = EN ، BO EN ∴
‫بالبرهان‬ DN = DE
DE=
1
2
EN ∴
)‫و.هـ.م‬ ( DE = OB , OB DE ∴
)1(
‫معطى‬ )2(
‫ضلعه‬ ‫توازي‬ ‫مثلث‬ ‫ضلعي‬ ‫منتصفي‬ ‫بني‬ ‫الواصلة‬ ‫املستقيم‬ ‫قطعة‬
.‫طوله‬ ‫نصف‬ ‫وطولها‬ ‫الثالث‬
1 /‫مبرهنة‬
1
2
1
2
B
E
A
D
N
O
2
1

120. 120
x ‫قيمه‬ ‫جد‬ : ‫المجاور‬ ‫الشكل‬ ‫في‬
/‫احلل‬
AB ‫منتصف‬ D
BC ‫منتصف‬ E
)1
)2
∴ 3x = (5x+4)
6x = 5x + 4 :2 ‫في‬ ‫الطرفين‬ ‫بضرب‬
x = 4∴
:‫المجاور‬ ‫الشكل‬ ‫في‬
‫؟‬m ∠ 1 = m ∠ 2 :‫ان‬ ‫هل‬ )1(
ABC ‫المثلث‬ ‫مساحة‬ ‫ما‬ ، DE ‫(2)جد‬
AB ‫منتصف‬ D/‫احلل‬
AC ‫منتصف‬ E
DE BC
( 1 ) ‫مثال‬
1
2
1
2
x ‫جد‬ ‫الشكل‬ ‫في‬
‫للطالب‬ ‫تمرين‬
( 2 ) ‫مثال‬
))1( ‫(مبرهنة‬
AB
C
E
D
5x+4
3x
B
A
C
D Ex
32 − 8
)3(
A
B C
D E
125
2X
2
x
1
{)1( ‫مبرهنة‬
1
2
DE = BC
DE AC
DE = AC ∴

121. 121
m ∠1 =m ∠2 )1
DE BC ‫الن‬
(AB)2
+ (BC)2
= (AC)2
(2x)2
+ x2
=
5x2
= 125 ⇒ x2
= 25
∴x = 5
∴ DE = BC .... ( 1 ‫)مبرهنة‬
‫المثلث‬ ‫مساحة‬ )3
= × BC × AB
= ×5×10
= 25 ‫مساحة‬ ‫وحدة‬
:‫فيه‬ ∆ ABC :‫المجاور‬ ‫الشكل‬ ‫في‬
. ‫جد‬ BC = 8cm ،‫الترتيب‬ ‫على‬ AC , BC , AB ‫االضالع‬ ‫منتصفات‬ H , E , D
. DH )1(
.‫اضالع‬ ‫متوازي‬ DECH ‫ان‬ ‫أثبت‬ )2(
‫معطى‬ .... ‫المثلث‬ ‫أضالع‬ ‫منصفات‬ H , E , D /‫احلل‬
DH = BC ∴
DH BC
DH = × 8 ∴
DH = 4 cm ∴
DH = EC = 4 cm∴
‫اضالع‬ ‫متوازي‬ DECH : ‫∴الشكل‬ DH EC
1
2
1
2
125( )
2
( 3 ) ‫مثال‬
1
21 ‫مبرهنة‬
1
2
C
A
B
DH
E
8 cm
.ABC ‫القائم‬ ∆ ‫على‬ ‫فيثاغورس‬ ‫مبرهنة‬ ‫نطبق‬ )2
‫متناظرة‬
‫المثلث‬ ‫مساحة‬
{
»‫ومتطابقني‬ ‫متوازيني‬ ‫متقابلني‬ ‫ضلعني‬ ‫فيه‬ ‫كان‬ ‫اذا‬ ‫أضالع‬ ‫متوازي‬ ‫الرباعي‬ ‫الشكل‬ ‫«يكون‬
1
2
=
5
2
⇒ BC = 5 ‫طول‬ ‫وحدة‬
⇒ DE =
1
2
(5) =
5
2
‫طول‬ ‫وحدة‬

122. 122
)1(......
)2(......
/‫المعطيات‬
DE BC , AB ‫منتصف‬ D :‫فيه‬ ∆ ABC
/‫أثباته‬ ‫المطلوب‬
AE = EC
/‫والبرهان‬ ‫العمل‬
H ‫نقطة‬ ‫في‬ DE ‫أمتداد‬ ‫فيالقي‬ C ‫نقطة‬ ‫من‬ ‫نرسم‬
‫اضالع‬ ‫متوازي‬ DBCH:‫الشكل‬ ∴
»‫األضالع‬ ‫متوازي‬ ‫تعريف‬ «
‫االضالع‬ ‫متوازي‬ ‫خواص‬ CH = BD∴
‫معطى‬ DA = BD
)‫مناظر‬ ‫وضلع‬ ‫(زاويتان‬ ‫متطابقان‬ CHE , ADE ‫∴المثلثان‬
) ‫م‬ . ‫هـ‬ .‫و‬ ( ‫متطابقة‬ ‫اشكال‬ ‫في‬ ‫متناظره‬ ‫...اجزاء‬ AE = EC :‫التطابق‬ ‫من‬
. AC = 6 cm , BC = 7 cm , AB = 5 cm ‫فيه‬ ∆ABC :‫الشكل‬ ‫في‬
. ∆MHD ‫محيط‬ ‫وما‬ AB ∥ DH ‫ان‬ ‫أثبت‬ AC ∥ MH , BC ∥ MD, AB ‫منتصف‬ M
/‫البرهان‬
‫معطى‬ MD ∥ BC , AB ‫منتصف‬ M
)1( ... 2 ‫مبرهنة‬ AD = DC∴
‫...معطى‬ MH∥ AC∵
.‫الثالث‬ ‫الضلع‬ ‫ينصف‬ ‫فيه‬ ٍ‫ثان‬ ‫لضلع‬ ً‫ا‬‫موازي‬ ‫مثلث‬ ‫أضالع‬ ‫أحد‬ ‫مبنتصف‬ ‫املار‬ ‫املستقيم‬
2 /‫مبرهنة‬
A
DEH
C B
‫مثال‬
A
BC
D
H
M
6 cm
5 cm
BD ‫يوازي‬ ً‫ا‬‫مستقيم‬
7 cm

123. 123
)2( ‫مبرهنة‬ ... BH = CH∴
: ‫على‬ ‫نحصل‬ )2(‫و‬ )1( ‫من‬
)1( ‫...مبرهنة‬ DH = AB , DH ∥AB
‫الثالثة‬ ‫أضالعه‬ ‫أطوال‬ ‫مجموع‬ ‫يساوي‬ ‫المثلث‬ ‫محيط‬
MH + HD + DM = ‫المثلث‬ ‫محيط‬ ∴
( × 6)+( × 5) + ( × 7) =
9 cm
‫هذه‬ ‫توفر‬ ‫عند‬ AC( ) ‫الوتر‬ ‫منتصف‬ ‫نقطة‬ D , B ‫في‬ ‫الزاوية‬ ‫قائم‬ ‫مثلث‬ ABC ‫المجاور‬ ‫الشكل‬ ‫في‬
BD = AD = DC : ‫على‬ ‫نحصل‬ ‫المعطيات‬
1
2
1
2
1
2
1
2
‫الوتر‬ ‫منتصف‬ ‫الى‬ ‫الزاوية‬ ‫القائم‬ ‫المثلث‬ ‫في‬ ‫القائمة‬ ‫رأس‬ ‫من‬ ‫المرسومة‬ ‫المستقيمة‬ ‫القطعة‬ ‫طول‬
. ‫الوتر‬ ‫طول‬ ‫نصف‬ ‫تساوي‬
3 /‫مبرهنة‬
A
BC
D
‫برهان‬ ‫بدون‬ ‫المبرهنة‬ ‫هذه‬ ‫سنقبل‬
6
2
+
5
2
+
7
2
+
18
2
=

124. 124
. AC ‫منتصف‬ D ‫فيه‬ ABC Δ : ‫المجاور‬ ‫الشكل‬ ‫في‬
BD ‫جد‬
x ‫قيمة‬ ‫إليجاد‬ /‫احلل‬
‫فيثاغورس‬ ‫مبرهنة‬ ‫نطبق‬
،‫األضالع‬ ‫متساوي‬ ‫مثلث‬ ADB ‫ان‬ ‫أثبت‬ ،B‫في‬ ‫الزاوية‬ ‫قائم‬ ABC
/‫احلل‬
‫منتصف‬ D ∵
3 ‫مبرهنه‬ BD=
1
2
AC ∴
) ‫االضالع‬ ‫(متساوي‬ ‫منتظم‬ ADB Δ ∴
‫المثلث‬ ‫زوايا‬ ‫من‬ ‫زاويه‬ ‫كل‬ ‫قياس‬
‫مثلث‬ ‫زوايا‬ ‫مجموع‬
m C=180o
− m B+m A( ) ∴
( 1 ) ‫مثال‬
AC( )
2
= AB( )
2
+ BC( )
2
2 5x( )
2
=42
+22
20x2
=20
⇒ x2
=1
⇒ x=1 x0( )
BD=
1
2
AC
∴ BD
1
2
x2 5= 5 cm
( 2 ) ‫مثال‬
A
BC
D
2cm
2
5X
4cm
AC
∴ BD= 4 cm
60o
= ADB
=180o
− 90o
+60o
( )
=180o
− 150o
∴ mc = 30o
A
BC
D
4 cm
8 cm
BD=
1
2
.
AC ‫منتصف‬ D ABC Δm∠C ‫جد‬ ‫ثم‬
60o
= ADB‫تساوي‬
∠
∠ ∠ ∠
∴ m C
AC = 8 ,

125. 125
: ‫ان‬ ‫أثبت‬ BC ‫منتصف‬ ‫نقطة‬ M ، ‫معين‬ ABCD /1‫س‬
: ‫فيه‬ ‫االضالع‬ ‫متساوي‬ ABC ∆ /2‫س‬
: ‫ان‬ ‫أثبت‬
: ‫المجاور‬ ‫الشكل‬ ‫في‬ /3‫س‬
) ‫الساقين‬ ‫(متساوي‬ AB = AC ‫فيه‬ ‫مثلث‬ ABC
: ‫فيه‬
MD ‫جد‬ ‫متنصف‬ ‫نقطه‬ M
5 1
OM =
1
2
AB, OM / / AB
AB ⊥ CH , AD ⊥ BC
DH / /AC
A
BC D
H
BC=12 cm , AD=8 cm
AB
A
BC D
M
A
BC
D
o
M

126. 126
: ‫فيه‬ ‫الساقني‬ ‫متساوي‬ ‫مثلث‬ ABC /4‫س‬
BC ‫منتصف‬ D , AB ‫منتصف‬ M , AB = AC
‫معني‬ AMDN : ‫ان‬ ‫أثبت‬ ‫منتصف‬ N ,
‫ان‬ ‫بحيث‬ AB ‫على‬ N ، M ‫النقطتان‬ ‫فرضت‬ ، ‫مثلث‬ ABC /5‫س‬
: ‫ان‬ ‫أثبت‬ O ‫في‬ AD , CM ‫وتقاطعت‬ D ‫النقطه‬ ‫في‬ BC ‫ونصفت‬
CM // DN )1
AD ‫منتصف‬ O )2
)3
N ‫في‬ CD ‫نصفت‬ ، P ‫في‬ BC ‫نصفت‬ ، O ‫في‬ ‫قطراه‬ ‫تقاطع‬ ، ‫أضالع‬ ‫متوازي‬ ABCD /6‫س‬
.‫أضالع‬ ‫متوازي‬ OPCN : ‫أن‬ ‫أثبت‬
AC
AM=MN=NB
MO=
1
4
MC

127. 127
‫أضالع‬ ‫على‬ ‫أعمدة‬ ‫أقيمت‬ ‫منتصف‬ P ، ‫منتصف‬ R ، ‫منتصف‬ G ‫فيه‬ ‫مثلث‬ ABC
OB = OA = OC : ‫ان‬ ‫على‬ ‫ذلك‬ ‫من‬ ‫نحصل‬ .O ‫نقطه‬ ‫في‬ ‫فالتقت‬ R , P , G ‫من‬ ‫المثلث‬
, , ‫منتصف‬ R , ‫منتصف‬ D , :‫الشكل‬ ‫في‬
. OR , OA ‫جد‬ AC=8 cm , OB=5 cm , OE ⊥ BC
BC , AB ‫الضلعين‬ ‫منتصف‬ E , D ‫حيث‬ OE ⊥ BC , OD ⊥ AB ∵ /‫احلل‬
. ‫منتصفاتها‬ ‫من‬ ‫المثلث‬ ‫أضالع‬ ‫على‬ ‫المقامة‬ ‫االعمدة‬ ‫ملتقى‬ ‫نقطه‬ 0 ∴
4 ‫مبرهنة‬ ...... OC=OB=OA
OA=5 cm
AC ‫منتصف‬ R ∵
‫القاعدة‬ ‫ومنتصف‬ ‫الساقين‬ ‫متساوي‬ ‫مثلث‬ ‫راس‬ ‫بين‬ ‫الواصل‬ ‫المستقيم‬ ‫قطعه‬ ... AC ⊥ OR ∴
. ‫القاعدة‬ ‫على‬ ‫عمودية‬ ‫تكون‬
AR=4 cm , R ‫في‬ ‫الزاوية‬ ‫قائم‬ ORA ∴
AO( )
2
= AR( )
2
+ RO( )
2
‫فيثاغورس‬
∴ RO = 3 cm
‫االبعاد‬ ‫متساوية‬ ‫تكون‬ ‫واحدة‬ ‫نقطة‬ ‫في‬ ‫تتالقى‬ ‫منتصفاتها‬ ‫من‬ ‫مثلث‬ ‫اضالع‬ ‫على‬ ‫المقامة‬ ‫االعمدة‬
.‫المثلث‬ ‫رؤوس‬ ‫عن‬
4 /‫مبرهنة‬
ACBCAB
‫مثال‬
ABACOD ⊥ AB
C
G
A
P
B
R
O
A
D
B
E
C
R
O
8
5
55
ABAB
25 = 16 + RO( )
2
BC ‫منتصف‬ E

128. 128
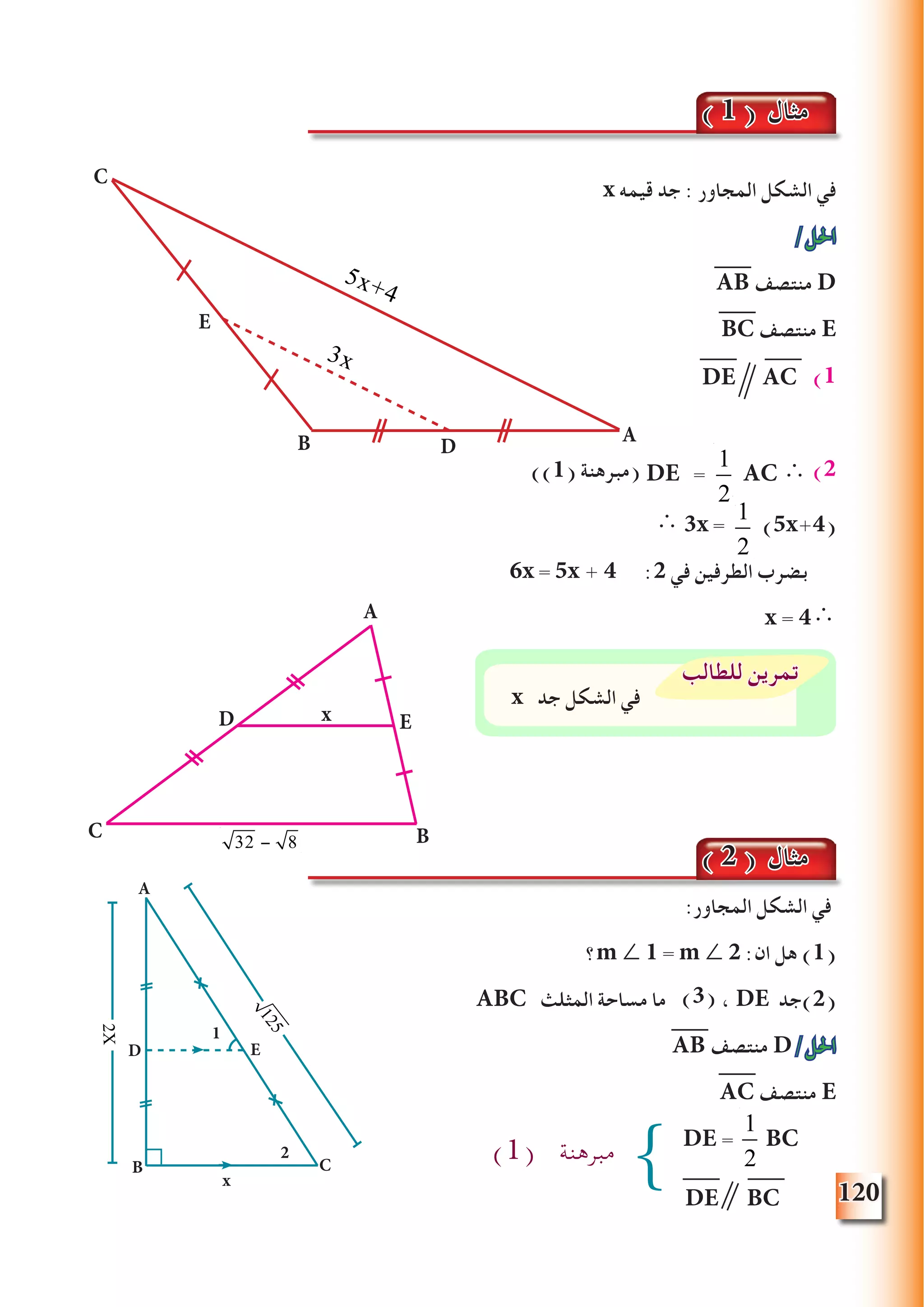
‫املثلث‬ ‫زوايا‬ ‫منصفات‬ ] 5 ‫ـ‬ 2[
‫املستقيم‬ ‫عن‬ ‫نقطه‬ ‫عد‬ُ‫ب‬ )5 ‫ـ‬ 1( ‫تعريف‬
. ‫المستقيم‬ ‫الى‬ ‫النقطة‬ ‫من‬ ‫المرسومة‬ ‫العمودية‬ ‫المستقيمة‬ ‫القطعة‬ ‫طول‬ ‫هو‬
AB ⊥ L , A ∉ L
‫عن‬ A ‫النقطة‬ ‫عد‬ُ‫ب‬ AB
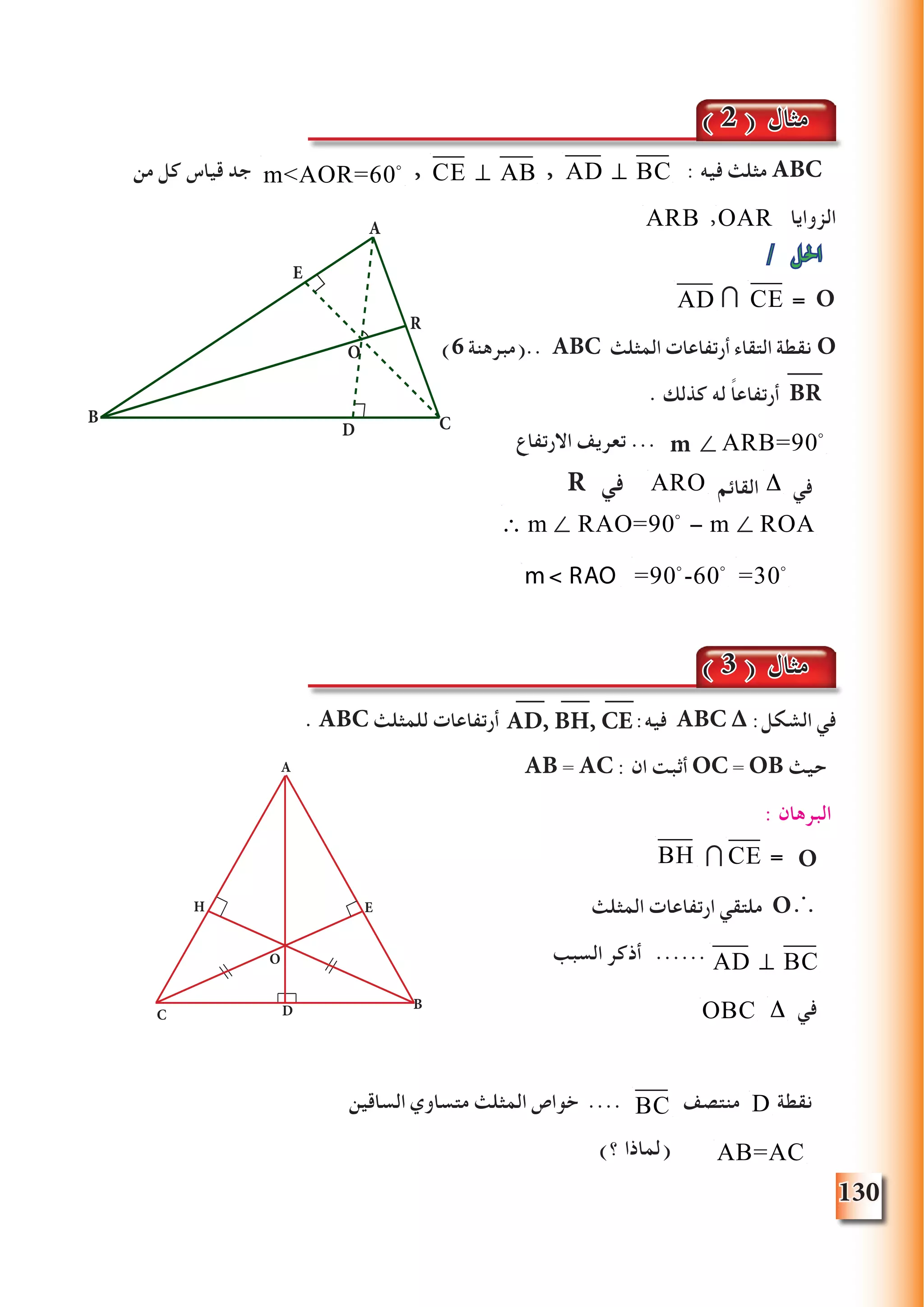
OC , OB , OA :‫فيه‬ ‫مثلث‬ ABC : ‫الشكل‬ ‫في‬
C , B , A ‫الزوايا‬ ‫منصفات‬
OG=OP=OR : ‫ان‬ ‫على‬ ‫نحصل‬ ‫المعطيات‬ ‫هذه‬ ‫من‬
O ‫نقطه‬ ‫من‬ ‫مرسومة‬ ‫أعمدة‬ OR , OP , OG ‫حيث‬
AC , BC , AB ‫على‬
5 - 2‫املثلث‬ ‫زوايا‬ ‫منصفات‬
. ‫أضالعه‬ ‫عن‬ ‫االبعاد‬ ‫متساوية‬ ‫تكون‬ ‫واحدة‬ ‫بنقطة‬ ‫تتالقى‬ ‫المثلث‬ ‫زوايا‬ ‫منصفات‬
5 /‫مبرهنة‬
A
B
L
L
A
G
B
PC
R
O

129. 129
x ‫قيمه‬ ‫جد‬ : ‫الشكل‬ ‫في‬
/ ‫احلل‬
B ‫زاوية‬ ‫تنصف‬ BO
C ‫زاوية‬ ‫تنصف‬ CO
‫منصفات‬ ‫التقاء‬ ‫نقطة‬ O∴
. ABC ‫المثلث‬ ‫زوايا‬
)A ‫زاوية‬ ‫تنصف‬ AO(
‫مثلث‬ ‫زاويا‬ ‫مجموع‬
x=
1
2
mA=180o
- mB+mC( )m B+m C( )
=180o
-130o
∴ mA = 50
xo
=25o
. ‫برهان‬ ‫بدون‬ ‫المبرهنة‬ ‫هذه‬ ‫سنقبل‬
:‫المجاور‬ ‫الشكل‬ ‫في‬
AN , CM , BO ‫الثالثة‬ ‫االرتفاعات‬
P ‫نقطة‬ ‫في‬ ‫التقت‬ ‫للمثلث‬
( 1 ) ‫مثال‬
x=
1
2
mA
A
O
C B
35ْ
35ْ
30ْ
30ْ
x
A∠
m ∠ ∠ ∠
m A∠
. ‫واحدة‬ ‫بنقطة‬ ‫تلتقي‬ ‫المثلث‬ ‫أرتفاعات‬
6 /‫مبرهنة‬
C
O
A
M B
N
P
=180°−(70°+ 60°)

130. 130
‫من‬ ‫كل‬ ‫قياس‬ ‫جد‬
mAOR=60o , CE ⊥ AB , AD ⊥ BC : ‫فيه‬ ‫مثلث‬ ABC
ARB ,OAR ‫الزوايا‬
/ ‫احلل‬
AD⋂
)6 ‫..(مبرهنة‬ ABC ‫المثلث‬ ‫أرتفاعات‬ ‫التقاء‬ ‫نقطة‬ O
. ‫كذلك‬ ‫له‬ ً‫ا‬‫أرتفاع‬ BR
‫االرتفاع‬ ‫تعريف‬ ...
mARB=90o
ARO ‫القائم‬ Δ ‫في‬
=90o
-60
=30o
. ABC ‫للمثلث‬ ‫أرتفاعات‬ :‫فيه‬ ABC ∆ :‫الشكل‬ ‫في‬
AB = AC : ‫ان‬ ‫أثبت‬ OC = OB ‫حيث‬
: ‫البرهان‬
BH ⋂CE = 0{ }O
‫المثلث‬ ‫ارتفاعات‬ ‫ملتقي‬ O∴
‫السبب‬ ‫أذكر‬ ......
OBC Δ ‫في‬
‫الساقين‬ ‫متساوي‬ ‫المثلث‬ ‫خواص‬ .... BC ‫منتصف‬ D ‫نقطة‬
)‫؟‬ ‫(لماذا‬ AB=AC
A
B
C D
EH
O
∠
∴ m RAO=90o
− m ROA∠
( 3 ) ‫مثال‬
AD, BH, CE
AD ⊥ BC
( 2 ) ‫مثال‬
A
E
B
D C
R
O
m ∠
=30o
CE = 0{ }O
R ‫في‬
m RAO

131. 131
5 - 3‫للمثلث‬ ‫املتوسطة‬ ‫القطع‬
)5 ‫ـ‬ 2( ‫تعريف‬
. ‫الرأس‬ ‫لذلك‬ ‫المقابل‬ ‫الضلع‬ ‫منتصف‬ ‫ونقطة‬ ‫المثلث‬ ‫رأس‬ ‫هما‬ ‫طرفاها‬ ‫التي‬ ‫المستقيمة‬ ‫القطعة‬ ‫هي‬
. ‫متوسطة‬ ‫مستقيمة‬ ‫قطع‬ ‫ثالث‬ ‫مثلث‬ ‫لكل‬ :‫مالحظة‬
.O ‫في‬ ‫تلتقي‬ ‫متوسطة‬ ‫قطع‬ BR, CG, AP : ABC‫المثلث‬ ‫في‬
، O ‫نقطة‬ ‫في‬ ‫تلتقيان‬ ‫متوسطتان‬ ‫قطعتان‬ AD , CE ‫فيه‬ ABC ‫المثلث‬ : ‫المجاور‬ ‫الشكل‬ ‫في‬
. AO , OE ‫جد‬ AD=6 cm ، CE = 9 cm
ABC ‫المثلث‬ ‫متوسطات‬ ‫ملتقي‬ O/ ‫احلل‬
OE=
1
2
OC ∴
OE =
1
3
CE
‫متوسطة‬ ‫قطعة‬ AD ‫كذلك‬
2 : 1 ‫بنسبة‬ ‫منها‬ ‫كل‬ ‫تقسم‬ ‫واحدة‬ ‫نقطة‬ ‫في‬ ‫تتالقى‬ ‫للمثلث‬ ‫المتوسطة‬ ‫المستقيمة‬ ‫القطع‬
. ‫الرأس‬ ‫جهة‬ ‫من‬
7 /‫مبرهنة‬
( 4 ) ‫مثال‬
A
C B
E
D
∴ OA =
2
3
AD =
2
3
× 6=4 cm
A
R
C
P
B
G
•
• •
•
O
2
1
2
1
=
CO
OG
=
BO
OR
=
AO
OP
=
2
1
∴ OE =
1
3
. 9=3 cm
O
OR =
1
2
BO
OR =
1
3
BR
OB =
2
3
BR
‫المتوسطة‬ ‫القطعة‬

132. 132
‫منتصفاتها‬ ‫من‬ ABC ‫المثلث‬ ‫أضالع‬ ‫على‬ ‫المقامة‬ ‫االعمدة‬ ‫التقاء‬ ‫نقطة‬ O : ‫الشكل‬ ‫في‬ /1‫س‬
.OA ‫جد‬ ، m ∠ COB = 60ْ
O ‫من‬ ‫يمر‬ ‫مستقيم‬ ‫رسم‬ ‫ثم‬ ،O ‫نقطة‬ ‫في‬ ‫المنصفان‬ ‫فألتقى‬ C , B ‫الزاويتان‬ ‫نصفت‬ ABC ∆ /2‫س‬
. AH = HO ‫ان‬ ‫أثبت‬ M‫في‬ BC ‫ويقطع‬ H ‫في‬ AB ‫ويقطع‬ AC ‫ويوازي‬
AC⋂ BD = 0{ }}O{ , AB=AD=DC , AD / / BC : ‫فيه‬ ‫منحرف‬ ‫شبه‬ ABCD /3‫س‬
BHC ‫الزواية‬ ‫ينصف‬
HO
u ruu
: ‫ان‬ ‫برهن‬
BA
u ruu
I CD
u ruu
= H{ } ،
, ABC ‫المثلث‬ ‫أرتفاعات‬ ‫التقاء‬ ‫نقطة‬ O , AD ⊥ BC :‫فيه‬ ABC ‫المثلث‬ : ‫الشكل‬ ‫في‬ /4‫س‬
. mCHA , mACH :‫جد‬ mBAC=70o
5 2
O
A
BC
60ْ
10
A
C B
H
D
O
BC = 10 cm
BA ∩
m ∠m ∠m ∠
cm

133. 133
⋂ BC= D{ } , mCOB=90o ، ‫املتوسطة‬ ‫القطع‬ ‫التقاء‬ ‫نقطة‬ O , ABC ‫املثلث‬ /5‫س‬
. AD ‫جد‬ BC=6 cm ,
: ‫كان‬ ‫فاذا‬ . DEF ∆ ‫في‬ ‫املتوسطة‬ ‫القطع‬ ‫التقاء‬ ‫نقطة‬ O : ‫أعاله‬ ‫الشكل‬ ‫في‬ /6‫س‬
‫؟‬ OF ‫ميثله‬ ‫التاليه‬ ‫املقادير‬ ‫من‬ ‫فأى‬ GF=6x2
+9y
a) 2x2
+9y b) 2x2
+3y c) 6x2
+9y d) 4x2
+6y
‫؟‬x ‫لقيمة‬ ‫الصحيحة‬ ‫االجابة‬ ‫أختر‬ LG=5x+3 ،WL=15x : ‫كان‬ ‫اذا‬ : ‫الشكل‬ ‫في‬ /7‫س‬
a) 0.3 b) 0.4 c) 0.6 d) 1.2
G
F E
D
O
F
G
D
W
R
L
AO

134. ‫الدائرة‬
Circle
. ‫الدائرة‬ ]6-1[
. ‫الدائرة‬ ) ‫(رسم‬ ‫تعيني‬ ‫كيفية‬ ]6-2[
. ‫االقواس‬ ]6-3[
. ‫التماس‬ ] 6 - 4[
A
B
C
D
N
O
A
B
O 2
O 1
1
‫ق‬‫ن‬
3
‫ق‬‫ن‬
‫ف‬‫ن‬‫ص‬‫م‬‫ال‬‫د‬‫و‬‫م‬‫ع‬‫ال‬
2
‫ق‬‫ن‬ O
r
r
r
‫الرياضية‬ ‫العالقة‬ ‫او‬ ‫الرمز‬ ‫املصطلح‬
r ‫القطر‬ ‫نصف‬
π ‫الثابتة‬ ‫النسبة‬
AB AB ‫القوس‬
6‫السادس‬ ‫الفصل‬

135. ]6 - 2[ ‫تعريف‬
‫قطر‬ ‫نصف‬
]6 - 3[ ‫تعريف‬
‫الدائرة‬ ‫وتر‬
]6 - 1[ ‫تعريف‬
‫الدائرة‬
]6 - 4[ ‫تعريف‬
‫الدائرة‬ ‫قطر‬
O
6
‫الدائرة‬
‫ورسمها‬ ‫حياته‬ ‫في‬ ‫عديدة‬ ‫مجاالت‬ ‫في‬ ‫واستخدمها‬ ‫خواصها‬ ‫درس‬ ‫حيث‬ ‫قديم‬ ‫زمن‬ ‫منذ‬ ‫الدائرة‬ ‫االنسان‬ ‫عرف‬
. ‫المتاحة‬ ‫الوسائل‬ ‫بأبسط‬
. ‫أخرى‬ ‫زاوية‬ ‫من‬ ‫الدائرة‬ ‫المرحلة‬ ‫هذه‬ ‫في‬ ‫ندرس‬ ‫وسوف‬
‫نقطة‬ ‫عن‬ ٍ‫ومتساو‬ ‫ثابت‬ ‫ببعد‬ ‫منها‬ ‫كل‬ ‫تبعد‬ ‫والتي‬ ‫المستوي‬ ‫نقاط‬ ‫مجموعة‬
. )Center = ‫(المركز‬ ‫تسمى‬ ‫ثابتة‬
.)Radius = r ‫القطر‬ ‫نصف‬ ‫طول‬ ‫الثابت‬ ‫البعد‬ ‫يسمى‬ (
.‫نقاطها‬ ‫من‬ ‫نقطة‬ ‫واية‬ ‫الدائرة‬ ‫مركز‬ ‫بين‬ ‫الواصلة‬ ‫المستقيم‬ ‫قطعة‬
.‫الدائرة‬ ‫نقاط‬ ‫من‬ ‫نقطتين‬ ‫أية‬ ‫بين‬ ‫الواصله‬ ‫المستقيم‬ ‫قطعة‬
.‫بمركزها‬ ‫المار‬ ‫الدائرة‬ ‫وتر‬
6 - 1 Circle )‫(الدائرة‬
‫الفصل‬
6
‫تعاريف‬ ]6 - 1 - 1[
A
B
C
D
N
O
r
‫ر‬‫ت‬‫و‬
‫ر‬‫ط‬‫ق‬

136. 136
‫من‬ ‫محدد‬ ‫غير‬ ‫عدد‬ ‫تعيين‬ ‫يمكن‬ A ‫مثل‬ ‫معلومة‬ ‫نقطة‬ ‫من‬ )1
. ‫الدوائر‬
‫واحدة‬ ‫دائرة‬ ‫تعييـن‬ ‫يمكن‬ ‫ال‬ B , A ‫مثل‬ ‫معلومتين‬ ‫نقطتين‬ ‫من‬ )2
) B , A ‫تحتوي‬ ‫الـدوائر‬ ‫مــن‬ ‫محــددة‬ ‫غير‬ ‫مجموعة‬ ‫(هناك‬
‫العمود‬ ‫على‬ ‫تقع‬ ‫نقطة‬ ‫أية‬ ‫المجموعة‬ ‫هذه‬ ‫مركز‬ ‫ويكون‬
. AB ‫للقطعة‬ ‫المنصف‬
. ‫دائرة‬ ‫أية‬ ‫تتعين‬ ‫ال‬ ‫واحدة‬ ‫أستقامة‬ ‫على‬ ‫نقاط‬ ‫ثالث‬ ‫من‬ - a )3
‫تتعين‬ ‫واحدة‬ ‫أستقامة‬ ‫على‬ ‫ليست‬ ‫نقاط‬ ‫ثالث‬ ‫من‬ - b
:‫اآلتية‬ ‫المبرهنة‬ ‫تنص‬ ‫كما‬ ‫فقط‬ ‫واحدة‬ ‫دائرة‬ )‫رسم‬ ‫(يمكن‬
‫برهان‬ ‫بدون‬ ‫المبرهنة‬ ‫نقبل‬ ‫سوف‬
:‫المجاور‬ ‫الشكل‬ ‫في‬ /‫توضيح‬
‫واحدة‬ ‫أستقامة‬ ‫على‬ ‫ليست‬ ‫نقاط‬ ‫ثالث‬ A , B , C
. ) ABC ‫المثلث‬ ‫رؤوس‬ ‫تشكل‬ ‫أنها‬ ‫(اي‬
BC , AB , AC ‫أضالعه‬ ‫منتصفات‬ ‫هي‬ P , N , M ‫والنقط‬
‫االضالع‬ ‫هذه‬ ‫على‬ ‫المقامة‬ ‫االعمدة‬ ‫ألتقت‬ ‫حيث‬ ‫الترتيب‬ ‫على‬
‫النقطة‬ ‫هذه‬ ‫فتكون‬ )O( ‫نقطة‬ ‫في‬ P , N , M ‫المنتصفات‬ ‫من‬
‫ومتساوية‬C,B,A‫المثلث‬‫برؤوس‬‫المارة‬‫الدائرة‬‫مركز‬)O(
. ً‫ا‬‫سابق‬ ‫مر‬ ‫كما‬ . ) r = OC = OB = OA( ‫عنها‬ ‫البعد‬
6 - 2‫الدائرة‬ )‫(رسم‬ ‫تعيني‬ ‫كيفية‬
. ‫واحدة‬ ‫دائرة‬ ‫بها‬ ‫تمر‬ ‫واحدة‬ ‫استقامة‬ ‫على‬ ‫ليست‬ ‫نقاط‬ ‫ثالث‬ ‫كل‬
8 /‫مبرهنة‬
A
A
B
M
P
C
O
N
AB
O1
1
‫نق‬
3
‫نق‬
‫المنصف‬ ‫العمود‬
2
‫نق‬
O2
O

137. 137
‫الهندسية‬ ‫االشكال‬ ‫خارج‬ ‫املرسومة‬ ‫الدائرة‬ ]6-5 [ /‫تعريف‬
.‫واحدة‬ ‫لدائرة‬ ‫تنتمي‬ ‫رؤوسه‬ ‫كانت‬ ‫أذا‬ )ً‫ا‬‫دائري‬ ً‫ا‬‫رباعي‬ ً‫ال‬‫(شك‬ ‫الرباعي‬ ‫الشكل‬ ‫يسمى‬
:‫المجاور‬ ‫الشكل‬ ‫في‬
. O ‫مركزها‬ ‫التي‬ ‫للدائرة‬ ‫تتنتمي‬ A , B , C , D ‫حيث‬ ‫دائري‬ ‫رباعي‬ ‫شكل‬ ABCD
. ‫دائرية‬ ‫هندسية‬ ‫اشكال‬ ‫تسمى‬ ‫واحدة‬ ‫دائرة‬ ‫برؤوسها‬ ‫تمر‬ ‫التي‬ ‫االخرى‬ ‫الهندسية‬ ‫االشكال‬ ‫وكذلك‬
‫مرسوم‬ ‫خماسي‬ ‫شكل‬ ABCDE ‫مرسوم‬ ‫مثلث‬ ABC
)‫دائري‬ ‫(خماسي‬ O ‫مركزها‬ ‫دائرة‬ ‫داخل‬ 0 ‫مركزها‬ ‫دائرة‬ ‫داخل‬
‫مالحظة‬:‫يلي‬ ‫كما‬ ‫آخر‬ ‫بأسلوب‬ 8 ‫مبرهنة‬ ‫فهم‬ ‫يمكن‬
‫تكون‬ )O( ‫واحدة‬ ‫بنقطة‬ ‫تلتقي‬ ‫منتصفاتها‬ ‫من‬ ‫مثلث‬ ‫أضالع‬ ‫على‬ ‫المقامة‬ ‫االعمدة‬ ‫ان‬
. ‫المثلث‬ ‫برؤوس‬ ‫تمر‬ ‫التي‬ ‫الدائرة‬ ‫مركز‬ ‫هي‬ ‫النقطة‬ ‫وهذه‬ .‫رؤوسه‬ ‫عن‬ ‫البعد‬ ‫متساوية‬
:‫تدريب‬
A
B
4
C
4
4
.)4cm ( ‫ضلعه‬ ‫طول‬ ‫االضالع‬ ‫متساوي‬ ‫مثلث‬ ‫برؤوس‬ ‫تمر‬ ‫دائرة‬ ‫أرسم‬
O
A
B
C
A
B
C
D
E
O
A
B
C
D
O

138. 138
: ‫الدائرة‬ ‫قوس‬
AB ‫ان‬ ‫نالحظ‬ ‫المجاور‬ ‫الشكل‬ ‫في‬ .‫الدائرة‬ ‫من‬ ‫جزء‬ ‫هو‬
. B , A ‫بالنقطتين‬ ‫الدائرة‬ ‫مع‬ ‫يشترك‬
‫انقسمت‬ ‫وبذلك‬ } B , A } = A B ∩ )‫(الدائرة‬ ‫ان‬ ‫اي‬
.ً‫ا‬‫قوس‬ ‫يسمى‬ ‫منهما‬ ‫كل‬ ‫جزئين‬ ‫الى‬ ‫الدائرة‬ ‫نقاط‬ ‫مجموعة‬
. ) Minor Arc AB ‫الثانوي‬ ‫(القوس‬ ‫االصغر‬ ‫القوس‬ -
. ) Major Arc ACB )‫الرئيسي‬ ‫القوس‬ ( ‫االكبر‬ ‫القوس‬ -
‫متساويين‬ ‫قوسين‬ ‫الى‬ ‫يقسمها‬ ‫الدائرة‬ ‫في‬ ‫قطر‬ ‫اي‬ ‫ان‬ ‫مالحظة‬ ‫مع‬
.Semi circle ‫الدائرة‬ ‫نصف‬ ‫منها‬ ‫كل‬ ‫يسمى‬
‫الدائرة‬ ‫نصف‬ ‫من‬ ‫أصغر‬ ‫االصغر‬ ‫القوس‬ :‫ان‬ ‫اي‬
.‫الدائرة‬ ‫نصف‬ ‫من‬ ‫اكبر‬ ‫فهو‬ ‫االكبر‬ ‫القوس‬ :‫اما‬
‫فقط‬ ‫بحرفين‬ ‫االصغر‬ ‫القوس‬ ‫عن‬ ‫التعبير‬ ‫على‬ ‫اتفق‬ ‫وقد‬
. AC ‫القوس‬ ‫في‬ ‫كما‬
: ‫توضيح‬
: ‫المجاور‬ ‫الشكل‬ ‫في‬
.O ‫مركزها‬ ‫التي‬ ‫الدائرة‬ ‫في‬ ‫مركزية‬ ‫زاوية‬ AOB ‫الزاوية‬ ‫تسمى‬
‫في‬ ‫قطرين‬ ‫نصفا‬ ‫وضلعاها‬ ‫الدائرة‬ ‫مركز‬ ‫هو‬ ‫الزاوية‬ ‫رأس‬ ‫ان‬ ‫اي‬
.‫الدائرة‬
‫الدائرة‬ ‫نقط‬ ‫من‬ ‫نقطة‬ ‫رأسها‬ ،‫محيطية‬ ‫زاوية‬ EDF ‫الزاوية‬ ‫تسمى‬
.‫الدائرة‬ ‫في‬ ‫وتران‬ ‫وضلعاها‬
6 - 3-‫املركزية‬ ‫الدائرة-الزوايا‬ ‫قوس‬
‫احمليطية‬ ‫الزوايا‬
A
B
O
C
A
B
C
D
O
A
B
D
O
E
F

139. 139
/‫المعطيات‬
.‫محيطية‬ ‫زاوية‬ CAB ،‫مركزية‬ ‫زاوية‬ COB , O ‫مركزها‬ ‫دائرة‬
/‫أثباته‬ ‫المطلوب‬
m ∠ COB = 2m ∠ CAB
/‫والبرهان‬ ‫العمل‬
.‫للدائرة‬ ً‫ا‬‫قطر‬ AD ‫نرسم‬
OA = OB ... ‫دائرة‬ ‫أقطار‬ ‫أنصاف‬
m ∠ 1 = m ∠ 2 ‫الساقين‬ ‫متساوي‬ ‫مثلث‬ ‫قاعدة‬ ‫زاويتا‬
m ∠ 3 + m ∠ 1 + m ∠ 2 = 1800
) ‫مثلث‬ ‫زوايا‬ ‫(مجموع‬
m ∠3 + 2m ∠2 =1800
⇐ m ∠1 ‫عن‬ ‫بالتعويض‬
]6 - 6 [‫تعريف‬
.‫بضلعيها‬ ‫القوس‬ ‫هذا‬ ‫يتحدد‬ ‫التي‬ ‫الزاوية‬ ‫اي‬ ‫المركزية‬ ‫زاويته‬ ‫قياس‬ ‫هو‬ ‫دائرة‬ ‫في‬ ‫قوس‬ ‫قياس‬
. ‫المجاور‬ ‫الشكل‬ ‫في‬ ‫كما‬
m (AB) = m ∠ AOB
‫قوسية‬ ‫درجة‬ ‫تسمى‬ ‫القوس‬ ‫قياس‬ ‫ووحدة‬
m ∠ AOB = 300
:‫كان‬ ‫فإذا‬
‫قوسية‬ ‫درجة‬ 30 ‫يكون‬ AB ‫قوسها‬ ‫قياس‬ ‫فأن‬
360-30 ‫هو‬ ACB ‫االكبر‬ ‫القوس‬ ‫قياس‬ ‫وأن‬
.‫قوسية‬ ‫درجة‬ 330 ‫أي‬
A B
O
30ْ
A
B
C
O
D
1
3
2
4
‫المشتركة‬ ‫المحيطية‬ ‫الزاوية‬ ‫قياس‬ ‫ضعف‬ ‫يساوي‬ ‫دائرة‬ ‫في‬ ‫المركزية‬ ‫الزاوية‬ ‫قياس‬
.‫نفسه‬ ‫بالقوس‬ ‫معها‬
9 /‫مبرهنة‬
C

140. 140
m ∠3 = 1800
- 2 m ∠2 .......1
m ∠ BOD + m ∠ 3 = 1800
‫مستقيمة‬ ‫زاوية‬
m BOD = 1800
- m ∠ 3
m ∠ BOD = 1800
- (1800
-2m ∠ 2) .... 1 ‫من‬
m ∠ BOD= 2m ∠ 2........2
‫ان‬ ‫نثبت‬ ‫الطريقة‬ ‫وبنفس‬
m ∠ COD= 2m ∠4........3
3 ‫و‬ 2 ‫المعادلتين‬ ‫بجمع‬
m ∠BOD + m ∠ COD = 2 m ∠2 + 2 m ∠ 4
) ‫م‬ . ‫هـ‬ . ‫(و‬ m COB = 2 m CAB ∴
: 9 ‫ملبرهنة‬ 1 ‫نتيجة‬
‫قوسها‬ ‫قياس‬ ‫نصف‬ ‫يساوي‬ ‫دائرة‬ ‫في‬ ‫المحيطية‬ ‫الزاوية‬ ‫قياس‬
m ∠ N ‫جد‬ :‫المجاور‬ ‫الشكل‬ ‫في‬
/‫احلل‬
OA = OB ‫دائرة‬ ‫اقطار‬ ‫انصاف‬ ∵
m ∠ ABO = m ∠ BAO ‫قاعدة‬ ‫زاويتا‬ ∴
m ∠ ABO = 500
‫الساقين‬ ‫متساوي‬ ‫مثلث‬ ∵
m ∠AOB = 1800
- 1000
‫مثلث‬ ‫زوايا‬ ∴
m ∠ AOB = 800
m ∠ AOB = 2 m ∠ N .......)9 ‫(مبرهنة‬
m ∠ N =
800
2
= 400
∴m ∠ N = 40ْ
(1 ) ‫مثال‬
A B
N
O
50ْ

141. 141
:x ‫قيمة‬ ‫جد‬ : ‫المجاور‬ ‫الشكل‬ ‫في‬
/‫احلل‬
m COB = 2 m A : 9 ‫مبرهنة‬ ∵
x + 300
= 2 x ∴
x = 300
: 9 ‫ملبرهنة‬ 2 ‫نتيجة‬
1800
= ‫دائري‬ ‫رباعي‬ ‫شكل‬ ‫أي‬ ‫في‬ ‫المتقابلتين‬ ‫الزاويتين‬ ‫قياسي‬ ‫مجموع‬
: ‫المجاور‬ ‫الشكل‬ ‫في‬
)‫دائرة‬ ‫داخل‬ ‫(مرسوم‬ ‫دائري‬ ‫رباعي‬ ‫شكل‬ ABCD
m ∠ A + m ∠ C = 1800
m ∠ B + m ∠ D = 1800
(2 ) ‫مثال‬
A
B
C
o
X
x+30
:‫تدريب‬:‫المجاور‬ ‫الشكل‬ ‫في‬
AB = BC
m ∠ ABC = 960
y ‫قيمة‬ ‫جد‬
A
B
C
O
D
y
96ْ
A B
C
O
D

142. 142
: ‫الشكل‬ ‫في‬
m ∠ A , m ∠ D‫جد‬
/‫احلل‬
‫دائري‬ ‫رباعي‬ ‫شكل‬ ABCD
m ∠ D + m ∠B = 1800
... 9 ‫مبرهنة‬ 2 ‫نتيجة‬
m ∠ D = 1800
-940
m ∠ D = 860
m ∠1 + m∠ ECD = 1800
])‫(مستقيمة‬ ‫واحدة‬ ‫أستقامة‬ ‫على‬ ‫[متجاورتان‬
m ∠ 1 = 1800
- 1000
m ∠ 1 = 800
m ∠A + m ∠1 = 1800
)‫دائري‬ ‫رباعي‬ ‫شكل‬ ‫في‬ ‫(متقابلتان‬
m ∠A = 1800
- 80
m ∠A = 1000
(3 ) ‫مثال‬
A
B
C
O
D
E
194ْ
100ْ
:‫تدريب‬: ‫المجاور‬ ‫الشكل‬ ‫في‬
.y , x ‫قيمة‬ ‫جد‬
O
A B
C
D
x+10
2y
xy

143. 143
/‫المعطيات‬
.‫فيها‬ ‫قطر‬ AB , O ‫مركزها‬ ‫دائرة‬
/‫اثباته‬ ‫المطلوب‬
m ∠ ACB = 900
/‫البرهان‬
‫مركزية‬ ‫زاوية‬ AOB
. )‫قطر‬ AB ‫الن‬ ‫مستقيمة‬ ‫زاوية‬ ( ........m ∠ AOB = 1800
‫المشتركة‬ ‫المحيطية‬ ‫قياس‬ ‫ضعف‬ ‫تساوي‬ ‫المركزية‬ ‫الزاوية‬ ‫قياس‬ ....... m ∠AOB = 2 m C
‫القوس‬ ‫بنفس‬ ‫معها‬
m ∠ C = 1800
2
= 900
) ‫م‬ . ‫هـ‬ . ‫(و‬
. Y ‫قيمة‬ ‫جد‬ ،‫فيها‬ ‫قطر‬ AB , O ‫مركزها‬ ‫دائرة‬
/‫احلل‬
m ∠ C = 900
..... 10 ‫مبرهنة‬
‫مثلث‬ ‫....زوايا‬ m ∠ A + m ∠ B = 1800
- m ∠ C
m ∠ A + m ∠B = 900
y + 2 y = 900
3y = 900
y = 300
AB
C
O
10 /‫مبرهنة‬
900
‫تساوي‬ ‫دائرة‬ ‫نصف‬ ‫في‬ ‫المرسومة‬ ‫المحيطية‬ ‫الزاوية‬ ‫قياس‬
(4 ) ‫مثال‬
2y
y
O
A
C
B

144. 144
AD = DC ‫أن‬ ‫أثبت‬ AB = BC ،‫فيها‬ ‫قطر‬ AB , O‫مركزها‬ ‫دائرة‬ ‫الشكل‬ ‫في‬
/ ‫احلل‬
/‫المعطيات‬
/‫أثباته‬ ‫المطلوب‬
/‫البرهان‬
( 10 ‫مبرهنة‬ ) ...... m ∠ 1 = 900
. ) D ‫في‬ ‫الزاوية‬ ‫قائما‬ ‫مثلثان‬ ( ....... BCD , ABD
‫معطى‬ ............ AB = BC
)‫قائم‬ ‫وضلع‬ ‫(وتر‬ ‫متطابقان‬ ...... ∆ CBD , ∆ ABD
‫المتطابقة‬ ‫االشكال‬ ‫في‬ ‫المتناظرة‬ ‫االجزاء‬ ‫تتساوى‬ .... AD = DC :‫على‬ ‫نحصل‬ ‫التطابق‬ ‫من‬
(5 ) ‫مثال‬
{‫للطالب‬ ‫تترك‬
A
B
C
o
21
D

145. 145
-: ‫االتية‬ ‫االشكال‬ ‫من‬ ‫شكل‬ ‫كل‬ ‫في‬ Y , X ‫قيمة‬ ‫جد‬ /1‫س‬
OD ∥ AC ، m∠ OAC = 60ْ ‫فيها‬ ‫قطر‬ AB ،)‫المجاور‬ ‫(الشكل‬ O ‫مركزها‬ ‫دائرة‬ /2‫س‬
m CD = m BD :‫ان‬ ‫أثبت‬ ‫ثم‬ m CD ‫جد‬
‫المثلث‬ ‫ان‬ ‫أثبت‬ m ∠ BAC = 300
‫كان‬ ‫فاذا‬ .O ‫مركزها‬ ‫دائرة‬ ‫داخل‬ ‫مرسوم‬ ‫مثلث‬ ABC/3‫س‬
. ‫االضالع‬ ‫متساوي‬ OBC
‫كان‬ ‫فاذا‬ ،AO ‫يوازي‬ BD ‫الوتر‬ ‫رسم‬ ، O ‫مركزها‬ ‫دائرة‬ ‫في‬ ‫قطرين‬ ‫نصفا‬ OB , OA /4‫س‬
AD ⊥OB :‫ان‬ ‫أثبت‬ m ∠ AOB = 600
‫المجاور‬ ‫الشكل‬ ‫س5/في‬
. m ∠ D ‫جد‬ ) a
. A ‫زاوية‬ ‫ينصف‬ AC ‫ان‬ ‫أثبت‬ ) b
6 1
A
B D
C
O
60˚
C
4y
y
x
O
B
A
BA
D
o
80˚20˚
C
D
B
C
O
A
4x
x
y

146. 146
/‫المعطيات‬
m CD = m AB
/‫أثباته‬ ‫المطلوب‬
m ∠ COD = m ∠ AOB
/‫البرهان‬
m AB = m ∠ AOB ...... 1
) ‫المركزية‬ ‫زاويته‬ ‫قياس‬ ‫هو‬ ‫القوس‬ ‫قياس‬ (
:‫كذلك‬
m CD = m ∠ COD ....2
‫معطاة‬ m CD = m AB .....3
:‫على‬ ‫نحصل‬ )3( ‫و‬ )2( ‫و‬ )1( ‫من‬
)‫م‬ . ‫هـ‬ . ‫(و‬ m ∠AOB = m ∠ COD
:11 ‫مبرهنة‬ ‫نتيجة‬
.‫متطابقتان‬ ‫المحيطيتين‬ ‫زاويتيهما‬ ‫فان‬ ‫دائرة‬ ‫في‬ ‫قوسان‬ ‫تطابق‬ ‫اذا‬
‫ثم‬ m ∠ DOB ‫جد‬ m CD = m BD , m ∠ COD = 500
‫فيها‬ ‫قطر‬ AB , O ‫مركزها‬ ‫دائرة‬
OD // AC ‫ان‬ ‫اثبت‬
/‫المعطيات‬
/ ‫أثباته‬ ‫المطلوب‬
‫متطابقتان‬ ‫المركزيتين‬ ‫زاويتيهما‬ ‫فان‬ ‫دائرة‬ ‫في‬ ‫قوسان‬ ‫تطابق‬ ‫اذا‬
11/‫مبرهنة‬
(1 ) ‫مثال‬
{‫للطالب‬ ‫تترك‬
o
A
BC
D

147. 147
/‫البرهان‬
‫معطى‬ m CD = m BD
m ∠ DOB = m ∠ COD..... ) 10 ‫مبرهنة‬ (
m ∠ DOB = 500
m ∠ COB = m ∠ COD + m ∠ DOB = 1000
) ‫المحيطية‬ ‫قياس‬ ‫ضعف‬ ‫المركزية‬ ‫قياس‬ (
m ∠ CAB = 1
2
m ∠ COB
= 500
‫ومتطابقتان‬ ‫متناظرتان‬ CAB , DOB ‫الزاويتان‬
CA // DO ∴
.‫برهان‬ ‫بدون‬ ‫المبرهنة‬ ‫هذه‬ ‫نقبل‬ ‫سوف‬
:‫توضيح‬
:‫المجاور‬ ‫الشكل‬ ‫في‬
‫فيها‬ ‫قطر‬ MD , O ‫مركزها‬ ‫دائرة‬ ‫في‬ ‫وتر‬ AB
MD ⊥ AB ‫ان‬ ‫بحيث‬
:‫ذلك‬ ‫من‬ ‫ينتج‬
)AC = BC) AB ‫الوتر‬ ‫ينصف‬ MD - 1
m BD = m AD - 2
m MB = m AM - 3
.‫قوسيه‬ ‫من‬ ً‫ال‬‫ك‬ ‫وينصف‬ ‫الوتر‬ ‫ينصف‬ ‫دائرة‬ ‫في‬ ‫وتر‬ ‫على‬ ‫العمودي‬ ‫القطر‬
12/‫مبرهنة‬
A
B D
C
o
50˚
o
AB
D
M
C

148. 148
(2 ) ‫مثال‬
(3 ) ‫مثال‬
{‫للطالب‬ ‫تترك‬
o
N
BO ‫جد‬ AB = 8 cm , OD = 3 cm , AB ⊥ OD , O ‫مركزها‬ ‫دائرة‬
/‫احلل‬
AB ⊥ OD ..... )‫(معطى‬
) 12 ‫مبرهنة‬ ( ...... AB ‫منتصف‬ D
BD = 4 cm
D ‫في‬ ‫الزاوية‬ ‫القائم‬ OBD ‫المثلث‬ ‫في‬
(OB)2
= (OD)2
+ (BD)2
..( ‫فيثاغورس‬‫مبرهنة‬)
= 9 + 16 = 25
BO = 5 cm
.O ‫المركز‬ ‫في‬ ‫متحدتان‬ ‫دائرتان‬
BD = AC :‫ان‬ ‫أثبت‬ BA ⊥ ON
/‫المعطيات‬
/ ‫أثباته‬ ‫المطلوب‬
/‫البرهان‬
ON ⊥ CD ‫الصغرى‬ ‫الدائرة‬ ‫في‬
CN = DN .... )1( 12 ‫مبرهنة‬
AN = BN ....)2( :‫الكبرى‬ ‫الدائرة‬ ‫في‬ ‫كذلك‬
:‫على‬ ‫نحصل‬ )2( ‫و‬ )1( ‫من‬
‫متساوية‬ ‫كميات‬ ‫طرحت‬ ‫اذا‬ AN - CN = BN - DN
‫متساوية‬ ‫النتائج‬ ‫تبقى‬ ‫متساوية‬ ‫اخرى‬ ‫من‬
AC = BD ∴
B D C
A
B
O
A
D 44
3

149. 149
.‫الوتر‬ ‫ذلك‬ ‫على‬ ً‫ا‬‫عمودي‬ ‫يكون‬ ‫الوتر‬ ‫بمنتصف‬ ‫المار‬ ‫الدائرة‬ ‫قطر‬
13/‫مبرهنه‬)12 ‫مبرهنة‬ ‫(عكس‬
‫مالحظة‬
BON , OAN ‫المثلثين‬ ‫تطابق‬ ‫من‬ ‫المبرهنة‬ ‫أثبات‬ ‫يمكن‬
/‫المعطيات‬
.N ‫في‬ AB ‫الوتر‬ ‫ينصف‬ CD ،‫فيها‬ ‫قطر‬ CD , O ‫مركزها‬ ‫دائرة‬ ‫في‬ ‫وتر‬ AB
/‫أثباته‬ ‫المطلوب‬
CD ⊥ AB
/‫البرهان‬
)‫قطرين‬ ‫(نصفا‬ OB , OA ‫نرسم‬
( ‫دائرة‬ ‫في‬ ‫قطرين‬ ‫نصفا‬ ).... OA = OB
) ‫معطى‬ ( ... AB ‫منتصف‬ N
) ‫الساقين‬ ‫متساوي‬ ‫مثلث‬ ‫(خواص‬ ... ON ⊥ AB
CD ⊥ AB ∴
) ‫م‬ . ‫هـ‬ . ‫(و‬
B
o
AN
D
C

150. 150
:‫المجاور‬ ‫الشكل‬ ‫في‬
D , O ‫مركزها‬ ‫دائرة‬ ‫في‬ ‫وتر‬ AB
m ∠ OBDm OBD = 300
, DO / /BC , AB ‫منتصف‬
‫االضالع‬ ‫متساوي‬ OBC ‫المثلث‬ ‫ان‬ ‫اثبت‬
/‫المعطيات‬
/‫أثباته‬ ‫المطلوب‬
/‫البرهان‬
) ‫معطى‬ ( .... AB ‫منتصف‬ D
) 13 ‫مبرهنة‬ ( ..... AB ⊥ OD
D ‫في‬ ‫الزاوية‬ ‫قائم‬ OBD ‫المثلث‬
) ‫معطى‬ (...... m ∠ OBD = 300
)1800
= ‫المثلث‬ ‫زوايا‬ ‫.....(مجموع‬ m ∠ BOD = 600
)‫معطى‬ ( ....... BC // DO ∵
)‫متبادلة‬ ( ... m ∠ OBC = m ∠ BOD
m ∠ OBC = 600
))OC = OB( ‫الساقين‬ ‫متساوي‬ ‫مثلث‬ ‫قاعدة‬ ‫زوايا‬ ( ...... m ∠ OBC = m ∠ OCB
)1800
= ‫المثلث‬ ‫زوايا‬ ‫.....(مجموع‬ m ∠ COB = 600
‫االضالع‬ ‫متساوي‬ BCO ‫المثلث‬ ∴
(4 ) ‫مثال‬
{‫للطالب‬ ‫تترك‬
o
30
60
AB
C
D

151. 151
m ∠ BDC ‫جد‬ ، CA = BC = AB :‫فيها‬ O ‫مركزها‬ ‫دائرة‬ :‫المجاور‬ ‫الشكل‬ ‫في‬ /1‫س‬
m∠ B , m ∠ C ، a ‫:قيمة‬ ‫جد‬ m BC = a , m AC = 96 :‫المجاور‬ ‫الشكل‬ ‫في‬ /2‫س‬
OD ‫جد‬ :‫المجاور‬ ‫الشكل‬ ‫في‬ /3‫س‬
∠ BAC ‫ينصف‬ AO : ‫ان‬ ‫برهن‬ ،O ‫مركزها‬ ‫دائرة‬ ‫في‬ ‫متطابقان‬ ‫وتران‬ AC , AB /4‫س‬
6 2
⁀ ⁀
A
BC
O
D
AB
C
O
a
96
32
AB
C
O
D 8

152. 152
b, a ‫جد‬ :‫المجاور‬ ‫الشكل‬ ‫/في‬ 5‫س‬
Yْ ‫قيمة‬ ‫جد‬ BC ∥ OA , BA ∥ CO :‫المجاور‬ ‫الشكل‬ ‫في‬ /6‫س‬
‫مع‬ ‫دائري‬ ‫رباعي‬ ‫شكل‬ ‫باكمال‬ ‫أخرى‬ ‫طريقة‬ ‫هناك‬ , OB ‫صل‬ ‫ثم‬ ، ‫معين‬ OCBA ‫ان‬ ‫أثبت‬ :‫تلميح‬
. C , B , A ‫النقط‬
y ‫قيمة‬ ‫جد‬ ، m ∠ D = 2y , m ∠ A = y + 30 :‫حيث‬ ‫دفترك‬ ‫في‬ ‫المجاور‬ ‫الشكل‬ ‫أنقل‬ /7‫س‬
. )4y 0
( ‫قياسها‬ ‫زاوية‬ ‫الشكل‬ ‫في‬ ‫أرسم‬ ‫ثم‬ ،
A B
C
D
b
a 3a
B
o
y˚ AC
1
2
o
D
A
B
C
2y
1
2
y +
30

153. 153
: O ‫مركزها‬ ‫التي‬ M ‫الدائرة‬ ‫ان‬ ‫أعاله‬ ‫الشكل‬ ‫في‬ ‫الحظ‬
A ‫نقطة‬ ‫في‬ M ‫للدائرة‬ ً‫ا‬‫مماس‬ L1
‫يسمى‬ } A} = M ∩ L1
: ‫فقط‬ ‫واحدة‬ ‫بنقطة‬ L1
‫مع‬ ‫تشترك‬ - 1
:‫فان‬ ‫ولذلك‬
‫للدائرة‬ ً‫ا‬‫مماس‬ ‫يسمى‬ ‫فقط‬ ‫واحدة‬ ‫بنقطة‬ ‫معها‬ ‫ويشترك‬ ‫الدائرة‬ ‫مستوي‬ ‫في‬ ‫مستقيم‬ ‫أي‬
.)‫التماس‬ ‫(نقطة‬ ‫النقطة‬ ‫تلك‬ ‫في‬
.‫للدائرة‬ ‫قاطع‬ L2
‫يسمى‬ } C , B } = M ∩ L2
- 2
. )‫الدائرة‬ ‫(خارج‬ ‫الدائرة‬ ‫يقطع‬ ‫وال‬ ‫يمس‬ ‫ال‬ , ∅ = M ∩ L3
- 3
6 - 4
ّ‫ماس‬ّ‫التـ‬
o
L3
A
B
C
M
‫متاس‬ ‫نقطة‬
L3
(‫والميس‬ ‫)اليقطع‬
(‫)قاطع‬
(‫)مماس‬
L2
L1

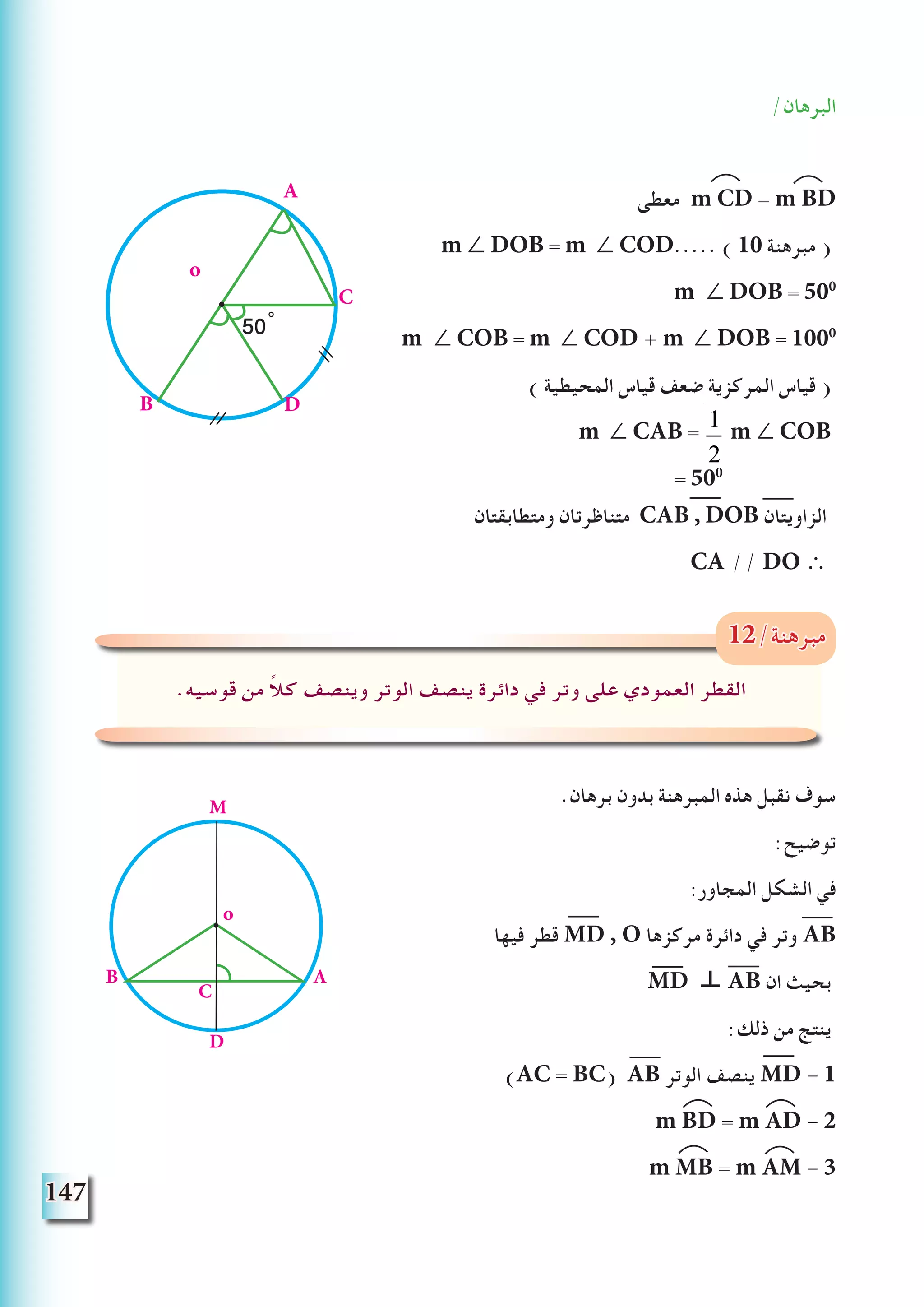
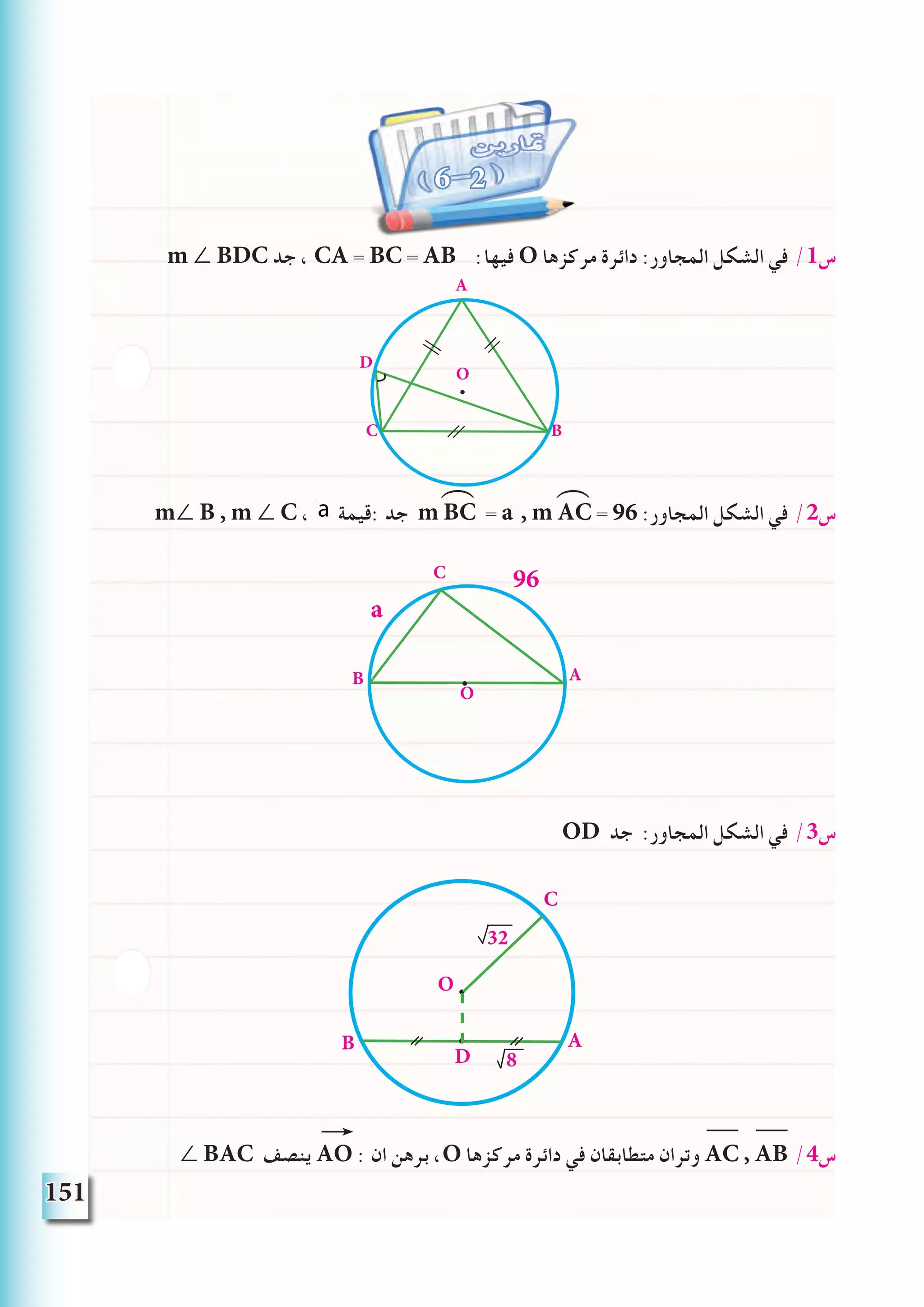
154. 154
‫كما‬ ً‫ا‬‫مشترك‬ ً‫ا‬‫مماس‬ ‫الحالة‬ ‫هذه‬ ‫في‬ ‫ويسمى‬ ‫الوقت‬ ‫نفس‬ ‫في‬ ‫دائرة‬ ‫من‬ ‫اكثر‬ ‫يمس‬ ‫قد‬ ‫المستقيم‬ ‫ان‬ ‫مالحظة‬ ‫مع‬
:‫االشكال‬ ‫في‬
‫الداخل‬ ‫من‬ ‫دائرتني‬ ‫متاس‬
‫اخلارج‬ ‫من‬ ‫دائرتني‬ ‫متاس‬
‫مشترك‬ ‫مماس‬
]6-7[ ‫تعريف‬
‫الجهة‬ ‫من‬ ‫التماس‬ ‫نقطة‬ ‫من‬ ‫المرسوم‬ ‫ووترها‬ ‫الدائرة‬ ‫بمماس‬ ‫المحددة‬ ‫الزاوية‬ ‫هي‬ :‫المماسية‬ ‫الزاوية‬
. ‫االخرى‬
‫زاوية‬ ABD ‫الزاوية‬ ‫تسمى‬ ‫للدائرة‬ ‫وتر‬ BA , O ‫مركزها‬ ‫التي‬ ‫للدائرة‬ ‫مماس‬ L : ‫الشكل‬ ‫في‬
.‫مماسية‬
‫أحد‬ ‫هو‬ ‫الذي‬ ‫للوتر‬ ‫المقابل‬ ‫القوس‬ ‫قياس‬ ‫نصف‬ ‫يساوي‬ ‫دائرة‬ ‫في‬ ‫المماسية‬ ‫الزاوية‬ ‫قياس‬ :‫اولية‬ ‫عبارة‬
. ‫المماسية‬ ‫الزاوية‬ ‫أضالع‬
⁀
A
B
C
D
O
L
mABD=
1
2
mABm ∠

155. 155
/‫المعطيات‬
.A ‫نقطة‬ ‫في‬ ‫الدائرة‬ ‫يمس‬ L ‫المستقيم‬ ،O ‫مركزها‬ ‫دائرة‬
/‫أثباته‬ ‫المطلوب‬
OA ⊥ L
/‫والبرهان‬ ‫العمل‬
AOB ‫القطر‬ ‫نرسم‬
( ‫الدائرة‬ ‫في‬ ‫قطر‬ AB ‫)الن‬ .... m ACB = 1800
( ‫اولية‬ ‫عبارة‬ )....m ∠ BADmABD=
1
2
mACB
m ∠m BAD =
1
2
×1800
= 900
) ‫م‬ . ‫هـ‬ . ‫(و‬ OA ⊥ L ∴
.N ‫نقطة‬ ‫في‬ L ⊥ ON , O ‫من‬ ‫نرسم‬ L ⊥ OA ‫يكن‬ ‫لم‬ ‫اذا‬ :‫آخر‬ ‫برهان‬
. AN = NP ‫ان‬ ‫بحيث‬ .P ‫النقطة‬ ‫الى‬ ‫أستقامتها‬ ‫على‬ AN ‫نمد‬
»‫بينهما‬ ‫محصورة‬ ‫وزاوية‬ ‫«ضلعان‬ .‫متطابقان‬ OAN , ONP ‫المثلثان‬
:‫على‬ ‫نحصل‬ ‫التطابق‬ ‫من‬
OA = OP
‫للدائرة‬ ∵
‫للدائرة‬ ∴
OA ⊥ L ∴
:‫أولية‬ ‫عبارة‬
.‫فقط‬ ‫واحد‬ ‫مماس‬ ‫رسم‬ ‫يمكن‬ ‫للدائرة‬ ‫تنتمي‬ ‫نقطة‬ ‫من‬ - 1
.‫الدائرة‬ ‫بمركز‬ ‫يمر‬ ‫التماس‬ ‫نقطة‬ ‫من‬ ‫الدائرة‬ ‫مماس‬ ‫على‬ ‫العمودي‬ ‫المستقيم‬ - 2
⁀
.‫التماس‬ ‫نقطة‬ ‫من‬ ‫المرسوم‬ ‫القطر‬ ‫نصف‬ ‫على‬ ‫عمود‬ ‫المماس‬
14/‫مبرهنة‬
A∈
P ∈
O
L
B
A
C
D
⁀
O
L
A PN

156. 156
)‫المجاور‬ ‫(الشكل‬ ،O ‫مركزها‬ ‫التي‬ ‫الدائرة‬ ‫في‬
A ‫في‬ ‫للدائرة‬ ‫مماس‬ AB
. m ∠ AOB ‫جد‬ ∠ ABO = 35ْ
‫معطى‬ ... A ‫في‬ ‫للدائرة‬ ‫مماس‬ AB ∵ / ‫احلل‬
. B ‫في‬ ‫الدائرة‬ ‫يمس‬ ، A ‫في‬ ‫الدائرة‬ ‫يمس‬ ، ‫فيها‬ ‫قطر‬ ، O ‫مركزها‬ ‫دائرة‬
‫ان‬ ‫أثبت‬
/‫المعطيات‬
/‫أثباته‬ ‫المطلوب‬
/‫البرهان‬
: ‫كذلك‬
: 2 ، 1 ‫من‬
∴ , ‫القاطع‬ ‫من‬ ‫واحدة‬ ‫جهه‬ ‫وعلى‬ ‫داخليتان‬ ‫الزاويتان‬ ‫وهاتان‬
‫من‬ ‫واحدة‬ ‫جهة‬ ‫في‬ ‫الواقعتان‬ ‫الداخليتان‬ ‫الزاويتان‬ ‫وكانت‬ ‫ثالث‬ ‫بمستقيم‬ ‫قطعا‬ ‫اذا‬ ‫مستقيمان‬ ‫(يتوازي‬
. )1800
‫مجموعهما‬ ‫القاطع‬
(2 ) ‫مثال‬
{‫للطالب‬ ‫تترك‬
ABDC//MN
(1 ) ‫مثال‬
m
o
A
B35˚
MNDC
DC//MN
AB
m 1+m 2=180o
A ‫في‬ ‫للدائرة‬ ‫مماس‬ MN ∵
AB ⊥ MN ∴13 ‫مبرهنة‬ .......
1.......
m 1=90o
∴
m 2=90o
∴2.......
AB ⊥ AO
∴ m OAB=90o
∴ m OBA=35o
∴ m AOB=90o
-35o
= 55o
180ْ = ‫مثلث‬ ‫زوايا‬ ‫مجموع‬
‫معطى‬
∠
∠
∠
∠
∠
∠ ∠
o2 1
C
AB
D
N
M
AB ⊥ MN ∴

157. 157
: ‫المجاور‬ ‫الشكل‬ ‫في‬
، A ‫في‬ ‫للدائرة‬ ‫مماس‬ AB
m ∠ OAC = 5N , m ∠ CAB = N
/‫احلل‬
A ‫في‬ ‫للدائرة‬ ‫مماس‬ AB
OA ⊥ AB ∴
) m ∠ OAB = 90ْ(
N + 5N = 90ْ
6N = 90ْ ⇒ N = 15ْ
m ∠ OAC = 5 × 15ْ = 75ْ
) ‫الدائرة‬ ‫اقطار‬ ‫انصاف‬ ( OA = OC ∴
‫الساقين‬ ‫متساوي‬ ‫مثلث‬ ‫قاعدة‬ ‫زاويتا‬ m ∠ OCA = 5N
∴ m ∠ OCA = 5 × 15ْ = 75ْ
) ‫المثلث‬ ‫زوايا‬ ‫مجموع‬ ( .... m ∠ OCA + m ∠ OAC + m ∠ AOC = 180ْ
75ْ + 75ْ + X = 180ْ
∴ X = 180ْ - 150ْ = 30ْ
(3 ) ‫مثال‬
o
x , N ‫قيمة‬ ‫جد‬ m ∠ AOC = x
o
B
C
A
•
N
o
X
5N

158. 158
: ‫الشكل‬ ‫في‬
BO , CO , AO : ‫هي‬ ‫المثلث‬ ‫زوايا‬ ‫منصفات‬
‫التي‬ ‫الدائرة‬ ‫مركز‬ O ‫فتكون‬ O ‫في‬ ‫التقت‬
. ABC ‫المثلث‬ ‫اضالع‬ ‫تمس‬
) ‫المثلث‬ ‫موضوع‬ ‫في‬ ‫ذلك‬ ‫درسنا‬ ‫(كما‬
OR = OQ = OP ‫ان‬ ‫اي‬
. ‫للدائرة‬ ‫قطر‬ ‫نصف‬ ‫يمثل‬ ‫منها‬ ‫وكل‬
o
A
‫المثلث‬ ‫اضالع‬ ‫تمس‬ ‫التي‬ ‫الدائرة‬ ‫مركز‬ ‫هي‬ ‫المثلث‬ ‫زوايا‬ ‫منصفات‬ ‫تقاطع‬ ‫نقطة‬
: 15 ‫مبرهنة‬ ‫نتيجة‬
: ‫توضيح‬
R
C
o
A
B
Q
P
B
: ‫توضيح‬
A ‫في‬ OA ⊥ AB
. ‫لدائرة‬ ‫قطر‬ ‫نصف‬ OA ‫حيث‬
: ‫ان‬ ‫على‬ ‫نحصل‬ ‫ذلك‬ ‫عند‬
. A ‫قي‬ ‫للدائرة‬ ‫مماس‬ AB
ً‫ا‬‫مماس‬ ‫يكون‬ ‫للدائرة‬ ‫المنتميه‬ ‫نهايته‬ ‫عند‬ ‫دائرة‬ ‫قطر‬ ‫نصف‬ ‫على‬ ‫العمودي‬ ‫المستقيم‬
. ‫للدائرة‬
15/‫مبرهنة‬. ) 14 ‫مبرهنة‬ ‫(عكس‬
‫برهان‬ ‫بدون‬ ‫المبرهنة‬ ‫نقبل‬ ‫سوف‬

159. 159
/ ‫المعطيات‬
AC ، AB ، A ∈∉ ‫للدائرة‬ ، O ‫مركزها‬ ‫دائرة‬
. A ‫من‬ ‫للدائرة‬ ‫مماسيتان‬ ‫قطعتان‬
/‫اثباته‬ ‫المطلوب‬
AB = AC
ABOC ‫الرباعي‬ ‫الشكل‬ ‫نكمل‬ /‫والبرهان‬ ‫العمل‬
AO ‫ونصل‬
) ‫(معطى‬ ...... C ،B ‫في‬ ‫الدائرة‬ ‫تمسان‬ AC ، AB ∵
) .... ‫على‬ ‫عمودي‬ ‫القطر‬ ‫نصف‬ ( ... OC ⊥ AC , AB ⊥ OB ∴
ACO ، ABO ∆∆ ‫في‬ ‫مشترك‬ ‫ضلع‬ OA
‫دائرة‬ ‫في‬ ‫قطرين‬ ‫نصفا‬ OC ≅ OB
)‫قائم‬ ‫وضلع‬ ‫(وتر‬ ‫الزاوية‬ ‫القائما‬ ‫المثلثان‬ ‫يتطابق‬ ∴
. AC = AB : ‫التطابق‬ ‫من‬
. ‫متطابقتان‬ ‫عنها‬ ‫خارجة‬ ‫نقطة‬ ‫من‬ ‫لدائرة‬ ‫المرسومتان‬ ‫المماسيتان‬ ‫القطعتان‬
16/‫مبرهنة‬
•
•
•
A
B
o
C
: ‫فانهما‬ ) ‫(مماسان‬ ‫او‬ ‫مماسيتان‬ ‫قطعتان‬ ‫عنها‬ ‫خارجة‬ ‫نقطة‬ ‫من‬ ‫لدائرة‬ ‫رسم‬ ‫اذا‬
. ‫متساويتين‬ ‫مركزيتين‬ ‫زاويتين‬ ‫تقابالن‬ - 1
‫تنصف‬ ‫الدائرة‬ ‫عن‬ ‫الخارجة‬ ‫والنقطة‬ ‫الدائرة‬ ‫مركز‬ ‫بين‬ ‫الواصلة‬ ‫المستقيم‬ ‫قطعة‬ - 2
. ‫المماسيتان‬ ‫القطعتان‬ ‫ضلعاها‬ ‫التي‬ ‫الزاوية‬
‫وتنصف‬ ‫عمودية‬ ‫عنها‬ ‫الخارجة‬ ‫والنقطة‬ ‫الدائرة‬ ‫مركز‬ ‫بين‬ ‫الواصلة‬ ‫المستقيم‬ ‫قطعة‬ - 3
. ‫التماس‬ ‫نقطتي‬ ‫بين‬ ‫الواصلة‬ ‫المستقيم‬ ‫قطعة‬
: 16 ‫مبرهنة‬ ‫نتيجة‬

160. 160
. BC ‫جد‬ ,‫للدائرة‬ ‫مماسات‬ CA ، BC ، BD , O ‫مركزها‬ ‫دائرة‬ : ‫المجاور‬ ‫الشكل‬ ‫في‬
/ ‫احلل‬
BN = BD ....‫عنها‬ ‫خارجة‬ ‫نقطة‬ ‫من‬ ‫لدائرة‬ ‫مماسان‬
∵
) ‫برهان‬ ‫بدون‬ ‫تقبل‬ (
: ‫المجاور‬ ‫الشكل‬ ‫في‬
B ‫في‬ ‫للدائرة‬ ‫مماس‬ ، O ‫مركزها‬ ‫دائرة‬
، ‫مماسية‬ ‫زاوية‬ ∠ ABC
‫وتر‬ ‫تقابل‬ ‫محيطية‬ ‫زاوية‬ ∠ BDC
.) ‫المماسية‬ ‫للزاوية‬ ‫(ضلع‬ BC ‫الدائرة‬
m ∠ ABC = m ∠ BDC
(4 ) ‫مثال‬
∴ BN=6 cm
CN=CA
∴ CN=4 cm
BC=CN
∴ BC=4+6=10 cm
‫الدائرة‬ ‫لوتر‬ ‫المقابلة‬ ‫المحيطية‬ ‫الزاوية‬ ‫قياس‬ ‫يساوي‬ ‫دائرة‬ ‫في‬ ‫المماسية‬ ‫الزاوية‬ ‫قياس‬
. ‫االخرى‬ ‫الجهة‬ ‫من‬ )‫الزاوية‬ ‫(ضلع‬
17/‫مبرهنة‬
•o
A
C
B
D
•
BA
•
•
•
•o
N
A
C B
D
6cm
4cm
+ NB

161. 161
: ‫المجاور‬ ‫الشكل‬ ‫في‬
m ∠ 3 , m ∠ 2 ‫جد‬
/ ‫احلل‬
C ‫في‬ ‫الدائرة‬ ‫تمس‬ AB ∵
)17 ‫(مبرهنة‬ ∴
m ∠ 1 = 74ْ
DE = CE ∵
) ‫الساقين‬ ‫متساوي‬ ‫مثلث‬ ‫خواص‬ ( ...... m ∠ 1 = m ∠ 2 ∴
m ∠ 2 = 74ْ ∴
180ْ = ‫مثلث‬ ‫زوايا‬ ‫مجموع‬ .... m ∠ 3 = 180ْ -(m ∠ 1+m ∠ 2(
m ∠ 3 = 180ْ -148ْ
m ∠ 3 = 32ْ
(5 ) ‫مثال‬
• O
ACB
D
E
740
1
2
3
m ∠ 1 = m ∠ ACE
:‫تدريب‬
CD //AB : ‫المجاور‬ ‫الشكل‬ ‫في‬
. x ‫قيمة‬ ‫جد‬•
AB
D C
O
x
3x

162. 162
‫المجاور‬ ‫الشكل‬ ‫في‬
m ∠ ABN ‫جد‬
/‫احلل‬
) ‫مماسية‬ ‫زاوية‬ ( ....m ∠ 1 = m ∠ N
m ∠ 1 = 50ْ ∴
)‫(معطى‬ ... CN = AN ∵
) ‫الساقين‬ ‫متساوي‬ ‫مثلث‬ ‫قاعدة‬ ‫زاويتا‬ ( ... m ∠ 2 = m ∠ 3 ∴
) ‫مثلث‬ ‫زوايا‬ ( .... m ∠ N + m ∠ 2 + m ∠ 3 = 180ْ ∴
m ∠ 2 ‫بـ‬ m ∠ 3 ‫إبدال‬
50ْ+ 2m ∠ 2 = 180ْ
2m ∠ 2 = 130ْ
m ∠ 2 = 65ْ ∴
: ABC ‫المثلث‬ ‫في‬
)‫مستقيمة‬ ‫زاوية‬ ( ... m ∠ 4 = 180ْ - m ∠ 3
m ∠ 4 = 180ْ - 65ْ = 115ْ ∴
m ∠ B = 180ْ -(m ∠ 1+m ∠ 4( ∴
m ∠ B = 180 ْ - 165 ْ = 15ْ ∴
(6 ) ‫مثال‬
•
••
N
A
50 o
B
C
O
1
4
2
3

163. 163
1، 2 : ‫المرقمة‬ ‫الزوايا‬ ‫قياسات‬ ‫جد‬ ‫المجاورين‬ ‫الشكلين‬ ‫في‬ /1‫س‬
‫الدائرة‬ ‫ويمس‬ ‫الكبرى‬ ‫الدائرة‬ ‫في‬ ‫وتر‬ AB ، O ‫المركز‬ ‫في‬ ‫متحدتان‬ ‫دائرتان‬ : ‫المجاور‬ ‫الشكل‬ ‫س2/في‬
AN = NB: ‫ان‬ ‫اثبت‬ N ‫في‬ ‫الصغرى‬
‫برؤوس‬ ‫المارة‬ ‫الدائرة‬ ‫يمس‬ AC ‫ان‬ ‫اثبت‬ ، AB ⊥ CD ‫رسم‬ ، C ‫في‬ ‫الزاوية‬ ‫قائم‬ ‫مثلث‬ ABC /3‫س‬
.BCD ‫المثلث‬
.ABC ‫المثلث‬ ‫محيط‬ ‫جد‬ : ‫المجاور‬ ‫الشكل‬ ‫في‬ /4‫س‬
6 3
AB
C
O
1
2
A
B
O
N
30ْ
O
AC
B
•
•
28ْ 2
44
E
2cm
O
B A
1.5cm
D
1
C
1.2cm
F

166. 166
7 - 2‫االحداثي‬ ‫املستوي‬ ‫في‬ ‫املسافة‬
Distance in The Coordinate Plane
‫المسافة‬ ‫نجد‬ ‫ان‬ ‫يمكن‬ ]7 - 2 - 1[
)‫الصادات‬ ‫محور‬ ‫يوازي‬ ( ‫عمودي‬ ‫مستقيم‬ ‫او‬ )‫السينات‬ ‫محور‬ ‫(يوازي‬ ‫افقي‬ ‫مستقيم‬ ‫على‬ ‫نقطتين‬ ‫بين‬
:ً‫ا‬‫سابق‬ ‫درست‬ ‫كما‬ ‫او‬ ‫المسطرة‬ ‫باستخدام‬
B ( x2
, y1
) , A ( x1
, y 1
( ‫حيث‬ ‫السينات‬ ‫محور‬ ‫يوازي‬ ‫معلوم‬ ‫لمستقيم‬ ‫تنتميان‬ A , B ‫كانت‬ ‫*اذا‬
. )1( ‫الشكل‬ ‫في‬ ‫كما‬ A , B ‫النقطتين‬ ‫بين‬ ‫البعد‬ ‫فان‬
AB =|x2
- x1
| ‫او‬ AB = | x1
- x2
| : ‫هو‬
‫محور‬ ‫يوازي‬ ‫معلوم‬ ‫لمستقيم‬ ‫تنتميان‬ A , B ‫كانت‬ ‫اذا‬ *
‫فان‬ B = (x 1
, y2
) ,A = (x1
, y1
( ‫حيث‬ ‫الصادات‬
. )2( ‫الشكل‬ ‫في‬ ‫كما‬ A , B ‫النقطتين‬ ‫بين‬ ‫البعد‬
AB =|y1
- y2
| ‫او‬ AB = | y2
- y1
| : ‫هو‬
B = (-2, 3) ,A = (5 , 3 ( ‫كان‬ ‫اذا‬ : ً‫ال‬‫فمث‬
AB = | x2
- x1
| = | -2 - 5 | = | -7 |= 7
A = (5, -3) , B = (5 , 8 (
AB = | y2
- y1
| = | 8 - (-3) | = | 11 | = 11
‫يوازي‬ ‫مستقيم‬ ‫الى‬ ‫وال‬ ‫السينات‬ ‫محور‬ ‫يوازي‬ ‫مستقيم‬ ‫الى‬ ‫التنتميان‬ A , B ‫النقطتان‬ ‫كانت‬ ‫اذا‬ : ‫واالن‬
‫؟‬ A , B ‫النقطتين‬ ‫بين‬ ‫المسافة‬ ‫نجد‬ ‫فكيف‬ . ‫الصادات‬ ‫محور‬
y
x- axis
{y1
| x2
- x1
|
y = y1
A ( x1
, y1
) B ( x2
, y1
)
)1(
x
A ( x1
, y1
)
{
x1
| y2
- y1
|
x = x1
y
)2(
x
B ( x1
, y2
)
: ‫فأن‬
‫كان‬ ‫اذا‬
: ‫فأن‬

167. 167
d=AB= X2 -X1( )
2
+ Y2 -Y1( )
2
d
‫االحداثي‬ ‫المستوي‬ ‫الى‬ ‫تنتميان‬ B (x2
, y2
) , A (x1
, y1
( : ‫لتكن‬
: ‫ان‬ ‫نجد‬ . E ‫في‬ ‫الزاوية‬ ‫قائم‬ AEB ‫المثلث‬ : ‫الشكل‬ ‫من‬
AE = | x2
- x1
| , BE = | y2
- y1
|
: ‫فثاغورس‬ ‫مبرهنة‬ ‫وحسب‬
)AB) 2
= (AE )2
+ (BE(2
‫نجد‬ BE , AE ‫عن‬ ‫وبالتعويض‬
)AB) 2
= (| x2
- x1
|)2
+ (| y2
- y1
| (2
)AB) 2
= (x2
- x1
)2
+ (y2
- y1
(2
=AB = (x2
- x1
)2
+ (y2
- y1
(2
|x|2
= x2
‫حيث‬
: ‫القانون‬ ‫تطبيقات‬ ‫بعض‬ ‫سنذكر‬ ‫المرحلة‬ ‫هذه‬ ‫في‬
. ‫واحدة‬ ‫استقامة‬ ‫على‬ A , B , C ‫مثل‬ ‫نقط‬ ‫ان‬ ‫اثبات‬ :ً‫ال‬‫او‬
: ‫الطريقة‬
. ‫االحداثي‬ ‫المستوي‬ ‫في‬ ‫المعطاة‬ ‫النقط‬ ‫نثبت‬ 
. ‫الناتج‬ ‫نبسط‬ ‫ثم‬ ‫نقطتين‬ ‫كل‬ ‫بين‬ ‫المسافة‬ ‫نجد‬ 
. ‫واحدة‬ ‫استقامة‬ ‫على‬ ‫النقط‬ ‫فان‬ ‫االجزاء‬ ‫مجموع‬ ‫يساوي‬ ‫الكل‬ ‫كان‬ ‫فاذا‬ 
‫االحداثي‬ ‫المستوي‬ ‫في‬ ‫النقطتين‬ ‫بين‬ ‫المسافة‬ ‫قانون‬ ]7 - 2 - 2[
y
A ( x1
, y1
)
| x2
- x1
|
B ( x2
, y2
)
X
E
| y2
- y1
|
‫نقطتين‬ ‫بين‬ ‫المسافة‬ ‫قانون‬ ‫تطبيقات‬ ‫بعض‬ ]7 - 2 - 3[

168. 168
‫واحدة‬ ‫استقامة‬ ‫على‬ ‫النقاط‬ ‫ان‬ ‫بين‬
/‫احلل‬
AB= 0+3( )
2
+ 1+2( )
2
= 3( )
2
+ 3( )
2
AB= 9+9 = 18 = 3 2
BC= 3-0( )
2
+ 4-1( )
2
= 3( )
2
+ 3( )
2
BC=3 2
AC= 3+3( )
2
+ 4+2( )
2
= 6( )
2
+ 6( )
2
= 36+36 = 72
AC=6 2
6 2 = 3 2 + 3 2
AC=AB+BC ‫اي‬
‫واحدة‬ ‫استقامة‬ ‫على‬ ‫تقع‬ ‫نقط‬ A , B , C :‫اذن‬
(1) ‫مثال‬
A= -3,-2( ),B= 0,1( ),C= 3,4( )
B ( 0 , 1 )
X
C ( 3 , 4 )
A ( -3 , -2 )
y d=AB= X2 -X1( )
2
+ Y2 -Y1( )
2
d = (x2
- x1
)2
+ (y2
- y1
(2

169. 169
‫واحد‬ ‫مستقيم‬ ‫خط‬ ‫على‬ ‫تقع‬ A -2,-1( ),B -1,0( ),C 2,3( ),D 4,5( ) : ‫النقط‬ ‫ان‬ ‫اثبت‬
/ ‫احلل‬
AB= -1+2( )
2
+ 0+1( )
2
= 1 + 1 = 2
BC= 2+1( )
2
+ 3-0( )
2
= 9 + 9 = 3 2
DC= 4-2( )
2
+ 5-3( )
2
= 4 + 4 = 2 2
AD ‫طول‬ ‫نجد‬ ‫واالن‬
AD= 4+2( )
2
+ 5+1( )
2
= 36 + 36 = 6 2
6 2 = 2 + 3 2 + 2 2 : ‫ان‬ ‫الحظ‬
AD = AB + BC + CD : ‫اي‬
‫واحد‬ ‫مستقيم‬ ‫على‬ ‫تقع‬ A , B , C , D ‫النقط‬ : ‫اذن‬
(2) ‫مثال‬
y
A
B
C
X
D
d=AB= X2 -X1( )
2
+ Y2 -Y1( )
2
d = (x2
- x1
)2
+ (y2
- y1
(2

170. 170
: ً‫ا‬‫ثاني‬
: ‫اضالعه‬ ‫اطوال‬ ‫حيث‬ ‫من‬ ‫المثلث‬ ‫نوع‬
. ‫االضالع‬ ‫مختلف‬ ‫او‬ ‫الساقين‬ ‫متساوي‬ ‫او‬ ‫االضالع‬ ‫متساوي‬ ‫اما‬ ‫فهو‬
A ( 2 , 4 ) , B (-4 , 2 ) , C) -1 , -2 ( ‫حيث‬ ‫اضالعه‬ ‫حيث‬ ‫من‬ A B C ‫المثلث‬ ‫نوع‬ ‫بين‬
/ ‫احلل‬
AB ≠ AC ≠ BC : ‫ان‬ ‫الحظ‬
‫االضالع‬ ‫مختلف‬ ‫المثلث‬ ∴
(3) ‫مثال‬
AB= 2+4( )
2
+ 4-2( )
2
= 36 + 4 = 2 10
AC= -1+4( )
2
+ -2+2( )
2
= 9 + 0 = 3
AC= -1+4( )
2
+ -2+2( )
2
= 9 + 0 = 3
BC= -1-2( )
2
+ -2-4( )
2
= 9 + 36 =
BC= -1-2( )
2
+ -2-4( )
2
= 9 + 36 = 45
y
A ( 2 , 4)
X
C ( -1 , -2)
B ( -4 , 2)
BC= 2+1( )
2
+ 3-0( )
2
= 9 + 9 = 3 25
d=AB= X2 -X1( )
2
+ Y2 -Y1( )
2
d = (x2
- x1
)2
+ (y2
- y1
(2
AC= -1+4( )
2
+ -2+2( )
2
= 9 + 0 = 3
BC= -1-2( )
2
+ -2-4( )
2
= 9 + 36 =−
16 25 = 5
AB = ( - 4 - 2 )2
+ ( 2 - 4) 2

171. 171
‫الساقين‬ ‫متساوي‬ A (3 ،-4 ) , B (5 ، -2 ) , C ) 5 ،-6 ( ‫رؤوسه‬ ‫الذي‬ ‫المثلث‬ ‫ان‬ ‫بين‬
/ ‫احلل‬
Q AB=AC ∵
‫الساقين‬ ‫متساوي‬ ABC ‫المثلث‬ ∴
: ً‫ا‬‫ثالث‬
‫الزاوية‬ ‫القائم‬ ‫المثلث‬ ‫أختبار‬
‫الزاوية‬ ‫قائم‬ ‫المثلث‬ ‫فان‬ ‫فيثاغورس‬ ‫مبرهنة‬ ‫تحققت‬ ‫فاذا‬ ، ‫اضالعه‬ ‫اطول‬ ‫نجد‬
. ‫الزاوية‬ ‫قائم‬ A (-2 , -2 ) , B (3 ,4 ) , C ) 3 , -2( ‫رؤوسه‬ ‫الذي‬ ‫المثلث‬ ‫ان‬ ‫بين‬
/ ‫احلل‬
d= x2 -x1( )
2
+ y2 -y1( )
2
(4) ‫مثال‬
d= x2 -x1( )
2
+ y2 -y1( )
2
AB= 5-3( )
2
+ -2+4( )
2
= 4 + 4 = 2
AB= 5-3( )
2
+ -2+4( )
2
= 4 + 4 = 2 2
BC= 5-5( )
2
+ -6+2( )
2
= 0 + 16 = 4
BC= 5-5( )
2
+ -6+2( )
2
= 0 + 16 = 4
AC= 5-3( )
2
+ -6+4( )
2
= 4 + 4 = 2
AC= 5-3( )
2
+ -6+4( )
2
= 4 + 4 = 2 2
y
c ( 5 , -6)
X
B ( 5 , -2)
A ( 3 , -4)
(5) ‫مثال‬
AB= 3+2( )
2
+ 4+2( )
2
= 25 + 36 = 61

172. 172
: ‫ان‬ ‫الحظ‬
AB( )
2
= AC( )
2
+ BC( )
2
: ‫اي‬
. C ‫في‬ ‫الزاوية‬ ‫قائم‬ ABC ‫المثلث‬ ∴
: ً‫ا‬‫رابع‬
‫أخرى‬ ‫تطبيقات‬
‫اضالع‬ ‫متوازي‬ ‫رؤوس‬ A (-2 , 3) ، B (-1 , 4) ،C (2 , -1) ، D(1 ,-2( : ‫النقط‬ ‫ان‬ ‫بين‬
.ABCD
/ ‫اجلل‬
∴AB=DC
∴
‫اضالع‬ ‫متوازي‬ ABCD ‫الشكل‬ ∴
AC= 3+2( )
2
+ -2+2( )
2
= 25 + 0
AC= 3+2( )
2
+ -2+2( )
2
= 25 + 0 = 25
BC= 3-3( )
2
+ -2-4( )
2
= 0 + 36 = 36
BC= 3-3( )
2
+ -2-4( )
2
= 0 + 36 =
y
X
B ( 3 , 4)
A ( -2 , -2) c (3 , -2) 61( )
2
= 25( )
2
+ 36( )
2
(6) ‫مثال‬
AB= -1+2( )
2
+ 4-3( )
2
= 1 + 1 = 2
AB= -1+2( )
2
+ 4-3( )
2
= 1 + 1 = 2
DC= 1-2( )
2
+ -2+1( )
2
= 1 + 1 = 2
DC= 1-2( )
2
+ -2+1( )
2
= 1 + 1 = 2
y
X
B
A
D
C
d= x2 -x1( )
2
+ y2 -y1( )
2
AD= 1+2( )
2
+ -2-3( )
2
= 9 + 25 = 34
BC= 2+1( )
2
+ -1-4( )
2
= 9 + 25 = 34
61 = 25 + 36
AD=BC

174. 174
. ‫منتصف‬ C ‫جد‬ B ( 5 , 1 ) ،A ( 3 , -5 ( ‫لتكن‬
/‫احلل‬
)Mid Point( ‫المنتصف‬ ‫نقطة‬
. B ‫النقطة‬ ‫احداثي‬ ‫فجد‬ A ( -1 , -2 ( ‫وكانت‬ ‫منتصف‬ ‫كانت‬ ‫اذا‬
/‫احلل‬
C=
x1 +x2
2
,
y1 +y2
2
⎛
⎝
⎜
⎞
⎠
⎟
3
2
,
-1
2
⎛
⎝
⎜
⎞
⎠
⎟ =
-1+x2
2
,
-2+y2
2
⎛
⎝
⎜
⎞
⎠
⎟ ⇒
3
2
=
-1+x2
2
⇒ -2+2x2 =6 ⇒ 2x2 =8 ⇒ x2 =4
-1
2
=
-2+y2
2
⇒ -4+2y2 =-2 ⇒ 2y2 =2 ⇒ y2 =1
∴ B = ( 4 , 1 )
(1) ‫مثال‬
(2) ‫مثال‬
C =
3
2
,
-1
2
⎛
⎝
⎜
⎞
⎠
⎟AB
M=
x1 +x2
2
,
y1 +y2
2
⎛
⎝
⎜
⎞
⎠
⎟
C =
3+5
2
,
-5+1
2
⎛
⎝
⎜
⎞
⎠
⎟
C =
8
2
,
-4
2
⎛
⎝
⎜
⎞
⎠
⎟
C = 4,-2( )
AB

175. 175
‫متوازي‬ ‫رؤوس‬ A (-2 , 3 ) ، B ( -1 , 4 ) ، C ( 2 , -1 ) ، D ( 1 ,- 2( ‫النقط‬ ‫ان‬ ‫بين‬
.‫المنتصف‬ ‫قانون‬ ‫باستخدام‬ ABCD ‫االضالع‬
/‫احلل‬
‫القطر‬ ‫منتصف‬ ‫نجد‬
M=
x1 +x2
2
,
y1 +y2
2
⎛
⎝
⎜
⎞
⎠
⎟
M1 =
-2+3
2
,
3+ -1( )
2
⎛
⎝
⎜
⎞
⎠
⎟
M1 =
-2+3
2
,
3+ -1( )
2
⎛
⎝
⎜
⎞
⎠
⎟
M1 = 0,1( )
BD ‫القطر‬ ‫منتصف‬ ‫نجد‬
M2 =
-1+1
2
,
4+ -2( )
2
⎛
⎝
⎜
⎞
⎠
⎟
M2 0,1( )
.‫االخر‬ ‫ينصف‬ ‫احدهما‬ ‫قطريه‬ ‫الن‬ ‫اضالع‬ ‫متوازي‬ ABCD ‫الشكل‬ M1 = M2 ∴
(3) ‫مثال‬
AC
y
X
B
A
D
C

176. 176
ABCD ‫الشكل‬ ‫كان‬ ‫اذا‬ D ‫النقطة‬ ّ‫احداثيي‬ ‫جد‬ A ( 4 , 0 ) ، B ( 6 , -6 ) ، C (-8 , 0( ‫لتكن‬
. ‫اضالع‬ ‫متوازي‬ ‫هو‬
/ ‫احلل‬
M=
x1 +x2
2
,
y1 +y2
2
⎛
⎝
⎜
⎞
⎠
⎟
AC ‫القطر‬ ‫منتصف‬ ‫نجد‬
M1 =
4+ -8( )
2
,
0+0
2
⎛
⎝
⎜
⎞
⎠
⎟
M1 = −2, 0( )
BD ‫القطر‬ ‫منتصف‬ ‫نجد‬
M2 =
x+6
2
,
y-6
2
⎛
⎝
⎜
⎞
⎠
⎟
‫االخر‬ ‫ينصف‬ ‫احدهما‬ ‫االضالع‬ ‫متوازي‬ ‫قطرا‬
∴ M2 = M1
: ‫اي‬
x+6
2
=-2 ⇒ x+6=-4
x=-10
y-6
2
=-2 ⇒ y-6=0
y=6
∴ D = −10,6( )
(4) ‫مثال‬
y-6
2
=-2 ⇒ y-6=0
A ( 4 , 0 )
D ( X , y )
c ( -8 , 0 )
B (6 , -6 )
y
X

177. 177
. ‫واحدة‬ ‫استقامة‬ ‫على‬ ‫تقع‬ A(-2,-2) ، B ( 2 , 1 ) ، C ( 6 , 4( : ‫النقاط‬ ‫ان‬ ‫بين‬ /1‫س‬
‫؟‬ A ( 6 , 8 ) ، B ( 0 , 0 ) ، C ( 0 , 8 ( :‫واحدة‬ ‫استقامة‬ ‫على‬ ‫تقع‬ ‫االتية‬ ‫النقط‬ ‫هل‬ /2‫س‬
.‫الدائرة‬ ‫هذه‬ ‫قطر‬ ‫طول‬ ‫جد‬ ‫لها‬ ‫تنتمي‬ A (-3 , -4 ( ‫والنقطة‬ O )6 , 8( ‫النقطة‬ ‫مركزها‬ ‫دائرة‬ /3‫س‬
‫الساقين‬ ‫«متساوي‬ A ( 2 ,-2) ، B ( 2 , 1 ) ، C ( 6 , 4 ( ‫رؤوسه‬ ‫الذي‬ ‫المثلث‬ ‫نوع‬ ‫بين‬ /4‫س‬
. » ‫االضالع‬ ‫مختلف‬ ، ‫االضالع‬ ‫متساوي‬
‫جد‬ ‫ثم‬ ‫الزاوية‬ ‫قائم‬ A ( 2 , -1 ) ، B ( 2 , 1 ) ، C ( -1 , 1( ‫رؤوسه‬ ‫الذي‬ ‫المثلث‬ ‫ان‬ ‫بين‬ /5‫س‬
. ‫المثلثة‬ ‫المنطقة‬ ‫مساحة‬
/6‫س‬
A ( -3 , 5 ) ، B ( 2 , 7 ) , C( 1 , 9) ،D (-4 , 7 ( ‫رؤوسه‬ ‫الذي‬ ‫الشكل‬ ‫ان‬ ‫بطريقتين‬ ‫بين‬
. ‫اضالع‬ ‫متوازي‬
/7‫س‬
D ‫الرابع‬ ‫الرأس‬ ‫احداثي‬ ‫جد‬ A(1 , 0) ، B(5 , 0) ، C(7 , 3( ‫رؤوسه‬ ‫اضالع‬ ‫متوازي‬ ABCD
/8‫س‬
‫المستقيمة‬ ‫القطعة‬ ‫طول‬ ‫ان‬ ‫من‬ ‫تحقق‬ A(6,4) ، B(-2,6) ، C(0,-4( ‫رؤوسه‬ ABC ‫مثلث‬
.‫الثالث‬ ‫الضلع‬ ‫طول‬ ‫نصف‬ ‫يساوي‬ ‫فيه‬ ‫ضلعين‬ ‫منتصفي‬ ‫بين‬ ‫الواصلة‬
/9‫س‬
‫القطعة‬ ‫طول‬ ‫ان‬ ‫من‬ ‫تحقق‬ A(0,10) ، B(6,8) ، C(-6,-8( ‫حيث‬ ‫مثلث‬ ABC
.‫الوتر‬ ‫طول‬ ‫نصف‬ ‫يساوي‬ ‫الوتر‬ ‫منتصف‬ ‫الى‬ ‫القائمة‬ ‫رأس‬ ‫من‬ ‫الواصلة‬ ‫المستقيمة‬
7 1

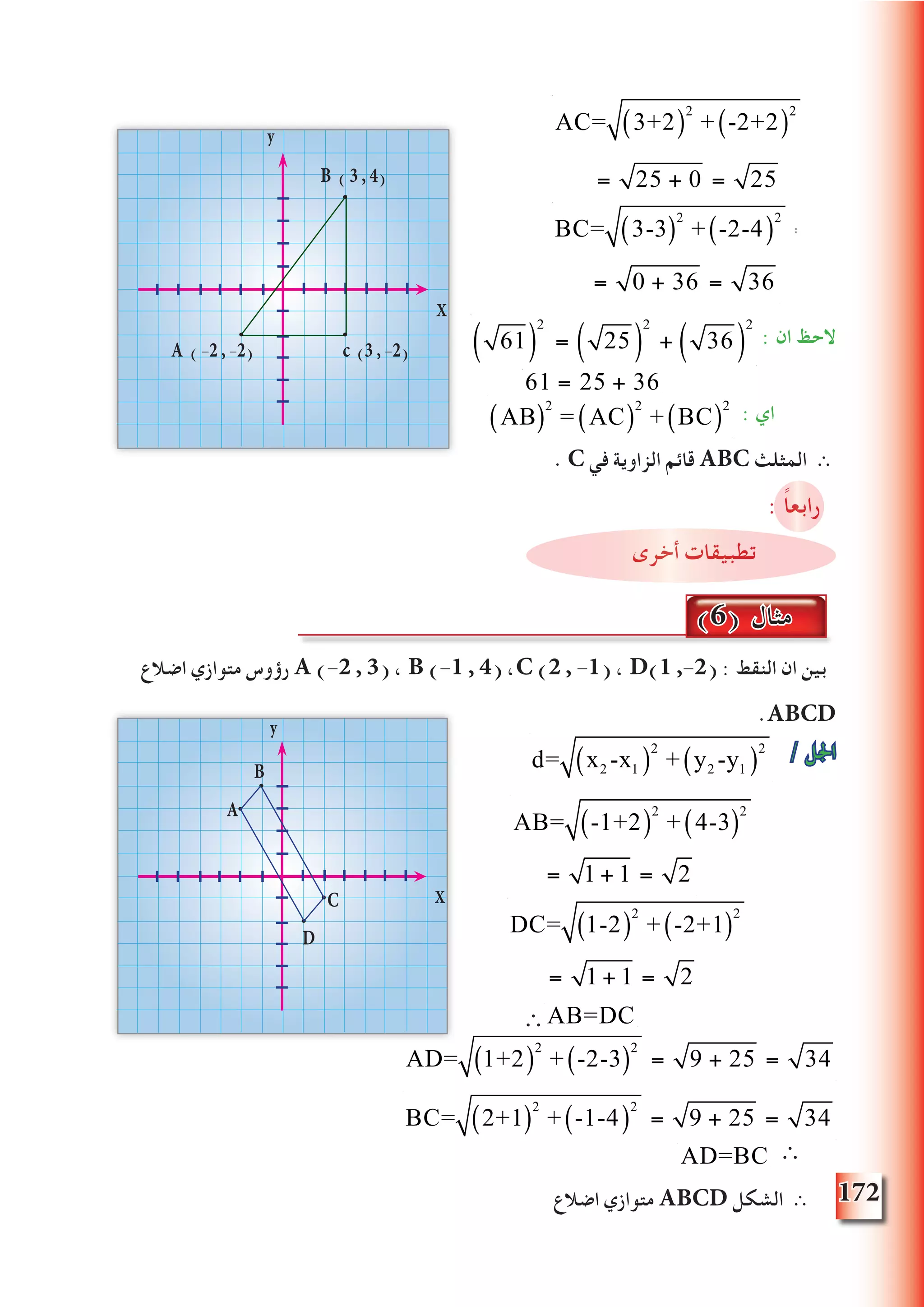
178. . ‫الهندسية‬ ‫التحويالت‬ ]8-1[
‫اآلنعكاس‬ ]8-2[
‫المستوي‬ ‫في‬ ‫مستقيم‬ ‫على‬ ‫اآلنعكاس‬ ]8-2-1[
‫اإلحداثي‬ ‫المستوي‬ ‫على‬ ‫اإلنعكاس‬ ]8-2-2[
‫اإلحداثي‬ ‫المستوي‬ ‫على‬ ‫اآلنسحاب‬ ]8-3[
‫الدوران‬ ]8-4[
‫نقطة‬ ‫حول‬ ٍ‫مستو‬ ‫على‬ ‫الدوران‬ ]8-4-1[
‫التكبير‬ ]8-5[
‫المتناسبة‬ ‫المجموعات‬ ]8-6[
‫التشابه‬ ]8-7[
‫الهندسية‬ ‫التحويالت‬
‫الرياضية‬ ‫العالقة‬ ‫او‬ ‫الرمز‬ ‫املصطلح‬
Rx
‫السيني‬ ‫احملور‬ ‫حول‬ ‫االنعكاس‬
Ry
‫الصادي‬ ‫احملور‬ ‫حول‬ ‫االنعكاس‬
R90ْ
90ْ ‫حول‬ ‫الدوران‬
D ‫التكبير‬
‫الثامن‬ ‫الفصل‬
8
‫االنسحاب‬T

179. ‫الهندسية‬ ‫التحويالت‬
‫الفصل‬
8
‫مقدمة‬
‫التناظر‬ ‫محور‬
‫الضلعين‬ ‫متطابق‬ ‫مثلث‬
‫تطابق‬ ‫يدرس‬ ‫الذي‬ ‫الهندسة‬ ‫فروع‬ ‫احد‬ ‫هي‬ ‫الهندسية‬ ‫التحويالت‬
‫متطابقان‬ ‫هندسيين‬ ‫لشكلين‬ ‫يقال‬ ‫حيث‬ ،‫الهندسية‬ ‫االشكال‬
‫التطابق‬ ‫وهذا‬ ‫االخر‬ ‫على‬ ‫نقاطهما‬ ‫من‬ ‫نقطة‬ ‫كل‬ ‫انطبقت‬ ‫اذا‬
‫فمثال‬ ‫جامدة‬ ‫او‬ ‫متحركة‬ ‫اجسام‬ ‫من‬ ‫الطبيعة‬ ‫في‬ ‫بما‬ ‫نالحظه‬
‫الكتاب‬ ‫وكذلك‬ ‫االخر‬ ‫على‬ ‫احدهما‬ ‫الفراشة‬ ‫جناحا‬ ‫ينطبق‬
‫تتطابق‬
‫وقوفك‬ ‫وعند‬ ‫التناظر‬ ‫محور‬ ‫نسميه‬ ‫محور‬ ‫بوساطة‬ ‫متناظرين‬ ‫نصفين‬ ‫الى‬ ‫ينقسم‬ ‫االنسان‬ ‫جسم‬ ‫وان‬ ‫اوراقه‬
‫ومن‬ ‫التناظر‬ ‫محور‬ ‫بمثابة‬ ‫المرآة‬ ‫خط‬ ‫وان‬ . ‫المرآة‬ ‫في‬ ‫تماما‬ ‫نفسها‬ ‫صورتك‬ ‫تشاهد‬ ‫مستوية‬ ‫مرآة‬ ‫امام‬
.‫هندسي‬ ‫شكل‬ ‫لكل‬ ‫التناظر‬ ‫محور‬ ‫نالحظ‬ ‫التالية‬ ‫االشكال‬ ‫خالل‬
‫بالتحويل‬ ‫يسمى‬ ‫نفسه‬ ‫المستوي‬ ‫في‬ ‫اخرى‬ ‫نقطة‬ ‫الى‬ ‫المستوي‬ ‫في‬ ‫نقطة‬ ‫كل‬ ‫ينقل‬ ‫الذي‬ ‫التحويل‬ ‫هذا‬ ‫ان‬
‫هذا‬ ‫في‬ ‫وسنتطرق‬ )Transltion( ‫واالنسحاب‬ , )Reflection( ‫االنعكاس‬ ‫أمثلته‬ ‫ومن‬ . ‫الهندسي‬
. ‫والتكبير‬ ‫كالدوران‬ ‫اخرى‬ ‫هندسية‬ ‫تحويالت‬ ‫إلى‬ ‫الفصل‬
8 - 1
‫المعين‬

180. 180
‫حيث‬ , R ‫التطبيق‬ ‫وأن‬ x ‫المستوي‬ ‫في‬ ‫مستقيم‬ L ‫أن‬ ‫نفرض‬
) a ∉ L) L ‫للمستقيم‬ ‫تنتمي‬ ‫ال‬ a ‫والنقطة‬ R : x x
ً‫ا‬‫آنعكاس‬ ‫يسمى‬ ‫هندسي‬ ‫تحويل‬ R ‫فان‬ .‫تقابل‬ ‫تطبيق‬ R ‫كان‬ ‫فاذا‬
.‫اآلنعكاس‬ ‫محور‬ ً‫ا‬‫أيض‬ L ‫ويسمى‬ RL
‫بالرمز‬ ‫له‬ ‫ونرمز‬ L ‫على‬
‫إحدى‬ ‫في‬ ‫الواقعة‬ ‫المستوي‬ ‫من‬ ‫النقط‬ ‫يحول‬ RL
‫أن‬ ‫الشكل‬ ‫من‬
‫الواقعة‬ ‫النقاط‬ ‫بينما‬ ‫منه‬ ‫األخرى‬ ‫الجهة‬ ‫الى‬ L ‫المستقيم‬ ‫جهتي‬
. a aَ ‫المستقيمة‬ ‫للقطعة‬ ‫العمودي‬ ‫المنصف‬ ‫هو‬ L ‫ويكون‬ . ‫موضعها‬ ‫في‬ ‫تبقى‬ ‫عليه‬
p1
(3 , 5 (‫النقطة‬ ‫صورة‬ ‫تكون‬ ‫المتعامد‬ ‫ثي‬ِ‫ا‬‫اإلحد‬ ‫المستوى‬ ‫في‬
‫.بعد‬ p2
(3 , -5 ( ‫)هي‬ x : axis) x ‫التناظر‬ ‫لمحور‬ ‫بالنسبة‬
‫بالنسبة‬ p2
‫النقطة‬ ‫بعد‬ ‫يساوي‬ x ‫لمحور‬ ‫بالنسبة‬ p1
‫النقطة‬
:‫التالية‬ ‫القاعدة‬ ‫إستنتاج‬ ‫يمكن‬ ‫عامة‬ ‫وبصورة‬ . x ‫لمحور‬
Rx
[( x , y )] = ( x , -y )
ً‫ا‬‫أيض‬ ‫الشكل‬ ‫ومن‬ . ) y = 0 (‫حيث‬ ) x : axis) x ‫السينات‬ ‫لمحور‬ ‫بالنسبة‬ ً‫ا‬‫آنعكاس‬ ‫يسمى‬ Rx
‫حيث‬
. p3
(-3 , 5 ( ‫هي‬ ) y : axis) y ‫الصادات‬ ‫لمحور‬ ‫بالنسبة‬ p1
(3 , 5 (‫النقطة‬ ‫صورة‬ ‫الحظ‬
‫الصادات‬ ‫محور‬ ‫عن‬ P3
‫النقطة‬ ‫بعد‬ ‫يساوي‬ ‫الصادات‬ ‫محور‬ ‫عن‬ ‫بالنسبة‬ P ‫النقطة‬ ‫بعد‬ ‫أن‬ ً‫ا‬‫أيض‬ ‫تالحظ‬ ‫كما‬
. ‫التالية‬ ‫القاعدة‬ ‫أستنتاج‬ ‫يسهل‬ ‫وهذا‬
Ry
[( x , y )] = ( -x , y )
. ) x = 0 ( ‫حيث‬ ) y : axis) y ‫الصادات‬ ‫لمحور‬ ‫بالنسبة‬ ً‫ا‬‫آنعكاس‬ ‫يسمى‬ Ry
‫حيث‬
8 - 2Reflection ‫االنعكاس‬
: ‫المستوي‬ ‫في‬ ‫مستقيم‬ ‫على‬ ‫االنعكاس‬ ]8 - 2 - 1[
: ‫االحداثي‬ ‫المستوى‬ ‫على‬ ‫االنعكاس‬ ]8 - 2 - 2[
x
y p1
( 3 , 5 )
p2
( 3 , -5 )
p3
( -3 , 5 )
a aَ
L

181. 181
(1) ‫مثال‬
:‫فجد‬ . p (3 , -4 ( ‫كانت‬ ‫اذا‬
.‫السينات‬ ‫لمحور‬ ‫بالنسبة‬ P ‫النقطة‬ ً‫ا‬‫آنعكاس‬ ‫صورة‬ )1
.‫الصادات‬ ‫لمحور‬ ‫بالنسبة‬ P ‫النقطة‬ ‫آنعكاس‬ ‫صورة‬ )2
/‫احلل‬
Rx
[( x , y )] = ( x , -y ( ‫القاعدة‬ ‫حسب‬ )1
⇒ Rx
[( 3 , -4 )] = ( 3 , -(-4)) = (3 , 4 (
‫القاعدة‬ ‫حسب‬ )2
Ry
[( x , y )] = ( -x , y (
⇒ Ry
[( 3 , -4 )] = ( -3 , -4 (
ABC ‫املثلث‬ ‫صورة‬ ‫فجد‬ C ( 0 , -3 ) , B ( 5 , 0 ) , A ( 3 , 2 ( ‫كانت‬ ‫اذا‬
. ً‫ا‬‫هندسي‬ ‫ه‬ّ‫ل‬‫ومث‬ ‫السينات‬ ‫محور‬ ‫في‬ ‫باالنعكاس‬ )1
. ً‫ا‬‫هندسي‬ ‫ه‬ّ‫ل‬‫ومث‬ ‫الصادات‬ ‫محور‬ ‫في‬ ‫باالنعكاس‬ )2
/ ‫احلل‬
‫السينات‬ ‫محور‬ ‫في‬ ‫انعكاس‬‫الصادات‬ ‫محور‬ ‫في‬ ‫انعكاس‬
Aَ = Rx
[( 3 , 2 )] = ( 3 , -2(Aً = Ry
[( 3 , 2 )] = ( -3 , 2(
Bَ = Rx
[( 5 , 0 )] = ( 5 , 0 (Bً = Ry
[( 5 , 0 )] = ( -5 , 0(
Cَ = Rx
[( 0 , -3 )] = ( 0 , 3 (Cً = Ry
[( 0 , -3 )] = ( 0 , -3 (
x
y
Aَ
Aً
Bَ
Bً
Cَ
Cً
(2) ‫مثال‬
A

182. 182
‫آنعكاس‬ ‫تأثير‬ ‫حتت‬ 2x - 3y = 6 ‫معادلته‬ ‫الذي‬ ‫املستقيم‬ ‫صورة‬ ‫جد‬
. ً‫ا‬‫هندسي‬ ‫ومثله‬ ‫السينات‬ ‫حملور‬ ‫بالنسبة‬ ) 1
. ً‫ا‬‫هندسي‬ ‫ومثله‬ ‫الصادات‬ ‫حملور‬ ‫بالنسبة‬ ) 2
‫بوضع‬ ‫املستقيم‬ ‫على‬ ‫نقطتني‬ ‫جند‬ / ‫احلل‬
x = 0
⇒ 2(0) - 3y = 6 ‫املستقيم‬ ‫معادلة‬ ‫في‬ ‫نعوضها‬
⇒ - 3y = 6
⇒ y =
6
-3
= ⇒ y = -2
⇒ 2x - 3(0) = 6 ‫املستقيم‬ ‫معادلة‬ ‫في‬ y = 0 ‫نعوض‬
⇒ 2x = 6
) 0 , -2( ، ) 3 , 0( ‫هما‬ ‫النقطتان‬ ∴
2x - 3y = 6 ‫املستقيم‬ ‫ميثل‬ L1
∴
1) Rx
[( 0 , -2 )] = ( 0 , 2 )
Rx
[( 3 , 0 )] = ( 3 ,0 (
2) Ry
[( 0 , -2 )] = ( 0 , -2 )
Ry
[( 3 , 0 )] = ( -3 ,0 (
‫يكون‬ ‫عندما‬ ‫الصادات‬ ‫محور‬ ‫في‬ ‫االنعكاس‬ ‫تأثير‬ ‫حتت‬ ABCD ‫الرباعي‬ ‫الشكل‬ ‫صورة‬ ‫جد‬
.ً‫ا‬‫هندسي‬ ‫ومثله‬ A ( 1 , 1 ) , B ( 4 , 1 ) , C ( 4 , 3 ) , D ( 1 , 3 (
Ry
[( 1 , 1 )] = ( -1 , 1 ( / ‫احلل‬
Ry
[( 4 , 1 )] = ( -4 , 1 (
Ry
[( 4 , 3 )] = ( -4 , 3 )
Ry
[( 1 , 3 )] = ( -1 , 3 (
⎤
⎦
⎥ ⇒ L2
⎤
⎦
⎥ ⇒ L3
(3) ‫مثال‬
(4) ‫مثال‬
⇒ x =
6
2
= ⇒ x = 3 y
x
L1
L2
L3
y
x
D
A B
CDَ
AَBَ
Cَ

183. 183
]8-1[ ‫تعريف‬
‫بحيث‬ pَ ‫الى‬ ‫المستوي‬ ‫في‬ P ‫نقطة‬ ‫كل‬ ‫ينقل‬ ‫هندسي‬ ‫تحويل‬ ‫هو‬
. ‫معلوم‬ ‫باتجاه‬ P Pَ ، ‫معينة‬ ‫مسافة‬ = P Pَ
‫السينات‬ ‫لمحور‬ ‫الموجب‬ ‫باالتجاه‬ ) 1 : ‫فأن‬
T ( x ,y ) = ( x + a , y )
‫السينات‬ ‫لمحور‬ ‫السالب‬ ‫باالتجاه‬ )2
T ( x ,y ) = ( x - a , y )
8 - 3Traslation ‫االنسحاب‬
: ‫االحداثي‬ ‫المستوي‬ ‫على‬ ‫االنسحاب‬ ]8 - 3 - 1[
: a ‫معينة‬ ‫مسافة‬ ‫انسحاب‬ ‫تاثير‬ ‫تحت‬ ) x , y ( ‫النقطة‬ ‫صورة‬ ]8 - 3 - 2[
‫الصادات‬ ‫حملور‬ ‫املوجب‬ ‫باالجتاه‬ )3
T( x , y ) = ( x , y + a )
‫الصادات‬ ‫حملور‬ ‫السالب‬ ‫باالجتاه‬ )3
T( x , y ) = ( x , y - a )
. ‫وحدات‬ ) 5( ‫مقداره‬ ‫أنسحاب‬ ‫تأثير‬ ‫حتت‬ ‫النقطة‬ ‫صورة‬ ‫فأوجد‬ ) -2 , 3( ‫النقطة‬ ‫كانت‬ ‫اذا‬
. ‫السينات‬ ‫حملور‬ ‫السالب‬ ‫باالجتاه‬ )b . ‫السينات‬ ‫حملور‬ ‫املوجب‬ ‫باالجتاه‬ )a
. ‫الصادات‬ ‫حملور‬ ‫السالب‬ ‫باالجتاه‬ )d . ‫الصادات‬ ‫حملور‬ ‫املوجب‬ ‫باالجتاه‬ )c
a = 5 (a / ‫احلل‬
T ( x , y ) = ( x + a , y )
T (-2 , 3 ) = (-2 + 5 , 3 ) = ( 3 , 3 )
(1) ‫مثال‬

184. 184
b) T ( x , y ) = ( x - a , y )
T (-2 , 3 ) = ( -2 -5 , 3 )
=(-7,3)
c) T ( x , y ) = ( x , y + a (
T(-2 , 3 ) = (-2 , 3 + 5 )
= (-2 , 8 )
d) T( x , y ) = ( x , y - a )
T(-2 , 3 ) = (-2 , 3 -5 (
= (-2,-2)
‫تعريف‬
]8-2[ ‫تعريف‬
a ‫مثل‬ ‫اخرى‬ ‫نقطة‬ ‫اي‬ ‫ويحول‬ ‫نفسها‬ ‫الى‬ O ‫النقطة‬ ‫يحول‬ ‫هندسي‬ ‫تحويل‬ ‫هو‬ ٍ‫مستو‬ ‫في‬ ‫الدوران‬
. ‫ثيتا‬ ‫تقرا‬ θ ‫الزاوية‬ ‫حيث‬ ʹa ‫النقطة‬ ‫الى‬
‫مالحظة‬: ‫على‬ ‫يحافظ‬ ‫االنسحاب‬
. ‫والتوازي‬ ‫الزاوية‬ ‫وقياس‬ ‫والبينية‬ ‫االستقامة‬
8 - 4Rotation ‫الدوران‬
: ‫االحداثي‬ ‫المستوي‬ ‫على‬ ‫الدوران‬ ]8 - 4 - 1

185. 185
: ‫وان‬
. ‫االصل‬ ‫نقطة‬ ‫حول‬ 90ْ ‫الدوران‬ ∗
. R 90ْ
( x , y ) = ( y , -x ( ‫الساعة‬ ‫عقارب‬ ‫باتجاه‬ ‫دوران‬ )1
R 90ْ
( x , y ) = ( -y , x ( ‫الساعة‬ ‫عقارب‬ ‫عكس‬ ‫باتجاه‬ ‫دوران‬ )2
. ) ‫دورة‬ ‫نصف‬ ( ‫االصل‬ ‫نقطة‬ ‫حول‬ 180ْ ‫الدوران‬ ∗
R 180ْ
( x , y ) = ( -x , -y ( ‫الساعة‬ ‫عقارب‬ ‫باتجاه‬ ‫دوران‬ )1
R 180ْ
( x , y ) = ( -x , -y ( ‫الساعة‬ ‫عقارب‬ ‫عكس‬ ‫باتجاه‬ ‫دوران‬ )2
. ‫االصل‬ ‫نقطة‬ ‫حول‬ 270ْ ‫الدوران‬ ∗
R 270ْ
( x , y ) = (- y , x ( ‫الساعة‬ ‫عقارب‬ ‫باتجاه‬ ‫دوران‬ )1
R 270ْ
( x , y ) = ( y , -x ( ‫الساعة‬ ‫عقارب‬ ‫عكس‬ ‫باتجاه‬ ‫دوران‬ )2
.‫النقطة‬ ‫صورة‬ ‫فجد‬ )-2 , 1( ‫النقطة‬ ‫كانت‬ ‫اذا‬
.‫االصل‬ ‫نقطة‬ ‫مركزه‬ ،90ُ ‫قياسها‬ ‫بزاوية‬ ‫دوران‬ ‫تأثير‬ ‫تحت‬ )1
. ‫الساعة‬ ‫عقارب‬ ‫باتجاه‬ )b . ‫الساعة‬ ‫عقارب‬ ‫عكس‬ ‫باتجاه‬ )a
a) R 90ْ
( x , y ) = ( -y , x ( /‫احلل‬
∴ R 90ْ
(-2 , 1 ) = (-1 , - 2
b) R 90ْ
( x , y ) = ( y , - x (
∴ R 90ْ
(-2 , 1 ) = (1 , 2 )
‫مثال‬
)

186. 186
.‫االصل‬ ‫نقطة‬ ‫مركزه‬ ، 180
o
‫قياسها‬ ‫بزاوية‬ ‫دوران‬ ‫تأثير‬ ‫تحت‬ )2
‫الساعة‬ ‫عقارب‬ ‫عكس‬ ‫باتجاه‬
/ ‫احلل‬
b) R 180ْ
(x,y)=(-x ,-y )
∴ R 180ْ
(-2 , 1 ) = (2 , - 1 )
.‫االصل‬ ‫نقطة‬ ‫مركزه‬ ، 270
o
‫قياسها‬ ‫بزاوية‬ ‫دوران‬ ‫تأثير‬ ‫تحت‬ )3
‫الساعة‬ ‫عقارب‬ ‫عكس‬ ‫باتجاه‬
b) R 270ْ
(x,y)=(y ,-x ( /‫احلل‬
∴ R 270ْ
(-2, 1)= (1 ,2)
‫اخرى‬ ‫نقطة‬ ‫اي‬ ‫ويحول‬ ‫نفسها‬ ‫الى‬ O ‫النقطة‬ ‫يحول‬ ‫وهو‬ K ‫ومعامله‬ O ‫مركزه‬ ‫هندسي‬ ‫تحويل‬ ‫هو‬
, Pَ (x1
, y 1
( . ‫الى‬ p (x , y ( ‫مثل‬
‫فان‬ K ‫،معامله‬ ‫االصل‬ ‫نقطة‬ O ‫مركزه‬ ، p (x , y ( ‫للنقطة‬ ‫التكبير‬ ‫كان‬ ‫اذا‬
D [P ( x ,y )] = ( Kx , Ky (
‫مالحظة‬:‫الدوران‬ ‫خواص‬ ‫بعض‬
.‫والتوازي‬ ‫الزوايا‬ ‫وقياس‬ ‫البينية‬ ‫و‬ ‫االستقامة‬ ‫على‬ ‫يحافظ‬
8 - 5Dilatation ‫التكبير‬
OPَ = KOP

187. 187
. 2 ‫ومعامله‬ ‫االصل‬ ‫نقطة‬ ‫مركزه‬ ‫تكبير‬ ‫تأثير‬ ‫حتت‬ p (3 ,4 ( ‫صورة‬ ‫جد‬
/‫احلل‬
p (3 , 4 (
K = 2
∵ D [P ( x , y )] = ( Kx , Ky (
∴ D [P ( 3 , 4 )] = (( 2 ( )3( , )2()4( (
= )6 , 8 (
. 3 ‫ومعامله‬ ‫االصل‬ ‫نقطة‬ ‫مركزه‬ ‫تكبير‬ ‫تأثير‬ ‫حتت‬ p (-2 , 3 ( ‫صورة‬ ‫جد‬
/‫احلل‬
p (-2 , 3 (
K =3
∵ D [P ( x , y )] = ( Kx , Ky (
∴ D [P ( -2 , 3 )] = ((3 ( )-2( , )3()3( (
= ) -6 , 9 (
.‫االستقامة‬ ‫على‬ ‫يحافظ‬ )1
.‫البينية‬ ‫على‬ ‫يحافظ‬ )2
.‫األبعاد‬ ‫نسب‬ ‫على‬ ‫يحافظ‬ )3
.‫الزوايا‬ ‫قياس‬ ‫على‬ ‫يحافظ‬ )4
(1) ‫مثال‬
(2 ) ‫مثال‬
: ‫التكبير‬ ‫خواص‬ ]8 - 5 - 1

188. 188
.‫االصل‬ ‫نقطة‬ ‫ومركزه‬ 2 ‫معامله‬ ‫تكبير‬ ‫تأثير‬ ‫تحت‬ ABC ∆ ‫صورة‬ ‫جد‬
. A ( 0 , 0 ) , B ( 4 , 0 ) , C ( 4 , 3 ( ‫حيث‬
/‫احلل‬
(3) ‫مثال‬
y
x
Aَ = A B Bَ
Cَ
C
K = 2
D(0,0) = (2(0),2(0)) = (0,0) = ʹA
D(4,0) = (2(4),2(0)) = (8,0) = ʹB
D(4,3) = (2(4),2(3)) = (8,6) = ʹC

189. 189
. p) 5 , -3( ‫النقطة‬ ‫صورة‬ ‫جد‬ )1
. ‫السينات‬ ‫محور‬ ‫على‬ ‫انعكاس‬ ‫تأثير‬ ‫تحت‬ )a
.‫الصادات‬ ‫محور‬ ‫على‬ ‫انعكاس‬ ‫تأثير‬ ‫تحت‬ )b
. ‫السينات‬ ‫لمحور‬ ‫الموجب‬ ‫باالتجاه‬ ‫وحدات‬ )3( ‫مقداره‬ ‫انسحاب‬ )c
. ‫الصادات‬ ‫لمحور‬ ‫السالب‬ ‫باالتجاه‬ ‫وحدات‬ )2( ‫مقداره‬ ‫انسحاب‬ )d
‫السينات‬ ‫محور‬ ‫في‬ ‫االنعكاس‬ ‫تأثير‬ ‫تحت‬ ABC ∆ ‫صورة‬ ‫جد‬ )2
C (4 , 5) , B ( 1 , 4 ) , A ( 1 , 2 ( ‫حيث‬
: ‫تأثير‬ ‫تحت‬ x - y - 4 = 0 ‫المستقيم‬ ‫صورة‬ ‫جد‬ )3
. ‫السينات‬ ‫محور‬ ‫على‬ ‫االنعكاس‬ )a
. ‫الصادات‬ ‫محور‬ ‫على‬ ‫االنعكاس‬ )b
8 1

190. 190
: ‫تأثير‬ ‫تحت‬ ) 2 , -1 ( ‫النقطة‬ ‫صورة‬ ‫جد‬ )4
.‫االصل‬ ‫نقطة‬ ‫ومركزه‬ .‫الساعة‬ ‫عقارب‬ ‫عكس‬ ‫باتجاه‬ 90ْ ‫بزاوية‬ ‫دوران‬ )a
.‫االصل‬ ‫نقطة‬ ‫ومركزه‬ .‫الساعة‬ ‫عقارب‬ ‫باتجاه‬ 90ْ ‫بزاوية‬ ‫دوران‬ )b
.‫االصل‬ ‫نقطة‬ ‫ومركزه‬ .‫الساعة‬ ‫عقارب‬ ‫عكس‬ ‫باتجاه‬ 180ْ ‫بزاوية‬ ‫دوران‬ ‫تأثير‬ ‫تحت‬ )c
.‫االصل‬ ‫نقطة‬ ‫ومركزه‬ .‫الساعة‬ ‫عقارب‬ ‫باتجاه‬ 180ْ ‫بزاوية‬ ‫دوران‬ ‫تأثير‬ ‫تحت‬ )d
. C(1 , 4 ) , B (-3 , 3 ) , A( - 2 , 1( ‫رؤوسه‬ ‫الذي‬ ‫المثلث‬ ‫انسحاب‬ ‫صورة‬ ‫جد‬ )5
. ‫السينات‬ ‫لمحور‬ ‫الموجب‬ ‫باالتجاه‬ ‫وحدات‬ )5( ‫قدرها‬ ‫مسافة‬
.)2( ‫ومعامله‬ ‫االصل‬ ‫نقطة‬ ‫مركزه‬ ‫تكبير‬ ‫تأثير‬ ‫تحت‬ p )-4 ,3( ‫النقطة‬ ‫صورة‬ ‫جد‬ )6
o ‫مركزه‬ ABC ‫المثلث‬ ‫صورة‬ ‫جد‬ C ( 0 , 6 ) , B ( 2 , 3 ) , A ( -1 , 1( ‫كانت‬ ‫اذا‬ )7
: ‫تكبيره‬ ‫ومعامل‬
a) k = 2
b) k = -2
c ) k =
1
2

191. 191
‫للمجموعتين‬ ‫فيقال‬ ‫متقابلتين‬ ‫مجموعتين‬ y = { c , d } , x = { a , b { ‫المجموعتان‬ ‫كانت‬ ‫اذا‬
‫كان‬ ‫اذا‬ ‫متناسبتان‬ ‫المتقابلتين‬
1( } 1 , 2 { , } 2 , 4 { . ‫متناسبة‬ ‫المجموعات‬ ‫اي‬ ‫بين‬
2( } 3 , 6 { , } 4 , 2 {
3( } 3 , 4 , 5 { , } 6 , 8 , 10 {
1( ‫متناسبة‬ / ‫احلل‬
2( ‫متناسبة‬ ‫غير‬
‫متناسبة‬
8 - 6‫املتناسبة‬ ‫املجموعات‬
‫مثال‬
a
c
=
b
d
1
2
=
1
2
3
4
≠
6
2
3
6
=
4
8
=
5
10
⇒
1
2
=
1
2
=
1
2
3(
2
4

192. 192
. ‫الرياضيات‬ ‫مادة‬ ‫عن‬ ‫منهم‬ ‫البعيدين‬ ‫حتى‬ ‫الناس‬ ‫من‬ ‫العظمى‬ ‫الغالبية‬ ‫لدى‬ ‫مفهوم‬ ‫التشابه‬ ‫مصطلح‬ ‫ان‬
- : ‫الهندسية‬ ‫االشكال‬ ‫موضوع‬ ‫وفي‬
‫المتناظرة‬ ‫اضالعهما‬ ‫اطوال‬ ‫وتناسبت‬ ‫متساوية‬ ‫زواياهما‬ ‫كانت‬ ‫اذا‬ ‫متشابهان‬ ‫انهما‬ ‫هندسيين‬ ‫لشكلين‬ ‫يقال‬
ً‫ال‬‫مث‬ . )‫المتساوية‬ ‫الزوايا‬ ‫تقابل‬ ‫(التي‬
. ‫متساوية‬ ‫زواياهما‬ ‫ان‬ ‫من‬ ‫بالرغم‬ B ‫المستطيل‬ ‫يشابه‬ ‫ال‬ A ‫المستطيل‬
-: ‫الشكل‬ ‫في‬ ‫فقط‬ ‫المتشابهة‬ ‫المثلثات‬ ‫على‬ ‫دراستنا‬ ‫في‬ ‫نقتصر‬ ‫وسوف‬
DEF , ABC
m ∠CAB = m ∠FDE
m ∠ABC = m ∠DEF
m ∠ACB = m ∠DFE
AB
DE
=
BC
DF
=
AC
DF
1(
2(
8 - 7‫التشابه‬
A
B C
D
E F
1cm
2cm
3cm
2cmA
B
△△ ‫متشابهان‬DEF , ABC
m ∠CAB = m ∠FDE
m ∠ABC = m ∠DEF
m ∠ACB = m ∠DFE
AB
DE
=
BC
DF
=
AC
DF

193. 193
. ‫االصل‬ ‫نقطة‬ ‫ومركزه‬ 3 ‫معامله‬ ‫بتكبير‬ OEF ‫للمثلث‬ ‫تكبير‬ OBC ‫املثلث‬ ‫كان‬ ‫اذا‬
‫؟‬ ‫متناسبة‬ ‫اضالعهما‬ ‫هل‬ ‫بني‬ ، F(3 , 3) ، E(3 , 0) ، O(0 , 0 ( ‫حيث‬
/‫احلل‬
FE = (3− 0)2
(0 − 0)2
= 3
OB = 9
OE = 3
BC = 9
FE = (3− 0)2
(0 − 0)2
= 3
OB = 9
OE = 3
BC = 9
+FE = (3− 0)2
(0 − 0)2
= 3
OB = 9
OE = 3
BC = 9
OF = (3− 0)2
+(3− 0)2
= 9 + 9 = 18 = 3 2
OC = (9 − 0)2
+(9 − 0)2
= 81+ 81 = 2(81) = 9 2
OB
OE
=
BC
EF
=
OC
OF
9
3
=
9
3
=
9 2
3 2
. ‫متناسبة‬ ‫االضالع‬ ∴
(1) ‫مثال‬
y
x
O(0 , 0)
C(9 , 9)
E(3 , 0) B(9 , 0)
F(3 , 3)
FE = (3− 0)2
(0 − 0)2
= 3
OB = 9
OE = 3
BC = 9
FE = (3− 0)2
(0 − 0)2
= 3
OB = 9
OE = 3
BC = 9
D(0,0) = (3(0),3(0)) = (0,0)
D(3,0) = (3(3),3(0)) = (9,0)
D(3,3) = (3(3),3(3)) = (9,9)

194. 194
‫مشابه‬ ‫الناجت‬ ‫املثلث‬ ‫فان‬ ‫االخرين‬ ‫ضلعيه‬ ‫ويقطع‬ ‫مثلث‬ ‫في‬ ً‫ا‬‫ضلع‬ ‫يوازي‬ ‫مستقيم‬ ‫رسم‬ ‫اذا‬
.‫االصلي‬ ‫للمثلث‬
‫لالطالع‬ 1 /‫مبرهنة‬
‫على‬ M , N ‫في‬ AC , AB ‫ضلعيه‬ ‫يقطع‬ MN ‫املستقيم‬ ، ABC ‫املثلث‬ ‫في‬ /‫المعطيات‬
MN
s ruu
/ /BC N، ‫الترتيب‬
ABC ‫املثلث‬ ‫يشابه‬ AMN ‫املثلث‬ ‫ان‬ /‫أثباته‬ ‫المطلوب‬
‫بحيث‬ A ‫مركزه‬ ‫تكبير‬ ‫أفرض‬ /‫البرهان‬
C → N , B → M
AB MN
s ruu
∴
C → N , B → M
AB MN
s ruu
∴
C → N , B → M
AB MN
s ruu
∴BC ‫صورة‬
MN
s ruu
∴
‫بالقياسات‬ ‫متساويه‬ ‫املتناظره‬ ‫املثلث‬ ‫زوايا‬ ∴
. ‫الزوايا‬ ‫قياس‬ ‫على‬ ‫يحافظ‬ ‫التكبير‬ ‫ألن‬
‫التكبير‬ ‫معامل‬ =
AM
AB
=
AN
AC
=
MN
BC
=
AM
AB
=
AN
AC
=
MN
BC
=
AM
AB
=
AN
AC
=
MN
BC
‫كذلك‬
‫متشابهان‬ ‫املثلثان‬ ∴
.‫زواياهما‬ ‫قياسات‬ ‫تساوت‬ ‫اذا‬ ‫املثلثان‬ ‫يتشابه‬
‫لالطالع‬ 2 /‫مبرهنة‬
‫فيهما‬ Aَ Bَ Cَ , ABC ‫املثلثان‬ /‫المعطيات‬
ʹA ʹB ʹC ‫املثلث‬ ‫يشابه‬ ABC‫املثلث‬ /‫أثباته‬ ‫المطلوب‬
A
C B
NM
NM
A
CB
Bَ Cَ
Aَ
m ∠ A = m ∠ ʹA
m ∠ B = m ∠ ʹB
m ∠ C = m ∠ ʹC

195. 195
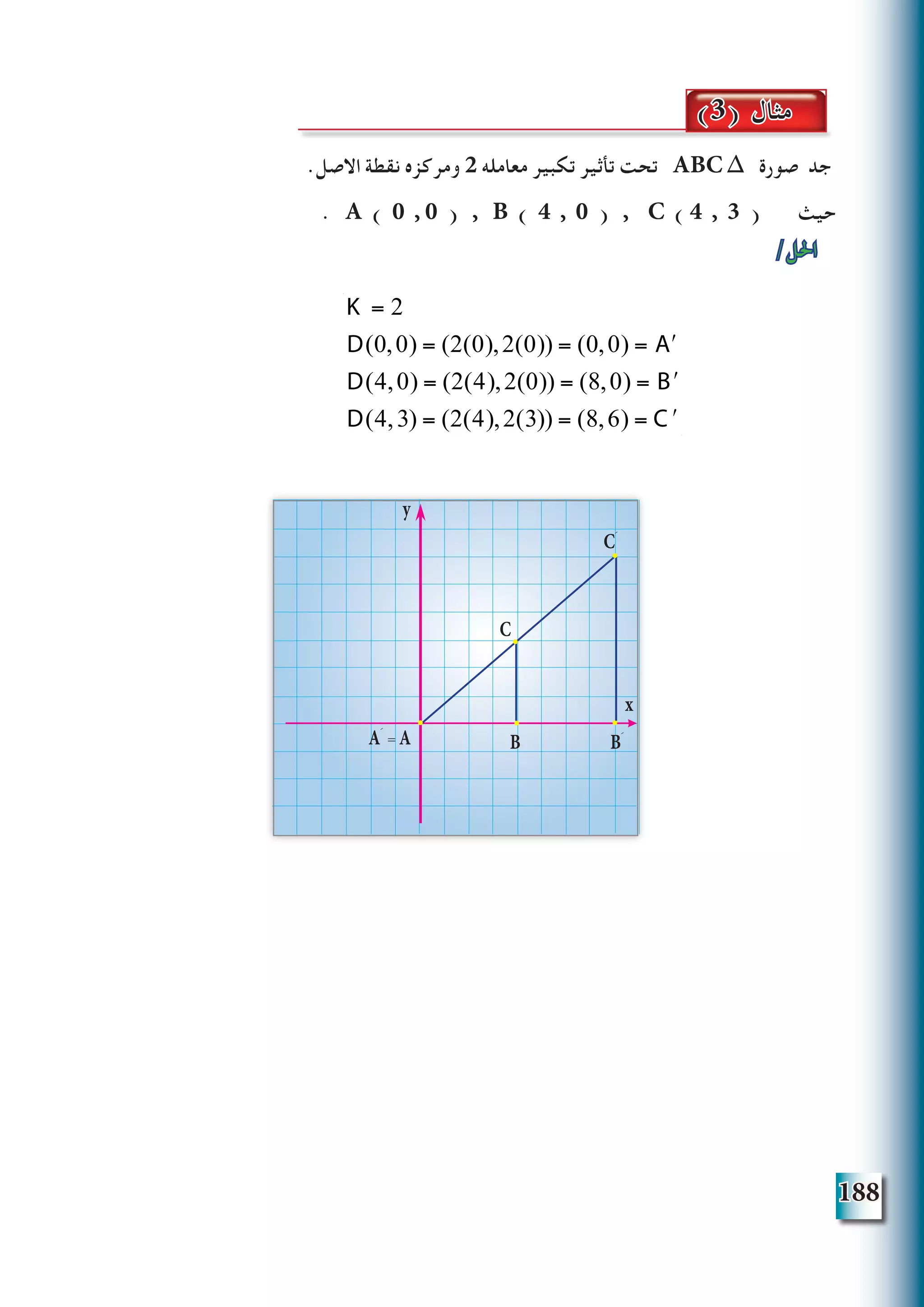
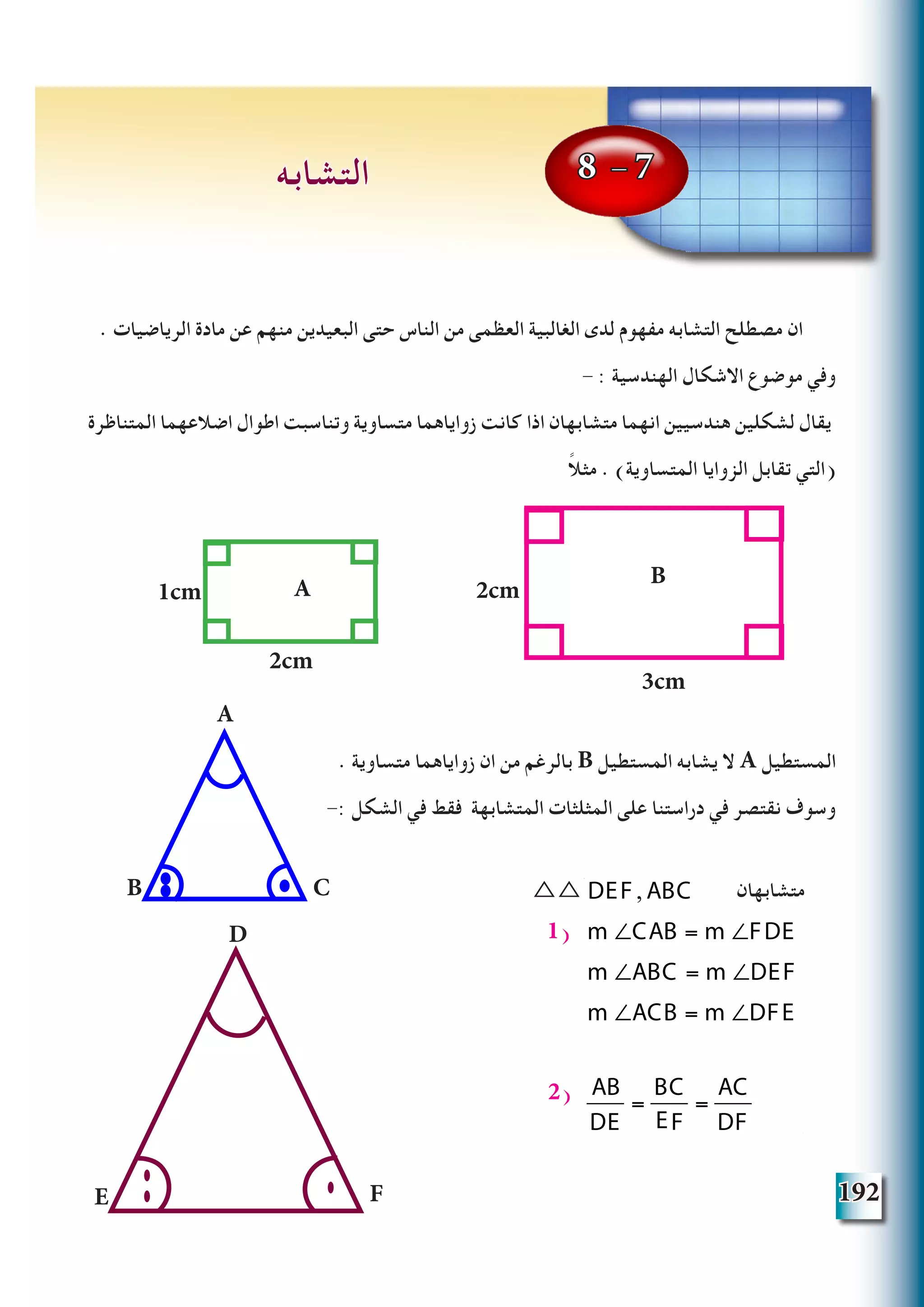
/‫البرهان‬
BC ∥ MN ‫وليكن‬ ، Aَ Bَ = AM ‫بحيث‬ AB ‫الى‬ ‫تنتمي‬ ‫نقطة‬ M ‫لتكن‬
]1 ‫[مبرهنة‬ ..... AMN ∆ ‫يشابه‬ ABC ∆ ∴
)‫متطابقان‬ ‫المثلثين‬ ‫(ألن‬ ...... Aَ Bَ Cَ ∆ ‫يشابه‬ AMN ∆ ‫لكن‬
) ‫م‬ . ‫هـ‬ . ‫و‬ ( Aَ Bَ Cَ ∆ ‫يشابه‬ ABC ∆ ∴
: ‫كان‬ ‫اذا‬
Aَ Bَ Cَ ∆ ‫يشابه‬ ABC ∆ ‫فان‬
‫فيهما‬ Aَ Bَ Cَ ∆ ‫و‬ ABC ∆
Aَ Bَ Cَ ∆ ‫يشابه‬ ABC ∆ ∴
. ‫اضالعهما‬ ‫أطوال‬ ‫تناسبت‬ ‫اذا‬ ‫المثلثان‬ ‫يتشابه‬
‫برهان‬ ‫بدون‬ ‫المبرهنة‬ ‫هذه‬ ‫سنقبل‬
3/‫مبرهنة‬
‫طوال‬ ‫وكان‬ ‫اخر‬ ‫مثلث‬ ‫في‬ ‫نظيرتها‬ ‫مثلث‬ ‫في‬ ‫زاوية‬ ‫طابقت‬ ‫اذا‬ ‫مثلثان‬ ‫يتشابه‬
. ‫بنظيرتها‬ ‫المحيطين‬ ‫الضلعين‬ ‫طولي‬ ‫مع‬ ‫متناسبين‬ ‫بها‬ ‫المحيطين‬ ‫الضلعين‬
‫برهان‬ ‫بدون‬ ‫المبرهنة‬ ‫هذه‬ ‫سنقبل‬
4/‫مبرهنة‬
A
Bَ Cَ
Aَ
CB
A
Bَ Cَ
Aَ
CB
AB
ʹA ʹB
=
AC
ʹA ʹC
=
BC
ʹB ʹC
m ∠ A = m ∠ ʹA
AB
ʹA ʹB
=
AC
ʹA ʹC

196. 196
،‫فيثاغورس‬ ‫مبرهنة‬ ‫بإسم‬ ‫يعرف‬ ‫المبرهنة‬ ‫من‬ )3( ‫والجزء‬
:‫المبرهنة‬ ‫هذه‬ ‫ونص‬
‫القائم‬ ‫المثلث‬ ‫في‬ ‫القائمين‬ ‫الضلعين‬ ‫طولي‬ ‫مربعي‬ ‫[مجموع‬
.]‫الوتر‬ ‫طول‬ ‫مربع‬ ‫يساوي‬ ‫الزاوية‬
‫فان‬ AM ⊥ BC ‫و‬ A ‫في‬ ‫الزاوية‬ ‫قائم‬ ABC ‫المثلث‬ ‫كان‬ ‫اذا‬
‫برهان‬ ‫بدون‬ ‫المبرهنة‬ ‫هذه‬ ‫سنقبل‬
5/‫مبرهنة‬
(AB) 2
= BC . BM
(AC) 2
= BC . CM
(BC )2
= (AB)2
+ ( AC) 2
. ‫قائمة‬ ∠ C ‫فان‬ : ‫كان‬ ‫اذا‬ ABC ‫المثلث‬ ‫في‬
‫برهان‬ ‫بدون‬ ‫المبرهنة‬ ‫هذه‬ ‫سنقبل‬
) ‫فيثاغورس‬ ‫مبرهنة‬ ‫عكس‬ ( 6/‫مبرهنة‬
(AB) 2
= (AC)2
+ ( BC)2
B
A
C
A
BC
M

197. 197
.‫الشكل‬ ‫على‬ ‫المبينة‬ ‫األطوال‬ ‫حسب‬ ABC ∆ ‫في‬ AC ، AB ‫جد‬ ‫الشكل‬ ‫في‬
/‫احلل‬
. AB = 3cm , BC = 4cm , AC = 5cm ‫المثلث‬ ‫في‬
‫ولماذا؟‬ ‫الزاوية‬ ‫قائم‬ ‫المثلث‬ ‫هل‬
/‫احلل‬
(BC)2
= (4) 2
= 16 cm
(AB)2
= (3) 2
= 9 cm
(AC)2
= (5) 2
= 25 cm
. B ‫في‬ ‫الزاوية‬ ‫قائم‬ ‫املثلث‬ ∴
(2) ‫مثال‬
AB( )
2
= AE( )
2
+ EB( )
2
AB( )
2
= 8( )
2
+ 15( )
2
AB( )
2
= 64 + 225
AB( )
2
= 289
AB =17
(AB) 2
= (AE)2
+ ( EB)2
AB = 17 cm
AC( )
2
= AE( )
2
+ EC( )
2
AC( )
2
= 64 + 36
AC( )
2
=100
AC =10
(AC) 2
= (AE)2
+ ( EC)2
AC = 10 cm
(3) ‫مثال‬
, ABC
(AC) 2
= (BC)2
+ ( AB)2
25 = 16 + 9
25 = 25
A
BC
E
8cm
15cm6cm
B
A
C
3
4
5

198. 198
8 2
/ 1‫س‬
m ∠ A = 70ْ ، m ∠ B = 40ْ ‫ان‬ ‫حيث‬ , DEF ‫المثلث‬ ‫يشابه‬ ABC ‫المثلث‬ ‫كان‬ ‫اذا‬
. C ‫زاوية‬ ‫قياس‬ )1 ‫جد‬
. E ‫زاوية‬ ‫قياس‬ )2
/2‫س‬
. x ‫قيمة‬ ‫جد‬ AC = 11cm ‫و‬ BC = 10cm ‫كان‬ ‫اذا‬ -: ‫الشكل‬ ‫في‬
/ 3‫س‬
N ∈ AC , E ∈ AB ‫النقطة‬ ‫وفيهما‬ ‫متشابهين‬ AEN ‫و‬ ABC ‫المثلثان‬ ‫كان‬ ‫اذا‬
. AN = 5cm , NC = 3cm , EB = 2cm , EN = 3cm
. AB )1 ‫جد‬
. BC )2
C
A
B
10cm
5cm
6cm
x
D E

199. 199
9‫التاسع‬ ‫الفصل‬
. ‫المثلثات‬ ]9-1[
. ‫المثلثية‬ ‫النسب‬ ]9-2[
. ‫الخاصة‬ ‫للزوايا‬ ‫المثلثية‬ ‫النسب‬ ]9-3[
‫ل‬‫ب‬‫ا‬‫ق‬‫م‬‫ل‬‫ا‬
‫ر‬‫ت‬‫و‬‫ل‬‫ا‬
‫ر‬‫و‬‫ا‬‫ج‬‫مل‬‫ا‬
A
B
C
θ
sin2
θ+cos2
θ=1
‫الرياضية‬ ‫العالقة‬ ‫او‬ ‫الرمز‬ ‫املصطلح‬
sin θ ‫الزاوية‬ ‫جيب‬
cos θ ‫الزاوية‬ ‫متام‬ ‫جيب‬
tan θ ‫الزاوية‬ ‫ظل‬
‫املثلثات‬ ‫حساب‬
Trigonometry

200. ‫مقدمة‬
:‫بانواعها‬ ‫يسمى‬ ‫زوايا‬ ‫ثالث‬ ‫من‬ ‫يتكون‬ ‫حيث‬ ‫وعناصره‬ ‫المثلث‬ ‫على‬ ‫تعرفت‬ ‫ان‬ ‫سبق‬
. )90ْ ‫من‬ ‫اقل‬ ‫اي‬ ‫حادة‬ ‫زواياه‬ ‫(جميع‬ ‫الزوايا‬ ‫حاد‬ ‫مثلث‬❈
.)90ْ=‫قائمة‬‫زاوية‬‫على‬‫(يحتوي‬‫الزواية‬‫قائم‬‫مثلث‬ ❈
.)90ْ ‫من‬‫اكبر‬‫اي‬‫منفرجة‬‫زواياه‬‫احدى‬(‫الزاوية‬‫منفرج‬‫مثلث‬ ❈
: ‫بانواعها‬ ‫يسمى‬ ‫اضالع‬ ‫وثالثة‬
. ‫االضالع‬ ‫مختلف‬ ‫مثلث‬- . ‫الساقين‬ ‫متساوي‬ ‫مثلث‬ - . ‫االضالع‬ ‫متساوي‬ ‫مثلث‬ -
‫يهمنا‬ ‫وما‬ ‫المثلثية‬ ‫بالنسب‬ ‫مايدعى‬ ‫العالقات‬ ‫هذه‬ ‫ومن‬ ‫واضالعه‬ ‫المثلث‬ ‫زوايا‬ ‫بين‬ ‫مهمة‬ ‫عالقات‬ ‫وهناك‬
. ‫الزاوية‬ ‫القائم‬ ‫المثلث‬ ‫هو‬ ‫الفصل‬ ‫هذا‬ ‫في‬
: ‫ان‬ ‫حيث‬ B ‫في‬ ‫الزاوية‬ ‫القائم‬ ABC ‫المثلث‬ ‫المجاور‬ ‫الشكل‬ ‫في‬ ‫الحظ‬
) ‫القائمة‬ ‫للزاوية‬ ‫(مقابل‬ ‫الوتر‬ ‫يدعى‬ ) AC ( ‫الضلع‬
. θ ‫للزاوية‬ ‫المقابل‬ ‫يدعى‬ )BC ( ‫والضلع‬
. θ ‫للزاوية‬ ‫المجاور‬ ‫فيدعى‬ ) AB ( ‫الضلع‬ ‫اما‬
‫فيثاغورس‬ ‫مبرهنة‬ ‫تدعى‬ ‫االضالع‬ ‫هذه‬ ‫اطوال‬ ‫بين‬ ‫تربط‬ ‫التي‬ ‫والمبرهنة‬
) AC)2
= (AB)2
+ (BC(2
‫حيث‬
θ
A B
C
‫المثلثات‬ ‫حساب‬
‫الفصل‬
9 - 1
9
+

201. 201
‫الحادتين‬ ‫الزاويتين‬ ‫احدى‬ θ ‫والزاوية‬ B ‫في‬ ‫الزاوية‬ ‫قائم‬ ABC ∆ ‫المجاور‬ ‫الشكل‬ ‫في‬
)sine( θ ‫الزاوية‬ ‫جيب‬
θ ‫الزاوية‬ ‫مقابل‬
‫الوتر‬
‫النسبة‬ ‫تدعى‬ )1
: ‫بشكل‬ ‫ويكتب‬
Sine ‫كلمة‬ ‫اختصار‬ Sin
) Cosine( θ ‫الزاوية‬ ‫تمام‬ ‫جيب‬
θ ‫الزاوية‬ ‫مجاور‬
‫الوتر‬
‫النسبة‬ ‫تدعى‬ )2
: ‫بشكل‬ ‫ويكتب‬
Cosine ‫كلمة‬ ‫اختصار‬ Cos
)Tangent( θ ‫الزاوية‬ ‫ظل‬
θ ‫الزاوية‬ ‫مجاور‬
θ ‫الزاوية‬ ‫مقابل‬
‫النسبة‬ ‫تدعى‬ )3
: ‫بشكل‬ ‫وتكتب‬
Tangent ‫كلمة‬ ‫اختصار‬ tan
. tan θ , cos θ , sin θ : ‫جد‬ : ‫الشكل‬ ‫في‬ ‫كما‬ ABC ‫مثلث‬
/‫احلل‬
θ
‫المقابل‬‫الوتر‬
‫املجاور‬
A B
C
9 - 2‫املثلثية‬ ‫النسب‬
sinθ =
BC
AC
cosθ =
AB
AC
tanθ =
BC
AB
(1) ‫مثال‬
sinθ =
BC
AC
⇒ sinθ =
4
5
cosθ =
AB
AC
⇒ cosθ =
3
5
tanθ =
BC
AB
⇒ tanθ =
4
3
4cm
5cm
3cm
A B
C
θ

202. 202
‫نجد‬ ‫فيثاغورس‬ ‫مبرهنة‬ ‫وباستخدام‬ ‫المجاور‬ ‫الشكل‬ ‫من‬
. ) AC)2
‫على‬ ‫بالقسمة‬ ‫و‬ ) BC)2
+ (AB)2
= ( AC)2
) sin θ) 2
+ (cos θ) 2
= 1
AC ‫على‬ ‫بالقسمة‬
tanA , sinA ‫فجد‬ cosA =
8
17
‫كانت‬ ‫اذا‬ B ‫في‬ ‫الزاوية‬ ‫القائم‬ ABC ∆ ‫في‬
17K = ‫الوتر‬ ، 8K = ‫المجاور‬ ∴ ، K 0 ‫حيث‬ ‫االولى‬ ‫الطريقة‬
) AB)2
+ (BC)2
= ( AC)2
‫فيثاغورس‬ ‫مبرهنة‬ ‫وحسب‬
) 8K) 2
+ (BC)2
= (17K)2
64K 2
+ (BC)2
= 289 K2
(BC )2
= 289K2
- 64K2
(BC )2
= 225K2
⇒ BC = 15K
θ
A B
C
9 - 3‫المثلثية‬ ‫العالقات‬ ‫بعض‬
(2) ‫مثال‬
BC
AC
⎛
⎝
⎜
⎞
⎠
⎟
2
+
AB
AC
⎛
⎝
⎜
⎞
⎠
⎟
2
=
AC
AC
⎛
⎝
⎜
⎞
⎠
⎟
2
tanθ =
BC
AC
tanθ =
BC
AC
AB
AC
tanθ =
sin θ
cos θ
tanθ =
BC
AC
tanθ =
BC
AC
AB
AC
tanθ =
sin θ
cos θ
cosA =
8K
17K
tanθ =
BC
AC
tanθ =
BC
AC
AB
AC
tanθ =
sin θ
cos θ

203. 203
‫الثانية‬ ‫الطريقة‬
BC( )
2
= 289K 2
− 64K 2
BC( )
2
= 225K 2
⇒ BC =15K
sin A =
15K
17K
=
15
17
tan A =
15K
8K
=
15
8
Asin A =
BC
AC
⇒
tan A =
BC
AB
BC( )
2
= 289K 2
− 64K 2
BC( )
2
= 225K 2
⇒ BC =15K
sin A =
15K
17K
=
15
17
tan A =
15K
8K
=
15
8
A⇒
A B
C
17
8
Qsin2
A + cos2
A =1
∴sin2
A +
8
17
⎛
⎝
⎜
⎞
⎠
⎟
2
=1
sin2
A =1−
64
289
sin A =
15
17
Qtan A =
sin A
cos A
tan A =
15
17
8
17
=
15
8
A
A
A
A
A
Qsin2
A + cos2
A =1
∴sin2
A +
8
17
⎛
⎝
⎜
⎞
⎠
⎟
2
=1
sin2
A =1−
64
289
sin A =
15
17
Qtan A =
sin A
cos A
tan A =
15
17
8
17
=
15
8
A
Qsin2
A + cos2
A =1
∴sin2
A +
8
17
⎛
⎝
⎜
⎞
⎠
⎟
2
=1
sin2
A =1−
64
289
sin A =
15
17
Qtan A =
sin A
cos A
tan A =
15
17
8
17
=
15
8
tanθ =
sin θ
cos θ
A
A
A
A B
C
17K
8K

204. 204
: ً‫ال‬‫او‬AB = BC‫ان‬‫بحيث‬B‫في‬‫الزاوية‬‫القائم‬ABC‫المثلث‬‫نرسم‬: 450
‫للزاوية‬ ‫المثلثية‬ ‫النسب‬
∵ m ∠ B = 900
⇒ m ∠ A+ m ∠ c = 900
∵ AB = BC
∴ m ∠ A = m ∠ C = 450
AB = BC = K 0 ‫ان‬ ‫نفرض‬
: ‫فثاغورس‬ ‫مبرهنة‬ ‫حسب‬
) AC )2
= (AB)2
+ ( BC)2
(AC )2
= K2
+ K2
(AC )2
= 2K2
AC = K
) 2cos45ْ + tan45ْ( 2
‫ناتج‬ ‫جد‬
/‫احلل‬
9 - 4‫اخلاصة‬ ‫للزوايا‬ ‫املثلثية‬ ‫النسب‬
Sin450
=
k
2k
⇒ Sin450
=
1
2
Cos450
=
k
2k
⇒ Cos450
=
1
2
tan450
=
k
k
⇒ tan 450
= 1
(1) ‫مثال‬
Q 2
1
2
+1
⎛
⎝⎜
⎞
⎠⎟
2
⇒ 2 2
1
2
+1
⎛
⎝
⎜
⎞
⎠
⎟
2
⇒ 2 +1( )
2
= 2( )
2
+ 2 2( )+1
= 2+ 2 2 +1
= 3+ 2 2
Qcos45ο
=
1
2
, tan45ο
= 1
Q 2
1
2
+1
⎛
⎝⎜
⎞
⎠⎟
2
⇒ 2 2
1
2
+1
⎛
⎝
⎜
⎞
⎠
⎟
2
⇒ 2 +1(
= 2( )
2
+ 2 2( )+1
= 2+ 2 2 +1
= 3+ 2 2
Q 2
1
2
+1
⎛
⎝⎜
⎞
⎠⎟
2
⇒ 2 2
1
2
+
⎛
⎝
⎜
= 2( )
2
+ 2 2( )+1
= 2+ 2 2 +1
= 3+ 2 2
∵
∵
A B
C
45ْ
45ْ
K
K
sin45ο
=
K
2K
⇒ sin45ο
=
1
2
cos45ο
=
K
2K
⇒ cos45ο
=
1
2
tan45ο
=
K
K
⇒ tan45ο
= 1
sin45ο
=
K
2K
⇒ sin45ο
=
1
2
cos45ο
=
K
2K
⇒ cos45ο
=
1
2
tan45ο
=
K
K
⇒ tan45ο
= 1
sin45ο
=
K
2K
⇒ sin45ο
=
1
2
cos45ο
=
K
2K
⇒ cos45ο
=
1
2
tan45ο
=
K
K
⇒ tan45ο
= 1
K
K
K

205. 205
:
(2) ‫مثال‬
‫كل‬‫قياس‬‫فيكون‬ 2k ‫ضلعه‬‫طول‬‫االضالع‬‫متساوي‬ ً‫ا‬‫مثلث‬‫نرسم‬ : 600
، 300
‫قياسها‬ ‫زاوية‬ ً‫ا‬‫ثاني‬
∴ BD = DC = K ‫وحدة‬ ‫المجاور‬ ‫الشكل‬ ‫الحظ‬ ‫فينصفه‬ AD ⊥ BC ‫نرسم‬ 600
‫منها‬ ‫زاويه‬
AD = K ‫بان‬ ‫نجد‬ ‫فيثاغورس‬ ‫مبرهنة‬ ‫وبستخدام‬ BAD = 300
‫الزاوية‬ ‫قياس‬ ‫وان‬
. x , y ∈ R ‫قيمة‬ ‫جد‬ ‫المجاور‬ ‫الشكل‬ ‫من‬
)a( /‫احلل‬
)b(
. 30ْ ‫للزواية‬ ‫مثلثية‬ ‫نسب‬ ‫باستخدام‬ ‫المثال‬ ‫حل‬ ‫حاول‬
AD = 3K
sin30ο
=
K
2K
⇒ sin30ο
=
1
2
cos30ο
=
3K
2K
⇒ cos30ο
=
3
2
tan30ο
=
K
3K
⇒ tan30ο
=
1
3
sin60ο
=
3K
2K
⇒ sin60ο
=
3
2
cos60ο
=
1
2
tan60ο
= 3
30ْ
K
30ْ
60ْ 60ْ
K
C
A
B
D
2K
40cm
y
60ْ
x
y
60ْ
x
Sin600
=
23
x
⇒
3
2
=
23
x
43=3x⇒x=4
tan60=
23
y
⇒3=
23
y
3y=23⇒y=2
cos60°
=
y
40
⇒
1
2
=
y
40
∴y =
40
2
⇒ y = 20
sin60°
=
x
40
⇒
3
2
=
x
40
∴2x = 40 3 ⇒ x = 20 3
sin60°
=
2 3
x
⇒
3
2
=
2 3
x
4 3 = 3 x ⇒ x = 4
tan60°
=
2 3
y
⇒ 3 =
2 3
y
∴ 3y = 2 3 ⇒ y = 2
sin30ο
=
K
2K
⇒ sin30ο
=
1
2
cos30ο
=
3K
2K
⇒ cos30ο
=
3
2
tan30ο
=
K
3K
⇒ tan30ο
=
1
3
sin60ο
=
3K
2K
⇒ sin60ο
=
3
2
cos60ο
=
1
2
tan60ο
= 3
sin30ο
=
K
2K
⇒ sin30ο
=
1
2
cos30ο
=
3K
2K
⇒ cos30ο
=
3
2
tan30ο
=
K
3K
⇒ tan30ο
=
1
3
sin60ο
=
3K
2K
⇒ sin60ο
=
3
2
cos60ο
=
1
2
tan60ο
= 3
sin30ο
=
K
2K
⇒ sin30ο
=
cos30ο
=
3K
2K
⇒ cos30
tan30ο
=
K
3K
⇒ tan30ο
sin60ο
=
3K
2K
⇒ sin60ο
cos60ο
=
1
2
tan60ο
= 3
sin30ο
=
K
2K
⇒ sin30ο
=
1
2
cos30ο
=
3K
2K
⇒ cos30ο
=
3
2
tan30ο
=
K
3K
⇒ tan30ο
=
1
3
sin60ο
=
3K
2K
⇒ sin60ο
=
3
2
cos60ο
=
1
2
tan60ο
= 3
sin30ο
=
K
2K
⇒ sin30ο
=
1
2
cos30ο
=
3K
2K
⇒ cos30ο
=
3
2
tan30ο
=
K
3K
⇒ tan30ο
=
1
3
sin60ο
=
3K
2K
⇒ sin60ο
=
3
2
cos60ο
=
1
2
tan60ο
= 3
K
K
K
K
cos60°
=
K
2K
tan60°
=
3K
K

206. 206
: ‫ياتي‬ ‫مما‬ ‫كل‬ ‫قيمة‬ ‫جد‬ / 1‫س‬
1) sin60ْ cos30ْ + cos60ْ sin30ْ
2) ( cos30ْ - sin45ْ ) ( sin60ْ + cos45ْ )
BC = 8cm , AB = 15cm ‫حيث‬ B ‫في‬ ‫الزاوية‬ ‫قائم‬ ‫مثلث‬ ABC / 2‫س‬
sin C , cos C , tanC ‫جد‬
a) cos2
30ْ - sin2
30ْ = cos60ْ ‫ان‬ ‫اثبت‬ /3‫س‬
b) 2 sin30ْ cos30ْ = sin60ْ
c )
: ‫المثلثين‬ ‫من‬ x , y ∈ R ‫جدقيمة‬ /4‫س‬
9 1
b(
10
y
x
45ْْ
10
y
x
30ْ
a(
1- cos60°
2
= sin30°

207. 207
‫االحصاء‬
Statistics
10
. ‫املبوبة‬ ‫غير‬ ‫للبيانات‬ ‫احلسابي‬ ‫الوسط‬ ]10-1[
.‫البسيط‬ ‫التكراري‬ ‫للتوزيع‬ ‫احلسابي‬ ‫الوسط‬ ]10-2[
.‫الفئات‬ ‫ذي‬ ‫التكراري‬ ‫للتوزيع‬ ‫احلسابي‬ ‫الوسط‬ ]10-3[
. ‫احلسابي‬ ‫الوسط‬ ‫وعيوب‬ ‫مزايا‬ ]10 - 4[
. ‫الوسيط‬ ]10-5[
. ‫الوسيط‬ ‫وعيوب‬ ‫مزايا‬ ]10-6[
. ‫املنوال‬ ]10-7[
. ‫املنوال‬ ‫وعيوب‬ ‫مزايا‬ ]10-8[
‫الرياضية‬ ‫العالقة‬ ‫او‬ ‫الرمز‬ ‫املصطلح‬
x x: ‫للقيم‬ ‫احلسابي‬ ‫الوسط‬
ME ‫الوسيط‬
MO ‫املنوال‬
‫العاشر‬ ‫الفصل‬x=
x1+x2+x3+...+xn
n
xi
+x2
+x3
+....+x7
7
x=

208. ‫مقدمة‬
‫الفصل‬
10
‫الظاهرة‬ ‫عن‬ ‫يعبر‬ ‫مقياس‬ ‫ايجاد‬ ‫الصعب‬ ‫من‬ ‫وكان‬ . ‫البيانات‬ ‫وتمثيل‬ ‫جمع‬ ‫طرق‬ ‫السابقة‬ ‫المراحل‬ ‫في‬ ‫درسنا‬
‫الميل‬ ‫وهذا‬ ، ‫القيم‬ ‫من‬ ‫كبير‬ ‫عدد‬ ‫حولها‬ ‫تتراكم‬ ‫واحدة‬ ‫قيمة‬ ‫اي‬ ‫مقياس‬ ‫عن‬ ‫سنبحث‬ ‫لذلك‬ ، ‫الدراسة‬ ‫موضوع‬
‫المركزية‬ ‫النزعة‬ ‫بمقياس‬ ‫القيمة‬ ‫تلك‬ ‫وتسمى‬ ‫البياني‬ ‫للتوزيع‬ ‫المركزية‬ ‫بالنزعة‬ ‫يسمى‬ ‫القيمة‬ ‫تلك‬ ‫حول‬
. )Measures of Central Tendency (
‫التوزيعات‬ ‫وصف‬ ‫في‬ ‫كبيرة‬ ‫اهمية‬ ‫ذات‬ ‫احصائية‬ ‫قيم‬ ‫هي‬ )‫المتوسطة‬ ‫(القيم‬ ‫المركزية‬ ‫النزعة‬ ‫مقاييس‬ ‫ان‬
: ‫هي‬ ‫المرحلة‬ ‫هذه‬ ‫في‬ ‫دراستها‬ ‫سنتناول‬ ‫التي‬ ‫المركزية‬ ‫النزعة‬ ‫مقاييس‬ ‫اهم‬ ‫ومن‬ ،‫البيانية‬
. Arithmatic Mean ‫الحسابي‬ ‫الوسط‬ - 1
.Median ‫الوسيط‬ - 2
. Mode ‫المنوال‬ - 3
. ‫وعيوبها‬ ‫ومزاياها‬ ‫استخراجها‬ ‫طريقة‬ ‫مبسط‬ , ‫بشكل‬
‫لبساطة‬ ً‫ا‬‫استخدام‬ ‫واكثرها‬ ً‫ا‬‫شيوع‬ ‫المركزية‬ ‫النزعة‬ ‫مقاييس‬ ‫اكثر‬ ‫المتوسط‬ ‫او‬ ‫الحسابي‬ ‫الوسط‬ ‫يعتبر‬
‫االصلية‬ ‫او‬ ‫االولية‬ ‫(البيانات‬ ‫المبوية‬ ‫غير‬ ‫للبيانات‬ ‫الحسابي‬ ‫للوسط‬ ً‫ا‬‫تعريف‬ ‫هنا‬ ‫نعطي‬ . ‫واستخراجه‬ ‫حسابه‬
)‫جدول‬ ‫بشكل‬ ‫توضع‬ ‫او‬ ‫تبوب‬ ‫ولم‬ ‫جمعت‬ ‫التي‬
]10-1[ ‫تعريف‬
‫على‬ ً‫ا‬‫مقسوم‬ ‫القيم‬ ‫مجموع‬ ‫بانه‬ ‫مبوبة‬ ‫غير‬ ‫لبيانات‬ ‫القيم‬ ‫من‬ ‫لمجموعة‬ ‫الحسابي‬ ‫الوسط‬ ‫يعرف‬
) X bar ‫بار‬ ‫أكس‬ ‫(ويقرأ‬ X ‫بالرمز‬ ‫عادة‬ ‫الحسابي‬ ‫للوسط‬ ‫ويرمز‬ ‫عددها‬
‫االحصاء‬

209. 209
: ‫يكون‬ ‫عندئذ‬ xi
:x1
, x2
, x3
, .... : xn
: ‫هي‬ xi
‫قيم‬ ‫من‬ n ‫لدينا‬ ‫كان‬ ‫فاذا‬
. ) 8 , 6 , 4 , 5 , 7 , 2 , 3 ( : ‫االتية‬ ‫لالعداد‬ ‫الحسابي‬ ‫الوسط‬ ‫اوجد‬
/ ‫احلل‬
: ‫هو‬ x ‫الحسابي‬ ‫الوسط‬
. ) 24 , 20 , 18 , 16 , 12 , 10 , 8 , 4 ( : ‫هي‬ ‫بالسنين‬ ‫اشخاص‬ ‫ثمانية‬ ‫اعمار‬ ‫كانت‬ ‫اذا‬
.‫العمارهم‬ ‫الحسابي‬ ‫الوسط‬ ‫جد‬
/‫احلل‬
(1) ‫مثال‬
10 - 1‫غير‬ ‫للبيانات‬ ‫احلسابي‬ ‫الوسط‬
‫املبوبة‬
x =
x1 + x2 + x3 + ...+ xn
n
x1
+ x2
+ x3
+ ....+ xn
n
X =
x =
x1 + x2 + x3 + ...+ xn
n
x1
+ x2
+ x3
+ ....+ x7
7
x =
x =
x1 + x2 + x3 + ...+ xn
n
3 + 2 + 7 + 5 +4 +6 + 8
7
x =
x=
x1 +x2 +x3 +...+xn
n
35
7
x = = 5
(2) ‫مثال‬
x =
x1 + x2 + x3 + ...+ xn
n
x1
+ x2
+ ....+ x8
8
x = , n = 8
x =
x1 + x2 + x3 + ... + xn
n
4 + 8 + 10 + 12 +16 +18 + 20 + 24
8
x = x=
x1 +x2 +x3 +...+xn
n
112
8
= = 14

210. 210
fi
‫تكرار‬ ‫من‬ n ‫ويقابلها‬Xi
:X1
, X2
, X3
, .... : Xn
: ‫هي‬ Xi
‫قيم‬ ‫من‬ n ‫لدينا‬ ‫كان‬ ‫اذا‬
. fi
:f1
, f2
, f3
, .... : fn
: ‫وهي‬
‫على‬ ً‫ا‬‫مقسوم‬ fi
‫المناظرة‬ ‫التكرارات‬ ‫في‬ X1
‫ضرب‬ ‫حواصل‬ ‫مجموع‬ ‫بانه‬ ‫الحسابي‬ ‫الوسط‬ ‫فيعرف‬
. ‫التكرارات‬ ‫مجموع‬
: ‫اي‬
: ‫شخص‬ )14( ‫العمار‬ ‫التالي‬ ‫التكراري‬ ‫للتوزيع‬ ‫الحسابي‬ ‫الوسط‬ ‫اوجد‬
‫العمر‬131098
‫االشخاص‬ ‫عدد‬2453
/ ‫احلل‬
x1
= 8 , f1
= 3 , x2
= 9 , f2
= 5 , ....
(3) ‫مثال‬
10 - 2‫للتوزيع‬ ‫احلسابي‬ ‫الوسط‬
‫البسيط‬ ‫التكراري‬
x =
x1 + x2 + x3 + ... + xn
n
x1
f1
+ x2
f2
+ x3
f3
+...+ xn
fn
f1
+ f2
+ f3
+...+ fn
x =
x =
x1 + x2 + x3 + ... + xn
n
x1
f1
+ x2
f2
+ x3
f3
+ x4
f4
f1
+ f2
+ f3
+ f4
x =
x =
x1 + x2 + x3 + ... + xn
n
)8()3( + )9()5( + )10()4( + )13()2(
3 + 5 + 4 + 2
x =
x =
x1 + x2 + x3 + ...+ xn
n
24 + 45 + 40 + 26
14
= x =
x1 + x2 + x3 +...+ xn
n
135
14
=

211. 211
: ‫االتي‬ ‫الجدول‬ ‫في‬ ‫كما‬ ‫السؤال‬ ‫حل‬ ‫يمكن‬
x1
f1
x1
f1
8 3 (8)(3)=24
9 5 (9)(5)=45
10 4 (10)(4)=40
13 2 (13)(2)=26
14 135
]10-2[ ‫تعريف‬
‫يرمز‬ ‫(والتي‬ ‫الفئات‬ ‫مراكز‬ ‫ضرب‬ ‫حواصل‬ ‫مجموع‬ ‫بأنه‬ ‫المبوبة‬ ‫للبيانات‬ ‫الحسابي‬ ‫الوسط‬ ‫يعرف‬
. ‫التكرارات‬ ‫مجموع‬ ‫على‬ ‫الناتج‬ ‫وقسمة‬ f i
‫المناظرة‬ ‫التكرارات‬ ‫في‬ )Xi
‫لها‬
‫المناظرة‬ ‫التكرارات‬ ‫وإن‬ x1
، x2
،x3
,.....xn
:‫التوالي‬ ‫على‬ ‫وهي‬ ‫الفئات‬ ‫مراكز‬ ‫من‬ n ‫لدينا‬ ‫كان‬ ‫فإذا‬
:‫اآلتي‬ ‫القانون‬ ‫بحسب‬ x ‫الحسابي‬ ‫الوسط‬ ‫يكون‬ ‫عندئذ‬ .‫التوالي‬ ‫على‬ f1
, f2
, f3
, ......fn
:‫هي‬ ‫لها‬
10 - 3‫للتوزيع‬ ‫احلسابي‬ ‫الوسط‬
‫الفئات‬ ‫ذي‬ ‫التكراري‬
x =
x1 + x2 + x3 + ... + xn
n
f1
x1
+ f2
x2
+ ... + xn
fn
f1
+ f2
+ f3
+... + fn
x =
∴x =
135
14
‫المجموع‬

212. 212
:‫التالية‬ ‫الخطوات‬ ‫نتبع‬ ‫المبوبة‬ ‫للبيانات‬ ‫الحسابي‬ ‫الوسط‬ ‫وإليجاد‬
.
xi
‫الفئات‬ ‫من‬ ‫فئة‬ ‫كل‬ ‫مركز‬ ‫نجد‬ )1
. fi
‫لها‬ ‫المناظر‬ ‫التكرار‬ ‫في‬ xi
‫فئة‬ ‫كل‬ ‫مركز‬ ‫نضرب‬ )2
.‫الضرب‬ ‫حواصل‬ ‫مجموع‬ ‫نجد‬ )3
‫مجموع‬ ‫على‬ ‫وقسمتها‬ ‫التكرارات‬ ‫في‬ ‫الفئات‬ ‫مراكز‬ ‫ضرب‬ ‫حواصل‬ ‫مجموع‬ ‫بقسمة‬ x ‫نجد‬ )4
. ‫التكرارات‬
.)kg( ‫غرام‬ ‫بالكيلو‬ ‫الوزن‬ ‫فئات‬ ‫حسب‬ ‫حاجة‬ 150 ‫توزيع‬ ‫يمثل‬ ‫التالي‬ ‫الجدول‬
‫الوزن‬ 15- 25- 35- 45- 55- 65-75
‫احلاجات‬ ‫عدد‬ 9 15 23 30 33 40
.‫للوزن‬ ‫الحسابي‬ ‫الوسط‬ ‫إحسب‬
:‫الفئات‬ ‫مراكز‬ ‫نجد‬ / ‫احلل‬
: x1
‫األولى‬ ‫الفئة‬ ‫مركز‬
:‫التالي‬ ‫اجلدول‬ ‫نعمل‬ ‫وهكذا‬ : x2
‫الثانية‬ ‫الفئة‬ ‫مركز‬
fi
xi
xi
‫الفئات‬ ‫مركز‬fi
‫التكرار‬‫الوزن‬ ‫فئات‬
(9)(20)=18020915-
(15)(30)= 450301525-
(23)(40)= 920402335-
(30)(50)= 1500503045-
(33)(60)= 1980603355-
(40)(70)= 2800704065-75
7830150
4 ‫مثال‬
x =
x1 + x2 + x3 +...+ xn
n x=
x1 +x2 +x3 +...+xn
n
40
2
15 + 25
2
x1
= = = 20
x =
x1 + x2 + x3 +...+ xn
n x=
x1 +x2 +x3 +...+xn
n
60
2
25 + 35
2
x2
= = = 30
‫المجموع‬

213. 213
:‫اآلتي‬ ‫التكراري‬ ‫اجلدول‬ ‫من‬ ‫احلسابي‬ ‫الوسط‬ ‫جد‬
‫الفئات‬ 60- 62- 64- 66- 68-70
‫التكرار‬ 5 18 42 27 8
:x1
‫األولى‬ ‫الفئة‬ ‫مركز‬ ‫جند‬ /‫احلل‬
:‫اآلتي‬ ‫اجلدول‬ ‫نعمل‬ :x2
‫الثانية‬ ‫الفئة‬ ‫مركز‬ ‫جند‬
fi
xi
xi
‫الفئات‬ ‫مركز‬fi
‫التكرار‬‫الفئات‬
(5)(61)=30561560-
(18)(63)=1134631862-
(42)(65)=2730654264-
(27)(67)=1809672766-
(8)(69)=55269868-
6530100
x =
x1 + x2 + x3 + ... + xn
n
f1
x1
+ f2
x2
+ ... + xn
fn
f1
+ f2
+ ... + fn
x =
x=
x1 +x2 +x3 +...+xn
n
7830
150
x = = 52.2kg
5 ‫مثال‬
x =
x1 + x2 + x3 +...+ xn
n x=
x1 +x2 +x3 +...+xn
n
122
2
60 + 62
2
x1
= = = 61
x =
x1 + x2 + x3 +...+ xn
n x=
x1 +x2 +x3 +...+xn
n
126
2
62 + 64
2
x2
= = = 63
x =
x1 + x2 + x3 + ... + xn
n
f1
x1
+ f2
x2
+ ... + xn
fn
f1
+ f2
+ ... + fn
x =
x=
x1 +x2 +x3 +...+xn
n
6530
100
x = = 65.3

214. 214
:‫املزايا‬ :ً‫ال‬‫أو‬
. ‫حسابه‬ ‫بسهولة‬ ‫يمتاز‬ *
.‫حسابه‬ ‫في‬ ‫القيم‬ ‫جميع‬ ‫تدخل‬ *
:‫العيوب‬ :ً‫ا‬‫ثاني‬
ً‫ا‬‫بياني‬ ‫إيجاده‬ ‫اليمكن‬ *
‫القيم‬ ‫لمعظم‬ ‫بالنسبة‬ ً‫ا‬‫جد‬ ‫صغيرة‬ ‫أو‬ ً‫ا‬‫جد‬ ‫كبيرة‬ ‫تكون‬ ‫التي‬ ‫المتطرفة‬ ‫او‬ ‫الشاذة‬ ‫بالقيم‬ ‫يتأثر‬ *
.‫الحسابي‬ ‫الوسط‬ ‫قيمة‬ ‫تخفض‬ ‫أو‬ ‫ترفع‬ ‫وبالتالي‬
‫الحسابي‬ ‫الوسط‬ ‫فيكون‬ ‫لها‬ ‫الحسابي‬ ‫الوسط‬ ‫وتجد‬ 1 , 3 , 7 , 9 , 10 :‫االتية‬ ‫االعداد‬ ‫لتأخذ‬ :ً‫ال‬‫مث‬
: ‫حيث‬ x ‫لها‬
‫االعداد‬ ‫لهذه‬ ‫الحسابي‬ ‫والوسط‬ 300 , 10 , 9 , 7 , 3 , 1 ‫االعداد‬ ‫فتكون‬ 300 ‫العدد‬ ‫لها‬ ‫اضفنا‬ ‫لو‬
‫يكون‬ ‫المرة‬ ‫هذه‬
‫للقيم‬ ‫بالنسبة‬ )55( ‫اصبح‬ ‫بينما‬ )6( ‫هو‬ 1 , 3 , 7 , 9 , 10 ‫للقيم‬ ‫الحسابي‬ ‫الوسط‬ ‫الحظ‬
.ً‫ا‬‫جد‬ ‫الصغيرة‬ ‫للقيم‬ ‫بالنسبة‬ ‫الشي‬ ‫ونفس‬ 1 , 3 , 7 , 9 ,10 , 300
10 - 4
‫احلسابي‬ ‫الوسط‬ ‫وعيوب‬ ‫مزايا‬
x =
x1 + x2 + x3 + ...+ xn
n
1 + 3 + 7 + 9 + 10
5
x = =x=
x1+x2+x3+...+xn
n
30
5
= 6
x =
x1 + x2 + x3 + ... + xn
n
1 + 3 + 7 + 9 + 10+300
6
x = =x=
x1+x2+x3+...+xn
n
330
6
= 55

215. 215
(1) ‫مثال‬
‫وسنقتصر‬ .‫المركزية‬ ‫النزعة‬ ‫مقاييس‬ ‫من‬ ‫آخر‬ ً‫ا‬‫مهم‬ ً‫ا‬‫قياس‬ ) ‫القيم‬ ( ‫البيانات‬ ‫من‬ ‫مجموعة‬ ‫وسيط‬ ‫يعتبر‬
. ‫المبوبة‬ ‫غير‬ ‫للبيانات‬ ‫الوسيط‬ ‫وايجاد‬ ‫تعريف‬ ‫على‬ ‫المرحلة‬ ‫لهذه‬ ‫دراستنا‬ ‫في‬
]10-3[ ‫تعريف‬
: ‫حالة‬ ‫في‬ x1
, x2
...., xn
: ‫القيم‬ ‫من‬ ‫مجموعة‬ ‫وسيط‬
‫فردي‬ ‫عدد‬ n :ً‫ال‬‫او‬
n+1
2
‫ترتيبه‬ ‫ويكون‬ ً‫ا‬‫تنازلي‬ ‫او‬ ً‫ا‬‫تصاعدي‬ ‫القيم‬ ‫ترتيب‬ ‫عند‬ ‫الوسط‬ ‫في‬ ‫تقع‬ ‫التي‬ ‫القيمة‬ ‫هو‬
‫زوجي‬ ‫عدد‬ n :ً‫ا‬‫ثاني‬
. ً‫ا‬‫تنازلي‬ ‫او‬ ً‫ا‬‫تصاعدي‬ ‫القيم‬ ‫ترتيب‬ ‫بعد‬ ‫الوسطيتين‬ ‫القيمتين‬ )‫(معدل‬ ‫منتصف‬ ‫في‬ ‫تقع‬ ‫التي‬ ‫القيمة‬ ‫هو‬
. ME ‫بالرمز‬ ‫للوسيط‬ ‫وسنرمز‬ ‫ترتيبها‬ ‫ويكون‬
3 , 2 , 4 , 6 , 5 :‫االتية‬ ‫للقيم‬ ‫الوسيط‬ ‫جد‬
‫الوسيط‬ ‫ترتيب‬ :‫يلي‬ ‫كما‬ ً‫ا‬‫تصاعدي‬ ‫القيم‬ ‫بترتيب‬ ‫نقوم‬ / ‫احلل‬
2 , 3 , 4 , 5 , 6
.‫الوسط‬ ‫في‬ ‫تقع‬ ‫الوسيط‬ ‫قيمة‬ ‫فان‬ )5( ‫فردي‬ ‫القيم‬ ‫عدد‬ ‫الن‬
∴ ME = 4
3 , 2 , 4 , 5 , 6 , 9 :‫االتية‬ ‫للقيم‬ ‫الوسيط‬ ‫جد‬
‫هما‬ ‫الوسيطين‬ ‫ترتيب‬ 2 , 3 , 4 , 5 , 6 , 9 :‫يلي‬ ‫كما‬ ً‫ا‬‫تصاعدي‬ ‫القيم‬ ‫بترتيب‬ ‫نقوم‬ / ‫احلل‬
: ‫واضح‬ ‫كما‬ ‫وهما‬ ‫الوسط‬ ‫في‬ ‫للقيمتين‬ ‫الحسابي‬ ‫الوسط‬ ‫هي‬ ‫الوسيط‬ ‫قيمة‬ ‫فان‬ )6( ‫زوجي‬ ‫القيم‬ ‫عدد‬ ‫الن‬
10 - 5‫الوسيط‬
(2) ‫مثال‬
ME = =x=
x1+x2+x3+...+xn
n
9
2
= 4.5x=
x1+x2+x3+...+xn
n
4 + 5
2
n
2
,
n
2
+1
n+1
2
⇒
5 +1
2
= 3
n
2
=
6
2
= 3,4

217. 217
‫المبوبة‬ ‫غير‬ ‫للبيانات‬ ‫تعريفه‬ ‫ويمكن‬ .‫المركزية‬ ‫النزعة‬ ‫مقاييس‬ ‫من‬ ‫مهما‬ َ‫آخر‬ ً‫ا‬‫مقياس‬ ‫المنوال‬ ‫يعتبر‬
.‫يلي‬ ‫كما‬
]10-4[ ‫تعريف‬
‫غيرها‬ ‫من‬ ‫اكثر‬ ‫تتكرر‬ ‫التي‬ ‫اي‬ ‫الشائعة‬ ‫القيمة‬ ‫هو‬ x1
, x2
...., xn
‫القيم‬ ‫مجموعة‬ ‫منوال‬
.MO ‫بالرمز‬ ‫للمنوال‬ ‫وسنرمز‬ . ‫المجموعة‬ ‫قيم‬ ‫ضمن‬
:‫االتية‬ ‫للقيم‬ ‫المنوال‬ ‫جد‬
11 , 9 , 5 , 4 , 8 , 6 , 9 ,13 , 1 2 , 7
/‫احلل‬
:‫فان‬ ‫لذا‬ ‫مرتين‬ ‫تكررت‬ )9( ‫القيمة‬ ‫ان‬ ‫الحظ‬
MO = 9
:‫االتية‬ ‫للقيم‬ ‫المنوال‬ ‫جد‬
10 ، 5 ، 5 ، 4 ، 7 ، 8 ،2 ، 12 ، 2 ، 3
/ ‫احلل‬
‫هما‬ ‫منواالن‬ ‫القيم‬ ‫لهذه‬ ‫فيكون‬ ‫مرتين‬ ‫تكررت‬ )2( ‫القيمة‬ ‫كذلك‬ ‫مرتين‬ ‫تكررت‬ )5( ‫القيمة‬ : ‫ان‬ ‫الحظ‬
: ‫اي‬ 5 , 2
MO = 2 , MO = 5
10- 7‫املنوال‬
(1) ‫مثال‬
(2) ‫مثال‬

218. 218
10 - 8‫املنوال‬ ‫وعيوب‬ ‫مزايا‬
‫االتية؟‬ ‫للقيم‬ ‫منوال‬ ‫يوجد‬ ‫هل‬
12 , 17 ,13 , 9 , 8 , 2 , 5 , 4 , 1
/ ‫احلل‬
. ‫القيم‬ ‫هذه‬ ‫من‬ ‫قيمة‬ ‫أية‬ ‫تكرار‬ ‫عدم‬ ‫هو‬ ‫والسبب‬ ‫منوال‬ ‫القيم‬ ‫لهذه‬ ‫ليس‬
‫املزايا‬ :ً‫ال‬‫او‬
.‫والحساب‬ ‫الفكرة‬ ‫حيث‬ ‫من‬ ‫بسيط‬ *
.‫المتطرفة‬ ‫او‬ ‫الشاذة‬ ‫بالقيم‬ ‫يتأثر‬ ‫ال‬ *
‫العيوب‬ :ً‫ا‬‫ثاني‬
. ‫منوال‬ ‫هناك‬ ‫يكون‬ ‫ال‬ ‫قد‬ *
.‫منوال‬ ‫من‬ ‫اكثر‬ ‫هناك‬ ‫يكون‬ ‫قد‬ *
(3) ‫مثال‬

219. 219
:‫يأتي‬ ‫مما‬ ‫لكل‬ ‫والمنوال‬ ‫الوسيط‬ ،‫الحسابي‬ ‫الوسط‬ ‫امكن‬ ‫ان‬ ‫جد‬ /1‫س‬
a) 11 , 20 , 5 , 8 , 12 , 17 , 9
b) 8 , 4 , 9 , 5 , 2 , 4 , 4 , 2 , 6 , 7 , 2
c) 12 , 24 , 16 , 20 ,10 , 8 ,18 , 4 , 20
d) 2 , 5 , 9 , 5 , 7 , 7 ,11 , 9 , 7
.‫الحسابي‬ ‫الوسط‬ ‫جد‬ ‫االتي‬ ‫الجدول‬ ‫من‬ /2‫س‬
201712796‫الوزن‬
756432‫العدد‬
:‫االتي‬ ‫التكراري‬ ‫الجدول‬ ‫من‬ ‫غرام‬ ‫بالكيلو‬ ً‫ا‬‫طالب‬ )40( ‫الوزان‬ ‫الحسابي‬ ‫الوسط‬ ‫اوجد‬ /3‫س‬
70- 8060-50-40-30-‫االوزان‬
6541510‫التكرار‬
:‫االتي‬ ‫الجدول‬ ‫في‬ ‫المعطاة‬ ‫للقيم‬ ‫الحسابي‬ ‫الوسط‬ ‫احسب‬ / 4‫س‬
20-2317-14-11-8-5-‫الفئة‬
5237911‫التكرار‬
10 1

220. ‫الفهرست‬
4 - 30........................... ‫التطبيقات‬ /‫االول‬ ‫الفصل‬
31 - 45 ..................... ‫الحقيقية‬ ‫االعداد‬ /‫الثاني‬ ‫الفصل‬
46 - 71......................... ‫الحدوديات‬ /‫الثالث‬ ‫الفصل‬
72 - 113......................... ‫المتباينات‬ /‫الرابع‬ ‫الفصل‬
114 - 133............... ‫المثلث‬ - ‫الهندسة‬ /‫الخامس‬ ‫الفصل‬
134 - 163......................... ‫الدائرة‬ /‫السادس‬ ‫الفصل‬
164 - 177................. ‫االحداثية‬ ‫/الهندسة‬ ‫السابع‬ ‫الفصل‬
178 - 198................. ‫التحويالت‬ ‫هندسة‬ /‫الثامن‬ ‫الفصل‬
199-206................... ‫المثلثات‬ ‫/حساب‬ ‫التاسع‬ ‫الفصل‬
207 - 219......................... ‫االحصاء‬ /‫العاشر‬ ‫الفصل‬