المستند يتناول موضوع المجموعات في نظرية المجموعات، مقدماً تعريفات وأمثلة حول كيفية تنظيم العناصر ضمن المجموعات وأنواعها. كما يستعرض مفهوم الانتساب والتعريفات الأساسية مثل المجموعة الجزئية والمجموعة الفارغة. بالإضافة إلى توضيح العلاقة بين المجموعات وعملياتها الأساسية.

4. ‫األسبوع‬‫تفاصٌل‬‫المفردات‬
‫األول‬‫المجموعات‬ ‫نظرٌة‬set theory
ً‫الثان‬‫أنواع‬ ‫ــــ‬ ‫المتجهات‬‫المتجهات‬ ‫جمع‬ ‫ــــ‬ ‫المتجهات‬vectors
‫الثالث‬‫العمودي‬ ‫المتجه‬‫المتجهات‬ ‫ضرب‬ ‫ـــ‬
‫الرابع‬‫المصفوفات‬matrices
‫الخامس‬‫المصفوفات‬ ‫ضرب‬
‫السادس‬‫المحددات‬.
‫السابع‬‫الخطٌة‬ ‫المعادالت‬ ‫لحل‬ ‫واستخدامه‬ ‫المصفوفة‬ ‫معكوس‬.
‫الثامن‬‫المصفوفة‬ ‫معكوس‬ ‫باستخدام‬ ‫المعادالت‬ ‫منظومة‬ ‫حل‬
‫العاشر‬‫الدوال‬‫ومشتقاتها‬‫الدوال‬ ‫ــــ‬‫الضمنٌة‬

5. ‫األسبوع‬‫تفاصٌل‬‫المفردات‬
‫عشر‬ ‫الحادي‬‫المثلثٌةـــ‬ ‫الدوال‬‫المثلثٌة‬ ‫الدوال‬ ‫مشتقة‬
‫عشر‬ ً‫الثان‬‫اللوغارٌتمٌة‬ ‫الدوال‬
‫عشر‬ ‫الثالث‬‫الجزئٌة‬ ‫المشتقات‬
‫الرابع‬‫عشر‬‫التكامل‬
‫عشر‬ ‫الخامس‬‫المحدد‬ ‫التكامل‬
‫عشر‬ ‫السادس‬‫والمثلثٌة‬ ‫واللوغارٌتمٌة‬ ‫االسٌه‬ ‫الدوال‬ ‫تكامل‬
‫عشر‬ ‫السابع‬‫التكامل‬ ‫طرق‬
‫عشر‬ ‫الثامن‬‫الكسور‬‫الجزئٌة‬
‫عشر‬ ‫التاسع‬‫التكامل‬ ‫تطبٌقات‬
‫العشرون‬‫التفاضلٌة‬ ‫المعادالت‬

6. ‫األسبوع‬‫تفاصٌل‬‫المفردات‬
‫والعشرون‬ ‫الحادي‬‫االولى‬ ‫المرتبة‬ ‫من‬ ‫التفاضلٌة‬ ‫المعادالت‬ ‫حل‬
‫والعشرون‬ ً‫الثان‬‫العددي‬ ‫التحلٌل‬(‫الحدود‬ ‫متعدد‬)
‫والعشرون‬ ‫الثالث‬‫الالخطٌة‬ ‫المعادالت‬ ‫حل‬
‫والعشرون‬ ‫الرابع‬‫نٌوتن‬ ‫طرٌقة‬-‫رافسون‬
‫والعشرون‬ ‫الخامس‬‫الخطٌة‬ ‫المعادالت‬ ‫حل‬
‫والعشرون‬ ‫السادس‬‫التكرارٌة‬ ‫الطرائق‬
‫والعشرون‬ ‫السابع‬‫العددي‬ ‫التفاضل‬
‫والعشرون‬ ‫الثامن‬‫العددي‬ ‫التكامل‬
‫والعشرون‬ ‫التاسع‬‫صٌغة‬ ‫ـــ‬ ‫التفاضلٌة‬ ‫للمعادالت‬ ‫العددٌة‬ ‫الحلول‬‫اوٌلر‬‫تاٌلرـــ‬ ‫صٌغة‬ ‫ـــ‬
‫المطورة‬ ‫اوٌلر‬ ‫طرٌقة‬
‫الثالثون‬

9. ‫المجموعات‬:-
‫كانتور‬ ‫الرٌاضٌات‬ ‫عالم‬ ‫كان‬ ‫عندما‬G.Cantor‫بعض‬ ‫على‬ ‫ٌشتغل‬
‫الرٌاضٌات‬ ً‫ف‬ ‫القضاٌا‬,‫عن‬ ‫وتعبر‬ ‫المترادفة‬ ‫الكلمات‬ ‫بعض‬ ‫هناك‬ ‫الحظ‬
‫مفهوم‬”‫األشٌاء‬ ‫من‬ ‫تجمع‬“‫ذلك‬ ‫تعبر‬ ‫لفظة‬ ‫اختٌار‬ ‫المفٌد‬ ‫من‬ ‫والحظ‬,
‫كلمة‬ ‫على‬ ‫اختٌاره‬ ‫ووقع‬(set( )‫مجموعة‬.)
‫فروع‬ ‫معظم‬ ً‫ف‬ ‫كبٌرة‬ ‫أهمٌة‬ ‫ذات‬ ‫المجموعات‬ ‫نظرٌة‬ ‫أصبحت‬ ‫وقد‬
‫التطبٌقات‬ ‫من‬ ‫كثٌر‬ ً‫وف‬ ‫الرٌاضٌات‬.
‫نظرٌة‬ ً‫ف‬ ‫أولٌة‬ ‫مقدمة‬ ‫على‬ ‫الفصل‬ ‫هذا‬ ‫ٌقتصر‬ ‫وسوف‬
‫المجموعات‬.

10. ‫المجموعة‬:-
‫متماٌزة‬ ‫أشٌاء‬ ‫من‬ ‫تاما‬ ‫تعرٌفا‬ ‫معرف‬ ‫تجمع‬ ً‫ه‬.‫من‬
‫كان‬ ‫أن‬ ‫ٌعرف‬ ‫شًء‬ ‫أي‬ ‫تحدٌد‬ ‫ٌمكن‬ ‫التعرٌف‬ ‫هذا‬
‫اآلراء‬ ‫تدخل‬ ‫ال‬ ‫أن‬ ‫بشرط‬ ‫ال‬ ‫أم‬ ‫المجموعة‬ ‫ضمن‬
‫المجموعة‬ ‫ضمن‬ ‫ٌكون‬ ‫أن‬ ً‫ف‬ ‫األهواء‬ ‫أو‬-‫ال‬ ‫أو‬
‫ٌكون‬.
‫الشًء‬ ‫كان‬ ‫أذا‬ ‫قاطعة‬ ‫الصفة‬ ‫تكون‬ ‫أن‬ ‫ٌجب‬ ‫أي‬
ً‫ٌنتم‬ ‫ال‬ ‫أو‬ ً‫ٌنتم‬,

11. ‫بعنصر‬ ‫للمجموعة‬ ‫المكونة‬ ‫االشٌاء‬ ‫من‬ ‫كل‬ ‫تسمٌة‬ ‫على‬ ‫اصطلح‬ ‫لقد‬
Elementً‫االلمان‬ ‫العالم‬ ‫وٌعد‬‫كانتور‬Cantor
ً‫ٌل‬ ‫بما‬ ‫ٌتصف‬ ‫اساسٌا‬ ‫مفهوما‬ ‫المجموعة‬ ‫اعتبر‬ ‫من‬ ‫اول‬:-
1-‫بذاته‬ ‫قائم‬ ً‫رٌاض‬ ‫كائن‬ ‫المجموعة‬.
2-‫متماٌزة‬ ‫المجموعة‬ ‫عناصر‬.
3-‫تعٌنا‬ ‫معٌنة‬ ‫المجموعة‬‫تاما‬.
4-‫علٌها‬ ‫اثر‬ ‫أي‬ ‫المجموعة‬ ‫عناصر‬ ‫فٌه‬ ‫تورد‬ ‫الذي‬ ‫للترتٌب‬ ‫لٌس‬.

12. ً‫ٌل‬ ‫ما‬ ً‫ف‬ ‫نبٌن‬‫المجموعة‬ ‫لتعٌن‬ ‫طرٌقتٌن‬:-
1-‫عناصرها‬ ‫جمٌع‬ ‫عرفت‬ ‫اذا‬ ‫المجموعة‬ ‫تتعٌن‬.‫كتابتها‬ ‫وعندئذ‬
‫متوسطٌن‬ ‫قوسٌن‬ ‫بٌن‬ ‫عناصرها‬ ‫جمٌع‬ ‫بذكر‬}{
‫عناصرها‬ ‫بٌن‬ ‫الفوارز‬ ‫وضع‬ ‫مع‬.
‫ا‬‫ال‬‫مث‬:‫كلمة‬ ‫حرف‬ ‫مجموعة‬(year)‫تكتب‬:-
},,,{ ryeax 

13. },5:{ nnnA  ‫موجب‬ ‫صحٌح‬ ‫عدد‬
2-‫بحٌث‬ ‫عناصرها‬ ‫تمٌز‬ ً‫الت‬ ‫الخواص‬ ‫كل‬ ‫بذكر‬ ‫المجموعة‬ ‫تعٌن‬ ‫ٌمكن‬
‫كان‬ ‫اذا‬ ‫ما‬ ‫قاطعة‬ ‫بصورة‬ ‫نحدد‬ ‫ان‬ ‫الخواص‬ ‫هذه‬ ‫باستخدام‬ ‫ٌمكن‬
ً‫ٌنتم‬ ‫اوال‬ ً‫ٌنتم‬ ‫ما‬ ‫عنصر‬.
‫ا‬‫ال‬‫مث‬:‫عنه‬ ‫التعبٌر‬ ‫ٌمكن‬ ‫السابق‬ ‫المثال‬:-
‫وتقرأ‬((‫العناصر‬ ‫كل‬ ‫مجموعة‬ ً‫ه‬,‫حٌث‬‫من‬ ‫حرف‬
‫كلمة‬ ‫حروف‬year))
xxx
}:{ xyearxx  ‫كلمة‬ ‫حروف‬ ‫من‬ ‫حرف‬
‫مثال‬2:‫تصغر‬ ً‫الت‬ ‫الموجبة‬ ‫الصحٌحة‬ ‫االعداد‬ ‫مجموعة‬
‫العدد‬(5.)‫تكتب‬:
A
}4,3,2,1{A

14. ‫ا‬‫ال‬‫مث‬:}‫موجب‬ ‫صحٌح‬ ‫عدد‬{=‫فان‬: x:xx
xx  5,1
‫أذا‬‫مجموعة‬ ‫من‬ ‫عنصرا‬ ‫كان‬‫فنقول‬‫إلى‬ ً‫ٌنتم‬ axax
‫بشكل‬ ‫وٌكتب‬‫وتقرأ‬‫إلى‬ ً‫تنتم‬. xaax
‫نقول‬ ‫فعندئذ‬ ‫المجموعة‬ ‫عناصر‬ ‫من‬ ‫عنصرا‬ ‫لٌس‬ ‫كان‬ ‫أذا‬ ‫أما‬
‫إلى‬ ً‫ٌنتم‬ ‫ال‬‫وٌكتب‬(‫االنتماء‬ ً‫نف‬) xxa
a

15. ‫بأنها‬ ‫عنصر‬ ‫أي‬ ‫على‬ ‫تحتوي‬ ‫ال‬ ً‫الت‬ ‫للمجموعة‬ ‫ٌقال‬‫مجموعة‬
‫أو‬‫الرمز‬{ }‫بدون‬‫فٌها‬ ‫عناصر‬.
‫وٌستخدم‬ ‫خالٌة‬‫الرمز‬ ‫عادة‬Øً‫خال‬ ‫ٌقرأ‬ ‫الذي‬

16. ‫منتهٌة‬ ‫انها‬ ‫ما‬ ‫لمجموعة‬ ‫ٌقال‬Finite‫او‬ ‫خالٌة‬ ‫كانت‬ ‫اذا‬
‫عددها‬ ‫ٌمكن‬ ‫عناصر‬ ‫على‬ ‫تحتوي‬ ‫كانت‬(‫نظرٌا‬ ‫ولو‬)ً‫وف‬
‫منتهٌة‬ ‫غٌر‬ ‫او‬ ‫النهاٌة‬ ‫انها‬ ‫للمجموعات‬ ‫ٌقال‬ ‫الحاالت‬ ‫هذه‬
Infinite.
‫ا‬‫ال‬‫مث‬:
1-‫من‬ ‫اقل‬ ً‫الت‬ ‫الطبٌعٌة‬ ‫االعداد‬ ‫مجموعة‬30‫مجموعة‬
‫منتهٌة‬
2-‫من‬ ‫اقل‬ ً‫الت‬ ‫الطبٌعٌة‬ ‫االعداد‬ ‫مجموعة‬30‫غٌر‬ ‫مجموعة‬
‫منتهٌة‬.

17. ‫مغلق‬ ‫بخط‬ ‫محاط‬ ‫مستو‬ ً‫ف‬ ‫بنقاط‬ ‫المجموعة‬ ‫تمثٌل‬ ‫ٌمكن‬
‫ٌمثل‬ ‫الذي‬ ‫الشكل‬ ‫وٌسمى‬ ‫مستطٌل‬ ‫أو‬ ‫مربع‬ ‫أو‬ ‫كدائرة‬
‫فٌنن‬ ‫مخطط‬ ‫الطرٌقة‬ ‫بهذه‬ ‫المجموعة‬.
‫برهنا‬ ‫فٌنن‬ ‫مخططات‬ ‫اعتبار‬ ‫ٌمكن‬ ‫ال‬ ‫انه‬ ‫إلى‬ ‫االنتباه‬ ‫ٌجب‬
‫كثٌر‬ ‫مفهوم‬ ‫أو‬ ‫برهانا‬ ‫إٌضاح‬ ً‫ف‬ ‫منها‬ ‫ٌستفاد‬ ‫بل‬ ‫رٌاضٌا‬
‫القضاٌا‬ ‫من‬.

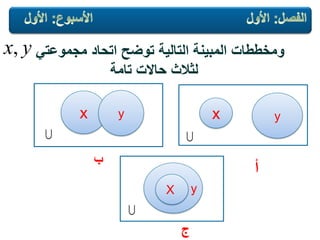
18. ً‫لمجموعت‬ ‫ٌقال‬) (‫اذا‬ ‫وفقط‬ ‫اذا‬ ‫متساوٌتان‬if and
onlyif‫العناصر‬ ‫نفس‬ ‫على‬ ‫احتوٌتا‬.
‫تكتب‬:-
][][ yxxxyx 
yx,
yx 

19. ‫األقل‬ ‫على‬ ‫وجد‬ ‫اذا‬ ‫متساوٌتان‬ ‫غٌر‬ ‫المجموعتان‬ ‫اما‬
‫الى‬ ً‫ٌنتم‬ ‫ال‬ ‫المجموعتٌن‬ ‫احدى‬ ً‫ف‬ ‫واحد‬ ‫عنصر‬
‫تكتب‬ ‫وعندئذ‬ ‫االخرى‬ ‫المجموعة‬:-
}1,2{B
BA 
yx 
‫ا‬‫ال‬‫مث‬:-
‫فأن‬:
}23:{ 2
 xxxA

20. yx 
xy 
][][ yxxxyx 
x
x
x
x
y
y
y
y
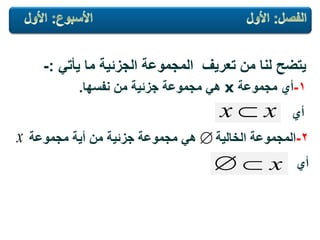
‫جزئٌة‬ ‫مجموعة‬ ‫ٌقال‬subset‫أذا‬ ‫المجموعة‬ ‫من‬
‫وتكتب‬ ‫إلى‬ ً‫ٌنتم‬ ‫عناصر‬ ‫من‬ ‫عنصر‬ ‫كل‬ ‫كان‬
‫وتقرأ‬(‫من‬ ‫جزئٌة‬ ‫مجموعة‬. )
‫وتكتب‬ ‫للمجموعة‬ ‫حاوٌة‬ ‫المجموعة‬ ‫بأن‬ ‫ٌقال‬ ‫كما‬
‫وٌمكن‬ً‫التال‬ ‫بالشكل‬ ‫الجزئٌة‬ ‫المجموعة‬ ‫تعرٌف‬ ‫كتابة‬:-

21. ً‫ٌأت‬ ‫ما‬ ‫الجزئٌة‬ ‫المجموعة‬ ‫تعرٌف‬ ‫من‬ ‫لنا‬ ‫ٌتضح‬:-
1-‫مجموعة‬ ‫أي‬x‫نفسها‬ ‫من‬ ‫جزئٌة‬ ‫مجموعة‬ ً‫ه‬.
xx 

x
x
‫أي‬
2-‫الخالٌة‬ ‫المجموعة‬‫من‬ ‫جزئٌة‬ ‫مجموعة‬ ً‫ه‬‫مجموعة‬ ‫أٌة‬
‫أي‬

22. }21,11,1,0{z
‫شاملة‬ ‫مجموعة‬ ‫اعتبار‬ ‫فٌمكن‬.....}..........3,2,1{U
U
‫قٌد‬ ‫تكون‬ ً‫الت‬ ‫المجموعات‬ ‫جمٌع‬ ‫فٌها‬ ‫تكون‬ ً‫الت‬ ‫المجوعة‬ ً‫ه‬
‫لها‬ ‫جزئٌة‬ ‫مجموعات‬ ‫المناقشة‬.
‫ب‬ ‫لها‬ ‫نرمز‬) (
‫مثال‬:-‫فأن‬ ‫صحٌحة‬ ‫اعداد‬ ‫من‬ ‫مجموعات‬ ‫من‬ ‫الحدٌث‬ ‫كان‬ ‫اذا‬
}5,4,3,2,1{x
}10,8,6,4,2{y

23. ‫قائم‬ ً‫رٌاض‬ ‫كائن‬ ‫المجموعة‬ ‫بأن‬ ‫بٌنا‬ ‫لقد‬‫بذاته‬.‫واآلن‬‫نستعرض‬
‫عالقة‬‫ببعضها‬ ‫المجموعات‬.‫األساسٌة‬ ‫العملٌات‬ ‫بعض‬ ‫سنعرف‬
ً‫الت‬‫معلومة‬ ‫مجموعات‬ ‫من‬ ‫جدٌدة‬ ‫مجموعات‬ ‫نشكل‬ ‫أن‬ ‫بواسطتها‬ ‫نستطٌع‬.
‫الجبرٌة‬ ‫األولٌة‬ ‫العملٌات‬ ‫ما‬ ‫حد‬ ‫إلى‬ ‫تشبه‬ ‫العملٌات‬ ‫وهذه‬‫على‬
‫األعداد‬.
‫مثل‬‫والضرب‬ ‫والطرح‬ ‫الجمع‬.

24. )}()(:{ yxxxxyx 
yx 
yx,
yx,
yx,
 xy
‫جمٌع‬ ‫من‬ ‫تتكون‬ ً‫الت‬ ‫المجموعة‬ ‫فان‬ ‫مجموعتٌن‬ ‫لتكن‬
‫المجموعتٌن‬ ‫أحدى‬ ً‫ف‬ ‫األقل‬ ‫على‬ ‫الموجودة‬ ‫العناصر‬
‫تسمى‬‫اتحاد‬‫المجموعتٌن‬
‫بالرمز‬ ‫المجموعتٌن‬ ‫التحاد‬ ‫وٌرمز‬
‫تقرأ‬ ً‫والت‬(‫اتحاد‬)‫رمز‬ ‫على‬ ‫وٌطلق‬‫عملٌة‬‫االتحاد‬.
‫وٌكون‬:

25. ً‫مجموعت‬ ‫اتحاد‬ ‫توضح‬ ‫التالٌة‬ ‫المبٌنة‬ ‫ومخططات‬
‫تامة‬ ‫حاالت‬ ‫لثالث‬
yX
x y x y
‫ج‬
‫أ‬
‫ب‬

 
yx,

26. ‫مثال‬:-‫كانت‬ ‫اذا‬
}9,8,7,6,4,3,2,1{yx 
‫فأن‬:
}4,3,2,1{x
}9,8,7,6,4,2{y

27. ‫مبرهنة‬:-
‫شاملة‬ ‫مجموعة‬ ‫لتكن‬,‫من‬ ‫جزئٌة‬ ‫مجموعات‬ ‫و‬
ni
n
i xxxxxx  ..........43211 
Uxyz ,,U
xxx 
xx 
xyyx  
UUx 
)()( zyxzyx  
‫فأن‬:-1
6
5
4
3
2

28. ‫جمٌع‬ ‫من‬ ‫تتكون‬ ً‫الت‬ ‫المجموعة‬ ‫فأن‬ ‫مجموعتٌن‬ ‫لتكن‬
‫تقاطع‬ ‫تسمى‬ ‫معا‬ ‫من‬ ‫كل‬ ‫الى‬ ً‫تنتم‬ ً‫الت‬ ‫العناصر‬
‫المجموعتٌن‬,‫تقاطع‬ ‫تقرأ‬ ً‫والت‬ ‫لها‬ ‫وٌرمز‬
,‫الرمز‬ ‫على‬ ‫ونطلق‬∩‫التقاطع‬ ‫رمز‬,‫كما‬ ‫عنه‬ ‫التعبٌر‬ ‫وٌمكن‬
ً‫ٌل‬:-
xy,
xy,
xy,yx
)}()(:{ yxxxxyx 
xy,
xy
‫مختلفة‬ ‫حاالت‬ ‫لثالث‬
‫المجموعتٌن‬ ‫تقاطع‬ ‫بٌن‬ ‫المظلل‬ ‫الجزء‬ ‫فٌن‬ ‫ومخطط‬

29. y
yxyx
x
yx  yx 
xyx 

30. ‫العدد‬ ‫مضاعفات‬ ‫أن‬ ‫نجد‬3‫العدد‬ ‫مضاعفات‬ ‫و‬2‫مجموعة‬ ‫وعلٌه‬
‫على‬ ‫القسمة‬ ‫تقبل‬ ً‫الت‬ ‫االعداد‬ ‫تضم‬ ‫التقاطع‬3,2‫المجموعة‬ ‫وستكون‬
‫العدد‬ ‫مضاعفات‬ ‫من‬6
},2:{2 nyyxxx 
.},.........6,4,2{2x
1x2x
},6:{21 nyyxxxx 
n ‫مثال‬:-‫و‬ ‫الطبٌعٌة‬ ‫االعداد‬ ‫مجموعة‬ ‫لتكن‬
},3:{1 nyyxxx 
‫الحل‬:-
....},.........2,1{n
.},.........9,6,3{1x

31. ‫فأن‬ ‫مجموعات‬ ‫ثالث‬ ‫لتكن‬
yx,
yx,
yx
xyz ,,
)()( zyxzyx  
‫تعرٌف‬:-
‫خالٌة‬ ‫مجموعة‬ ‫المجموعتٌن‬ ‫نقاط‬ ‫مجموعة‬ ‫كان‬ ‫اذا‬,‫أي‬
‫منفصلتان‬ ‫مجموعتان‬ ‫أن‬ ‫ٌقال‬ ‫فعندئذ‬disjoint
‫مبرهنات‬:-
xxx 
xyyx  
1
2
3

32. U
c
x
xU
Ux
xU
c
x
x,c
x
x
‫المجموعة‬ ‫من‬ ‫جزئٌة‬ ‫مجموعة‬ ‫أن‬ ‫لنفرض‬‫الشاملة‬.
‫تسمى‬ ‫إلى‬ ً‫تنتم‬ ‫ال‬ ً‫الت‬ ‫العناصر‬ ‫من‬ ‫المكونة‬ ‫فالمجموعة‬
‫انه‬ ‫أي‬ ‫بالرمز‬ ‫ط‬ ‫وٌرمز‬ ‫إلى‬ ‫بالنسبة‬ ‫المجموعة‬ ‫متممة‬:-
‫وٌوضح‬ ً‫الثان‬ ‫فٌن‬ ‫ومخطط‬‫متممة‬
},;{ xxUxxxc


33. U
}2:{)2  yyy
ً‫زوج‬ ‫عدد‬
}2,1,0,1{......,}2:{,.......}5,4,3{)2  yyyy c
‫مثال‬:-
‫الصحٌحة‬ ‫األعداد‬ ‫مجموعة‬ ً‫ه‬ ‫كان‬ ‫أذا‬,‫مما‬ ‫كل‬ ‫متممة‬ ‫فجد‬
ً‫ٌأت‬:-}:{)1 xxx 
‫الحل‬:-
......}3,1,1,3,5{...........}4,2,0,2,4{......,)1  n
xx

34. ‫أن‬ ‫أي‬ ‫أو‬ ‫لها‬ ‫وٌرمز‬
},{/ yxxxxyx 
xy,
xy
xyy x
yx/yx
‫لتكن‬‫مجموعتٌن‬‫تحتوي‬ ً‫الت‬ ‫المجموعة‬ ‫فان‬
‫إلى‬ ‫المنتمٌة‬ ‫وغٌر‬ ‫إلى‬ ‫المنتمٌة‬ ‫العناصر‬ ‫على‬
‫على‬ ‫فضلة‬ ‫تسمى‬‫على‬ ‫فرق‬ ‫أو‬

35. x yyx x
‫حاالت‬ ‫أربع‬ ً‫ف‬ ‫مجموعتٌن‬ ‫فضلة‬ ‫ٌوضح‬ ‫فٌن‬ ‫مخطط‬

xyx /

yx /yx /xy /
xy y

36. }6,3,2{y
xy /
‫مثال‬:-‫كانت‬ ‫اذا‬
}6,5,4,3,2,1{x
‫فأن‬:-
}5,4,1{/ yx

37. ً‫وه‬ ‫الكمٌات‬ ‫من‬ ‫نوعٌن‬ ‫مع‬ ‫العملٌة‬ ‫حٌاتنا‬ ً‫ف‬ ‫نتعامل‬ ‫نحن‬:-
1-‫الكمٌات‬(‫المقادٌر‬)‫القٌاسٌة‬scalars
ً‫حقٌق‬ ‫عدد‬ ً‫ه‬ ً‫الت‬ ‫بقٌمتها‬ ‫تتحدد‬ ً‫الت‬ ً‫وه‬,‫الحجم‬ ‫ا‬‫ال‬‫مث‬,‫الكتلة‬
,‫الحرارة‬ ‫درجات‬,‫المساحات‬.
2-‫المتجهة‬ ‫الكمٌات‬....-:vectors
‫تحدٌدها‬ ‫ٌتطلب‬ ً‫الت‬ ‫الكمٌات‬ ً‫وه‬:-
‫أ‬-‫قٌمتها‬(‫الطول‬....length)
‫ب‬-‫اتجاه‬....direction

38. ‫جسم‬‫الدقٌقة‬ ً‫ف‬ ‫امتار‬ ‫خمسة‬ ‫بسرعة‬ ‫ٌتحرك‬
‫وبزاوٌة‬‫مقدارها‬30‫فٌمكن‬ً‫ف‬ ‫كما‬ ‫هندسٌا‬ ‫تمثٌلها‬
ً‫التال‬ ‫الشكل‬:
‫المتجه‬ ‫تمثٌل‬ ‫وكٌفٌة‬ ‫المتجه‬ ‫الكمٌات‬ ً‫ه‬ ‫دراسته‬ ‫ٌهمنا‬ ‫والذي‬
‫المتجهات‬ ‫لها‬ ‫تخضع‬ ً‫الت‬ ‫الجبرٌة‬ ‫والعملٌات‬ ‫هندسٌا‬.
‫ومثال‬:-

39. y
X
u
0
0 x
•30
u0
305
<
u ‫حٌث‬:‫مسار‬ ‫ٌمثل‬ ‫والمستقٌم‬ ‫الدقٌقة‬ ‫نهاٌة‬ ً‫ف‬ ‫الجسم‬ ‫موقع‬
‫بالرمز‬ ‫عنه‬ ‫وٌعبر‬ ‫الجسم‬
ً‫حقٌق‬ ‫عدد‬ ‫أي‬ ‫تمثٌل‬ ‫ٌمكن‬x‫على‬ ‫نقطة‬ ‫لتمثٌل‬ ‫تستخدم‬ ‫ان‬ ‫ٌمكن‬
ً‫التال‬ ‫الشكل‬ ً‫ف‬ ‫كما‬ ‫مستقٌم‬

40. ً‫ف‬ ‫نقطة‬ ‫لتمثٌل‬ ‫ٌستخدم‬ ‫الحقٌقة‬ ‫األعداد‬ ‫من‬ ً‫والثالث‬
ً‫التال‬ ‫الشكل‬ ً‫ف‬ ‫كما‬ ‫فضاء‬
‫لتمثٌل‬ ‫تستخدم‬ ‫أن‬ ‫ٌمكن‬ ‫الحقٌقة‬ ‫األعداد‬ ‫من‬ ‫زوج‬ ‫أي‬ ‫وان‬
ً‫التال‬ ‫الشكل‬ ً‫ف‬ ‫كما‬ ‫مستوى‬ ً‫ف‬ ‫نقطة‬:
x
x
y
y
y
x
x
y
x
z
z
),( yx
),,( zyx
),( yx
),,( zyx

41. ]86
2
1
3[],51102[],253[],17[  ba
ً‫الصف‬ ‫المتجه‬:-‫صف‬ ً‫ف‬ ‫مرتبة‬ ‫حقٌقة‬ ‫اعداد‬ ‫مجموعة‬ ‫عن‬ ‫عبارة‬
‫فوازر‬ ‫بدون‬ ‫او‬ ‫بفوارز‬ ‫بعضها‬ ‫عن‬ ‫مفصولة‬ ‫وتكتب‬ ‫واحد‬ ‫سطر‬ ‫او‬
‫مركبة‬ ‫المتجه‬ ً‫ف‬ ‫عدد‬ ‫كل‬ ‫على‬ ‫وٌطلق‬ ‫كبٌرٌن‬ ‫قوسٌن‬ ‫داخل‬
component‫عنصر‬ ‫أو‬element
‫مثال‬:
‫مركبتٌن‬ ‫من‬ ‫االول‬ ‫المتجه‬ ‫ٌتألف‬ ً‫صف‬ ‫متجه‬,‫ثالث‬ ً‫والثان‬
‫مركبات‬,‫مركبات‬ ‫ست‬ ‫من‬ ‫والرابع‬ ‫مركبات‬ ‫اربعة‬ ‫من‬ ‫والثالث‬

42. ‫تعرٌف‬:-‫من‬ ‫مكون‬ ً‫الصف‬ ‫المتجه‬ ‫كان‬ ‫اذا‬) (‫فٌقال‬ ‫المركبات‬ ‫من‬
‫المرتبة‬ ‫من‬ ‫له‬
Vn
ordern‫البعد‬ ‫ذو‬ ‫انه‬ ‫أو‬nensionaln )dim(
‫صغٌرة‬ ‫بحروف‬ ‫مركبة‬ ‫ولكل‬ ‫كبٌرة‬ ‫بحروف‬ ‫للمتجه‬ ‫نرمز‬ ‫وعادة‬
‫الدلٌل‬ ‫ٌسمى‬ ‫المركبة‬ ‫او‬ ‫العنصر‬ ‫االسفل‬ ‫والقٌم‬,ً‫ف‬ ‫ترتٌبه‬ ً‫ٌعن‬
‫المتجه‬
],......,,[ 21 naaaA 
‫ا‬‫ال‬‫مث‬

43. ‫البعد‬ ‫نفس‬ ‫من‬ ‫كانا‬ ‫أذا‬ ‫وفقط‬ ‫أذا‬ ‫الصفٌان‬ ‫المتجهان‬ ‫ٌتساوى‬
‫متساوٌة‬ ‫المتناظرة‬ ‫مركباتهما‬ ‫وكانت‬.‫كان‬ ‫فإذا‬
],.........,[ 21 nbbbB 
‫فأن‬:‫كان‬ ‫إذا‬ ‫وفقط‬ ‫إذا‬
nn bababa  ,........., 2211
‫ا‬‫ال‬‫مث‬:
]32[],352[],3
4
10
[  CBA
‫فأن‬:cbA 
BA
‫تعرٌف‬:-
],.........,[ 21 naaaA 

44. ‫مثال‬:‫قٌمة‬ ‫جد‬‫أن‬ ‫بحٌث‬:
]3124[]7]122[ yx 
‫التعرٌف‬ ‫من‬:
3
7
,22  yx
‫الصفري‬ ‫المتجه‬:
‫صفري‬ ‫متجه‬ ‫أصفار‬ ‫مركباته‬ ‫أو‬ ‫عناصره‬ ‫جمٌع‬ ‫الذي‬ ‫للمتجه‬ ‫ٌقال‬
)0.,.........0,0(0 
xy,
73,42  yx
‫له‬ ‫وٌرمز‬‫بالرمز‬0‫أن‬ ‫أي‬

45. ‫المتجهات‬ ‫جمع‬
‫البعد‬ ‫ذو‬ ‫متجهٌن‬ً‫ٌل‬ ‫كما‬ ‫جمعهما‬ ‫حاصل‬ ‫فٌعرف‬
)............,(),..,.........( 211 nn xxxuyyv 
)...,.........,( 2211 nn yxyxyxvu 
‫ا‬‫ال‬‫مث‬:‫لتكن‬)3,2,0(),5,2,1(  AB‫فأن‬:
)8,0,1( BA
n
‫كان‬ ‫أذا‬

46. ‫قٌاسٌة‬ ‫بكمٌة‬ ‫متجه‬ ‫ضرب‬multiplication by scalar
‫كان‬ ‫أذا‬),........( 1 nxxu ,‫ثابت‬ ‫عدد‬ ‫البعد‬ ‫ذو‬ ‫متجه‬,ً‫ٌل‬ ‫كما‬ ‫ٌعرف‬ ‫فأن‬:-
),......,,(),,.........( 211 nn cxcxcxxxccu 
‫مثال‬:‫لٌكن‬:-
)20,5,15( 
nc,cu
)4,1,3(,5  uc
)4,1,3(5 cu

47. wvu ,,
cvcuvuc  )()3
uv,
Dvcuvu 
vu
),....( 11 nn yxyxvu 
n,c ‫مبرهنة‬:-‫كان‬ ‫أذا‬‫البعد‬ ‫نفس‬ ‫من‬ ‫متجهات‬‫عدد‬,‫فأن‬:-
)())(1 wvuwvu 
uvvu )2
‫لٌكن‬‫البعد‬ ‫نفس‬ ‫من‬ ‫متجهٌن‬,‫من‬ ‫طرح‬ ‫ٌعرف‬
‫متجه‬ ‫بأنه‬
‫كان‬ ‫أذا‬ ‫وعلٌه‬:),,.........(,),,.........( 11 nn xxuyyv 
‫تعرٌف‬:-

48. ‫للمتجهات‬ ً‫الخط‬ ‫التركٌب‬
linear combination of vectors
nvvv ,,........., 21
nccc ,,........., 21
nnvcvcvcv ............2211 
nvvv ,,........., 21
‫مثال‬:‫لتكن‬)4,1,1(),3,0,2(),1,2,1(2 321  vvv
‫ولتكن‬2,3,2 321  ccc
v
‫البعد‬ ‫نفس‬ ‫ذات‬ ‫متجهات‬ ‫لتكن‬,‫ولتكن‬
‫حقٌقٌة‬ ‫أعداد‬,‫فالمتجه‬,‫حٌث‬
‫للمتجهات‬ ً‫خط‬ ‫تركٌب‬ ‫ٌسمى‬

49. )4,1,1)(2()3,0,2(3)1,2,1(2 v
v‫هو‬ ً‫الخط‬ ‫فالتركٌب‬
)1,2,6( 
)8,2,2()9,0,6()2,4,2( 

50. ‫المعتمدة‬ ‫المتجهات‬‫ا‬‫ا‬ٌ‫خط‬
Linearly dependent vectors
nvvv ...,,........., 21
nccc .,........., 21
0.........2211  nnvcvcvc
0...........0............ 212211  nnn cccvcvcvc
‫البعد‬ ‫نفس‬ ‫متجهات‬ ‫لتكن‬,ً‫ا‬ٌ‫خط‬ ‫معتمدة‬ ‫أنها‬ ‫فٌقال‬
‫قٌاسٌة‬ ‫كمٌات‬ ‫وجدت‬ ‫أذا‬,‫أصفار‬ ‫جمٌعها‬ ‫لٌست‬,
‫أن‬ ‫بحٌث‬:
ً‫ا‬ٌ‫خط‬ ‫مستقلة‬ ‫أنها‬ ‫ٌقال‬ ‫ذلك‬ ‫وبعكس‬Linearly independent vectors
‫أن‬ ‫أي‬:

51. )0,0,0(),1,6,5(),0,2,1( 321  vvv321 ,, vvv
)0,0,0()0,2,1(0)1,6,5(0)0,0,0(1 
)2,7,0,0(),1,3,5,0(),4,3,2,6( 321  vvv
321, vvv
‫الحل‬:
‫حقٌقٌة‬ ‫قٌم‬ ‫نفرض‬zyx ,,
)0,0,0,0()2,7,0,0()1,3,5,0()4,3,2,6(  zyx
‫فالمتجهات‬
‫ا‬‫ا‬ٌ‫خط‬ ‫معتمدة‬‫ألن‬
‫مثال‬:‫لٌكن‬
‫ا‬‫ا‬ٌ‫خط‬ ‫معتمدة‬ ‫أم‬ ‫مستقلة‬ ‫المتجهات‬ ‫هل‬.
)0,0,0,0()24,733,52,6(  zyxzyxyxx
‫مثال‬:‫لتكن‬

52. ‫فأن‬ ‫وعلٌه‬:
06 x
‫خطٌة‬ ‫مستقلة‬ ‫فالمتجهات‬ ‫وعلٌه‬.
0 zyx
321 ,, vvv
024  zyx
0733  zyx
052  yx
‫على‬ ‫نحصل‬ ‫المعادالت‬ ‫وبحل‬

53. 1-‫كان‬ ‫أذا‬)1,2,8(),7,6,3( uvvuvuvu  ,2,3
2-‫قٌمة‬ ‫جد‬)3,2(),4( xy  xy,
3-‫؟ولماذا؟‬ً‫ا‬ٌ‫خط‬ ‫مستقلة‬ ‫أم‬ ‫معتمدة‬ ‫التالٌة‬ ‫المتجهات‬ ‫هل‬
)2,1(),1,2(),3,0( 321  vvv
‫فجد‬
‫كان‬ ‫أذا‬
)1,0,0,0(),0,1,0,0( 43  vv
)0,0,1,0(),0,0,0,1( 21  vv
)7,0,2(),3,1,0( 21  vv
1
3
2

54. 

















na
a
a
2
1
naaa ........, 21 n A
‫واحد‬ ‫سطر‬ ً‫ف‬ ‫مكتوبة‬ ‫مركبات‬ ً‫ه‬ ‫أعداد‬ ‫بصورة‬ ‫متجه‬ ‫أي‬ ‫عن‬ ‫التعبٌر‬ ‫ٌمكن‬
‫وٌمكن‬‫واحد‬ ‫عمود‬ ً‫ف‬ ‫كتابتها‬,‫العمودي‬ ‫بالمتجه‬ ‫علٌه‬ ‫ٌطلق‬ ‫وعندئذ‬‫وكل‬‫التعارف‬
‫والقواعد‬‫تنطبق‬ ً‫الصف‬ ‫المتجه‬ ‫تخص‬ ً‫الت‬ ‫والمبرهنات‬‫المتجهات‬ ‫على‬‫العمودٌة‬
‫مجموعة‬‫واحد‬ ‫عمود‬ ً‫ف‬ ‫مرتبة‬ ‫حقٌقة‬ ‫أعداد‬ ‫من‬
‫مركباته‬ ‫الذي‬ ‫المرتبة‬ ‫من‬ ‫العمودي‬ ‫فالمتجه‬
A 
‫العمودي‬ ‫المتجه‬ ‫تعرٌف‬:-

55. ‫المتجهات‬ ‫ضرب‬the multiplication of vectors
uv,


















ny
y
y
2
1
nuv
uv
v u
‫لٌكن‬‫متجهٌن‬‫نفس‬ ‫من‬‫الرتبة‬‫نعبر‬‫عن‬‫و‬ ً‫صف‬ ‫بشكل‬‫عمودي‬ ‫بشكل‬
‫نعرف‬ً‫القٌاس‬ ‫الضرب‬ ‫حاصل‬scalar-productً‫الداخل‬ ‫أو‬inner‫للمتجهٌن‬
‫له‬ ‫ٌرمز‬ ‫والذي‬‫عدد‬ ‫بأنه‬‫نحصل‬ ً‫حقٌق‬‫من‬ ‫مركبة‬ ‫كل‬ ‫ضرب‬ ‫حواصل‬ ‫مجموع‬ ‫من‬ ‫علٌه‬
‫من‬ ‫نظٌرتها‬ ‫مع‬‫كان‬ ‫أذا‬ ‫أي‬:
u ).......,,( 21 nxxx , v 

56. ‫فأن‬:
nnyxyxyxuv  ..........2211
‫ا‬‫ال‬‫مث‬:‫كان‬ ‫أذا‬)2,1,1(,
3
1
2











 vu‫فأن‬
7612 uv
i
n
i
i yx

1

57. ‫مبرهنات‬:-
ACABCBA  )(
(ً‫حقٌق‬ ‫عدد‬K)
‫المتجه‬ ‫قٌمة‬:
]...,.........,[ 21 naaaA 
nbc,n
n
‫كان‬ ‫أذا‬A‫عمودٌة‬ ‫متجهات‬ ‫ولٌكن‬ ‫الرتبة‬ ‫ذي‬ ً‫صف‬ ‫متجه‬‫من‬‫الرتبة‬
‫فان‬:
0. AA
).()( BAKKBA 
).()( BAXBKA 
‫واتجاه‬ ‫قٌمة‬ ‫متجه‬ ‫لكل‬,‫طوله‬ ‫ٌناسب‬ ً‫حقٌق‬ ‫عدد‬ ً‫ه‬ ‫المتجه‬ ‫قٌمة‬ ‫وان‬‫قٌمته‬ ‫مع‬.
‫وٌعرف‬:-‫لٌكن‬A‫الرتبة‬ ‫من‬ ‫ا‬‫ا‬‫متجه‬
3
2
1

58. ‫قٌمة‬ ‫تعرف‬A,ً‫ٌل‬ ‫بما‬ ‫لها‬ ‫ٌرمز‬ ً‫والت‬: A
22
2
2
1 ....... naaaA 
‫مثال‬:‫لٌكن‬]2,2,4,1[ A‫جد‬A
544161 A
‫الوحدة‬ ‫متجه‬ ‫للمتجه‬ ‫ٌقال‬(‫احدي‬ ‫الو‬ ‫أو‬unit vector)‫كان‬ ‫أذا‬
‫تعرٌف‬:
‫مثال‬:‫لٌكن‬
1u
]
6
1
,
2
1
,
3
2
,
6
1
,
2
1
[ U
‫مالحظة‬:‫كان‬ ‫أذا‬A‫فأن‬ ‫صفري‬ ‫غٌر‬ ‫ا‬‫ا‬‫متجه‬‫واحدي‬ ‫متجه‬ ‫هو‬. A
A
1
u
1
36
1
4
1
9
4
36
1
4
1
u

59. ‫مبرهنة‬
‫فٌثاغورس‬ ‫مبرهنة‬
Pythagoras theorem
222
vuvu 
vu,
uxxA .
‫أن‬ ‫أي‬vu.0 
xn ً‫حقٌق‬ ‫عدد‬ ‫كان‬ ‫أذا‬,A‫ذو‬ ‫متجه‬‫البعد‬‫فأن‬
‫متعامدان‬ ‫متجهٌن‬ ‫كان‬ ‫أذا‬‫فأن‬

60. 1-‫كان‬ ‫أذا‬)3,2,0(),4,1,3(),0,1,2(  uvw
u
2-‫متعامدٌن‬ ‫فٌها‬ ‫ٌكون‬ ‫التالٌة‬ ‫الحاالت‬ ‫من‬ ‫أي‬uv,
)1,3,2(,)1,1,1(  vu
wvy 22 vu 
v
)2,
2
1
,3(,)7,2,5(  vu
)5,1,2(,)1,2,1(  vu
‫جد‬
1 2
3 4
1
2
3

61. 3-‫متعامدٌن‬ ‫التالٌٌن‬ ‫المتجهٌن‬ ‫تجعل‬ ً‫الت‬ ‫قٌم‬ ‫جد‬
)7,2),31((,)2,
2
1
,1( xvxu 
4-‫البعد‬ ‫ذات‬ ‫متجهٌن‬ ‫كانت‬ ‫أذا‬‫فان‬
BABA 
vu,
x
n

62. ‫أن‬‫المصفوفة‬ ‫مفهوم‬matrix‫حٌث‬ ‫المهمة‬ ‫الرٌاضٌة‬ ‫المفاهٌم‬ ‫من‬
‫الخطٌة‬ ‫البرمجة‬ ‫منها‬ ‫عدٌدة‬ ‫مجاالت‬ ً‫ف‬ ‫تستخدم‬linear
programming‫الخطٌة‬ ‫المعادالت‬ ‫انظمة‬ ‫وحل‬linear
equations‫واإلحصاء‬statistic‫والجبر‬ً‫الخط‬linear
algebra
‫تعرٌف‬‫المصفوفة‬matrixThe:-
‫سطور‬ ‫أو‬ ‫صفوف‬ ً‫ف‬ ‫مرتبة‬ ‫كمٌات‬ ‫او‬ ‫اعداد‬ ‫مجموعة‬ ‫أنها‬rows))
‫واعمدة‬(columns)ً‫التال‬ ‫الجدول‬ ً‫ف‬ ‫كما‬

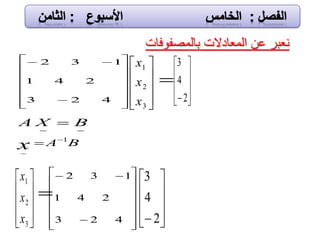
63. ‫األعداد‬ ‫أو‬ ‫الكمٌات‬ ‫من‬ ‫كل‬,‫ٌسمى‬ ‫المجموعة‬ ‫هذه‬ ‫تشكل‬ ً‫والت‬
‫عنصرا‬‫المصفوفة‬ ‫لعناصر‬ ‫المرافقة‬ ‫األرقام‬ ‫على‬ ‫وٌطلق‬ ‫المصفوفة‬ ً‫ف‬‫األدلة‬ً‫الت‬ ً‫وه‬
‫الصف‬ ‫ترتٌب‬ ‫على‬ ‫ٌدل‬ ‫الٌسار‬ ‫من‬ ‫األول‬ ‫فالرقم‬ ‫المصفوفة‬ ً‫ف‬ ‫عنصر‬ ‫كل‬ ‫موقع‬ ‫تحدد‬
‫العمود‬ ‫ٌمثل‬ ً‫الثان‬ ‫والرقم‬ ‫العنصر‬ ‫فٌه‬ ‫ٌقع‬ ‫الذي‬
‫بالرمز‬ ‫للمصفوفة‬ ‫ٌرمز‬ ‫كما‬




























mnm
m
n
n
aaa
aaa
aaa
....
.....
.....
2
1
22 2
2 1
11 2
1 1
mnaaa .........1211
nmaij *][
A 

64. ‫لتكن‬A‫اسطرها‬ ‫عدد‬ ‫مصفوفة‬m‫أعمدتها‬ ‫وعدد‬n‫التالٌة‬ ‫الصورة‬ ً‫ف‬ ‫كما‬
njmiaijA ,....1,,....1),( 
‫أن‬ ‫فنقول‬A‫رتبة‬ ‫ذات‬ ‫مصفوفة‬(m*n)‫وتقرأ‬(mً‫ف‬n)
‫رتبتها‬3*2
















43
10
21
ً‫ل‬‫مث‬:‫المصفوفة‬A

65. ‫عمود‬ ‫أو‬ ‫واحد‬ ‫صف‬ ‫ذات‬ ‫مصفوفة‬ ‫متجه‬ ‫كل‬ ‫اعتبار‬ ‫أمكانٌة‬
‫مركباته‬ ‫عدد‬ ‫الذي‬ ً‫الصف‬ ‫فالمتجه‬ ‫واحد‬n‫ذات‬ ‫مصفوفة‬ ‫هو‬
‫سعة‬1*n,‫مركباته‬ ‫عدد‬ ‫الذي‬ ‫العمودي‬ ‫والمتجه‬mً‫ه‬
‫سعة‬ ‫ذات‬ ‫مصفوفة‬m*1.‫للصف‬ ‫ا‬‫ة‬‫عاد‬ ‫ٌرمز‬iً‫ف‬
‫المصفوفة‬A‫أن‬ ‫أي‬ ‫بالرمز‬: )(iA
].......[ 21)( iniii aaaA 
‫للعمود‬ ‫ٌرمز‬ ‫كما‬j‫أي‬ ‫بالرمز‬)( jA




















n j
j
j
a
a
a
2
1
)( jA 

66. ‫مركبة‬ ‫أعداد‬ ‫أو‬ ‫جبرٌة‬ ‫أو‬ ‫مثلثٌه‬ ‫ا‬‫ا‬‫نسب‬ ‫تمثل‬ ‫أن‬ ‫ٌمكن‬ ‫المصفوفة‬ ‫عناصر‬
(complex number)‫مصفوفات‬ ‫حتى‬ ‫أو‬ ‫تكامالت‬ ‫أو‬ ‫مشتقاته‬ ‫أو‬
‫عادة‬ ‫لها‬ ‫وٌرمز‬ ‫صفرا‬ ‫فٌها‬ ‫عنصر‬ ‫كل‬ ‫ٌكون‬ ً‫الت‬ ‫المصفوفة‬ ً‫ه‬O‫وتكون‬
‫البحث‬ ‫سٌاق‬ ‫من‬ ‫مستمدة‬ ‫مرتبتها‬
‫واحد‬ ‫صف‬ ‫من‬ ‫المكونة‬ ‫المصفوفة‬ ً‫ه‬

67. ‫واحد‬ ‫عمود‬ ‫من‬ ‫المكونة‬ ‫المصفوفة‬ ً‫ه‬.
‫أعمدتها‬ ‫لعدد‬ ‫ا‬‫ا‬‫مساو‬ ‫صفوفها‬ ‫عدد‬ ‫ٌكون‬ ً‫الت‬ ‫المصفوفة‬ ً‫ه‬.‫وعندئذ‬
‫المرتبة‬ ‫من‬ ‫مصفوفة‬ ‫لها‬ ‫ٌقال‬n‫سعة‬ ‫أو‬n*n))

68. ‫على‬ ‫الواقعة‬ ‫العناصر‬ ‫من‬ ‫المؤلف‬ ‫بأنه‬ ‫المربعة‬ ‫المصفوفة‬ ً‫ف‬ ‫ٌعرف‬
‫العنصر‬ ً‫ف‬ ً‫والمنته‬ ‫الٌسرى‬ ‫العلٌا‬ ‫الزاوٌة‬ ً‫ف‬ ‫بالعنصر‬ ‫المبتدئ‬ ‫القطر‬
‫المصفوفة‬ ‫من‬ ‫الٌمنى‬ ‫السفلى‬ ‫الزاوٌة‬ ً‫ف‬.ً‫الرئٌس‬ ‫القطر‬ ‫عناصر‬ ‫أن‬ ‫أي‬
ً‫ه‬ ‫المرتبة‬ ‫ذو‬ ‫المربعة‬ ‫المصفوفة‬ ً‫ف‬: ][aijA n
nnaaaa ........,, 332211
‫الزاوٌة‬ ً‫ف‬ ‫بالعنصر‬ ‫المبتدئة‬ ‫العناصر‬ ‫من‬ ‫ٌتألف‬ ‫فانه‬ ‫الثانوي‬ ‫القطر‬ ‫أما‬
‫من‬ ‫الٌمنى‬ ‫العلٌا‬ ‫الزاوٌة‬ ً‫ف‬ ‫الواقع‬ ‫العنصر‬ ً‫ف‬ ‫والمنتهٌة‬ ‫الٌسرى‬ ‫السفلى‬
‫المصفوفة‬.

69. ‫أصفار‬ ً‫الرئٌس‬ ‫القطر‬ ‫على‬ ‫التقع‬ ً‫الت‬ ‫عناصرها‬ ‫جمٌع‬ ‫مربعة‬ ‫مصفوفة‬ ً‫ه‬
‫المصفوفة‬ ‫مثل‬:

















500
020
001
‫بالرمز‬ ‫المرتبة‬ ‫من‬ ‫القطرٌة‬ ‫المصفوفة‬ ‫عن‬ ‫نعبر‬ ‫أن‬ ‫وٌمكن‬][aign
],........,[ 2211 nnaaadiag

70. ‫القطرٌة‬ ‫للمصفوفة‬ ‫ٌقال‬daig (1 , 1 , ....1)‫المرتبة‬ ‫من‬n‫مصفوفة‬
‫ذاتٌة‬(‫وأحدٌة‬ ‫مصفوفة‬ ‫أو‬(I dentity matrix‫ا‬‫ة‬‫عاد‬ ‫لها‬ ‫وٌرمز‬
nI
















100
010
001
‫الرتبة‬ ‫نفس‬ ‫ذات‬ ‫مصفوفتان‬ ‫لتكن‬m*n
‫متساوٌة‬ ‫المتناظرة‬ ‫عناصرهما‬ ‫كانت‬ ‫أذا‬ ‫وفقط‬ ‫أذا‬ ‫متساوٌتٌن‬ ‫المصفوفتٌن‬ ‫بأن‬ ‫فٌقال‬.
nmnm aijAbijB ** )(,)( 
‫تعرٌف‬:-
‫ا‬‫ال‬‫فمث‬
3I 
‫تعرٌف‬:-

71. ‫أن‬ ‫أخر‬ ‫وبتعبٌر‬:
jibijaijbijaij nmnm ,)()( ** 
‫مثال‬:‫كان‬ ‫أذا‬












01
3
2
1
‫فالمصفوفتان‬‫متساوٌتان‬ AB,
B , A












01
3
4
1

72. ‫مثال‬:‫كانت‬ ‫أذا‬

















112
201
321



















112
201
zyx
321  zyxBA
B 
, A 

73. ‫حٌث‬ ‫المصفوفات‬ ‫كافة‬ ‫على‬ ‫أجرائها‬ ‫ٌمكن‬ ‫ال‬ ‫المصفوفات‬ ‫جمع‬ ‫عملٌة‬ ‫أن‬
‫الرتبة‬ ‫نفس‬ ‫من‬ ‫تكونا‬ ‫أن‬ ‫مصفوفتٌن‬ ‫جمع‬ ‫شرط‬ ‫ٌلزم‬.
‫رتبة‬ ‫ذات‬ ‫مصفوفتان‬ nmnm aijAbijB ** )(,)( nm*
‫له‬ ‫ٌرمز‬ ‫والذي‬ ‫جمعهما‬ ‫حاصل‬ ‫فنعرف‬A+Bً‫ٌل‬ ‫كما‬
nmbijaijBA *)( 
‫الطرٌقة‬ ‫بنفس‬ ‫بٌنهما‬ ‫الفرق‬ ‫نعرف‬ ‫كما‬BA
nmbijaijBA *)( 
‫تعرٌف‬:‫لتكن‬

74. ‫مثال‬:
,
22
01
32


















B
‫فأن‬:
,
02
43
41
















 BA
2*3

















20
42
13
A
2*3



















42
41
25
BA
2*32*3

75. ‫ولٌكن‬ ‫مصفوفة‬ ‫لٌكن‬c‫ثابتة‬ ‫كمٌة‬,ً‫ٌل‬ ‫كما‬ ‫فنعرف‬ nmaijA *)(
nmcaijcA *)(
cA
‫مثال‬:‫لٌكن‬












12
13
A
2*2
,‫جد‬3A












36
39
3A
2*2

76. ‫مبرهنة‬:‫كمٌات‬ ‫ولٌكن‬ ‫الرتبة‬ ‫نفس‬ ‫من‬ ‫مصفوفتٌن‬ ‫لتكن‬
‫قٌاسٌة‬
AB,nm*hk,
KBKABAk  )(
)()( hAKAKh 
0.0,.1  AAA
hAKAAhK  )(
3
4
2
1
‫فأن‬

77. 1-‫لٌكن‬













111
210
C
‫جد‬:-CBA 243 
2-‫من‬ ‫كل‬ ‫قٌمة‬ ‫جد‬dcba ,,,













cba
ba
2
1
3
,
403
152









 
A ,
510
321












B
‫كان‬ ‫أذا‬












dc
ba
23
2












dc
a
23
13

78. 









 
53
41x
3-‫صحٌحة‬ ‫المعطاة‬ ‫المساواة‬ ‫تجعل‬ ً‫الت‬ ‫المجاهٌل‬ ‫قٌم‬ ‫جد‬
4-‫المصفوفة‬ ‫جد‬A‫المعادلة‬ ‫تحقق‬ ً‫الت‬












4210
5143












514
432
y
x













5103
3211
A

79. ‫تعرٌف‬:‫لٌكن‬nmaijA *)(‫رتبة‬ ‫ذات‬ ‫مصفوفة‬m*n
‫رتبة‬ ‫ذات‬ ‫مصفوفة‬n*r

















mnm
n
aa
aa
A
...........
.
.
.
.............
1
111

















nrn
r
bb
bb
B
.........
.
.
.
..........
1
111
rnbijB *)(

80. ‫للمصفوفة‬ ‫العمودٌة‬ ‫المتجهات‬ ‫و‬B
mAA ...,.........1
rBB ,,.........1
‫أن‬ ‫أي‬:
rmcijAB *)(



















r
m
m
mm
r
BABABA
BABABA
AB
.........
.
.
.........
1
1
2
1
1
1
m*n
‫الصفٌة‬ ‫المتجهات‬ ‫كان‬ ‫اذا‬A
‫فأن‬:

81. 


















nj
j
j
in
ini
i
j
i
b
b
b
aaaBAcij
.
.).......(
2
1
2
1
‫حٌث‬:
‫مالحظة‬:
‫ضرب‬ ‫حاصل‬ ‫إلٌجاد‬A b‫المصفوفة‬ ‫أعمدة‬ ‫عدد‬ ‫ٌكون‬ ‫أن‬ ‫ٌجب‬
A‫صفوف‬ ‫عدد‬ ‫ٌساوي‬B‫الضرب‬ ‫حاصل‬ ‫أٌجاد‬ ‫الٌمكن‬ ‫وبخالفه‬

82. ‫مثال‬:‫لٌكن‬
,
011
321













B
3*2 2*2
‫فأن‬:











23
2221
13
1211
ccc
ccc
3*2












13
21
A
AB

83. ‫أن‬ ‫حٌث‬:
1)1(*)2()1(*)1(
1
1
)21(11 






c
9)0(*)1()3(*)3(
0
3
)13(23 





c
5)1(*)1()2(*)3(
1
2
)13(22 





c
4)1(*)1()1(*)3(
1
1
)13(21 






c
3)0(*)2()3(*)1(
0
3
)31(13 





c
4)1(*)2()2(*)1(
1
2
)21(12 





c

84. ‫فأن‬ ‫وعلٌه‬:









 

954
341
AB
3*2
‫ولكن‬BA‫مصفوفة‬ ‫األعمدة‬ ‫عدد‬ ‫ألنه‬ ‫معرف‬ ‫غٌر‬B‫عدد‬ ‫ٌساوي‬ ‫ال‬
‫المصفوفة‬ ‫صفوف‬A.
‫مالحظة‬:

85. ‫مثال‬:‫لٌكن‬
,
231
512










B
‫فأن‬:















12
21
43
AB
3*3














21
43
A



















1255
150
231510










231
512

86. ‫أن‬ ‫فنالحظ‬AB‫رتبة‬ ‫ذات‬ ‫مصفوفة‬3*3‫الن‬:
3*33*2
2*3
)( ABBA 
‫أٌجاد‬ ‫وٌمكن‬BA‫الن‬:
2*22*3
3*2
)(BAAB 











231
512
BA
3*2 2*3 2*2











124
1515

















12
21
43

87. ACABCBA  )(
‫رتبة‬n*r‫ولتكن‬c‫رتبة‬ ‫ذات‬ ‫مصفوفة‬r*n‫فأن‬:
)()( BCACAB 
‫فأن‬
nnaijA *)(
AAIAI nn 
‫مالحظة‬:‫أعاله‬ ‫المثال‬ ‫من‬ ‫نستنتج‬AB≠BA
‫مبرهنة‬1:‫لتكن‬A‫رتبة‬ ‫ذات‬ ‫مصفوفة‬m*n
‫من‬ ‫كل‬ ‫ولتكن‬B,C‫رتبة‬ ‫ذات‬ ‫مصفوفة‬n*r
‫فان‬:
‫مبرهنة‬2:‫لتكن‬A‫رتبة‬ ‫ذات‬ ‫مصفوفة‬m*n‫ولتكن‬B‫ذات‬ ‫مصفوفة‬
‫مبرهنة‬3:‫لتكن‬‫مربعة‬ ‫مصفوفة‬

88. ‫مثال‬:
T
A T
A



















73
51
02











 
750
312
‫فأن‬
2*3
3*2
‫لتكن‬A‫رتبة‬ ‫ذات‬ ‫مصفوفة‬m*n,‫المصفوفة‬ ‫مبدلة‬ ‫تعرف‬A‫المصفوفة‬ ‫بأنها‬
‫لها‬ ‫المناظرة‬ ‫عمده‬ ‫باال‬ ‫الصفوف‬ ‫أبدال‬ ‫من‬ ‫الحاصلة‬.
‫المصفوفة‬ ‫لمبدلة‬ ‫عادة‬ ‫وٌرمز‬A‫بالرمز‬,‫سعتها‬ ‫واضح‬n*m
‫الموضع‬ ً‫ف‬ ‫العنصر‬ ‫وان‬(i , j)‫من‬ ‫العنصر‬ ‫هو‬A‫الموضع‬ ً‫ف‬(i ,j)
A
T
A 

89. ‫مبرهنة‬1:‫لكل‬A
AA TT
)(
‫مبرهنة‬2:B,A‫الرتبة‬ ‫نفس‬ ‫من‬ ‫مصفوفتٌن‬
TTT
BABA  )(
‫مبرهنة‬3:‫كانت‬ ‫اذا‬A‫رتبة‬ ‫ذات‬m*n‫و‬B‫رتبة‬ ‫ذات‬ ‫مصفوفة‬n*p‫فأن‬
TTT
ABAB )(
‫تعرٌف‬:‫المربعة‬ ‫للمصفوفة‬ ‫ٌقال‬A‫متماثلة‬ ‫بأنها‬symmetric‫أذا‬
‫كانت‬AAT 
‫و‬‫كانت‬ ‫أذا‬ ‫انه‬ ‫اضح‬A‫متماثلة‬,‫فأن‬aijaij 

90. ‫المربعة‬ ‫للمصفوفة‬ ‫ٌقال‬A‫متماثلة‬ ‫بأنها‬,‫تخالفٌه‬skew-symmetric‫أذا‬
ً‫الرئٌس‬ ‫القطر‬ ‫عناصر‬ ‫وان‬ ‫أن‬ ‫أي‬ ‫كان‬
‫صفر‬ ‫تساوي‬.
T
AA aijaij 
‫تعرٌف‬:

91. 1-‫كانت‬ ‫أذا‬:
















 41
13
21
‫جد‬:CABBCA )(),(
A,B‫واحدة‬ ‫رتبة‬ ‫ذات‬ ‫مصفوفتٌن‬,‫ولٌكن‬AB=BA.‫أن‬ ‫اثبت‬
222
.2)( BBAABA 












103
142












112
011
A B C,
 
2-‫لتكن‬:
22
))(( BABABA 
,
1
2

92. 3-‫لٌكن‬:
















511
201
312
‫جد‬:ABBABA TT
,,
3-‫لٌكن‬:
















100
110
111
‫جد‬:2
,AAAT
4-‫المصفوفات‬ ‫باستعمال‬ ‫آالتٌة‬ ‫المعادالت‬ ‫نظام‬ ‫اكتب‬:
42  zyx
B
A, )001(
A
6534  zyx
0 yx

93. ‫حقٌقٌة‬ ‫أعداد‬ ‫عن‬ ‫عبارة‬ ‫القٌمة‬ ‫تكون‬ ‫أن‬ ‫وٌمكن‬.‫دالة‬ ‫اعتباره‬ ‫ٌمكن‬ ‫والمحدد‬
function.‫مربعة‬ ‫مصفوفة‬ ‫منطلقها‬,‫ومستقرها‬
‫فأن‬ ‫وعلٌة‬ ‫الحقٌقٌة‬ ‫األعداد‬
‫حقٌقٌة‬ ‫أعداد‬‫معرفة‬ ‫مصفوفة‬‫دالة‬
‫المحدد‬
‫تعرٌف‬:‫رتبة‬ ‫ذات‬ ‫مربعة‬ ‫مصفوفة‬ ‫لكل‬n*n‫معٌنة‬ ‫قٌمة‬,‫القٌمة‬ ‫وهذه‬
‫محدد‬ ‫اسم‬ ‫علٌها‬ ‫ٌطلق‬DETERMINANT.
RMD=

94. )(ADet A
ً‫ٌل‬ ‫كما‬:
bcad
dc
ba
A 
‫الثانٌة‬ ‫بالمرتبة‬ ‫الخاصة‬ ‫الطرٌقة‬ ‫تسمى‬ ‫الطرٌقة‬ ‫هذه‬.
‫تعرٌف‬:











dc
ba
A
‫رتبة‬ ‫من‬ ‫مصفوفة‬2*2‫المصفوفة‬ ‫محدد‬ ‫نعرف‬A‫والذي‬
‫أو‬ ‫أو‬ ‫له‬ ‫ٌرمز‬)(AD

95. ‫مثال‬:










42
13
‫فأن‬:
)1)(2(
A 
10
A )4)(3( 


96. ‫تعرٌف‬:‫لتكن‬
















33
3231
23
2221
13
1211
aaa
aaa
aaa
‫رتبة‬ ‫ذات‬ ‫مربعة‬ ‫مصفوفة‬3*3
‫نعرف‬ً‫ٌل‬ ‫كما‬: A
32
31
22
21
13
aa
aa
a
  3*3aijA  
A
33
32
23
22
11
aa
aa
a 
33
31
23
21
12
aa
aa
a 

97. ‫الثانٌة‬ ‫الرتبة‬ ‫ذات‬ ‫محددات‬ ‫إلى‬ ‫تحولت‬ ‫حٌث‬.
‫وٌمكن‬)()()()( 131312121111 ADaADaADaAD 
11A
‫المرافق‬ ‫المحدد‬*‫العنصر‬*‫العنصر‬ ‫أشاره‬
11a
A
ji
 )1(
‫المصفوفة‬ ‫من‬ ‫الحاصلة‬ ‫المصففة‬ ‫ٌمثل‬A‫العمود‬ ‫و‬ ‫األول‬ ‫الصف‬ ‫حذف‬ ‫بعد‬
‫للعنصر‬ ‫المرافق‬ ‫المحدد‬ ‫وٌسمى‬ ‫األول‬
‫الصٌغة‬ ‫تكون‬ ‫أو‬ ‫العامة‬ ‫الطرٌقة‬ ‫وهذه‬,‫باالعتماد‬ ‫محدد‬ ‫أي‬ ‫فك‬ ‫ٌمكن‬
‫وتكون‬ ‫عمود‬ ‫أو‬ ‫صف‬ ‫أي‬ ‫على‬
‫أشاره‬‫ٌكون‬ ‫أن‬ ‫أما‬ ‫العنصر‬‫أشاره‬‫العنصر‬j , i‫تكون‬

98. ‫كان‬ ‫فإذا‬i+j‫سالبة‬ ‫تكون‬ ‫فردي‬,‫موجبة‬ ‫تكون‬ ً‫زوج‬ ‫كانت‬ ‫إذا‬ ‫أما‬
‫اإلشارات‬ ‫جدول‬ ‫من‬ ‫أو‬



















‫االصفار‬ ‫من‬ ‫عدد‬ ‫اكبر‬ ‫ٌتضمن‬ ‫عمود‬ ‫أو‬ ‫صف‬ ‫نختار‬ ‫أن‬ ‫ٌفضل‬.

99. ‫الثالثة‬ ‫الرتبة‬ ‫من‬ ‫محدد‬ ‫قٌمة‬ ‫إلٌجاد‬ ‫الخاصة‬ ‫الطرٌقة‬
333231
232221
131211
aaa
aaa
aaa
A 
3231
2221
1211
aa
aa
aa
322113312312332211 aaaaaaaaa 
122133112332132231 aaaaaaaaa 

100. ‫مثال‬:‫لٌكن‬

















432
141
201
A
‫فأن‬:
32
41
2
42
11
0
43
14
1)( AD
310316)83(20316 

101. ‫أو‬:
432
141
201
A
32
41
01
03166016 
3

102. ‫لٌكن‬:




















44434241
34333231
24232221
14131211
aaaa
aaaa
aaaa
aaaa
A 4*4)(aij

103. 444341
343331
242321
12
444342
343332
242322
11
aaa
aaa
aaa
a
aaa
aaa
aaa
aA 
‫األول‬ ‫الصف‬ ‫إلى‬ ‫نسبة‬ ‫نعرف‬
‫الثالثة‬ ‫المرتبة‬ ‫من‬ ‫محددات‬ ‫إلى‬ ‫تحولت‬ ‫حٌث‬.
A
434241
333231
232221
14
444241
343231
242221
13
aaa
aaa
aaa
a
aaa
aaa
aaa
a 

104. ‫اإلشارات‬ ‫جدول‬ ‫ٌكون‬ ‫حٌث‬
























‫الرتبة‬ ‫ذات‬ ‫المحددات‬ ‫قٌمة‬ ‫أٌجاد‬ ‫ٌمكن‬ ‫األسلوب‬ ‫وبنفس‬(n)‫من‬ ‫أكثر‬(4)....

105. ‫صف‬ ‫عناصر‬ ‫ضربت‬ ‫أذا‬(‫عمود‬ ‫أو‬)‫المصفوفة‬A‫عدد‬ ً‫ف‬X‫المحدد‬ ‫فقٌمة‬
ً‫ه‬ ‫الجدٌد‬. AX

















101
012
261
A

















101
012
6183
B ‫ولٌكن‬
‫وسنذكر‬ ‫المحددات‬ ‫أٌجاد‬ ً‫ف‬ ‫تساعدنا‬ ً‫الت‬ ‫المحددات‬ ‫خواص‬ ‫أهم‬ ‫سنذكر‬
‫بمثال‬ ‫منها‬ ‫كل‬ ‫وسنوضح‬ ‫براهٌن‬ ‫بدون‬ ‫الخواص‬.
1-‫األولى‬ ‫الخاصٌة‬:
‫مثال‬:‫لٌكن‬

106. ‫حٌث‬B‫المصفوفة‬A‫األول‬ ‫الصف‬ ‫عناصر‬ ‫ضرب‬ ‫بعد‬*3
01
12
6
11
02
18
10
01
3



B
‫صف‬ ‫عناصر‬ ‫جمٌع‬ ‫اشتركت‬ ‫أذا‬(‫عمود‬ ‫أو‬)‫اخراجة‬ ‫ٌمكن‬ ‫معٌن‬ ‫بمقدار‬
‫المحدد‬ ‫من‬ ‫مشترك‬ ‫كعامل‬
A3
 











 

01
12
2
11
02
6
10
01
13
‫نالحظ‬ ‫هذا‬ ‫من‬:

107. ‫المصفوفة‬ ‫محدد‬A‫المبدلة‬ ‫محدد‬ ‫ٌساوي‬.
T
AA 
‫مثال‬:‫كان‬ ‫أذا‬


















141
131
502
T
A


















115
430
112
A‫فأن‬
‫وأن‬
33,33  AAT
2-‫الثانٌة‬ ‫الخاصٌة‬:
‫أن‬ ‫أي‬:

108. ‫صف‬ ‫عناصر‬ ‫جمٌع‬ ‫كان‬ ‫أذا‬(‫عمود‬ ‫أو‬)‫للمصفوفة‬ ‫ما‬A‫أصفارا‬
‫فأن‬0A
‫مثال‬:‫كان‬ ‫ذا‬




















165
243
000
A
0
65
43
0
15
23
0
16
24
0 



A
3-‫الثالثة‬ ‫الخاصٌة‬:

109. ‫صفان‬ ‫أبدل‬ ‫أذا‬(‫عمودان‬ ‫أو‬)‫األخر‬ ‫مكان‬ ‫احدهما‬ ‫متجاوران‬.‫قٌمة‬ ‫فأن‬
‫فقط‬ ‫إشارتها‬ ‫تتغٌر‬ ‫المحدد‬.
‫مثال‬:‫كان‬ ‫أذا‬

















103
211
120
A
17A ‫فأن‬:
ً‫ه‬ ‫الجدٌدة‬ ‫فالمصفوفة‬ ‫األخر‬ ‫مكان‬ ‫منهما‬ ‫كل‬ ‫والثالث‬ ً‫الثان‬ ‫العمود‬ ‫أبدلنا‬ ‫لو‬

















013
121
210
B
BA  17B ‫فأن‬:‫منها‬:
4-‫الرابعة‬ ‫الخاصٌة‬:

110. ‫صفٌن‬ ‫تطابق‬ ‫أذا‬(‫عمودٌن‬ ‫أو‬)‫المصفوفة‬ ‫من‬ ‫مضاعفاتهما‬ ‫من‬ ‫أو‬A.
‫فأن‬0A
‫مثال‬:‫كان‬ ‫أذا‬




















123
354
123
A
0A ‫فأن‬:
5-‫الخامسة‬ ‫الخاصٌة‬:

111. ‫مثال‬:




















123
354
123
A
‫العلٌا‬ ‫الرتب‬ ‫من‬ ‫المحدد‬ ‫قٌمة‬ ‫إٌجاد‬ ‫عملٌة‬ ‫علٌنا‬ ‫تسهل‬ ‫الخاصٌة‬ ‫وهذه‬.
6-‫صف‬ ‫عناصر‬ ‫ضربت‬ ‫أذا‬(‫عمود‬ ‫أو‬)‫عدد‬ ً‫ف‬ ‫المصفوفة‬X.‫إلى‬ ‫وأضٌفت‬
‫صف‬ ‫من‬ ‫لها‬ ‫المناظرة‬ ‫العناصر‬(‫عمود‬ ‫أو‬)‫تتغٌر‬ ‫ال‬ ‫المحدد‬ ‫فقٌمة‬ ‫أخر‬

112. ‫الثالث‬ ‫الصف‬ ‫بضرب‬(-1)*‫المحدد‬ ‫ٌكون‬ ‫األول‬ ‫للصف‬ ‫واضافتة‬
0
123
354
000


A
‫عمود‬ ‫أو‬ ‫صف‬ ‫عناصر‬ ‫جمٌع‬ ‫كانت‬ ‫أذا‬=‫ا‬‫ا‬‫صفر‬
‫المحدد‬ ‫قٌم‬ ‫فأن‬=‫ا‬‫ا‬‫صفر‬

113. 7-‫القطر‬ ‫عناصر‬ ‫ضرب‬ ‫حاصل‬ ‫ٌساوي‬ ‫المربعة‬ ‫القطرٌة‬ ‫المصفوفة‬ ‫محدد‬.
abc
c
b
a

00
00
00
‫ٌساوي‬ ‫الواحدٌة‬ ‫المصفوفة‬ ‫محدد‬1.
1nI
‫مثال‬:
‫نتٌجة‬:
‫أن‬ ‫أي‬

114. 8-‫كانت‬ ‫أذا‬B,A‫رتبة‬ ‫ذات‬ ‫مربعتٌن‬ ‫مصفوفتٌن‬n*n.
‫محددٌهما‬ ‫ضرب‬ ‫حاصل‬ ‫ٌساوي‬ ‫ضربهما‬ ‫حاصل‬ ‫محدد‬ ‫فأن‬
BAAB 
‫نتٌجة‬:
1
A
1
A

115. ‫الخطٌة‬ ‫المعادالت‬ ‫أنظمة‬ ‫حل‬ ً‫ف‬ ‫هو‬ ‫للمحددات‬ ‫المهمة‬ ‫االستخدامات‬ ‫من‬
‫بالصٌغة‬ ‫المعادالت‬ ‫كانت‬ ‫فإذا‬
11212111 ....... bxaxaxa nn 


mnmnm bxaxaxa  ......2211

116. ً‫ٌل‬ ‫كما‬ ‫المصفوفات‬ ‫بصٌغة‬ ‫المعادلة‬ ‫نظام‬ ‫كتابة‬ ‫ٌمكن‬:
















mnm
n
n
aa
aa
aa
......
.
.
.......
.......
1
221
111
‫المعامالت‬ ‫مصفوفة‬ ‫تسمى‬ ‫فالمصفوفة‬
‫سنتعرف‬ ‫البند‬ ً‫ف‬ ‫أما‬ ‫الحذف‬ ‫أو‬ ‫التعوٌض‬ ‫بطرٌقة‬ ‫أما‬ ‫اآلتٌة‬ ‫المعادالت‬ ‫حل‬ ‫ٌمكن‬
‫أو‬ ‫المحددات‬ ‫باستخدام‬ ‫المعادالت‬ ‫حل‬ ‫على‬
nmaijA *)(
















mb
b
b
.
.
2
1
















mx
x
x
.
.
2
1

‫كرامر‬ ‫قاعدة‬Cramer rule

117. ‫الصٌغة‬ ‫حسب‬ ‫المجهولة‬ ‫القٌم‬ ‫حل‬ ‫على‬ ‫تنص‬ ‫حٌث‬
ni
A
A
x i
i ,.......2,1, 
‫العمود‬ ‫أبدال‬ ‫بعد‬ ‫المعادالت‬ ‫محدد‬ ‫أن‬ ‫حٌث‬(i)‫الثابتة‬ ‫بالقٌم‬
‫مثال‬1:‫المحددات‬ ‫باستخدام‬ ‫اآلتٌة‬ ‫الخطٌة‬ ‫المعادالت‬ ‫نظام‬ ‫حل‬
523  yx
0 yx
iA

118. 5
11
23










 
 AA
2,1 i
A
A
x i
i
5
10
25
11 









 
 AA
1
5
51

A
A
x

119. 1
5
52



A
A
y
‫و‬‫األٌمن‬ ‫الطرف‬ ‫مع‬ ‫تطابقها‬ ‫وبٌان‬ ‫المعادلة‬ ً‫ف‬ ‫بالتعوٌض‬ ‫الحل‬ ‫من‬ ‫التحقق‬ ‫ٌمكن‬
5
01
53
22 










 AA

120. ‫مثال‬:‫المحددات‬ ‫باستخدام‬ ً‫األت‬ ‫الخطٌة‬ ‫المعادالت‬ ‫نظام‬ ‫حل‬
32  zyx
1086  zyx
34  yx
‫الحل‬:















 

014
186
112
A

121. 28
14
12
1
14
86
)1( A
14
013
1810
113
1 

A
28
034
1106
132
2 

A

122. 28
314
1086
312
3 A
1
1
28
141

A
A
x
1
28
282

A
A
y 1
28
283



A
A
z

123. 1-‫التالٌة‬ ‫المحددات‬ ‫قٌم‬ ‫جد‬
200
010
004
137
110
000
0211
1021
0025

1
32

124. 2-‫أن‬ ‫اثبت‬
))()((
1
1
1
2
2
2
bcacab
cc
bb
aa

3-‫أن‬ ‫اثبت‬ ‫المحدد‬ ‫فك‬ ‫بدون‬
0
11
11
11




bca
acb
cba

125. 4-‫المحدد‬ ‫باستخدام‬ ‫اآلتٌة‬ ‫الخطٌة‬ ‫المعادالت‬ ‫أنظمة‬ ‫حل‬(‫كرامر‬ ‫طرٌقة‬)
1 zy
0 zyx
03  zyx
zyx 332 
123  yzx
zxy 223 
1
2

126. ‫لتكن‬A‫المرتبة‬ ‫من‬ ‫مربعة‬ ‫مصفوفة‬n.‫للمصفوفة‬ ‫ٌقال‬B‫أنها‬
‫المصفوفة‬ ‫عكس‬A‫كان‬ ‫أذا‬ ‫وفقط‬ ‫أذا‬
‫أن‬ ‫ٌقال‬ ‫وعندئذ‬A‫المصفوفة‬ ‫لمعكوس‬ ‫وٌرمز‬ ‫للعكس‬ ‫قابلة‬A‫بالرمز‬A-1
‫معكوس‬ ‫المربعة‬ ‫للمصفوفة‬ ‫ٌكون‬ ‫ال‬ ‫قد‬ ‫انه‬ ‫نؤكد‬ ‫أن‬ ‫ٌجب‬,‫كل‬ ‫لٌس‬ ‫أي‬
‫للعكس‬ ‫قابلة‬ ‫مربعة‬ ‫مصفوفة‬
‫مبرهنة‬:-‫لتكن‬A,B‫المرتبة‬ ‫من‬ ‫مربعتٌن‬ ‫مصفوفتٌن‬n,‫قابلة‬ ‫منهما‬ ‫كل‬ ‫ولتكن‬
‫فأن‬ ‫للعكس‬AB‫وان‬ ‫للعكس‬ ‫قابلة‬(AB)-1=B-1 A-1
nIBAAB 
‫تعرٌف‬:-
‫من‬ ‫له‬ ‫لما‬ ‫المصفوفات‬ ً‫ف‬ ‫المهمة‬ ‫المواضٌع‬ ‫من‬ ‫المربعة‬ ‫المصفوفة‬ ‫عكس‬
‫الخطٌة‬ ‫المعادالت‬ ‫حل‬ ً‫ف‬ ‫فائدة‬.

127. ‫المصفوفة‬ ‫معكوس‬ ‫إلٌجاد‬ ‫طرق‬ ‫عدة‬ ‫هناك‬A‫ٌمكن‬ ‫أذا‬ ‫للعكس‬ ‫القابلة‬
‫رتبة‬ ‫من‬ ‫المصفوفات‬ ‫إلٌجاد‬ ‫التعرٌف‬ ‫استخدام‬2*2‫أو‬3*3‫من‬ ‫ولكن‬
‫ذلك‬ ‫من‬ ‫أعلى‬ ‫رتبها‬ ‫كانت‬ ‫أذا‬ ‫الصعوبة‬.
‫طرٌقة‬ ‫أو‬ ‫المحددات‬ ‫طرٌقة‬ ‫استخدام‬ ‫ٌمكن‬ ‫أو‬‫كاوسن‬Guassn.
‫التعرٌف‬ ‫صٌغة‬:-
𝐷 𝐴 = 𝐴 = 𝑎𝑑 − 𝑏𝑐 ≠ 0
‫لٌكن‬𝐴 =
𝑎 𝑏
𝑐 𝑑
‫مرتبة‬ ‫ذات‬ ‫مربعة‬ ‫مصفوفة‬2*2
‫ولٌكن‬:
‫مصفوفة‬ ‫أٌجاد‬ ‫هو‬ ‫هدفنا‬𝑥 =
𝑥 𝑦
𝑧 𝑤

128. IXAAX 










dc
ba
01  bwaybzax
‫المصفوفة‬ ً‫ف‬ ‫نضعه‬ ‫ثم‬ ‫المجاهٌل‬ ‫نوجد‬x‫تمثل‬ ً‫والت‬
(‫المصفوفة‬ ‫معكوس‬A)
wzyx ,,,1
A
‫أن‬ ‫بحٌث‬:










10
01











wz
yx
‫وان‬:
10  dwcydzcx

129. =
𝐴 =
2 1
4 3
𝑥 𝑦
𝑧 𝑤
‫الحل‬:-
2 1
4 3
𝑥 𝑦
𝑧 𝑤
1 0
0 1
2𝑥 + 𝑧 = 1 2𝑦 + 𝑤 = 0
4x+3z=0 , 4y+3w=1
‫على‬ ‫نحصل‬ ‫المعادالت‬ ‫وبحل‬
𝑥 = 1, 𝑦 = −
1
2
,z=-1,w=1
‫نفرض‬A-1=
‫مثال‬1:-‫لٌكن‬,‫فجد‬1-A

130. 01.1
3
1
.3 A
‫فأن‬ ‫وعلٌه‬:-
‫مثال‬2:-
‫الحل‬:-
𝐴;1
=
1 − 1
2
−1 1
𝐴 =
3 1
1 1
3
‫كان‬ ‫اذا‬,‫جد‬𝐴;1
‫الن‬ ‫موجود‬ ‫غٌر‬ 𝐴;1

131. ‫كانت‬ ‫أذا‬ ‫الطرٌقة‬ ‫وبنفس‬A‫رتبة‬ ‫ذات‬ ‫مربعة‬ ‫مصفوفة‬3*3,
│A│≠0,‫خطٌة‬ ‫لمعادالت‬ ‫أنظمة‬ ‫ثلث‬ ‫على‬ ‫سنحصل‬,‫وكل‬
‫مجاهٌل‬ ‫ثلث‬ ‫ٌضم‬ ‫نظام‬,‫على‬ ‫نحصل‬ ‫الثلث‬ ‫األنظمة‬ ‫هذه‬ ‫وبحل‬
A-1.
‫أو‬ ‫العامة‬ ‫الصٌغة‬ ً‫سنعط‬(‫العام‬ ‫القانون‬)‫إلٌجاد‬‫مصفوفة‬ ‫معكوس‬
‫رتبة‬ ‫ذات‬ ‫مربعة‬n*n.
‫لتكن‬(A=(aij‫رتبة‬ ‫ذات‬ ‫مربعة‬ ‫مصفوفة‬n*n,‫ولٌكن‬
d(a)≠0.‫فأن‬A‫للكسر‬ ‫قابلة‬.

132. ),1(
)(
)()1(1
nji
AD
AijD
A
TJI





 



A
Aadj
A
)(1

‫وان‬:
‫أو‬:
‫من‬ ‫الحاصل‬ ‫المصفوفة‬ ‫ٌمثل‬ ‫أن‬ ‫حٌث‬A‫الصف‬ ‫حذف‬ ‫بعد‬i
‫والعمود‬j.‫العنصر‬ ‫محدد‬ ‫وٌسمى‬aij
Aij

133. 















432
101
021
32
01
0
42
11
2
43
10
1 A
‫مثال‬:-‫جد‬‫المصفوفة‬ ‫معكوس‬
‫الحل‬:-
42
11
)( 12 AD
3
43
10
)( 11 AD
743 
A

134. 3
32
01
)( 13 AD
1
32
21
)( 23 AD
4
42
01
)( 22 AD
8
43
02
)( 21 AD

135. 2
10
02
)( 3 1 AD





















7
2
7
1
7
3
7
1
7
4
7
2
7
2
7
8
7
3




















212
148
323
7
11


A
2
01
21
)( 33 AD
1
11
01
)( 32 AD
𝑇

136. ‫التالٌة‬ ‫المصفوفات‬ ‫معكوس‬ ‫جد‬:-
𝐴 =
2 1 2
0 3 − 1
4 1 1
𝐵 =
2 4 3
−1 3 0
0 2 1
C=















3000
0100
0020
0004

137. ‫المحددات‬ ‫بند‬ ً‫ف‬ ‫ذكرت‬ ‫كما‬ ‫معادالت‬ ‫منظومة‬ ‫لدٌنا‬ ‫لتكن‬
= BXA
‫إن‬ ‫حٌث‬A=‫المعادالت‬ ‫مصفوفة‬.
X=‫المتغٌرات‬ ‫متجه‬.
B=‫الثانٌة‬ ‫القٌمة‬ ‫متجه‬.
‫عندما‬‫تكون‬A‫قابلة‬‫للعكس‬
B1-= AXA1-A
X = A-1 B

138. ‫مثال‬:-‫أآلتٌه‬ ‫الخطٌة‬ ‫المعادالت‬ ‫منظومة‬ ‫لحل‬ ‫المصفوفة‬ ‫معكوس‬ ‫طرٌقة‬ ‫استخدم‬
X1 + X2 + X3 = 7
X1 + 2X2 + 3X3 = 16
X1 + 3X2 + 4X3 = 22
‫الحل‬:-‫مرتبة‬ ‫المعادالت‬
ً‫التال‬ ‫بالشكل‬ ‫بالمصفوفة‬ ‫المعادالت‬ ‫منظومة‬ ‫عن‬ ‫التعبٌر‬ ‫ٌمكن‬
1 1 1
1 2 3
1 3 4
𝑥1
𝑥2
𝑥3
=
7
16
22
A 𝑋= 𝑏
𝑥1
𝑥2
𝑥3
=
1 1 1
1 2 3
1 3 4
-1 7
16
22

139. Mij
ji
ijij

 )1(
‫المرافقة‬ ‫المعامالت‬ ‫مصفوفة‬ ‫أٌجاد‬ ‫ٌتطلب‬adjA
‫أن‬ ‫حٌث‬A‫فأن‬ ‫لذلك‬ ‫متماثلة‬ ‫مصفوفة‬:
A
Aadj
A
)(1

1)34(
41
31
)1(
21
2112 


1)98(
43
32
)1(
11
11 



140. 1)23(
31
21
)1(
31
3113 


1)12(
21
11
)1(
33
33 


2)13(
31
11
)1(
32
3223 


3)14(
41
11
)1(
22
22 



141. 



















121
231
111
)( BBAadj
‫فأن‬ ‫وعلٌه‬:
ً‫ٌعن‬ ‫وهذا‬:1,3,3 123  xxx










3
3
1










22
16
7



















121
231
111










3
2
1
x
x
x



















121
231
111

A
Aadj
A
)(1

1)1)(1()1)(1()1)(1(131312121111   aaaA
 

142. ‫مثال‬2:-‫الخطٌة‬ ‫المعادالت‬ ‫منظومة‬ ‫لحل‬ ‫المصفوفة‬ ‫معكوس‬ ‫طرٌقة‬ ‫استخدم‬
‫طرٌقة‬ ‫باستخدام‬ ‫النتٌجة‬ ‫صحة‬ ‫من‬ ‫تحقق‬ ‫ثم‬ ‫اآلتٌة‬‫كرامر‬(‫المحددات‬. )
-2x1 + 3x2 – 3 = x3
x1 + 2x3 + 4x2 = 4
3x1 – 2x2 + 4x3 +2 = 0
‫الحل‬:-‫المعادالت‬ ‫ترتٌب‬
-2x1 + 3x2 – x3 = 3
x1 + 4x2 + 2x3 = 4
3x1 – 2x2 + 4x3 = -2

143. ‫بالمصفوفات‬ ‫المعادالت‬ ‫عن‬ ‫نعبر‬


















423
241
132










 2
4
3


















423
241
132










3
2
1
x
x
x
BAx
1



 BXA










2
4
3











3
2
1
x
x
x


144. Mij
ji
ij

 )1(
‫أٌجاد‬ ‫ٌتطلب‬A-1
adj (A)=1-A
│A│
‫الصٌغة‬ ‫وفق‬ ‫المرافقة‬ ‫المعادالت‬ ‫مصفوفة‬ ‫أٌجاد‬ ‫ٌتطلب‬
𝐵 =
20 2 14
−10 − 5 5
10 3 − 11

145. ‫نجد‬ ‫ثم‬│A│
20131312121111   aaaA
𝑎𝑑𝑗 𝐴 = 𝐵 𝑇
=
20 − 10 10
2 − 5 3
14 5 − 11
𝐴;1
=
−1 1
2
− 1
2
− 1
10
1
4
− 3
20
7
10
− 1
4
11
20

146. 𝑋1
𝑋2
𝑋3
=
−1 1
2
− 1
2
− 1
10
1
4
− 3
20
7
10
− 1
4
11
20
3
4
−2
=
0
1
0
ً‫ٌعن‬ ‫وهذا‬𝑋3=0, 𝑋2 = 1, 𝑋1=0
‫اٌجاد‬ ‫فالمطلوب‬ ‫المحددات‬ ‫باستخدام‬ ‫اما‬𝐴3 , 𝐴2 , 𝐴1 , 𝐴
𝐴 =-20

147. 𝐴1 =
3 3 − 1
4 4 2
−2 − 2 4
=0,
𝐴2 =
−2 3 − 1
1 4 2
3 − 2 4
=-20
𝐴3 =
−2 3 3
1 4 4
3 − 2 − 2
=0

148. 𝑋1=
𝑋2=
𝑋3=
𝐴1
𝐴
=
𝐴2
𝐴
=
𝐴3
𝐴
=
0
;20
= 0
0
;20
= 0
;20
;20
= +1
𝑋1=0
𝑋2=+1
𝑋3=0
‫المصفوفة‬ ‫معكوس‬ ‫باستخدام‬ ‫علٌها‬ ‫حصلنا‬ ً‫الت‬ ‫النتٌجة‬ ‫نفس‬ ً‫وه‬

149. ‫السؤال‬ ً‫ف‬ ‫المعادالت‬ ‫منظومة‬ ‫حل‬
‫الرابع‬‫صفحة‬(45)‫باستخدام‬
‫المصفوفة‬ ‫معكوس‬

150. ‫بصٌغة‬ ‫تكتب‬ ً‫الت‬ ‫الدوال‬ ‫أن‬((y= f(x)‫الصٌغة‬ ‫بهذه‬ ‫تكتب‬ ً‫الت‬ ‫والدالة‬
‫المتغٌر‬ ‫ٌكتب‬ ‫حٌث‬ ‫صرٌحة‬ ‫دالة‬ ‫تسمى‬y‫بداللة‬ ‫وواضحة‬ ‫جلٌة‬ ‫بصورة‬
‫المتغٌر‬x.
‫المتغٌرٌن‬ ‫بٌن‬ ‫علقات‬ ‫هناك‬ ‫توجد‬ ‫ولكن‬y,x‫عن‬ ‫التعبٌر‬ ‫الصعب‬ ‫من‬y
‫بداللة‬x.
‫التالٌة‬ ‫العلقات‬ ‫مثل‬y2x + xy2 = 3
X2 + y2 = x y + 2
‫الدوال‬ ‫مشتقة‬ ‫وإلٌجاد‬ ‫الضمنٌة‬ ‫الدوال‬ ‫اسم‬ ‫علٌها‬ ‫ٌطلق‬ ‫الدوال‬ ‫من‬ ‫النوع‬ ‫وهذا‬
‫اآلتٌة‬ ‫الطرٌقة‬ ‫نستخدم‬ ‫الضمنٌة‬
((‫إلى‬ ‫بالنسبة‬ ‫المعادلة‬ ‫حدود‬ ‫من‬ ‫حد‬ ‫كل‬ ‫نشتق‬x‫نعامل‬ ‫حٌث‬y‫إلى‬ ‫كدالة‬x
‫نستخرج‬ ‫وبعدها‬d y / d x))
ً‫الضمن‬ ‫التفاضل‬ ‫بطرٌقة‬ ‫الطرٌقة‬ ‫هذه‬ ‫وتدعى‬

151. 1 𝑋2
+
1
2
xy + 𝑦3
=0
‫مثال‬:‫األتٌة‬ ‫الدوال‬ ‫من‬ ‫لكل‬ ‫جد‬dx
dy
03)1.()1.(
2
1
2
2





dx
dy
yy
dx
dy
xx
03
22
2
2

dx
dy
y
y
dx
dyx
x
yx
dx
dy
y
dx
dy
x  46
2
2
6
4
yx
yx
dx
dy




152. 2
3
xxyyx 7104 233

70)1()2(123 222
 y
dx
dy
yx
dx
dy
yx
73)212( 222
 xyxyy
dx
dy
xyy
xy
dx
dy
212
73
2
22



034 22
 xyxyx
0)1()2()1(338 2
 y
dx
dy
yxy
dy
dx
xx
yxy
dx
dy
xy
dx
dy
x 3823 2

yxyxyx
dx
dy
38)23( 2

xyx
yxy
dy
dx
23
382




153. 1
2
3
4
5
6
7
dx
dy
‫جد‬‫اآلتٌة‬ ‫الدوال‬ ‫من‬ ‫لكل‬:
52
3
)2
1
( x
x
xy 
22
4)1( xxy 
x
x
y
1
5


yyxyx 52 33

yx
yx
x
2
22



34
2)32( yx 
xxu
u
y 25,
1 2
3


154. 3
2
1
‫أخر‬ ‫إلى‬ ‫ضلع‬ ‫نسبة‬ ‫عن‬ ‫عبارة‬ ً‫ه‬,‫الزاوٌة‬ ‫القائم‬ ‫المثلث‬ ً‫فف‬a b c
a b
c
ac
bc
xy  sin
ac
ab
xy  cos
ab
bc
x
x
xy 
cos
sin
tan
‫المثلثٌة‬ ‫النسب‬:

155. 1
2
3
‫التالٌة‬ ‫األمثلة‬ ً‫ف‬ ‫كما‬ ‫مثلثٌه‬ ‫دالة‬ ‫تدعى‬ ‫المثلثٌة‬ ‫النسب‬ ‫هذه‬ ‫من‬ ‫أكثر‬ ‫أو‬ ‫واحده‬ ‫على‬ ‫تحتوي‬ ‫دالة‬ ‫كل‬:-
)2cos(4)3sin( xxy 
)3sin(3)4cot( xxy 
xxyy csc)cot( 
4
6
5
ab
ac
x
xy 
cos
1
sec
bc
ac
x
xy 
sin
1
csc
bc
ab
x
x
x
xy 
sin
cos
tan
1
cot

156. 1
2
3
4
5
1cossin 22
 xx
xx 22
sec1tan 
xx 22
csc1cot 
xxx cossin22sin 
 xx 2cos1
2
1
sin2


157. 6
7
8
9
 xx 2cos1
2
1
cos2

xxx 22
sincos2cos 
;
sec
1
cos;
csc
1
sin
x
x
x
x 
x
x
x
x
x
x
sin
cos
cot,
cos
sin
tan 
);cos()cos();sin()sin( xxxx 
);cot()cot();tan()tan( xxxx 
);csc()csc(;sec)sec( xxxx 

158. 1
1‫أن‬ ‫حٌث‬ ‫كانت‬ ‫أذا‬‫فأن‬: )sin(uy )(xfu 
d
du
u
dx
dy
).cos(
‫مثال‬:‫التالٌة‬ ‫الدوال‬ ‫من‬ ‫لكل‬ ‫اوجد‬dx
dy
)3sin( xy 
3).3cos( x
dx
dy

)3cos(3 x

159. 2
3
)1sin( 2
 xy
2
1
2
)1sin(  xy
xxx
dx
dy
2.)1(
2
1
.)1cos( 2
1
22
1
2


1
)1cos(
2
2



x
xx
)6(sin2
xy 
  6).6cos(.)6sin(2 xxy 
)6cos().6sin(12 xx

160. 2
1
2
‫أن‬ ‫حٌث‬ ‫كانت‬ ‫أذا‬‫فأن‬: )cos(uy )(xfu 
dx
du
u
dx
dy
).sin(
)
1
cos( 2
x
xy 
)cos( 2
1
2

 xxy
)
2
1
2).(sin( 2
3
2
1
2

 xxxx
dx
dy
)3cos(
1
x
y 
  2
1
)3cos(

 xy

161. 3
3
))5cos(sin( xy 
5).5cos()).5sin(sin( xx
dx
dy

)5cos().5sin(sin(5 xx
‫أن‬ ‫حٌث‬ ‫كانت‬ ‫أذا‬‫فأن‬: )tan(uy )(xfu 
dx
du
u
dx
dy
).(sec2

  )3).3sin(.()3cos(
2
1 2
3
xx
dx
dy


  2
3
)3cos()3sin(
2
3 
 xx

162. 4
5
6
‫أن‬ ‫حٌث‬ ‫كانت‬ ‫أذا‬‫فأن‬: )sec(uy )(xfu 
dx
du
uu
dx
dy
).tan().sec(
‫أن‬ ‫حٌث‬ ‫كانت‬ ‫أذا‬‫فأن‬:
‫أن‬ ‫حٌث‬ ‫كانت‬ ‫أذا‬‫فأن‬:
)cot(uy )(xfu 
dx
du
u
dx
dy
).(csc2

)csc(uy )(xfu 
dx
du
uu
dx
dy
).cot().csc(

163. 1-
2-
3-
4-
‫جد‬
dx
dy
‫االتٌة‬ ‫الدوال‬ ‫من‬ ‫لكل‬
)(sin)2sin( 22
xxxxy 
1
)2cos(
2


x
x
y
)3(sin2)3(cos2 22
xxy 
)2cos()2sin( xyyx 

164. 5-
6-
7-
9-
8-
22
))5(csc()sec( xxy 
1)4(tan
1
2


x
y
)2sin()sin(2
yyx 
30)tan(2
 xyx
))2cot(sin( xy 

165. -1
-2Ln
r
a annLog 
‫العدد‬ ‫لنتج‬ ‫لألساس‬ ‫كأس‬ ‫رفع‬ ‫لو‬ ‫الذي‬ ‫العدد‬ ‫ذلك‬ ‫هو‬ ‫اللوغارٌتم‬ ‫تعرٌف‬.‫وٌكون‬
‫اللوغارٌتمات‬ ‫من‬ ‫نوعان‬ ‫وهناك‬:‫ــــ‬
‫األساس‬ ‫ٌكون‬ ‫وفٌه‬ ‫االعتٌادي‬ ‫اللوغارٌتم‬10‫له‬ ‫وٌرمز‬‫ب‬
‫ب‬ ‫له‬ ‫وٌرمز‬ ‫األساس‬ ‫ٌكون‬ ‫وفٌه‬ ً‫الطبٌع‬ ‫اللوغارٌتم‬
Log

166. ‫تفاضل‬(‫المشتقة‬)‫دالة‬‫حٌث‬ ‫كانت‬ ‫إذا‬ ً‫الطبٌع‬ ‫اللوغارٌتم‬‫إن‬𝒖 = 𝒇 𝒙
vLnuLnvuLn  )(
dx
du
udx
dy
.
1

uLnnuLn n

vLnuLn
v
u
Ln )(
1
3
2
𝒚 = 𝑳𝒏(𝒖)
‫فأن‬:

167. 2
232
)1)(1(  xxLny
232
)1()1(  xLnxLny
)1(2)1( 32
 xLnxLn
1
6
1
2
3
2
2




x
x
x
x
dx
dy
‫مثال‬:-‫التالٌة‬ ‫الدوال‬ ‫من‬ ‫لكل‬ ‫جد‬:-
)2( 2
xxLny 
)22.(
2
1
2


 x
xxdx
dy
1
𝑑𝑦
𝑑𝑥
= 𝑦 𝑥
𝑥:2
:𝐿𝑛(𝑥:2)
‫فأن‬ ‫اللوغارٌتم‬ ‫خواص‬ ‫بتطبٌق‬

168. 3 )2(cos xLny 
)2cos(
)2sin(2
)2).2sin(.(
)2cos(
1
x
x
x
xdx
dy

)2tan(2 x
‫العملٌات‬ ‫ٌبسط‬ ‫اللوغارٌتم‬‫اللوغارٌتم‬ ‫نأخذ‬ ‫متغٌر‬ ‫أس‬ ‫متغٌر‬ ‫ٌكون‬ ‫وعندما‬
‫للطرفٌن‬‫نشتق‬ ‫ثم‬‫الطرفٌن‬
4
x
xy )2( 

169. x
xLnLny )2( 
)2(  xxLn
1).2()1.(
2
1
.
1


 xLn
x
x
dx
dy
y








 )2(
2
xLn
x
x
y
dx
dy








 )2(
)2(
)2( xLn
x
x
x
x

170. Lnyx 
x
ey 
2121
. xxxx
eee 

‫لألساس‬ ‫آسٌة‬ ‫دالة‬ ‫تدعى‬ ‫وهذه‬e‫واألس‬x‫اللوغارٌتمٌة‬ ‫الدالة‬ ‫معكوس‬ ً‫ه‬ ‫اآلسٌة‬ ‫والدالة‬
‫فان‬ ‫كانت‬ ‫إذا‬
ueLn u

ue
uLn

x
x
e
e
1

21
2
1
xx
x
x
e
e
e 

1-
2- 5-
4-
3-

171. 1
‫اآلسٌة‬ ‫الدالة‬ ‫مشتقة‬:-‫أن‬ ‫حٌث‬ ‫كانت‬ ‫أذا‬
u
ey )(xfu ‫فأن‬:
dx
du
e
dx
dy u
.
‫أمثلة‬:‫جد‬dx
dy
‫األتٌة‬ ‫الدوال‬ ‫من‬ ‫لكل‬
22
32 xxx
eey  
)6()22.(
22
32
xexe
dx
dy xxx
 
22
32
6)22( xxx
xeex  

172. 3
2
xx
ey 2cos4sin 

)2).(2sin()4.(4.(cos2cos4sin
xxe
dx
dy xx
 
xx
exx 2cos4sin
)2sin(2)4cos(4( 

)4sin44cos2(2
xxey x

  2.).4sin44cos2(4).4cos(44).4sin((2. 22 xx
exxxxe
dx
dy

)4sin(8)4cos(4)4cos(164sin8 2222
xeexxexe xxxx

))4(cos(20 2
xe x


173. 4
5
x
x
e
e
Lny


1
)1( xx
eLnLne 
1..
1
1
1..
1 x
x
x
x
e
e
e
edx
dy


x
x
e
e


1
1
30 yLnx
Lnee
30 yx
xy  30
1
dx
dy

174. 1-
2-
5-
4-
3-
7-
6-
8-
10
)(Lnxy 
)sec(tan xxLny 
2 2
2.3(  xxLny
x
x
Lny



1
1
2
1 2
yLnxxLny 
2
1
1
x
x
Lny



2
tan)4( 2 x
xxy 
22
)1(
2
1
xLnLnxy 

175. 9
10
11
12
13
14
15
LnxyLnx 2)1()1( 
x
x
Lny
sin1
sin1



)(sin yxLny 
LnxeLny x

)(LnxLney x

13 2

 x
exy
1)3(sin 22
 xy
exy

176. 16
18
17
x
y
xey
sin
x
y
Lne yx

x
xy cos
)3( 

177. ‫دالة‬ ‫الواقع‬ ً‫ف‬ ‫تكون‬ ‫والثانٌة‬ ‫األولى‬ ‫الحالتٌن‬ ‫من‬ ‫كل‬ ً‫وف‬‫اشتقاقها‬ ‫وٌمكن‬ ‫واحد‬ ‫لمتغٌر‬
‫المناسبة‬ ‫االشتقاق‬ ‫وقوانٌن‬ ‫قواعد‬ ‫إلى‬ ‫ا‬‫ا‬‫استناد‬‫ا‬‫ا‬‫سابق‬ ‫والمعروفة‬.
),( yxfz xy,xy,
xy
yx
xy,
z
x
yzx x
‫أن‬ ‫وبما‬ ‫المستقلٌن‬ ‫المتغٌرٌن‬ ً‫ف‬ ‫دالة‬ ‫لتكن‬‫متغٌران‬
‫أن‬ ‫ٌمكننا‬ ‫فأننا‬ ‫مستقالن‬:-
1-‫ثابتة‬ ‫وتترك‬ ‫تتغٌر‬ ‫أن‬ ‫ل‬ ‫نسمح‬.
2-‫ثابتة‬ ‫وتترك‬ ‫تتغٌر‬ ‫أن‬ ‫ل‬ ‫نسمح‬.
3-‫واحد‬ ‫أن‬ ً‫ف‬ ‫ٌتغٌران‬ ‫أن‬ ‫ل‬ ‫نسمح‬.
‫بالنسبة‬ ‫ومشتقتها‬ ً‫ف‬ ‫دالة‬ ‫تكون‬ ‫فعندئذ‬ ‫ثابتة‬ ‫بقاء‬ ‫مع‬ ‫تغٌرت‬ ‫فإذا‬
ً‫ه‬ ‫إلى‬:

178. ‫الجزئٌة‬ ‫بالمشتقة‬ ‫وتسمى‬‫األولى‬‫ل‬z‫بالنسبة‬‫إلى‬.x
‫أذا‬ ‫أما‬‫تغٌرت‬y‫بقاء‬ ‫مع‬x‫فان‬ ‫ثابتة‬zً‫ف‬ ‫دالة‬ ‫تكون‬y‫بالنسبة‬ ‫ومشتقتها‬‫ل‬yً‫ه‬:-
‫الجزئٌة‬ ‫بالمشتقة‬ ‫وتسمى‬‫األولى‬‫ل‬z‫بالنسبة‬‫إلى‬y‫أذا‬ ‫أما‬‫كانت‬z
ً‫ف‬ ‫كدالة‬ ً‫ضمن‬ ‫بشكل‬ ‫معرفة‬x ,y‫بالعلقة‬‫فانه‬‫ٌمكن‬‫أٌجاد‬
‫المشتقتٌن‬‫الجزئٌتٌن‬‫درسناها‬ ً‫الت‬ ً‫الضمن‬ ‫االشتقاق‬ ‫قاعة‬ ‫باستخدام‬ً‫ا‬‫سابق‬.
x
yxfyxxf
x
x
z




 ),(),(
0lim
y
yxfxyxf
x
z




 ),(),(
0lim
0),,( zyxf
y
z
x
z




,

179. hg
yy
xx
yxz
2020
6006
63_1 22







63 22
 yxz
42
)43( yxz 
‫أمثلة‬:-‫جد‬
1
2
yy 2020 


xx 6006 


32
)43(16 yx 
)4()43(4 32
yx 


32
)43(24 yxx 
)6()43(4 32
xyx 


x
z
y
z




,ً‫ٌأت‬ ‫مما‬ ‫لكل‬:-

180. 4
3
)2(sec122).2(sec60 22
yy 


)3sin(120)3).3sin((4 xx 


yx 83 


yx 34 


)2tan(6))3cos(4( yxz 
22
432 yxyxz 

181. )32sin( yxz 
2
2
122 2
)2()(
y
x
x
y
yxyx
y


 
2
2
221 2
)()2(
x
y
y
x
xyxy 

 
2121
yxxyz 

6
5
)32cos(3)30).(32cos( yxyx 


)32cos(2)02).(32cos( yxyx 


x
y
y
x
z
22
2 

182. ‫ضمنٌة‬ ‫الدالة‬‫ت‬‫الضمنٌة‬ ‫الدالة‬ ‫حدود‬ ‫من‬ ‫حد‬ ‫كل‬ ‫شتق‬Z‫إلى‬ ‫بالنسبة‬x‫معتبرٌن‬y‫أن‬ ‫حٌث‬ ‫ثابت‬
z
x
z
x
x
z





2
2
x
x
z
z 22 


0202 



x
z
zx
25222
 zyx
xyxxyx
xexe 


 22
)0(
)2(
2
yxe xyx


 
7
8
xyx
ez 

2

183. 1 zxyzxy
z
y
z
y
y
z





2
2
9
xy
zy
xy
zy








zyxy 


)(
0






x
z
xz
x
z
yy
‫إلى‬ ‫بالنسبة‬x
0220 



y
z
zy
‫إلى‬ ‫بالنسبة‬ ‫ا‬‫ا‬ٌ‫ضمن‬ ‫نشتق‬ ‫ثم‬y‫أن‬ ‫معتبرٌن‬x‫ثابت‬:

184. 0))1(( 






y
z
xz
y
z
yx
zxxy
y
z



)(
‫ثم‬‫ضمنٌا‬ ‫نشتق‬z‫بالنسبة‬‫إلى‬y‫معتبرٌن‬‫أن‬x‫ثابت‬
zy
yx
xy
zx
y
z









185. ‫جد‬‫التالٌة‬ ‫الدوال‬ ‫من‬ ‫لكل‬:-
23
2
3
46
yx
yx
z



)43ln( 2
yxz 
)tan(
x
y
z 
))4)(cos(3sin( yxz 
22
x
y
y
x
z 
1
2
3
5
4
6
x
z
y
z




,
22
32 yxyxz 

186. ‫أذا‬‫كانت‬‫اثبت‬‫أن‬
‫أذا‬‫كانت‬‫اثبت‬‫أن‬1





y
z
y
x
z
x
z
y
z
y
x
z
x 





0 xyxzyz
063 23
 xyzyxz
369_4 222
 zyx
7
8
9
10
11
12 22
yxLnz 
22
yxz 
22
2
6 yx
exz 


187. ‫المجاالت‬ ً‫ف‬ ‫االستخدام‬ ‫والكثٌرة‬ ‫المهمة‬ ‫الرٌاضٌة‬ ‫المفاهٌم‬ ‫من‬ ‫التكامل‬ ‫موضوع‬ ‫إن‬
‫األخرى‬ ‫والعلوم‬ ‫واإلحصائٌة‬ ‫الهندسٌة‬.
‫مهمٌن‬ ‫معنٌٌن‬ ‫على‬ ‫ٌدل‬ ‫التكامل‬,‫المشتقة‬ ‫بمعكوس‬ ‫ٌسمى‬ ‫ما‬ ‫األول‬anti-dreviative‫أو‬
‫المحدد‬ ‫غٌر‬ ‫التكامل‬indefinite integral.‫المساحات‬ ‫بإٌجاد‬ ‫ٌتعلق‬ ً‫الثان‬ ‫والمعنى‬
‫واإلحصائٌة‬ ‫الهندسٌة‬ ‫التطبٌقات‬ ‫من‬ ‫كثٌر‬ ً‫وف‬ ‫المنحنٌات‬ ‫وأطوال‬ ‫والحجوم‬,‫ٌطلق‬ ‫والذي‬
‫اسم‬ ‫علٌه‬‫المحدد‬ ‫التكامل‬definite integral
‫الدالة‬ ‫إٌجاد‬ ‫عملٌة‬ ‫أن‬f(x)‫التفاضلٌة‬ ‫دالتها‬ ً‫الت‬(‫مشتقتها‬)f(x)‫بالتكامل‬ ‫تدعى‬,‫وتكتب‬
ً‫التال‬ ‫بالشكل‬ ‫الرموز‬:

188.   cxfdxxf )()(
‫إن‬ ‫حٌث‬:‫تكامل‬ ‫ٌقرأ‬f(x)‫المتغٌر‬ ‫إلى‬ ‫بالنسبة‬x
F(x):‫التكامل‬ ‫ٌسمى‬
F(x)+c:‫قٌمة‬ ‫ٌسمى‬(‫ناتج‬)‫التكامل‬,c‫هذا‬ ‫وٌعرف‬ ‫للتكامل‬ ‫ثابت‬
‫المحدد‬ ‫غٌر‬ ‫بالتكامل‬ ‫التكامل‬ ‫من‬ ‫النوع‬.
  cxfdxxf )()(
‫فٌكون‬ ‫المحدد‬ ‫التكامل‬ ‫أما‬:
 b
a
b
a
xfdxxf  )()(
‫أن‬ ‫حٌث‬:
a , b:‫التكامل‬ ‫حدود‬ ‫تسمى‬a ≤ b
a:‫األدنى‬ ‫الحد‬
b:‫األعلى‬ ‫الحد‬

189. ‫أن‬ ‫حٌث‬‫القوس‬ ‫داخل‬ ‫مشتقة‬
‫وان‬n≠-1
)(xf 
1
5
4
3
2
    c
n
xf
dxxfxf
n
n




 1
)(
)()(
1
c
n
x
dxx
n
n




 1
1
     dxxgdxxfdxxgxf )()()()( 
   ckxdxkkdx
  cxdx

190. c
x
dxx 




 2
2
3
cxx
x
 3
3
2
3
cx
xx
 3
2
2
3
23
   dxxdxdxx 322
dxxx )32( 2
1
2

191. ctc
t
dttdtt   2
52
5
2
3
3
5
2
2
5
3
dx
xx
x )1
11
( 2
3
4
dxxxx )1( 2
1
23




 


dxdxxdxxdxx
2
1
23
cx
xxx




2
114
2
1
14

192. ‫التكامل‬ ‫أٌجاد‬ ً‫ف‬ ‫ومشتقة‬ ‫القوس‬ ‫قاعدة‬ ‫بتطبٌق‬
5 dxxxx )22()32( 22

    c
n
xf
dxxfxf
n
n




 1
)(
)()(
1
c
xx



3
)32( 32

193. dxxx 22
1
3
)2( 
dxxx 23
3)2(
3
1
 
cxc
x


 2
3
3
2
3
3
)2(
9
2
2
3
)2(
3
1
6
7 xdxx 102
)3( 
xdxx 2)3(
2
1 102
 
c
x



11
)3(
2
1 112

194. dxxxx )1()2( 2

dxxxxdxxxx )22()2(
2
1
)1()2( 2
1
22
1
2
 
c
xx



2
3
)2(
2
1 2
3
2
cxx  2
3
2
)2(
3
1
8
9 dxx 5
)
2
1
1( 
dxx )
2
1
()
2
1
1(2 5
 
c
x
c
x





3
)
2
1
1(
6
)
2
1
1(
2
66

195. 10 dxxx 232
)1( 
  dxxxxx 23222232
)1()1)((3)1()(3)( 
dxxxxx 2246
)133(  
dxxxxx 2468
33  
dxxdxxdxxdxx   2468
33
c
xxxx

35
3
7
3
9
3579

196. 2
1
2
2
1
2
)101(
10
1
2
1
)101(
20
1
y
y



ydyy 2
1
2
)101(

 
  2
101 y
ydy
11
12 dx
x
xxx

 25
dxxxxx 2
1
25
)(

 

197. dxxdxxdxx   2
1
2
3
2
9
cxxxc
xxx
 2
3
2
5
2
112
3
2
5
2
11
3
2
5
2
11
2
2
3
2
5
2
11

198. 2
3
4
5
6
1 dxx
2
dxxx 324
)1( 
dxx
3 5
dtttt )23
2
1
( 45
 

dxxx )1)(2( 
dxx
3

199. 7
8 dxxxx )1()2( 42

dxx

 2
)23(
9
10
11
dx
x
x
 3
5
2
  2
)1( t
dt
xdxx )31( 2
 

200. 14
13
12 dx
x
x
 

2
)2(
42
 


23
4
)1(
10
3
25
t
dt
dx
x
xx
dx
x
xx


3
4
3
25

201. ‫كانت‬ ‫أذا‬f(x)‫المغلقة‬ ‫الفترة‬ ‫على‬ ‫مستمرة‬ ‫دالة‬[ a, b]‫ولتكن‬f(x)‫كل‬ ‫أن‬ ‫بحٌث‬ ‫دالة‬x
ً‫ف‬[a , b ]‫مشتقة‬f(x)‫فان‬:
b
a
b
a
xfdxxf  )()(
‫حٌث‬‫أن‬a<b
F(x)):‫المشتقة‬ ‫معكوس‬f(x
‫وان‬:‫التكامل‬ ‫ناتج‬ ً‫ف‬ ‫التعوٌض‬ ً‫ٌعن‬f(x)‫كل‬ ‫ٌدل‬x‫األعلى‬ ‫بالحد‬b‫ٌطرح‬ ‫ثم‬
‫كل‬ ‫ٌدل‬ ‫ناتج‬ ‫منه‬x‫األدنى‬ ‫الحد‬((a
b
axf )(
)()( afbf 

202. ‫مساحات‬ ‫أٌجاد‬ ً‫ف‬ ‫ٌستعمل‬ ‫وهو‬ ‫المحدد‬ ‫للتكامل‬ ‫كثٌرة‬ ‫تطبٌقات‬ ‫وهناك‬
‫منحنٌن‬ ‫بٌن‬ ‫المحصورة‬ ‫المنطقة‬,‫للدالة‬ ً‫المنحن‬ ‫تحت‬ ‫المساحة‬ ‫أٌجاد‬ ً‫وف‬
,‫الدورانٌة‬ ‫المساحات‬ ‫حجوم‬ ‫أٌجاد‬ ً‫وف‬,‫لألجسام‬ ‫السطحٌة‬ ‫والمساحات‬
‫وهندسٌة‬ ‫فٌزٌاوٌة‬ ‫تطبٌقات‬ ً‫وف‬ ‫المنحنٌات‬ ‫أطوال‬ ‫أٌجاد‬ ً‫وف‬ ‫الدورانٌة‬
‫كثٌرة‬ ‫وإحصائٌة‬.
 
3
1
2
)543( dxxx1

203.   
3
1
3
1
3
1
2
543 dxxdxdxx
0101626 
)2(5)19(2127 
   )13(5)13(21352 22333
1
3
1
23
1
3
 xxx
  3
1
3
1
2
3
1
3
5
2
4
3
3 x
xx

2 dxxxx )33( 2
1
1
3


204.    

1
1
1
1
1
1
2
1
1
3
33 dxxdxdxxdxx
   1
1
2
1
1
3
1
1
4
3
23
3
4
  x
xxx
)1(1(3
2
)1(1
)1(1(
4
)1(1 22
33
44





460)2(0 
3  
0
2
2
21 t
tdt

205. 1)31(
2
1
)91(
2
1

tdtt 2
10
2
2
)21(


 
tdtt 4)21(
4
1 2
10
2
2


 
 0
2
2
1
2
2
1
)21(
4
1



t
0
2
2
21
2
1
 t
22
)2(21)0(21(
2
1


206. 4 dxx )1(
3
1
2

 3
1
3
1
3
1
33
1
2
3
x
x
dxdxx  
3
32
2
3
26
)13(
3
13 33




207. 2
1 dxxx )25(
2
0
2

dxxx )3(
2
2
3

3 dxx
4
0

208. 6
5
4 dxxx )35(
0
1
2

dxx 
1
0
45
dx
x
4
1
3

209. ‫المشتقة‬ ‫مواضٌع‬ ً‫ف‬ ‫درسنا‬ ‫كما‬(‫التفاضل‬)‫من‬ ‫لكل‬ ‫المشتقة‬ ‫أٌجاد‬ ‫قوانٌن‬
‫والمثلثٌة‬ ‫واللوغارتمٌة‬ ‫اآلسٌة‬ ‫الدوال‬,‫هذه‬ ‫لتكامل‬ ‫مناظرة‬ ‫قوانٌن‬ ‫فهناك‬
‫المشتقة‬ ‫لقوانٌن‬ ‫معكوس‬ ‫وتكون‬ ‫الدوال‬.
ً‫األت‬ ‫التكامالت‬ ‫لحساب‬ ‫القوانٌن‬ ‫هذه‬ ‫ومن‬:-
:u′‫الدالة‬ ‫مشتقة‬
1 cuLndxu
u

1
‫أن‬ ‫حٌث‬u:‫دالة‬xًٌ
3
2 cedxue uu
 .
  cudxuu )cos().sin(

210. 4
5
6
8
7
cudxuu  )(sin).(cos
cudxuu  )(tan).(sec2
cudxuu  )(sec)(tan)(sec
cudxuu  cot).(csc2
cudxuu  cot).(csc2

211.   x
dx
1
cxLn
x
dx



  1
1
1
  3
2
41 x
dxx
cxLndx
x
x


 
3
3
2
41
12
1
41
12
2
1
2

212. dx
x
x
  2sin1
2cos
cxLndx
x
x


  2sin1
2
1
2
2sin1
2cos
2
1
3
4  

)2(
)1(
2
xx
x
cxxLndx
xx
x



  2
2
1
)2(
)22(
2
1 2
2

213. cee xx
 2
2
1
5 dxee xx
)( 2 

dxedxe xx


 2
dxedxe xx
)1()1(2.
2
1 2
 

6 dxxe xx
)1()2( 2



214. dxxe xx
)22(
2
1 )2( 2
 

ce xx
  )2( 2
2
1
7  x
dxe x
cecedxxedxxe xxxx


 22
2
1
.2.
2
1
2
1
2
1
2
1
2
1
dxxe x
)3cos()3sin(
8

215. dxxe x
3).3cos(.
3
1 )3sin(

ce x
 )3sin(
3
1
9 dx
x
)
3
sin(
dx
x
)
3
1
).(
3
sin(3
c
x
c
x






 )
3
cos(3)
3
cos(3

216. c
x
dx
x




 )
2
3
tan(2
2
1
).
2
3
(2sec2
10   dxx)31cos(
dxx )3).(31(cos
3
1

cx  )31cos(
3
1
11 dx
x
)
2
3
(2sec



217. 12  xdxx cossin
c
x

2
sin2
xdx
2
sin13
‫النسب‬ ‫خواص‬ ‫باستخدام‬
)2cos1(
2
1
sin2
xx 
dxx)2cos1(
2
1
 
  dxx)2cos1(
2
1

218.   dxxdx 2).2cos(
2
1
2
1
cx
x
 )2sin(
4
1
2
14 dx
x
x
 3
sin
cos
dxxx )cos()(sin 3



  c
x




2
)sin( 2

219. 15 xdxxx sin)cos(sin 2
 
xdxxxxx sin)coscossin2(sin 22
 
1cossin 22
 xx
xdxxxdxxdxxx cossin2sinsin)cossin21( 2
  
c
x

3
sin
2cos
3
16 xdx
2
tan

220.    dxxdxdxx 22
sec)1(sec
cxx  2
tan

221. 4
3
2
1 dx
x
Lnx

 5
)4(
dxex 2
)1( 
dx
xLnx
dx
e
e

2
dx
x
Lnx

3
)(

222. 5 dx
ee
ee
xx
xx
 



9
7
6
8
10
dx
x
x
 2
3
sin
cos
 dxxxx  )cos()5sin( 22
 xdxtan
 xdxcot
xdx
3
tan

223. ‫تفاضل‬(‫مشتقة‬)‫هو‬ ً‫األت‬ ‫الضرب‬ ‫حاصل‬
vduudvvud  )(
‫أن‬ ‫على‬ ‫نحصل‬ ‫الطرفٌن‬ ‫تكامل‬ ‫وعند‬
   vduudvvud )(
1
   )1........(..........cvduuvudv
  vduudvcuv

224. ‫انمبػذح‬(1)‫رحذٌذ‬ ‫ثؼذ‬ ‫رطجٍمٓب‬ ٍ‫ًٌٔك‬ ‫ثبنزجزئخ‬ ‫انزكبيم‬ ‫رذػى‬(u)ٔ(d v)‫صى‬
ٍ‫ي‬ ‫كم‬ ‫أٌجبد‬(v , du )‫سلى‬ ‫ثبنمبػذح‬ ‫َؼٕض‬ ‫صى‬(1)‫انزكبيم‬ ‫لًٍخ‬ ‫ػهى‬ ‫نُحصم‬
‫انًطهٕة‬.
‫رقم‬ ‫القاعدة‬ ‫وتطبٌق‬(1)‫الدوال‬ ‫منها‬ ‫حاالت‬ ً‫ف‬‫اللوغارٌتمٌة‬
,‫المثلثٌة‬ ‫الدوال‬,‫المثلثٌة‬ ‫الدوال‬ ‫معكوس‬,‫ضرب‬ ‫حاالت‬ ً‫وف‬
‫دالتٌن‬......‫الخ‬.
1 Lnxdx
   cvduuvudv

225. Lnxulet  dxdv ;
dx
x
du
1
   dxdv
xv 
cdx
x
xxLnxdxxLn   )
1
())(()(
  cdxxLnx
cxxLnx 

226. 2 xLnxdx
   cvduuvudv
Lnxulet  xdxdv ;
dx
x
du
1
   
2
;
2
x
vxdxdv
dx
x
xx
LnxxLnxdx
1
.
2
)
2
(
22
 
 xdxLnx
x
2
1
2
2

227. c
x
Lnx
x

22
1
2
22
c
x
Lnx
x

42
22
3 dxxxdxxx   2
1
)1(1
   cvduuvudv
xulet  dxxdv 2
1
)1(; 

228. dxdu  2
32
3
)1(
3
2
2
3
)1(
; x
x
v 


cdxxxxdxxxudv 





   2
3
2
3
)1(
3
2
)1(
3
2
1
c
x
xx 


2
5
)1(
3
2
)1(
3
2 2
5
2
3
cxxx  2
5
2
3
)1(
15
4
)1(
3
2

229. 4 xdxex
sin
   cvduuvudv
x
eulet  xdxdv sin, 
dxexexdxeudv xxx
  cos)(cossin
   xvxdxdvdxedu x
cossin;
‫ل‬ ‫التجزئة‬ ‫قاعدة‬ ‫نشتق‬ ‫ثم‬
dxex
 cos)(

230. cxx
e
xdxe
x
x
 )cos(sin
2
sin
xdxdv cos, 
x
eulet 
dxedu x
 xv sin
cxdxexexexdxe xxxx
  sinsincossin
cxxexdxe xx
 )cos(sinsin2

231. 5 Lnxdxx
2
   cvduuvudv
Lnxu  dxxdv 2
; 
dx
x
du
1

3
;
3
2 x
vdxxdv  
cdx
x
x
Lnx
x
Lnxdxxudv   
1
33
33
2

232. cxLnx
x
 3
3
9
1
3
c
x
Ln
x

33
1
3
33

233. 5
3
4
2
1 dx
x
x )
1
( 
 dxLnx)cos(
dxxex

xdxx cos2

Lnxdxx
2

234. ‫دوال‬ ‫على‬ ‫تحتوي‬ ‫تكامالت‬ ‫على‬ ‫التعرف‬ ‫سٌتم‬
)(
)(
)(
xg
xf
xh 
‫من‬ ‫كل‬ ‫أن‬ ‫حٌث‬f(x),g(x)‫الحدود‬ ‫متعددة‬,g)x(≠0
‫جد‬ ‫ا‬‫ال‬‫فمث‬:
 

32
35
2
xx
x
ً‫ٌل‬ ‫بما‬ ‫الطرٌقة‬ ‫وتتلخص‬ ‫الكسر‬ ‫نجزء‬ ‫أو‬ ‫نفصل‬ ‫الممكن‬ ‫من‬:
32
35
2


xx
x

235. 13)1)(3(
35
32
35
2









x
B
x
A
xx
x
xx
x
)3()1(35  xBxAx
)3()( BAxBA 
BA5
BA 33 
‫وعلٌه‬
‫السابقتٌن‬ ‫المعادلتٌن‬ ‫وبحل‬‫نحصل‬
3A,2B
 





1
2
3
3
32
35
2
x
dx
x
dx
dx
xx
x

236. cxxLn  23
)1()3(
cxLnxLn  1233
  2
)2(x
xdx
22
)2()2()2( 



 x
B
x
A
x
x
BAAxx  2

237. 1A
202  BBA
dx
x
dx
xx
xdx
 



 )2(
2
)2(
1
)2( 2
cdxxxLn  
2
)2(22
c
x
xLn 




1
)2(
22
1
22  xLn

238. 5
3
4
2
1  92
x
dx
  542
xx
xdx
  2
)1(x
xdx
  )2)(1( xx
xdx
dx
x
x
 

1
32
2

239. ‫فان‬‫المساحة‬ ‫قانون‬
 dxxfA )(
ً‫ٌل‬ ‫بما‬ ‫الحل‬ ‫خطوات‬ ‫وتتلخص‬:
1-‫الدالة‬ ً‫منحن‬ ‫نرسم‬y=f(x)‫قٌم‬ ‫تحدٌد‬ ‫خالل‬ ‫من‬(x)‫قٌم‬ ‫واستخراج‬(y).
3-‫أذا‬‫الدالة‬ ‫كانت‬y=f(x)‫سالبة‬,‫تقع‬ ‫إٌجادها‬ ‫المطلوبة‬ ‫المساحة‬ ‫أن‬ ‫أخر‬ ‫بمعنى‬‫تحت‬
‫الصٌغة‬ ‫وفق‬ ‫تحسب‬ ‫المساحة‬ ‫فأن‬ ‫السٌنات‬ ‫محور‬‫االتٌة‬
4-‫السالبة‬ ‫المساحة‬ ‫من‬ ‫للتخلص‬ ‫المطلوبة‬ ‫القٌم‬ ‫اخذ‬ ‫أو‬
2-‫الدالة‬ ‫كانت‬ ‫أذا‬y=f(x)‫موجبة‬,‫المساحة‬ ‫أن‬ ‫أخر‬ ‫بمعنى‬‫المطلوب‬‫فوق‬ ‫تقع‬ ‫إٌجادها‬
‫محور‬‫السٌنات‬

b
c
dxxfAArea )(

240. ‫يضبل‬:‫انذانخ‬ ًُ‫يُح‬ ٍٍ‫ث‬ ‫انًحصٕسح‬ ‫انًُطمخ‬ ‫يضبحخ‬ ‫جذ‬14)( 3
 xxfy
51)1(4)1( 3
f
X
1
2
3
Y
5
33
109
‫نرسم‬ً‫منحن‬‫الدالة‬
1 2 3
10
20
30
110
‫والمستقٌمٌن‬ ‫السٌنات‬ ‫ومحور‬x=3,x=1‫؟‬
‫الحل‬:
14 3
 xy
A

241.  
3
1
3
1
4
4
4 x
x
A 
‫المطلوبة‬ ‫المنطقة‬ ‫أن‬ ‫بما‬(‫موجبة‬ ‫الدالة‬)‫فان‬ ‫السٌنات‬ ‫محور‬ ‫فوق‬ ‫تقع‬b=3,a=1
dxxA )14(
3
1
3
 
 
3
1
3
1
3
4 dxdxx
unitesquare82280 
)13)(13( 44


242. ‫نرسم‬‫الدالة‬ ً‫منحن‬y=f(x)
X
0
1
2
3
Y
3
2
3
6 A
‫جد‬‫الدالة‬ ً‫منحن‬ ‫بٌن‬ ‫المحصورة‬ ‫المنطقة‬ ‫مساحة‬
‫والمستقٌمٌن‬ ‫السٌنات‬ ‫ومحور‬x=3,x=0‫؟‬
1 2 3
2
4
6
32)( 2
 xxyxf
‫الحل‬:-
‫مثال‬:
32)( 2
 xxyxf
63)3(23)3( 2
f
33)2(22)2( 2
f
23)1(21)1( 1
f
33)0(20)0( 0
f

243. ‫السٌنات‬ ‫محور‬ ‫فوق‬ ‫تقع‬ ‫مساحتها‬ ‫أٌجاد‬ ‫المطلوب‬ ‫المنطقة‬ ‫ان‬ ‫بما‬(‫موجبة‬ ‫الدالة‬)‫فان‬ ‫لذلك‬b=3,a=0
 
3
0
2
)32( dxxxA
unitesquare9999 






 )0(30
3
0
)3(33
3
3 2
3
2
3

3
0
23
)3
2
2
3
( x
xx

  
3
0
3
0
3
0
2
32 dxxdxdxx

244. Y
-4
X
-15)( 2
 xyxf
A
-1 1 2
-1
-2
-3
-4
‫مثال‬:
‫نرسم‬‫الدالة‬ ً‫منحن‬y=f(x) ‫الحل‬:
152)2( 2
f
451)1( 2
f
550)0( 2
f
4515)1()1( 2
 xf
52
xy ‫الدالة‬ ً‫بمنحن‬ ‫المحددة‬ ‫المنطقة‬ ‫مساحة‬ ‫جد‬‫السٌنات‬ ‫ومحور‬
‫والمستقٌمٌن‬x=2,x=-1‫؟‬

245. ‫السٌنات‬ ‫محور‬ ‫أسفل‬ ‫تقع‬ ‫المطلوبة‬ ‫المنطقة‬ ‫مساحة‬ ‫أن‬ ‫بما‬(‫السالبة‬ ‫الدالة‬)‫فان‬ ‫لذلك‬
a=-1,b=2
dxxA )5(
2
1
2
 
3155
3
1
10
3
8

))1(5
3
)1(
)2(5
3
2
(
33















2
1
3
)5
3
(  x
x
 

2
1
2
1
2
)5( dxdxx
unitesqure12

246. 2
4)( xyxf 
2-‫الدالة‬ ً‫منحن‬ ‫بٌن‬ ‫المحصورة‬ ‫المنطقة‬ ‫مساحة‬ ‫جد‬ ‫اآلتٌة‬ ‫التمارٌن‬ ‫من‬ ‫لكل‬f(x)‫المعطاة‬
‫والمستقٌمٌن‬ ‫السٌنات‬ ‫ومحور‬x=b , x=a‫منها‬ ‫كل‬ ‫إزاء‬ ‫المؤشرة‬ ‫النقاط‬ ً‫ف‬:-
3,1,3)( 2
 baxxxf
2,0,
)32(
14
)( 2


 ba
x
xf
3
4
2
1
4,2,2)( 2
 baxxxf
3,1,652)( 23
 baxxxxf
1-‫ومحور‬ ‫الدالة‬ ً‫منحن‬ ‫بٌن‬ ‫المحصورة‬ ‫المنطقة‬ ‫مساحة‬ ‫جد‬
‫السٌنات‬.

247. ‫الدالة‬ ً‫منحن‬ ‫بٌن‬ ‫المحصورة‬ ‫المنطقة‬ ‫مساحة‬ ‫جد‬f(x)‫ومحور‬ ‫المعطاة‬‫السٌنات‬
9)( 2
xxf
5

248. ‫معادلته‬ ‫الذي‬ ً‫المنحن‬ ‫قوس‬ ‫حساب‬ ‫منا‬ ‫طلب‬ ‫انه‬ ‫لنفرض‬y=f(x)‫النقطة‬ ‫من‬(a , c)‫إلى‬
‫النقطة‬(b ,d )‫أدناه‬ ‫الشكل‬ ً‫ف‬ ‫موضح‬ ‫كما‬:
‫وحساب‬ ‫معلومتٌن‬ ‫نقطتٌن‬ ‫بٌن‬ ‫مستقٌم‬ ‫قطعة‬ ‫طول‬ ‫أٌجاد‬ ‫قانون‬ ‫باستخدام‬ ‫ٌتم‬ ‫ذلك‬ ‫فان‬
‫التفاضل‬,‫بالرمز‬ ً‫المنحن‬ ‫قوس‬ ‫لطول‬ ‫رمزنا‬ ‫فإذا‬(L)‫اآلتٌة‬ ‫الصٌغة‬ ‫ٌأخذ‬ ‫القانون‬ ‫فان‬
dx
dx
dy
L
b
a
2
)(1 
Y=f(x)
b, da ,c

249. dy
dy
dx
L
d
c
2
)(1 
‫مثال‬:‫النقطة‬ ‫من‬ ً‫المنحن‬ ‫طول‬ ‫جد‬((0,0‫النقطة‬ ‫إلى‬
2
3
3
2
xy )
3
16
,4(
dx
dx
dy
L
b
a
2
)(1 
‫الحل‬:
2
1
2
1
2
3
3
2
xx
dx
dy

2
3
3
2
xy 
‫بالشكل‬ ً‫المنحن‬ ‫معادلة‬ ‫كانت‬ ‫أذا‬ ‫أما‬x=f(y)‫الصٌغة‬ ‫حسب‬ ‫ٌحسب‬ ً‫المنحن‬ ‫طول‬ ‫فان‬
‫اآلتٌة‬

250. dxxL  
4
0
2
1
(1
  unite155
3
2













 15
3
2
)01()41(
3
2 2
3
2
3
2
3

4
0
2
3
2
3
)1( x

dxxdxx  
4
0
2
14
0
)1(1

251. 2-ً‫المنحن‬ ‫قوس‬ ‫طول‬ ‫جد‬‫النقطة‬ ‫من‬x=0‫النقطة‬ ‫إلى‬x=3.
13 2
3
 xy
2
3
2
)2(
3
1
 xy
1-ً‫المنحن‬ ‫قوس‬ ‫طول‬ ‫احسب‬‫النقطة‬ ‫من‬x=0‫النقطة‬ ‫إلى‬x=4.

252. ‫التطبٌقٌة‬ ‫الرٌاضٌات‬ ‫مواضٌع‬ ‫أهم‬ ‫من‬ ‫التفاضلٌة‬ ‫المعادالت‬ ‫تعتبر‬,‫هذا‬ ‫دراسة‬ ‫بدأت‬ ‫وقد‬
‫دراسة‬ ً‫ف‬ ‫أساسٌة‬ ‫التفاضلٌة‬ ‫المعادالت‬ ‫والتكامل‬ ‫التفاضل‬ ‫موضوع‬ ‫وجد‬ ‫منذ‬ ‫الموضوع‬
‫األخرى‬ ‫التطبٌقٌة‬ ‫العلوم‬ ‫وكافة‬ ‫والهندسة‬ ‫الفٌزٌاء‬ ‫مواضٌع‬.
‫عالقة‬ ‫بأنها‬ ‫التفاضلٌة‬ ‫المعادلة‬ ‫وتعرف‬(‫معادلة‬)‫مشتقات‬ ‫من‬ ‫أكثر‬ ‫أو‬ ‫مشتقة‬ ‫على‬ ‫تحتوي‬
‫معلومة‬ ‫غٌر‬ ‫دالة‬,‫تعتمد‬ ً‫الت‬ ‫المستقلة‬ ‫المتغٌرات‬ ‫بعض‬ ‫مع‬ ‫نفسها‬ ‫الدالة‬ ‫تتضمن‬ ‫وقد‬
‫الدالة‬ ‫علٌها‬.
‫الفصل‬:‫األسبوع‬ ‫الثامن‬:‫العشرون‬
033 2
2
3
3
 xzy
dx
yd
dx
yd
2
1
xy
dx
dy
dx
yd
sin34)( 3
2

3
4
xy
dx
dy
dx
yd
sin34)( 3
2







3)( 4
3
3
dx
dy
dx
yd

253. ‫فمػ‬ ‫االػزٍبدٌخ‬ ‫انزفبظهٍخ‬ ‫انًؼبدالد‬ ‫ػهى‬ ‫انًشحهخ‬ ِ‫ْز‬ ً‫ف‬ ‫دساصزُب‬ ‫رمزصش‬ ‫ٔصٕف‬.
‫ولٌكن‬ ‫مستقل‬ ‫متغٌر‬ ‫بٌن‬ ‫عالقة‬ ً‫ه‬x‫معروفة‬ ‫الغٌر‬ ‫ودالته‬y‫مشتقات‬ ‫وبعض‬y‫بالنسبة‬
‫إلى‬x‫التالٌة‬ ‫بالصٌغة‬ ‫المعادلة‬ ‫هذه‬ ‫كتابة‬ ‫وٌمكن‬:-
‫هما‬ ‫نوعٌن‬ ‫إلى‬ ‫تقسم‬ ‫التفاضلٌة‬ ‫المعادالت‬ ‫أن‬:-
1-‫االعتٌادٌة‬ ‫التفاضلٌة‬ ‫المعادالت‬
2-‫الجزئٌة‬ ‫التفاضلٌة‬ ‫المعادالت‬
‫الفصل‬:‫األسبوع‬ ‫الثامن‬:‫العشرون‬

254. ‫حٌث‬‫أن‬:
0....).,.........,,,,,( )()4(
 n
yyyyyyxF
n
n
n
dx
yd
y
dx
yd
y
dx
dy
y  ,........., 2
2
0sin)4(
 yxyyy
03  x
ey
0)(  xyy
2
1 3
‫الفصل‬:‫األسبوع‬ ‫الثامن‬:‫العشرون‬

255. 1-‫التفاضلٌة‬ ‫المعادلة‬ ‫رتبة‬:equationorder differenatial
‫المعادلة‬ ً‫ف‬ ‫مشتقة‬ ‫اعلى‬ ‫رتبة‬ ‫بانها‬ ‫التفاضلٌة‬ ‫المعادلة‬ ‫رتبة‬ ‫تعرف‬
‫فالمعادلة‬1‫االولى‬ ‫الرتبة‬ ‫من‬ ‫تفاضلٌة‬ ‫معادلة‬ ً‫ه‬ ‫اعله‬
‫والمعادلة‬2‫الثانٌة‬ ‫الرتبة‬ ‫من‬ ‫تفاضلٌة‬ ‫معادلة‬ ً‫ه‬ ‫اعله‬
‫والمعادلة‬3‫الرابعة‬ ‫الرتبة‬ ‫من‬ ‫تفاضلٌة‬ ‫معادلة‬ ً‫ه‬ ‫اعله‬
2-‫التفاضلٌة‬ ‫المعادلة‬ ‫درجة‬degree of differenatial equation
‫التفاضلٌة‬ ‫المعادلة‬ ‫درجة‬ ‫تعرف‬‫أعلى‬ ‫أس‬ ‫بأنها‬‫التفاضلٌة‬ ‫المعادلة‬ ً‫ف‬ ‫موجودة‬ ‫مشتقة‬
‫فالمعادلة‬1‫أعله‬‫الرتبة‬ ‫من‬ ‫تفاضلٌة‬ ‫معادلة‬ ً‫ه‬‫األولى‬‫الثانٌة‬ ‫والدرجة‬
‫والمعادلة‬2‫أعله‬‫والدرجة‬ ‫الثانٌة‬ ‫الرتبة‬ ‫من‬ ‫تفاضلٌة‬ ‫معادلة‬ ً‫ه‬‫األولى‬
‫والمعادلة‬3‫أعله‬‫والدرجة‬ ‫الرابعة‬ ‫الرتبة‬ ‫من‬ ‫تفاضلٌة‬ ‫معادلة‬ ً‫ه‬‫األولى‬
‫تعارٌف‬:
‫الفصل‬:‫األسبوع‬ ‫الثامن‬:‫العشرون‬

256. 3-‫الجزئٌة‬ ‫التفاضلٌة‬ ‫المعادلة‬partial differenatial equation
‫أذا‬‫هناك‬ ‫كان‬‫أكثر‬‫بٌن‬ ‫العلقة‬ ‫فان‬ ً ‫مثل‬ ‫مستقل‬ ‫متغٌر‬ ‫من‬
‫المعروفة‬ ‫غٌر‬ ‫ودالتها‬ ‫المتغٌرات‬ ‫هذه‬y‫ومشتقات‬y‫بالنسبة‬ ‫الجزئٌة‬‫إلى‬
‫جزئٌة‬ ‫تفاضلٌة‬ ‫معادلة‬ ‫تسمى‬.
),,,(......... xzv
xzv ,,.........,
‫ٌقال‬‫للدالة‬y=g(x)‫بأنها‬‫التفاضلٌة‬ ‫للمعادلة‬ ‫حل‬‫أذا‬‫الدالة‬ ‫كانت‬
‫المعادلة‬ ‫تلك‬ ‫تحقق‬ ‫ومشتقاتها‬.‫بعبارة‬‫أخرى‬‫التفاضلٌة‬ ‫المعادلة‬ ‫بحل‬ ‫ٌقصد‬‫أٌجاد‬‫دالة‬‫أو‬‫علقة‬
‫التعوٌض‬ ‫ٌؤدي‬ ‫بحٌث‬ ‫التفاضلٌة‬ ‫المشتقات‬ ‫من‬ ‫والخالٌة‬ ‫فٌها‬ ‫الواردة‬ ‫المتغٌرات‬ ‫بٌن‬‫إلى‬
‫المعادلة‬ ً‫طرف‬ ‫اختصار‬‫إلى‬‫متطابقٌن‬ ‫مقدارٌن‬.
‫التفاضلٌة‬ ‫المعادالت‬ ‫حل‬:
‫الفصل‬:‫األسبوع‬ ‫الثامن‬:‫العشرون‬

257. ‫التفاضلٌة‬ ‫للمعادلة‬ ‫حل‬ ً‫ه‬ ‫الدالة‬‫اآلتٌة‬
‫ٌنتج‬ ‫التفاضلٌة‬ ‫المعادلة‬ ً‫ف‬ ‫ومشتقتها‬ ‫الدالة‬ ‫عن‬ ‫بالتعوٌض‬‫أن‬
52
 x
ey
010)5(2)02( 22
 xx
ee
‫الطرف‬‫األٌمن‬=‫األٌسر‬ ‫الطرف‬
52
 x
ey‫التفاضلٌة‬ ‫المعادلة‬ ‫حل‬ ‫هو‬‫أعاله‬
‫مثال‬1:
00 
0101022 2
 xx
ee
‫الفصل‬:‫األسبوع‬ ‫الثامن‬:‫العشرون‬

258. ‫مثال‬2:
‫التفاضلٌة‬ ‫للمعادلة‬ ً‫ه‬ ‫الدالة‬
‫وذلك‬‫أذا‬ ‫ألنه‬‫عن‬ ‫عوضنا‬y‫الطرف‬ ً‫ف‬ ‫ومشتقتها‬‫األٌسر‬‫ٌنتج‬‫أن‬
xxxx 62)2)(3( 32

‫الطرف‬‫األٌسر‬=‫األٌمن‬ ‫الطرف‬
32
xyxx
dx
dy
y 62 3

dx
dy
‫األٌسر‬ ‫الطرف‬=‫األٌمن‬ ‫الطرف‬
xxxx 6262 33

‫الفصل‬:‫األسبوع‬ ‫الثامن‬:‫العشرون‬

259. ‫مالحظة‬:‫أحٌانا‬‫هناك‬ ‫ٌكون‬‫أكثر‬‫التفاضلٌة‬ ‫المعادلة‬ ‫لنفس‬ ‫واحد‬ ‫حل‬ ‫من‬,‫جمٌع‬ ‫مجموعة‬
‫التفاضلٌة‬ ‫للمعادلة‬ ‫العام‬ ‫بالحل‬ ‫تسمى‬ ‫المعادلة‬ ‫لتلك‬ ‫المختلفة‬ ‫الحلول‬.
‫مثال‬3:‫لتكن‬‫التفاضلٌة‬ ‫للمعادلة‬ ‫العام‬ ‫فالحل‬‫هو‬
‫حٌث‬‫أن‬c‫ثابتة‬ ‫كمٌة‬
22  xycxxy  22
‫االختٌارٌة‬ ‫الثوابت‬ ‫حذف‬:‫عند‬‫أٌجاد‬‫وجدنا‬ ‫تفاضلٌة‬ ‫لمعادلة‬ ‫العام‬ ‫الحل‬‫أن‬‫ٌحتوي‬ ‫الحل‬ ‫هذا‬
‫الثوابت‬ ‫من‬ ‫عدد‬ ‫على‬.‫واآلن‬‫مسالة‬ ً‫ف‬ ‫نبحث‬ ‫سوف‬‫أٌجاد‬‫التفاضلٌة‬ ‫المعادلة‬ً‫أعط‬ ‫أذا‬
‫الناتجة‬ ‫التفاضلٌة‬ ‫المعادلة‬ ‫ورتبة‬ ‫العام‬ ‫حلها‬ ‫مجموعة‬.
‫مثال‬1:‫العام‬ ‫حلها‬ ً‫الت‬ ‫التفاضلٌة‬ ‫المعادلة‬ ‫جد‬
‫حٌث‬‫أن‬a=‫ثابتة‬ ‫كمٌة‬.
)( xaxy 
‫الفصل‬:‫األسبوع‬ ‫الثامن‬:‫العشرون‬

260. 1..).........( xaxy 
‫فبإجراء‬‫التفاضل‬ ‫عملٌة‬(‫المشتقة‬)‫على‬ ‫نحصل‬
xyaxay 22 
‫عن‬ ‫بالتعوٌض‬(a)‫العلقة‬ ً‫ف‬1‫أعله‬‫على‬ ‫نحصل‬‫أن‬
))2(( xxyxy 
‫نستنج‬ ‫ذلك‬ ‫ومن‬‫أن‬‫المعادلة‬2‫الرتبة‬ ‫من‬ ‫تفاضلٌة‬ ‫معادلة‬ ً‫ه‬‫األولى‬‫الدرجة‬ ‫ومن‬‫األولى‬
‫ملحظة‬ ‫ٌمكن‬ ‫ومنها‬‫أن‬‫المعادلة‬1‫رقم‬ ‫التفاضلٌة‬ ‫للمعادلة‬ ‫العام‬ ‫الحل‬ ‫مجموعة‬ ‫تمثل‬2‫وذلك‬
‫التعوٌض‬ ‫عند‬ً‫ف‬ ‫عن‬‫على‬ ‫نحصل‬ ‫التفاضلٌة‬ ‫المعادلة‬‫أن‬ yy ,
2
xaxy 
02
 xyyx
2
xyxy 
‫األٌمن‬ ‫الطرف‬=‫األٌس‬ ‫الطرف‬‫ر‬
‫الفصل‬:‫األسبوع‬ ‫الثامن‬:‫العشرون‬

261. ‫يضبل‬2:ٛ٘ َ‫اٌؼا‬ ‫دٍٙا‬ ٟ‫اٌر‬ ‫اٌّؼادٌح‬ ‫جذ‬
ْ‫أ‬ ‫د١ث‬B,A‫اخر١اس٠ح‬ ‫ثٛاتد‬.
xx
BeAey 32
 
‫نشتق‬‫مرتٌن‬ ‫العام‬ ‫الحل‬(‫عدد‬ ‫بقدر‬‫الثوابت‬)‫على‬ ‫فنحصل‬‫أن‬
1...............32 xx
BeAey  
)3()2( 32 xx
BeAey  
‫الثانٌة‬ ‫المشتقة‬ ‫نجد‬ ‫ثم‬,‫حٌث‬‫أن‬‫المشتقة‬ ‫مشتقة‬ ً‫ه‬ ‫الثانٌة‬ ‫المشتقة‬‫األولى‬
3............94 32 xx
BeAey 
‫الثابت‬ ‫نحذف‬ ً‫ولك‬A‫المعادلة‬ ‫ضرب‬ ‫ٌتم‬1ً‫ف‬2‫رقم‬ ‫المعادلة‬ ‫مع‬ ‫وجمعها‬2
4.............52 3x
Beyy 
‫الحل‬:
2...............32 32 xx
BeAey 
‫الفصل‬:‫األسبوع‬ ‫الثامن‬:‫العشرون‬

262. ‫رقم‬ ‫المعادلة‬ ‫ضرب‬ ‫ٌتم‬ ‫وكذلك‬2ً‫ف‬2‫رقم‬ ‫معادلة‬ ‫مع‬ ‫وجمعها‬3ً‫ماٌل‬ ‫ٌنتج‬
5...............152 3x
Beyy 
‫ا‬‫لقاعدة‬:‫إلٌجاد‬‫التفاضلٌة‬ ‫المعادلة‬‫أذا‬‫على‬ ‫ٌحتوي‬ ‫الذي‬ ‫العام‬ ‫حلها‬ ‫مجموعة‬ ‫علم‬n))‫الثوابت‬ ‫من‬
‫ا‬‫عملٌات‬ ‫نجري‬ ‫الختٌارٌة‬‫التفاضل‬(‫أٌجاد‬‫المشتقات‬)‫بالتتابع‬‫إلى‬((n‫لدٌنا‬ ‫فتتكون‬ ‫المراتب‬ ‫من‬
((n‫المعادالت‬ ‫هذه‬ ‫نحل‬ ‫ثم‬ ‫المعادالت‬ ‫من‬‫إلٌجاد‬‫بداللة‬ ‫االختٌارٌة‬ ‫الثوابت‬(y , x‫ومشتقات‬y
‫بالنسبة‬‫إلى‬xً‫ة‬‫عاد‬ ً‫والت‬ ‫التفاضلٌة‬ ‫المعادلة‬ ‫على‬ ‫لنحصل‬ ‫العام‬ ‫الحل‬ ً‫ف‬ ‫تعوٌضها‬ ‫ثم‬‫تأخذ‬
ً‫التال‬ ‫الشكل‬:
0),,,,(  xyyyyf
‫التالٌة‬ ‫القاعدة‬ ‫نستنتج‬ ‫المثالٌن‬ ‫هذٌن‬ ‫ومن‬:
06  yyy
)2(32 yyyy 
‫الفصل‬:‫األسبوع‬ ‫الثامن‬:‫العشرون‬

263. ‫يضبل‬3:ٛ٘ َ‫اٌؼا‬ ‫دٍٙا‬ ٟ‫اٌر‬ ‫اٌرفاػٍ١ح‬ ‫اٌّؼادٌح‬ ‫جذ‬
1............4 3
BxAxy 
‫الحل‬:‫نشتق‬‫الثوابت‬ ‫بعدد‬ ‫العام‬ ‫الحل‬(‫العام‬ ‫الحل‬ ‫نشتق‬ ‫لذلك‬‫األولى‬‫والثانٌة‬)
2............12 2
BxAxy 
‫المعادلة‬ ‫من‬3‫على‬ ‫نحصل‬‫أن‬:
x
y
B
24


‫عن‬ ‫وبالتعوٌض‬Bً‫ف‬‫المعادلة‬2‫على‬ ‫نحصل‬‫أن‬:2
24
12 x
x
y
yA


‫أن‬ ‫ٌنتج‬:
3.................240 Bxy 
xyyA 
2
1
‫الفصل‬:‫األسبوع‬ ‫الثامن‬:‫العشرون‬

264. ٓ‫ػ‬ ‫ٚتاٌرؼٛ٠غ‬B , A‫اٌرفاػٍ١ح‬ ‫اٌّؼادٌح‬ ٍٝ‫ػ‬ ً‫ٔذظ‬ َ‫اٌؼا‬ ً‫اٌذ‬ ٟ‫ف‬ ‫٠ساٚ٠ّٙا‬ ‫تّا‬
3
)
24
(4)
2
1
( x
x
y
xxyyy


‫التفاضلٌة‬ ‫المعادلة‬ ‫على‬ ‫نحصل‬ ‫التبسٌط‬ ‫وبعد‬
0332
 yyyx
xyyA 
2
1
‫الفصل‬:‫األسبوع‬ ‫الثامن‬:‫العشرون‬

265. 1-‫اآلتٌة‬ ‫المعادالت‬ ‫من‬ ‫كل‬ ‫ودرجة‬ ‫رتبة‬ ‫جد‬:
2
1
3
4
yy )4(
0)3(
yyy
yexy 222
)( 
xey x
32

xy 3
5
‫الفصل‬:‫األسبوع‬ ‫الثامن‬:‫العشرون‬

266. 2-‫هو‬ ‫العام‬ ‫حلها‬ ً‫الت‬ ‫التفاضلٌة‬ ‫المعادلة‬ ‫جد‬
2
1
3
4 cBxAxy  2
)3sin( xBAey x

BAxy 
2
AAxy 
‫الفصل‬:‫األسبوع‬ ‫الثامن‬:‫العشرون‬

267. 1
‫الفصل‬:‫الثامن‬‫األسبوع‬:‫العشرون‬ ‫و‬ ‫الحادي‬
‫على‬ ‫ذلك‬ ‫وٌعتمد‬ ‫المعادالت‬ ‫من‬ ‫النوع‬ ‫هذا‬ ‫لحل‬ ‫طرق‬ ‫عدة‬ ‫هناك‬‫المعادالت‬ ‫إن‬‫وفٌما‬ ‫التفاضلٌة‬
‫الطرق‬ ‫تلك‬ ً‫ٌل‬:-
‫المتغٌرٌن‬ ‫فصل‬:-variables separable
‫التالٌة‬ ‫التفاضلٌة‬ ‫معادلة‬ ‫وضع‬ ‫أمكن‬ ‫إذا‬
..................).........().( xNxM
dx
dy

‫إن‬ ‫إذ‬M(X)‫لــ‬ ‫دالة‬X‫وان‬N(y)‫لــ‬ ‫دالة‬y‫نضع‬ ‫المعادالت‬ ‫من‬ ‫النوع‬ ‫هذا‬ ‫ولحل‬
‫وبالشكل‬ ‫المعادلة‬ً‫التال‬
dxxM
yn
dy
)(
)(
1
1

268. ‫انفصلت‬ ‫المتغٌرات‬ ‫ان‬ ‫اي‬,‫للطرفٌن‬ ‫التكامل‬ ‫وٌاخذ‬
  cdxxM
dx
dy
)(
‫ان‬ ‫اذ‬c‫اختٌاري‬ ‫ثابت‬
‫مثال‬:-‫التالٌة‬ ‫التفاضلٌة‬ ‫المعادالت‬ ‫حل‬ ‫اوجد‬:-
1 x
dx
dy

xdxdy 
   cxdxdy
c
x
y 
2
2
‫الفصل‬:‫الثامن‬‫األسبوع‬:‫العشرون‬ ‫و‬ ‫الحادي‬

269. 2 yx
e
dx
dy 
 2 ‫عندما‬0,0  xy
yx
ee
dx
dy
.2

dxe
ex
dy x2

cdxedye xy
 
 2
cee xy
  2
2
1
‫الفصل‬:‫الثامن‬‫األسبوع‬:‫العشرون‬ ‫و‬ ‫الحادي‬

270. ‫ٚػٕذِا‬x=0,y=0ْ‫فأ‬
-e0 = 1/2 e0 + c c = -1 – 1/2 = - 3/2
ٛ٘ ‫اٌرفاػٍ١ح‬ ‫تاٌّؼادٌح‬ ‫اٌخاص‬ ً‫اٌذ‬ ْ‫فأ‬ ٗ١ٍ‫ٚػ‬
-e-y 1/2 e2x
e-y = 3/2 – 1/2 e2x
3
𝐝𝐲
𝐝𝐱
= −𝟐𝐱 𝐭𝐚𝐧 𝐲
xdx
y
dy
2
tan

2
,0  yx 𝜋 ‫عندما‬
  cxdxdy
y
y
2
sin
cos
‫الفصل‬:‫الثامن‬‫األسبوع‬:‫العشرون‬ ‫و‬ ‫الحادي‬

271. ‫الفصل‬:‫األسبوع‬ ‫الثامن‬:‫العشرون‬ ‫و‬ ‫الحادي‬
cxyLn  2
sin
cLn  0
2
sin
0c
2
sin xyLn 
‫عن‬ ‫وبالتعوٌض‬
‫هو‬ ‫للمعادلة‬ ‫الخاص‬ ‫الحل‬ ‫فان‬
0,
2
 xy 𝜋𝜋
4

272. ‫الجزئٌة‬ ‫الكسور‬ ‫باستخدام‬
‫إن‬ ‫أي‬
‫الفصل‬:‫األسبوع‬ ‫الثامن‬:‫العشرون‬ ‫و‬ ‫الحادي‬

273. ْ‫إ‬ ‫ٔفشع‬ ‫اٌّؼادالخ‬ ِٓ ‫إٌٛع‬ ‫٘زا‬ ً‫ٌٚذ‬:-
y = vx
𝑑𝑦
𝑑𝑥
= 𝑥
𝑑𝑣
𝑑𝑥
+v
ْ‫إ‬ ٞ‫أ‬:-
x
𝑑𝑣
𝑑𝑥
+ v = g v
‫٠ٕرج‬ ‫اٌّرغ١شاخ‬ ً‫ٚتفظ‬:-
𝑑𝑣
𝑔 𝑣 − 𝑣
=
𝑑𝑥
𝑥
2
ً‫االت‬ ‫بالشكل‬ ‫وضعها‬ ‫ٌمكن‬ ً‫الت‬ ‫التفاضلٌة‬ ‫المعادلة‬ ً‫وه‬
𝑑𝑦
𝑑𝑥
= 𝑔(
𝑦
𝑥
)
‫الفصل‬:‫األسبوع‬ ‫الثامن‬:‫العشرون‬ ‫و‬ ‫الحادي‬

274. ً‫ٔذظ‬ ٓ١‫ٌٍطشف‬ ًِ‫اٌرىا‬ ‫تأخز‬ ٚ:-
𝑑𝑣
𝑔 𝑣 − 𝑣
=
𝑑𝑥
𝑥
+ 𝑐
ٓ‫ػ‬ ‫اٌرؼٛ٠غ‬ ُ‫٠ر‬ ُ‫ث‬
𝑦
𝑥
=vٓ٠‫اٌّرغ١ش‬ ‫تذالٌح‬ ‫اٌّؼادٌح‬ ٍٝ‫ػ‬ ‫ٌٍذظٛي‬x , y.
‫ايضهخ‬:-‫اٌراٌ١ح‬ ‫اٌرفاػٍ١ح‬ ‫ٌٍّؼادالخ‬ ً‫اٌذ‬ ‫اٚجذ‬:-
𝑦 =
𝑥 2 : 𝑦 2
𝑥 𝑦
𝑦 =
𝑥2
𝑥𝑦
+
𝑦2
𝑥𝑦
=
𝑥
𝑦
+
𝑦
𝑥
𝑑𝑦
𝑑𝑥
= 𝑥
𝑑𝑣
𝑑𝑥
+ 𝑣
x
𝑑𝑣
𝑑𝑥
+ 𝑣 =
𝑥
𝑣𝑥
+
𝑣𝑥
𝑥
‫الفصل‬:‫األسبوع‬ ‫الثامن‬:‫العشرون‬ ‫و‬ ‫الحادي‬
1
‫ان‬ ‫بفرض‬y=vx‫فان‬

275. ‫الفصل‬:‫األسبوع‬ ‫الثامن‬:‫العشرون‬ ‫و‬ ‫الحادي‬
x
𝒅𝒗
𝒅𝒙
= +𝐯 =
𝟏
𝒗
+ 𝒗
𝒗𝒅𝒙 =
𝒅𝒙
𝒙
𝐯𝐝𝐯 =
𝐝𝐱
𝐱
+ 𝐜
𝑣2
2
= ln 𝑥 + 𝑐 𝑣2
= 2 ln 𝑥 + 2𝑐
𝒙
𝒅𝒗
𝒅𝒙
=
𝟏
𝒗

276. 𝟐𝒙𝒚 𝒚 − 𝒚 𝟐
+𝒙 𝟐
= 𝟎
𝟐𝒚 −
𝒚 𝟐
𝒙𝒚
+
𝒙 𝟐
𝒙𝒚
= 𝟎
𝟐𝒚 −
𝒚
𝒙
−
𝒙
𝒚
= 𝟎
𝒚 = 𝒗𝒙 →
𝒅𝒚
𝒅𝒙
= 𝒗 + 𝒙
𝒅𝒗
𝒅𝒙
𝟐 𝒗 + 𝒙
𝒅𝒗
𝒅𝒙
=
𝒗𝒙
𝒙
+
𝒙
𝒗𝒙
𝟐𝒗 + 𝟐𝒙
𝒅𝒗
𝒅𝒙
= 𝒗 +
𝟏
𝒗
𝟐𝒙
𝒅𝒗
𝒅𝒙
=
𝟏
𝒗
− 𝒗 =
𝟏 − 𝒗 𝟐
𝒗
→
𝟐𝒗 𝒅𝒗
𝟏 − 𝒗 𝟐
=
𝒅𝒙
𝒙
2
‫الفصل‬:‫األسبوع‬ ‫الثامن‬:‫العشرون‬ ‫و‬ ‫الحادي‬

277. ‫الفصل‬:‫األسبوع‬ ‫الثامن‬:‫العشرون‬ ‫و‬ ‫الحادي‬
ln 1 − 𝑣2 = ln 𝑥 + 𝑐
ln
1;𝑣2
𝑥
= 𝑐
1;𝑣2
𝑥
= 𝑒 𝑐 = 𝑐1
1 −
𝑦2
𝑥2
𝑥
= 𝑐1
𝑥2 − 𝑦2
𝑥
= 𝑐1 𝑦2 − 𝑥2
= 𝑥𝑐1

278. 𝒙 𝟐
+ 𝟑𝒚 𝟐
𝒅𝒙 − 𝟐𝒙𝒚 𝒅𝒚 = 𝟎
𝑑𝑦
𝑑𝑥
=
𝑥2
+ 3𝑦2
2𝑥𝑦
=
𝑥
2𝑦
+
3𝑦
2𝑥
y = v x‫ٔفشع‬ْ‫ا‬
𝑑𝑦
𝑑𝑥
= 𝑣 + 𝑥
𝑑𝑣
𝑑𝑥
𝑣 + 𝑥
𝑑𝑣
𝑑𝑥
=
𝑥
2𝑦
+
3
2
𝑦
𝑥
𝑥
𝑑𝑣
𝑑𝑥
=
2
2𝑣
+
3
2
𝑣 − 𝑣 =
1
2𝑣
+
1
2
𝑣 =
1 + 𝑣2
2𝑣
2𝑣 𝑑𝑥
1 + 𝑣2
=
𝑑𝑥
𝑥
3
‫الفصل‬:‫األسبوع‬ ‫الثامن‬:‫العشرون‬ ‫و‬ ‫الحادي‬

279. ln 1 + 𝑣2
= ln 𝑥 + 𝑐
ln
1 + 𝑣2
𝑥
= 𝑐
1 + 𝑣2
𝑥
= 𝑒 𝑐
= 𝑐
ٓ‫ػ‬ ‫ٚتاٌرؼٛ٠غ‬vً‫ٔذظ‬:-
1 +
𝑦2
𝑥2
𝑥
= 𝑐
𝑥2
+ 𝑦2
𝑥
= 𝑐
𝑥2
+ 𝑦2
= 𝑐𝑥
‫الفصل‬:‫الثامن‬‫األسبوع‬:‫العشرون‬ ‫و‬ ‫الحادي‬

280. 𝑑𝑦
𝑑𝑥
+ 𝑝 𝑥 𝑦 = 𝑄(𝑥)
ْ‫ا‬ ‫د١ث‬p(x),Q(x)‫ٌــــــ‬ ‫دٚاي‬ ‫ّ٘ا‬(x) .ً‫ِث‬ ‫داٌح‬ ‫ا٠جاد‬ ‫ٔذاٚي‬ ‫اٌّؼادٌح‬ ٖ‫٘ز‬ ً‫ٌٚذ‬
I(x)‫ِشرمح‬ ‫اال٠سش‬ ‫اٌطشف‬ ‫٠ظثخ‬ ‫اٌذاٌح‬ ٖ‫تٙار‬ ‫اٌّؼادٌح‬ ‫ػشب‬ ‫ػٕذ‬ ‫تذ١ث‬
‫ػشب‬ ً‫داط‬I(x).yْ‫فا‬:-
I(x)
𝑑𝑦
𝑑𝑥
+I(x) p(x) =I(x) Q(x)
ْ‫إ‬ ٞ‫أ‬:-
I x
𝑑𝑦
𝑑𝑥
+ I x p x y =
𝑑(𝐼 − 𝑦)
𝑑𝑥
3
‫الفصل‬:‫األسبوع‬ ‫الثامن‬:‫العشرون‬ ‫و‬ ‫الحادي‬
ً‫التال‬ ‫بالشكل‬ ‫تكون‬ ً‫الت‬ ‫المعادلة‬ ً‫وه‬

281. ‫الفصل‬:‫األسبوع‬ ‫الثامن‬:‫العشرون‬ ‫و‬ ‫الحادي‬
‫ٌنتج‬ ‫الحدود‬ ‫واختصار‬ ‫االٌمن‬ ‫الطرف‬ ‫فتح‬ ‫وعند‬:-
𝑑I(x)
𝑑𝑥
= I x . p x
‫ٌنتج‬ ‫المتغٌرات‬ ‫وبفصل‬:-
𝑑𝐼(𝑥)
𝑑𝑥
= 𝑝 𝑥 𝑑𝑥
ln(𝐼 𝑥 ) = 𝑝(𝑥) 𝑑𝑥 + ln 𝑐
𝐼 𝑥 = 𝑐 𝑒 𝑝(𝑥) 𝑑𝑥
𝐼 𝑥 = 𝑒 𝑝 𝑥 𝑑𝑥
ً‫التكامل‬ ‫بالعامل‬ ‫الدالة‬ ‫هذه‬ ‫وتسمى‬(Integration factor)‫هذا‬ ‫وباستعمال‬
ً‫ٌل‬ ‫كما‬ ً‫االول‬ ‫العلقة‬ ‫تصبح‬ ‫العامل‬:-
‫عندما‬c=1‫فان‬

282. 𝑑(𝐼 𝑥 . 𝑦)
𝑑𝑥
= 𝐼 𝑥 𝑄(𝑥)
ًِ‫اٌرىا‬ َ‫تاسرخذا‬ ‫ٚٔذٍٙا‬:-
𝐼 𝑥 . 𝑦 = 𝐼(𝑥) . 𝑄 𝑥 𝑑𝑥 + 𝑐
‫الفصل‬:‫األسبوع‬ ‫الثامن‬:‫العشرون‬ ‫و‬ ‫الحادي‬

283. 𝑑𝑦
𝑑𝑥
+ 𝑦 = 𝑒 𝑥
P(x) = 1 → 𝑝(𝑥) 𝑑𝑥 = 𝑥
ٍِٟ‫اٌرىا‬ ًِ‫فاٌؼا‬IFٛ٘𝑒 𝑥
‫٠ٕرج‬ ٍِٟ‫اٌرىا‬ ًِ‫تاٌؼا‬ ‫اٌرفاػٍ١ح‬ ‫اٌّؼادٌح‬ ٟ‫ؽشف‬ ‫ٚتؼشب‬:-
𝑑𝑦
𝑑𝑥
+ 𝑦 𝑒 𝑥
= 1
𝑑
𝑑𝑥
𝑦 𝑒 𝑥 = 1
𝑦 𝑒 𝑥
= 𝑥 + 𝑐
1
‫الفصل‬:‫األسبوع‬ ‫الثامن‬:‫العشرون‬ ‫و‬ ‫الحادي‬
‫مثال‬:-‫التالٌة‬ ‫التفاضلٌة‬ ‫للمعادالت‬ ‫العام‬ ‫الحل‬ ‫اوجد‬:-

284. 2 𝑑𝑦
𝑑𝑥
+
𝑦
𝑥
= 𝑥2

x
xp
1
)(
‫الفصل‬:‫األسبوع‬ ‫الثامن‬:‫العشرون‬ ‫و‬ ‫الحادي‬
𝑝(𝑥) 𝑑𝑥 =
1
𝑥
𝑑𝑥 = ln 𝑥
𝐼 . 𝐹 𝑒ln 𝑥
= 𝑥
𝑥
𝑑𝑦
𝑑𝑥
+
𝑦
𝑥
= 𝑥2
− 𝑥
𝑥𝑦 =
𝑥4
4
+ 𝑐

285. 𝑥
𝑑𝑦
𝑑𝑥
+ 2𝑦 = 𝑥4
𝑑𝑦
𝑑𝑥
+
2
𝑥
𝑦 = 𝑥3
P(x) = 2/x → 𝑝(𝑥) 𝑑𝑥 =
2
𝑥
𝑑𝑥 = 2 ln 𝑥
I . F =𝑒2 ln 𝑥
= 𝑥2
𝑥2 𝑑𝑦
𝑑𝑥
+
2
𝑥
𝑦 = 𝑥5
𝑑 𝑦𝑥2 = 𝑥5
𝑦𝑥2=
𝑥6
6
+ 𝑐
3
‫الفصل‬:‫األسبوع‬ ‫الثامن‬:‫العشرون‬ ‫و‬ ‫الحادي‬

286. ٌٟٛٔ‫تش‬ ‫تّؼادٌح‬ ‫ذؼشف‬ ‫اٌراٌ١ح‬ ‫اٌّؼادٌح‬ ْ‫إ‬:-
𝑑𝑦
𝑑𝑥
+ 𝑝𝑦 = 𝑄 𝑦 𝑛
ْ‫إ‬ ‫ار‬Q , p‫ٌــــ‬ ‫دٚاي‬)x(‫فمؾ‬)n‫ثاتد‬(‫ّ٘ا‬ ‫اٌّؼادٌح‬ ٖ‫ٌٙار‬ ْ‫داٌرا‬ ‫ٕٚ٘ان‬:-
1-‫ػٕذِا‬n=1ٓ٠‫اٌّرغ١ش‬ ً‫فظ‬ ‫تطش٠مح‬ ً‫ٚذذ‬ ‫إٌّفظٍح‬ ‫ٔٛع‬ ِٓ ‫اٌّؼادٌح‬ ْٛ‫ذى‬.
2-‫ػٕذِا‬n≠1ٟ‫ف‬ ‫اٌّؼادٌح‬ ٟ‫ؽشف‬ ‫ٔؼشب‬𝑦1;𝑛
‫إٌاذج‬ ْٛ‫ف١ى‬:-
𝑦;𝑛
𝑑𝑦
𝑑𝑥
+ 𝑝𝑦1;𝑛 = 𝑄
ْ‫إ‬ ْ‫اال‬ ‫ٌٕفشع‬𝑍 = 𝑦1;𝑛
ْٛ‫ف١ى‬
𝑑𝑧
𝑑𝑥
= 1 − 𝑛 𝑦;𝑛
𝑑𝑦
𝑑𝑥
ْٛ‫٠ى‬ ‫ٚتاٌرؼٛ٠غ‬
1
1;𝑛
𝑑𝑧
𝑑𝑥
+ 𝑝𝑧 = 1 − 𝑛 𝑄
‫الفصل‬:‫األسبوع‬ ‫الثامن‬:‫العشرون‬ ‫و‬ ‫الحادي‬

287. ‫تـــ‬ ‫اٌّؼادٌح‬ ‫ٔؼشب‬𝑦;2ْٛ‫ذى‬𝑦;2 𝑑𝑦
𝑑𝑥
+
1
𝑥𝑦
= 1
ْ‫إ‬ ‫ٔفشع‬)𝑧 = 𝑦;1(ْٛ‫فرى‬)
𝑑𝑧
𝑑𝑥
= −𝑦;2 𝑑𝑦
𝑑𝑥
(ْٛ‫٠ى‬ ‫ٚتاٌرؼٛ٠غ‬
−
𝑑𝑧
𝑑𝑥
+
𝑧
𝑥
= 1
𝑑𝑧
𝑑𝑥
−
𝑧
𝑥
= −1
1
‫الفصل‬:‫األسبوع‬ ‫الثامن‬:‫العشرون‬ ‫و‬ ‫الحادي‬
‫أو‬
1
1 − 𝑛
=
𝑑𝑧
𝑑𝑥
+ 𝑝𝑧 = 𝑄
‫لـــ‬ ‫خطٌة‬ ‫معادلة‬ ً‫ه‬ ‫االخٌرة‬ ‫المعادلة‬ ‫وان‬Z‫بإٌجاد‬ ‫الحل‬ ‫ونواصل‬
ً‫التكامل‬ ‫العامل‬𝐼 . 𝐹 = 𝑒 1;𝑛 𝑝 𝑑𝑥
‫مثال‬:-‫التالٌة‬ ‫التفاضلٌة‬ ‫المعادالت‬ ‫حل‬....𝑑𝑦
𝑑𝑥
+
𝑦
𝑥
= 𝑦2

288. p(x) = 1/x , 𝑝 𝑥 𝑑𝑥 = −
𝑑𝑥
𝑥
= ln 𝑥
ْ‫ا‬ ٞ‫ا‬:-
𝐼 . 𝐹 = 𝑒 𝑝 𝑥 𝑑𝑥
= 𝑒; ln 𝑥
=
1
𝑥
‫٠ٕرج‬ ٍِٟ‫اٌرىا‬ ًِ‫تاٌؼا‬ ‫ٚتاٌؼشب‬:-
𝑧
𝑥
= − ln 𝑥 + 𝑐
1 + 𝑥𝑦 ln 𝑥 = 𝑐𝑦
‫الفصل‬:‫األسبوع‬ ‫الثامن‬:‫العشرون‬ ‫و‬ ‫الحادي‬

289. ‫الفصل‬:‫األسبوع‬ ‫الثامن‬:‫العشرون‬ ‫و‬ ‫الحادي‬
2 𝑑𝑦
𝑑𝑥
− 𝑦 tan 𝑥 =
sin 𝑥 .cos2 𝑥
𝑦2
ً‫ف‬ ‫المعادلة‬ ‫نضرب‬𝑦2‫على‬ ‫نحصل‬:-
𝑦2
𝑑𝑦
𝑑𝑥
− 𝑦3 tan 𝑥 = sin 𝑥 cos2 𝑥
‫نفرض‬‫ان‬← 𝑧 = 𝑦3𝑑𝑧
𝑑𝑥
= 3𝑦2 𝑑𝑦
𝑑𝑥
‫وبالتعوٌض‬
1
3
𝑑𝑧
𝑑𝑥
− 𝑧 tan 𝑥 = sin 𝑥 cos2 𝑥
𝑑𝑧
𝑑𝑥
− 3 tan 𝑥 . 𝑧 = sin 𝑥 cos2 𝑥
∴p(x)=-3tan → 𝑝𝑥 = −3 tan 𝑥 𝑑𝑥 = −3 ln cos 𝑥
I . F =𝑒 𝑝 𝑥 𝑑𝑥
= 𝑒ln cos3 𝑥 = cos3 𝑥

290. 𝑑
𝑑𝑥
𝑧 cos3 𝑥 = 3 sin 𝑥 cos5 𝑥
𝑧 cos3
𝑥 =
;3
6
cos6
𝑥 + 𝑐
2𝑦3
cos3
𝑥 + cos6
𝑥 = 𝑐
‫الفصل‬:‫األسبوع‬ ‫الثامن‬:‫العشرون‬ ‫و‬ ‫الحادي‬

291. ‫ٔٛع‬ ِٓ ‫اٌرفاػٍ١ح‬ ‫اٌّؼادٌح‬ ‫وأد‬ ‫ارا‬
M(x , y) dx + N(x , y) dy =0
ْ‫ا‬ ‫تذ١ث‬
𝑑𝑀
𝑑𝑦
=
𝑑𝑁
𝑑𝑥
‫ذاِح‬ ّٝ‫ذس‬ ‫اٌرفاػٍ١ح‬ ‫اٌّؼادٌح‬ ْ‫فأ‬.
ً‫ِث‬ ‫داٌح‬ ‫تئ٠جاد‬ ‫٠رٍخض‬ ً‫اٌذ‬ ‫اسٍٛب‬ ْ‫ٚا‬f(x , y)ْ‫إ‬ ‫تذ١ث‬:-
𝑀 𝑥, 𝑦 =
𝑑 𝑓(𝑥,𝑦)
𝑑𝑥
, 𝑁 𝑥, 𝑦 =
𝑑 𝑓(𝑥,𝑦)
𝑑𝑦
4
‫الفصل‬:‫األسبوع‬ ‫الثامن‬:‫العشرون‬ ‫و‬ ‫الحادي‬

292. 𝑦2
𝑑𝑥 + 2𝑥𝑦 𝑑𝑦 = 0
𝑀 𝑥, 𝑦 = 𝑦2
→
𝑑𝑀
𝑑𝑦
= 2𝑦
𝑁 𝑥, 𝑦 = 2𝑥𝑦 →
𝑑𝑁
𝑑𝑥
= 2𝑦
‫ذاِح‬ ‫اٌرفاػٍ١ح‬ ‫اٌّؼادٌح‬ ْ‫فا‬
‫اٌذاٌح‬ ‫ا٠جاد‬ ‫ٌٚغشع‬f (x , y)ْ‫إ‬ ‫ٔالدظ‬
𝑑 𝑥𝑦2
= 2𝑥𝑦 𝑑𝑦 + 𝑦2
𝑑𝑥
‫ٚتاٌرؼٛ٠غ‬𝑑 𝑥𝑦2
= 0
𝑥𝑦2
= 𝑐
1
‫الفصل‬:‫األسبوع‬ ‫الثامن‬:‫العشرون‬ ‫و‬ ‫الحادي‬
‫مثال‬:-‫التالٌة‬ ‫التفاضلٌة‬ ‫المعادالت‬ ‫حل‬ ‫اوجد‬:-

293. ‫الفصل‬:‫األسبوع‬ ‫الثامن‬:‫العشرون‬ ‫و‬ ‫الحادي‬
2
𝑀 𝑥, 𝑦 = 3𝑥2 + 2𝑥𝑦 →
𝑑𝑀
𝑑𝑦
= 3𝑥2 + 2𝑥
𝑁 𝑥, 𝑦 = 𝑥3 + 𝑥2 + 2𝑦 →
𝑑𝑁
𝑑𝑥
= 3𝑥2 + 2𝑥
‫ان‬ ‫بما‬
𝑑𝑁
𝑑𝑥
=
𝑑𝑀
𝑑𝑦
‫تامة‬ ‫فالمعادلة‬
𝑑 𝑓(𝑥,𝑦)
𝑑𝑥
= 3𝑥2
+ 2𝑥𝑦 → (1)
𝑑 𝑓(𝑥,𝑦)
𝑑𝑦
= 𝑁 𝑥, 𝑦 = 𝑥3 + 𝑥2 + 2𝑦 → (2)
3𝑥2
𝑦 + 2𝑥𝑦 𝑑𝑥 + 𝑥3
+ 𝑥2
+ 2𝑦 𝑑𝑦 = 0

294. ‫ٌٍّؼادٌح‬ ًِ‫اٌرىا‬ ‫ػٍّ١ح‬ ‫ٚتئجشاء‬)1(ً‫ٔذظ‬....
𝑓 𝑥, 𝑦 = 𝑥3 𝑦 + 𝑥2 𝑦 → 3
‫اٌّؼادٌح‬ ‫ٔىرة‬ ُ‫ث‬)3(ً‫تاٌشى‬......
𝑓 𝑥, 𝑦 = 𝑥3 𝑦 + 𝑥2 𝑦 + ∅(𝑦) → (4)
‫الفصل‬:‫األسبوع‬ ‫الثامن‬:‫العشرون‬ ‫و‬ ‫الحادي‬
‫معرفة‬ ‫نود‬ ‫اننا‬ ‫اذ‬∅(𝑦)‫لـــ‬ ‫المشتقة‬ ‫واٌجاد‬y‫للمعادلة‬((4‫ٌنتج‬:-
𝑑 𝑓(𝑥, 𝑦)
𝑑𝑦
= 𝑥3 + 𝑥2 + ∅(𝑦)
‫معادلة‬ ‫وبمساواة‬(5)‫معادلة‬ ‫مع‬(2)‫ٌنتج‬:-
𝑥3 + 𝑥2 + 2𝑦 = 𝑥3 + 𝑥2 + ∅(𝑦)

295. ْ‫إ‬ ‫ٔجذ‬∅ 𝑦 = 2𝑦ْ‫ا‬ ٞ‫أ‬:‫ـــــ‬
∅ 𝑦 = 𝑦2
+ 𝑐
‫اٌذاٌح‬ ْٛ‫ٚذى‬𝑓 (𝑥, 𝑦)ٍٟ٠ ‫وّا‬:-
𝑓 𝑥, 𝑦 = 𝑥3 𝑦 + 𝑦2 + 𝑦2 + 𝑐
ٛ٘ ‫ذفاػٍٙا‬ ٟ‫اٌر‬:-
𝑀 𝑥, 𝑦 𝑑𝑥 + 𝑁 𝑥, 𝑦 𝑑𝑦
ٛ٘ َ‫اٌؼا‬ ً‫اٌذ‬ ‫ٚ٠ظثخ‬:-
𝑥3
𝑦 + 𝑥2
𝑦 + 𝑦2
= 𝐶
‫الفصل‬:‫األسبوع‬ ‫الثامن‬:‫العشرون‬ ‫و‬ ‫الحادي‬

296. 2
3
1
4
5
6
7
‫الفصل‬:‫األسبوع‬ ‫الثامن‬:‫العشرون‬ ‫و‬ ‫الحادي‬
𝑑𝑦
𝑑𝑥
+ 𝑥𝑦 = 𝑥𝑦2
𝑥 Ln 𝑥 𝑦 = 𝑦
𝑥2
+ 𝑦2
𝑑𝑥 + 2𝑥𝑦 𝑑𝑦 = 0
𝑦 =
𝑦
𝑥
+ cos(
𝑦 − 𝑥
𝑥
)
𝑑𝑦
𝑑𝑥
+
𝑦
𝑥
= 𝑦2
𝑑𝑦
𝑑𝑥
=
2𝑥 + 2𝑦 − 2
3𝑥 + 𝑦 − 5
2𝑥𝑦 𝑑𝑥 + 𝑥2 + 1 𝑑𝑦 = 0

297. ‫يطهٕثخ‬ ‫ػذدٌخ‬ ‫َزبئج‬ ‫حضبة‬ ‫غشق‬ ‫ٔرمٍٍى‬ ‫دساصخ‬ ًٍ‫ٌزع‬ ‫انؼذدي‬ ‫انزحهٍم‬ ٌ‫إ‬
‫يؼبنجخ‬ ‫ػهى‬ ٍ‫ي‬ ‫جزءا‬ ‫انؼذدي‬ ‫انزحهٍم‬ ‫ٌٔؼزجش‬ ‫يؼطبح‬ ‫ػذدٌخ‬ ‫ثٍبَبد‬ ٍ‫ي‬
ٔ ‫انًؼهٕيبد‬,ًْ ‫انًطهٕثخ‬ ‫ٔانُزبئج‬ ‫انًذخالد‬ ‫رًضم‬ ‫انًؼطبح‬ ‫انجٍبَبد‬ ‫فزؼزجش‬
ً‫انحضبث‬ ‫ثبنُظبو‬ ‫رًضم‬ ‫انحضبة‬ ‫ٔغشٌمخ‬ ‫انًخشجبد‬,‫انؼذدي‬ ‫انزحهٍم‬ ٌ‫إ‬ ‫كًب‬
‫نًضبئم‬ ‫ػذدٌخ‬ ‫حهٕل‬ ‫ػهى‬ ‫انٕصٕل‬ ‫غشق‬ ‫ٔرحهٍم‬ ‫ٔٔصف‬ ‫ثبشزمبق‬ ‫ٌزؼهك‬
‫االػزٍبدٌخ‬ ‫انججشٌخ‬ ‫انزحهٍهٍخ‬ ‫ثبنطشق‬ ‫حهٓب‬ ‫ػبدح‬ ‫ٌصؼت‬ ‫سٌبظٍخ‬.
‫الفصل‬:‫التاسع‬‫األسبوع‬:‫العشرون‬ ‫و‬ ً‫الثان‬
‫قٌاس‬ ‫اجهزة‬ ‫من‬ ً‫تأت‬ ‫عادة‬ ‫ألنها‬ ‫صحٌحة‬ ‫المدخلة‬ ‫البٌانات‬ ‫تكون‬ ‫ما‬ ‫نادرا‬
‫اخر‬ ‫أو‬ ‫نوع‬ ‫من‬,‫هناك‬ ‫إن‬ ‫كما‬ ‫اٌضا‬ ‫اخطاء‬ ‫على‬ ‫تشمل‬ ‫فالمعلومات‬ ‫لذلك‬
‫االخطاء‬ ‫انواع‬ ً‫ٌأت‬ ‫وفٌما‬ ‫الحسابٌة‬ ‫الطرٌقة‬ ‫من‬ ً‫تأت‬ ‫اخرى‬ ‫اخطاء‬.

298. ‫االخطبء‬ ‫إَاع‬:-
ْ‫إ‬ ‫ٌٕفشع‬xْ‫ٚا‬ ‫اٌّؼثٛؽ‬ ‫اٌؼذد‬ ً‫ذّث‬x‫ٌٍؼذد‬ ‫اٌرمش٠ث١ح‬ ‫اٌم١ّح‬ ً‫ذّث‬
xٟ‫٠أذ‬ ‫وّا‬ ‫٠ؼشف‬ ‫اٌّطٍك‬ ‫اٌخطأ‬ ْ‫فا‬:-
E= ±(x – x^)
‫تاٌؼاللح‬ ‫٠ؼشف‬ ٟ‫إٌسث‬ ‫اٌخطأ‬ ْ‫إ‬ ُ‫و‬
𝐸𝑟 =
𝐸
𝑥
= 1 −
𝑥∩
𝑥
‫الفصل‬:‫التاسع‬‫األسبوع‬:‫العشرون‬ ‫و‬ ً‫الثان‬
‫تلك‬ ‫انواع‬ ً‫ٌل‬ ‫ما‬ ً‫وف‬‫االخطاء‬:

299. ‫انزمشٌت‬ ‫اخطبء‬:-Round –off Errors
‫تؼغ‬ ٟ‫ف‬ ‫ٚخاطح‬ ‫اٌّشاذة‬ ِٓ ‫ٌؼذد‬ ٓ١‫ِؼ‬ ‫ػذد‬ ‫٠مشب‬ ‫ػٕذِا‬
‫اٌّسرخذِح‬ ‫اٌذاسة‬ ‫آٌح‬ ‫ذسرٛػة‬ ‫ال‬ ‫ػٕذِا‬ ‫اٌذسات١ح‬ ‫اٌؼٍّ١اخ‬
‫اٌؼذد‬ ‫٠مشب‬ ‫فّثال‬ ُ‫اٌشل‬ ‫رٌه‬ ‫ٌّشاذة‬123567‫استؼح‬ ٌٝ‫إ‬
ٍٟ٠ ‫وّا‬ ‫ِشاذة‬1236.ٖ‫ٚ٘ز‬ ‫وسٛس‬ ‫االػذاد‬ ٖ‫٘ز‬ ْٛ‫ذى‬ ‫ٚلذ‬
‫إٌسثح‬ ‫فّثال‬ ‫اٌمطغ‬ ٌٝ‫إ‬ ‫لاتٍح‬ ‫اٌىسٛس‬
1
3
‫تؼغ‬ ٟ‫ف‬ ‫ذىرة‬
ْ‫األد١ا‬0.33ٚ‫أ‬0.333.
1
‫الفصل‬:‫التاسع‬‫األسبوع‬:‫العشرون‬ ‫و‬ ً‫الثان‬

300. ‫الفصل‬:‫التاسع‬‫األسبوع‬:‫العشرون‬ ‫و‬ ً‫الثان‬
2‫االنقطاع‬ ‫اخطاء‬:-
‫تكامل‬ ‫اٌجاد‬ ‫مثال‬ ‫نهائٌة‬ ‫ال‬ ‫بعملٌة‬ ‫منتهٌة‬ ‫عملٌة‬ ‫استبدال‬ ‫من‬ ‫ٌنشأ‬
‫الحقا‬ ‫ستذكر‬ ً‫الت‬ ‫فروق‬ ‫معادلة‬ ‫باستخدام‬ ‫تفاضلٌة‬ ‫معادلة‬,‫حساب‬ ‫أو‬
‫مجموعة‬ ‫بتقرٌب‬ ‫محدود‬ ‫تكامل‬.
3‫واآللة‬ ‫االنسان‬ ‫من‬ ‫تنتج‬ ً‫الت‬ ‫االخطاء‬:-
ٔ‫أ‬ ‫انًؼهٕيبد‬ ‫َمم‬ ‫خالل‬ ٍ‫ي‬ ‫او‬ ‫اخطبء‬ ‫رحذس‬ ٌ‫إ‬ ‫انؼذدٌخ‬ ‫انؼًهٍبد‬ ‫جًٍغ‬ ً‫ف‬ ‫َزٕلغ‬
ٌ‫إ‬ ٍ‫يًك‬ ‫انجذأل‬ ‫ٔحزى‬ ‫حضبثٍخ‬ ‫ػًهٍبد‬ ‫رُفٍز‬ ٍ‫ي‬ ‫خبغئخ‬ ‫َزبئج‬ ‫ػهى‬ ‫انحصٕل‬
ٍ‫ًٌك‬ ‫خطأ‬ ‫ٌحذس‬ ‫فمذ‬ ‫االنكزشٍَٔخ‬ ‫انحبصجبد‬ ‫اصزخذاو‬ ‫ػُذ‬ ‫ايب‬ ‫اخطبء‬ ‫ػهى‬ ‫رحزٕي‬
ْٕ ‫انخطأ‬ ‫صجت‬ ٌ‫كب‬ ‫ارا‬ ‫خبصخ‬ ‫انزذلٍك‬ ‫خالل‬ ٍ‫ي‬ ‫انزمهٍهٓب‬ ٔ‫أ‬ ‫يُٓب‬ ‫انزخهص‬
‫ػهٍٓب‬ ‫صٍطشح‬ ‫ُْبن‬ ‫فهٍش‬ ‫انحبصجبد‬ ‫صججٓب‬ ً‫انز‬ ‫االخطبء‬ ‫ايب‬ ّ‫َفض‬ ٌ‫االَضب‬.

301. ‫يضبل‬(1: )-
ٞ‫أ‬ ‫اٌؼذد‬ ‫ٔفس‬ ٍٝ‫ػ‬ ‫لسّٕا‬ ُ‫ث‬ ‫ػذد‬ ٟ‫ف‬ ‫ِؼ١ٕح‬ ‫ل١ّح‬ ‫ػشتٕا‬ ‫ارا‬
(0.76 X 0.06) ÷ 0.06 = 0.76
‫االطٍ١ح‬ ‫اٌم١ّح‬ ‫ذٕرج‬ ‫فال‬ ‫ػٍّ١ح‬ ً‫و‬ ٟ‫ف‬ ‫اٌرمش٠ة‬ ‫اجش٠ٕا‬ ٌٛ ٓ‫ٌٚى‬
(0.76 X 0.06) ÷ 0.06 = 0.05 ÷ 0.06 = 0.83 ≠ 0.76
ٛ٘ ‫اٌرمش٠ة‬ ِٓ ‫اٌخطأ‬ ‫ِمذاس‬ ْٛ‫ٚ٠ى‬...
E = 0.83 – 0.76 = 0.07
‫الفصل‬:‫التاسع‬‫األسبوع‬:‫العشرون‬ ‫و‬ ً‫الثان‬

302. ‫يضبل‬(2:)-
‫حضبة‬ ‫اسدَب‬ ٕ‫ن‬𝒆
𝟏
𝟑‫انذانخ‬ ‫يؼكٕس‬ ٍ‫ي‬ ‫فمػ‬ ‫حذٔد‬ ‫نخًضخ‬𝒆 𝒙
‫انحبصجبد‬ ٌ‫ٔا‬
‫ػششٌخ‬ ‫يشارت‬ ‫ألسثؼخ‬ ‫رجشي‬,‫االخطبء‬ ‫لٍى‬ ‫أجذ‬.
𝑓 𝑥 = 𝑒 𝑥 , 𝑥 =
1
3
‫جؼٍٕا‬ ٍٛ‫ف‬x=0.3333‫ٌٍم١ّح‬ ‫ورمش٠ة‬
1
3
‫اٌذاٌح‬ ٟ‫ف‬ ٟ‫اترذائ‬ ‫خطأ‬ ‫فٕٙان‬f (x)ْ‫إ‬ ٞ‫أ‬
𝐸1 = 𝑒0.3333 − 𝑒
1
3
= 𝑒0.3333
− 𝑒0.333333
= 𝑒0.3333
1 − 𝑒0.0000333
= 0.0000465196
‫دساب‬ ‫ٚػٕذ‬𝑒 𝑥ٞ‫أ‬ ٌٝٚ‫اال‬ ‫دذٚد‬ ‫ٌخّسح‬:-
𝑓 𝑥 = 1 + 𝑥 +
𝑥2
2!
+
𝑥3
3!
+
𝑥4
4!
‫الفصل‬:‫التاسع‬‫األسبوع‬:‫العشرون‬ ‫و‬ ً‫الثان‬

303. 𝑓 𝑥 = 1 +
1
3
+
(
1
3
)2
2!
+
(
1
3
)3
3!
+
(
1
3
)4
4!
= 1.396090535
𝑓 0.3333
= 1 + 0.3333 +
(0.3333)2
2!
+
(0.3333)3
3!
+
(0.3333)4
4!
= 1.396043828
𝐸2 = 1.396090535 − 1.396043828 = 0.000046707
ٍٟ‫اٌى‬ ‫اٌخطأ‬
𝐸 = 𝐸1 + 𝐸2
= −0.0000465196 + 0.000046707
= 0.000000188
‫الفصل‬:‫التاسع‬‫األسبوع‬:‫العشرون‬ ‫و‬ ً‫الثان‬

304. ‫الفصل‬:‫التاسع‬‫األسبوع‬:‫العشرون‬ ‫و‬ ً‫الثان‬
ً‫الت‬ ‫الحسابٌة‬ ‫العملٌات‬ ‫بعض‬ ‫اجراء‬ ‫ٌسهل‬ ‫الذي‬ ‫ابسط‬ ‫دوال‬ ‫من‬ ‫بطائفة‬ ‫دالة‬ ‫تقرٌب‬ ‫ٌمثل‬
‫االمثلة‬ ً‫ف‬ ‫توضٌحها‬ ‫ٌمكن‬ ‫اخرى‬ ‫فوائد‬ ‫له‬ ‫التقرٌب‬ ‫هذا‬ ‫إن‬ ‫كما‬ ‫والتكامل‬ ‫كالتفاضل‬ ‫ها‬ ‫تحتاج‬
‫التالٌة‬:-
‫مثال‬:-‫قٌمة‬ ‫إلٌجاد‬ ‫حاجة‬ ‫لدٌنا‬ ‫كان‬ ‫لو‬(30.5)sin‫غٌر‬ ‫القٌمة‬ ‫هذه‬ ‫وان‬
‫إن‬ ‫نجد‬ ‫بٌنما‬ ‫الجدول‬ ً‫ف‬ ‫موجودة‬sin (30)‫و‬sin(31)‫تخمٌن‬ ‫فٌمكن‬ ‫معلومة‬
‫القٌمتٌن‬ ‫بتوسط‬ ‫القٌمة‬ ‫تلك‬30 , 31‫أي‬
𝐬𝐢𝐧(𝟑𝟎) + 𝐬𝐢𝐧(𝟑𝟏)
𝟐
= 𝟎. 𝟓𝟎𝟕𝟓𝟏𝟗𝟎𝟒
‫الحقٌقٌة‬ ‫للقٌمة‬ ‫مطابقة‬ ‫غٌر‬ ‫القٌمة‬ ‫هذه‬,‫تقرٌب‬ ‫ووجدنا‬ ‫اكثر‬ ‫قٌم‬ ‫استخدمنا‬ ‫لو‬ ‫ولكن‬
‫القٌمتٌن‬ ‫متوسط‬ ‫من‬ ‫الحقٌقة‬ ‫إلى‬ ‫اقرب‬ ‫منها‬
‫الحدود‬ ‫متعددة‬ ً‫ه‬ ‫للتقرٌب‬ ‫ا‬‫ا‬‫استخدام‬ ‫الدوال‬ ‫اكثر‬ ‫إن‬(polynomials)‫والدوال‬
‫ا‬‫ا‬‫استخدام‬ ‫اكثرها‬ ً‫ه‬ ‫الحدود‬ ‫متعددة‬ ‫ولك‬ ‫النسبٌة‬ ‫االسٌة‬ ‫والدوال‬ ‫المثلثٌة‬.

305. ‫الفصل‬:‫التاسع‬‫األسبوع‬:‫العشرون‬ ‫و‬ ً‫الثان‬
‫مثال‬(2:)-‫كان‬ ‫اذا‬y= f (x)ً‫التال‬ ‫الجدول‬ ً‫ف‬ ‫المبٌنة‬ ‫النقاط‬ ‫عند‬ ‫قٌمتها‬ ‫معلوم‬:-
X = 1 2 4 5
0 2 12 21=F (x)
‫قٌمة‬ ‫احسب‬f(3)‫للنقاط‬ ً‫التربٌع‬ ‫االستكمال‬ ‫باستخدام‬(1,2,4)ً‫التربٌع‬ ‫واالستكمال‬
‫للنقاط‬(5,4,2)‫للنقاط‬ ‫التربٌعٌة‬ ‫االشكال‬ ‫باستخدام‬(4,2,1)
‫إن‬ ‫نفرض‬
𝑓 𝑥 = 𝑎0 + 𝑎1 𝑥1 + 𝑎2 𝑥2
)1.........(..........)1( 210 aaaf 
)2..(..........42)2( 210 aaaf 
)3...(..........164)4( 210 aaaf 
‫على‬ ‫نحصل‬ ‫آنٌا‬ ‫المعادالت‬ ‫هذه‬ ‫وبحل‬:-
1210 ,1,0  aaa

306. ‫الفصل‬:‫التاسع‬‫األسبوع‬:‫العشرون‬ ‫و‬ ً‫الثان‬
‫ان‬ ‫أي‬:
2
)( xxxf 
693)3( f
‫للنقاط‬ ً‫التربٌع‬ ‫االستكمال‬ ‫وباستخدام‬(5,4,2)
‫نفرض‬‫ان‬:2
2110)( xaxaaxf 
𝑓 2 = 𝑎0 + 2𝑎1 + 4𝑎2 →(1)
𝑓 4 = 𝑎0 + 4𝑎1 + 16𝑎2 →(2)
𝑓 6 = 𝑎0 + 5𝑎1 + 25𝑎2 → (𝟑)

307. ٓ١‫اٌساتمر‬ ٓ١‫إٌر١جر‬ َ‫ٚتاسرخذا‬
𝑓 3 =
6 + 5.667
2
= 5.83
𝑓 𝑥 =
8
3
− 3𝑥 +
4
3
𝑥2
𝑓 3 =
8
3
− 9 + 12 =
17
3
= 5.667
‫وبحل‬‫على‬ ‫نحصل‬ ‫آنٌا‬ ‫المعادالت‬ ‫هذه‬:-
𝑎0 =
8
3
, 𝑎1 = −3 , 𝑎2 =
4
3
‫الفصل‬:‫التاسع‬‫األسبوع‬:‫العشرون‬ ‫و‬ ً‫الثان‬

308. 1‫كشاَج‬ ‫ال‬ ‫صٍغخ‬:Lagrange Formula
‫الفصل‬:‫التاسع‬‫األسبوع‬:‫العشرون‬ ‫و‬ ً‫الثان‬
‫منها‬ ‫احلدود‬ ‫متعدد‬ ‫تستخدم‬ ‫اليت‬ ‫الصوغ‬ ‫من‬ ‫العديد‬ ‫هناك‬:-

309. ‫الفصل‬:‫التاسع‬‫األسبوع‬:‫العشرون‬ ‫و‬ ً‫الثان‬
‫مثال‬:-‫للدالة‬ ‫الحدود‬ ‫كثٌر‬ ‫كانت‬ ‫اذا‬f (x)ً‫التال‬ ‫الجدول‬ ً‫ف‬ ‫المعرفة‬:
x = 1 3 4 6
f (x) = 2 10 15 8
‫الحدود‬ ‫متعددة‬ ‫على‬ ‫الحصول‬ ‫فٌمكن‬f (x)ً‫ٌل‬ ‫كما‬:
𝐿0 𝑥 =
(𝑥 − 3)(𝑥 − 4)(𝑥 − 6)
(1 − 3)(1 − 4)(1 − 6)
= −
1
30
𝑥 − 3 𝑥 − 4 𝑥 − 6
𝐿1 𝑥 =
(𝑥 − 1)(𝑥 − 4)(𝑥 − 6)
(3 − 1)(3 − 4)(3 − 6)
=
1
6
(𝑥 − 1)(𝑥 − 4)(𝑥 − 6)
𝐿2 𝑥 =
(𝑥 − 1)(𝑥 − 3)(𝑥 − 6)
(4 − 1)(4 − 3)(4 − 6)
= −
1
6
(𝑥 − 1)(𝑥 − 3)(𝑥 − 6)
𝐿3 𝑥 =
(𝑥 − 1)(𝑥 − 3)(𝑥 − 4)
(6 − 1)(6 − 3)(6 − 4)
=
1
30
(𝑥 − 1)(𝑥 − 3)(𝑥 − 4)

310. 𝑝 𝑥 = −
1
30
𝑥 − 3 𝑥 − 4 𝑥 − 6 𝑥2
+
1
6
𝑥 − 1 𝑥 − 4 𝑥 − 6 𝑥10 −
1
6
𝑥 − 1 𝑥 − 3 𝑥 − 4 𝑥15
+
1
30
𝑥 − 1 𝑥 − 3 𝑥 − 4 𝑥8
ً‫ٔذظ‬ ‫اٌرثس١ؾ‬ ‫ٚتؼذ‬
𝑝 𝑥 = 0.6𝑥3 + 5.4𝑥2 − 9.36667𝑥 + 6.6
‫الفصل‬:‫التاسع‬‫األسبوع‬:‫العشرون‬ ‫و‬ ً‫الثان‬

311. ‫الفصل‬:‫التاسع‬‫األسبوع‬:‫العشرون‬ ‫و‬ ً‫الثان‬
‫مثال‬:-‫للدالة‬ ً‫التال‬ ‫الجدول‬ ‫من‬f (x)‫قٌمة‬ ‫قدر‬f (0.6)‫كرانج‬ ‫ال‬ ‫صٌغة‬ ‫باستخدام‬
‫االستكمالٌة‬.
x : 0.4 0.5 0.7 0.8
f(x) : - 0.9116291 -0.693147 - 0.356675 -0.233144
𝐿0 0.6 =
(0.6 − 0.5)(0.6 − 0.7)(0.6 − 0.8)
(0.4 − 0.5)(0.4 − 0.7)(0.4 − 0.8)
= −
1
6
𝐿1 0.6 =
(0.6 − 0.4)(0.6 − 0.7)(0.6 − 0.8)
(0.5 − 0.4)(0.5 − 0.7)(0.5 − 0.8)
=
2
3
𝐿2 0.6 =
(0.6 − 0.4)(0.6 − 0.5)(0.6 − 0.8)
(0.7 − 0.4)(0.7 − 0.5)(0.7 − 0.8)
=
2
3
𝐿3 0.6 = −
1
6
𝑓 0.6 = −
1
6
−0.916291 +
2
3
−0.693147 +
2
3
− −0.356673
−
1
6
−0.233141 = −0.509975

312. ‫الفصل‬:‫التاسع‬‫األسبوع‬:‫العشرون‬ ‫و‬ ً‫الثان‬
2‫انفشٔق‬ ‫جذأل‬:Differences table
‫انذانخ‬ ‫نمٍى‬ ‫ٔانزمشٌت‬ ‫االصزكًبل‬ ‫اٌجبد‬ ً‫ف‬ ‫انًًٓخ‬ ‫انؼٕايم‬ ٍ‫ي‬ ‫انفشٔق‬ ‫رؼزجش‬f (x)ًْٔ
ٍٍ‫َٕػ‬ ‫ػهى‬:-
‫أ‬-‫االيبيٍخ‬ ‫انفشٔق‬:Forward differences
ٓ١‫ٔمطر‬ ٞ‫أ‬ ٓ١‫ت‬ ‫اٌّسافح‬ ْ‫إ‬ ‫تذ١ث‬ ‫ِشذثح‬ ‫إٌماؽ‬ ‫ِجّٛع‬ ْ‫إ‬ ‫ٔفشع‬
ٞٚ‫ٚذسا‬ ‫ثاترح‬ ٓ١‫ِرراٌ١ر‬hْ‫إ‬ ٞ‫أ‬.
𝑥1 = 𝑥0 + 𝑕
𝑥2 = 𝑥1 + 𝑕 = 𝑥0 + 2𝑕
𝑥𝑖 = 𝑥0 + 𝑖𝑕 𝑖 = 0,1,2,3, … … . , 𝑛
‫االِاِ١ح‬ ‫اٌفشٚق‬ ًِ‫ِؼا‬ ‫ف١ؼشف‬∆‫اٌراٌ١ح‬ ‫تاٌؼالِح‬
∆ 𝑓 𝑥 = 𝑓 𝑥 + 𝑕 + 𝑓(𝑥)

313. ٌ‫إ‬ ‫أي‬
∆ 𝑓0= 𝑓1 − 𝑓0
∆ 𝑓1 = 𝑓2 − 𝑓1
‫اٌثأ١ح‬ ‫االِاِ١ح‬ ‫اٌفشٚق‬ َ‫ا‬∆2 𝑓‫تاٌؼاللح‬ ‫ذؼشف‬
∆2 𝑓 𝑥 = ∆ (∆ 𝑓(𝑥))
= ∆ (𝑓 𝑥 + 𝑕 − 𝑓(𝑥))
= ∆ 𝑓 𝑥 + 2𝑕 − 2 𝑓 𝑥 + 𝑕 + 𝑓 𝑥
= 𝑓 𝑥 + 2𝑕 − 𝑓 𝑥 + 𝑕 − 𝑓 𝑥 + 𝑕 − 𝑓 𝑥
= 𝑓 𝑥 + 2𝑕 − 2 𝑓 𝑥 + 𝑕 + 𝑓(𝑥)
‫ا٠جاد‬ ٓ‫٠ّى‬ ‫االسٍٛب‬ ‫ٚتٕفس‬∆3 𝑓(𝑥)ْ‫فأ‬ َ‫ػا‬ ً‫ٚتشى‬
∆ 𝑛:1 𝑓 𝑥 = ∆ (∆ 𝑛 𝑓(𝑥))
‫الفصل‬:‫التاسع‬‫األسبوع‬:‫العشرون‬ ‫و‬ ً‫الثان‬

314. ‫اسرخذِٕا‬ ‫فارا‬𝑦1 = 𝑓1 = 𝑓(𝑥1)ْ‫فا‬:
∆ 𝑦𝑖 = 𝑦𝑖 + 1 − 𝑦𝑖
∆2 𝑦𝑖 = 𝑦𝑖:2 − 2𝑦𝑖:1 + 𝑦1 = ∆ ∆ 𝑦𝑖 = ∆ (𝑦𝑖:1 − 𝑦𝑖)
ْ‫فأ‬ َ‫ػا‬ ً‫ٚتشى‬:-∆ 𝑘 𝑦𝑖 = ∆ 𝑘;1 𝑦𝑖:1 − ∆ 𝑘;1 𝑦𝑖
‫اٌفشٚق‬ ‫تجذٚي‬ ّٝ‫٠س‬ ‫اٌجذٚي‬ ٟ‫ف‬ ‫اٌفشٚق‬ ‫ذٍه‬ ‫ٚػغ‬ ‫ٚػٕذ‬difference tableُ١‫ٌم‬y
‫اٌّؼطاج‬:-
𝒙𝒊 𝒚𝒊 ∆ ∆ 𝟐 ∆ 𝟑 ∆ 𝟒 ∆ 𝟓
𝑥0 𝑦0 ∆ 𝑦0
𝑥1 𝑦1 ∆ 𝑦1 ∆2 𝑦0 ∆3 𝑦0
𝑥2 𝑦2 ∆ 𝑦2 ∆2
𝑦1 ∆3
𝑦1 ∆4
𝑦0
𝑥3 𝑦3 ∆𝑦3 ∆2 𝑦2 ∆3 𝑦2 ∆4 𝑦1 ∆5 𝑦0
𝑥4 𝑦4 ∆𝑦4 ∆2
𝑦3
𝑥5 𝑦5
‫الفصل‬:‫التاسع‬‫األسبوع‬:‫العشرون‬ ‫و‬ ً‫الثان‬

315. ‫يضبل‬:-‫انزبنٍخ‬ ‫نهمٍى‬ ‫االيبيٍخ‬ ‫انفشٔق‬ ‫جذٔل‬ ‫اكزت‬:-
x = 2 3 4 5 6
f (x) = 5 10 17 26 37
𝒙𝒊 𝒚𝒊 ∆ ∆ 𝟐 ∆ 𝟑
2 5
3 10 5
4 17 7 2
5 26 9 2 0
6 37 11 2 0
‫الفصل‬:‫التاسع‬‫األسبوع‬:‫العشرون‬ ‫و‬ ً‫الثان‬

316. ‫وأد‬ ‫ارا‬)xi , fi(‫اٌّؼشفح‬ ‫إٌماؽ‬ ً‫ذّث‬,ٌٝٚ‫اال‬ ‫اٌخٍف١ح‬ ‫اٌفشٚق‬ ْ‫فا‬𝛻‫ٚاٌثأ١ح‬
𝛻2‫اٌّشذثح‬ ِٓٚKٟ٘𝛻 𝑘ٟ‫واالذ‬ ‫ذؼشف‬:-
𝛻 𝑓𝑖 = 𝑓𝑖 − 𝑓𝑖 − 1
𝛻2 𝑓𝑖 = 𝛻 𝛻 𝑓𝑖 = 𝛻 𝑓𝑖 − 𝑓𝑖 − 1 = 𝛻𝑓𝑖 − 𝛻 𝑓𝑖
𝛻 𝑘
𝑓𝑖 = 𝛻 𝑘;1
𝑓𝑖 − 𝛻 𝑘;1
𝑓𝑖 − 1
‫اسرخذِٕا‬ ‫ٚارا‬𝑓1 = 𝑦1ْ‫فأ‬
𝛻 𝑘 𝑦𝑖 = 𝛻 𝑘;1 𝑦𝑖 − 𝛻 𝑘;1 𝑦𝑖;1
‫ب‬
‫الفصل‬:‫التاسع‬‫األسبوع‬:‫العشرون‬ ‫و‬ ً‫الثان‬

317. ُ١‫ٌم‬ ‫اٌخٍف١ح‬ ‫اٌفشٚق‬ ‫جذٚي‬ ّٝ‫٠س‬ ‫جذٚي‬ ٟ‫ف‬ ‫اٌفشٚق‬ ‫ذٍه‬ ‫ٚػغ‬ ‫ٚػٕذ‬y
ٍٟ٠ ‫ٚوّا‬ ‫اٌّؼطاج‬:-
𝑥𝑖 𝑦𝑖 𝛻 𝛻2
𝛻3
𝛻4
𝛻5
𝑥0 𝑦0
𝑥1 𝑦1 𝛻𝑦1
𝑥2 𝑦2 𝛻𝑦2 𝛻2
𝑦2
𝑥3 𝑦3 𝛻𝑦3 𝛻2
𝑦3 𝛻3
𝑦3
𝑥4 𝑦4 𝛻𝑦4 𝛻2
𝑦4 𝛻3
𝑦4 𝛻4
𝑦4
𝑥5 𝑦5 𝛻𝑦5 𝛻2
𝑦5 𝛻3
𝑦5 𝛻4
𝑦5 𝛻5
𝑦5
‫الفصل‬:‫التاسع‬‫األسبوع‬:‫العشرون‬ ‫و‬ ً‫الثان‬

318. ‫يضبل‬:‫انفشٔق‬ ‫أجذ‬𝛻3
𝑦4 , 𝛻2
𝑦2 , 𝛻𝑦4 𝑦4‫انزبنٍخ‬ ‫انمٍى‬ ‫جذٔل‬ ٍ‫ي‬:
x : 2 3 4 5 6
f (x) : 5 10 14 26 37
𝛻 𝑦4 = 𝑦4 − 𝑦3 = 37 − 26 = 11
𝛻2 𝑦2 = 𝛻 𝑦2 − 𝛻 𝑦1 = 𝑦2 − 𝑦1 − 𝑦1 − 𝑦0
= 17 − 10 − 10 − 5 = 7 − 5 = 2
𝛻3 𝑦4 = 𝛻2 𝑦4 − 𝛻2 𝑦3
= 𝛻 𝑦4 − 𝛻 𝑦3 − 𝛻 𝑦3 + 𝛻 𝑦2
= 𝑦4 − 𝑦3 − 2 𝑦3 − 𝑦2 + 𝑦2 − 𝑦1
= 37 − 26 − 2 26 − 17 + (17 − 10)
= 11 − 18 + 7 = 0
‫الفصل‬:‫التاسع‬‫األسبوع‬:‫العشرون‬ ‫و‬ ً‫الثان‬

319. ‫لٍى‬ ‫كبَذ‬ ‫ارا‬x‫انًضبفبد‬ ‫يزضبٌٔخ‬,‫انذانخ‬ ‫رمذٌش‬ ‫ٔإلٌجبد‬f (x)‫لًٍخ‬ ‫ػُذ‬
‫انحذٔد‬ ‫يزؼذد‬ ‫فُجذ‬ ‫يؼهٕيخ‬ ‫غٍش‬p (x)‫صٍغخ‬ ‫ثبصزخذاو‬ ‫انًؼهٕيخ‬ ‫نهمٍى‬
‫ًْب‬ ٍٍ‫َٕػ‬ ‫ػهى‬ ًْٔ ٍ‫ٍَٕر‬:-
‫أ‬-‫االيبيٍخ‬ ‫نهفشٔق‬ ٍ‫ٍَٕر‬ ‫صٍغ‬:-Newton forward formula
‫دذٚد‬ ‫ِرؼذد‬ ‫إل٠جاد‬ ‫اٌظ١غح‬ ٖ‫٘ز‬ َ‫ذسرخذ‬p (x)‫ٌٍذاٌح‬ ‫ورمش٠ة‬f (x)ُ١‫ل‬ ْٛ‫ذى‬ ‫ػٕذِا‬
𝑥 𝑛, … … , 𝑥1, 𝑥0 ‫ثاترح‬ ‫تّسافح‬ ‫ِرثاػذج‬ h ْ‫إ‬ ٞ‫𝑕𝑕أ‬ = 𝑥𝑖 − 𝑥𝑖;1 . ‫ط١غح‬ ‫وراتح‬ ْ‫فثاإلِىا‬
ٍٟ٠ ‫وّا‬ ‫االِاِ١ح‬ ‫ٌٍفشٚق‬ ٓ‫ٔ١ٛذ‬:-
𝑝 𝑥 = 𝑦0 + 𝑥 − 𝑥0
∆ 𝑦0
𝑖! 𝑕
+ 𝑥 − 𝑥0 𝑥 − 𝑥1
∆2
𝑦0
2! 𝑕2
+ ⋯ ∙∙∙∙∙
+ 𝑥 − 𝑥0 𝑥 − 𝑥1 … … … (𝑥 − 𝑥 𝑛;1)
∆ 𝑛
𝑦0
𝑛! 𝑕 𝑛
3
‫الفصل‬:‫التاسع‬‫األسبوع‬:‫العشرون‬ ‫و‬ ً‫الثان‬

320. ‫يضبل‬(1:)-‫نهذانخ‬ ‫انزمشٌجٍخ‬ ‫انمًٍخ‬ ‫أجذ‬f (x)‫ػُذيب‬x=3.4 , x=2.5ً‫انزبن‬ ‫انجذٔل‬ ً‫ف‬ ‫انًؼهًخ‬ ‫نهمٍى‬:
x : 2 3 4 5 6
f : 5 10 17 26 37
ْٕ ‫االيبيٍخ‬ ‫انفشٔق‬ ‫جذٔل‬ ٌ‫إ‬:-
𝒙𝒊 𝒚𝒊 ∆ ∆ 𝟐
∆ 𝟑
∆ 𝟒
2 5
3 10 5
4 17 7 2
5 26 9 2 0
6 37 11 2 0 0
‫انزبنٍخ‬ ‫انحذٔد‬ ‫يمذاس‬ ‫ػهى‬ ‫َحصم‬ ٍ‫ٍَٕر‬ ‫صٍغ‬ ‫ٔثزطجٍك‬:
𝒑 𝒙 = 𝟓 + 𝒙 − 𝟐
𝟓
𝟏! 𝟏
+ 𝒙 − 𝟐 𝒙 − 𝟑
𝟐
𝟐! 𝟏 𝟐
+ 𝒙 − 𝟐 𝒙 − 𝟑 𝒙 − 𝟒
𝟎
𝟑! 𝟏 𝟑
+ 𝟎 = 𝒙 𝟐
+ 𝟏
ٌ‫إ‬ ‫أي‬:-
𝒑 𝟐. 𝟓 = (𝟐. 𝟓) 𝟐
+𝟏 = 𝟕. 𝟐𝟓
𝒑 𝟑. 𝟒 = (𝟑. 𝟒) 𝟐
+𝟏 = 𝟏𝟐. 𝟓𝟔
‫الفصل‬:‫التاسع‬‫األسبوع‬:‫العشرون‬ ‫و‬ ً‫الثان‬

321. ‫يضبل‬(2)ً‫انزبن‬ ‫االيبيٍخ‬ ‫انفشٔق‬ ‫نجذٔل‬ ‫انضبنضخ‬ ‫انذسجخ‬ ٍ‫ي‬ ‫انحذٔد‬ ‫يزؼذد‬ ‫أجذ‬
𝒙𝒊 𝒚𝒊 ∆𝒚 𝒌 ∆ 𝟐 𝒚 𝒌 ∆ 𝟑 𝒚 𝒌
4 1
6 3 2
8 8 5 3
10 20 12 7 4
ٍٝ‫ػ‬ ً‫ٔذظ‬ ٓ‫ٔ١ٛذ‬ ‫ط١غح‬ ‫ٚترطث١ك‬:-
𝑝 𝑥 = 1 +
2
2
𝑥 − 4 +
3
8
𝑥 − 4 𝑥 − 6
+
4
48
𝑥 − 4 𝑥 − 6 𝑥 − 8
=
1
24
(2𝑥3
− 27𝑥2
+ 142𝑥 − 240)
‫الفصل‬:‫التاسع‬‫األسبوع‬:‫العشرون‬ ‫و‬ ً‫الثان‬

322. ‫ٌــ‬ ‫اٌرمش٠ث١ح‬ ‫اٌم١ّح‬ ‫إل٠جاد‬f (x)ْٛ‫ذى‬ ‫ػٕذِا‬x‫اٌجذاٚي‬ ‫ٔٙا٠ح‬ ‫لشب‬
ٚ‫ا‬(𝑥 𝑛;1 , 𝑥 𝑛) ‫اٌم١ّح‬ ْ‫إ‬ ‫د١ث‬ ‫اٌخٍف١ح‬ ٓ‫ٔ١ٛذ‬ ‫ط١غح‬ َ‫ٔسرخذ‬ ‫فإٔٔا‬
ْ‫ٚا‬ ‫االِاِ١ح‬ ٓ‫ٔ١ٛذ‬ ‫ط١غح‬ ِٓ ‫اٌذم١م١ح‬ ‫اٌم١ّح‬ ٌٝ‫إ‬ ‫الشب‬ ْٛ‫ذى‬ ‫اٌرمش٠ث١ح‬
‫اٌساتمح‬ ‫ٌٍظ١غح‬ ٗ‫ِشات‬ ‫اٌظ١غح‬ ٖ‫٘ار‬)‫االِاِ١ح‬ ٓ‫ٔ١ٛذ‬ ‫ط١غح‬(‫تاٌرؼٛ٠غ‬
ٓ‫ػ‬∆‫تـ‬𝛻ٍٟ٠ ‫وّا‬ ‫وراترٙا‬ ٓ‫٠ّى‬ ‫اٌظ١غح‬ ٖ‫٘ار‬ ْ‫ٚا‬:-
𝑄 𝑥 = 𝑦𝑛 + 𝑥 − 𝑥 𝑛
𝛻 𝑦𝑛
1! 𝑕
+ 𝑥 − 𝑥 𝑛 𝑥 − 𝑥 𝑛;1
𝛻2
𝑦𝑛
2! 𝑕2
+ ⋯ ∙∙∙ + 𝑥 − 𝑥 𝑛 𝑥 − 𝑥 𝑛;1 … (𝑥 − 𝑥1)
𝛻2 𝑦𝑛
2! 𝑕 𝑛
‫ب‬‫الخلفٌة‬ ‫للفروق‬ ‫نٌوتن‬ ‫صٌغة‬Neutron's Backward Formula
‫الفصل‬:‫التاسع‬‫األسبوع‬:‫العشرون‬ ‫و‬ ً‫الثان‬

323. ‫نـ‬ ‫انزمشٌجٍخ‬ ‫انمًٍخ‬ ‫أجذ‬𝐜𝐨𝐬(𝟎. 𝟐𝟓)‫لٍى‬ ٌٕ‫رك‬ ‫ػُذيب‬𝐜𝐨𝐬(𝒙)‫انًؼهٕيخ‬
ً‫انزبن‬ ‫انجذٔل‬ ً‫ف‬ ‫انًٕظحخ‬ ًْ:-
𝑥 ∶ 0 0.1 0.2 0.3
cos 𝑥 ∶ 1 0.995 0.98007 0.95534
‫اٌم١ّح‬ ْ‫إ‬ ‫٠رؼخ‬0.25ٓ١‫ت‬ ‫ذمغ‬)0.2 , 0.3(َ‫ٔسرخذ‬ ‫ٌزٌه‬ ‫اٌجذٚي‬ ‫ٔٙا٠ح‬ ‫لشب‬ ٞ‫أ‬
‫اٌخٍف١ح‬ ٓ‫ٔ١ٛذ‬ ‫ط١غح‬,ْ‫إ‬ ‫ار‬= 0.1 h‫اٌخٍف١ح‬ ‫اٌفشٚق‬ ‫جذٚي‬ ٓ٠ٛ‫ذى‬ ‫اٚال‬ ‫ٚ٠جة‬
.𝒙 𝐜𝐨𝐬(𝒙) 𝜵 𝜵 𝟐 𝜵 𝟑
0 1
0.1 0.995 -0.005
0.2 0.98007 -0.01493 -0.00993
0.3 0.95534 -0.02473 -0.0098 0.00013
‫مثال‬:
‫الفصل‬:‫التاسع‬‫األسبوع‬:‫العشرون‬ ‫و‬ ً‫الثان‬

324. ‫انصٍغخ‬ ً‫ف‬ ‫انفشٔق‬ ِ‫ْز‬ ‫ٔثزؼٌٕط‬.
𝑸 𝒙 = 𝒚 𝟑 + 𝒙 − 𝒙 𝟑
𝜵 𝒚 𝟑
𝒉
+ (𝒙 − 𝒙 𝟑)(𝒙 − 𝒙 𝟐)
𝜵 𝟐
𝒚 𝟑
𝟐! 𝒉 𝟐
+(𝒙 − 𝒙 𝟑)(𝒙 − 𝒙 𝟐)(𝒙 − 𝒙 𝟏)
𝜵 𝟐 𝒚 𝟑
𝟑! ‫ا‬
𝟑
𝑸 𝒙 = 𝟎. 𝟗𝟓𝟓𝟑𝟒 + 𝒙 − 𝟎. 𝟑
−𝟎. 𝟎𝟐𝟒𝟕𝟑
𝟎. 𝟏
+ (𝒙 − 𝟎. 𝟑)(𝒙
− 𝟎. 𝟐)
−𝟎. 𝟎𝟎𝟗𝟖
𝟐! (𝟎. 𝟏) 𝟐
+(𝒙 − 𝟎. 𝟑)(𝒙 − 𝟎. 𝟐)(𝒙 − 𝟎. 𝟏)
𝟎. 𝟎𝟎𝟎𝟏𝟑
𝟑! (𝟎. 𝟏) 𝟑
𝑸 𝒙 = 𝒙 𝟑 − 𝟎. 𝟓𝟎𝟑𝒙 𝟐 + 𝟎. 𝟎𝟎𝟎𝟎𝟖𝒙 + 𝟏
ٍ‫ػ‬ ‫ٔثبنزؼٌٕط‬0.25‫ػهى‬ ‫َحصم‬
𝑸 𝟎. 𝟐𝟓 = 𝟎. 𝟗𝟔𝟖𝟗𝟏
ٌ‫إ‬ ‫أي‬:-𝐜𝐨𝐬(𝟎. 𝟐𝟓) ≅ 𝟎. 𝟗𝟔𝟖𝟗
‫انًعجٕغخ‬ ‫انمًٍخ‬ ‫رضبٔي‬ ًْٔ.
‫الفصل‬:‫التاسع‬‫األسبوع‬:‫العشرون‬ ‫و‬ ً‫الثان‬

325. ‫يضبل‬:‫اٌذاٌح‬ ٟٕ‫ِٕذ‬ ٍٝ‫ػ‬ ‫إٌماؽ‬ ‫تؼغ‬ ٟ‫٠ؼط‬ ٌٟ‫اٌرا‬ ‫اٌجذٚي‬y = f (x)
x : 4 6 8 10
y : 1 3 8 20
‫اٚجذ‬f (9)‫اٌخٍف١ح‬ ٓ‫ٔ١ٛذ‬ ‫ط١غح‬ َ‫تاسرخذا‬.
‫اٌخٍف١ح‬ ‫اٌفشٚق‬ ‫جذٚي‬ ‫ٔجذ‬
𝒙 𝒚 𝜵 𝜵 𝟐 𝜵 𝟑
4 1
6 3
8 8 5 3
10 20 12 7 4
‫الفصل‬:‫التاسع‬‫األسبوع‬:‫العشرون‬ ‫و‬ ً‫الثان‬

326. h=2‫اٌخٍف١ح‬ ٓ‫ٔ١ٛذ‬ ‫ط١غح‬ ‫ٚترطث١ك‬
𝑄 𝑥 = 𝑦3 + 𝑥 − 𝑥3
𝛻 𝑦3
ℎ
+ 𝑥 − 𝑥3 𝑥 − 𝑥2
𝛻2 𝑦3
2! ℎ2
+(𝑥 − 𝑥3)(𝑥 − 𝑥2)(𝑥 − 𝑥1)
𝛻3
𝑦3
3! 𝑕3
= 20 + 𝑥 − 10
12
2
+ 𝑥 − 10 𝑥 − 8
7
2! 22
+(𝑥 − 10)(𝑥 − 8)(𝑥 − 6)
4
3! 23
= 20 + 6 𝑥 − 6 +
7
8
𝑥 − 10 𝑥 − 8
+
1
12
(𝑥 − 10)(𝑥 − 8)(𝑥 − 6)
𝐹 9 = 𝑄 9 =
103
8
= 12.875
‫الفصل‬:‫التاسع‬‫األسبوع‬:‫العشرون‬ ‫و‬ ً‫الثان‬

327. ‫ٌم١ّح‬ ‫ذمش٠ة‬ ‫ادسة‬f (1.25)‫ػٍّد‬ ‫ارا‬
𝑓 0 , 𝑓 1 = 6 , 𝑓 3 = 34
, 𝑓 7 = 162
1
3
2
‫الفصل‬:‫التاسع‬‫األسبوع‬:‫العشرون‬ ‫و‬ ً‫الثان‬
‫الدالة‬ ‫لدٌك‬ ‫كانت‬ ‫اذا‬𝑓 𝑥 = 𝑥3 − 6𝑥2 + 3𝑥 − 0.4 − 149‫قٌمة‬ ‫احسب‬f
(x)‫عندما‬x=4.71‫عشرٌة‬ ‫مراتب‬ ‫لثلثة‬,‫الخطأ‬ ‫قٌمة‬ ‫واحسب‬.
‫التالٌة‬ ‫الحسابات‬ ‫ناتج‬ ‫اوجد‬:-
‫أ‬-‫بالضبط‬
‫ب‬-‫الخطأ‬ ‫حدد‬ ‫ثم‬ ‫ارقام‬ ‫لثلثة‬ ‫بالتقرٌب‬
a – 14.1+0.0981
b – 0.0218 * 197

328. 6
4
5
‫الفصل‬:‫التاسع‬‫األسبوع‬:‫العشرون‬ ‫و‬ ً‫الثان‬
‫قٌمة‬ ‫احسب‬ ‫ثم‬ ً‫التال‬ ‫للجدول‬ ‫تكعٌبٌة‬ ‫حدود‬ ‫إلٌجاد‬ ‫الكرانج‬ ‫صٌغة‬ ‫استخدم‬
‫عند‬ ‫الحدود‬ ‫كثٌرة‬x = 2.5
x : 0 1 4 6
y : 1 -1 1 -1
‫الثالثة‬ ‫الدرجة‬ ‫من‬ ‫حدود‬ ‫متعدد‬ ‫إلٌجاد‬ ‫االمامٌة‬ ‫نٌوتن‬ ‫صٌغة‬ ‫استخدم‬,‫اذا‬
‫التالٌة‬ ‫القٌم‬ ‫لدٌك‬ ‫توفرت‬:-
x : 3 4 5 6
y : 6 24 60 120
‫نهمٍى‬ ‫انشاثؼخ‬ ‫انذسجخ‬ ٍ‫ي‬ ‫حذٔد‬ ‫يزؼذد‬ ‫انخهفٍخإلٌجبد‬ ٍ‫ٍَٕر‬ ‫صٍغخ‬ ‫اصزخذو‬:-
x : 1 2 3 4 5
y : 1 -1 1 -1 1
‫انمًٍخ‬ ‫رمشٌت‬ ‫أجذ‬ ‫صى‬(3.5)

329. ‫خطٍخ‬ ‫انال‬ ‫انًؼبدالد‬ ‫حم‬:-Linear Equations–Non
‫انذسجخ‬ ٍ‫ي‬ ‫ٔاحذ‬ ‫حذ‬ ‫االلم‬ ‫ػهى‬ ‫فٍٓب‬ ٌٕ‫ٌك‬ ً‫انز‬ ‫انًؼبدالد‬ ًْ ‫خطٍخ‬ ‫انال‬ ‫انًؼبدالد‬
‫يضم‬ ‫نٕغبسٌزًٍخ‬ ٔ‫أ‬ ‫ٔيضهضٍخ‬ ٔ‫أ‬ ‫اصٍخ‬ ‫دٔال‬ ٔ‫أ‬ ‫اكضش‬ ٔ‫أ‬ ‫انضبٍَخ‬:-
𝑥2 + 3𝑥 − 1 = 0
𝑥 − sin 𝑥 = 0
𝑒 𝑥
− log 𝑥2
= 0
ً‫ا‬‫ِؼثٛؽ‬ ً‫ال‬‫د‬ ‫اٌّؼادٌح‬ ً‫د‬ ٌٝ‫إ‬ ٞ‫ذؤد‬ ‫ِثاششج‬ ً‫ا‬‫ط١غ‬ َ‫ذسرخذ‬ ٟ‫اٌر‬ ‫اٌّؼشٚفح‬ ‫ٚاٌطشق‬
‫اٌّؼادالخ‬ ِٓ ً‫ا‬‫جذ‬ ‫ِذذٚد‬ ‫ػذد‬ ٍٝ‫ػ‬ ‫اال‬ ‫ذطثك‬ ‫ال‬ ‫ؽشق‬ ٟ٘

330. ٟ‫ٚاٌر‬ ‫اٌرىشاس٠ح‬ ‫تاٌطشق‬ ّٝ‫ذس‬ ٟ‫اٌر‬ ‫اٌؼذد٠ح‬ ‫ؽشق‬ ‫تؼغ‬ ‫ٚسٕرٕاٚي‬
‫جزٚس‬ ‫ا٠جاد‬ ٌٝ‫إ‬ ‫ػادج‬ ٞ‫ذؤد‬)ّٝ‫٠س‬a‫اٌّؼادٌح‬ ‫جزس‬f (x)=0‫ارا‬
ْ‫وا‬f (x)=0(ٞ‫ذؤد‬ ْ‫اد١ا‬ ٟ‫ٚف‬ ‫اٌّؼثٛؽح‬ ‫اٌجزٚس‬ ِٓ ً‫ا‬‫جذ‬ ‫لش٠ثح‬
‫اٌّؼثٛؽح‬ ‫اٌجزٚس‬ ٖ‫٘ار‬ ٌٝ‫إ‬.
‫اترذائ١ح‬ ‫ذمش٠ث١ح‬ ‫ل١ّح‬ ‫ذفرشع‬ ‫د١ث‬X0‫اٌظ١غح‬ َ‫اسرخذا‬ ‫٠ىشس‬ ُ‫ث‬
‫اٌّؼثٛؽح‬ ‫اٌجزٚس‬ ‫الشب‬ ‫ل١ّح‬ ٍٝ‫ػ‬ ‫ٌٍذظٛي‬ ‫ِشاخ‬ ‫ػذج‬.
‫انحم‬ ‫غشائك‬:-
‫اٌالخط١ح‬ ‫اٌّؼادالخ‬ ‫جزٚس‬ ‫ا٠جاد‬ ‫ؽشائك‬ ِٓ ‫وث١ش‬ ‫ػذد‬ ‫ٕ٘ان‬
ً‫ا‬ِ‫اسرخذا‬ ‫اٌطشق‬ ‫اوثش‬ ‫ٚسٕزوش‬.

331. ‫انٕصطى‬ ‫انمًٍخ‬ ‫يجشُْخ‬:-MeanValue theorem
‫انذانخ‬ ‫نذٌُب‬ ‫كبَذ‬ ٕ‫ن‬y = f (x)‫نالشزمبق‬ ‫لبثهخ‬,ٌ‫َمطزب‬ ‫ُْبن‬ ٌ‫إ‬ ‫كًب‬(a , b)
‫انذانخ‬ ِ‫نٓز‬,ٍ‫ٔنزك‬aٌ‫فأ‬ ‫ثًٍُٓب‬ ‫ٔصطى‬ ‫لًٍخ‬:-
𝑓(0)
𝑓 𝑏 ;𝑓(𝑎)
𝑏;𝑎
ٟ٘ ‫ذىشاس٠ح‬ ‫ط١غح‬ ٍٝ‫ػ‬ ‫ف١ٙا‬ ً‫ٔذظ‬ ‫اٌالخط١ح‬ ‫اٌّؼادالخ‬ ً‫د‬ ‫ؽشائك‬ ‫اغٍة‬ ْ‫إ‬ ٍَٛ‫اٌّؼ‬ ِٓ
𝑋 𝑛:1 = 𝑋 𝑛 −
𝑓(𝑥 𝑛)
𝑘
𝑛 = 0,1,2, … … …
َ‫ذسرخذ‬ ‫اٌرطشق‬ ٜ‫ادذ‬ ْ‫ٚا‬k‫تطش٠مح‬ ّٝ‫ذس‬ ٟ‫ٚاٌر‬ ‫اٌم١ّح‬ ‫ٌٕظش٠ح‬ ‫اٌؼالِح‬:-
1
‫المتغٌر‬ ‫القاطع‬(Variable Secant)‫سٌكرر‬ ‫الذي‬ ‫الجذر‬ ‫قٌمة‬ ‫تصبح‬ ‫اذ‬
‫هو‬ ً‫الحقٌق‬ ‫الجذر‬ ‫من‬ ‫قرٌبة‬ ‫قٌمة‬ ‫على‬ ‫للحصول‬:-

332. 𝑥 𝑛:1 = 𝑥 𝑛 −
𝑓(𝑥 𝑛)
𝑓 𝑥 𝑛 −𝑓(𝑓 𝑛−1)
𝑥 𝑛−𝑥 𝑛−1
ٍٟ٠ ‫وّا‬ ‫اٌظ١غح‬ ‫ذظثخ‬ ‫ٚتزٌه‬:-
𝑥 𝑛;1 = 𝑥 𝑛 − 𝑓(𝑥 𝑛)
𝑥 𝑛;𝑥 𝑛−1
𝑓 𝑥 𝑛 ;𝑓(𝑥 𝑛−1)
‫يضبل‬:-‫يجبل‬ ً‫ف‬ ‫انٕالؼخ‬ ‫انجزٔس‬ ‫جذ‬(1,5.0)‫انزبنٍخ‬ ‫انالخطٍخ‬ ‫نهًؼبدنخ‬-:
𝒙 + 𝒆;𝟐𝒙
− 𝟏 = 𝟎
‫اٌّجاي‬ ّٓ‫ػ‬ ٓ١‫ٔمطر‬ ٞ‫أ‬ ‫تافرشاع‬(0.5 , 1)ٓ‫ٌٚرى‬X0=0.5ْ‫ٚا‬X1=0.9
𝑥2 = 𝑥1 − 𝑓(𝑥1)
𝑥1;𝑥0
𝑓 𝑥1 ;𝑓(𝑥0)
= 0.9 − 𝑓(0.9)
0.9;0.5
𝑓 0.9 ;𝑓(0.5)

333. 𝑓 0.9 = 0.9 + 𝑒;0.8 − 1 = 0.065298888 ْ‫ا‬ ‫ار‬
𝑓 0.5 = 0.5 + 𝑒;1 − 1 = −0.13210558
𝑥2 = 0.9 − 0.065298888
0.9 − 0.5
0.197419446
= 0.7677
𝑓 0.7677 = −0.016933 ْ‫ا‬ ‫ار‬
ٟ٘ ‫جذ٠ذج‬ ‫ل١ّح‬ ‫ا٠جاد‬ ‫٠جة‬ ٗ١ٍ‫ٚػ‬ ‫طفش‬ ٞٚ‫ذسا‬ ‫ال‬X3‫ٕ٘ا‬ َ‫ٚٔسرخذ‬X2=0.7677ٚ
X1=0.9ْ‫إ‬ ‫ٔجذ‬ ‫اٌرؼٛ٠غ‬ ‫ٚػٕذ‬X3=0.79494ْ‫إ‬ ‫ٚار‬f(0.79494)≠0‫ٚٔسرّش‬
‫اٌؼٍّ١اخ‬ ٖ‫٘ز‬ ‫٠ٛػخ‬ ٟ‫ا٢ذ‬ ‫ٚاٌجذٚي‬ ‫جذ٠ذج‬ ُ١‫ل‬ ‫ترٌٛ١ذ‬
𝑋 𝑛;1 𝑋 𝑛 𝑥 𝑛:1 𝑓(𝑚)
0.5 0.9 0.7677 -0.016933
0.9 0.7677 0.79494 -0.001103
0.7677 0.79494 0.79685 0.0000231
0.79494 0.79685 0.79681 0.00000003
ٟ٘ ‫اٌجذاٚي‬ ْ‫إ‬ ٞ‫أ‬0.79681‫اخزٔا‬ ٌٛ ٓ‫ٌٚى‬X0=0.6,X1=0.6ِٓ ‫اسشع‬ ‫اٌجزس‬ ‫سٕجذ‬
‫اٌساتك‬

334. ‫انزكشاس‬ ‫غشٌمخ‬:-Iterative Method
‫اٌّؼادالخ‬ ً‫ٌذ‬ ‫اٌطش٠مح‬ ٖ‫٘ز‬ َ‫ذسرخذ‬f (x)=0ٟ٘ ‫خاطح‬ ‫طٛسج‬ ٟ‫ف‬ ‫اٌّؼادٌح‬ ‫تٛػغ‬ ‫ٚرٌه‬:-
X = g (x)
‫اٌّؼادٌح‬ ْ‫ٚا‬f (x)=0ً‫ال‬‫فّث‬ ‫اٌطشق‬ ِٓ ‫وث١ش‬ ‫تؼذد‬ ‫اٌخاطح‬ ‫تاٌظٛسج‬ ‫ٚػؼٙا‬ ٓ‫٠ّى‬
𝑥3
− 2 = 0‫اٌراٌ١ح‬ ‫تاٌطشق‬ ‫ٚػؼٙا‬ ٓ‫٠ّى‬:
𝑥 = 𝑥3 − 2𝑥 + 𝑥
𝑥 =
2;𝑥3:5𝑥
5
𝑥 =
2
𝑥2
‫ِٕاسثح‬ ‫تم١ّح‬ ‫ٔثذأ‬ ُ‫ث‬X=X0‫اٌؼاللح‬ َ‫تاسرخذا‬ ‫ذمش٠ثاخ‬ ِٓ ‫سٍسٍح‬ ْٛ‫ٚو‬
𝑋 𝑛;1 = 𝑔 𝑥 𝑛 𝑛 = 0,1,2, … … …
‫اٌّرراٌ١ح‬ ٖ‫ٌٙز‬ ْ‫ِا‬ ‫ارا‬ ٗٔ‫ا‬ ‫اٌٛاػخ‬ ِٓٚX0 , X1 , X2 , …..‫غا٠ح‬Limitٛ٘mْ‫فأ‬m
‫اٌّؼادٌح‬ ‫جزس‬ ْٛ‫٠ى‬x = g (x)ْ‫أل‬m = g (m).
2

335. ‫يضبل‬:-‫ٌٍّؼادٌح‬ ٟ‫اٌذم١م‬ ‫اٌجزس‬ ‫اٚجذ‬𝑋3 − 2 = 0‫اٌرىشاس‬ ‫تطش٠مح‬
)1(𝑥 = 𝑥3
− 2 + 𝑥 … … … …
)2(𝑥 =
2;𝑥3:5𝑥
5
… … … …
‫االترذائ١ح‬ ‫اٌم١ّح‬ ‫ٚتاخر١اس‬X0=1.2َ‫تاسرخذا‬)1(
𝑥 𝑛:1 = 𝑥 𝑛
3 − 2 + 𝑥 𝑛
𝑥0 = 1.2
𝑥1 = (1.2)3−2 + 1.2 = 0.928
𝑥2 = (0.928)3−2 + 0.928 = −0.273
𝑥3 = = −2.293
𝑥4 = = −16.349

336. َ‫تاسرخذا‬)2(
𝑥 𝑛:1 =
2;𝑥 𝑛
3:5𝑥 𝑛
5
𝑥0 = 1.2
𝑥1 =
2; 1.2 3:5(1.2)
5
= 1.2544
𝑥2 =
2;(1.2544)3:5(1.2544)
5
= 1.2596
𝑥3 = = 0.2599
𝑥4 = = 1.25992
‫ٌٍظ١غح‬ ‫اٌظذ١خ‬ ‫اٌجزس‬ ٛ‫ٔذ‬ ً‫ال‬‫فؼ‬ ‫ذرماسب‬ ‫اٌّثاٌ١ح‬ ُ١‫اٌم‬ ْ‫إ‬ ‫ٚٔجذ‬)2(
𝑚 = 2
3

337. ٍ‫ٍَٕر‬ ‫غشٌمخ‬–ٌٕ‫سافض‬Newton –Raphson Method
‫ثبنصٕسح‬ ً‫ال‬ٔ‫ا‬ ‫انًؼبدنخ‬ ‫َعغ‬ ‫انطشٌمخ‬ ِ‫ثٓز‬ ‫انًؼبدنخ‬ ‫نحم‬(f (x)=0)‫رمشٌجٍخ‬ ‫لًٍخ‬ ‫َٕٔجذ‬
‫اثزذائٍخ‬X0ٍٍ‫انمًٍز‬ ٍٍ‫ث‬ ً‫ب‬‫ٔالؼ‬ ‫انصحٍح‬ ‫انجزس‬ ٍ‫ي‬ ‫ثبنمشة‬x=b , x=a‫رمشٌجبد‬ ‫َٕجذ‬ ‫صى‬
‫يززبنٍخ‬
X1 , X2 , ……., Xn‫انزبنٍخ‬ ‫انؼاللبد‬ ‫ٔحضت‬:-
∆=
𝑓(𝑥0)
𝑓(𝑥0)
𝑥1 = 𝑥0 − ∆= 𝑥0 −
𝑓(𝑥0)
𝑓(𝑥0)
𝑥2 = 𝑥1 −
𝑓(𝑥1)
𝑓(𝑥1)
𝑥3< 𝑥2 −
𝑓 𝑥2
𝑓 𝑥2
ْ‫فأ‬ َ‫ػا‬ ً‫تشى‬
𝑥 𝑛:1 = 𝑥 𝑛 −
𝑓 𝑥 𝑛
𝑓 𝑥 𝑛
𝑛 = 0,1,2, … .
3

338. ‫يضبل‬(1):-‫نهًؼبدنخ‬ ً‫ا‬‫جزس‬ ‫اسلبو‬ ‫ألسثؼخ‬ ‫أجذ‬𝒙 𝟒
− 𝒙 = 𝟏𝟎ٍ‫ي‬ ‫ثبنمشة‬
x=2‫نيوتن‬‫بطريقة‬–‫افسون‬‫ر‬.
𝑓 𝑥 = 𝑥4
− 𝑥 − 10 = 0
𝑓 0 = −10 < 0
𝑓 1 = −10 < 0
𝑓 2 = 4 > 0
ٓ٠‫جزس‬ ‫ٌٙا‬ ‫اٌّؼادٌح‬ ْ‫إ‬ ٞ‫أ‬x = 2ٚ‫أ‬x = 1ٌٝ‫إ‬ ‫الشب‬ ْٛ‫٠ى‬ ْ‫إ‬ ‫ٚذرٛلغ‬x = 2ٟ‫ٚاٌر‬
‫االترذائ١ح‬ ‫اٌم١ّح‬ ً‫ذّث‬X0.
10)( 4
 xxxf
14)( 3
 xxf
14
103
4
10
)(
)(
3
4
3
4
1






 
n
n
n
nn
n
n
n
nn
x
x
x
xx
x
xf
xf
xx

339. ‫على‬ ‫نحصل‬ ‫مرات‬ ‫عدة‬ ‫الصٌغ‬ ‫وبتطبٌق‬:-
𝑥1 = 1.871 𝑥3 = 1.85578
𝑥2 = 1.855585 𝑥4 = 1.85558452522
‫المتتالٌتٌن‬ ‫القٌمتٌن‬ ‫بٌن‬ ‫للفرق‬ ‫المطلقة‬ ‫القٌمة‬ ‫وان‬𝑥 𝑛 − 𝑥 𝑛;1ً‫ا‬‫صفر‬ ‫اصبح‬
𝑥4 − 𝑥3 = 0.0000000477478

340. ‫يضبل‬(2: )-‫أجذ‬ٍ‫ٍَٕر‬ ‫ثطشٌمخ‬–‫سافش‬‫نهًؼبدنخ‬ ‫جزس‬ ‫اصغش‬𝒆;𝒙 = 𝐬𝐢𝐧 𝒙‫ٔنضالس‬
‫ػششٌخ‬ ‫اسلبو‬.
ٓ١١ٕ‫ٌٍّٕذ‬ ٟ‫ذمش٠ث‬ ُ‫ٚتشس‬( 𝑦 = 𝑒;𝑥 , 𝑦 = sin 𝑥) ‫ٔجذ‬ ‫اٌم١ّح‬ ْ‫إ‬ ‫اٌرمش٠ث١ح‬
ٟ٘ ‫اٌّؼطاج‬ ‫ٌٍّؼادٌح‬ ‫جزس‬ ‫اطغش‬ ً‫ذمات‬ ٟ‫اٌر‬ ‫اٌرماؽغ‬ ‫ٌٕمطح‬ ٟٕ١‫اٌس‬ ٓ١١‫االدذاث‬)X0=0.6(.
𝑓 𝑥 = 𝑒;𝑥 − sin 𝑥
𝑓 𝑥 = −𝑥;𝑥 − sin 𝑥
𝑥 𝑛:1 = 𝑥 𝑛 −
𝑒−𝑥 𝑛;sin 𝑥 𝑛
;𝑒−𝑥 𝑛;cos 𝑥 𝑛
𝑥0 = 0.6
𝑥1 = 0.5885
𝑥2 = 0.58853274
ْ‫ال‬ ‫اٌرىشاس٠ح‬ ‫اٌظ١غح‬ ‫ذطث١ك‬ ٓ‫ػ‬ ‫ٚٔرٛلف‬
∆= 𝑥2 − 𝑥1 = 0.5883274 − 0.5885 = 0.00000327
‫اٌظفش‬ ِٓ ‫ذمرشب‬ ً‫ا‬‫جذ‬ ‫طغ١شج‬ ‫وّ١ح‬ ٟ٘ٚ.

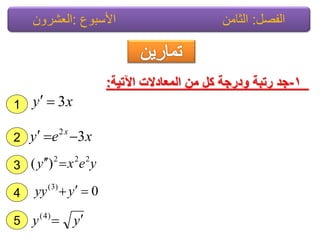
341. 1
2
3
‫المجال‬ ‫ضمن‬ ‫المعادلة‬ ‫جذر‬ ‫إلٌجاد‬ ‫القاطع‬ ‫طرٌقة‬ ‫استخدم‬[3 , 2].
𝒙 𝟑 − 𝟓𝒙 = 𝟎
‫نٌوتن‬ ‫طرٌقة‬ ‫استخدم‬–‫المعادلة‬ ‫جذر‬ ‫إلٌجاد‬ ‫رافس‬𝒙 = 𝒆;𝒙 ‫ارقام‬ ‫ألربعة‬
‫عشرٌة‬.
‫نٌوتن‬ ‫طرٌقة‬ ‫استخدم‬–‫المعادلة‬ ‫جذر‬ ‫إلٌجاد‬ ‫رافسون‬𝒙 𝒍𝒏 𝒙 = 𝟏‫لخمسة‬
‫عشرٌة‬ ‫ارقام‬.

342. ً‫التال‬ ً‫الخط‬ ‫النظام‬ ‫لدٌنا‬ ‫كان‬ ‫اذا‬:
a 11 x1+a12 x2 + …+a1n xn = b1
.
.
.
am1 x1 + am2 x2 +…+ amn= bn
a21 x1+a22 x2 +…+a2n xn = b2
‫ٌظم‬ ‫الذي‬mً‫ف‬ ‫المعادالت‬ ‫من‬n‫هذا‬ ‫كتابة‬ ‫اوٌمكن‬ ‫المجاهٌل‬ ‫من‬
ً‫ٌأت‬ ‫كما‬ ‫المصفوفات‬ ‫بصٌغة‬ ‫النظام‬:

343. 𝐀 =
𝑎11 𝑎12 … … 𝑎1𝑛
𝑎21
⋮
𝑎22 … …
⋮
𝑎2𝑛
⋮
𝑎 𝑚1 𝑎 𝑚2 … … 𝑎 𝑚𝑛
, 𝑥 =
𝑥1
𝑥2
⋮
𝑥 𝑛
, 𝐵 =
𝑏1
𝑏2
⋮
𝑏 𝑚
‫فإرا‬ ‫انخطٍخ‬ ‫انًؼبيالد‬ ‫نًُظٕيخ‬ ‫حم‬ ‫ػهى‬ ‫يُٓب‬ ‫انحصٕل‬ ٍ‫ًٌك‬ ً‫انز‬ ‫انطشق‬ ‫إَاع‬ ‫اثضػ‬ ًْٔ
ِ‫ٌذ‬ ‫انًز‬ ‫ثبنًصفٕفخ‬ ‫رضًى‬ ً‫انز‬ ٍّ‫انزبن‬ ‫ثبنصٕسح‬ ‫انُظبو‬ ‫كزجُب‬Augmented matrix
‫للحل‬ ‫المباشرة‬ ‫الطرائق‬:direct method of solution
1

344. 

















nn
n
n
bamamam
baaa
baaa
.......
.
.
..........
..........
21
222212
111211
‫العناصر‬ ‫ونجعل‬‫مساوٌة‬‫االول‬ ‫الصف‬ ‫عناصر‬ ‫ٌضرب‬ ‫وذلك‬ ‫للصفر‬ً‫ف‬
‫وطرحها‬ ‫العنصر‬ً‫الثان‬ ‫الصف‬ ‫عناصر‬ ‫من‬,‫االول‬ ‫الصف‬ ‫عناصر‬ ‫وضرب‬ً‫ف‬
‫وطرحه‬ ‫العنصر‬‫النظام‬ ‫على‬ ‫لنحصل‬ ‫الصفوف‬ ‫لجمٌع‬ ‫وهكذا‬ ‫الثالث‬ ‫الصف‬ ‫من‬
21311 ,.... aaam
11
21
a
a
11
31
a
a

345. ‫ٚ٘ىزا‬ ‫اٌثاٌث‬ ‫اٌظف‬ ِٓ ‫إٌاذج‬ ‫ٚؽشح‬ ‫تاٌؼٕظش‬ ٟٔ‫اٌثا‬ ‫اٌظف‬‫اٌظفٛف‬ ‫ٌجّ١غ‬




















nn
n
n
bmamama
baaa
baaaa
.......0
.
.
..........0
..........
32
222322
11131211
322 .....ama 
22
32
a
a


‫نحصل‬ ‫االسلوب‬ ‫وبنفس‬‫العناصر‬‫عناصر‬ ‫بضرب‬ ‫اصفار‬
‫المصفوفة‬ ‫على‬ ‫لنحصل‬

346. ‫تصبح‬ ‫وبذلك‬‫وبالتعوٌض‬ً‫باق‬ ‫على‬ ‫نحصل‬ ‫المعادالت‬ ً‫باق‬ ً‫ف‬‫المجاهٌل‬
‫الطرٌقه‬ ‫توضح‬ ‫التالٌه‬ ‫واالمثله‬.
























nmn
n
n
n
dc
dcc
dccc
dcccc
:........000
.
.
:......00
:......0
:......
3333
222322
11131211
mn
n
n
c
d
x 

347. ‫مثال‬:1‫كاوس‬ ‫بطرٌقة‬ ‫التالٌه‬ ‫المعادالت‬ ‫منظومة‬ ‫حل‬ ‫اوجد‬:
02 321  xxx
923 321  xxx
3334 321  xxx
ً‫ه‬ ‫المعادالت‬ ‫النظام‬ ‫المحددة‬ ‫المصفوفة‬ ‫ان‬:
















3:334
9:213
0:121

348. ٟ‫ف‬ ‫االٚي‬ ‫اٌظف‬ ‫ػٕاطش‬ ‫تؼشب‬3ٟٔ‫اٌثا‬ ‫اٌظف‬ ‫ػٕاطش‬ ِٓ ‫ٚؽشدٙا‬,‫وّا‬
ٟ‫ف‬ ‫االٚي‬ ‫اٌظف‬ ‫ػٕاطش‬ ‫ٔؼشب‬4‫٠ٕرج‬ ‫اٌثاٌث‬ ‫اٌظف‬ ‫ػٕاطش‬ ِٓ ‫ٚؽشدٙا‬
ً‫الثان‬ ‫الصف‬ ‫عناصر‬ ‫وبضرب‬‫أي‬‫ٌنتج‬ ‫الثالث‬ ‫الصف‬ ‫عناصر‬ ‫من‬ ‫وتطرح‬:














3:750
9:570
0:121
7
5
7
5



















7
24
:
7
24
00
9:570
0:121

349. ‫ان‬ ‫اذ‬:
1
7
24
7
24
33 

 xx
‫وان‬:
957 32  xx
2
7
14
957 22 

 xx
‫وان‬:
02 321  xxx
3014 11  xx
‫أي‬‫ان‬‫هو‬ ‫الحل‬ ‫مجموعة‬(1,-2,3)

350. ‫يضبل‬2:‫واٚس‬ ‫تطش٠مح‬ ٗ١ٌ‫اٌرا‬ ٗ١‫اٌخط‬ ‫اٌّؼادالخ‬ ‫ِٕظِٛح‬ ً‫د‬ ‫اٚجذ‬
22 321  xxx
535 321  xxx
922 321  xxx
ً‫ه‬ ‫المعادالت‬ ‫لنظام‬ ‫المحدودة‬ ‫المصفوفة‬ ‫ان‬:










 9:212
5:135
2:121

351. ٟ‫ف‬ ‫االٚي‬ ‫اٌظف‬ ‫ػٕاطش‬ ‫ٔؼشب‬5‫ٔؼشب‬ ‫وّا‬ ٟٔ‫اٌثا‬ ‫اٌظف‬ ‫ػٕاطش‬ ِٓ ‫ٚٔطشدٙا‬
ٟ‫ف‬ ‫االٚي‬ ‫اٌظف‬ ‫ػٕاطش‬2‫٠ٕرج‬ ‫االٚي‬ ‫اٌظف‬ ‫ػٕاطش‬ ِٓ ‫ٚٔطشدٙا‬:-














5:050
5:470
2:121
ً‫ف‬ ً‫الثان‬ ‫الصف‬ ‫عناصر‬ ‫نضرب‬7
5
7
5 
ٚ‫ا‬‫ٌنتج‬ ‫الثالث‬ ‫الصف‬ ‫عناصر‬ ‫من‬ ‫ونطرح‬

















7
60
:
7
20
00
5:470
2:121

352. ‫ان‬ ‫اذ‬:
‫وان‬:
‫وان‬:
3
7
60
7
20
33  xx
547 32  xx
1775127 222  xxx
22 321  xxx
1232 11  xx
ً‫ه‬ ‫الحل‬ ‫مجموعة‬ ‫ان‬ ‫أي‬(3,-1,1)
‫مالحظة‬:‫ٌكون‬ ‫عندما‬ ‫استخدامها‬ ‫الٌمكن‬ ‫كاوس‬ ‫طرٌقة‬ ‫ان‬011a

353. 2
‫المصفوفة‬ ‫تحلٌل‬ ‫على‬ ‫تعتمد‬ ‫الطرٌقة‬ ‫هذه‬ ‫ان‬A‫الى‬‫اي‬ ‫مثلثٌن‬ ‫عاملٌن‬ ‫ضرب‬ ‫حاصل‬:
ULA .
َّ‫ارا‬L=(Lij)‫صفهى‬ ٍّ‫يضهض‬ ‫يصفٕفخ‬ ًْ
L=(uij)‫ػهٍب‬ ٍّ‫يضهض‬ ‫يصفٕفخ‬ ًْ
‫نهًصفٕفخ‬ ٌّ‫انمطش‬ ‫انؼُبصش‬ ٌٕ‫رك‬ ٌ‫ا‬ ‫كشٔاد‬ ‫غشٌمخ‬ ‫رشزشغ‬ ‫حٍش‬U‫انٕاحذ‬ ًْ
Uii=1 i=1,2,…N
ٍٍ‫انًصفٕفز‬ ‫لطشي‬ ‫ػُبصش‬ ٌٕ‫رك‬ ٌ‫ا‬ ً‫جٕنضك‬ ‫غشٌمخ‬ ‫رشزشغ‬ ٍٍ‫ح‬ ً‫ف‬L,Uٌّٔ‫يزضب‬
Lii=Uii
‫يُٓب‬ ‫ألصهٕة‬ ‫رٕظٍح‬ ً‫ٌه‬ ‫ٔفًٍب‬
ّ‫نهًصفٕف‬ ‫ٌمبل‬(A)‫لًٍخ‬ ٌ‫ٔا‬ ّ‫يزًبصه‬ ّ‫يصفٕف‬ ‫كبَذ‬ ‫ارا‬ ‫لطؼب‬ ّ‫يٕجج‬ ‫ثأَٓب‬𝒙 𝑻 ay
‫صفشي‬ ‫غٍش‬ ّ‫يٕجج‬y.

354. ‫المثلثٌة‬ ‫المصفوفات‬ ‫اٌجاد‬:
‫القطرٌة‬ ‫العناصر‬ ‫ان‬ ‫ٌنتج‬ ‫قطعا‬ ‫موجبه‬ ‫مصفوفة‬ ‫على‬ ً‫جولسك‬ ‫طرٌقة‬ ‫تطبٌق‬ ‫فعند‬ً‫ف‬
U,L‫موجبه‬ ‫جمٌعها‬‫وان‬:
T
LLLUA 
‫وٌمكن‬‫السفلٌة‬ ‫المثلثٌة‬ ‫المصفوفة‬ ‫عناصر‬ ‫حساب‬L‫الترتٌب‬ ‫حسب‬ ‫اخر‬ ‫بعد‬ ‫عمود‬
‫التالٌه‬ ‫بالصٌغه‬:
‫القطرٌه‬ ‫غٌر‬ ‫للعناصر‬
aL 11
kj
j
k ik
ij
ij IIaij
I
L 



1
1
(
1

355. ‫مثال‬:‫المصفوفة‬ ‫حل‬Aً‫جولسك‬ ‫بطرٌقة‬ ‫التالٌة‬













5.375.21
75.225.41
114
A
‫الحل‬:











333231
2221
11
0
00
III
II
I
A










33
3222
312111
00
0
I
II
III
241111  aL
5.0
2
1
11
21
21 
L
a
L

356. 5.0
2
1
11
21
31 
L
a
L
2)5.0(25.4 22
212222  LaL
1)5.1)(5.0(5.32
21
2
313332  LLaL
‫فأن‬ ‫وعلٌه‬











15.15.0
025.0
002
L , U









 
100
5.120
5.05.02

357. ٌ‫ا‬ ‫ار‬ ً‫انخط‬ ‫انُظبو‬ ‫حم‬ ‫انًطهٕة‬ ٌ‫كب‬ ‫ارا‬A‫لطؼب‬ ّ‫يٕجج‬ ّ‫يصفٕف‬,‫فجؼذ‬
ِ‫انصٕس‬ ‫اٌجبد‬
bAx 
T
LLA 
‫الى‬ ً‫الخط‬ ‫النظام‬ ‫نحلل‬bxLLT

ً‫ٌعن‬ ‫وهذا‬
‫ولحل‬‫أي‬ ً‫االمام‬ ‫بالتعوٌض‬ ‫السابق‬ ً‫المثلث‬ ‫النظام‬:
‫لحل‬
bLz 
‫حٌث‬zxLT

bLz 

358. ‫فان‬:
1111 Lbz 
niLijzjb
L
z
i
j
i
ii
i ,......,3,2,1,
1 1
1






 


‫النظام‬ ‫ولحل‬zxLT
‫فان‬:
nnnn Lzx 
1,......1,
1






 
niLjixjz
L
x
n
iij
i
ii
i
‫ان‬ ‫باعتبار‬
T
LU ‫ان‬ ‫اذ‬LjiUij 

359. ‫مثال‬3:ً‫جولسك‬ ‫بطرٌقة‬ ً‫التال‬ ً‫الخط‬ ‫النموذج‬ ‫حل‬ ‫اوجد‬
8
2
1
4 321  xxx
6
8
5
4
5
321  xxx
4
10
9
8
5
2
1
321  xxx
‫الحل‬:



















16
9
8
5
2
1
8
5
4
5
1
2
1
14
A ,











4
6
8
b ,











3
2
1
x
x
x
x

360. 










333231
2221
11
0
00
LLL
LL
L
A










33
2322
131211
00
0
L
LL
LLL
241111  aL
2
1
11
21
21 
L
a
L
4
1
2
21
11
31
31 
L
a
L

361. 1
4
1
4
52
212222  LaL
2
1
8
4
)
2
1
.
4
1
8
5
(1)(
1
213132
22
32  LLa
L
L
2
1
16
4
4
1
16
1
16
9
32
2
313333  LLaL

















2
1
2
1
4
1
01
2
1
002
L ,



















2
1
00
2
1
10
4
1
2
1
2
LU

362. ‫قٌم‬ ‫والٌجاد‬X‫التالتٌٌن‬ ‫العالقتٌن‬ ‫نستخدم‬
 bLz
















2
1
2
1
4
1
01
2
1
002










3
2
1
z
z
z











4
6
8
4
2
8
1 z
4)4.
2
1
6(12 z






 
2
1
3 34
21
1
j
jzjLz 2)214(2 

363. ‫قٌم‬ ‫اما‬x‫التالٌة‬ ‫العالقة‬ ‫حسب‬ ‫اٌجادها‬ ‫فٌمكن‬
zxLT



















2
1
00
2
1
10
4
1
2
1
2










3
2
1
x
x
x











2
4
4
4
21
2
3 x

364. 2)4.
2
1
4(
1
1
2 x


3
2
1 )4(
2
1
j
Ljixjx )4.
4
1
2.
2
1
4(
2
1
 )114(
2
1

11x

365. ً‫ف‬‫الطرائق‬‫المباشرة‬‫نجري‬‫عدد‬‫محدد‬‫من‬‫العملٌات‬‫الجبرٌة‬‫للوصول‬‫إلى‬‫الحل‬
‫المطلوب‬‫أما‬ً‫ف‬‫الطرائق‬‫التكرارٌة‬‫فإننا‬‫نبدأ‬‫بتقرٌب‬ً‫أول‬‫ثم‬‫نحاول‬‫تحسٌنه‬‫بعدد‬‫من‬
‫المرات‬‫إلى‬‫أن‬‫نصل‬‫إلى‬‫حل‬‫دقٌق‬.‫وتستخدم‬‫هذه‬‫الطرائق‬‫عند‬‫حل‬‫النظم‬‫الخطٌة‬
‫الكبٌرة‬‫أي‬ً‫الت‬‫تحوي‬‫عدد‬‫كبٌر‬‫من‬‫المعادالت‬‫اوالمجاهٌل‬‫ومن‬‫هذه‬‫الطرق‬
‫طرٌقة‬ً‫جاكوب‬(‫التقرٌبات‬‫المتتابعة‬)(Jacobi's method)
‫تقةدٌرات‬ ‫بإعطةاء‬ ‫الطرٌقةة‬ ‫هذه‬ ‫خطوات‬ ‫تبدأ‬(‫تخمٌنةات‬)‫للمجاهٌةل‬ ‫أولٌةة‬xi‫مةثال‬xi‫ثةم‬
ً‫هة‬ ‫جدٌةدة‬ ‫قةٌم‬ ‫علةى‬ ‫للحصول‬ ‫المعادالت‬ ‫منظومة‬ ً‫ف‬ ‫القٌم‬ ‫هذه‬ ‫تعوض‬xiً‫فة‬ ‫ونعةوض‬
‫ةدة‬‫ة‬ٌ‫جد‬ ‫ةدٌرات‬‫ة‬‫تق‬ ‫ةى‬‫ة‬‫عل‬ ‫ةول‬‫ة‬‫للحص‬ ‫ةادالت‬‫ة‬‫المع‬ ‫ةة‬‫ة‬‫مجموع‬ً‫ة‬‫ة‬‫ه‬xi‫ةتمر‬‫ة‬‫وتس‬‫أي‬ ‫ةد‬‫ة‬‫نج‬ ‫ال‬ ‫ةٌن‬‫ة‬‫لح‬
‫قٌم‬ ً‫ف‬ ‫تغٌٌر‬xi‫التكرارٌة‬ ‫العملٌات‬ ‫خالصة‬ ‫تمثل‬ ‫العالقة‬ ‫أن‬ ‫أي‬

366. ‫قٌم‬ ‫تصبح‬ ‫بان‬ ‫المطلوبة‬ ‫الدقة‬ ‫على‬ ‫الحصول‬ ‫لحٌن‬x‫تقرٌبا‬ ‫ثابتة‬.
ni
a
aijxb
x
ii
j
k
ji
k
i .,,.........2,1
)(
)1(





‫مثال‬:‫استخدم‬‫خمس‬‫تقرٌبات‬ً‫ف‬‫إٌجاد‬‫مجموعة‬‫الحلول‬‫لمنظومة‬‫المعادالت‬‫التالٌة‬‫باستخدام‬‫طرٌقة‬ً‫جاكوب‬
1124 321  xxx
1642 321  xxx
32 21  xx
‫تبدل‬‫المعادلتٌن‬‫الثانٌة‬‫والثالثة‬‫الن‬‫وتصبح‬‫المعادالت‬ً‫كاآلت‬ 033a

367. 1124 321  xxx
1642 321  xxx
32 21  xx
 ........... 1
‫أن‬ ‫نجد‬ ‫العالقة‬ ‫هذه‬ ‫ومن‬
321
4
1
2
1
4
11
xxx 
12
2
1
2
3
xx 
213
4
1
2
1
4 xxx 
 ........... 2

368. ‫نختا‬‫ر‬ً‫اآلت‬ ‫األولٌة‬ ‫التقرٌبات‬ ‫متجه‬:
),,( )0(
3
)0(
2
)0(
1
)0(
xxxx 
)111(
‫السابقة‬ ‫المعادالت‬ ً‫ف‬ ‫وبالتعوٌض‬(2)‫ٌنتج‬:
2
4
1
2
1
4
11)1(
1 x
2
2
1
2
3)1(
2 x
4
13
4
1
2
1
4)1(
3 x

369. ‫ان‬ ‫اي‬:
)
4
13
22()1(
x
‫السابقة‬ ‫المعادالت‬ ً‫ف‬ ‫أخرى‬ ‫مرة‬ ‫وبالتعوٌض‬(2)‫للمتجه‬‫ٌنتج‬:-
)1(
x
16
15
)
9
13
(
4
1
)2(
2
1
4
11)2(
1 x
2
5
)2(
2
1
2
3)2(
2 x
2
5
)2(
4
1
)2(
2
1
4)2(
3 x

370. 3x2x1xK
1 110
13/4221
5/25/215/162
3 7/8 63/32 93/32
133/128 31/16 393/1284
517/256 767/256519/5125
ً‫التال‬ ‫القٌم‬ ‫جدول‬ ‫على‬ ‫فنحصل‬ ‫التكراري‬ ‫بالتعوٌض‬ ‫وتستمر‬:-
‫ونالحظ‬‫أن‬‫التقرٌبات‬‫المحسبة‬ً‫ف‬‫التكرار‬‫الخامس‬‫تختلف‬‫عن‬‫الحل‬‫المضبوط‬
((3,2,1‫بحدود‬%1‫وٌمكن‬‫زٌادة‬‫عدد‬‫التكرارات‬‫أكثر‬‫للحصول‬‫على‬
‫الدقة‬‫المطلوبة‬.

371. ‫التالٌة‬ ‫المعادالت‬ ‫منظومة‬ ‫لحل‬ ً‫جاكوب‬ ‫طرٌقة‬ ‫استخدم‬ ‫مثال‬2:
535 321  xxx
22 321  xxx
922 321  xxx
‫تقرٌبات‬ ‫أربعة‬ ‫ا‬‫ا‬‫معتمد‬)111()0(
x
‫أن‬ ‫نجد‬ ‫السابقة‬ ‫المعادالت‬ ‫من‬
321
5
1
5
3
1 xxx 
312
2
1
2
1
1 xxx 
213
2
1
2
9
xxx 

372. ‫ٌنتج‬ ‫االولى‬ ‫وبالتعوٌض‬
5
1
5
1
5
3
1)1(
1 x
0
2
1
2
1
1)1(
2 x
4
2
1
1
2
9)1(
3 x
)401()1(
x
5
1
5
4
1)4(
5
1
1)2(
1 x

373. 2
3
)4(
2
1
2
1
1)2(
2 x
2
7
1
2
9)2(
3 x
)
2
7
2
3
5
1
()2(
x
5
6
10
12
10
7
10
9
1)
2
7
(
5
1
)
2
3
(
5
3
1)3(
3 x
20
17
4
7
10
1
1)
2
7
(
2
1
)
5
1
(
2
1
1)3(
2 x
20
71
4
3
5
1
2
9
)
2
3
(
2
1
5
1
2
9)3(
3 x

374. 1
2
‫المصفوفة‬ ‫حلل‬ ً‫جولسك‬ ‫طرٌقة‬ ‫استخدم‬A‫بالصورة‬ ‫مصفوفتٌن‬ ‫ضرب‬ ‫حاصل‬ ‫الى‬ ‫التالٌة‬
T
LLA ‫ان‬ ‫اذ‬L‫سفلى‬ ‫مثلثٌة‬ ‫مصفوفة‬














210
121
012
A
‫المعادالت‬ ‫منظمومة‬ ‫لحل‬ ً‫جاكوب‬ ‫طرٌقة‬ ‫استخدم‬
24 21 xx
64 321  xxx
24 32  xx

375. ‫هناك‬‫بعض‬‫الصٌغ‬‫العددٌة‬ً‫الت‬ً‫تعط‬‫قٌما‬‫تقرٌبٌة‬‫للمشتقة‬‫األولى‬‫والثانٌة‬
‫والدرجات‬‫العلٌا‬‫عند‬‫إحدى‬‫نقاط‬‫الجدول‬.
‫إذا‬‫كانت‬‫داله‬‫لها‬‫قٌم‬‫معلومة‬‫عند‬‫بعض‬‫النقاط‬ً‫ف‬‫جدول‬‫ذو‬‫مسافات‬
‫متساوٌة‬‫والمطلوب‬‫أن‬‫نجد‬‫مشتقة‬‫الدالة‬‫عند‬‫إحدى‬‫نقاط‬‫الجدول‬‫أو‬
‫نقطة‬‫غٌرها‬.
)(xf
)(xf
‫أن‬ ‫االستكمال‬ ‫فصل‬ ً‫ف‬ ‫الخطٌة‬ ‫المعامالت‬ ‫بٌن‬ ‫العالقات‬ ‫خالل‬ ‫من‬
)1log( hD

376. ‫أن‬ ‫إذ‬D‫األمامٌة‬ ‫الفروق‬ ‫معامل‬ ‫هو‬ ‫التفاضل‬ ‫معامل‬ ‫هو‬
dx
d
D ,
iii yyy 
)1log(
1

h
D
‫على‬ ‫نحصل‬ ‫تاٌلر‬ ‫متسلسلة‬ ‫وباستخدام‬
........)
3
1
2
1
(
1 32

h
D
‫أن‬ ‫أي‬:
1...............).....(
3
1
)(
2
1
)(
1
)()( 32






 xfxfxf
h
xfxDf
‫األمامٌة‬ ‫الفروق‬ ‫بداللة‬ ‫للدالة‬ ‫األولى‬ ‫المشتقة‬ ً‫تعط‬ ‫الصٌغة‬ ‫فهذه‬
‫ومسافة‬h.
)(xfk


377. ‫من‬ ‫علٌها‬ ‫الحصول‬ ‫ٌمكن‬ ‫للمشتقة‬ ‫مبسطة‬ ‫تقرٌبٌة‬ ‫أخرى‬ ‫صٌغة‬ ‫وهناك‬
‫العالقة‬ ‫من‬ ‫المشتقة‬ ‫حساب‬ ً‫ف‬ ً‫األساس‬ ‫الحد‬(1(
)(xf 
2..............
)()(
)(
1
)( 00
00
h
xfhxf
xf
h
xf


‫الحصول‬ ‫ٌمكن‬ ‫للمشتقة‬ ‫مبسطة‬ ‫ثالثة‬ ‫تقرٌبه‬ ‫صٌغة‬ ‫هناك‬ ‫كما‬
‫العالقة‬ ‫تشبه‬ ‫الخلفٌة‬ ‫الفروق‬ ‫بداللة‬ ‫علٌها‬(1)‫بداللة‬ ً‫تعط‬ ً‫الت‬
ً‫ه‬ ‫األمامٌة‬ ‫الفروق‬
)(xf 
)(xf 
3...........
)()(
)(
1
)( 00
00
h
hxfxf
xf
h
xf



378. ‫مثال‬:‫الصٌغتٌن‬ ‫استخدم‬2,3‫للدالة‬ ‫الخلفٌة‬ ‫األمامٌة‬ ‫للفروق‬xxf sin)( 0 
‫عندما‬h=0.1‫عند‬x=1
‫الصٌغة‬ ‫باستخدام‬(2(
10
)()(
)( 0
0



xfhxf
xf
49736.0
1.0
841471.0891207.0
1.0
)1sin()11sin(
)( 



 xf
‫الصٌغة‬ ‫باستخدام‬(3(
h
hxfxf
xf
)()(
)( 00
0


1.0
)9.0sin()1sin( 
 58148.0
1.0
783327.0841471.0



379. ‫البٌانات‬ ‫بجداول‬ ‫لٌست‬ ‫نقاط‬ ‫عند‬ ‫للمشتقات‬ ‫عددٌة‬ ‫صٌغ‬:
‫موجودة‬ ‫غٌر‬ ‫نقطة‬ ‫عند‬ ‫المختلفة‬ ‫المشتقات‬ ‫على‬ ‫الحصول‬ ً‫ف‬ ‫المقٌدة‬ ‫العالقات‬ ‫بعض‬ ً‫ٌل‬ ‫فٌما‬
ً‫ف‬ ‫موجودة‬ ‫لٌست‬ ‫نقاط‬ ‫عند‬ ‫للدالة‬ ‫قٌم‬ ‫على‬ ‫للحصول‬ ‫االستكمال‬ ‫صٌغ‬ ‫مستخدمٌن‬ ‫بالجدول‬
‫التالٌة‬ ‫العالقة‬ ‫ا‬‫ال‬‫فمث‬ ‫المطلوبة‬ ‫الصٌغة‬ ‫تعطٌنا‬ ‫مرات‬ ‫عدة‬ ‫الصٌغ‬ ‫هذه‬ ‫فاضلنا‬ ‫فإذا‬ ‫الجدول‬
‫لنٌوتن‬ ‫األمامٌة‬ ‫للفروق‬
0
0
ycy i
k
i
k
ik  
..............
2
)1(
0
2
00 

 y
kk
yky
i

380. ‫أن‬ ‫إذ‬:
khxxxxfy kkk  0,)(
‫لل‬ ‫بالنسبة‬ ‫العالقة‬ ً‫طرف‬ ‫فاضلنا‬ ‫فإذا‬k‫ٌنتج‬:
dx
d
h
d
dx
d
d
d
d
kxk
 .
)()(
)()(
k
x
k
k
k
k
k
xfhxfh
d
xdf
h
d
xdf
d
dy

‫فان‬ ‫وعلٌه‬
...........)263(
6
1
)12(
2
1
)( 0
33
0
2
0  ykkykyxfh k

381. 4..............).)263(
6
1
)
2
1
((
1
)( 0
32
0
2
0  ykkyky
h
yxf kk
‫الدالة‬ ‫وبمفاضلة‬(4(‫نحصل‬:
  5.............................)1(
1
)( 0
3
0
2
2
 yky
h
yxf kk
‫الدالة‬ ‫وبمفاضلة‬(5(‫نحصل‬:
  ........................)1(
1
0
4
0
3
3
 yky
h
y k
‫فان‬ ‫بالجدول‬ ‫تكن‬ ‫لم‬ ‫بٌنما‬ ‫فان‬ ‫الجدول‬ ً‫ف‬ ‫نقطة‬ ‫كان‬ ‫فإذا‬kx0k0k

382. ‫مثال‬:‫النقاط‬ ‫عند‬ ‫قٌمتها‬ ‫معلومة‬ ‫دالة‬ ‫أن‬ ‫افرض‬)(xf
10864:x
20831:f
‫اوجد‬:‫النقاط‬ ‫عند‬
yyy  ,,4,5.4.  xx
32
yx
14
122010
47588
3236

383. ‫أ‬-‫النقطة‬ ‫عند‬:






 .......)263(
6
1
)
2
1
(
1
)( 0
32
0
2
0 ykkyky
h
xf k
12
11
4)263(
6
1
)3)(
2
1
1(2
2
1
)4( 





y
4
1
)43(
4
1
)4( y
2
1
)4(
8
1
)4( y
4x

384. ‫ب‬-‫النقطة‬ ‫عند‬5.4x
ً‫ه‬ ‫نقطة‬ ‫واقرب‬ ‫الجدول‬ ً‫ف‬ ‫موجودة‬ ‫لٌست‬x=4
4
1
2
45.4


h
48
41
......)4)(2
4
6
16
3
(
6
1
3)
2
1
4
1
(2
2
1
)5.4( 





y
0)4)(1
4
1
(3(
4
1
)5.4( y
2
1
)4(
8
1
)5.4( y

385. ‫لـ‬ ‫التقرٌبٌة‬ ‫القٌمة‬ ‫على‬ ‫الحصول‬ ‫ٌمكن‬
b
a
dxxf )(‫بالتكامالت‬ ‫أو‬ ‫معٌنة‬ ‫صٌغ‬ ‫باستخدام‬
‫المٌكانٌكٌة‬,‫أجراء‬ ‫الصعب‬ ‫من‬ ‫ٌكون‬ ‫عندما‬ ‫التقرٌبٌة‬ ‫التكامل‬ ‫قٌمة‬ ‫حساب‬ ‫ضرورة‬ ‫وتبرز‬
‫عددٌة‬ ‫لقٌم‬ ‫بجدول‬ ‫التكامل‬ ‫دالة‬ ‫تعرف‬ ‫عندما‬ ‫أو‬,ً‫ه‬ ‫الصٌغ‬ ‫هذه‬ ‫بعض‬ ً‫ٌل‬ ‫وفٌما‬:-
‫بالمحور‬ ‫األسفل‬ ‫ومن‬ ً‫بالمنحن‬ ‫األعلى‬ ‫من‬ ‫المحددة‬ ‫المساحة‬ ‫لتكن‬
‫أن‬ ‫حٌث‬ ‫منها‬ ‫شرٌحة‬ ‫كل‬ ‫عرض‬ ‫الشرائح‬ ‫من‬ ‫إلى‬
)(xfy )(x
axbx  ,,
‫العادٌة‬ ‫بالطرق‬ ‫التكامل‬,‫ابتدائٌة‬ ‫بدوال‬ ‫محدد‬ ‫الغٌر‬ ‫التكامل‬ ‫عن‬ ‫التعبٌر‬ ‫ٌتعذر‬ ‫عندما‬ ‫أو‬
‫الجانبٌن‬ ‫ومن‬‫بالمستقٌمٌن‬‫المساحة‬ ‫هذه‬ ‫نقسم‬ ‫ثم‬
)(n)(h
n
ab
h



386. ‫أدناه‬ ‫بالشكل‬ ‫موضح‬ ‫كما‬:
hna )1( 
np0p
1p
2p
h
a ha ha 2

387. ‫أعاله‬ ‫الشكل‬ ً‫ف‬ ‫الشرائح‬ ‫لمساحات‬ ‫التقرٌب‬ ‫وباستخدام‬,‫مساحة‬ ‫صٌغة‬ ‫باستخدام‬
‫المنحرف‬ ‫الشبه‬‫للتكامل‬ ‫التقرٌبٌة‬ ‫القٌمة‬ ‫على‬ ‫نحصل‬(ً‫المنحن‬ ‫تحت‬ ‫المساحة‬)
 )()1((2).....2(2)(2)(
2
)( bfhnafhafthafaf
h
dxxf
b
a

 abhbfaf
h
 );()(
2
‫التالٌة‬ ‫للصٌغة‬ ‫ا‬‫ا‬‫وفق‬:

388. ‫مثال‬:‫المنحرف‬ ‫شبه‬ ‫بطرٌقة‬ ً‫التال‬ ‫للتكامل‬ ‫التقرٌبٌة‬ ‫القٌمة‬ ‫اوجد‬dxx )1(
1
0
3

‫الحل‬:
‫أن‬ ‫نجد‬ ‫التكامل‬ ‫خالل‬ ‫من‬1,0,01 10  xxh
‫وان‬:
1)( 3
xxf
‫وعلٌه‬:
‫أن‬ ‫أي‬
1
2)(,1)( 10  xfxf
5.1
2
3
)21(
2
1
)1(
1
0
3
 dxx

389. ‫للتكامل‬ ‫تقرٌبٌة‬ ‫قٌمة‬ ‫جد‬dxxI )1(
2
0
2
 
5)2()(,1)()(,2 100  fxfxfxfh
3)51(
2
1
I
‫مثال‬:

390. ‫أن‬ ‫افرضنا‬ ‫أذا‬‫وان‬: axbx  02 ,
2
1
ba
x


‫أن‬ ‫أي‬:hxxxx  0112
‫معلومة‬ ‫جمٌعها‬ ‫أن‬ ‫فرضنا‬ ‫وإذا‬,‫فان‬
‫الدالة‬ ً‫منحن‬ ‫تحت‬ ‫المطلوبة‬ ‫المساحة‬ ‫تقرٌب‬ ‫أساس‬ ‫على‬ ‫تقوم‬ ‫سمبسون‬ ‫قاعدة‬
‫بالنقاط‬ ‫ٌمر‬ ‫الذي‬ ‫الحدود‬ ‫متعدد‬ ً‫منحن‬ ‫تحت‬ ‫بالمساحة‬:
)(),(),( 012 xfxfxf
)(xf
)(2 xp
))(,()),(,()),(,( 001122 xfxxfxxfx

391. ‫أن‬ ‫وبما‬:2
2102 )( xcxccxp 
‫أن‬ ‫أي‬:dxxcccdxxpI x
x
x
b
a
)()( 2
2102
2
0
 
‫الدالة‬ ً‫ف‬ ‫الثالث‬ ‫بالنقاط‬ ‫بالتعوٌض‬ ‫قٌم‬ ‫على‬ ‫الحصول‬ ‫ٌمكن‬ ‫إذ‬. 012 ,, ccc
‫على‬ ‫نحصل‬ ‫الصٌغة‬ ‫تحلٌل‬ ‫بعد‬
ً‫التال‬ ‫الشكل‬ ‫وحسب‬:
)(2 xp
  )1......(....................)()(4)(
3
210 xfxfxf
h
I 

392. ‫أن‬ ‫إذ‬:
22
02
1201
xxab
xxxxh




‫الصٌغة‬ ‫وتسمى‬(1)}‫البسٌطة‬ ‫سمبسون‬ ‫بصٌغة‬{

393. ‫مثال‬:‫سمبسون‬ ‫بقاعدة‬ ً‫التال‬ ‫التكامل‬ ‫قٌمة‬ ‫احسب‬
dxxxxI )572( 2
3
1
3
 
0112120 ,2
2
31
,3,1 xxxxhxxx 


25)(,9)(,1)( 210  xfxfxf
   
3
62
25)9(41
3
1
)3()2(4)1(
3
1
 fffI

394. ‫مثال‬2:‫عندما‬ ‫سمبسون‬ ‫قاعدة‬ ‫باستخدام‬ ً‫األت‬ ‫التكامل‬ ‫قٌمة‬ ‫احسب‬4n=  
2
1
0
2
1 x
dx
 )()3(4)2(2)(4)(
3
)( bfhafhafhafaf
h
dxxf
b
a

8
1
4
1
2
1





n
ab
h
8
1
8
1
8
1
0  ha
4
1
8
2
02  ha
8
3
8
3
03  ha

395. ))
2
1
()
8
3
(4)
4
1
(2)
8
1
(4)0((
3
8
1
1
2
1
0
2
fffff
x
dx


)
)
2
1
(1
1
)
8
3
(1
1
4
)
4
1
(1
1
2
)
8
1
(1
4
01
1
(
24
1
2222
2










untiesqure4637.0)
5
4
73
256
17
32
65
256
1(
24
1

2
1
8
4
04  ha

396. 1-‫قٌم‬ ‫بعض‬ ً‫ٌعط‬ ً‫التال‬ ‫الجدول‬)(xfy 
2.116.112.108.1:x
28.0290.0295.0295.0:y
‫بأن‬ ‫ا‬‫ا‬‫علم‬ ‫عندما‬ ‫الدالة‬ ‫مشتقة‬ ‫إلٌجاد‬ ‫والخلفٌة‬ ‫األمامٌة‬ ‫الفروق‬ ‫طرٌقة‬ ‫استخدم‬5.2x1.0. h
2-‫عندما‬ ‫سمبسون‬ ‫بطرٌقة‬ ً‫التال‬ ‫التكامل‬ ‫قٌمة‬ ‫إلٌجاد‬ ‫أرقام‬ ‫لثالثة‬ ‫احسب‬2n
dx
x
 
1
0
2
1
1
3-ً‫التال‬ ‫للتكامل‬ ‫تقرٌب‬ ‫إلٌجاد‬ ‫عندما‬ ‫ا‬‫ا‬‫متخد‬ ‫المنحرف‬ ‫شبه‬ ‫قاعدة‬ ‫استخدم‬5.0h2n
dx
x
e x
 
2
1
1

397. ‫التفاضلٌة‬ ‫المعادالت‬ ‫حل‬ ‫طرائق‬ ‫الى‬ ‫التطرق‬ ‫تم‬ ‫السابقة‬ ‫الفصول‬ ً‫ف‬,‫منها‬ ‫التحلٌلٌة‬ ‫بالطرق‬
‫المتغٌرات‬ ‫فصل‬,‫وغٌرها‬ ً‫التكامل‬ ‫والعامل‬,‫نحصل‬ ً‫الت‬ ‫التفاضلٌة‬ ‫المعادالت‬ ‫معظم‬ ‫ولكن‬
‫التحلٌلٌة‬ ‫بالطرق‬ ‫حلها‬ ‫اٌجاد‬ ‫الٌمكن‬ ‫الذي‬ ‫النوع‬ ‫من‬ ً‫ه‬ ‫التطبٌقٌة‬ ‫العملٌة‬ ‫الحٌاة‬ ً‫ف‬ ‫علٌها‬
‫لهذه‬ ‫حل‬ ‫الٌجاد‬ ‫العددٌة‬ ‫الطرق‬ ‫استخدام‬ ‫باالمكان‬ ‫فانه‬ ‫للحل‬ ‫عددٌة‬ ‫قٌم‬ ‫اٌجاد‬ ‫المطلوب‬ ‫وان‬
‫التفاضلٌة‬ ‫المعادالت‬.

398. 1‫اوٌلر‬ ‫صٌغة‬‫التفاضلٌة‬ ‫المعادالت‬ ‫لدٌنا‬ ‫افترض‬
),( yxfy  , 00)( yxf 
‫التالٌة‬ ‫اوٌلر‬ ‫صٌغة‬ ً‫ه‬ ‫التفاضلٌة‬ ‫المعادلة‬ ‫لحل‬ ‫التقرٌبٌة‬ ‫الطرائق‬ ‫ابسط‬ ‫فأن‬
),(1 nnnn yxhfyy 
‫قٌمة‬ ‫نجد‬ ‫اذ‬1ny‫التقرٌبٌة‬ ‫القٌمة‬ ً‫ه‬ ً‫الت‬
‫عندما‬ ‫ل‬y1 nxx‫وان‬nn xxh  1

399. ‫مثال‬:‫قٌمة‬ ‫اوجد‬)2,0(f‫التفاضلٌة‬ ‫للمعادلة‬ xyxf )(‫بان‬ ً‫ا‬‫علم‬
5.0)0( f
00x , 5.0)( 0 xf , 2.01x 2.0h
),( 0001 yxhfyy 
5.0)5.00(2.05.0  x

400. ‫مثال‬2:-‫التفاضلٌة‬ ‫للمعادلة‬ ‫التقرٌبٌة‬ ‫القٌمة‬ ‫جد‬ ‫أو‬)1*1(f2
)( xyxf 
‫بان‬ ‫ا‬‫ا‬‫علم‬2)1( f
21.01*1,1 010  yhxx
),()1*1( 0001 yxhfyfy 
4.2)4(1.02 
‫مالحظة‬:-‫الحقٌقٌة‬ ‫القٌم‬ ‫عن‬ ‫بعٌدة‬ ‫تقرٌبٌة‬ ‫قٌم‬ ً‫تعط‬ ‫اوٌلر‬ ‫صٌغة‬ ‫أن‬,‫أجرٌت‬ ‫لذلك‬
‫مطوره‬ ‫أخرى‬ ‫صٌغ‬ ‫عنها‬ ‫ونتجت‬ ‫علٌها‬ ‫التعدٌالت‬ ‫بعض‬.

401. ً‫ٌأت‬ ‫وكما‬ ‫إلٌجاد‬ ‫تاٌلر‬ ‫مفكوك‬ ‫استخدام‬ ‫باإلمكان‬: )( 0 hxf 
....)(
!2
)()()( 0
2
000  xf
h
xfhxfhxf
‫قٌمه‬ ‫على‬ ‫تعتمد‬ ً‫الت‬ ‫المتسلسلة‬ ‫هذه‬ ‫من‬ ‫الحدود‬ ‫تلك‬ ‫بعض‬ ‫استخدام‬ ‫وباإلمكان‬h
‫الحدود‬ ‫من‬ ‫قلٌل‬ ‫عدد‬ ‫إلى‬ ‫تحتاج‬ ‫صغٌره‬ ‫كانت‬ ‫فكلما‬
ً‫ه‬ ‫تاٌلر‬ ‫صٌغه‬ ‫وان‬ ً‫تقرٌب‬ ‫الناتج‬ ‫وسٌكون‬:
),(1 nnnnnn yxhfyyhyy 
nnnn y
h
yhyy 
!2
2
1 ‫أن‬ ‫أي‬:

402. ‫مثال‬:-‫الثانٌة‬ ‫الرتبة‬ ‫من‬ ‫تاٌلر‬ ‫صٌغه‬ ‫باستخدام‬ ‫التقرٌبٌة‬ ‫القٌمة‬ ‫اوجد‬
‫بان‬ ‫علما‬ ‫للمعادلة‬ ‫الخامسة‬ ‫والرتبة‬
)1.1(f
yy 2)1( f
‫الحل‬:-
yyyyxf  ,),(
yyy
dy
yxdf
dx
yxdf
y  .
),(),(
‫أن‬ ‫أي‬:
nnnnnnn y
h
hyyy
h
yhyy
!2!2
22
1 
81.1)
2
12.0
1.01(2
!2
0
2
001  y
h
hyyy

403. ً‫فه‬ ‫الخامسة‬ ‫ألمرتبه‬ ‫أما‬
)5(
5
)4(
432
1
!5!4!3!2
nnnnnnn y
h
y
h
y
h
y
h
yhyy 
‫للمثال‬ ‫وبالنسبة‬
yyyyyy  )5()4(
,,
‫أن‬ ‫أي‬:
nnnnnnn y
h
y
h
y
h
y
h
y
h
yy
!5!4!3!21
5432
1 
‫على‬ ‫نحصل‬ ‫عن‬ ‫التعوٌض‬ ‫وعند‬: 01.0,0 0  yhn
80967.1
!5
)1.0(
!4
)1.0(
!3
)1.0(
!2
)1.0(
1.01
5432
1 





y

404. ‫دقٌقه‬ ‫تكون‬ ‫ال‬ ‫القٌم‬ ‫وهذه‬ ‫التقرٌبٌة‬ ‫القٌم‬ ‫لحساب‬ ‫قٌم‬ ‫تستخدم‬ ‫اوٌلر‬ ‫طرٌقة‬ ‫أن‬
‫احتساب‬ ‫بإعادة‬ ‫وذلك‬ ‫ألنقطه‬ ً‫ف‬ ‫ألداله‬ ‫قٌمة‬ ‫تحسٌن‬ ‫فٌمكن‬ ‫عام‬ ‫بشكل‬
ً‫ٌأت‬ ‫كما‬ ‫الفترة‬ ‫ونهاٌة‬ ‫بداٌة‬ ‫مٌل‬ ‫معدل‬ ‫بدالله‬ ‫المستقٌم‬ ‫الخط‬ ‫معادله‬ ‫من‬ ‫قٌمه‬:-
1ny ny
1ny1nx
1ny
  )2.(..........),(),(
2
1
111   nnnnnn yxfyxfhyy
‫العالقة‬ ‫ضمن‬ ‫معروفه‬ ‫غٌر‬ ‫قٌمه‬ ‫أن‬(2)‫اوٌلر‬ ‫طرٌقة‬ ‫باستخدام‬ ‫تخمٌنها‬ ‫وٌتم‬ 1ny
‫ألتكرارٌه‬ ‫الطرق‬ ‫احد‬ ‫باستخدام‬ ‫ل‬ ‫متعاقبة‬ ‫قٌم‬ ‫حساب‬ ‫أعادة‬ ‫وٌمكن‬1ny
‫العالقة‬ ‫كتابة‬ ‫أعادة‬ ‫فٌمكن‬ ‫ل‬ ‫أولٌه‬ ‫قٌمه‬ ‫تمثل‬ ‫ولتكن‬(2) 1ny
ً‫التال‬ ‫بالشكل‬:
)0(
1ny
 )(
11
)1(
1 ,(),( r
nnnnn
r
n yxfyxf
n
h
yy 

 

405. ‫تكون‬ ‫أن‬ ‫تتطلب‬ ‫ألنها‬ ‫قلٌله‬ ‫فائدتها‬ ‫العملٌة‬ ‫الناحٌة‬ ‫من‬ ‫اوٌلر‬ ‫طرٌقه‬ ‫أن‬‫قٌمه‬h‫جدا‬ ‫صغٌره‬
‫الجٌدة‬ ‫ألدقه‬ ‫على‬ ‫للحصول‬,‫تحتاج‬ ‫ال‬ ‫حٌث‬ ‫اقل‬ ‫وبجهد‬ ‫الجٌدة‬ ‫ألدقه‬ ً‫فتعط‬ ‫الطرٌقة‬ ‫هذه‬ ‫أما‬
‫مرات‬ ‫عدة‬ ‫الدالة‬ ‫قٌمة‬ ‫أٌجاد‬ ‫وإنما‬ ‫تاٌلر‬ ‫صٌغة‬ ً‫ف‬ ‫كما‬ ‫مشتقات‬ ‫حساب‬ ‫إلى‬
‫المطلوب‬ ‫للمجال‬ ‫الصغٌرة‬ ‫فترات‬ ‫من‬ ‫فتره‬ ‫لكل‬ ‫مختارة‬ ‫لنقاط‬.
),( yxf
‫راٌخ‬ ‫لطرٌقة‬ ‫مختلفة‬ ‫صٌغ‬ ‫توجد‬-‫واستخداما‬ ‫شٌوعا‬ ‫أكثرها‬ ‫وان‬ ‫رتب‬ ‫أربعه‬ ‫أو‬ ‫كوتا‬
‫ٌعتمد‬ ‫اشتقاقها‬ ‫وان‬ ‫االستخدام‬ ‫وسهله‬ ‫دقٌقه‬ ‫نتائج‬ ً‫تعط‬ ‫حٌث‬ ‫الرابعة‬ ‫الرتبة‬ ‫صٌغة‬ ً‫ه‬
‫اوٌلر‬ ‫وطرٌقة‬ ‫تاٌلر‬ ‫مفكوك‬ ‫على‬.

406. ً‫ه‬ ‫الرابعة‬ ‫للرتبة‬ ‫الصٌغة‬ ‫وان‬
)22(
6
4321 kkkk
h
yy nn 
),(1 nn yxfk 
)
2
,
2
( 12 k
h
y
h
xfk nn 
)
2
,
2
( 23 k
h
y
h
xfk nn 
),( 34 hkyhxfk nn 

407. ‫مثال‬:-‫راٌخ‬ ‫طرٌقه‬ ‫تستخدم‬-‫التفاضلٌة‬ ‫المعادلة‬ ‫لحل‬ ‫الرابعة‬ ‫الرتبة‬ ‫من‬ ‫كوتا‬x
y
xy
2

‫من‬1.2 1‫عندما‬h=0.04‫مره‬,h=0.1‫وان‬ ‫أخرى‬ ‫مره‬25.00 y
25.01 00  yx
)22(
6
432101 kkkk
h
yy 
‫الحل‬:-
‫حٌث‬ ‫نحسب‬ ‫وإلٌجاد‬n=0‫أن‬ ‫أي‬ 1y1234 ,,, kkkk
0
0
0001
2
),(
x
y
xyxfk 
875.0
)1)(2(
25.1
1)25.0,1( f

408. )
2
,
2
( 1002 k
h
y
h
xfk 






 )875.0(
2
04.0
25.0,
2
04.0
1f
8889.0)2675.0,02.1(  f
)
2
,
2
( 2003 k
h
y
h
xfk 
)8889.0(
2
04.0
25.0,
2
04.0
1(  f
8889.0
)02.1(2
2678.0
02.1)2678.0,02.1(  f
),( 3004 hkyhxfk 

409. ))8889.0(04.025.0,04.01(4  fk
)2856.0,04.1(f
9027.0
)04.1(2
2856.0
04.1 
 9027.0)8889.0(2)8889.0(2875.0
6
04.0
25.01 y
2856.0
‫فان‬ ‫وعلٌه‬:
ً‫ٌل‬ ‫وكما‬ ‫مستخدمٌن‬ ‫أخرى‬ ‫مره‬ ‫حساب‬ ‫ٌعاد‬ ‫قٌمه‬ ‫ولحساب‬: 2y1234 ,,, kkkk1y
9027.0)2856.0,04.1(),( 111  fyxfk

410. 9167.0)3037.0,06.1()
2
,
2
( 1112  fk
h
y
h
xfk
9167.0)3139.0,06.1()
2
,
2
( 2113  fk
h
y
h
xfk
9308.0)3223.0,08.1(),( 3114  fhkyhxfk
)2(
6
432112 kkkk
h
yy 
 9308.0)9167.0(29027.0
6
04.0
2856.02 y
3223.0

411. ‫ٌمثل‬ ً‫األت‬ ‫الجدول‬ ‫حساب‬ ‫ٌمكن‬ ‫األسلوب‬ ‫وبنفس‬
‫عندما‬ ‫العددٌة‬ ‫النتائج‬h=0.4
3456 ,,, yyyy
25.01
2855529.004.1
3222224.008.1
3600233.012.1
3989685.016.1
4390694.02.1
x y

412. ‫وعندما‬h=0.1
25.01
3409806.01.1
4390697.02.1
yx