يتعلق المستند بمذكرة دراسية لأستاذ الرياضيات أحمد الشمري للصف السادس، متضمنة تمارين وحلول لمختلف الموضوعات الرياضية من الفصل الدراسي 2017-2016. يغطي المحتوى مفاهيم أساسية مثل العدد ومبدأ العد، التباديل، التوافيق، والغرض، كما يقدم أمثلة وتمارين لحلها. تُستخدم نتائج حلول هذه التمارين في تطبيقات رياضية متعددة.

1. ‫األستاذ‬‫الشمري‬ ‫أحمد‬ :
07704516937
‫المرسل‬‫الطباعية‬ ‫للخدمات‬
‫المنصور‬–‫دراغ‬ ‫حي‬ ‫جامع‬ ‫مجاور‬
07703458937
‫ملزمة‬‫الرياضيات‬
‫االدبي‬ ‫السادس‬
2017-2016
‫مفصل‬ ‫شرح‬
‫التمارين‬ ‫حلول‬
‫الوزارية‬ ‫االسئلة‬ ‫حلول‬
‫اثرائية‬ ‫امثلة‬

2. / ‫الشمري‬ ‫احمد‬ ‫األستاذ‬077045169372/ ‫الطباعية‬ ‫للخدمات‬ ‫المرسل‬07703458937
:)‫الحدين‬ ‫ذات‬ ‫االول(مبرهنة‬ ‫الفصل‬
1-‫االساسي‬ ‫العد‬ ‫مبدأ‬.......................................................................................................5
2-‫التمارين‬ ‫حلول‬1-1....................................................................................................7
3-‫العدد‬ ‫مضروب‬:.......................................................................................................8
4-‫التباديل‬:.................................................................................................................9
5-‫التمارين‬ ‫حلول‬2-1....................................................................................................10
6-‫التوافيق‬:................................................................................................................12
7-‫التمارين‬ ‫حلول‬3-1....................................................................................................14
8-:‫الحدين‬ ‫ذو‬ ‫مبرهنة‬....................................................................................................71
9-‫التمارين‬ ‫حلول‬4-1....................................................................................................20
‫الثاني‬ ‫الفصل‬:)‫(الغاية‬
1-:‫الغايات‬.................................................................................................................25
2-‫التمارين‬ ‫حلول‬1-2....................................................................................................30
3-:‫االستمرارية‬...........................................................................................................33
4-‫التمارين‬ ‫حلول‬2-2....................................................................................................35
‫ال‬:)‫(المشتقة‬ ‫الثالث‬ ‫فصل‬
1-‫المشتقة‬...................................................................................................................41
2-‫تمارين‬ ‫حلول‬1-3......................................................................................................44
3-‫االشتقاق‬ ‫مبادئ‬..........................................................................................................74
4-‫تمارين‬ ‫حلول‬2-3......................................................................................................84
5-:‫للمشتقة‬ ‫والفيزياوية‬ ‫الهندسية‬ ‫التطبيقات‬..............................................................................50
6-:‫االقتصاد‬ ‫في‬ ‫المشتقة‬ ‫تطبيقات‬ ‫بعض‬.................................................................................35
7-‫تمارين‬ ‫حلول‬3-3......................................................................................................35
8-‫والصغرى‬ ‫العظمى‬ ‫النهايات‬............................................................................................65
9-‫تمارين‬ ‫حلول‬4-3......................................................................................................95
10-:‫االنقالب‬ ‫ونقاط‬ ‫والتحدب‬ ‫التقعر‬....................................................................................26
11-‫تمارين‬ ‫حلول‬5-3....................................................................................................26
12-:‫الدوال‬ ‫رسم‬..........................................................................................................56
13-‫تمارين‬ ‫حلول‬6-3....................................................................................................76
14-:‫والصغرى‬ ‫العظمى‬ ‫النهايات‬ ‫على‬ ‫تطبيقات‬........................................................................71
15-‫تمارين‬ ‫حلول‬7-3....................................................................................................47
:)‫(التكامل‬ ‫الرابع‬ ‫الفصل‬
1-:‫المحدد‬ ‫غير‬ ‫التكامل‬....................................................................................................83
2-‫حل‬‫و‬‫تمارين‬ ‫ل‬1-4.......................................................................................................58
3-‫المحدد‬ ‫غير‬ ‫للتكامل‬ ‫الهندسية‬ ‫التطبيقات‬................................................................................88
4-:‫المحدد‬ ‫غير‬ ‫للتكامل‬ ‫االقتصادية‬ ‫التطبيقات‬............................................................................19
5-‫تمارين‬ ‫حلول‬2-4.......................................................................................................29
6-:‫المحدد‬ ‫التكامل‬..........................................................................................................59
7-‫تمارين‬ ‫حلول‬3-4.......................................................................................................69
8-‫السينات‬ ‫ومحور‬ ‫المنحني‬ ‫بين‬ ‫المساحة‬..................................................................................001
9-‫المساحة‬‫دالتين‬ ‫منحني‬ ‫بين‬...............................................................................................021
10-‫تمارين‬ ‫حلول‬4-4....................................................................................................031
‫االثرائية‬ ‫االمثلة‬:..............................................................................................................061

3. / ‫الشمري‬ ‫احمد‬ ‫األستاذ‬077045169373/ ‫الطباعية‬ ‫للخدمات‬ ‫المرسل‬07703458937
‫األستاذ‬‫الشمري‬ ‫أحمد‬ :
07704516937
‫والنشر‬ ‫للطباعة‬ ‫المرسل‬
‫المنصور‬–‫دراغ‬ ‫حي‬ ‫جامع‬ ‫مجاور‬
07703458937
‫ملزمة‬‫الرياضيات‬
‫االدبي‬ ‫السادس‬
2017-2016
‫الفصل‬‫االول‬
‫الحدين‬ ‫ذات‬ ‫مبرهنة‬

4. ‫أدبي‬ ‫سادس‬‫االول‬ ‫الفصل‬‫االساسي‬ ‫العد‬ ‫مبدأ‬
/ ‫الشمري‬ ‫احمد‬ ‫األستاذ‬077045169374/ ‫الطباعية‬ ‫للخدمات‬ ‫المرسل‬07703458937

5. ‫أدبي‬ ‫سادس‬‫االول‬ ‫الفصل‬‫االساسي‬ ‫العد‬ ‫مبدأ‬
/ ‫الشمري‬ ‫احمد‬ ‫األستاذ‬077045169375/ ‫الطباعية‬ ‫للخدمات‬ ‫المرسل‬07703458937
:)‫الحدين‬ ‫ذات‬ ‫االول(مبرهنة‬ ‫الفصل‬
1-‫(مبد‬‫أ‬:)‫االساسي‬ ‫العد‬‫به‬ ‫ويقصد‬‫اساليب‬ ‫اتباع‬‫المعادالت‬ ‫استخدام‬ ‫بدون‬ ‫الحساب‬ ‫عمليات‬ ‫اجراء‬ ‫في‬ ‫االساسية‬ ‫العد‬:
‫مثال‬1/‫الزرقاء‬ ‫الصناديق‬ ‫عدد‬ ‫فكم‬ ‫زرقاء‬ ‫صناديق‬ ‫اربع‬ ‫منها‬ ‫كل‬ ‫بداخل‬ ‫بيضاء‬ ‫صناديق‬ ‫ثالثة‬ ‫لدينا‬‫؟‬
/‫الحل‬‫خالل‬ ‫من‬‫االساسي‬ ‫العد‬ ‫مبدء‬‫ن‬‫قوم‬‫ب‬‫ابيض‬ ‫صندوق‬ ‫كل‬ ‫في‬ ‫الزرقاء‬ ‫الصناديق‬ ‫بعدد‬ ‫البيضاء‬ ‫الصناديق‬ ‫عدد‬ ‫ضرب‬‫و‬‫يساوي‬ ‫الناتج‬‫عدد‬
:‫مبين‬ ‫كما‬ ‫الكلي‬ ‫الزرقاء‬ ‫الصناديق‬
‫البيضاء‬ ‫الصناديق‬ ‫عدد‬=3
‫ابيض‬ ‫صندوق‬ ‫لكل‬ ‫الزرقاء‬ ‫الصناديق‬ ‫عد‬=4
‫عدد‬‫الكلي‬ ‫الصناديق‬=3.4=12‫صندوق‬
‫مثال‬2/‫للدر‬ ‫محل‬ ‫صاحب‬ ‫اعلن‬‫الدر‬ ‫من‬ ‫انواع‬ ‫خمسة‬ ‫لديه‬ ‫يوجد‬ ‫ان‬ ‫الهوائية‬ ‫اجات‬‫ثالثة‬ ‫يوجد‬ ‫نوع‬ ‫كل‬ ‫ومن‬ ‫اجات‬‫احجام‬
‫در‬ ‫ست‬ ‫يوجد‬ ‫حجم‬ ‫كل‬ ‫ومن‬‫الدر‬ ‫عدد‬ ‫فكم‬ ‫اجات‬.‫المحل‬ ‫في‬ ‫اجات‬
/‫الحل‬‫نوع‬ ‫كل‬ ‫ان‬ ‫بما‬‫د‬‫ر‬‫در‬ ‫ستة‬ ‫يحوي‬ ‫حجم‬ ‫وكل‬ ‫احجام‬ ‫ثالثة‬ ‫يحوي‬ ‫اجات‬:‫فان‬ ‫اجات‬
‫الدر‬ ‫انواع‬ ‫عدد‬‫اجات‬=5
‫االحجام‬ ‫عدد‬‫نوع‬ ‫لكل‬=3‫الدر‬ ‫عدد‬‫الكلي‬ ‫اجات‬=5.3.6=90.‫اجة‬‫در‬
‫حجم‬ ‫لكل‬ ‫الدراجات‬ ‫عدد‬=6
‫مثال‬3/‫يحوي‬ ‫للمالبس‬ ‫محل‬5‫يوجد‬ ‫موديل‬ ‫كل‬ ‫وفي‬ ‫الرجالية‬ ‫البدالت‬ ‫من‬ ‫مختلفة‬ ‫موديالت‬10‫الوان‬ ‫سبعة‬ ‫ولديه‬ ‫قياسات‬
.‫الكلي‬ ‫الرجالية‬ ‫البدالت‬ ‫عدد‬ ‫فكم‬ ‫قياس‬ ‫كل‬ ‫في‬
/‫الحل‬‫الموديالت‬ ‫عدد‬=5
‫موديل‬ ‫لكل‬ ‫القياسات‬ ‫عدد‬=10‫الكلي‬ ‫البدالت‬ ‫عدد‬=5.10.7=350.‫بدلة‬
‫قياس‬ ‫لكل‬ ‫االلوان‬ ‫عدد‬=7
‫مثال‬4/‫لديه‬ ‫ساعات‬ ‫محل‬ ‫صاحب‬10‫فيها‬ ‫ماركة‬ ‫وكل‬ ‫مختلفة‬ ‫ماركات‬5‫فيه‬ ‫حجم‬ ‫وكل‬ ‫احجام‬7‫في‬ ‫ساعة‬ ‫فكم‬ ‫الوان‬
‫المحل‬‫(وزاري‬2012)‫اول‬ ‫دور‬
/‫الحل‬‫عدد‬‫الماركات‬=10
‫لكل‬ ‫االحجام‬ ‫عدد‬‫ماركة‬=5‫الكلي‬ ‫الساعات‬ ‫عدد‬=10.5.7=350‫ساعة‬
‫عدد‬‫االلوان‬‫حجم‬ ‫لكل‬=7
: )‫(الطرق‬ ‫االختيارات‬‫مبد‬ ‫باستخدام‬‫أ‬‫الطرق‬ ‫عدد‬ ‫ايجاد‬ ‫يمكننا‬ ‫االساسي‬ ‫العد‬‫لتوزيع‬ ‫اتباعها‬ ‫الممكن‬‫العناصر‬ ‫من‬ ‫مجموعة‬
‫الخانات‬ ‫من‬ ‫مجموعة‬ ‫على‬.
‫مثال‬5/‫الرقمين‬ ‫باستخدام‬ ‫مرتبتين‬ ‫من‬ ‫عدد‬ ‫لتكوين‬ ‫المتوفرة‬ ‫االختيارات‬ ‫هي‬ ‫ما‬3‫و‬5.‫نفسه‬ ‫العدد‬ ‫في‬ ‫الرقم‬ ‫بتكرار‬ ‫ويسمح‬
/‫الحل‬‫العشرات‬ ‫مرتبة‬ ‫طرق‬ ‫عدد‬=2
‫االحاد‬ ‫مرتبة‬ ‫طرق‬ ‫عدد‬=2
‫الكلية‬ ‫الطرق‬ ‫عدد‬=2.2=4‫طرق‬[
‫مثال‬6/‫االرقام‬ ‫باستخدام‬ ‫مرتبتين‬ ‫من‬ ‫عدد‬ ‫لتكوين‬ ‫المتوفرة‬ ‫االختيارات‬ ‫هي‬ ‫ما‬1‫و‬2‫و‬3‫العدد‬ ‫في‬ ‫الرقم‬ ‫بتكرار‬ ‫ويسمح‬
.‫نفسه‬
/‫الحل‬‫العشرات‬ ‫مرتبة‬ ‫طرق‬ ‫عدد‬=3
‫االحاد‬ ‫مرتبة‬ ‫طرق‬ ‫عدد‬=3
‫الكلية‬ ‫الطرق‬ ‫عدد‬=3.3=9‫طرق‬
‫مثال‬7/‫االرقام‬ ‫باستخدام‬ ‫مراتب‬ ‫ثالثة‬ ‫من‬ ‫عدد‬ ‫لتكوين‬ ‫المتوفرة‬ ‫االختيارات‬ ‫هي‬ ‫ما‬1‫و‬2‫و‬3‫و‬4‫و‬5‫بتكرار‬ ‫ويسمح‬
.‫نفسه‬ ‫العدد‬ ‫في‬ ‫الرقم‬
/‫الحل‬‫المئات‬ ‫مرتبة‬ ‫طرق‬ ‫عدد‬=5
‫العشرات‬ ‫مرتبة‬ ‫طرق‬ ‫عدد‬=5‫الكلية‬ ‫الطرق‬ ‫عدد‬=5.5.5=125‫طريقة‬
‫االحاد‬ ‫مرتبة‬ ‫طرق‬ ‫عدد‬=5
‫تكرا‬ ‫عدم‬ ‫السؤال‬ ‫في‬ ‫منا‬ ‫طلب‬ ‫واذا‬ ‫خانة‬ ‫من‬ ‫اكثر‬ ‫في‬ ‫الرقم‬ ‫بتكرار‬ ‫نسمح‬ ‫كنا‬ ‫السابقة‬ ‫االمثلة‬ ‫في‬ ‫الحظ‬‫فاننا‬ ‫رقم‬ ‫اي‬ ‫ر‬‫واهم‬ ‫مختلف‬ ‫اسلوب‬ ‫نتبع‬
‫االحرف‬ ‫عدد‬ ‫ليكون‬ ‫الدال‬ ‫حرف‬ ‫نحذف‬ ‫(بغداد‬ ‫المكررة‬ ‫العناصر‬ ‫حذف‬ ‫خطوة‬4‫االحرف‬ ‫عدد‬ ‫ليكون‬ ‫الزاء‬ ‫حرف‬ ‫نحذف‬ ‫زيزفون‬ ,5‫سلسبيل‬ ,
‫االحرف‬ ‫عدد‬ ‫ليكون‬ ‫والالم‬ ‫السين‬ ‫محذف‬4)

6. ‫أدبي‬ ‫سادس‬‫االول‬ ‫الفصل‬‫االساسي‬ ‫العد‬ ‫مبدأ‬
/ ‫الشمري‬ ‫احمد‬ ‫األستاذ‬077045169376/ ‫الطباعية‬ ‫للخدمات‬ ‫المرسل‬07703458937
‫مثال‬8/‫الرقمين‬ ‫باستخدام‬ ‫مرتبتين‬ ‫من‬ ‫عدد‬ ‫لتكوين‬ ‫المتوفرة‬ ‫االختيارات‬ ‫هي‬ ‫ما‬3‫و‬5.‫رقم‬ ‫اي‬ ‫تكرار‬ ‫بدون‬
/‫الحل‬‫العشرات‬ ‫مرتبة‬ ‫طرق‬ ‫عدد‬=2
‫االحاد‬ ‫مرتبة‬ ‫طرق‬ ‫عدد‬=1
‫الكلية‬ ‫الطرق‬ ‫عدد‬=2.1=2‫طريقة‬
‫مثال‬9/‫االرقام‬ ‫باستخدام‬ ‫مرتبتين‬ ‫من‬ ‫عدد‬ ‫لتكوين‬ ‫المتوفرة‬ ‫االختيارات‬ ‫هي‬ ‫ما‬1‫و‬2‫و‬3.‫رقم‬ ‫اي‬ ‫تكرار‬ ‫بدون‬
/‫الحل‬‫العشرات‬ ‫مرتبة‬ ‫طرق‬ ‫عدد‬=3
‫االحاد‬ ‫مرتبة‬ ‫طرق‬ ‫عدد‬=2
‫الكلي‬ ‫الطرق‬ ‫عدد‬=3.2=6‫طرق‬
‫مثال‬10/‫االرقام‬ ‫باستخدام‬ ‫مراتب‬ ‫ثالثة‬ ‫من‬ ‫عدد‬ ‫لتكوين‬ ‫المتوفرة‬ ‫االختيارات‬ ‫هي‬ ‫ما‬1‫و‬2‫و‬3‫و‬4‫و‬5‫اي‬ ‫تكرار‬ ‫بدون‬
.‫رقم‬
/‫الحل‬‫المئات‬ ‫مرتبة‬ ‫طرق‬ ‫عدد‬=5
‫العشرات‬ ‫مرتبة‬ ‫طرق‬ ‫عدد‬=4‫االختيارات‬ ‫عدد‬=5.4.3=60‫طريقة‬
‫االحاد‬ ‫مرتبة‬ ‫طرق‬ ‫عدد‬=3
‫مثال‬11/‫الحروف‬ ‫لدينا‬ ‫كان‬ ‫اذا‬(‫ز‬ , ‫هـ‬ , ‫د‬ , ‫ج‬ , ‫ب‬ , ‫أ‬)‫تتكون‬ ‫بحيث‬ ‫تكوينها‬ ‫يمكننا‬ )‫معنى‬ ‫بدون‬ ‫او‬ ‫(بمعنى‬ ‫كلمة‬ ‫فكم‬
.‫الواحدة‬ ‫الكلمة‬ ‫في‬ ‫الحرف‬ ‫بتكرار‬ ‫يسمح‬ ‫ال‬ ‫ان‬ ‫على‬ ‫حروف‬ ‫اربعة‬ ‫من‬
/‫الحل‬‫الكلمة‬ ‫في‬ ‫االول‬ ‫الحرف‬ ‫طرق‬ ‫عدد‬=6
‫الكلمة‬ ‫في‬ ‫الثاني‬ ‫الحرف‬ ‫طرق‬ ‫عدد‬=5‫الكلية‬ ‫الطرق‬ ‫عدد‬=6.5.4.3=360‫كلمة‬
‫الكلمة‬ ‫في‬ ‫الثالث‬ ‫الحرف‬ ‫طرق‬ ‫عدد‬=4
‫الكلمة‬ ‫في‬ ‫الرابع‬ ‫الحرف‬ ‫طرق‬ ‫عدد‬=3
‫مثال‬12/‫فتاة‬ ‫لدى‬ ‫كان‬ ‫اذا‬6‫و‬ ‫االلوان‬ ‫مختلفة‬ ‫قمصان‬7‫و‬ ‫االلوان‬ ‫مختلفة‬ ‫تنورات‬4‫مكون‬ ‫زي‬ ‫فبكم‬ ‫مختلفة‬ ‫احذية‬ ‫ازواج‬
.‫تستخدم‬ ‫ان‬ ‫للفتاة‬ ‫يمكن‬ ‫وحذاء‬ ‫وتنورة‬ ‫قميص‬ ‫من‬
‫واحد‬ ‫خانة‬ ‫على‬ ‫عناصر‬ ‫مجموعة‬ ‫توزيع‬ ‫طرق‬ ‫عدد‬ : ‫توضيح‬.‫المجموعة‬ ‫في‬ ‫العناصر‬ ‫عدد‬ ‫يساوي‬ ‫ة‬
/‫الحل‬‫القميص‬ ‫طرق‬ ‫عدد‬=6
‫التنورة‬ ‫طرق‬ ‫عدد‬=7‫الكلية‬ ‫الطرق‬ ‫عدد‬=6.7.4=168‫زي‬
‫الحذاء‬ ‫زوج‬ ‫طرق‬ ‫عدد‬=4
‫مثال‬13/‫بفرض‬ ‫يستخدم‬ ‫ان‬ ‫يمكنه‬ ‫زي‬ ‫فكم‬ ‫احذية‬ ‫واربعة‬ ‫بنطلونات‬ ‫وخمسة‬ ‫تيشيرتات‬ ‫وثالثة‬ ‫قمصان‬ ‫اربعة‬ ‫لشاب‬ ‫كان‬ ‫اذا‬
.‫شيرت‬ ‫تي‬ ‫او‬ ‫قميص‬ ‫اما‬ ‫يرتدي‬ ‫انه‬
/‫الحل‬‫تيشيرتات‬ ‫ومجموعة‬ ‫قمصان‬ ‫مجموعة‬ ‫لدينا‬ ‫المثال‬ ‫هذا‬ ‫في‬‫عدد‬ ‫مجموع‬ ‫يساوي‬ ‫الخانة‬ ‫هذه‬ ‫طرق‬ ‫عدد‬ ‫يكون‬ ‫لذلك‬ ‫الخانة‬ ‫نفس‬ ‫في‬ ‫تندرج‬
‫والتيشيرتات‬ ‫القمصان‬ ‫عناصر‬:
‫والتيشيرتات‬ ‫القمصان‬ ‫خانة‬ ‫طرق‬ ‫عدد‬=3+4=7
‫البنطلونات‬ ‫طرق‬ ‫عدد‬=5‫الكلية‬ ‫الطرق‬ ‫عدد‬=7.5.4=140‫زي‬
‫االحذية‬ ‫طرق‬ ‫عدد‬=4
‫مثال‬14/‫من‬ ‫اقل‬ ‫يكون‬ ‫ان‬ ‫على‬ ‫مراتب‬ ‫ثالثة‬ ‫من‬ ‫عددا‬ ‫تكوين‬ ‫يمكن‬ ‫طريقة‬ ‫بكم‬500‫االرقام‬ ‫باستخدام‬(1,2,3,4,
5,6,7):‫كان‬ ‫اذا‬
1–.‫نفسه‬ ‫العدد‬ ‫في‬ ‫الرقم‬ ‫بتكرار‬ ‫يسمح‬
2–.‫نفسه‬ ‫العدد‬ ‫في‬ ‫الرقم‬ ‫بتكرار‬ ‫يسمح‬ ‫ال‬
‫السؤال‬ : ‫توضيح‬‫يشترط‬‫من‬ ‫اقل‬ ‫العدد‬ ‫يكون‬ ‫ان‬500‫و‬‫االرقام‬ ‫وضع‬ ‫نستطيع‬ ‫ال‬ ‫اننا‬ ‫يعني‬ ‫هذا‬7‫و‬6‫و‬5‫عدد‬ ‫يكون‬ ‫وبذلك‬ ‫المئات‬ ‫خانة‬ ‫في‬
‫وهي‬ ‫فقط‬ ‫ارقام‬ ‫اربعة‬ ‫هي‬ ‫المئات‬ ‫لخانة‬ ‫الممكنة‬ ‫االرقام‬1‫و‬2‫و‬3‫و‬4.
/‫الحل‬‫أ‬–:‫الرقم‬ ‫بتكرار‬ ‫يسمح‬
‫في‬ ‫الطرق‬ ‫عدد‬‫مرتبة‬‫المئات‬=4
‫في‬ ‫الطرق‬ ‫عدد‬‫مرتبة‬‫العشرات‬=7‫الكلية‬ ‫الطرق‬ ‫عدد‬=4.7.7=196‫طريقة‬
‫في‬ ‫الطرق‬ ‫عدد‬‫مرتبة‬‫االحاد‬=7
‫ب‬–:‫الرقم‬ ‫بتكرار‬ ‫يسمح‬ ‫ال‬
‫المئات‬ ‫خانة‬ ‫طرق‬ ‫عدد‬=4
‫العشرات‬ ‫خانة‬ ‫طرق‬ ‫عدد‬=6‫الكلية‬ ‫الطرق‬ ‫عدد‬=4.5.6=120‫طريقة‬
‫االحاد‬ ‫خانة‬ ‫طرق‬ ‫عدد‬=5

7. ‫أدبي‬ ‫سادس‬‫االول‬ ‫الفصل‬‫االساسي‬ ‫العد‬ ‫مبدأ‬
/ ‫الشمري‬ ‫احمد‬ ‫األستاذ‬077045169377/ ‫الطباعية‬ ‫للخدمات‬ ‫المرسل‬07703458937
‫مثال‬15/‫االرقام‬ ‫باستخدام‬ ‫تكوينه‬ ‫يمكن‬ ‫مراتب‬ ‫ثالثة‬ ‫من‬ ‫رمزه‬ ‫مكون‬ ‫عددا‬ ‫كم‬(1,2,3,4,5,6,7):‫بحيث‬
a)‫العدد‬ ‫في‬ ‫الرقم‬ ‫وتكرار‬ ‫زوجيا‬ ‫العدد‬ ‫يكون‬‫غير‬.‫به‬ ‫مسموح‬(‫تمهيدي‬2014)
b).‫به‬ ‫مسموح‬ ‫العدد‬ ‫في‬ ‫الرقم‬ ‫وتكرار‬ ‫فرديا‬ ‫العدد‬ ‫يكون‬‫(وزاري‬2013)‫ثاني‬ ‫دور‬
/‫الحل‬a)‫االحاد‬ ‫مرتبة‬ ‫طرق‬ ‫عدد‬=3
‫العشرات‬ ‫مرتبة‬ ‫طرق‬ ‫عدد‬=6‫الكلية‬ ‫الطرق‬ ‫عدد‬=3.6.5=90‫طريقة‬
‫المئات‬ ‫مرتبة‬ ‫طرق‬ ‫عدد‬=5
/ ‫مالحظة‬( ‫االرقام‬ ‫احد‬ ‫تحوي‬ ‫االحاد‬ ‫مرتبة‬2‫و‬4‫و‬6‫يساوي‬ ‫االحاد‬ ‫مرتبة‬ ‫طرق‬ ‫عدد‬ ‫اي‬ )3.
b)‫االحاد‬ ‫مرتبة‬ ‫طرق‬ ‫عدد‬=4
‫العشرات‬ ‫مرتبة‬ ‫طرق‬ ‫عدد‬=7
‫المئات‬ ‫مرتبة‬ ‫طرق‬ ‫عدد‬=7
‫الكلية‬ ‫الطرق‬ ‫عدد‬=4.7.7=196‫طريقة‬
/ ‫مالحظة‬(‫االرقام‬ ‫احد‬ ‫تحوي‬ ‫االحاد‬ ‫مرتبة‬1‫و‬3‫و‬5‫و‬7‫يساوي‬ ‫االحاد‬ ‫مرتبة‬ ‫طرق‬ ‫عدد‬ ‫اي‬ )4.
‫تمارين‬ ‫حلول‬1-1
1-‫احمد‬ ‫لدى‬5‫و‬ ‫مختلفة‬ ‫سترات‬6‫و‬ ‫مختلفة‬ ‫بنطلونات‬8‫سترة‬ ‫من‬ ‫مكون‬ ‫احمد‬ ‫به‬ ‫يظهر‬ ‫مختلف‬ ‫زي‬ ‫فبكم‬ ‫مختلفة‬ ‫قمصان‬
.‫وقميص‬ ‫وبنطلون‬(‫تمهيدي‬2013,‫وزاري‬2011)‫اول‬ ‫دور‬
/‫ج‬‫السترات‬ ‫طرق‬ ‫عدد‬=5
‫البنطلونات‬ ‫طرق‬ ‫عدد‬=6‫الزي‬ ‫طرق‬ ‫عدد‬=5.6.8=240‫ز‬‫ي‬
‫القمصان‬ ‫طرق‬ ‫عدد‬=8
2-‫الحروف‬ ‫لدينا‬ ‫كان‬ ‫اذا‬(‫أ‬–‫ل‬–‫ع‬–‫ق‬–‫ك‬–) ‫ب‬‫هذه‬ ‫من‬ )‫معنى‬ ‫بدون‬ ‫او‬ ‫(بمعنى‬ ‫احرف‬ ‫اربعة‬ ‫من‬ ‫مكونة‬ ‫كلمة‬ ‫كم‬
‫الحروف‬‫ع‬.‫الواحدة‬ ‫الكلمة‬ ‫في‬ ‫الحرف‬ ‫بتكرار‬ ‫يسمح‬ ‫ال‬ ‫ان‬ ‫لى‬
/‫ج‬‫االول‬ ‫الحرف‬ ‫طرق‬ ‫عدد‬=6
‫الثاني‬ ‫الحرف‬ ‫طرق‬ ‫عدد‬=5‫الكلمات‬ ‫عدد‬=6.5.4.3=360‫كلمة‬
‫الثالث‬ ‫الحرف‬ ‫طرق‬ ‫عدد‬=4
‫الرابع‬ ‫الحرف‬ ‫طرق‬ ‫عدد‬=3
3-‫وظائف‬ ‫ثالثة‬ ‫لشغل‬ ‫اشخاص‬ ‫عشرة‬ ‫بين‬ ‫من‬ ‫اشخاص‬ ‫ثالث‬ ‫اختيار‬ ‫يمكن‬ ‫طريقة‬ ‫بكم‬‫معينة‬‫مختلفة‬.
/‫ج‬‫االولى‬ ‫الوظيفة‬ ‫طرق‬ ‫عدد‬=10
‫الثانية‬ ‫الوظيفة‬ ‫طرق‬ ‫عدد‬=9‫الوظائف‬ ‫شغل‬ ‫طرق‬ ‫عدد‬=10.9.8=720‫طريقة‬
‫الثالثة‬ ‫الوظيفة‬ ‫طرق‬ ‫عدد‬=8
4-‫االرقام‬ ‫باستخدام‬ ‫تكوينه‬ ‫يمكن‬ ‫ارقام‬ ‫ثالثة‬ ‫من‬ ‫رمزه‬ ‫مكون‬ ‫عددا‬ ‫كم‬9,8,7,6,5,4,3
‫أ‬–.‫نفسه‬ ‫العدد‬ ‫في‬ ‫للرقم‬ ‫مسموح‬ ‫غير‬ ‫والتكرار‬ ‫فرديا‬ ‫العدد‬ ‫يكون‬ ‫ان‬ ‫على‬
‫ب‬–.‫نفسه‬ ‫العدد‬ ‫في‬ ‫للرقم‬ ‫به‬ ‫مسموح‬ ‫والتكرار‬ ‫زوجيا‬ ‫العدد‬ ‫يكون‬ ‫ان‬ ‫على‬
/‫ج‬‫أ‬-‫االحاد‬ ‫مرتبة‬ ‫طرق‬ ‫عدد‬=4
‫العشرات‬ ‫مرتبة‬ ‫طرق‬ ‫عدد‬=6‫الكلية‬ ‫الطرق‬ ‫عدد‬=4.6.5=120‫طريقة‬
‫المئات‬ ‫مرتبة‬ ‫طرق‬ ‫عدد‬=5
‫ب‬-‫االحاد‬ ‫مرتبة‬ ‫طرق‬ ‫عدد‬=3
‫العشرات‬ ‫مرتبة‬ ‫طرق‬ ‫عدد‬=7‫الكلية‬ ‫الطرق‬ ‫عدد‬=3.7.7=147‫طريقة‬
‫المئات‬ ‫مرتبة‬ ‫طرق‬ ‫عدد‬=7
5-‫االرقام‬ ‫باستخدام‬ ‫تكوينه‬ ‫يمكن‬ ‫مراتب‬ ‫ثالث‬ ‫من‬ ‫مكون‬ ‫رمزه‬ ‫يكون‬ ‫عددا‬ ‫كم‬1,2,3,4,5,6,7
‫أ‬–‫اكبر‬ ‫العدد‬ ‫يكون‬ ‫ان‬ ‫على‬‫من‬500.‫نفسه‬ ‫العدد‬ ‫في‬ ‫للرقم‬ ‫به‬ ‫مسموح‬ ‫والتكرار‬
‫ب‬–‫من‬ ‫اصغر‬ ‫العدد‬ ‫يكون‬ ‫ان‬ ‫على‬400.‫نفسه‬ ‫العدد‬ ‫في‬ ‫للرقم‬ ‫به‬ ‫مسموح‬ ‫غير‬ ‫والتكرار‬
/‫الحل‬
‫أ‬-‫االحاد‬ ‫مرتبة‬ ‫طرق‬ ‫عدد‬=7
‫العشرات‬ ‫مرتبة‬ ‫طرق‬ ‫عدد‬=7‫الكلية‬ ‫الطرق‬ ‫عدد‬=3.7.7=147‫عدد‬
‫المئات‬ ‫مرتبة‬ ‫طرق‬ ‫عدد‬=3
‫ب‬-‫االحاد‬ ‫مرتبة‬ ‫طرق‬ ‫عدد‬=5
‫العشرات‬ ‫مرتبة‬ ‫طرق‬ ‫عدد‬=6‫الكلية‬ ‫الطرق‬ ‫عدد‬=3.6.5=90‫عدد‬
‫المئات‬ ‫مرتبة‬ ‫طرق‬ ‫عدد‬=3

8. ‫أدبي‬ ‫سادس‬‫االول‬ ‫الفصل‬‫التباديل‬
/ ‫الشمري‬ ‫احمد‬ ‫األستاذ‬077045169378/ ‫الطباعية‬ ‫للخدمات‬ ‫المرسل‬07703458937
2-)‫(المفكوك‬ ‫العدد‬ ‫مضروب‬:‫او‬ ! ‫بـ‬ ‫اما‬ ‫له‬ ‫ويرمز‬ ‫تسبقه‬ ‫التي‬ ‫االعداد‬ ‫في‬ ‫العدد‬ ‫ضرب‬ ‫حاصل‬ ‫هو‬L‫ان‬ ‫فرضنا‬ ‫واذا‬
n‫مفكوك‬ ‫فان‬ ‫طبيعي‬ ‫عدد‬n‫هو‬n!: ‫حيث‬ ‫او‬
n! = n . (n-1) . (n-2) . ……. . 1
‫مثال‬1/‫العدد‬ ‫مفكوك‬ ‫جد‬4‫؟‬
/‫ج‬4! = 4 . 3 . 2 . 1 = 24
‫مثال‬2/‫االعداد‬ ‫مفكوك‬ ‫جد‬5,3‫؟‬
5! = 5 . 4 . 3 . 2 . 1 = 120
3! = 3 . 2 . 1 = 6
‫مثال‬3/‫التالية‬ ‫المعادلة‬ ‫قيمة‬ ‫جد‬
9!
7!
‫؟‬
9!
7!
=
9 . 8 . 7!
7!
= 𝟗 . 𝟖 = 𝟕𝟐
‫مثال‬4/‫المعادلة‬ ‫ناتج‬ ‫جد‬
100!
99!
‫؟‬
100!
99!
=
100 .99!
99!
= 𝟏𝟎𝟎
‫مثال‬5/‫قيمة‬ ‫جد‬n‫المعادلة‬ ‫تحقق‬ ‫التي‬
n!
(n−2)!
= 6.‫(وزاري‬2011)‫اول‬ ‫دور‬
/‫الحل‬:‫فان‬ ‫العدد‬ ‫مفكوك‬ ‫تعريف‬ ‫من‬
n! = n . (n-1) . (n-2)!
‫قيمة‬ ‫عن‬ ‫نستعيض‬ ‫ان‬ ‫يمكننا‬ ‫بذلك‬n!:‫مبين‬ ‫كما‬
n . (n−1) . (n−2)!
(n−2)!
= 6
n(n-1)-6 = 0 ⟹ n2
– n - 6 = 0 ⟹ (n+2)(n-3) = 0
n = -2 ‫مفكوك‬ ‫له‬ ‫يوجد‬ ‫ال‬ ‫السالب‬ ‫العدد‬ ‫الن‬ ‫دائما‬ ‫تهمل‬
∴ n = 3
‫مثال‬6/‫قيمة‬ ‫جد‬n‫المعادلة‬ ‫تحقق‬ ‫التي‬(n+1)! = 24
/‫الحل‬‫هو‬ ‫المعادلة‬ ‫طرفي‬ ‫احد‬ ‫ان‬ ‫بما‬‫وليس‬ ‫عدد‬‫الرقم‬ ‫يساوي‬ ‫مفكوكه‬ ‫يكون‬ ‫الذي‬ ‫العدد‬ ‫نجد‬ ‫ان‬ ‫يجب‬ ‫فاننا‬ ‫مفكوك‬24‫الضرب‬ ‫خالل‬ ‫من‬
:‫العكسي‬
1 . 2 = 2
2 . 3 = 6
6 . 4 = 24 ∴ 4! = 24
: ‫اذا‬(n+1)! = 4!
n+1 = 4 ≫ ∴ n = 3
‫قوانين‬:‫المفكوك‬
1) 0! = 1 ‫يساوي‬ ‫الصفر‬ ‫مفكوك‬1
2) 1! = 1 ‫يساوي‬ ‫الواحد‬ ‫مفكوك‬1
3) 2! = 2 ‫يساوي‬ ‫االثنين‬ ‫مفكوك‬2
4) n! = n . (n-1)! = n . (n-1) . (n-2)!
:‫ان‬ ‫اي‬
6! = 6 . 5! = 6 . 5 . 4! = 6 . 5 . 4 . 3! = 6 . 5 . 4 . 3 . 2!
: ‫التساوي‬ ‫قانون‬‫كان‬ ‫اذا‬n! = k!‫فان‬n‫تساوي‬k
n

9. ‫أدبي‬ ‫سادس‬‫االول‬ ‫الفصل‬‫التباديل‬
/ ‫الشمري‬ ‫احمد‬ ‫األستاذ‬077045169379/ ‫الطباعية‬ ‫للخدمات‬ ‫المرسل‬07703458937
3-:‫التباديل‬‫بشرط‬ ‫عناصر‬ ‫لمجموعة‬ ‫الطرق‬ ‫عدد‬ ‫حساب‬ ‫في‬ ‫التباديل‬ ‫معادلة‬ ‫تستخدم‬‫مسموح‬ ‫غير‬ ‫التكرار‬‫و‬‫الترتيب‬
‫بنظر‬ ‫مأخوذ‬‫االعتبار‬:
‫التباديل‬ ‫قانون‬:𝐏𝐫
𝐧
=
𝐧!
( 𝐧−𝐫)!
‫تباديل‬ ‫وتقرأ‬n‫مأخوذة‬r‫مرة‬ ‫كل‬ ‫في‬:‫حيث‬
Pr
n
= ‫الكلي‬ ‫الطرق‬ ‫عدد‬ (rPn
)
n = ‫عدد‬‫ال‬‫اكبر‬ ‫ايهما‬ ‫المراتب‬ ‫عدد‬ ‫او‬ ‫عناصر‬
r = ‫عدد‬‫ال‬‫اقل‬ ‫ايهما‬ ‫المراتب‬ ‫عدد‬ ‫او‬ ‫عناصر‬
‫مثال‬1/‫النشاء‬ ‫الطرق‬ ‫عدد‬ ‫جد‬( ‫االرقام‬ ‫مجموعة‬ ‫باستخدام‬ ‫مراتب‬ ‫ثالثة‬ ‫من‬ ‫رقم‬1‫و‬2‫و‬3‫و‬4‫و‬5‫تكرار‬ ‫عدم‬ ‫بشرط‬ )
.‫نفسه‬ ‫العدد‬ ‫في‬ ‫الرقم‬
/‫الحل‬n=5&r=3
𝐏𝟑
𝟓
=
𝟓!
(𝟓−𝟑)!
=
𝟓!
𝟐!
=
𝟓.𝟒.𝟑.𝟐!
𝟐!
= 60 ‫طريقة‬ ‫طريقة‬ 60 ‫يساوي‬ ‫الكلية‬ ‫الطرق‬ ‫عدد‬ ‫اذا‬
‫مثال‬2/‫تكرار‬ ‫عدم‬ ‫بشرط‬ )‫هـ‬ , ‫د‬ , ‫ج‬ , ‫ب‬ , ‫(أ‬ ‫االحرف‬ ‫مجموعة‬ ‫باستخدام‬ ‫حروف‬ ‫اربعة‬ ‫من‬ ‫كلمة‬ ‫النشاء‬ ‫الطرق‬ ‫عدد‬ ‫جد‬
.‫نفسها‬ ‫الكلمة‬ ‫في‬ ‫الحرف‬
P4
5
=
5!
(5−4)!
=
5!
1!
= 5.4.3.2 = 120 ‫كلمة‬
‫مثال‬3/:‫يأتي‬ ‫مما‬ ‫كل‬ ‫احسب‬P0
10
,P4
4
,P3
4
a) P0
10
=
10!
(10−0)!
=
10!
10!
= 1
b) P4
4
=
4!
(4−4)!
=
4!
0!
=
4!
1
= 4.3.2 = 24
c) P3
4
=
4!
(4−3)!
=
4!
1!
=
4.3.2
1
= 24
d) P1
4
=
4!
(4−1)!
=
4!
3!
=
4.3!
3!
= 4
‫مثال‬4/‫توزيع‬ ‫طرق‬ ‫عدد‬ ‫ما‬5‫وظائف‬ ‫خمسة‬ ‫على‬ ‫اشخاص‬‫مختلفة‬.‫واحدة‬ ‫وظيفة‬ ‫شخص‬ ‫لكل‬ ‫بحيث‬
P5
5
=
𝟓!
( 𝟓−𝟓)!
= 5! = 5.4.3.2 = 120 ‫طريقة‬
.‫مهم‬ ‫الترتيب‬ ‫فان‬ ‫مختلفون‬ ‫واالشخاص‬ ‫مختلفة‬ ‫الوظائف‬ ‫ان‬ ‫بما‬ /‫مالحظة‬
‫مثال‬5/‫قيمة‬ ‫جد‬n‫عندما‬P2
n
= 42
/‫ج‬42𝐏𝟐
𝐧
=
𝐧!
(𝐧−𝟐)!
=
𝐧.(𝐧−𝟏).(𝐧−𝟐)!
(𝐧−𝟐)!
=
n.(n-1) = 42 ⟹ n2
– n – 42 = 0 ⟹ (n +6) (n – 7) = 0
n = -6 ‫تهمل‬ ⟹ ∴ n = 7
‫مثال‬6/‫قيمة‬ ‫جد‬r:‫عندما‬
a) P3
6
= P𝑟
6
b) P4
5
= P𝑟
5
/‫ج‬a)P3
6
= P𝑟
6
6!
(6−3)!
=
6!
(6−r)!
⟹ (6 − 3)! = (6 − r)! ⟹ 6-3 = 6 – r ⟹ ∴ r = 3
b)P4
5
= P𝑟
5
5!
(5−4)!
=
5!
(5−r)!
⟹ (5 − 4)! = (5 − r)! ⟹ 5 - 4 = 5 – r ⟹ ∴ r = 4

10. ‫أدبي‬ ‫سادس‬‫االول‬ ‫الفصل‬‫التباديل‬
/ ‫الشمري‬ ‫احمد‬ ‫األستاذ‬0770451693710/ ‫الطباعية‬ ‫للخدمات‬ ‫المرسل‬07703458937
‫مثال‬7/‫من‬ ‫كل‬ ‫قيمة‬ ‫جد‬P3
6
,P5
8
,P7
15
a) P3
6
=
6!
(6−3)!
=
6!
3!
=
6.5.4.3!
3!
= 120
b) P5
8
=
8!
(8−5)!
=
8!
3!
=
8.76.5.4.3!
3!
= 6720
c) P7
15
=
15!
(15−7)!
=
15.14.13.12.11.10.9.8!
8!
= 32432400
‫مثال‬8/‫االرقام‬ ‫بين‬ ‫من‬ ‫مأخوذة‬ ‫ارقام‬ ‫ثالثة‬ ‫من‬ ‫مكون‬ ‫منها‬ ‫كل‬ ‫رمز‬ ‫التي‬ ‫االعداد‬ ‫عدد‬ ‫ما‬3,4,5,6,7,8:‫بشرط‬
‫أ‬–.‫نفسه‬ ‫العدد‬ ‫في‬ ‫الرقم‬ ‫تكرار‬ ‫دون‬
‫ب‬–.‫نفسه‬ ‫العدد‬ ‫في‬ ‫الرقم‬ ‫تكرار‬ ‫يمكن‬
/‫الحل‬‫أ‬–
P3
6
=
6!
(6−3)!
=
6.5.4.3!
3!
= 120 ‫عدد‬
‫ب‬-
‫االحاد‬ ‫مرتبة‬ ‫طرق‬ ‫عدد‬=6
‫العشرات‬ ‫مرتبة‬ ‫طرق‬ ‫عدد‬=6‫الكلية‬ ‫الطرق‬ ‫عدد‬=6.6.6=216‫طريقة‬
‫المئات‬ ‫مرتبة‬ ‫طرق‬ ‫عدد‬=6
‫التمارين‬ ‫حلول‬2-1
1-: ‫من‬ ‫كل‬ ‫قيمة‬ ‫احسب‬
‫أ‬–
7!
5!
=
7.6.5!
5!
= 42
‫ب‬-
=
10!
6!
−
9!
5!
=
10.9.8.7.6!
6!
−
9.8.7.6.5!
5!
= 5040 − 3024 = 2016
2-‫ج‬‫قيمة‬ ‫د‬n: ‫كان‬ ‫اذا‬
‫أ‬-n! = 5040
1 1
2 2
6 3
24 4
120 5
720 6
5040 7
‫ب‬-P2
n
= 72
P2
n
=
n!
(n−2)!
=
n.(n−1).(n−2)!
(n−2)!
= n.(n-1) = n2 – n = 72
n2 – n – 72 = 0 ⟹ (n + 8)(n-9) = 0 ⟹ n = -8 ‫تهمل‬ , ∴ n = 9
7=n∴
‫ق‬‫ان‬‫و‬:‫المساواة‬ ‫ن‬‫كان‬ ‫اذا‬Pr
n
=Pk
n
‫فان‬r = K
10 9
56

11. ‫أدبي‬ ‫سادس‬‫االول‬ ‫الفصل‬‫التباديل‬
/ ‫الشمري‬ ‫احمد‬ ‫األستاذ‬0770451693711/ ‫الطباعية‬ ‫للخدمات‬ ‫المرسل‬07703458937
‫ج‬-P5
n
= 8 . P4
n
‫(وزاري‬2013)‫اول‬ ‫دور‬(‫تمهيدي‬2014)
P5
n
= 8 . P4
n
⟹
n!
(n−5)!
= 8 .
n!
(n−4)!
⟹ (n – 4)! = 8 . (n - 5)!
(n – 4) . (n - 5)! = 8 . (n - 5)! ⟹ n - 4 = 8 ⟹ ∴ n = 12
‫د‬-= 30
(n+1)!
(n−1)!
‫(وزاري‬2013‫دور‬‫ثاني‬)
(n+1)!
(n−1)!
=
(n+1) . (n+1−1) .(n+1−2)!
(n−1)!
=
(n+1) . (n) .(n−1)!
(n−1)!
= n (n + 1) = 30
n2 + n - 30 = 0 ⟹ (n - 5)(n + 6) = 0 ⟹ n = -6 ‫تهمل‬
, ∴ n = 5
3-‫المجموعة‬ ‫لدينا‬ ‫كانت‬ ‫اذا‬(7,6,5,4,3,2,1)=x‫تكوينه‬ ‫يمكن‬ ‫مراتب‬ ‫ثالثة‬ ‫من‬ ‫مكون‬ ‫رمزه‬ ‫عددا‬ ‫فكم‬
:‫كان‬ ‫اذا‬
a)‫بدون‬‫الرقم‬ ‫تكرار‬‫نفسه‬ ‫العدد‬ ‫في‬‫؟‬‫عدد‬210=
7.6.5.4!
4!
=
7!
(7−3)!
P3
7
=
b)‫الرقم‬ ‫بتكرار‬ ‫يسمح‬‫العدد‬ ‫في‬‫نفسه‬‫؟‬
‫االحاد‬ ‫مرتبة‬ ‫طرق‬ ‫عدد‬=7
‫العشرات‬ ‫مرتبة‬ ‫طرق‬ ‫عدد‬=7‫الكلية‬ ‫الطرق‬ ‫عدد‬=343‫عدد‬
‫المئات‬ ‫مرتبة‬ ‫طرق‬ ‫عدد‬=7
c)‫من‬ ‫اصغر‬400‫الرقم‬ ‫تكرار‬ ‫بدون‬‫نفسه‬ ‫العدد‬ ‫في‬‫؟‬
‫المئات‬ ‫مرتبة‬ ‫طرق‬ ‫عدد‬=3
‫العشرات‬ ‫مرتبة‬ ‫طرق‬ ‫عدد‬=6‫الكلية‬ ‫الطرق‬ ‫عدد‬=90‫عدد‬
‫االحاد‬ ‫مرتبة‬ ‫طرق‬ ‫عدد‬=5
d)‫من‬ ‫اكبر‬200‫الرقم‬ ‫بتكرار‬ ‫ويسمح‬‫نفسه‬ ‫العدد‬ ‫في‬‫؟‬
‫المئات‬ ‫مرتبة‬ ‫طرق‬ ‫عدد‬=6
‫العشرات‬ ‫مرتبة‬ ‫طرق‬ ‫عدد‬=7‫الكلية‬ ‫الطرق‬ ‫عدد‬=294‫عدد‬
‫االحاد‬ ‫مرتبة‬ ‫طرق‬ ‫عدد‬=7
e)‫الرقم‬ ‫تكرار‬ ‫بدون‬ ‫زوجيا‬ ‫عددا‬‫نفسه‬ ‫العدد‬ ‫في‬‫؟‬
‫االحاد‬ ‫مرتبة‬ ‫طرق‬ ‫عدد‬=3
‫العشرات‬ ‫مرتبة‬ ‫طرق‬ ‫عدد‬=6‫الكلية‬ ‫الطرق‬ ‫عدد‬=90‫عدد‬
‫المئات‬ ‫مرتبة‬ ‫طرق‬ ‫عدد‬=5
f)‫الرقم‬ ‫بتكرار‬ ‫ويسمح‬ ‫فرديا‬ ‫عددا‬‫نفسه‬ ‫العدد‬ ‫في‬‫؟‬
‫المئات‬ ‫مرتبة‬ ‫طرق‬ ‫عدد‬=4
‫العشرات‬ ‫مرتبة‬ ‫طرق‬ ‫عدد‬=7‫الكلية‬ ‫الطرق‬ ‫عدد‬=196‫عدد‬
‫االحاد‬ ‫مرتبة‬ ‫طرق‬ ‫عدد‬=7
4-‫يجر‬‫ى‬‫انتخاب‬ ‫الصفوف‬ ‫احد‬ ‫في‬‫ا‬‫في‬ ‫مراكز‬ ‫ثالثة‬ ‫على‬‫الرئيس‬ ‫ونائب‬ ‫الرئيس‬ ‫هي‬ ‫الصف‬ ‫لجان‬ ‫احدى‬‫ما‬ ‫السر‬ ‫وامين‬
‫اذا‬ ‫االنتخابات‬ ‫عنها‬ ‫تسفر‬ ‫التي‬ ‫النتائج‬ ‫عدد‬‫االنتخابات‬ ‫في‬ ‫المشاركين‬ ‫الطالب‬ ‫عدد‬ ‫ان‬ ‫علم‬‫طالب؟‬ ‫عشرة‬
/‫ج‬‫مسموح‬ ‫غير‬ ‫والتكرار‬ ‫مهم‬ ‫الترتيب‬:
P3
10
=
10!
(10−3)!
=
10.9.8.7!
7!
= 720 ‫نتيجة‬
5-‫كلمة‬ ‫كم‬‫الحروف‬ ‫مختلفة‬‫قار؟‬ ‫ذي‬ ‫كلمة‬ ‫حروف‬ ‫بين‬ ‫من‬ ‫حروف‬ ‫ثالثة‬ ‫من‬ ‫مكونة‬
/‫ج‬
P3
5
=
5!
(5−3)!
=
5.4.3.2!
2!
= 60 ‫كلمة‬
6-‫صف‬ ‫في‬ ‫طالب‬ ‫خمسة‬ ‫يجلس‬ ‫ان‬ ‫يمكن‬ ‫طريقة‬ ‫بكم‬‫من‬‫ثمانية‬‫كراسي‬‫؟‬
/‫ج‬‫وكذلك‬ ‫مسموح‬ ‫غير‬ ‫التكرار‬‫ال‬‫ترتيب‬‫مهم‬:
P5
8
=
8!
(8−5)!
=
8.7.6.5.4.3!
3!
= 6720 ‫طريقة‬

12. ‫أدبي‬ ‫سادس‬‫االول‬ ‫الفصل‬‫التوافيق‬
/ ‫الشمري‬ ‫احمد‬ ‫األستاذ‬0770451693712/ ‫الطباعية‬ ‫للخدمات‬ ‫المرسل‬07703458937
4-: ‫التوافيق‬‫طرق‬ ‫عدد‬ ‫حساب‬ ‫في‬ ‫التوافيق‬ ‫معادلة‬ ‫تستخدم‬‫ترتيب‬:‫بشرط‬ ‫عناصر‬ ‫مجموعة‬
1-.‫مسموح‬ ‫غير‬ ‫التكرار‬
2-.‫االعتبار‬ ‫بنظر‬ ‫مأخوذ‬ ‫غير‬ ‫الترتيب‬
‫التوافيق‬ ‫قانون‬𝐂 𝐫
𝐧
=
𝐧!
𝐫! . (𝐧−𝐫)!
‫توافيق‬ ‫وتقرأ‬n‫مأخوذة‬r‫مرة‬ ‫كل‬ ‫في‬
Cr
n
‫الكلي‬ ‫الطرق‬ ‫عدد‬=
n = ‫عدد‬ ‫او‬ ‫المجموعة‬ ‫عناصر‬ ‫عدد‬‫اكبر‬ ‫ايهما‬ ‫المراتب‬
r = ‫اقل‬ ‫ايهما‬ ‫المراتب‬ ‫عدد‬ ‫او‬ ‫المجموعة‬ ‫عناصر‬ ‫عدد‬
:‫مبين‬ ‫كما‬ ‫التوافيق‬ ‫رمز‬ ‫كتابة‬ ‫ويمكن‬
(
n
r
) ‫أو‬ C(n, r)
‫مثال‬1/‫االمتحانية‬ ‫الورقة‬ ‫في‬ ‫االسئلة‬ ‫عدد‬ ‫كان‬ ‫اذا‬8‫عن‬ ‫االجابة‬ ‫والمطلوب‬6‫االسئلة؟‬ ‫حل‬ ‫طرق‬ ‫عدد‬ ‫فكم‬ ‫فقط‬ ‫اسئلة‬
/‫ج‬:‫مبين‬ ‫كما‬ ‫التوافيق‬ ‫قانون‬ ‫نستخدم‬ ‫فاننا‬ ‫االمتحاني‬ ‫الدفتر‬ ‫في‬ ‫سؤال‬ ‫اي‬ ‫حل‬ ‫تكرار‬ ‫يمكن‬ ‫وال‬ ‫مهم‬ ‫غير‬ ‫االسئلة‬ ‫حل‬ ‫ترتيب‬ ‫ان‬ ‫بما‬
n = 8 & r = 6
C6
8
=
8!
6! . (8−6)!
=
8.7.6!
6! . 2!
= 28‫طريقة‬
‫مثال‬2/‫فيها‬ ‫مجموعة‬ ‫من‬ ‫بنقطتين‬ ‫تحديدها‬ ‫يمكن‬ ‫التي‬ ‫المستقيم‬ ‫قطع‬ ‫عدد‬ ‫كم‬6‫استقامة‬ ‫على‬ ‫نقاط‬ ‫ثالث‬ ‫توجد‬ ‫وال‬ ‫نقاط‬
‫واحدة؟‬‫(تمهيدي‬2005)
/‫ج‬
C2
6
=
6!
2! . (6−2)!
=
6.5.4!
2 . 4!
= 15
‫مثال‬3/‫يأتي‬ ‫ما‬ ‫ناتج‬ ‫جد‬C12
15
,C3
15
,C0
8
,C4
5
,C5
5
a) C12
15
=
15!
12! . (15−12)!
=
15.14.13.12!
12! . 3!
=
15.14.13
3.2
= 5.7.13 = 455
b) C3
15
=
15!
3! . (15−3)!
=
15.14.13.12!
3! . 12!
=
15.14.13
3.2
= 5.7.13 = 455
c)C0
8
=
8!
0! . (8−0)!
=
8!
1 . 8!
= 1
d) C4
5
=
5!
4! . (5−4)!
=
5 .4!
4! . 1!
= 5
e) C5
5
=
5!
5! . (5−5)!
=
5!
5! . 0!
=
5!
5! . 1
= 1
‫مثال‬4/‫يأتي‬ ‫ما‬ ‫احسب‬C5
13
,C0
10
,C20
20
/‫ج‬
a) C5
13
=
13!
5! . (13−5)!
=
13.12.11.10.9.8!
5! . 8!
=
13.12.11.10.9
5.4.3.2
= 13.11.9 = 1287
b) C0
10
=
10!
0! . (10−0)!
= 1
c) C20
20
=
20!
20! . (20−20)!
= 1
‫قانو‬:‫التوافيق‬ ‫ن‬𝐂 𝐧−𝐫
𝐧
=𝐂 𝐫
𝐧

13. ‫أدبي‬ ‫سادس‬‫االول‬ ‫الفصل‬‫التوافيق‬
/ ‫الشمري‬ ‫احمد‬ ‫األستاذ‬0770451693713/ ‫الطباعية‬ ‫للخدمات‬ ‫المرسل‬07703458937
‫مثال‬5/‫قيمة‬ ‫جد‬n‫كان‬ ‫اذا‬(n+1
3
)=2(n
2
)‫؟‬(‫وزاري‬2012‫اول‬ ‫دور‬)
2(n
2
) = (n+1
3
) ⟹ 2.
n!
2! . (n−2)!
=
(n+1)!
3! . ((n+1)−3)!
2.
n!
2! . (n−2)!
=
(n+1).(n+1−1)!
3! . (n−2)!
⟹ 1 =
(n+1)
3.2
⟹ (n + 1) = 6
n = 6 - 1 ⟹ ∴ n = 5
‫مثال‬6/‫من‬ ‫مكونة‬ ‫لجنة‬ ‫اختيار‬ ‫يمكن‬ ‫طريقة‬ ‫بكم‬5‫و‬ ‫طالبات‬7‫من‬ ‫مكونة‬ ‫مجموعة‬ ‫بين‬ ‫من‬ ‫طالب‬8‫و‬ ‫طالبات‬10‫طالب؟‬
/‫ج‬‫خمس‬ ‫اختيار‬ ‫طرق‬ ‫عدد‬‫طالبات‬‫ثمانية‬ ‫من‬=C5
8
‫سبع‬ ‫اختيار‬ ‫طرق‬ ‫عدد‬‫طالب‬‫عشرة‬ ‫من‬=C7
10
C5
8
. C7
10
=
8!
5! . (8−5)!
.
10!
7! . (10−7)!
=
8.7.6.5!
5! . (3)!
.
10.9.8.7!
7! . (3)!
=
8.7.6.5!
5! . (3)!
.
10.9.8.7!
7! . 3 .2
= 8.7.10.3.4 = 6720‫طريقة‬
‫مثال‬7/‫يحوي‬ ‫صندوق‬6‫و‬ ‫حمراء‬ ‫كرات‬4)‫(اختيار‬ ‫سحب‬ ‫يراد‬ ‫بيضاء‬ ‫كرات‬5‫تكون‬ ‫ان‬ ‫بشرط‬ ‫كرات‬3‫كرات‬‫منها‬
‫فقط‬ ‫حمراء‬,‫السحب؟‬ ‫اجراء‬ ‫يمكن‬ ‫طريقة‬ ‫بكم‬‫(تمهيدي‬2013)
/‫ج‬‫اختيار‬ ‫طرق‬ ‫عدد‬3‫من‬ ‫حمراء‬ ‫كرات‬6‫كرات‬=C3
6
‫ا‬ ‫طرق‬ ‫عدد‬‫من‬ ‫بيضاء‬ ‫كرتين‬ ‫ختيار‬4‫كرات‬=C2
4
C3
6
. C2
4
=
6!
3! . (6−3)!
.
4!
2! . (4−2)!
=
6.5.4.3!
3! . 3.2
.
4.3.2!
2! . 2!
= 5 . 4 . 2 . 3 = 120
‫مثال‬8/‫يمكن‬ ‫طريقة‬ ‫بكم‬ , ‫سكر‬ ‫اكياس‬ ‫وخمسة‬ ‫الشاي‬ ‫من‬ ‫علب‬ ‫واربع‬ ‫الحليب‬ ‫مادة‬ ‫من‬ ‫علب‬ ‫ستة‬ ‫يوجد‬ ‫المخازن‬ ‫احد‬ ‫في‬
‫سكر‬ ‫اكياس‬ ‫واربعة‬ ‫شاي‬ ‫علب‬ ‫وثالث‬ ‫حليب‬ ‫علبتي‬ ‫تحوي‬ ‫طلبية‬ ‫تجهيز‬‫؟‬
/‫الحل‬‫ستة‬ ‫من‬ ‫حليب‬ ‫علبتي‬ ‫اختيار‬ ‫طرق‬ ‫عدد‬=C2
6
‫اربع‬ ‫من‬ ‫شاي‬ ‫علب‬ ‫ثالث‬ ‫اختيار‬ ‫طرق‬ ‫عدد‬=C3
4
‫اختيار‬ ‫طرق‬ ‫عدد‬‫خمسة‬ ‫من‬ ‫سكر‬ ‫اكياس‬ ‫اربع‬=C4
5
C2
6
. C3
4
. C4
5
=
6!
2! . (6−2)!
.
4!
3! . (4−3)!
.
5!
4! . (5−4)!
= 15 . 4 . 5 = 300 ‫طريقة‬
‫مثال‬9/‫يحوي‬ ‫صندوق‬6‫و‬ ‫حمراء‬ ‫كرات‬4)‫(اختيار‬ ‫سحب‬ ‫يراد‬ ‫بيضاء‬ ‫كرات‬5‫ت‬ ‫ان‬ ‫بشرط‬ ‫كرات‬‫ح‬‫و‬‫ي‬‫االقل‬ ‫على‬3
‫فقط‬ ‫حمراء‬ ‫كرات‬,‫السحب؟‬ ‫اجراء‬ ‫يمكن‬ ‫طريقة‬ ‫بكم‬
/‫ج‬‫األقل‬ ‫على‬3‫من‬ ‫(نبدء‬ ‫حمراء‬3‫ونزيد‬)
1)]‫من‬ ‫حمراء‬ ‫ثالث‬‫ستة‬[‫و‬]‫من‬ ‫بيضاء‬ ‫اثنان‬‫اربعة‬[=. 𝐂 𝟑
𝟔
𝐂 𝟐
𝟒
2)]‫من‬ ‫حمراء‬ ‫اربع‬‫ستة‬[‫و‬]‫من‬ ‫بيضاء‬ ‫واحدة‬‫اربعة‬[=. 𝐂 𝟒
𝟔
𝐂 𝟏
𝟒
3)]‫من‬ ‫حمراء‬ ‫خمسة‬‫ستة‬[‫و‬]‫من‬ ‫بيضاء‬ ‫صفر‬‫اربعة‬[=. 𝐂 𝟓
𝟔
𝐂 𝟎
𝟒
C3
6
. C2
4
+ C4
6
. C1
4
+ C5
6
. C0
4
=
6!
3! . (6−3)!
.
4!
2! . (4−2)!
+
6!
4! . (6−4)!
.
4!
1! . (4−1)!
+
6!
5! . (6−5)!
.
4!
0! . (4−0)!
=
6.5.4.3!
3! . 3.2
.
4.3.2
2 .2
+
6.5.4!
4! . 2
.
4.3!
3!
+
6.5!
5!
.
4!
4!
= 20 . 6 + 15 . 4+ 6*1 = 120 + 60+6 = 186 ‫طريقة‬
‫المجموع‬=5( ‫البيضاء‬4)( ‫الحمراء‬6)
523
514
505
2

14. ‫أدبي‬ ‫سادس‬‫االول‬ ‫الفصل‬‫التوافيق‬
/ ‫الشمري‬ ‫احمد‬ ‫األستاذ‬0770451693714/ ‫الطباعية‬ ‫للخدمات‬ ‫المرسل‬07703458937
‫مثال‬10/‫لدينا‬ ‫كان‬ ‫اذا‬‫تحوي‬ ‫مجموعة‬‫ثالث‬‫و‬ ‫سيارات‬‫تحوي‬ ‫مجموعة‬‫خمسة‬‫دراجات‬‫كم‬ ,‫مجموعة‬‫تكوينها‬ ‫يمكن‬ ‫رباعية‬
‫المجموعتين‬ ‫عناصر‬ ‫من‬‫ان‬ ‫بشرط‬‫االكثر‬ ‫على‬ ‫تحوي‬‫دراجتين‬‫؟‬
/‫الحل‬‫االكثر‬ ‫على‬2‫دراجة‬‫من‬ ‫(نبدء‬2)‫وننزل‬
1)]‫من‬ ‫سيارتين‬3[‫و‬]‫من‬ ‫دراجتين‬5[=. C2
3
C2
5
2)]‫ثال‬‫ث‬‫سيار‬‫ات‬‫من‬3[‫و‬]‫دراجة‬‫من‬5[=. C3
3
C1
5
3)‫فقط‬ ‫ثالثة‬ ‫عددها‬ ‫الن‬ ‫سيارات‬ ‫ثالث‬ ‫من‬ ‫اكثر‬ ‫اختيار‬ ‫يمكن‬ ‫ال‬
C2
5
. C2
3
+ C1
5
. C3
3
=
5!
2! . (5−2)!
.
3!
2! . (3−2)!
+
5!
1! . (5−1)!
.
3!
3! . (3−3)!
=
5.4.3!
2 . 3!
.
3.2
2
+
5.4!
4!
.
3!
3!
= 10 . 3 + 5 . 1 = 30 + 5 = 35 ‫مجموعة‬
‫ح‬‫تمارين‬ ‫لول‬3-1
1-: ‫من‬ ‫كل‬ ‫قيمة‬ ‫جد‬
a) C5
11
=
11!
5! . (11−5)!
=
11.10.9.8.7.6!
5.4.3.2! . 6!
=11.3.2.7=462
b) C(18,18) =
18!
18! . (18−18)!
= 1
c) (7
0
) =
7!
0! . (7−0)!
= 1
d)
1
210
[P3
7
+ P4
7
] =
1
210
[
7!
(7−3)!
+
7!
(7−4)!
] =
1
210
[
7.6.5.4!
4!
+
7.6.5.4.3!
3!
]
=
1
210
[210 + 840] =
1050
210
= 5
2-‫قيمة‬ ‫جد‬n‫كان‬ ‫اذا‬C20
n
= C35
n
(2012‫دور‬3)
/‫ج‬‫ان‬ ‫بما‬Cr
n
= Cn−r
n
:‫اذا‬
∵ r = 20 , n – r = 35 , n – 20 = 35
∴ n = 35 + 20 = 55
3-:‫خاطئة‬ ‫منها‬ ‫واي‬ ‫صائبة‬ ‫االتية‬ ‫العبارات‬ ‫اي‬
a) C6
16
= C4
10
C6
16
=
16!
6! . (16−6)!
=
16.15.14.13.12.11.10!
6.5.4.3.2 . 10!
= 8.7.13.11 = 8008
C4
10
=
10!
4! . 6!
=
10.9.8.7.6!
4.3.2 . 6!
= 10.3.7 = 210 ⟹ ∴ C6
16
≠ C4
10
‫خاطئة‬ ‫العبارة‬
b) C23
25
=
P2
25
2!
(‫تمهيدي‬2005)
𝟐𝟓!
𝟐𝟑! .(𝟐𝟓−𝟐𝟑)!
=
𝟐𝟓!
(𝟐𝟓−𝟐)!
.
𝟏
𝟐!
⟹ 𝟐𝟓!
𝟐𝟑! . 𝟐!
=
𝟐𝟓!
𝟐𝟑!
.
𝟏
𝟐!
‫صائبة‬ ‫العبارة‬
c) (n
4
) = (n
6
) ∴ n = 10
‫ان‬ ‫بما‬Cr
n
= Cn−r
n
:‫اذا‬
∵ r = 4 , n - 6 = 4 , n = 4+ 6
∴ n = 10 ‫صائبة‬ ‫العبارة‬
‫المجموع‬=4‫سيارات‬(3)‫دراجات‬(5)
422
431
4‫تهمل‬0‫تهمل‬

15. ‫أدبي‬ ‫سادس‬‫االول‬ ‫الفصل‬‫التوافيق‬
/ ‫الشمري‬ ‫احمد‬ ‫األستاذ‬0770451693715/ ‫الطباعية‬ ‫للخدمات‬ ‫المرسل‬07703458937
d)‫تكوينها‬ ‫يمكن‬ ‫والتي‬ ‫عناصر‬ ‫ثالثة‬ ‫على‬ ‫تحتوي‬ ‫التي‬ ‫الجزئية‬ ‫المجموعات‬ ‫عدد‬‫عناصرها‬ ‫عدد‬ ‫مجموعة‬ ‫من‬10‫هو‬C3
10
‫صائبة‬ ‫العبارة‬
e)‫هو‬ ‫منهم‬ ‫ثالثة‬ ‫اختيار‬ ‫طرق‬ ‫عدد‬ ‫يكون‬ ‫متمايزين‬ ‫غير‬ ‫اشخاص‬ ‫سبعة‬P3
7
‫خاطئة‬ ‫العبارة‬
: ‫مالحظة‬‫متمايزين‬ ‫غير‬ ‫اشخاص‬ ‫تحوي‬ ‫الفرعية‬ ‫المجموعة‬ ‫الن‬)‫(متشابهين‬‫غير‬ ‫الترتيب‬ ‫اذا‬‫ض‬.‫بالتوافيق‬ ‫والحل‬ ‫روري‬
f)‫بين‬ ‫من‬ ‫شخصين‬ ‫اختيار‬ ‫طرق‬ ‫عدد‬‫يساوي‬ ‫االختيار‬ ‫عند‬ ‫الترتيب‬ ‫مراعاة‬ ‫دون‬ ‫اشخاص‬ ‫ستة‬15.‫طريقة‬
C2
6
=
6!
2! . (6−2)!
=
6.5.4!
2! . 4!
= 15
‫صائبة‬ ‫العبارة‬
g) P0
3
− 2 = -1
R.H.S = P0
3
− 2 =
𝟑!
(𝟑−𝟎)!
- 2 . 0! =
𝟑!
𝟑!
– 2 . 1 = 1-2 = -1 = L.H.S ‫صائبة‬ ‫العبارة‬
h)‫لكل‬Nn , r ∈‫كان‬ ‫اذا‬Pr
5
= Pn
5
‫فان‬n = r
Pr
5
= Pn
5
𝟓!
( 𝟓−𝐫)!
=
𝟓!
( 𝟓−𝐧)!
( 𝟓 − 𝐫)! = ( 𝟓 − 𝐧)! ‫بطرفين‬ ‫وسطين‬
( 𝟓 − 𝐫) = ( 𝟓 − 𝐧) ⟹ 𝟓 − r = 5 − n ∴ r = n‫صائبة‬ ‫العبارة‬
4-:‫يأتي‬ ‫مما‬ ‫كل‬ ‫في‬ ‫الصحيحة‬ ‫االجابة‬ ‫اختر‬
a)‫عشرة‬ ‫بين‬ ‫من‬ ‫ثالثية‬ ‫لجنة‬ ‫اختيار‬ ‫طرق‬ ‫عدد‬‫يساوي‬ ‫اشخاص‬
‫الصحيح‬ ‫الجواب‬𝐂 𝟑
𝟏𝟎
‫اي‬‫رقم‬2
b)‫كان‬ ‫اذا‬n‫عناصرها‬ ‫عدد‬ ‫مجموعة‬ ‫من‬ ‫تكوينها‬ ‫يمكن‬ ‫التي‬ ‫الثنائية‬ ‫الجزئية‬ ‫المجموعات‬ ‫عدد‬6‫فان‬n: ‫يساوي‬
𝐂 𝟐
𝟔
=
𝟔!
𝟐! . (𝟔−𝟐)!
=
𝟔.𝟓.𝟒!
𝟐! . 𝟒!
= 15 1 ‫رقم‬ ‫الصحيح‬ ‫الجواب‬
c)‫يساوي‬ ‫سداسي‬ ‫مضلع‬ ‫رؤوس‬ ‫من‬ ‫رأسين‬ ‫بين‬ ‫تصل‬ ‫ان‬ ‫يمكن‬ ‫التي‬ ‫المستقيمة‬ ‫القطع‬ ‫عدد‬
‫رقم‬ ‫الصحيح‬ ‫الجواب‬2𝐂 𝟐
𝟔
d) ( 𝟔𝟖
𝟖
) ÷ 𝐂 𝟔𝟎
𝟔𝟖
= 𝐂 𝟖
𝟔𝟖
÷ 𝐂 𝟔𝟎
𝟔𝟖
= 𝟏
‫ان‬ ‫بما‬Cr
n
= Cn−r
n
‫فان‬C8
68
= C60
68
‫رقم‬ ‫الصحيح‬ ‫الجواب‬3
e)‫االرقام‬ ‫لدينا‬ ‫كان‬ ‫اذا‬1,2,3,4,5,6,7,8,9‫فان‬‫من‬ ‫رمزها‬ ‫المكون‬ ‫االعداد‬ ‫عدد‬‫اربعة‬‫ارقام‬‫مختلفة‬‫هذه‬ ‫بين‬ ‫من‬
: ‫هو‬ ‫االرقام‬
P4
9
=
9!
(9−4)!
=
9.8.7.6.5!
5!
= 9.8.7.6 = 3024 ‫رقم‬ ‫الصحيح‬ ‫4الجواب‬
5-‫بين‬ ‫من‬ ‫اعضاء‬ ‫ستة‬ ‫من‬ ‫لجنة‬ ‫تشكيل‬ ‫يراد‬5‫و‬ ‫طالب‬8‫على‬ ‫محتوية‬ ‫اللجنة‬ ‫تكون‬ ‫ان‬ ‫يمكن‬ ‫طريقة‬ ‫فبكم‬ ‫مدرسين‬
‫اثنين‬ ‫مدرسين‬‫فقط‬‫؟‬(2013‫اول‬ ‫دور‬)
C2
8
. C4
5
=
8!
2! . (8−2)!
. 5 =
8.7.6!
2! . 6!
. 5 =
8.7
2
. 5 = 4 . 7 . 5 = 140‫يقة‬‫طر‬
4
0
0

16. ‫أدبي‬ ‫سادس‬‫االول‬ ‫الفصل‬‫التوافيق‬
/ ‫الشمري‬ ‫احمد‬ ‫األستاذ‬0770451693716/ ‫الطباعية‬ ‫للخدمات‬ ‫المرسل‬07703458937
6-‫يحوي‬ ‫صندوق‬4‫و‬ ‫حمراء‬ ‫كرات‬8‫كرات‬ ‫ثالث‬ ‫سحبت‬ ‫بيضاء‬ ‫كرات‬‫معا‬‫سحب‬ ‫طرق‬ ‫عدد‬ ‫جد‬:(2012)‫اول‬ ‫دور‬
1).‫بيضاء‬ ‫وواحدة‬ ‫حمراء‬ ‫اثنتان‬
2).‫حمراء‬ ‫اثنتان‬ ‫االقل‬ ‫على‬
/‫ج‬1)‫بيضاء‬ ‫وواحدة‬ ‫حمراء‬ ‫اثنتان‬:‫والحمراء‬ ‫البيضاء‬ ‫بين‬ ‫مهم‬ ‫غير‬ ‫الترتيب‬ ‫اي‬ ‫معا‬ ‫تسحب‬ ‫الكرات‬ ‫ان‬ ‫بما‬
1) 𝐂 𝟐
𝟒
. 𝐂 𝟏
𝟖
=
𝟒!
𝟐! . (𝟒−𝟐)!
. 𝟖 =
𝟒.𝟑.𝟐!
𝟐! . 𝟐!
. 8 = 2.3.8 = 48
2)‫حمراء‬ ‫اثنتان‬ ‫االقل‬ ‫على‬
‫ا‬: ‫بيضاء‬ ‫وواحدة‬ ‫حمراء‬ ‫ثنتان‬C2
4
. C1
8
‫بيضاء‬ ‫كرات‬ ‫بدون‬ ‫فقط‬ ‫حمراء‬ ‫ثالثة‬:C3
4
. C0
8
C2
4
. C1
8
+ C3
4
. C0
8
= 6 . 8 + 4 . 1 = 48 + 4 = 52 ‫طريقة‬
7-‫هو‬ ‫ما‬ ‫مادة‬ ‫امتحان‬ ‫اسئلة‬ ‫عدد‬ ‫كان‬ ‫اذا‬10‫حل‬ ‫المطلوب‬ ‫وكان‬ ‫اسئلة‬7‫نختار‬ ‫ان‬ ‫على‬ ‫منها‬ ‫اسئلة‬4‫االولى‬ ‫الخمسة‬ ‫من‬
‫االجابة؟‬ ‫يمكن‬ ‫طريقة‬ ‫فبكم‬ ,
/‫ج‬
C4
5
. C3
5
= 5 .
5!
3! . (5−3)!
= 5 .
5.4.3!
3! . 2!
= 50‫طريقة‬
2

17. ‫ادبي‬ ‫سادس‬‫االول‬ ‫الفصل‬‫االثرائية‬ ‫االمثلة‬
/ ‫الشمري‬ ‫احمد‬ ‫األستاذ‬0770451693717/ ‫الطباعية‬ ‫للخدمات‬ ‫المرسل‬07703458937
3-‫ذ‬ ‫مبرهنة‬‫ات‬:‫الحدين‬‫تح‬ ‫في‬ ‫المبرهنة‬ ‫هذه‬ ‫تستخدم‬‫من‬ ‫تتكون‬ ‫التي‬ ‫المعادالت‬ ‫ليل‬‫طرح‬ ‫او‬ ‫جمع‬‫الي‬ ‫مرفوعين‬ ‫حدين‬
‫قوة‬n
y)±(x‫وقانونها‬:‫هو‬
(x + y)n
= ∑ Ci
n
. x(n−i)
. y(i)n
i=0
‫مثال‬1/‫مفكوك‬ ‫جد‬2
)x+y(:‫الحدين‬ ‫ذات‬ ‫مبرهنة‬ ‫باستخدام‬
(x+y)2
= C0
2
. x(2−0)
. y(0)
+ C1
2
. x(2−1)
. y(1)
+ C2
2
. x(2−2)
. y(2)
(x+y)2
= x2
+2 x . y + y2
‫مثال‬2/‫مفكوك‬ ‫جد‬2
)y-x(:‫الحدين‬ ‫ذات‬ ‫مبرهنة‬ ‫باستخدام‬
(x-y)2
= (𝐱 + (−𝐲))
𝟐
= 𝐂 𝟎
𝟐
. 𝐱(𝟐−𝟎)
. (−𝐲)(𝟎)
+ 𝐂 𝟏
𝟐
. 𝐱(𝟐−𝟏)
. (−𝐲)(𝟏)
+ 𝐂 𝟐
𝟐
. 𝐱(𝟐−𝟐)
. (−𝐲)(𝟐)
(x-y)2
= 𝐱 𝟐
- 𝟐 𝐱 . 𝐲 + 𝐲 𝟐
‫اذا‬ / ‫مالحظة‬.‫وهكذا‬ ‫سالب‬ ‫حد‬ ‫ويليه‬ ‫موجب‬ ‫حد‬ ‫اول‬ ‫فان‬ ‫طرح‬ ‫االقواس‬ ‫داخل‬ ‫كان‬ ‫اذا‬ ‫اما‬ ‫موجبة‬ ‫المفكوك‬ ‫حدود‬ ‫فكل‬ ‫جمع‬ ‫االقواس‬ ‫داخل‬ ‫كان‬
‫مثال‬3/‫مفكوك‬ ‫جد‬4
)x+y(:‫الحدين‬ ‫ذات‬ ‫مبرهنة‬ ‫باستخدام‬
(x+y)4
= C0
4
. x4
+ C1
4
. x3
. y + C2
4
. x2
. y2
+ C3
4
. x . y3
+ C4
4
. y4
(x+y)4
= x4
+ 4 . x3
. y +6 . x2
. y2
+ 4 . x . y3
+ y4
‫مثال‬4/‫مفكوك‬ ‫جد‬4
)y-x(:‫الحدين‬ ‫ذات‬ ‫مبرهنة‬ ‫باستخدام‬
(x-y)4
= C0
4
. x4
- C1
4
. x3
. y + C2
4
. x2
. y2
− C3
4
. x . y3
+ C4
4
. y4
(x-y)4
= x4
- 4 . x3
. y +6 . x2
. y2
− 4 . x . y3
+ y4
‫مثال‬5/‫مفكوك‬ ‫جد‬3
)y-x(‫الحدين‬ ‫ذات‬ ‫مبرهنة‬ ‫باستخدام‬
(x-y)3
= C0
3
. x3
- C1
3
. x2
. y + C2
3
. x . y2
− C3
3
. y3
(x-y)3
= x3
- 3 . x2
. y + 3 . x . y2
− y3
:‫مالحظات‬‫الخطوات‬ ‫من‬ ‫العديد‬ ‫نختصر‬ ‫ان‬ ‫يمكننا‬ ‫التالية‬ ‫المالحظات‬ ‫خالل‬ ‫من‬:
1-‫يساوي‬ ‫المفكوك‬ ‫حدود‬ ‫عدد‬n+1.
2-‫اسس‬ ‫مجموع‬x‫و‬y‫يساوي‬ ‫حد‬ ‫كل‬ ‫في‬n.
3-‫االول‬ ‫المتغير‬ ‫اس‬ ‫يكون‬ ‫حد‬ ‫اول‬ ‫في‬x‫يساوي‬n.‫حد‬ ‫اخر‬ ‫في‬ ‫صفر‬ ‫اسه‬ ‫ليصبح‬ ‫التالية‬ ‫الحدود‬ ‫في‬ ‫تدريجيا‬ ‫ويتناقص‬
4-‫المتغير‬ ‫اس‬ ‫يكون‬ ‫حد‬ ‫اول‬ ‫في‬y‫يساوي‬ ‫اسه‬ ‫ليصبح‬ ‫تدريجيا‬ ‫ويتزايد‬ ‫صفر‬ ‫يساوي‬n.‫حد‬ ‫اخر‬ ‫في‬
5-‫والح‬ ‫موجبة‬ ‫دائما‬ ‫الفردية‬ ‫الحدود‬ ‫فان‬ ‫طرح‬ ‫لدينا‬ ‫كان‬ ‫اذا‬.‫سالبة‬ ‫دوما‬ ‫الزوجية‬ ‫دود‬
6-‫التوافقيات‬ ‫قيم‬‫الحد‬ ‫حول‬‫ود‬‫الوسطي‬‫ة‬.‫متساوية‬
7-‫توافقية‬ ‫واخر‬ ‫توافقية‬ ‫اول‬=1
8-‫االخير‬ ‫قبل‬ ‫وما‬ ‫الثاني‬ ‫الحد‬ ‫توافقية‬ ‫قيمة‬=n
:‫مبين‬ ‫كما‬
(x+y)4
= C0
4
. x4
+ C1
4
. x3
. y + C2
4
. x2
. y2
+ C3
4
. x . y3
+ C4
4
. y4
‫مثال‬6/‫مفكوك‬ ‫جد‬5
)y-x(.
(x - y)5
= C0
5
. x5
- C1
5
. x4
. y + C2
5
. x3
. y2
− C3
5
. x2
. y3
+ C4
5
. x . y4
- C5
5
. y5
= x5
- 5 . x4
. y + 10 . x3
. y2
− 10 . x2
. y3
+ 5 . x . y4
- y5
‫مثال‬7/‫مفكوك‬ ‫جد‬4
)3a + b(.
(3a + b)4
= C0
4
. (3a)4
+ C1
4
. (3a)3
. b+ C2
4
. (3a)2
. b2
+ C3
4
. 3a . b3
+ C4
4
. b4
= 81 a4
+ 4 . 27 a3
. b+ 6 . 9 a2
. b2
+ 4 . 3a . b3
+ b4
= 81 a4
+ 108 a3
. b + 54 . a2
. b2
+ 12 . a . b3
+ b4
‫اس‬x‫يساوي‬n‫واس‬y
‫صفر‬ ‫يساوي‬ ‫اس‬x‫واحد‬ ‫ينقص‬
‫واس‬y‫واحد‬ ‫يزداد‬ ‫اس‬x‫يساوي‬0‫واس‬y
‫يساوي‬n

18. ‫ادبي‬ ‫سادس‬‫االول‬ ‫الفصل‬‫االثرائية‬ ‫االمثلة‬
/ ‫الشمري‬ ‫احمد‬ ‫األستاذ‬0770451693718/ ‫الطباعية‬ ‫للخدمات‬ ‫المرسل‬07703458937
‫مثال‬8/‫قيمة‬ ‫جد‬3
)101(
/‫ج‬:‫ليصبح‬ ‫المقدار‬ ‫بتبسيط‬ ‫نقوم‬
(101)3
= (100 + 1)3
= C0
3
. 1003
+ C1
3
. 1002
. 1 + C2
3
. 100 . 12
+ C3
3
. 13
= 1003
+ 3 . 1002
+ 3 . 100 + 1= 1000000 + 30000 + 300 + 1= 1030301
‫مثال‬9/‫قيمة‬ ‫جد‬5
)0.99(
(0.99)5
= (
99
100
)5
=
995
1005 =
(100−1)5
1005
‫مفكوك‬ ‫ايجاد‬:‫البسط‬
(100 − 1)5
= 1005
- 5.1004
+ 10.1003
- 10.1002
+ 5.100-1 = 9509900499
∴ (0.99)5
=
9509900499
1005 = 0. 9509900499
:‫العام‬ ‫الحد‬ ‫قانون‬‫المفكوك‬ ‫في‬ ‫معين‬ ‫حد‬ ‫اليجاد‬ ‫يستخدم‬ ‫قانون‬ ‫وهو‬‫و‬‫اذا‬‫فرضنا‬‫هو‬ ‫الحد‬ ‫تسلسل‬ ‫ان‬r‫فيرمز‬‫الحد‬ ‫لذلك‬
‫بالرمز‬𝐏𝐫:‫هي‬ ‫ومعادلته‬
𝐏𝐫 = 𝐂 𝐫−𝟏
𝐧
. 𝐱(𝐧−𝐫+𝟏)
. 𝐲(𝐫−𝟏)
‫حيث‬r‫و‬ ‫المفكوك‬ ‫في‬ ‫المطلوب‬ ‫الحد‬ ‫تسلسل‬ ‫تمثل‬n‫المفكوك‬ ‫اس‬ ‫تمثل‬‫تسلسله‬ ‫حد‬ ‫اول‬ (1‫تسلسله‬ ‫حد‬ ‫واخر‬n+1)
‫مثال‬10/‫مفكوك‬ ‫في‬ ‫الثالث‬ ‫الحد‬ ‫جد‬5
)2x +(
P3 = C3−1
5
. x(5−3+1)
. 2(3−1)
= C2
5
. x3
. 22
= 10 . x3
. 4 = 40 x3
‫مثال‬11/‫مفكوك‬ ‫في‬ ‫الثاني‬ ‫الحد‬ ‫جد‬4
)3-a(
P2 = C2−1
4
. a(4−2+1)
. (−3)(2−1)
C1
4
. a3
. (−3)1
= 4 . a3
. (−3) = -12 a3
‫مثال‬12/‫مفكوك‬ ‫في‬ ‫الخامس‬ ‫الحد‬ ‫جد‬8
)x-2(
P5 = C5−1
8
. 2(8−5+1)
. (−x)(5−1)
= C4
8
. 24
. (−x)4
=
8.7.6.5.4!
4.3.2! . 4!
. 16 . x4
= 70 . 16 . x4
= 1120 x4
‫مثال‬13/‫مفكوك‬ ‫في‬ ‫االوسط‬ ‫الحد‬ ‫جد‬6
)x+3(
/ ‫ج‬‫يساوي‬ ‫المفكوك‬ ‫حدود‬ ‫عدد‬ ‫ان‬ ‫بما‬n+1‫اي‬7‫الرابع‬ ‫الحد‬ ‫هو‬ ‫االوسط‬ ‫الحد‬ ‫فان‬:
P4 = C4−1
6
. x(6−4+1)
. (3)(4−1)
= C3
6
. x3
. 27 = 20 . 27 . x3
= 540 x3
‫كان‬ ‫اذا‬ /‫مالحظة‬n‫هو‬ ‫االوسط‬ ‫الحد‬ ‫تسلسل‬ ‫فان‬ ‫زوجي‬ ‫عدد‬
𝐧+𝟏
𝟐
‫مثال‬14/‫مفكوك‬ ‫في‬ ‫االوسط‬ ‫الحد‬ ‫جد‬6
)3-x(
/ ‫ج‬‫يساوي‬ ‫المفكوك‬ ‫حدود‬ ‫عدد‬ ‫ان‬ ‫بما‬n+1‫اي‬7‫الرابع‬ ‫الحد‬ ‫هو‬ ‫االوسط‬ ‫الحد‬ ‫فان‬:
P4 = C4−1
6
. x(6−4+1)
. (−3)(4−1)
= C3
6
. x3
. (−27) = − 20 . 27 . x3
= - 540 x3
‫مثال‬15/‫مفكوك‬ ‫في‬ ‫االوسط‬ ‫الحد‬ ‫جد‬7
)3x+(
/ ‫ج‬‫يساوي‬ ‫المفكوك‬ ‫حدود‬ ‫عدد‬ ‫ان‬ ‫بما‬n+1‫اي‬8‫والخامس‬ ‫الرابع‬ ‫الحدين‬ ‫هو‬ ‫االوسط‬ ‫الحد‬ ‫فان‬:
P4 = C4−1
7
. x(7−4+1)
. (3)(4−1)
= C3
7
. x4
. (27) =
7.6.5.4!
3.2! . 4!
. 27 . x4
= 35 . 27 . x4
= 945 x4
P5 = C5−1
7
. x(7−5+1)
. (3)(5−1)
= C4
7
. x3
. (81) =
7!
4! . 3!
. 81. x3
=
7.6.5.4!
4! . 3!
.81. x3
= 35 . 81 . x3
= 2835x3
‫مثال‬16/‫المتغير‬ ‫يحوي‬ ‫الذي‬ ‫الحد‬ ‫جد‬4
x‫مفكوك‬ ‫في‬6
)3x+(
/ ‫ج‬‫ان‬ ‫نفرض‬‫تسلسل‬‫تسلسله‬ ‫المطلوب‬ ‫الحد‬=r:‫مبين‬ ‫كما‬ ‫المعادلة‬ ‫ونكتب‬
Pr = Cr−1
6
. x(6−r+1)
. (3)(r−1)

19. ‫ادبي‬ ‫سادس‬‫االول‬ ‫الفصل‬‫االثرائية‬ ‫االمثلة‬
/ ‫الشمري‬ ‫احمد‬ ‫األستاذ‬0770451693719/ ‫الطباعية‬ ‫للخدمات‬ ‫المرسل‬07703458937
‫المتغير‬ ‫هو‬ ‫المطلوب‬ ‫ان‬ ‫بما‬4
x: ‫فان‬
x(6−r+1)
= x4
6 − r + 1 = 4 ‫االسس‬ ‫تساوت‬ ‫االساسات‬ ‫وتساوت‬ ‫كميتان‬ ‫تساوت‬ ‫اذا‬
∴ r = 6 + 1 - 4 = 3
‫المتغير‬ ‫يحوي‬ ‫الذي‬ ‫الحد‬ ‫اذا‬4x‫الثالث‬ ‫الحد‬ ‫هو‬:‫مبين‬ ‫كما‬ ‫الحد‬ ‫هذا‬ ‫بايجاد‬ ‫االن‬ ‫ونقوم‬
P3 = C3−1
6
. x(6−3+1)
. (3)(3−1)
= C2
6
. x4
. (3)2)
= 15 . x4
. 9 = 135 x4
‫مثال‬17/‫يحوي‬ ‫الذي‬ ‫الحد‬ ‫جد‬8
a‫مفكوك‬ ‫في‬8
)2
a+3(.‫معامله‬ ‫جد‬ ‫ثم‬‫(وزاري‬2012)‫ثالث‬ ‫دور‬
/ ‫ج‬
Pr = Cr−1
8
. 3(8−r+1)
. (a2
)(r−1)
‫المتغير‬ ‫هو‬ ‫المطلوب‬ ‫ان‬ ‫بما‬8
a: ‫فان‬
(a2
)(r−1)
= a8
⟹ (a)2(r−1)
= a8
2(r − 1) = 8 ‫االسس‬ ‫تساوت‬ ‫االساسات‬ ‫وتساوت‬ ‫كميتان‬ ‫تساوت‬ ‫اذا‬
r − 1 = 4 ⟹ ∴ r = 5
‫المتغير‬ ‫يحوي‬ ‫الذي‬ ‫الحد‬ ‫اذا‬8
a‫الخامس‬ ‫الحد‬ ‫هو‬‫هو‬ ‫ومعامله‬Cr−1
8
. 3(8−r+1)
C5−1
8
. 3(8−5+1)
= C4
8
. 34
=
8.7.6.5.4!
4.3.2! . 4!
. 81 = 70 . 81 = 5670 ‫الخامس‬ ‫الحد‬ ‫معامل‬
‫مثال‬18/‫من‬ ‫الخالي‬ ‫الحد‬ ‫جد‬x‫مفكوك‬ ‫في‬15
)x2
−
1
x
(.‫(وزاري‬2013‫دور‬)‫ثاني‬
/ ‫ج‬
Pr = Cr−1
15
. (x2
)(15−r+1)
. (−
1
x
)(r−1)
= Cr−1
15
(x)2(16−r)
.(−1)(r−1)
(x)−(r−1)
= Cr−1
15
. x(32−2r)−(r−1)
. (−1)(r−1)
= Cr−1
15
. x(33−3r)
. (−1)(r−1)
‫من‬ ‫الخالي‬ ‫الحد‬ ‫هو‬ ‫المطلوب‬ ‫ان‬ ‫بما‬x‫اس‬ ‫فان‬x:‫ان‬ ‫اي‬ ‫صفر‬ ‫يساوي‬
x(33−3r)
= x0
33 - 3r = 0 ‫تساوت‬ ‫اذا‬‫االساسات‬ ‫وتساوت‬ ‫قيمتان‬‫االسس‬ ‫تساوت‬
∴ r = 11
‫من‬ ‫الخالي‬ ‫الحد‬ ‫اذا‬x‫عشر‬ ‫الحادي‬ ‫الحد‬ ‫هو‬
𝐏𝟏𝟏 = 𝐂 𝟏𝟏−𝟏
𝟏𝟓
. (𝐱 𝟐
)(𝟏𝟓−𝟏𝟏+𝟏)
.(−
𝟏
𝐱
)(𝟏𝟏−𝟏)
= C10
15
.(x2)
5
. (−
1
x
)10
P11 =
15.14.13.12.11.10!
10! . 5.4.3.2
. x10
. (
1
x10) =
15.14.13.12.11
5.4.3.2
= 3003 ‫عشر‬ ‫الحادي‬ ‫الحد‬ ‫معامل‬
‫مثال‬19/‫مفكوك‬ ‫في‬ ‫االوسط‬ ‫الحد‬ ‫جد‬8
)3-x(‫(وزاري‬2011‫دور‬‫اول‬)
/‫ج‬‫الخامس‬ ‫هو‬ ‫االوسط‬ ‫الحد‬
P5 = C4
8
. x4
. (−3)4
=
8.7.6.5.4!
4.3.2! . 4!
.81. x4
= 70. 81. x4
= 5670 x4
‫مثال‬20/‫المقدار‬ ‫بسط‬4
a)-+ (24
(2+a)‫عندما‬ ‫المقدار‬ ‫قيمة‬ ‫جد‬ ‫ثم‬ ‫صورة‬ ‫ابسط‬ ‫الى‬a = √3.
/‫ج‬‫قوسين‬ ‫جمع‬ ‫حاصل‬ ‫من‬ ‫مكون‬ ‫المقدار‬ ‫ان‬ ‫بما‬‫مترافقين‬2 + a‫و‬2 - a‫االس‬ ‫لنفس‬ ‫مرفوعين‬‫قوس‬ ‫كل‬ ‫حدود‬ ‫فان‬ ‫باالشارة‬ ‫ويختلفان‬
:‫مبين‬ ‫كما‬ ‫االشارات‬ ‫تختلف‬ ‫ولكن‬ ‫االخر‬ ‫القوس‬ ‫حدود‬ ‫تساوي‬
(2+a)4
= P1 + P2 + P3 + P4 + P5
(2-a)4
= P1 - P2 + P3 - P4 + P5
‫بالجمع‬:5P2+3P2+1P2=4
a)-2+ (4
+a)2(
= 2(P1 + P3 + P5)
‫والخامس‬ ‫والثالث‬ ‫االول‬ ‫الحدود‬ ‫قيمة‬ ‫بايجاد‬ ‫نقوم‬ ‫االن‬‫فقط‬‫ال‬ ‫من‬‫مقدار‬4)a+2(:‫مبين‬ ‫كما‬

20. ‫ادبي‬ ‫سادس‬‫االول‬ ‫الفصل‬‫االثرائية‬ ‫االمثلة‬
/ ‫الشمري‬ ‫احمد‬ ‫األستاذ‬0770451693720/ ‫الطباعية‬ ‫للخدمات‬ ‫المرسل‬07703458937
P1 = C1−1
4
. 2(4−1+1)
. a(1−1)
= C0
4
. 24
. a0
= 16
P3 = C3−1
4
. 2(4−3+1)
. a(3−1)
= C2
4
. 22
. a2
= 24 a2
P5 = C5−1
4
. 2(4−5+1)
. a(5−1)
= C4
4
. 20
. a4
= a4
∴ (2+a)4
+ (2-a)4
= 2(16 + 24 a2
+ a4
)
‫عندما‬a = √3:‫تساوي‬ ‫المقدار‬ ‫قيمة‬ ‫فان‬
2(16 + 24 (√3)2
+ (√3)4
) = 2(16 + 24 . 3 + 9) = 2(97) = 194
‫فردي‬ ‫الزوجية(الجمع‬ ‫الحدود‬ ‫مجموع‬ ‫ضعف‬ ‫هو‬ ‫الطرح‬ ‫وناتج‬ ‫الفردية‬ ‫الحدود‬ ‫مجموع‬ ‫ضعف‬ ‫هو‬ ‫الجمع‬ ‫ناتج‬ /‫مالحظة‬.)‫زوجي‬ ‫والطرح‬
‫مثال‬21/‫المقدار‬ ‫بسط‬5
)
1
a
-a(-5
)
1
a
+a(‫صورة‬ ‫ابسط‬ ‫الى‬.
/‫ج‬:‫الزوجية‬ ‫الحدود‬ ‫مجموع‬ ‫ضعف‬ ‫هو‬ ‫الطرح‬ ‫ناتج‬
(a +
1
a
)5
- (a -
1
a
)5
= 2(P2+P4+P6)
P2 = 𝐂 𝟐−𝟏
𝟓
. a(𝟓−𝟐+𝟏)
. (
1
a
)(𝟐−𝟏)
= C1
5
. a4
. a−1
= 5 a3
P4 = C4−1
5
. a(5−4+1)
. (
1
a
)(4−1)
= C3
5
. a2
. a−3
= 10 a-1
=
10
a
P6 = C6−1
5
. a(5−6+1)
. (
1
a
)(6−1)
= C5
5
. a−5
= a-5
=
1
a5
(a +
1
a
)5
- (a -
1
a
)5
= 2 (5 a3
+
10
a
+
1
a5)
1 – 4 ‫تمارين‬ ‫حلول‬
1-‫جد‬:‫يأتي‬ ‫مما‬ ‫كل‬ ‫مفكوك‬
a) (3a –b)4
= C0
4
. (3a)4
- C1
4
. (3a)3
. b + C2
4
. (3a)2
. b2
− C3
4
. (3a). b3
+ C4
4
. b4
= 1 . 81a4
- 4 . 27 a3
. b + 6 . 9a2
. b2
− 4 . 3a . b3
+ 1 . b4
= 81a4
- 108 a3
. b + 54 a2
. b2
− 12a . b3
+ b4
b) (3x2
+ 2y)3
= C0
3
. (3x2
)3
+ C1
3
. (3x2
)2
. 2y + C2
3
. (3x2). (2y)2
+ C3
3
. (2y)3
= 27 x6
+ 3 . 9x4
. 2y + 3 . 3x2
. 4y2
+ 8y3
= 𝟐𝟕 𝐱 𝟔
+ 𝟓𝟒𝐱 𝟒
. 𝐲 + 𝟑𝟔𝐱 𝟐
. 𝐲 𝟐
+ 𝟖𝐲 𝟑
c) (2x –
1
2x
)
6
= C0
6
. (2x)6
- C1
6
. (2x)5
. (
1
2x
) + C2
6
. (2x)4
. (
1
2x
)2
− C3
6
. (2x)3
. (
1
2x
)3
+
C4
6
. (2x)2
. (
1
2x
)4
- C5
6
. 2x. (
1
2x
)5
+ C6
6
. (
1
2x
)6
= 64x6
– 6. 32x5
. (
1
2x
) + 15 . 16x4
.
1
4x2 − 20 . 8x3
.
1
8x3 + 15 . 4x2
.
1
16x4 -
6 . 2x.
1
32x5 +
1
64x6
= 64x6
–96 x4
+60 x2
− 20 +
15
4x2 -
6
16x4 +
1
64x6
2-‫مفكوك‬ ‫في‬ ‫الثالث‬ ‫الحد‬ ‫جد‬7
)2
3y-x(.‫(تمهيدي‬2013)(‫تمهيدي‬4201)
/‫ج‬
P3 = C2
7
. x5
. (−3y2
)2
= 21 .x5 . 9y4
= 189 . x5
. y4
16x4

21. ‫ادبي‬ ‫سادس‬‫االول‬ ‫الفصل‬‫االثرائية‬ ‫االمثلة‬
/ ‫الشمري‬ ‫احمد‬ ‫األستاذ‬0770451693721/ ‫الطباعية‬ ‫للخدمات‬ ‫المرسل‬07703458937
3-‫مفكوك‬ ‫في‬ ‫السادس‬ ‫الحد‬ ‫جد‬(
x2
2
−
x
3
)8
/‫ج‬
P6 = C5
8
. (
x2
2
)3
. (−
x
3
)5
= 56 .
x6
8
.
−x5
243
=
−7
243
. x11
4-‫مفكوك‬ ‫في‬ ‫االوسط‬ ‫الحد‬ ‫جد‬( a −
2
a
)12
.‫(وزاري‬2012‫دور‬2)
/‫ج‬‫يساوي‬ ‫المفكوك‬ ‫حدود‬ ‫عدد‬13‫الحد‬ ‫هو‬ ‫االوسط‬ ‫الحد‬ ‫ان‬ ‫اي‬‫السابع‬:
P7 = C6
12
. a6
. (−
2
a
)6
=
12.11.10.9.8.7.6!
6.5.4.3.2 .6!
. a6
.
64
a6 = 11.2.3.2.7 . 64 = 59136
5-‫مفكوك‬ ‫في‬ ‫االوسطين‬ ‫الحدين‬ ‫جد‬(2a − 1)7
‫(وزاري‬2015)‫اول‬ ‫دور‬
/‫ج‬‫االول‬ ‫االوسط‬ ‫الحد‬ ‫ان‬ ‫اي‬ ‫ثمانية‬ ‫يساوي‬ ‫المفكوك‬ ‫حدود‬ ‫عدد‬4‫والثاني‬5:
P4 = C3
7
. (2a)4
. (−1)3
= 35 . 16 a 4
. (−1) = -560 . a4
P5 = C4
7
. (2a)3
. (−1)4
= 35 . 8 a 3
. (+1) = 280 . a3
6-‫على‬ ‫يحوي‬ ‫الذي‬ ‫الحد‬ ‫جد‬4
x‫مفكوك‬ ‫في‬(1 + x2
)6
.‫معامله‬ ‫جد‬ ‫ثم‬‫(وزاري‬2012)‫ثاني‬ ‫دور‬
/‫ج‬
Pr = Cr−1
6
. 1(6−r+1)
. (x2
)(r−1)
= Cr−1
6
. 1(6−r+1)
. (x)2(r−1)
(x)2(r−1)
= x4
‫اذا‬.‫االسس‬ ‫تساوت‬ ‫االساسات‬ ‫تساوت‬
2(r − 1) = 4 ⟹ r − 1 = 2 ⟹ ∴ r = 3
:‫المعامل‬ ‫ايجاد‬
P3 = C2
6
. 14
. x4
= 15 x4
7-‫معامل‬ ‫جد‬2
x‫مفكوك‬ ‫في‬( x3
+
2
x2)9
.‫(وزاري‬2013)‫اول‬ ‫دور‬‫(وزاري‬5201)‫اول‬ ‫دور‬
/‫ج‬
Pr = Cr−1
9
. (x3
)(9−r+1)
. (
2
x2)(r−1)
= Cr−1
9
. (x)3(10−r)
.
2(r−1)
x2(r−1)
= Cr−1
9
. (x)(30−3r)
.(2)(r−1)
. x(2−2r)
= Cr−1
9
. (x)(30−3r)+(2−2r)
. 2(r−1)
(x)(30−3r)+(2−2r)
= x2
x2
‫يحوي‬ ‫الذي‬ ‫هو‬ ‫المطلوب‬ ‫الحد‬ ‫ان‬ ‫بما‬
(30 − 3r) + (2 − 2r) = 2 ‫االسس‬ ‫تساوت‬ ‫االساسات‬ ‫وتساوت‬ ‫قيمتان‬ ‫تساوت‬ ‫اذا‬
32 – 5r = 2 ⟹ 5r = 30 ⟹ ∴ r = 6
:‫المعامل‬ ‫ايجاد‬
P6 = C5
9
. (x3
)4
. (
2
x2)5
=
9.8.7.6.5!
5! . 4.3.2
. x12
.
32
x10 = 3.7.6 . x2
. (32) = 4032 . x2
‫المعامل‬=4032

22. ‫ادبي‬ ‫سادس‬‫االول‬ ‫الفصل‬‫االثرائية‬ ‫االمثلة‬
/ ‫الشمري‬ ‫احمد‬ ‫األستاذ‬0770451693722/ ‫الطباعية‬ ‫للخدمات‬ ‫المرسل‬07703458937
8-‫من‬ ‫الخالي‬ ‫الحد‬ ‫جد‬x‫مفكوك‬ ‫في‬( x2
+
2
x3)10
/‫ج‬
Pr = Cr−1
10
. (x2
)(10−r+1)
. (
2
x3)(r−1)
= Cr−1
10
. (x)2(11−r)
.
2(r−1)
x3(r−1)
Pr = Cr−1
10
. (x)2(11−r)
. x−3(r−1)
. (2)(r−1)
= Cr−1
10
. (x)(22−2r)
. x(3−3r).(2)(r−1)
Pr = Cr−1
10
. (x)
(22−2r)+(3−3r)
. (2)(r−1)
(x)(22−2r)+(3−3r)
= x0
x0
‫اي‬ x ‫هو‬ ‫المطلوب‬ ‫الحد‬‫من‬ ‫الخالي‬ ‫الحد‬
(22 − 2r) + (3 − 3r) = 0 ‫االسس‬ ‫تساوت‬ ‫االساسات‬ ‫وتساوت‬ ‫قيمتان‬ ‫تساوت‬ ‫اذا‬
25 – 5r = 0 ⟹ 5r = 25 ⟹ ∴ r = 5
P5 = C5−1
10
. (x)2(11−5)
.
2(5−1)
x3(5−1) = C4
10
. (x)12
.
24
x12 =
10.9.8.7.6!
4.3.2 . 6!
. 16
= 10.3.7 . 16 = 3360
9-‫قيمة‬ ‫جد‬4
)99(.‫الحدين‬ ‫ذي‬ ‫مبرهنة‬ ‫باستخدام‬
/‫ج‬
(99)4
= (100 -1)4
= C0
4
. 1004
+ C1
4
. 1003
. (−1)+ C2
4
. 1002
. (−1)2
+ C3
4
. 100 . (−1)3
+C4
4
. (−1)4
= 1004
- 4 . 1003
+ 6 . 1002
− 4 . 100 + 1 = 100000000 – 4000000 + 60000 − 400 +1
∴ (99)4
= 96059601
10-‫قيمة‬ ‫جد‬4
)98(–4
)102(
/‫ج‬
(102)4
– (98)4
= (100+2)4
– (100-2)4
(100+2)4
– (100-2)4
= 2P4 + 2P2 ‫الزوجية‬ ‫الحدود‬ ‫مجموع‬ ‫ضعف‬ ‫هو‬ ‫الطرح‬ ‫ناتج‬
P2 = C1
4
. 1003
. 2 = 4 . 1003
. 2 = 8000000
P4 = C3
4
. 100 . 23
= 4 . 100 . 8 = 3200
(102)4
– (98)4
= 2(8000000+3200) = 2(8003200) = 16006400
11-‫قيمة‬ ‫جد‬+ (2 − √3)7
(2 + √3)7
/‫ج‬‫الفردية‬ ‫الحدود‬ ‫ضعف‬ ‫هو‬ ‫الجمع‬ ‫ناتج‬
(2 + √3)7
+ (2 − √3)7
= 2(P1+P3+P5+P7)
P1 = C0
7
. 27
. (√3)0
= 128
P3 = C2
7
. 25
. (√3)
2
= 21 .32 .3 = 2016
P5 = C4
7
. 23
. (√3)
4
=
7.6.5.4!
4! . 3.2
. 8 .9 = 35 . 72 = 2520
P7 = C6
7
. 2 . (√3)
6
= 7.2 .27 = 378
(2 + √3)7
+ (2 − √3)7
= 2(128 + 2016 + 2520 + 378) = 10084

23. ‫ادبي‬ ‫سادس‬‫االول‬ ‫الفصل‬‫االثرائية‬ ‫االمثلة‬
/ ‫الشمري‬ ‫احمد‬ ‫األستاذ‬0770451693723/ ‫الطباعية‬ ‫للخدمات‬ ‫المرسل‬07703458937
‫الوزارية‬ ‫االسئلة‬
1)‫يجلس‬ ‫ان‬ ‫يمكن‬ ‫طريقة‬ ‫بكم‬10.‫فقط‬ ‫مقاعد‬ ‫اربع‬ ‫في‬ ‫طالب‬2012-2
2)‫بتكرار‬ ‫السماح‬ ‫دون‬ )‫معنى‬ ‫بدون‬ ‫او‬ ‫(بمعنى‬ ‫زيزفون‬ ‫كلمة‬ ‫احرف‬ ‫من‬ ‫حروف‬ ‫ثالثة‬ ‫من‬ ‫تكوينها‬ ‫يمكن‬ ‫كلمة‬ ‫كم‬
.‫الواحدة‬ ‫الكلمة‬ ‫في‬ ‫الحروف‬2013-3
3)‫بدون‬ )‫معنى‬ ‫بدون‬ ‫او‬ ‫(بمعنى‬ ‫بغداد‬ ‫كلمة‬ ‫حروف‬ ‫من‬ ‫انشائها‬ ‫يمكن‬ ‫والتي‬ ‫احرف‬ ‫ثالثة‬ ‫من‬ ‫المكونة‬ ‫الكلمات‬ ‫عدد‬ ‫كم‬
.‫الواحدة‬ ‫الكلمة‬ ‫في‬ ‫الحرف‬ ‫تكرار‬
4)‫يجلس‬ ‫ان‬ ‫يمكن‬ ‫طريقة‬ ‫بكم‬10.‫فقط‬ ‫مقاعد‬ ‫اربع‬ ‫في‬ ‫طالب‬2012-2
5)‫االمتحان‬ ‫ورقة‬ ‫في‬ ‫االسئلة‬ ‫عدد‬ ‫كان‬ ‫اذا‬6‫خم‬ ‫عن‬ ‫االجابة‬ ‫والمطلوب‬ ‫اسئلة‬‫ذلك؟‬ ‫يمكن‬ ‫طريقة‬ ‫فبكم‬ ‫اسئلة‬ ‫سة‬2012-3
6)‫يحوي‬ ‫صندوق‬10‫و‬ ‫حمراء‬ ‫كرات‬5‫سحب‬ ‫يراد‬ ‫بيضاء‬ ‫كرات‬ ‫وثالث‬ ‫خضراء‬ ‫كرات‬5‫ضمن‬ ‫تكون‬ ‫ان‬ ‫على‬ ‫كرات‬
‫لذلك؟‬ ‫طريقة‬ ‫فكم‬ ‫خضراء‬ ‫واحدة‬ ‫وكرة‬ ‫حمراء‬ ‫كرتين‬ ‫السحبة‬2012-2
7)‫قيمة‬ ‫جد‬n‫كان‬ ‫اذا‬( 𝐧+𝟏
𝟒
)=6( 𝐧
𝟑
)‫؟‬2012-2
8)‫اذا‬‫االمتحان‬ ‫ورقة‬ ‫في‬ ‫االسئلة‬ ‫عدد‬ ‫كان‬6‫ذلك؟‬ ‫يمكن‬ ‫طريقة‬ ‫فبكم‬ ‫اسئلة‬ ‫خمسة‬ ‫عن‬ ‫االجابة‬ ‫والمطلوب‬ ‫اسئلة‬2012-3
9)‫ك‬‫م‬‫كلمة‬‫يمكن‬‫تكوينها‬‫مكونة‬‫من‬‫اربعة‬‫حروف‬‫مختلفة‬‫من‬‫كلمة‬)‫سنكفيكهم‬(2014-‫ت‬
10)‫كم‬‫كلمة‬‫بمعنى‬‫او‬‫بدون‬‫معنى‬‫يمكن‬‫تكوينها‬‫من‬‫كلمة‬)‫سنكفيكهم‬(‫مكونة‬‫من‬‫اربع‬‫أحرف‬‫على‬‫ان‬‫ال‬‫يسمح‬‫بتكرار‬
‫الحرف‬‫في‬‫الكلمة‬‫نفسها؟‬2015-2
11)‫بكم‬‫طريقة‬‫يمكن‬‫اختيار‬‫اربعة‬‫اشخاص‬‫من‬‫بين‬‫عشرة‬‫اشخاص‬‫لشغل‬‫اربعة‬‫وظائف‬‫معينة‬‫مختلفة‬2014-1
12)‫كم‬‫قطعة‬‫مستقيم‬‫يمكن‬‫تحديدها‬‫بنقطتين‬‫من‬‫مجموعة‬‫فيها‬7‫نقاط‬‫وال‬‫توجد‬‫ثالث‬‫نقاط‬‫على‬‫استقامة‬‫واحدة‬2014-1
13)‫اذا‬‫كان‬‫لدى‬‫فتاة‬7‫قمصان‬‫مختلفة‬‫االلوان‬‫و‬5‫تنورات‬‫مختلفة‬‫االلوان‬‫و‬3‫احذية‬‫مختلفة‬‫فبكم‬‫زي‬‫مكون‬‫من‬‫قميص‬
‫وتنورة‬‫وحذاء‬‫يمكن‬‫تظهر‬‫به‬‫الفتاة‬.2014-2
14)‫كيس‬‫فيه‬10‫كرات‬‫حمراء‬‫و‬6‫بيضاء‬‫سحبت‬‫منه‬4‫كرات‬‫معا‬‫دون‬‫ارجاع‬,‫ما‬‫عدد‬‫الطرق‬‫التي‬‫تكون‬‫فيها‬‫الكرات‬
‫المسحوبة‬‫من‬‫نفس‬‫اللون‬2015-1
15)‫كم‬‫عدد‬‫رمزه‬‫مكون‬‫من‬3‫ارقام‬‫يمكن‬‫تكوينه‬‫باستخدام‬‫االرقام‬2,3,4,5,6,7,8,9‫على‬‫ان‬‫يكون‬‫العدد‬‫فرديا‬
‫والتكرار‬‫غير‬‫مسموح‬‫فيه‬‫للرقم‬2015-1
16)‫بكم‬‫طريقة‬‫يمكن‬‫اختيار‬‫لجنة‬‫مكونة‬‫من‬3‫موظفين‬‫وموظفتين‬‫من‬‫بين‬10‫موظفين‬‫وخمسة‬‫موظفات‬2015-2
17)‫كم‬‫عدد‬‫ا‬‫زوجيا‬‫مكون‬‫من‬4‫مراتب‬‫يمكن‬‫تكوينه‬‫من‬‫االرقام‬( 0,1,2,3,4,5,6,7)‫مع‬‫عدم‬‫السماح‬‫بتكرار‬‫الرقم‬.
18)‫اذا‬‫كان‬3(n!) = 360‫جد‬‫قيمة‬n‫؟‬2015-3
19)‫ما‬‫عدد‬‫طرق‬‫اختيار‬‫وفد‬‫من‬4‫اشخاص‬‫نختارهم‬‫من‬‫بين‬6‫رجال‬‫و‬7‫نساء‬‫علما‬‫ان‬‫الوفد‬‫مناصفة‬‫من‬‫كل‬‫جنس‬
2015-3
20)‫جد‬‫قيمة‬n‫اذا‬‫كان‬n! = 6(n-2)!2014-1
21)‫جد‬‫قيمة‬n‫اذا‬‫علمت‬‫ان‬2P2
n
=C3
𝑛+1
2015-3
22)‫ج‬‫د‬‫قيمة‬n‫اذا‬‫علمت‬‫ان‬= 2P2
3
n!
(n−2)!
2015-1
23)‫جد‬‫قيمة‬[P2
8
+ P3
8
]
1
56
2014-2
24)‫جد‬‫مفكوك‬8
)2y–2
3x(2014-1
25)‫هل‬‫يوجد‬‫حد‬‫خالي‬‫من‬x‫في‬‫مفكوك‬15)−
1
x2
2x(‫بين‬‫ذلك‬.2014-2‫الحل‬‫مثال‬18‫صفحة‬19
26)‫جد‬‫الحدين‬‫االوسطين‬‫في‬‫مفكوك‬(2 −
x
2
)
9
2015-3
27)‫من‬ ‫مكونة‬ ‫الطالب‬ ‫من‬ ‫مجموعة‬10‫و‬ ‫طالب‬8‫من‬ ‫مؤلفة‬ ‫لجنة‬ ‫تشكيل‬ ‫يراد‬ ‫طالبات‬7‫االنشطة‬ ‫الدارة‬ ‫اعضاء‬
‫من‬ ‫تكونت‬ ‫اذا‬ ‫اللجنة‬ ‫اختيار‬ ‫يمكن‬ ‫طريقة‬ ‫بكم‬ , ‫الطالبية‬4‫و‬ ‫طالب‬3.‫طالبات‬2016-1
28)‫من‬ ‫مكون‬ ‫رمزه‬ ‫عدد‬ ‫كم‬3‫واكبر‬ ‫مراتب‬‫من‬600‫االرقام‬ ‫من‬ ‫تكوينه‬ ‫يمكن‬4,5,6,7,8:‫كان‬ ‫اذا‬
‫به‬ ‫مسموح‬ ‫التكرار‬‫به‬ ‫مسموح‬ ‫غير‬ ‫التكرار‬2016-1
29)‫من‬ ‫الخالي‬ ‫الحد‬ ‫جد‬x‫مفكوك‬ ‫في‬( x +
2
x2)6
.2016-1

24. ‫ادبي‬ ‫سادس‬‫االول‬ ‫الفصل‬‫االثرائية‬ ‫االمثلة‬
/ ‫الشمري‬ ‫احمد‬ ‫األستاذ‬0770451693724/ ‫الطباعية‬ ‫للخدمات‬ ‫المرسل‬07703458937
30)( ‫لجنة‬ ‫فيها‬ ‫تكون‬ ‫التي‬ ‫الطرق‬ ‫عدد‬ ‫ما‬4‫بين‬ ‫من‬ ‫نختارهم‬ )‫اشخاص‬10‫و‬ ‫رجال‬6‫من‬ ‫اللجنة‬ ‫تتكون‬ ‫ان‬ ‫على‬ ‫نساء‬
‫واحد؟‬ ‫جنس‬2016-‫ت‬
31)‫كان‬ ‫اذا‬2C2
n+1
= C3
n+2
‫قيمة‬ ‫فجد‬n.2016-‫ت‬
32)‫(ستنتصرون)؟‬ ‫كلمة‬ ‫من‬ ‫تكوينها‬ ‫يمكن‬ ‫مختلفة‬ ‫حروف‬ ‫ثالثة‬ ‫من‬ ‫مكونة‬ ‫كلمة‬ ‫كم‬2016-2
33)‫اذا‬( ‫هنالك‬ ‫كان‬7( ‫سوى‬ ‫يجدوا‬ ‫ولم‬ ‫يتوظفوا‬ ‫ان‬ ‫يريدون‬ ‫خريجين‬ )3‫الوظائف؟‬ ‫اشغال‬ ‫يمكن‬ ‫طريقة‬ ‫فبكم‬ ،‫وظائف‬ )
2016-2
34)‫قيمة‬ ‫جد‬n:‫حيث‬P3
n+1
=7 P2
n
2016-2
35)‫الحروف‬ ‫تكون‬ ‫ان‬ ‫على‬ )‫(فأسقيناكموه‬ ‫كلمة‬ ‫من‬ ‫تكوينها‬ ‫يمكن‬ ‫حروف‬ ‫ثالثة‬ ‫من‬ ‫مكونة‬ ‫معنى‬ ‫بدون‬ ‫او‬ ‫بمعنى‬ ‫كلمة‬ ‫كم‬
‫مختلفة؟‬2016-3
36)‫جد‬‫الحد‬‫االوسط‬‫من‬‫مفكوك‬(m −
1
m
)
14
2016-3
37)‫قيمة‬ ‫جد‬n‫كان‬ ‫اذا‬( 𝐧+𝟏
𝟒
)=3( 𝐧
𝟑
)‫؟‬2016-3

25. 1
‫األستاذ‬‫الشمري‬ ‫أحمد‬ :
07704516937
‫المرسل‬‫الطباعية‬ ‫للخدمات‬
‫المنصور‬–‫دراغ‬ ‫حي‬ ‫جامع‬ ‫مجاور‬
07703458937
‫ملزمة‬‫الرياضيات‬
‫االدبي‬ ‫السادس‬
2017-2016
‫الثاني‬ ‫الفصل‬
‫واالستمرارية‬ ‫الغايات‬

26. ‫الثاني‬ ‫الفصل‬ ‫أدبي‬ ‫سادس‬‫الغاية‬
26

27. ‫الثاني‬ ‫الفصل‬ ‫أدبي‬ ‫سادس‬‫الغاية‬
27
:)‫واالستمرارية‬ ‫الثاني(الغايات‬ ‫الفصل‬
(‫الغاية‬:)‫الغاية‬‫الدالة‬ ‫ناتج‬ ‫قيمة‬ ‫يمثل‬ ‫رياضي‬ ‫تعبير‬f(x)‫متغيرها‬ ‫يقترب‬ ‫عندما‬‫المستقل‬x‫معين‬ ‫مقدار‬ ‫من‬a‫وتكتب‬
:‫التالية‬ ‫بالصيغة‬
𝐥𝐢𝐦
𝐱→𝐚
f(x)
‫غاية‬ ‫وتقرأ‬f(x)‫عندما‬x‫من‬ ‫تقترب‬a
‫مثال‬1/‫الدالة‬ ‫غاية‬ ‫جد‬2x + 1–2
x‫عندما‬x‫من‬ ‫يقترب‬1.
/‫ج‬‫قيمة‬ ‫نعوض‬x‫بواحد‬:‫مبين‬ ‫كما‬lim
x→1
(x2
− 2x + 1) = 1 − 2 + 1 = 0
‫عندما‬ ‫الدالة‬ ‫غاية‬ ‫ان‬ ‫اي‬x‫من‬ ‫تقترب‬1‫قيمة‬ ‫وهي‬ ‫صفر‬ ‫تساوي‬
‫عندما‬ ‫للغاية‬ ‫اخرى‬ ‫قيمة‬ ‫يوجد‬ ‫ال‬ ‫اي‬ ‫وحيدة‬x → 1:‫مبين‬ ‫كما‬
‫مثال‬2/‫الدالة‬ ‫غاية‬ ‫جد‬
1
x2+ 1
‫عندما‬x‫من‬ ‫تقترب‬-1.
/‫الحل‬‫المتغير‬ ‫على‬ ‫قسمة‬ ‫عملية‬ ‫تحوي‬ ‫الدالة‬ ‫ان‬ ‫بما‬x‫عندما‬ ‫للدالة‬ ‫فحص‬ ‫عمل‬ ‫الى‬ ‫نحتاج‬ ‫فاننا‬x‫من‬ ‫تقترب‬-1
lim
x→−1
1
x2 + 1
=
1
(−1)2 + 1
=
1
2
‫عندما‬ ‫الدالة‬ ‫غاية‬ ‫ان‬ ‫نقول‬ ‫اذا‬ ‫حقيقي‬ ‫عدد‬ ‫الناتج‬ ‫ان‬ ‫بما‬x‫من‬ ‫تقترب‬-1‫وتساوي‬ ‫موجودة‬
𝟏
𝟐
.
‫مثال‬3/‫الدالة‬ ‫غاية‬ ‫جد‬
x2−x
x
‫عندما‬x‫من‬ ‫تقترب‬0.
/‫الحل‬‫عندما‬x‫الى‬ ‫ننتقل‬ ‫لذلك‬ ‫معرف‬ ‫غير‬ ‫عدد‬ ‫وهذا‬ ‫صفر‬ ‫يساوي‬ ‫المقام‬ ‫فان‬ ‫صفر‬ ‫تساوي‬‫التبسيط‬‫مبين‬ ‫كما‬:
lim
x→0
x2−x
x
=
x(x−1)
x
= lim
x→0
(x − 1) = 0 − 1 = −1
‫عندما‬ ‫غاية‬ ‫للدالة‬ ‫اذا‬x → 0‫وتساوي‬-1:‫مبين‬ ‫كما‬
‫مثال‬4/‫قيمة‬ ‫جد‬(x3
+ 2x + 3)lim
x→−2
.‫(وزاري‬2012)‫اول‬ ‫دور‬
/‫الحل‬
lim
x→−2
(x3
+ 2x + 3) = (-2)3
+ 2 . (-2) + 3 = -8 – 4 + 3 = -9
:‫معرفة‬ ‫الغير‬ ‫القيم‬
1–‫مثل‬ ‫صفر‬ ‫على‬ ‫القسمة‬
𝐱
𝟎
‫و‬
𝟎
𝟎
.
2–‫سالبة‬ ‫لقيمة‬ ‫الزوجي‬ ‫الجذر‬√−5
4
.
‫ناتج‬ ‫من‬ ‫اكثر‬ ‫يوجد‬ ‫ال‬ : ‫الغاية‬ ‫وحدانية‬‫معين‬ ‫عدد‬ ‫عند‬ ‫الغاية‬ ‫لقيمة‬ ‫واحد‬

28. ‫الثاني‬ ‫الفصل‬ ‫أدبي‬ ‫سادس‬‫الغاية‬
28
‫مثال‬5/‫الدالة‬ ‫غاية‬ ‫جد‬
x−1
x2− 1
‫عندما‬x‫من‬ ‫تقترب‬1.
/‫الحل‬‫المتغير‬ ‫على‬ ‫قسمة‬ ‫عملية‬ ‫تحوي‬ ‫الدالة‬ ‫ان‬ ‫بما‬x‫عندما‬ ‫للدالة‬ ‫فحص‬ ‫عمل‬ ‫الى‬ ‫نحتاج‬ ‫فاننا‬x‫من‬ ‫تقترب‬1
lim
x→1
x − 1
x2 − 1
=
0
1 − 1
=
0
0
‫الدالة‬ ‫تحليل‬ ‫الى‬ ‫ننتقل‬ ‫فاننا‬ ‫حقيقي‬ ‫عدد‬ ‫يمثل‬ ‫ال‬ ‫المقدار‬ ‫وهذا‬ ‫صفر‬ ‫على‬ ‫قسمة‬ ‫يحوي‬ ‫الناتج‬ ‫ان‬ ‫بما‬:
lim
x→1
x−1
(x− 1)(x+ 1)
=
1
x+ 1
=
1
2
‫مثال‬6/‫الدالة‬ ‫غاية‬ ‫جد‬
x2−4
x− 2
‫عندما‬x‫من‬ ‫تقترب‬2.‫(وزاري‬2014)‫اول‬ ‫دور‬
/‫الحل‬‫عندما‬ ‫صفر‬ ‫يساوي‬ ‫المقام‬ ‫ان‬ ‫بما‬x‫تساوي‬2:‫التحليل‬ ‫الى‬ ‫ننتقل‬
lim
x→2
x2−4
x− 2
=
(x−2)(x+2)
x− 2
= lim
x→2
(x + 2) = 2 + 2 = 4
‫منها‬ ‫تقترب‬ ‫قيمة‬ ‫اي‬ ‫عند‬ ‫الثابتة‬ ‫القيمة‬ ‫غاية‬ /‫مالحظة‬x:‫الثابتة‬ ‫القيمة‬ ‫تساوي‬
lim
x→a
c = c a , c ∈ R
lim
x→0
5 = 5
lim
x→2
1 = 1
‫مثال‬7/‫جد‬‫قيمة‬lim
x→2
x3− 8
x2−4
:‫(تمهيدي‬2013)
/‫الحل‬‫عندما‬ ‫صفر‬ ‫يساوي‬ ‫المقام‬ ‫ان‬ ‫بما‬x‫تساوي‬2:‫التحليل‬ ‫الى‬ ‫ننتقل‬
lim
x→2
x3− 8
x2−4
= lim
x→2
x3− 23
x2−22 = lim
x→2
(x−2)(x2+2x+4)
(x−2)(x+2)
= lim
x→2
x2+2x+4
x+2
=
4+4+4
4
= 3
‫مثال‬8/‫قيمة‬ ‫جد‬lim
x→0
√x+2 −√2
x
:
/‫الحل‬‫عندما‬ ‫صفر‬ ‫يساوي‬ ‫المقام‬ ‫ان‬ ‫بما‬x‫تساوي‬0:‫التحليل‬ ‫الى‬ ‫ننتقل‬
:‫البسط‬ ‫بمرافق‬ ‫نضرب‬
lim
x→0
√x+2 −√2
x
.
√x+2 +√2
√x+2 +√2
lim
x→0
(x+2)−2
x .(√x+2 +√2)
= lim
x→0
x
x .(√x+2 +√2 )
= lim
x→0
1
√x+2 +√2
=
1
√2 +√2
=
1
2√2
‫مثال‬9/‫جد‬‫قيمة‬lim
x→3
√x+1 −2
x−3
:‫(وزاري‬2013‫ثاني‬ ‫دور‬2012)‫ثالث‬ ‫دور‬
/‫الحل‬‫عندما‬ ‫صفر‬ ‫يساوي‬ ‫المقام‬ ‫ان‬ ‫بما‬x‫تساوي‬3:‫التحليل‬ ‫الى‬ ‫ننتقل‬
:‫البسط‬ ‫بمرافق‬ ‫نضرب‬
lim
x→3
√x + 1 − 2
x − 3
.
√x + 1 + 2
√x + 1 + 2
= lim
x→3
(x + 1) − 4
(x − 3). (√x + 1 + 2)
= lim
x→3
x−3
(x−3).(√x+1 +2)
= lim
x→3
1
√x+1 +2
=
1
√4 +2
=
1
4

29. ‫الثاني‬ ‫الفصل‬ ‫أدبي‬ ‫سادس‬‫الغاية‬
29
‫مثال‬10/‫قيمة‬ ‫جد‬lim
x→3
x3 −27
x2+2x−15
.‫(وزاري‬2011)‫اول‬ ‫دور‬
/‫الحل‬‫مكعبين‬ ‫بين‬ ‫فرق‬ ‫البسط‬ ‫نحلل‬
lim
x→3
x3 −27
x2+2x−15
= lim
x→3
(x −3)(x2 + 3x+9)
(x−3)(x+5)
= lim
x→3
x2 + 3x+9
x+5
=
9+ 9+9
3+5
=
27
8
‫مثال‬11/‫قيمة‬ ‫جد‬lim
x→1
x − 1
√x − 1
.(2005)
/‫الحل‬:‫مربعين‬ ‫بين‬ ‫فرق‬ ‫البسط‬ ‫نحلل‬
lim
x→1
x − 1
√x − 1
= lim
x→1
(√x – 1)(√x + 1)
√x − 1
= lim
x→1
√x + 1 = 1 + 1 = 2
‫مثال‬12/‫كانت‬ ‫اذا‬lim
x→1
(x2
− 2x + a)‫تساوي‬4‫جد‬‫قيمة‬a.
/‫الحل‬
lim
x→1
(x2
− 2x + a) = 4
1-2+a = 4 ⟹ -1 + a = 4 ⟹ a = 5
‫مثال‬13/‫كانت‬ ‫اذا‬lim
x→1
a(x−1)
x2− 1
‫تساوي‬1‫جد‬‫قيمة‬a‫عندما‬ ‫الدالة‬ ‫غاية‬ ‫جد‬ ‫ثم‬ ‫ومن‬x‫من‬ ‫تقترب‬2.
/‫الحل‬
lim
x→1
a(x−1)
x2− 1
= lim
x→1
a(x−1)
(x−1)(x+1)
= lim
x→1
a
x+1
= 1
a
(1+1)
= 1 ⟹ a = 2
‫عندما‬ ‫الدالة‬ ‫غاية‬x‫من‬ ‫يقترب‬2:‫هي‬
lim
x→2
2
x+1
=
2
2+1
=
2
3
‫مثال‬14/‫كانت‬ ‫اذا‬f(x) =
ax2 + bx
x
‫وكانت‬lim
x→0
f(x) = 4‫و‬lim
x→1
f(x) = 5‫قيمتي‬ ‫جد‬a‫و‬b
.‫الحقيقيتين‬
/‫الحل‬
lim
x→0
ax2 + bx
x
= 4 ⟹ lim
x→0
x(ax + b)
x
= 4 ⟹ lim
x→0
(ax+b) = 4
a(0) + b = 4 ⟹ ∴ b = 4
lim
x→1
ax2 + bx
x
= 5 ⟹ lim
x→1
(ax+b) = 5 ⟹ a(1) + b = 5 ⟹ a + 4 = 5
∴ a = 1
‫مثال‬15/‫كانت‬ ‫اذا‬= 2a + 3lim
x→1
x2+3x−1
x+2
‫جد‬‫قيمة‬a.‫(وزاري‬2013)‫اول‬ ‫دور‬
/‫الحل‬
lim
x→1
x2+3x−1
x+2
=
1+3−1
1+2
= 1
2a +3 = 1 ⟹ 2a = 1 -3 = -2 ⟹ a =
−2
2
= -1

30. ‫الثاني‬ ‫الفصل‬ ‫أدبي‬ ‫سادس‬‫الغاية‬
30
‫مثال‬16/‫كانت‬ ‫اذا‬f(x) = 6x2
+ ax + b‫وكانت‬lim
x→1
f(x) = 6‫و‬lim
x→2
f(x) = 29‫جد‬‫قيمة‬a‫و‬b.
/‫الحل‬‫(تمهيدي‬2005)
lim
x→1
(6x2
+ ax + b) = 6 ⟹ 6 + a + b = 6 ⟹ b + a = 0 ……
lim
x→2
(6x2
+ ax + b) = 29 ⟹ 24 + 2a + b = 29 ⟹ 2a + b = 5 ……
‫معادلة‬ ‫نطرح‬‫من‬
2a + b = 5
a + b = 0
a = 5 ‫بالطرح‬
‫قيمة‬ ‫نعوض‬a‫المعادلة‬ ‫في‬:
b + a= 0 ⟹ b + 5 = 0 ⟹ b = -5
:‫المركبة‬ ‫الدوال‬‫باقي‬ ‫عن‬ ‫مستقل‬ ‫مجال‬ ‫يملك‬ ‫منها‬ ‫كل‬ ‫اقسام‬ ‫عدة‬ ‫من‬ ‫تتكون‬ ‫التي‬ ‫الدوال‬ ‫وهي‬:‫االخرى‬ ‫الدوال‬ ‫مجاالت‬
‫مثال‬17/‫الدالة‬ ‫غاية‬ ‫جد‬f(x) = { x2
x ≤ 1
x x > 1
‫عندما‬x‫من‬ ‫تقترب‬3,0,1-.
1-‫عندما‬x‫من‬ ‫يقترب‬3‫نستخدم‬:‫الثانية‬ ‫الدالة‬lim
x→3
f(x) = lim
x→3
x = 3
2-‫عندما‬x‫من‬ ‫تقترب‬0‫نستخدم‬:‫االولى‬ ‫الدالة‬lim
x→0
f(x) = lim
x→0
x2
= 0
3-‫عندما‬x‫من‬ ‫تقترب‬-1‫نستخدم‬:‫االولى‬ ‫الدالة‬lim
x→−1
f(x) = lim
x→−1
x2
= 1
‫اليسار‬ ‫وغاية‬ ‫اليمين‬ ‫غاية‬:‫لدينا‬ ‫كان‬ ‫اذا‬‫من‬ ‫مركبة‬ ‫دالة‬‫تكون‬ ‫االفتراضية‬ ‫االلتقاء‬ ‫نقطة‬ ‫عند‬ ‫الدالة‬ ‫غاية‬ ‫فان‬ ‫دالتين‬
‫الدالة‬ ‫غاية‬ ‫فان‬ ‫السابق‬ ‫المثال‬ ‫وفي‬ ‫متساويتين‬ ‫االفتراضية‬ ‫االلتقاء‬ ‫نقطة‬ ‫عند‬ ‫الدالتين‬ ‫غاية‬ ‫كانت‬ ‫اذا‬ ‫موجودة‬x‫غاية‬ ‫تسمى‬
‫الدالة‬ ‫وغاية‬ ‫اليمين‬2
x‫هي‬ ‫االفتراضية‬ ‫االلتقاء‬ ‫ونقطة‬ ‫اليسار‬ ‫غاية‬ ‫تسمى‬0:
L1 = lim
x→0+
x = 0 ‫اليمين‬ ‫غاية‬
L2 = lim
x→0− x2 = 0 = L1 ‫اليسار‬ ‫غاية‬
‫ان‬ ‫بما‬1L=2L‫عندما‬ ‫الدالة‬ ‫غاية‬ ‫فان‬x.‫موجودة‬ ‫الغاية‬ ‫ان‬ ‫اي‬ ‫صفر‬ ‫تساوي‬ ‫الصفر‬ ‫من‬ ‫تقترب‬
‫مثال‬2/‫لتكن‬f(x) = { x2
+ 1 x ≥ 1
2x − 1 x < 1
‫عندما‬ ‫غاية‬ ‫للدالة‬ ‫هل‬x‫من‬ ‫يقترب‬1.
/‫الحل‬‫عند‬ ‫االفتراضية‬ ‫االلتقاء‬ ‫نقطة‬1‫لذا‬.‫اليسار‬ ‫ودالة‬ ‫اليمين‬ ‫دالة‬ ‫نحسب‬
L1 = lim
x→1+
(x2
+ 1) = 1 +1 = 2
L2 = lim
x→1− (2x − 1) = 2 - 1 = 1 ≠ L1
‫من‬ ‫يقترب‬1 x ‫عندما‬ ‫غاية‬ ‫تملك‬ ‫ال‬ ‫الدالة‬ ‫ان‬
‫مثال‬3/‫للدالة‬ ‫هل‬f(x) = { x2
+ 1 x ≥ 1
2x x < 1
‫عندما‬ ‫غاية‬x → 1:
/‫الحل‬
L1 = lim
x→1+
( x2
+ 1) = 1 +1 = 2
L2 = lim
x→1− 2x = 2 = L1 x → 1 ‫عندما‬ ‫غاية‬ ‫تملك‬ ‫الدالة‬

31. ‫الثاني‬ ‫الفصل‬ ‫أدبي‬ ‫سادس‬‫الغاية‬
31
‫مثال‬4/‫لتكن‬f(x) = { x2
+ 2 x > 1
2x + a x ≤ 1
‫وان‬lim
x→1
f(x)‫موجودة‬‫قيمة‬ ‫جد‬a‫حيث‬R∈a.
/‫الحل‬‫موجودة‬ ‫الغاية‬ ‫ان‬ ‫بما‬‫عندما‬x = 1‫فان‬:‫ان‬ ‫اي‬ ‫اليسار‬ ‫غاية‬ ‫تساوي‬ ‫اليمين‬ ‫غاية‬
lim
x→1+
( x2
+ 2) = lim
x→1− (2x + a)
12
+ 2 = 2 . 1 + a ⟹ 3 = 2 + a ⟹ a = 3 -2 = 1
‫مثال‬5/‫لتكن‬f(x) = { x2
+ a x > 1
b − 2x x ≤ 1
‫وكانت‬lim
x→1
f(x)‫وان‬ ‫موجودة‬lim
x→−1
f(x) = 5‫قيمتي‬ ‫جد‬
R∈a‫و‬b.
/‫الحل‬
lim
x→−1
f(x) = lim
x→−1
(b − 2x) = 5
‫قيمة‬ ‫نعوض‬x = -1‫لـ‬ ‫جذر‬ ‫او‬ ‫قسمة‬ ‫تحوي‬ ‫ال‬ ‫الدالة‬ ‫كون‬x
(b − 2 . (−1)) = 5 ⟹ b + 2 = 5 ⟹ b = 3
lim
x→1+
(x2
+ a) = lim
x→1− (3 − 2x) ⟹ 1 + a = 3 − 2 ⟹ a = 1 – 1 = 0
‫مثال‬6/‫لتكن‬f(x) = {
6 − x x < 1
x 2
x ≥ 1
‫عندما‬ ‫غاية‬ ‫للدالة‬ ‫هل‬x‫من‬ ‫يقترب‬1.‫(تمهيدي‬2005)
/‫الحل‬
L1 = lim
x→1+
(6 − x) = 6 – 1 = 5
L2 = lim
x→1− x 2
= 1 ≠ L1 1 ‫من‬ ‫يقترب‬ x ‫عندما‬ ‫غاية‬ ‫للدالة‬ ‫ليس‬
‫مثال‬7/‫لتكن‬f(x) = {
x − 2 x < 3
x 2
− 8 x ≥ 3
‫عندما‬ ‫غاية‬ ‫للدالة‬ ‫هل‬x‫من‬ ‫يقترب‬0,3,5.
/‫الحل‬
‫عندما‬x‫من‬ ‫يقترب‬0:
lim
x→0
(x − 2) = -2 ‫للدالة‬ ‫غاية‬ ‫يوجد‬
‫عندما‬x‫من‬ ‫يقترب‬3:
L1 = lim
x→3+
(x 2
− 8) = 9 - 8 = 1
L2 = lim
x→3− (x − 2) = 3 − 2 =1 = L1 3 ‫من‬ ‫يقترب‬ x ‫عندما‬ ‫غاية‬ ‫للدالة‬
‫عندما‬x‫من‬ ‫يقترب‬5:
lim
x→5
(x 2
− 8) = 25 – 8 = 17
‫مثال‬8/‫لتكن‬f(x) = {
1 − x x < 2
x + 1 x ≥ 2
‫عندما‬ ‫غاية‬ ‫للدالة‬ ‫هل‬x‫من‬ ‫يقترب‬2‫عند‬ ‫الدالة‬ ‫غاية‬ ‫جد‬ ‫ثم‬x → −1
‫عند‬ ‫و‬x→4
.
/‫الحل‬‫أ‬-
L1 = lim
x→2+
(1 − x) = 1 - 2 = -1
L2 = lim
x→2− (x + 1) = 2 + 1 = 3 ≠ L1 ‫غاية‬ ‫للدالة‬ ‫ليس‬∴
‫ب‬-‫عندما‬ ‫الغاية‬x→−1
:lim
x→−1
(1 − x) = 1 + 1 = 2
‫ج‬-‫عندما‬ ‫الغاية‬x→4
:lim
x→4
(x + 1) = 4 + 1 = 5

32. ‫الثاني‬ ‫الفصل‬ ‫أدبي‬ ‫سادس‬‫الغاية‬
32
‫تمارين‬ ‫حلول‬1–2
1–:‫يأتي‬ ‫مما‬ ‫كل‬ ‫قيمة‬ ‫جد‬
1) lim
x→−1
(x3
+ 2x + 3) = )-1(3 + 2(-1) +3 = -1 -2 +3 = 0
2) lim
x→0
x4+1
x+1
=
0+1
0+1
= 1
3) lim
x→−2
x2+2x
x2−x−6
lim
x→−2
x(x+2)
(x+2)(x−3)
= lim
x→−2
x
(x−3)
=
−2
(−2−3)
=
2
5
‫(وزاري‬5201‫دور‬2)
4) lim
x→1
x4−1
x−1
= lim
x→1
(x2−1)(x2+1)
x−1
= lim
x→1
(x−1)(x+1)(x2+1)
x−1
= lim
x→1
(x + 1)(x2
+ 1)
=(1+1)(1+1) = 4 )‫اول‬ ‫دور‬ 2013 ‫(وزاري‬
5) lim
x→3
x3−27
x2+2x−15
‫(وزاري‬2011)‫اول‬ ‫دور‬
lim
x→3
x3−27
x2+2x−15
= lim
x→3
(x−3)(x2+3x+9)
(x−3)(x+5)
= lim
x→3
(x2+3x+9)
(x+5)
=
9+9+9
3+5
=
27
8
6) lim
x→√2
x2−2
x−√2
= lim
x→√2
(x−√2)(x+√2)
x−√2
= lim
x→√2
(x + √2) = √2+ √2 = 2√2
7) lim
x→1
x3+7x2−8x
3x2−3
= lim
x→1
x (x2
+7x−8)
3(x2−1)
= lim
x→1
x(x−1)(x+8)
3(x−1)(x+1)
= lim
x→1
x(x+8)
3(x+1)
=
1(1+8)
3(1+1)
=
9
6
=
3
2
8) lim
x→−2
x3+ 8
x4−16
= lim
x→−2
(x+2)(x2−2x+4)
(x2−4)(x2+4)
= lim
x→−2
(x+2)(x2−2x+4)
(x−2)(x+2)(x2+4)
= lim
x→−2
x2−2x+4
(x−2)(x2+4)
=
4+4+4
−4(4+4)
= -
12
32
= -
3
8
)3 ‫دور‬ 2015 ‫(وزاري‬
9) lim
x→1
x2−1
√x−1
= lim
x→1
(x−1)(x+1)
√x−1
= lim
x→1
(√x−1)(√x+1)(x+1)
√x−1
‫(وزاري‬2012)‫ثاني‬ ‫دور‬
= lim
x→1
[(√x + 1)(x + 1)] = 2 . 2 = 4
10) lim
x→1
x2−9
√3x−3
=
1−9
√3−3
=
−8
√3−3
)1 ‫دور‬ 2014 ‫(وزاري‬
‫عندما‬ ‫طلب‬ ‫الكتاب‬ ‫في‬x‫تقترب‬‫من‬1‫عندما‬ ‫يطلب‬ ‫ما‬ ‫غالبا‬ ‫االسئلة‬ ‫هذه‬ ‫مثل‬ ‫في‬ ‫ولكن‬ ‫مباشرة‬ ‫التعويض‬ ‫ويمكننا‬ ‫صفر‬ ‫المقام‬ ‫يجعل‬ ‫ال‬ ‫وهذا‬x
‫من‬ ‫تقترب‬3:‫مبين‬ ‫كما‬ ‫التحليل‬ ‫الى‬ ‫ونذهب‬ ‫صفر‬ ‫المقام‬ ‫سيصبح‬ ‫عندها‬
lim
x→3
x2−9
√3x−3
= lim
x→3
(x−3)(x+3)
√3(√x− √3)
= lim
x→3
(√x−√3)(x+√3)(x+3)
√3(√x− √3)
‫نحلل‬(𝐱 − 𝟑)‫مربعين‬ ‫بين‬ ‫فرق‬
= lim
x→3
(√x+√3)(x+3)
√3
=
(√3+√3)(3+3)
√3
=
2 . √3 . 6
√3
=12
11) lim
x→−1
x2+ x
√x+10−3
= lim
x→−1
x( x+1)
√x+10−3
:‫المقام‬ ‫بمرافق‬ ‫نضرب‬

33. ‫الثاني‬ ‫الفصل‬ ‫أدبي‬ ‫سادس‬‫الغاية‬
33
lim
x→−1
x( x + 1)
√x + 10 − 3
√x + 10 + 3
√x + 10 + 3
= lim
x→−1
x( x + 1)(√x + 10 + 3)
(x + 10 − 9)
lim
x→−1
x( x+1)(√x+10+3)
(x+1)
= lim
x→−1
(x (√x + 10 + 3)) = -1 (√9 + 3) = -1(3+3) = -6
2–‫كان‬ ‫اذا‬lim
x→4
x2−2x+6
x+3
= 3a − 4‫قيمة‬ ‫جد‬a‫حيث‬a ∈ R.
lim
x→4
x2−2x+6
x+3
= 3a − 4 ⟹
16−8+6
4+3
= 3a − 4
14
7
= 3a − 4 ⟹ 2 = 3a − 4 ⟹ 3a = 2+4 ⟹ a =
6
3
= 2
3-‫كانت‬ ‫اذا‬lim
x→a
x2−a2
x−a
= 8‫قيمة‬ ‫جد‬a‫حــــيث‬a ∈ R.‫(وزاري‬2011)‫اول‬ ‫دور‬
lim
x→a
x2−a2
x−a
= 8 = lim
x→a
(x−a)(x+a)
x−a
= 8
lim
x→a
(x + a) = 8 ⟹ a + a = 8 ⟹ 2a = 8 ⟹ a = 4
4–‫كانت‬ ‫اذا‬+ bx2
ax=f(x)‫وكانت‬lim f(x) = 5
x→1
‫و‬lim f(x) = 8
x→−2
‫قيمتي‬ ‫جد‬a‫و‬b.‫الحقيقيتين‬
(2013)‫ثاني‬ ‫دور‬(2014‫دور‬2)(2015‫دور‬3)
lim
x→1
(ax2
+ bx) = a + b = 5
a + b = 5 ………❶
lim
x→−2
(ax2
+ bx) = 4a − 2b = 8
4a − 2b = 8 ….…❷
‫المعادلة‬ ‫نضرب‬❶‫ب‬‫ـ‬2‫المعادلة‬ ‫مع‬ ‫ونجمع‬❷:
2a + 2b = 10
4a − 2b = 8
6a = 18 ‫بالجمع‬
∴ a =
18
6
= 3
‫قيمة‬ ‫نعوض‬a‫المعادلة‬ ‫في‬❷:
4(3) − 2b = 8 ⟹ 12 − 2b = 8
2b = 12 – 8 ⟹ b =
4
2
⟹ b = 2
5-‫لتكن‬f(x) = { x2
− 3 x > 2
2 − 2x x ≤ 2
‫للدالة‬ ‫هل‬f‫عند‬ ‫غاية‬2.‫ذلك‬ ‫بين‬ ‫؟‬‫جد‬ ‫ثم‬lim
x→1
f(x).(‫تمهيدي‬2014)
a)
L1 = lim
x→2+
(x 2
− 3) = 4 - 3 = 1
L2 = lim
x→2− (2 − 2x) = 2- 4 = −2 ≠ L1 2 ‫عند‬ ‫غاية‬ ‫للدالة‬ ‫ليس‬ ‫اذا‬
b)
lim
x→1
f(x) = lim
x→1
(2 − 2x) = 2 – 2 .1 = 0

34. ‫الثاني‬ ‫الفصل‬ ‫أدبي‬ ‫سادس‬‫الغاية‬
34
6-‫لتكن‬f(x) = { x2
+ 1 x ≥ 2
2 − x x < 2
‫عندما‬ ‫غاية‬ ‫للدالة‬ ‫هل‬x→2
.‫ذلك‬ ‫بين‬ ‫؟‬
/‫الحل‬
L1 = lim
x→2+
(x 2
+ 1) = 4 + 1 = 5
L2 = lim
x→2− (2 − x) = 2- 2 = 0 ≠ L1 2 ‫عند‬ ‫غاية‬ ‫للدالة‬ ‫ليس‬ ‫اذا‬
7-‫لتكن‬f(x) = {
a + 2x x ≤ −1
3 − x2
x > −1
‫وكانت‬lim
x→−1
f(x)‫قيمة‬ ‫جد‬ , ‫موجودة‬a‫حيث‬R∈a.
‫(وزاري‬2012‫دور‬‫اول‬)
/‫الحل‬‫عندما‬ ‫موجودة‬ ‫الغاية‬ ‫ان‬ ‫بما‬x‫من‬ ‫تقترب‬-1‫اذا‬:‫اليسار‬ ‫غاية‬ ‫تساوي‬ ‫اليمين‬ ‫غاية‬
L1 = L2
lim
x→−1+
(3 − x2) = lim
x→−1− (a + 2x)
3 – (−1)2
= a - 2 ⟹ 3 - 1 = a – 2 ⟹ a = 2 + 2 = 4
8-‫لتكن‬f(x) = {
3x + a x ≥ 3
x2
− b x < 3
‫وكانت‬lim
x→3
f(x)‫وان‬ ‫موجودة‬f(√2) = 5‫قيمة‬ ‫جد‬ ,R∈a , b.
/‫الحل‬
f(√2) = x2
− b = 5 ⟹ (√2)2
− b = 5 ⟹ 2 – b = 5 ⟹ b = 2 -5
b = -3
‫ان‬ ‫بما‬lim
x→3
f(x).‫اليسار‬ ‫غاية‬ ‫تساوي‬ ‫اليمين‬ ‫غاية‬ ‫اذا‬ ‫موجودة‬
lim
x→3− (x2
− b) = lim
x→3+
(x2
+ a) ⟹ 32
- (-3) = 9 + a
9 + 3 = 9 + a ⟹ a = 3

35. ‫ادبي‬ ‫سادس‬‫الثاني‬ ‫الفصل‬‫االثرائية‬ ‫االمثلة‬
35
2-(‫االستمرارية‬:)‫نقطة‬ ‫في‬ ‫ان‬ ‫وذكرنا‬ ‫المركبة‬ ‫الدوال‬ ‫على‬ ‫وتعرفنا‬ ‫الغايات‬ ‫السابق‬ ‫الموضوع‬ ‫في‬ ‫تناولنا‬‫االلتقاء‬
‫االفتراضية‬‫غاية‬ ‫تملك‬ ‫دوال‬ ‫هناك‬ ‫ان‬ ‫والحظنا‬ ‫النقطة‬ ‫هذه‬ ‫عند‬ ‫غاية‬ ‫للدالة‬ ‫فان‬ ‫اليسار‬ ‫غاية‬ ‫تساوي‬ ‫اليمين‬ ‫غاية‬ ‫كانت‬ ‫اذا‬
‫سنح‬ ‫حيث‬ ‫االن‬ ‫الموضوع‬ ‫هذه‬ ‫من‬ ‫وسنستفيد‬ ‫غاية‬ ‫تملك‬ ‫ال‬ ‫واخرى‬‫في‬ ‫فراغ‬ ‫يوجد‬ ‫ام‬ ‫معينة‬ ‫نقطة‬ ‫في‬ ‫مستمرة‬ ‫الدالة‬ ‫ان‬ ‫هل‬ ‫دد‬
:‫التاليين‬ ‫الرسمين‬ ‫في‬ ‫مبين‬ ‫كما‬ ‫المنحني‬
‫اذا‬ /‫مالحظة‬‫للمتغير‬ ‫جذر‬ ‫او‬ ‫قسمة‬ ‫تحوي‬ ‫ال‬ ‫الدالة‬ ‫كانت‬x‫كل‬ ‫هو‬ ‫الدالة‬ ‫مجال‬ ‫فان‬R.
‫مثال‬1/‫كانت‬ ‫اذا‬+32
x=f(x)‫ان‬ ‫هل‬f‫عن‬ ‫مستمرة‬‫ـــــ‬‫د‬1=x‫؟‬‫(وزاري‬2012)‫ثالث‬ ‫دور‬
/‫الحل‬‫الدالة‬ ‫مجال‬f‫هو‬R.‫الدالة‬ ‫مجال‬ ‫الى‬ ‫ينتمي‬ ‫والواحد‬
1) f(1) = 12
+ 3 = 4
2) lim
x→1
f(x) = 12
+ 3 = 4
3) f(1) = lim
x→1
f(x) = 4
‫مثال‬2/‫لتكن‬f(x) = {
2x + 3 x < 0
x2
+ 1 x ≥ 0
‫هل‬f‫عند‬ ‫مستمرة‬x = 0.‫(وزاري‬2013)‫اول‬ ‫دور‬
/‫الحل‬‫الدالة‬ ‫مجال‬f‫هو‬R.‫الدالة‬ ‫مجال‬ ‫الى‬ ‫ينتمي‬ ‫والصفر‬
‫الدالة‬ ‫مجال‬ ‫الى‬ ‫ينتمي‬ ‫الصفر‬ ‫ان‬ ‫بما‬ /‫مالحظة‬𝐱 ≥ 𝟎‫الدالة‬ ‫على‬ ‫االول‬ ‫الشرط‬ ‫نطبق‬ ‫فاننا‬𝐱 𝟐
+ 𝟏:
1) f(0) = 02
+ 1 = 1
2) L1 = lim
x→0−
f(x) = 02
+ 1= 1 :‫اليمين‬ ‫غاية‬
L2 = lim
x→0+
f(x) = 2 . 0 + 3 = 3 ≠ L1 ‫اليسار‬ ‫غاية‬
.‫الشروط‬ ‫باقي‬ ‫الجراء‬ ‫داعي‬ ‫وال‬ ‫مستمرة‬ ‫غير‬ ‫الدالة‬ ‫فان‬ ‫شرط‬ ‫اي‬ ‫يتحقق‬ ‫لم‬ ‫اذا‬ /‫مالحظة‬
‫مثال‬3/‫لتكن‬f(x) = {
2 − x x < −1
2x2
+ 1 x ≥ −1
‫الدالة‬ ‫استمرارية‬ ‫ابحث‬f‫عند‬x = -1.
/‫الحل‬‫الدالة‬ ‫مجال‬f‫هو‬R‫و‬-1.‫الدالة‬ ‫مجال‬ ‫الى‬ ‫ينتمي‬
1) f(-1) = 2(-1)2
+ 1 = 2 +1 = 3
2) L1 = lim
x→(−1)+
f(x) = 2.(-1)2
+ 1= 3 : ‫اليمين‬ ‫غاية‬
L2 = lim
x→(−1)−
f(x) = 2 – (-1) = 2 +1 = 3 : ‫اليسار‬ ‫غاية‬
:‫االستمرارية‬ ‫شروط‬‫كانت‬ ‫اذا‬f(x)‫دالة‬‫وكان‬a‫الدالة‬ ‫مجال‬ ‫الى‬ ‫ينتمي‬‫فاننا‬‫عند‬ ‫مستمرة‬ ‫الدالة‬ ‫ان‬ ‫نقول‬a=x
:‫التالية‬ ‫الثالث‬ ‫الشروط‬ ‫تحققت‬ ‫اذا‬
1) f(a) ‫وحقيقية‬ ‫.موجودة‬
2) lim
x→a
f(x) ‫وحقيقية‬ ‫.موجودة‬
lim
x→a+
f(x) = lim
x→a− f(x) ‫ان‬ ‫اي‬‫اليسار‬ ‫غاية‬ ‫تساوي‬ ‫اليمين‬ ‫غاية‬
3) lim
x→a
f(x) = f(a)
‫عندما‬ ‫مستمرة‬ ‫غير‬ ‫الدالة‬ ‫هذه‬x‫تساوي‬1 ‫عندما‬ ‫مستمرة‬ ‫الدالة‬ ‫هذه‬x‫تساوي‬1
‫اذا‬f‫عند‬ ‫مستمرة‬1=x
‫الدالة‬ ‫اذا‬f‫عند‬ ‫مستمرة‬ ‫غير‬0=x.

36. ‫ادبي‬ ‫سادس‬‫الثاني‬ ‫الفصل‬‫االثرائية‬ ‫االمثلة‬
36
∵ L1 = L2 = 3 ⟹ ∴ lim
x→−1
f(x) = 3
3) f(−1) = lim
x→−1
f(x) = 3
‫مثال‬4/‫لتكن‬f(x) = {
3x + 1 x ≥ −1
x2
x < −1
‫(وزاري‬2012)‫ثاني‬ ‫دور‬
‫أ‬-‫الدالة‬ ‫استمرارية‬ ‫ابحث‬f‫عند‬x = -1.
‫ب‬-‫عندما‬ ‫غاية‬ ‫للدالة‬ ‫هل‬x → 4.‫ذلك‬ ‫بين‬ ‫؟‬
/‫الحل‬‫أ‬–‫الدالة‬ ‫مجال‬f‫هو‬R‫والـ‬-1.‫الدالة‬ ‫مجال‬ ‫الى‬ ‫ينتمي‬
1) f(-1) = 3(-1) + 1 = -3 +1 = -2
2) L1 = lim
x→(−1)+
f(x) = 3(-1) + 1= -2
L2 = lim
x→(−1)−
f(x) = (-1)2
= 1 ≠ L1
‫ب‬-‫الـ‬4‫الدالة‬ ‫مجال‬ ‫الى‬ ‫تنتمي‬3x + 1
lim
x→4
(3x + 1) = 3(4) +1 = 13
‫مثال‬5/‫الدالة‬ ‫استمرارية‬ ‫ابحث‬f(x) =
x
x+1
‫عند‬x = 1.‫(وزاري‬2014‫دور‬1)
/‫الحل‬‫هو‬ ‫للدالة‬ ‫مجال‬ ‫اوسع‬R‫عدا‬:‫صفر‬ ‫المقام‬ ‫تجعل‬ ‫التي‬ ‫القيم‬
x + 1 = 0 ⟹ x = -1
∴‫هو‬ ‫الدالة‬ ‫مجال‬R‫عدا‬-1‫وتكتب‬R{-1}‫اذا‬1.‫الدالة‬ ‫مجال‬ ‫الى‬ ‫ينتمي‬
1) f(1) =
1
1+1
=
1
2
2) lim
x→1
f(x) =
x
x+1
=
1
1+1
=
1
2
3) f(1) = lim
x→1
f(x) =
1
2
‫مثال‬6/‫الدالة‬ ‫استمرارية‬ ‫ابحث‬f(x) =
x+3
x2+1
‫عند‬x = 1.(‫تمهيدي‬2014)
/‫الحل‬‫هو‬ ‫للدالة‬ ‫مجال‬ ‫اوسع‬R‫عدا‬:‫صفر‬ ‫المقام‬ ‫تجعل‬ ‫التي‬ ‫القيم‬
x2
+ 1 = 0 ⟹ x2
= −1
‫قيم‬ ‫كل‬ ‫الدالة‬ ‫مجال‬R‫والـ‬1:‫الدالة‬ ‫مجال‬ ‫الى‬ ‫ينتمي‬
1) f(1) =
1+3
1+1
=
4
2
= 2
2) lim
x→1
x+3
x2+1
=
1+3
1+1
=
4
2
= 2
3) f(1) = lim
x→1
f(x) = 2
‫مثال‬7/‫الدالة‬ ‫استمرارية‬ ‫ابحث‬f(x) = ǀx +2ǀ‫عند‬x = -2.
/‫الحل‬‫هو‬ ‫للدالة‬ ‫مجال‬ ‫اوسع‬R‫والـ‬-2:‫الدالة‬ ‫مجال‬ ‫الى‬ ‫ينتمي‬
‫المطلق‬ ‫عالمة‬ ‫بدون‬ ‫نفسها‬ ‫الدالة‬ ‫يحوي‬ ‫االول‬ ‫قسمين‬ ‫الى‬ ‫الدالة‬ ‫بتجزئة‬ ‫نقوم‬ ‫مطلقة‬ ‫قيم‬ ‫تحوي‬ ‫التي‬ ‫الدوال‬ ‫في‬ /‫مالحظة‬(x +2)‫يحوي‬ ‫والثاني‬
‫بـ‬ ‫مضروبة‬ ‫الدالة‬-1‫قيمة‬ ‫ونحسب‬ ‫بالصفر‬ ‫الدالة‬ ‫نساوي‬ ‫حيث‬ ‫مجالهما‬ ‫ونحسب‬x:
x + 2 = 0 ⟹ x = -2
∴ f(x) = {
x + 2 x ≥ −2
−(x + 2) x < −2
‫الدالة‬ ‫اذا‬f‫عند‬ ‫مستمرة‬1-=x.
‫الدالة‬ ‫اذا‬f‫غير‬‫عند‬ ‫مستمرة‬1-=x.
‫اذا‬f‫عند‬ ‫مستمرة‬1=x.
‫اذا‬f‫عند‬ ‫مستمرة‬1=x.

37. ‫ادبي‬ ‫سادس‬‫الثاني‬ ‫الفصل‬‫االثرائية‬ ‫االمثلة‬
37
1) f(-2) = −2 + 2 = 0
2) L1 = lim
x→(−2)+
f(x) = −2 + 2 = 0
L2 = lim f(x)
x→(−2)−
= −(−2 + 2) = 0= L1
3) f(-2) = lim f(x)
x→−2
= 0
‫مثال‬8/‫لتكن‬f(x) = {x2
− 1 x ≥ 1
a − x x < 1
‫قيمة‬ ‫جد‬a ∈ R‫كانت‬ ‫اذا‬f‫عند‬ ‫مستمرة‬x = 1.
/‫الحل‬‫عند‬ ‫مستمرة‬ ‫الدالة‬ ‫ان‬ ‫بما‬x = 1:‫اليسار‬ ‫غاية‬ ‫تساوي‬ ‫اليمين‬ ‫غاية‬ ‫اذا‬
lim
x→(1)+
(x2
− 1) = lim
x→(1)−
(a − x)
(1)2
− 1 = a − 1
0 = a − 1 ⟹ a = 1
‫مثال‬9/‫لتكن‬f(x) = { 𝑎x2
+ 2 x ≥ 1
bx x < 1
‫قيمة‬ ‫جد‬a,b ∈ R‫كانت‬ ‫اذا‬f‫عند‬ ‫مستمرة‬x = 1‫و‬f(-1) = -4
/‫الحل‬‫قيمة‬ ‫لها‬ ‫تنتمي‬ ‫التي‬ ‫الدالة‬ ‫نختار‬ ‫حيث‬ ‫النقطة‬ ‫بتعويض‬ ‫دائما‬ ‫نبدأ‬x = -1
f(-1) = b(-1) = -4 ⟹ - b = -4 ⟹ b = 4
‫عند‬ ‫مستمرة‬ ‫الدالة‬x = 1‫تساوي‬ ‫اليمين‬ ‫غاية‬ ‫اذا‬‫غ‬.‫اليسار‬ ‫اية‬
lim
x→(1)+
(ax2
+ 2) = lim
x→(1)−
(4x)
a(1)2
+ 2 = 4(1) ⟹ a + 2 = 4 ⟹ a = 4 – 2 = 2
‫التمارين‬ ‫حلول‬2-2
1-‫لتكن‬+ 32
+ x3
x=f(x)‫عند‬ ‫الدالة‬ ‫استمرارية‬ ‫ابحث‬3=x.
/‫الحل‬‫الدالة‬ ‫مجال‬R
1) f(3) = 33
+ 32
+ 3 = 27+9+3 = 39
2) lim
x→3
f(x) = 33
+ 32
+ 3 = 39
3) f(3) = lim
x→3
f(x) = 39
2-‫لتكن‬f(x) =
x2
x2+1
‫ان‬ ‫اثبت‬f.‫مجالها‬ ‫في‬ ‫مستمرة‬
/‫الحل‬‫قيم‬ ‫كل‬ ‫الدالة‬ ‫مجال‬R‫ونفرض‬a‫الى‬ ‫ينتمي‬ ‫حقيقي‬ ‫عدد‬R:‫فان‬
1) f(a) =
a2
a2+1
2) lim
x→a
f(x) =
a2
a2+1
3) f(a) = lim
x→a
f(x) =
a2
a2+1
4)
‫اذا‬f‫عند‬ ‫مستمرة‬2-=x.
‫اذا‬f‫عند‬ ‫مستمرة‬3=x.
‫اذا‬f. ‫مجالها‬ ‫في‬ ‫مستمرة‬

38. ‫ادبي‬ ‫سادس‬‫الثاني‬ ‫الفصل‬‫االثرائية‬ ‫االمثلة‬
38
3-‫لتكن‬3
x=f(x).‫مجالها‬ ‫في‬ ‫الدالة‬ ‫استمرارية‬ ‫ابحث‬
/‫الحل‬‫هو‬ ‫للدالة‬ ‫مجال‬ ‫اوسع‬R‫ولتكن‬a‫الى‬ ‫ينتمي‬ ‫حقيقي‬ ‫عدد‬R:
1) f(a) = a3
2) lim
x→a
f(x) = a3
3) f(a) = lim
x→a
f(x) = a3
[
4-‫لتكن‬f(x) = {x2
− 2 x ≥ −1
3x + 1 x < −1
‫الدالة‬ ‫استمرارية‬ ‫ابحث‬f‫عند‬x = -1.‫(وزاري‬2011)‫اول‬ ‫دور‬
/‫الحل‬‫الدالة‬ ‫مجال‬f‫هو‬R‫والعدد‬-1.‫الدالة‬ ‫مجال‬ ‫الى‬ ‫ينتمي‬
1) f(-1) = (-1)2
- 2 = 1- 2 = -1
2) L1 = lim
x→(−1)+
f(x) = (-1) 2
-2= 1- 2= -1
L2 = lim
x→(−1)−
f(x) =3(-1) +1= -3 +1= -2 ≠ L1
5-‫لتكن‬ǀf(x) =ǀx - 2‫عنـــــــد‬ ‫الدالــــــة‬ ‫استمرارية‬ ‫ابحث‬x = 2.
/‫الحل‬‫قيم‬ ‫كل‬ ‫الدالة‬ ‫مجال‬R‫والـ‬2:‫الدالة‬ ‫مجال‬ ‫الى‬ ‫تنتمي‬
x-2 = 0 ⟹ x = 2
f(x) = {
x − 2 x ≥ 2
−(x − 2) x < 2
1) f(2) = 2 - 2 = 0
2) L1 = lim
x→(2)+
f(x) = 2 -2 = 0
L2 = lim
x→(2)−
f(x) =-(2-2) = 0 = L1
3) f(2) = lim
x→2
f(x) = 0
6-‫لتكن‬f(x) = {
1 − 2x x ≤ 2
1 − x2
x > 2
‫ان‬ ‫اثبت‬f‫عند‬ ‫مستمرة‬x = 2.(2012)‫اول‬ ‫دور‬(2015‫دور‬2)
/‫الحل‬‫الدالة‬ ‫مجال‬f‫هو‬R‫والعدد‬2.‫الدالة‬ ‫مجال‬ ‫الى‬ ‫ينتمي‬
1) f(2) = 1 – 2(2) = 1- 4 = -3
2) L1 = lim
x→(2)+
f(x) = 1- (2)2
= 1- 4 = -3
L2 = lim
x→(2)− f(x) =1 – 2(2) =-3 = L1
3) f(2) = lim
x→2
f(x) = -3
7-‫لتكن‬f(x) = {
ax + 3 x ≥ 1
3x2
+ 1 x < 1
‫قيمة‬ ‫جد‬a ∈ R‫كانت‬ ‫اذا‬f‫عند‬ ‫مستمرة‬x = 1.
/‫الحل‬‫عند‬ ‫مستمرة‬ ‫الدالة‬ ‫ان‬ ‫بما‬x = 1:‫اليسار‬ ‫غاية‬ ‫تساوي‬ ‫اليمين‬ ‫غاية‬ ‫اذا‬
lim
x→(1)+
(ax + 3) = lim
x→(1)−
(3x2
+ 1)
a(1) + 3 = 3(1)2
+ 1
a + 3 = 4 ⟹ a = 4 − 3 = 1
‫اذا‬f. ‫مجالها‬ ‫في‬ ‫مستمرة‬
‫الدالة‬ ‫اذا‬f‫عند‬ ‫مستمرة‬ ‫غير‬1-=x.
‫الدالة‬ ‫اذا‬f‫عند‬ ‫مستمرة‬2=x.
‫الدالة‬ ‫اذا‬f‫عند‬ ‫مستمرة‬2=x.

39. ‫ادبي‬ ‫سادس‬‫الثاني‬ ‫الفصل‬‫االثرائية‬ ‫االمثلة‬
39
8-‫لتكن‬f(x) = {
2x + b x ≤ −1
x2
+ a x > −1
‫قيمتي‬ ‫جد‬a‫و‬b‫كانت‬ ‫اذا‬ ‫الحقيقيتين‬f‫عندما‬ ‫مستمرة‬x = -1‫وان‬
f(2) = 7.‫(وزاري‬2012‫دور‬‫ثالث‬)(‫تمهيدي‬2014)2016-3
/‫الحل‬
f(2) = 22
+ a = 7 ⟹ 4 + a = 7 ⟹ a = 7- 4 ⟹ a = 3
‫عند‬ ‫مستمرة‬ ‫الدالة‬x = -1‫تساوي‬ ‫اليمين‬ ‫غاية‬ ‫اذا‬‫غ‬.‫اليسار‬ ‫اية‬
lim
x→(−1)+
(x2
+ a) = lim
x→(−1)−
(2x + b)
(-1)2
+ 3 = 2(−1) + b ⟹ 1 + 3 = −2 + b ⟹ b = 1+3 + 2 ⟹ b = 6

40. ‫ادبي‬ ‫سادس‬‫الثاني‬ ‫الفصل‬‫االثرائية‬ ‫االمثلة‬
40
‫الوزارية‬ ‫األسئلة‬
1):‫التالية‬ ‫الغايات‬ ‫من‬ ‫غاية‬ ‫كل‬ ‫قيمة‬ ‫جد‬
lim
x→2
x2−2𝑥
x2−3x−10
2014-2 , lim
x→2
x4−81
x−3
2015-1 , lim
x→1
√x+3−2
x−1
2016-1
lim
√z
→−3
z−9
√z+3
2016-2 , lim
x→4
x2−16
√4x−4
2016-3
2)‫لتكن‬f(x) = {
7 − 2x x < −1
2x2
+ 3 x ≥ −1
‫هل‬f‫عند‬ ‫مستمرة‬x = -1.‫ذلك‬ ‫بين‬ ‫؟‬2014-2
3)‫كانت‬ ‫اذا‬lim
x→5
x2−25
x2−8x+15
= −3𝑎 + 11‫قيمة‬ ‫جد‬a.2015-1
4)‫كانت‬ ‫اذا‬lim
x→n
x2−𝑛2
𝑥−𝑛
= 10‫قيمة‬ ‫جد‬a.2015-2
5)‫لتكن‬f(x) = { x2
+ 1 x < −1
2x − 2 x ≥ −1
‫ان‬ ‫حيث‬ 𝑓: 𝑅 → 𝑅2015-1
a.‫الدالة‬ ‫استمرارية‬ ‫ابحث‬f‫عندما‬x → 3.
b.‫عند‬ ‫الغاية‬ ‫جد‬x = -2.
6)‫لتكن‬f(x) = {
2x + a x ≥ 2
x2
− b x < 2
‫وكانت‬lim
x→2
f(x)‫موجودة‬f(√2) = 5‫فم‬‫ا‬‫قيمة‬b ,a‫الحقيقيتين‬.
2015-2
7)‫كانت‬ ‫اذا‬f(x) = {2a + x2
x ≥ 1
2x + b x < 1
‫وكانت‬f(x)‫عند‬ ‫مستمرة‬x = 1‫موجودة‬f(2) = 6‫ج‬‫ـــــــ‬‫د‬
‫قيمتي‬b ,a.‫الحقيقيتين‬2015-3
8)‫كان‬ ‫اذا‬lim
x→5
x2−2x−15
x−5
= 3a − 4‫قيمة‬ ‫جد‬a.2016-‫ت‬
9): ‫أن‬ ‫علمت‬ ‫اذا‬f(x) = {
2x + 3 x ≥ 1
x2
− 2 x < 1
,1)‫عند‬ ‫غاية‬ ‫للدالة‬ ‫هل‬1‫؟‬2)‫جد‬lim
x→3
f(x)
10)‫ليكن‬f(x) = {x2
+ 1 x > −1
1 − x x ≤ −1
,‫هل‬‫ا‬‫لدالة‬‫مستمرة‬x = -1‫؟‬2016-‫ت‬
11)‫لتكن‬f(x) = {x2
− 1 x > 3
5 + x x ≤ 3
(a‫عند‬ ‫الدالة‬ ‫استمرارية‬ ‫ابحث‬x = 3
b)‫عندما‬ ‫الدالة‬ ‫غاية‬ ‫جد‬x = 22016-1
12)‫كانت‬ ‫اذا‬+ bx + 32
f(x) = ax‫دالة‬‫وكانت‬lim f(x) = 8
x→1
‫و‬lim f(x) = 4
x→−1
‫قيم‬ ‫جد‬‫ـــــــــــــ‬‫تي‬
b ∈ R‫و‬a.2016-1
13)‫لتكن‬f(x) = {3x2
− 10 x > 3
5 + x x ≤ 3
‫مستمرة‬ ‫الدالة‬ ‫ان‬ ‫اثبت‬‫عند‬x = 32016-2
14)‫لتكن‬f(x) = {
2x + b x ≤ −1
x2
+ a x > −1
‫قيمتي‬ ‫جد‬a‫و‬b‫كانت‬ ‫اذا‬ ‫الحقيقيتين‬f‫عندمـــــــا‬ ‫مستمرة‬x = -2‫وان‬
f(2) = 7.2016-2
15)‫لتكن‬f(x) = {x2
− 1 x > 3
x + 5 x ≤ 3
‫عندما‬ ‫غاية‬ ‫للدالة‬ ‫هل‬x → 32016-3

41. /‫الشمري‬ ‫أحمد‬ :‫األستاذ‬077045169371‫المرسل‬‫الطباعية‬ ‫للخدمات‬/07703458937
‫األستاذ‬‫الشمري‬ ‫أحمد‬ :
07704516937
‫المرسل‬‫الطباعية‬ ‫للخدمات‬
‫المنصور‬–‫دراغ‬ ‫حي‬ ‫جامع‬ ‫مجاور‬
07703458937
‫ملزمة‬‫الرياضيات‬
‫االدبي‬ ‫السادس‬
2017-2016
‫الثالث‬ ‫الفصل‬
‫المشتقة‬

42. /‫الشمري‬ ‫أحمد‬ :‫األستاذ‬0770451693742‫المرسل‬‫الطباعية‬ ‫للخدمات‬/07703458937

43. ‫الفص‬ ‫أدبي‬ ‫سادس‬‫المشتقة‬ ‫الثالث‬ ‫ل‬
/‫الشمري‬ ‫أحمد‬ :‫األستاذ‬0770451693743‫المرسل‬‫الطباعية‬ ‫للخدمات‬/07703458937
:)‫الثالث(االشتقاق‬ ‫الفصل‬
3-(‫المشتقة‬:)‫لها‬ ‫ويرمز‬ ‫نقطة‬ ‫اي‬ ‫عند‬ ‫للدالة‬ ‫المماس‬ ‫ميل‬ ‫معادلة‬ ‫المشتقة‬ ‫تمثل‬
dy
dx
‫او‬f̅(x)‫او‬y̅
:‫هو‬ ‫وقانونها‬
f̅(xo) = lim
∆x→0
f(xo+∆x)− f(xo)
∆x
‫مثال‬1/‫كان‬ ‫اذا‬f(x) = x2
‫جد‬f̅(2).
‫ا‬/‫لحل‬
f̅(xo) = lim
∆x→0
f(xo+∆x)− f(xo)
∆x
‫القانون‬
f̅(2) = lim
∆x→0
f(2+∆x)− f(2)
∆x
‫التطبيق‬
‫نعوض‬𝐟(𝟐 + ∆𝐱)‫رمز‬ ‫كل‬ ‫نستبدل‬ ‫اي‬x‫بـ‬𝟐 + ∆𝐱‫الدالة‬ ‫في‬f(x)‫نعوض‬ ‫وكذلك‬f(2)‫رمز‬ ‫كل‬ ‫نستبدل‬ ‫اي‬x‫الدالة‬ ‫في‬f(x)‫بـ‬2‫كما‬
:‫مبين‬
f̅(2) = lim
∆x→0
(2+∆x)2− (2)2
∆x
‫التعويض‬
‫يحوي‬ ‫المقام‬ ‫ان‬ ‫بما‬∆𝐱:‫التبسيط‬ ‫الى‬ ‫نلجأ‬ ‫لذلك‬ ‫صفر‬ ‫قيمة‬ ‫تعويض‬ ‫يمكننا‬ ‫ال‬
f̅(2) = lim
∆x→0
4 + 4∆x + ∆x2 − 4
∆x
‫التبسيط‬
= lim
∆x→0
4∆x + ∆x2
∆x
‫مشترك‬ ‫عامل‬ ∆x
= lim
∆x→0
∆x(4 +∆x)
∆x
= lim
∆x→0
(4 + ∆x) = 4 + 0 = 4
‫مثال‬2/‫الدالــة‬ ‫مشتقة‬ ‫جد‬ ‫التعريف‬ ‫باستخدام‬f(x) = x2
+ x + 1‫عندما‬x = 1.
/‫الحل‬
f̅(x) = lim
∆x→0
f(xo+∆x)− f(xo)
∆x
‫القانون‬
f̅(1) = lim
∆x→0
f(1+∆x)− f(1)
∆x
‫التطبيق‬
f̅(1) = lim
∆x→0
(1+∆x)2+ (1+∆x)+1−[1 + 1 + 1]
∆x
‫التعويض‬
f̅(1) = lim
∆x→0
1+2∆x+ ∆x2+1+∆x+1−3
∆x
‫التبسيط‬
f̅(1) = lim
∆x→0
3∆x+ ∆x2
∆x
= lim
∆x→0
∆x(3 +∆x)
∆x
‫مشترك‬ ‫عامل‬ ∆x
f̅(1) = lim
∆x→0
(3 + ∆x) = 3 + 0 = 3

44. ‫الفص‬ ‫أدبي‬ ‫سادس‬‫المشتقة‬ ‫الثالث‬ ‫ل‬
/‫الشمري‬ ‫أحمد‬ :‫األستاذ‬0770451693744‫المرسل‬‫الطباعية‬ ‫للخدمات‬/07703458937
‫مثال‬3/‫الدالــة‬ ‫مشتقة‬ ‫جد‬ ‫التعريف‬ ‫باستخدام‬f(x) =
1
x
.
/‫الحل‬
f̅(xo) = lim
∆x→0
f(xo+∆x)− f(xo)
∆x
‫القانون‬
f̅(x) = lim
∆x→0
f(x+∆x)− f(x)
∆x
‫التطبيق‬
‫البسط‬ ‫ناتج‬ ‫قيمة‬ ‫بحساب‬ ‫نقوم‬𝐟(𝐱 + ∆𝐱) − 𝐟(𝐱)
f̅(x) = lim
∆x→0
1
x+∆x
−
1
x
∆x
= lim
∆x→0
x−(x+∆x)
x(x+∆x)
∆x
= lim
∆x→0
x−x−∆x
x(x+∆x)
∆x
=lim
∆x→0
−∆x
x(x+∆x)
∆x
1
f̅(x) = lim
∆x→0
−∆x
x(x+∆x)
.
1
∆x
= lim
∆x→0
−1
x2+ x ∆x
=
−1
x2+ x (0)
= −
1
x2 ‫الدالة‬ ‫مشتقة‬
‫مثال‬4/‫الدالــة‬ ‫مشتقة‬ ‫جد‬ ‫التعريف‬ ‫باستخدام‬f(x) = √x
/‫الحل‬
f̅(x) = lim
∆x→0
f(xo+∆x)− f(xo)
∆x
‫الق‬‫انون‬
= lim
∆x→0
√x+∆x − √x
∆x
‫التعويض‬
= lim
∆x→0
√x+∆x − √x
∆x
.
√x+∆x+ √x
√x+∆x+ √x
‫البسط‬ ‫بمرافق‬ ‫نضرب‬
= lim
∆x→0
(x+∆x)− x
∆x .(√x+∆x+ √x)
= lim
∆x→0
x + ∆x − x
∆x .(√x+∆x+ √x)
‫تبسيط‬
= lim
∆x→0
∆x
∆x .(√x+∆x+ √x)
= lim
∆x→0
1
√x+∆x + √x
=
1
√x+0 + √x
f̅(x) =
1
√x + √x
=
1
2√x
:‫للمشتقة‬ ‫الهندسي‬ ‫التفسير‬‫ان‬‫معرفة‬ ‫نقطة‬ ‫عند‬ ‫الدالة‬ ‫مشتقة‬
‫فان‬ ‫وكذلك‬ ‫النقطة‬ ‫تلك‬ ‫عند‬ ‫الدالة‬ ‫لمنحني‬ ‫المماس‬ ‫ميل‬ ‫تساوي‬
‫لـ‬ ‫قيمة‬ ‫اي‬ ‫عند‬ ‫الدالة‬ ‫مشتقة‬x‫للدالة‬ ‫المماس‬ ‫ميل‬ ‫معادلة‬ ‫تساوي‬
:‫التالي‬ ‫الرسم‬ ‫في‬ ‫مبين‬ ‫كما‬ ‫نقطة‬ ‫اي‬ ‫عند‬
‫القيمة‬ ‫كانت‬ ‫كلما‬∆x‫ميل‬ ‫يمثل‬ ‫المستقيم‬ ‫الخط‬ ‫ميل‬ ‫كان‬ ‫كلما‬ ‫صغيرة‬
‫للد‬ ‫المماس‬‫كانت‬ ‫واذا‬ ‫معينة‬ ‫نقطة‬ ‫عند‬ ‫الة‬∆x‫فان‬ ‫الصفر‬ ‫من‬ ‫تقترب‬
‫ال‬ ‫ناتج‬‫غاية‬‫ي‬‫المماس‬ ‫ميل‬ ‫مثل‬.‫المشتقة‬ ‫تسمية‬ ‫عليها‬ ‫ويطلق‬
: ‫المستقيم‬ ‫الخط‬ ‫معادلة‬)1x-m(x=1y–y
: ‫حيث‬m‫ميل‬ ‫تمثل‬, ‫المستقيم‬1y‫و‬1x‫نقطة‬ ‫احداثيات‬‫معلومة‬.‫المستقيم‬ ‫على‬
‫مالحظة‬1:‫معاد‬ ‫لدينا‬ ‫كان‬ ‫اذا‬( ‫بصيغــــــة‬ ‫مستقيم‬ ‫لة‬Ay + Bx + C = 0)‫معامل‬ ‫سالب‬ ‫يساوي‬ ‫المستقيم‬ ‫ميل‬ ‫فان‬x
‫معامل‬ ‫على‬ ‫مقسوم‬y:‫مبين‬ ‫كما‬m =
−𝐁
𝐀
‫مالحظة‬2:‫على‬ ‫العمود‬ ‫ميل‬‫مستقيم‬‫ي‬‫ميل‬ ‫مقلوب‬ ‫ساوي‬‫المستقيم‬.‫االشارة‬ ‫بعكس‬
‫مثال‬5/‫كات‬ ‫اذا‬f(x) = 2x2
+ 3x + 1‫التعريف‬ ‫باستخدام‬ ‫جد‬f̅(2).‫النقطة‬ ‫هذه‬ ‫عند‬ ‫للمنحني‬ ‫المماس‬ ‫معادلة‬ ‫جد‬ ‫ثم‬
/‫الحل‬‫قيمة‬ ‫نحسب‬f̅(2)
x
∆x
f(x)
f(x+∆x)
f(x + ∆x) − f(x)

45. ‫الفص‬ ‫أدبي‬ ‫سادس‬‫المشتقة‬ ‫الثالث‬ ‫ل‬
/‫الشمري‬ ‫أحمد‬ :‫األستاذ‬0770451693745‫المرسل‬‫الطباعية‬ ‫للخدمات‬/07703458937
f̅(2) = lim
∆x→0
f(2 + ∆x) − f(2)
∆x
f̅(2) = lim
∆x→0
2(2+∆x)2 + 3(2+∆x)+ 1−(2(2)2 + 3(2)+ 1)
∆x
= lim
∆x→0
2(4+4∆x+ ∆x2)+ 6+3∆x + 1−15
∆x
= lim
∆x→0
𝟖 + 8∆x + 2∆x2 + 𝟔 +3∆x + 𝟏 −15
∆x
= lim
∆x→0
11∆x +2∆x2 + 15 −15
∆x
= lim
∆x→0
11∆x+2∆x2
∆x
= lim
∆x→0
∆x(11+2∆x)
∆x
= lim
∆x→0
(11 + 2∆x) = 11 + 2 (0) = 11 ‫المماس‬ ‫ميل‬
‫الدالة‬ ‫من‬f(x)‫عندما‬x1‫تساوي‬2‫قيمة‬ ‫نحسب‬y1:
y1 = f(2) = 2(2)2
+ 3(2) + 1 = 15
‫قيم‬ ‫نعوض‬x1‫و‬y1‫و‬m:‫المستقيم‬ ‫معادلة‬ ‫في‬
y − 15 = 11(x − 2) ⟹ y − 15 = 11x – 22 ⟹ y - 11x + 22 - 15 = 0
y - 11x + 7 = 0 2 ‫النقطة‬ ‫عند‬ ‫للمنحني‬ ‫المماس‬ ‫معادلة‬
‫الفيزياو‬ ‫التطبيقات‬:‫للمشتقة‬ ‫ية‬‫االجسام‬ ‫حركة‬ ‫منها‬ ‫التطبيقات‬ ‫من‬ ‫العديد‬ ‫في‬ ‫المشتقة‬ ‫من‬ ‫االستفادة‬ ‫يمكننا‬‫مستقيم‬ ‫خط‬ ‫على‬:
1‫االزاحة‬ ‫دالة‬ (f(t)‫قطعه‬ ‫التي‬ ‫المسافة‬ ‫أو‬ ‫البعد‬ , ‫الموضع‬ ‫لتحديد‬ ‫الزمن.)تستخدم‬ ‫بداللة‬ ‫تكون‬(‫البداية‬ ‫نقطة‬ ‫من‬ ‫الجسم‬ ‫ا‬
2‫السرعة‬ ‫دالة‬ (v(t)=‫الزمن‬ ‫الى‬ ‫بالنسبة‬ ‫االزاحة‬ ‫دالة‬ ‫مشتقة‬:v(t) = f̅(t)
3‫التعجيل‬ ‫دالة‬ (a(t)=:‫الزمن‬ ‫الى‬ ‫بالنسبة‬ ‫السرعة‬ ‫دالة‬ ‫مشتقة‬a(t) = v̅(t)
‫الحركة‬ ‫بداية‬ ‫عند‬t = 0
‫يصله‬ ‫مسافة‬ ‫واوطئ‬ ‫واعلى‬ ‫واكبر‬ ‫اقل‬‫الجسم‬‫عندما‬v(t) = 0
‫عندما‬ ‫الجسم‬ ‫يصلها‬ ‫سرعة‬ ‫واكبر‬ ‫اقل‬a(t) = 0
‫موجبة‬ ‫قيمته‬ ‫دائما‬ ‫الزمن‬.‫يهمل‬ ‫والسالب‬
:‫التالية‬ ‫النقاط‬ ‫احدى‬ ‫سيذكر‬ ‫فانه‬ ‫الزمن‬ ‫يحدد‬ ‫ولم‬ ‫التعجيل‬ ‫او‬ ‫السرعة‬ ‫او‬ ‫البعد‬ ‫طلب‬ ‫اذا‬
o‫الزمن‬ ‫نعوض‬ : ‫الحركة‬ ‫بدء‬t = 0.
o‫سرعته‬ ‫تكون‬ ‫عندما‬k‫السرعة‬ ‫دالة‬ ‫في‬ ‫نعوض‬ :v(t) = k‫ونحسب‬t.‫ونعوضه‬
o‫تعجيله‬ ‫يكون‬ ‫عندما‬k‫التعجيل‬ ‫دالة‬ ‫في‬ ‫نعوض‬ :a(t) = k‫ونحسب‬t.‫ونعوضه‬
o‫المسافة‬ ‫تكون‬ : ‫االنطالق‬ ‫او‬ ‫البداية‬ ‫لنقطة‬ ‫عودته‬ ‫عند‬f(t) = 0.‫ونعوضه‬ ‫الزمن‬ ‫ونحسب‬
‫مثال‬6/‫لتكن‬+32
2t=f(t)‫وسرعته‬ ‫الجسم‬ ‫موقع‬ ‫جد‬ ‫باالمتار‬ ‫لحظة‬ ‫اي‬ ‫في‬ ‫جسم‬ ‫حركة‬ ‫تمثل‬‫بعد‬2.‫الحركة‬ ‫بدأ‬ ‫من‬ ‫ثانية‬
/‫الحل‬‫بعد‬ ‫الجسم‬ ‫موقع‬ ‫ان‬2‫االزاحة‬ ‫يعني‬ ‫ثانية‬f(t)‫مرور‬ ‫بعد‬2:‫الدالة‬ ‫من‬ ‫مباشرة‬ ‫ونحسبها‬ ‫ثانية‬
f(2) = 2(2)2
+ 3 = 8 + 3 = 11 m 2 ‫الثانية‬ ‫في‬ ‫الجسم‬ ‫موقع‬
‫بحساب‬ ‫نقوم‬ ‫فاننا‬ ‫ثانيتين‬ ‫مرور‬ ‫بعد‬ ‫الجسم‬ ‫سرعة‬ ‫لحساب‬ ‫واالن‬f̅( 𝟐) = 𝐯(𝟐):
v(2) = f̅(2) = lim
∆t→0
f(2+∆t)− f(2)
∆t
= lim
∆t→0
2(2+∆t)2 +3−( 2(2)2
+ 3 )
∆t
= lim
∆t→0
2(4 + 4∆t + ∆t2) +3−11
∆t
= lim
∆t→0
8 + 8∆t + 2∆t2− 8
∆t
= lim
∆t→0
8∆t + 2∆t2
∆t
= lim
∆t→0
∆t(8 + 2∆t)
∆t
= lim
∆t→0
(8 + 2∆t) = 8
m
sec
‫ثانيتين‬ ‫مرور‬ ‫بعد‬ ‫الجسم‬ ‫سرعة‬

46. ‫الفص‬ ‫أدبي‬ ‫سادس‬‫المشتقة‬ ‫الثالث‬ ‫ل‬
/‫الشمري‬ ‫أحمد‬ :‫األستاذ‬0770451693746‫المرسل‬‫الطباعية‬ ‫للخدمات‬/07703458937
‫مثال‬7/‫لتكن‬2
3t=v(t)‫لجسم‬ ‫السرعة‬ ‫دالة‬ ‫تمثل‬‫المتر‬ ‫بوحدات‬‫وال‬‫ثانية‬‫بعد‬ ‫التعجيل‬ ‫جد‬ ,2.‫ثانية‬
/‫الحل‬‫السرعة‬ ‫دالة‬ ‫مشتقة‬ ‫هو‬ ‫التعجيل‬:
a(2) = v̅(2) = lim
∆t→0
f(2+∆t)− f(2)
∆t
= lim
∆t→0
3(2+∆t)2 − 3(2)2
∆t
= lim
∆t→0
3(4 + 4∆t + ∆t2)−12
∆t
= lim
∆t→0
12 + 12∆t + 3∆t2 −12
∆t
= lim
∆t→0
12∆t + 3∆t2
∆t
= lim
∆t→0
∆t(12 + 3∆t)
∆t
= lim
∆t→0
(12 + 3∆t) = 12 + 3(0) = 12
m
sec2 ‫التعجيل‬
‫تمارين‬ ‫حلول‬1-3
1-‫الدالة‬ ‫مشتقة‬ ‫جد‬f(x) = x2
+ 5x‫احسب‬ ‫ثم‬ ‫التعريف‬ ‫باستخدام‬f̅(3)‫و‬f̅(0).
f̅(x) = lim
∆x→0
f(x+∆x)− f(x)
∆x
= lim
∆x→0
(x+∆x)2+ 5(x+∆x)− (x2+5x)
∆x
= lim
∆x→0
x2+ 2x∆x + ∆x2+ 5x + 5∆x−x2− 5x
∆x
= lim
∆x→0
2x∆x + ∆x2
+ 5∆x
∆x
= lim
∆x→0
∆x(2x +∆x + 5 )
∆x
= lim
∆x→0
(2x + ∆x + 5) = 2x + 0 + 5
f̅(x) = 2x + 5 ⟹ f̅(3) = 2(3) + 5 = 11 ⟹ f̅(0) = 2 . 0 + 5 = 5
2-‫المش‬ ‫جد‬‫يأتي‬ ‫مما‬ ‫لكل‬ ‫التعريف‬ ‫بطريقة‬ ‫تقة‬
a(f(x) =
3
x−1
b(f(x) = √x + 1
/‫الحل‬a(
f̅(x) = lim
∆x→0
f(x+∆x)− f(x)
∆x
f̅(x) = lim
∆x→0
3
𝑥+∆𝑥−1
−
3
𝑥−1
∆𝑥
= lim
∆x→0
3(x−1)− 3(x+∆x−1)
(x+∆x−1)(x−1)
∆x
= lim
∆x→0
3x−3− 3x− 3∆x+ 3
(x+∆x−1)(x−1)
∆x
= lim
∆x→0
−3∆x
(x+∆x−1)(x−1)
∆x
1
f̅(x) = lim
∆x→0
− 3 . ∆x
(x+∆x−1)(x−1)
.
1
∆x
f̅(x) = lim
∆x→0
−3
(x + ∆x − 1)(x − 1)
=
−3
(x − 1)(x − 1)
=
−3
(x − 1)2
b(
f̅(x) = lim
∆x→0
f(x+∆x)− f(x)
∆x
= lim
∆x→0
√x+∆x+1 − √x+1
∆x
= lim
∆x→0
√x+∆x+1− √x+1
∆x
.
√x+∆x+1 + √x+1
√x+∆x+1+√x+1
‫البسط‬ ‫بمرافق‬ ‫نضرب‬

47. ‫الفص‬ ‫أدبي‬ ‫سادس‬‫المشتقة‬ ‫الثالث‬ ‫ل‬
/‫الشمري‬ ‫أحمد‬ :‫األستاذ‬0770451693747‫المرسل‬‫الطباعية‬ ‫للخدمات‬/07703458937
= lim
∆x→0
(x+∆x+1)− (x+1)
∆x .(√x+∆x+1+ √x+1)
= lim
∆x→0
x + ∆x + 1 – x −1
∆x .(√x+∆x+1+ √x+1)
= lim
∆x→0
∆x
∆x .(√x+∆x+1+ √x+1)
= lim
∆x→0
1
√x+∆x+1+ √x+1
f̅(x) =
1
√x+0+1 + √x+1
=
1
√x+1 + √x+1
=
1
2√x+1
=
1
2√x+1
3-‫كانت‬ ‫اذا‬f(x) = x2
- 3x- 4‫جد‬f̅(x)‫عند‬ ‫الدالة‬ ‫لمنحني‬ ‫المماس‬ ‫معادلة‬ ‫جد‬ ‫ثم‬ ‫التعريف‬ ‫مستخدما‬x=1.
/‫الحل‬
f̅(x) = lim
∆x→0
f(x+∆x)− f(x)
∆x
‫القانون‬
= lim
∆x→0
(x+∆x)2−3(x+∆x)−4−(x2− 3x −4)
∆x
= lim
∆x→0
x2+2x∆x+∆x2−3x−3∆x−4 − x2 + 3x +4
∆x
= lim
∆x→0
2x∆x+∆x2−3∆x
∆x
= lim
∆x→0
∆x(2x+∆x−3)
∆x
‫مشترك‬ ‫عامل‬ ∆x
= lim
∆x→0
∆x(2x+∆x−3)
∆x
= lim
∆x→0
(2x + ∆x − 3) = 2x − 3
m = f̅(1) = 2 . 1 − 3 = -1 x =1 ‫عند‬ ‫المماس‬ ‫ميل‬
‫قيمة‬ ‫نحسب‬1y‫عندما‬1=1x‫الدالة‬ ‫من‬:
y1 = f(1) = 12
– 3(1) - 4 = -6
: ‫المستقيم‬ ‫معادلة‬)1x-m(x=1y–y
y − (−6) = −1(x − 1)
y + 6 = -x +1
y + x + 5 = 0 x=1 ‫عندما‬ ‫المماس‬ ‫معادلة‬
4-‫حيث‬ ‫العالقة‬ ‫وفق‬ ‫يتحرك‬ ‫جسم‬f‫بالدالة‬ ‫معطاة‬ ‫باالمتار‬ ‫االزاحة‬+ 2t +12
t=f(t)‫بعد‬ ‫الجسم‬ ‫سرعة‬ ‫جد‬ ,3‫ثواني‬
.‫الحركة‬ ‫بدأ‬ ‫من‬‫(وزاري‬2014‫دور‬1‫االشتقاق‬ ‫بقواعد‬ ‫يحل‬)
/‫الحل‬‫هي‬ ‫ثواني‬ ‫ثالث‬ ‫بعد‬ ‫السرعة‬f̅(3)
f̅(3) = lim
∆t→0
f(3+∆t)− f(3)
∆t
= lim
∆t→0
(3+∆t)2 + 2(3+∆t) +1−(32 + 2.3 +1)
∆t
= lim
∆t→0
32+ 2 .3 .∆t + ∆t2 + 6 + 2∆t +1−( 9 + 6 + 1)
∆t
= lim
∆t→0
𝟗 +6∆t + ∆t2 + 𝟔 + 2∆t +𝟏 − 16
∆t
= lim
∆t→0
6∆t + ∆t2 + 2∆t +16 − 16
∆t
f̅(3) = lim
∆t→0
8∆t + ∆t2
∆t
= lim
∆t→0
∆t(8 +∆t)
∆t
= lim
∆t→0
(8 + ∆t) = 8 + 0 = 8
‫متر‬
‫ثانية‬

48. ‫الفص‬ ‫أدبي‬ ‫سادس‬‫المشتقة‬ ‫الثالث‬ ‫ل‬
/‫الشمري‬ ‫أحمد‬ :‫األستاذ‬0770451693748‫المرسل‬‫الطباعية‬ ‫للخدمات‬/07703458937
5-‫بالعالقـة‬ ‫معطاة‬ ‫السرعة‬ ‫كانت‬ ‫اذا‬+ t + 12
t=v(t)‫عند‬ ‫التعجيل‬ ‫جد‬ , ‫م/ثا‬1=t.‫ثانية‬
/‫الحل‬‫عندما‬ ‫التعجيل‬t=1‫ثا‬‫يساوي‬ ‫نية‬v̅(1):
v̅(1) = lim
∆t→0
v(1+∆t)− v(1)
∆t
v̅(1) = lim
∆t→0
(1+∆t)2 + (1+∆t) +1−(12 + 1 +1 )
∆t
v̅(1) = lim
∆t→0
𝟏 + 2∆t + ∆t2 + 𝟏 + ∆t + 𝟏 − 𝟑
∆t
= lim
∆t→0
3∆t + ∆t2
∆t
v̅(1) = lim
∆t→0
3∆t + ∆t2
∆t
= lim
∆t→0
∆t(3 +∆t)
∆t
‫مشترك‬ ‫عامل‬ ∆t
= lim
∆t→0
(3 + ∆t) = 3 + 0 = 3
‫متر‬
‫ثانية‬
2 t = 1 sec ‫عند‬ ‫التعجيل‬

49. ‫قواعد‬ ‫الثالث‬ ‫الفصل‬ ‫أدبي‬ ‫سادس‬‫االشتقاق‬
/‫الشمري‬ ‫أحمد‬ :‫األستاذ‬0770451693749‫المرسل‬‫الطباعية‬ ‫للخدمات‬/07703458937
‫قواعد‬:‫االشتقاق‬‫باستخدام‬ ‫الدالة‬ ‫مشتقة‬ ‫ايجاد‬ ‫كيفية‬ ‫السابق‬ ‫الموضوع‬ ‫في‬ ‫تعلمنا‬‫كيفية‬ ‫سنتعلم‬ ‫واالن‬ ‫التعريف‬‫ايجاد‬
.‫القواعد‬ ‫باستخدام‬ ‫المشتقة‬
‫لتكن‬n
x=f(x):‫هي‬ ‫الدالة‬ ‫مشتقة‬ ‫فان‬
f̅( 𝐱) = 𝐧 . 𝐱 𝐧−𝟏
‫لتكن‬ /‫مثال‬3
x=f(x):‫الدالة‬ ‫مشتقة‬ ‫جد‬
f̅(x) = 3 . x3−1
= 3x2
‫لتكن‬ /‫مثال‬f(x) = x:‫الدالة‬ ‫مشتقة‬ ‫جد‬
f̅(x) = 1 . x1−1
= 1
‫لتكن‬ /‫مثال‬f(x) = √x23
:‫الدالة‬ ‫مشتقة‬ ‫جد‬
f (x) = √x23
= x
2
3
f̅(x) =
2
3
. x
2
3−1
=
2
3
. x
−1
3 =
2
3 √x3
:‫االشتقاق‬ ‫قوانين‬
1(:‫صفر‬ ‫تساوي‬ ‫الثابت‬ ‫مشتقة‬
/‫مثال‬‫لتكن‬f(x) = 12:‫الدالة‬ ‫مشتقة‬ ‫جد‬f̅(x) = 0
2(‫د‬ ‫في‬ ‫المضروب‬ ‫الثابت‬ ‫مشتقة‬‫الة‬:‫الدالة‬ ‫مشتقة‬ ‫في‬ ‫الثابت‬ ‫تساوي‬
/‫مثال‬‫لتكن‬3x2
=f(x):‫الدالة‬ ‫مشتقة‬ ‫جد‬fˊ
6x=3 . 2x2−1
=)x(
/‫مثال‬‫لتكن‬2x4
=f(x):‫الدالة‬ ‫مشتقة‬ ‫جد‬fˊ
8x3
=2 . 4x4−1
=)x(
3(‫مشتقة‬‫جمع‬:‫مشتقاتها‬ ‫طرح‬ ‫او‬ ‫جمع‬ ‫يساوي‬ ‫دالتين‬ ‫طرح‬ ‫او‬
/‫مثال‬‫لتكن‬x +1+x2
-3
x=f(x):‫الدالة‬ ‫مشتقة‬ ‫جد‬
f̅(x) = 3x3−1
− 2x2−1
+ 1x1−1
+ 0= 3x2
− 2x1
+ 1x0
= 3x2
− 2x + 1
/‫مثال‬‫لتكن‬3+x2
-3
2x=f(x):‫الدالة‬ ‫مشتقة‬ ‫جد‬
f̅(x) = 2(3x3−1
) − 2(x)2−1
+ 0 = 6x2
− 2x
4(‫مشتقة‬‫ال‬‫اال‬ ‫تساوي‬ ‫اس‬ ‫الى‬ ‫المرفوعة‬ ‫دالة‬‫واحد‬ ‫ناقص‬ ‫لالس‬ ‫مرفوعة‬ ‫بالدالة‬ ‫مضروب‬ ‫س‬:‫القوس‬ ‫داخل‬ ‫مشتقة‬ ‫في‬
/‫مثال‬‫لتكن‬f(x) = (x2
− 2)3
:‫الدالة‬ ‫مشتقة‬ ‫جد‬
f̅(x) = 3(x2
− 2)3−1
.(2x)= 6x(x2
− 2)2
/‫مثال‬‫لتكن‬f(x) = √x4 + 1
4
:‫الدالة‬ ‫مشتقة‬ ‫جد‬
f(x) = √x4 + 1
4
= (x4
+ 1)
1
4
f̅(x) =
1
4
(x4
+ 1)
1
4
−1
. (4x4−1
+ 0) =
1
4
(x4
+ 1)
−3
4 . (4x3
) =
4 x3
4 √(x4 + 1)34
f̅(x) =
x3
√(x4 + 1)34
5(‫االول‬ ‫في‬ ‫الثاني‬ ‫مشتقة‬ ‫زائدا‬ ‫الثاني‬ ‫في‬ ‫االول‬ ‫مشتقة‬ ‫تساوي‬ ‫دالتين‬ ‫ضرب‬ ‫حاصل‬ ‫مشتقة‬:
/‫مثال‬‫لتكن‬f(x) = (x2
-2)(x+3)‫م‬ ‫جد‬:‫الدالة‬ ‫شتقة‬
f̅(x) =(x2
- 2)(x1−1
+ 0) + (x+3)(2x2−1
- 0) =(x2
- 2)(1) + (x + 3)(2x)
f̅(x) =(x2
- 2) + (2x2
+ 6x) = x2
-2 + 2x2
+ 6x = 3x2
+ 6x – 2

50. ‫قواعد‬ ‫الثالث‬ ‫الفصل‬ ‫أدبي‬ ‫سادس‬‫االشتقاق‬
/‫الشمري‬ ‫أحمد‬ :‫األستاذ‬0770451693750‫المرسل‬‫الطباعية‬ ‫للخدمات‬/07703458937
6(‫يساوي‬ ‫دالتين‬ ‫قسمة‬ ‫مشتقة‬)‫تقسيم‬ (‫المقام‬ ‫مشتقة‬ ‫في‬ ‫البسط‬ ‫ناقص‬ ‫البسط‬ ‫مشتقة‬ ‫في‬ ‫المقام‬:‫المقام‬ ‫مربع‬
/‫مثال‬‫لتكن‬f(x) =
x2
x+3
:‫الدالة‬ ‫مشتقة‬ ‫جد‬
f̅(x) =
(x+3)(2x)− (x2) (1)
(x+3)2 =
2x2+6x− x2
x2+6x+9
=
x2+6x
x2+6x+9
‫مثال‬1/:‫يأتي‬ ‫مما‬ ‫كل‬ ‫مشتقة‬ ‫جد‬
a) f(x)= (x3
+ x2
+ x +1)5
f̅(x) = 5(x3
+ x2
+ x + 1)4
. (3x2
+ 2x + 1)
b) f(x)= √x2 − 2x + 1 ( ‫وزاري‬2012‫دور‬1 )
f(x) = (x2 − 2x + 1)
1
2
f̅(x) =
1
2
(x2
− 2x + 1)−
1
2 . (2x - 2) =
1
2
(x2 − 2x + 1)
−
1
2
. 2(x-1)
f̅(x) =
(x−1)
√x2−2x+1
=
(x−1)
√(x−1)(x−1)
=
(x−1)
√(x−1)2
=
(x−1)
ǀx−1ǀ
c) f(x) = (
x
x+1
)4
x=1 ‫عند‬ ‫المشتقة‬ ‫جد‬ ‫وزاري‬2012‫دور‬1( )
f̅(x) = 4(
x
x+1
)3
(
(x+1) .1−x(1+0)
(x+1)2 ) = 4(
x
x+1
)
3
(
x+1−x
(x+1)2)
f̅(x) = 4(
x
x+1
)3
(
1
(x+1)2) = 4
x3
(x+1)3 (
1
(x+1)2) =
4 x3
(x+1)5
f̅(1) =
4 . 13
(1+1)5 =
4
32
=
1
8
: ‫المشتقة‬ ‫مشتقة‬‫الى‬ ‫نحتاج‬ ‫التطبيقات‬ ‫بعض‬ ‫في‬ ‫ولكن‬ ‫للدالة‬ ‫االولى‬ ‫المشتقة‬ ‫مع‬ ‫نتعامل‬ ‫كنا‬ ‫السابقة‬ ‫االمثلة‬ ‫كل‬ ‫في‬
‫الثانية‬ ‫المشتقة‬)‫الثالثة‬ ‫او‬(‫الخ‬ ‫الرابعة‬ ‫او‬‫للدالة‬:‫التالية‬ ‫الرموز‬ ‫باحد‬ ‫لها‬ ‫ونرمز‬
d2y
dx2 ‫او‬ f̅̅ (x) ‫او‬ y̅̅
‫مثال‬3/‫كانت‬ ‫اذا‬3+3
+ 5x4
x=y‫جد‬y̅‫و‬y̅̅
y̅ = 4x3 + 15x2
⟹ y̅̅ = 3.4x2
+ 2.15x = 12x2
+ 30x
‫مثال‬4/‫كانت‬ ‫اذا‬f(x) = 2x3
+ 4 +
3
x
‫جد‬f̅(x)‫و‬f̅̅(x):
f̅ (x) = 6x2
+
−3
x2 ⟹ f̅̅ (x) = 12x +
6x
x4
‫تمارين‬ ‫حلول‬2-3
1-:‫ازائها‬ ‫المؤشر‬ ‫العدد‬ ‫عند‬ ‫التالية‬ ‫الدوال‬ ‫من‬ ‫كل‬ ‫مشتقة‬ ‫القواعد‬ ‫باستخدام‬ ‫جد‬
a) f(x)= x3
-4x2
+ x – 1 , x = 1
f̅(x) = 3x2
– 8x +1 ⟹ f̅(1) = 3. 12
– 8. 1 +1 = -4
b) f(x) = (4-x) (x2
+3) , x = 2 ‫وزاري‬(3201‫دور‬1‫و‬2201‫دور‬3‫و‬1201‫دور‬1)
f̅ (x) = (4-x) . 2x + (x2
+3) . (-1) = 8x - 2x2
- x2
- 3 = 8x -3x2
- 3
f̅ (2) = 8 . 2 - 3. 22
– 3 =16 – 12 - 3 =1

51. ‫قواعد‬ ‫الثالث‬ ‫الفصل‬ ‫أدبي‬ ‫سادس‬‫االشتقاق‬
/‫الشمري‬ ‫أحمد‬ :‫األستاذ‬0770451693751‫المرسل‬‫الطباعية‬ ‫للخدمات‬/07703458937
c) f(x) =
4−5x
x2+ x + 1
, x = -1
f̅ (x) =
(x2+x+1) . (−5) − (4−5x) . (2x+1)
(x2+ x + 1)2 =
−5x2−5x−5 − (8x−10x2+ 4−5x)
(x2+ x + 1)2
f̅ (x) =
−5x2−5x−5 − 8x+10x2− 4 + 5x
(x2+ x + 1)2
=
5x2 − 8x− 9
(x2+ x + 1)2 =
5(−1)2 − 8(−1)− 9
((−1)2+ (−1) + 1)2
f̅ (-1) =
5+ 8− 9
(1−1 + 1)2 =
4
(1)2 = 4
d) f(x) =
1
√2x+1
, x = 0
f(x) = (2x + 1)−
1
2 ⟹ f̅ (x) = −
1
2
(2x + 1)−
1
2
−1
. 2 = −(2x + 1)−
3
2
=
−1
√(2x+1)3
⟹ f̅ (0) =
−1
√(2 .0 +1)3
=
−1
√(1)3
= -1
e) f(x) = x +
3
x2 + 2
, x = -1 ‫(وزاري‬2013‫دور‬1)
f̅ (x) = 1 +
0−3(2x)
(x2 + 2)2 = 1 −
6x
(x2 + 2)2 = 1 −
6(−1)
((−1) 2 + 2)2
f̅ (-1) = 1 −
6(−1)
((−1)2 + 2)2 = 1 +
6
(1 + 2)2 = 1 +
6
9
= 1 +
2
3
=
5
3
2-‫كانت‬ ‫اذا‬f(x) = (x2
− 4)4
‫جد‬f̅(x)‫و‬f̅̅(x)‫عند‬x = 2.
/‫الحل‬‫ايجاد‬f̅(2):f(x) = (x2
− 4)4
f̅ (x) = 4(x2
− 4)3
. 2x = 8x(x2
− 4)3
f̅ (2)= 8 . 2 . (22
− 4)3
= 16 . (4 − 4)3
= 16 . (0)3
= 0
‫ايجاد‬f̅̅(2):
f̅ (x)= 8x (x2
− 4)3
f̅̅(x) = 8x . 3(x2
− 4)
2
. 2x + 8(x2
− 4)3
= 48x2 .(x2 − 4)
2
+ 8(x2
− 4)3
f̅̅(2) = 48(22
) . (22
− 4)
2
+ 8(22
− 4)3
= 48(4) .(0)2
+ 8(0)3
= 0
3-‫كانت‬ ‫اذا‬f(x) = (x3
+ 3x2
− 3)
3
2‫جد‬f̅(x)‫و‬f̅(2).
/‫الحل‬
f̅(x) =
3
2
(x3
+ 3x2
− 3)
3
2
−1
. (3x2
+6x) =
3
2
(x3
+ 3x2
− 3)
1
2 . (3x2
+6x)
f̅(x) =
3
2
√ x3 + 3x2 − 3 . (3x2
+6x)
f̅(2) =
3
2
√ 23
+ 3 . 22
− 3 .(3. 22
+6. 2)=
3
2
√8 + 12 − 3 . (3. 4 +12)
f̅(2) =
3
2
√17 . (24)= 36 √17

52. ‫أدبي‬ ‫سادس‬‫المشتقة‬ ‫قواعد‬ ‫تطبيقات‬ ‫الثالث‬ ‫الفصل‬
/‫الشمري‬ ‫أحمد‬ :‫األستاذ‬0770451693752‫المرسل‬‫الطباعية‬ ‫للخدمات‬/07703458937
‫الم‬ ‫قواعد‬ ‫باستخدام‬ ‫والفيزياوية‬ ‫الهندسية‬ ‫التطبيقات‬:‫شتقة‬
‫مثال‬1/‫الدالة‬ ‫لمنحني‬ ‫المماس‬ ‫معادلة‬ ‫جد‬f(x) = x2
-5x+2‫عند‬x= 1.(‫تمهيدي‬2014)
/‫الحل‬‫االحداثي‬ ‫تعريف‬y‫عند‬ ‫للنقطة‬x = 1
y1 = f(1) = 12
– 5(1) + 2 = -2 (1,-2 ) ‫النقطة‬ ∴
f̅(x) = 2x − 5 ⟹ f̅(1) = 2(1) − 5 = -3 = m x = 1 ‫ال‬ ‫ميل‬‫عند‬ ‫مماس‬
: ‫المستقيم‬ ‫معادلة‬)1x–m ( x=1y–y
y − (−2) = −3(x − 1) ⟹ y + 2 = -3x +3 ⟹ y +3x -1 = 0 ........‫المماس‬ ‫معادلة‬
‫مثال‬2/‫الدالة‬ ‫لمنحني‬ ‫المماس‬ ‫معادلة‬ ‫جد‬f(x) = √x + 3
3
‫عند‬x= 5.‫)وزاري‬2014‫دور‬2(
/‫الحل‬‫االحداثي‬ ‫تعريف‬y‫للن‬‫عند‬ ‫قطة‬x = 5
y1 = f(5) = √5 + 3
3
= √8
3
= 2 (2 , 5) ‫النقطة‬ ∴
f(x) = (x + 3)
1
3
f̅(x) =
1
3
(x + 3)
1
3
−1
(1) =
1
3
(x + 3)
−2
3 = 1
3 (x+3)
2
3
=
1
3 √(x+3)23
f̅(5) =
1
3 ( √5+3
3
)2
=
1
3 ( √8
3
)
2 =
1
3 (2 )2 =
1
3 .4
=
1
12
= m x = 5 ‫عند‬ ‫المماس‬ ‫ميل‬
: ‫المستقيم‬ ‫معادلة‬)1x–m ( x=1y–y
y − 2 =
1
12
(x − 5) ⟹ 12(y – 2) = (x -5) ⟹ 12y - 24 = x – 5
12y - x -19 = 0 ..............‫المماس‬ ‫معادلة‬
‫مثال‬3/‫المما‬ ‫معادلة‬ ‫جد‬‫الدالة‬ ‫لمنحني‬ ‫المماس‬ ‫على‬ ‫والعمود‬ ‫س‬f(x) =
2x+1
3−x
‫عند‬y= 5.‫)وزاري‬2013‫دور‬2(
/‫الحل‬‫االحداثي‬ ‫تعريف‬x‫عند‬ ‫للنقطة‬y = 5
y1 = f(x) =
2x+1
3−x
= 5
2x + 1 = 5(3 − x) ⟹ 2x + 1 = 15−5x ⟹ 2x + 5x = 15−1
7x = 14 ⇒ x =
14
7
= 2 (5 , 2) ‫النقطة‬ ∴
f̅(x) =
(3−x) .2−(2x+1)(−1)
(3−x)2 =
6−2x+2x+1
(3−x)2 =
7
(3−x)2
f̅(2) =
7
(3−2)2 =
7
1
= 7 = m x = 2 ‫عند‬ ‫المماس‬ ‫ميل‬
: ‫المستقيم‬ ‫معادلة‬)1x–m ( x=1y–y
y -5 = 7(x -2) ⟹ y - 5 = 7x - 14 ⟹ y - 7x + 9 = 0 ..............‫المماس‬ ‫معادلة‬
‫المماس‬ ‫على‬ ‫العمود‬ ‫ميل‬=
−1
7
=m
y − 5 =
−1
7
(x − 2) ⟹ 7(y - 5) = -1(x -2) ⟹ 7y - 35 = -x + 2
7y + x - 37 = 0 ........‫المماس‬ ‫على‬ ‫العمود‬ ‫معادلة‬
‫مثال‬4/‫الدالة‬ ‫لمنحني‬ ‫المماس‬ ‫معادلة‬ ‫جد‬f(x) = x2
+ 1‫ع‬.‫الصادات‬ ‫محور‬ ‫مع‬ ‫تقاطعه‬ ‫نقطة‬ ‫ند‬
‫محور‬ ‫او‬ ‫الصادات‬ ‫محور‬ ‫مع‬ ‫التقاطع‬ ‫نقطة‬ ‫في‬ /‫توضيح‬y‫فان‬x = 0‫قيمة‬ ‫ونحسب‬y‫المحور‬ ‫او‬ ‫السينات‬ ‫محور‬ ‫مع‬ ‫التقاطع‬ ‫نقطة‬ ‫في‬ ‫اما‬x‫فان‬
y = 0‫قيمة‬ ‫ونحسب‬‫قيم‬ ‫او‬x.
/‫الحل‬‫فان‬ ‫الصادات‬ ‫محور‬ ‫مع‬ ‫المنحني‬ ‫تقاطع‬ ‫نقطة‬ ‫في‬x = 0:

53. ‫أدبي‬ ‫سادس‬‫المشتقة‬ ‫قواعد‬ ‫تطبيقات‬ ‫الثالث‬ ‫الفصل‬
/‫الشمري‬ ‫أحمد‬ :‫األستاذ‬0770451693753‫المرسل‬‫الطباعية‬ ‫للخدمات‬/07703458937
y1 = f(0) = 02
+ 1 = 1
∴‫نقطة‬‫هي‬ ‫الصادات‬ ‫محور‬ ‫مع‬ ‫التقاطع‬)1,0(
f̅(x) = 2x ⟹ f̅(0) = 2 . 0 = 0 ‫افقي‬ ‫خط‬ ‫المماس‬
: ‫المستقيم‬ ‫معادلة‬)1x–m ( x=1y–y
y − 1 = 0 (x − 0) ⟹ y -1 = 0 ⟹ y = 1 .............. ‫المماس‬ ‫معادلة‬
‫مثال‬5/‫المنحني‬ ‫الى‬ ‫تنتمي‬ ‫نقطة‬ ‫جد‬4x + 5-x2
=f(x)‫والتي‬
‫معادلته‬ ‫الذي‬ ‫المستقيم‬ ‫يوازي‬ ‫المماس‬ ‫عندها‬y = - 3 - 2x
)2013‫دور‬1,2016‫دور‬2(
‫لتصبح‬ ‫بالصفر‬ ‫نساويها‬ ‫حيث‬ ‫المستقيم‬ ‫معادلة‬ ‫نرتب‬y + 2x +3 = 0
‫معامل‬x‫هو‬2‫ومعامل‬y‫هو‬1
/‫الحل‬‫يساو‬ ‫المستقيم‬ ‫ميل‬‫معامل‬ ‫سالب‬ ‫ي‬x‫معامل‬ ‫على‬ ‫مقسوم‬y:
m =
−(2)
1
= -2 ‫المعلوم‬ ‫المستقيم‬ ‫ميل‬
f̅(x) = 2x - 4 = -2 ‫المستقيم‬ ‫ميل‬=‫بالتوازي‬ ‫للمنحني‬ ‫المماس‬ ‫ميل‬
2x = 4-2= 2 ⟹ x = 1
y = f(1) = 12
– 4(1) + 5 = 1 -4 + 5 = 2 x = 1 ‫و‬ y = 2 ‫المطلوبة‬ ‫النقطة‬ ‫اذا‬
‫مثال‬6/‫الدالة‬ ‫كانت‬ ‫اذا‬f(x) = x2
+ ax + b‫عند‬ ‫للمنحني‬ ‫المماس‬ ‫ميل‬ ‫وكان‬x = -1‫هو‬4‫بالنقطة‬ ‫يمر‬ ‫المنحني‬ ‫وكان‬
)2,-3‫قيمة‬ ‫(جد‬a‫و‬b.‫)وزاري‬2012(‫اول‬ ‫دور‬
/‫الحل‬
f(x) = x2
+ax + b ⟹ f̅(x) = 2x + a
‫عند‬ ‫المماس‬ ‫ميل‬x = -1‫هو‬4:
f̅(−1) = 2(−1) + a = 4 ⟹ -2 + a = 4 ⟹ a = 6
) ‫النقطة‬2,-3(:‫للمنحني‬ ‫تنتمي‬
f(-3) = (-3)2
+6(-3) + b = 2 ⟹ 9 – 18 + b = 2 ⟹ b = 9 + 2 = 11
‫مثال‬7/‫العالقة‬ ‫وفق‬ ‫مستقيم‬ ‫خط‬ ‫على‬ ‫يتحرك‬ ‫جسم‬+ 4t + 12
+ 3t3
t=s(t)‫حيث‬s(t)‫والدقائق‬ ‫باالمتار‬ ‫تقاس‬
‫بعد‬ ‫وتعجيله‬ ‫وسرعته‬ ‫موضعه‬ ‫جد‬5.‫الحركة‬ ‫بدأ‬ ‫من‬ ‫دقائق‬
/‫الحل‬:‫الموقع‬ ‫لتحديد‬ ‫المعادلة‬ ‫في‬ ‫خمسة‬ ‫الرقم‬ ‫نعوض‬ ‫فاننا‬ ‫الدقائق‬ ‫تستخدم‬ ‫المعادلة‬ ‫ان‬ ‫بما‬
s(5) = 53
+ 3(5)2
+ 4(5) + 1= 125 + 75 + 20 + 1 = 221 ‫متر‬
‫السرع‬ ‫دالة‬‫ة‬v(t)‫االزاحة‬ ‫دالة‬ ‫مشتقة‬ ‫تساوي‬s(t):
v(t) = s̅(t) = 3t2
+ 6t + 4
v(5) = 3(5)2
+ 6(5) + 4 = 75 + 30 + 4 = 109
‫متر‬
‫دقيقة‬
‫التعجيل‬ ‫دالة‬a(t)‫السرعة‬ ‫دالة‬ ‫مشتقة‬ ‫تساوي‬v(t):
a(t) = v̅(t) = 6t + 6 ⟹ a(5) = 6(5) + 6 = 30 + 6 = 36
‫متر‬
‫دقيقة‬
2
‫مثال‬8/‫العالقة‬ ‫وفق‬ ‫مستقيم‬ ‫خط‬ ‫على‬ ‫جسم‬ ‫يتحرك‬20t + 120-2
t=s(t)‫بالساعة‬ ‫والزمن‬ ‫بالكيلومتر‬ ‫البعد‬ ‫يقاس‬ ‫حيث‬
:‫احسب‬
1(.‫ساعات‬ ‫خمس‬ ‫بعد‬ ‫السرعة‬
2(.‫صفرا‬ ‫سرعته‬ ‫تصبح‬ ‫عندما‬ ‫بعده‬
/‫الحل‬1(‫السرعة‬ ‫دالة‬v(t)‫االزاحة‬ ‫دالة‬ ‫مشتقة‬ ‫تساوي‬s(t):

54. ‫أدبي‬ ‫سادس‬‫المشتقة‬ ‫قواعد‬ ‫تطبيقات‬ ‫الثالث‬ ‫الفصل‬
/‫الشمري‬ ‫أحمد‬ :‫األستاذ‬0770451693754‫المرسل‬‫الطباعية‬ ‫للخدمات‬/07703458937
v(t) = s̅ (t) = 2t – 20 ⟹ v(5) = 2(5) - 20 = -10
‫كيلومتر‬
‫ساعة‬
2(‫قيمة‬ ‫نحسب‬ ‫صفر‬ ‫السرعة‬ ‫تكون‬ ‫عندما‬t:
v(t) = 2(t) - 20 = 0 ⟹ 2t = 20 ⟹ t = 10 ‫ساعة‬
‫السرعة‬ ‫عند‬ ‫الزمن‬ ‫نعوض‬0:‫البعد‬ ‫اليجاد‬ ‫االزاحة‬ ‫دالة‬ ‫في‬
s(10) = 102
– 20(10) + 120 = 100 – 200 + 120 = 20 ‫كيلومتر‬
‫مثال‬9/‫العالقة‬ ‫وفق‬ ‫مستقيم‬ ‫خط‬ ‫على‬ ‫جسم‬ ‫يتحرك‬s(t) = √2t + 1‫سرعته‬ ‫تصبح‬ ‫حتى‬ ‫يستغرقه‬ ‫الذي‬ ‫الزمن‬ ‫أوجد‬
1
3
.‫بالثانية‬ ‫متر‬‫)وزاري‬2013‫و‬ ‫تمهيدي‬2012‫دور‬1(
/‫الحل‬
s(t) = √2t + 1 = (2t + 1)
1
2
‫السرعة‬ ‫دالة‬v(t)‫االزاحة‬ ‫دالة‬ ‫مشتقة‬ ‫تساوي‬s(t):
v(t) =
1
√2t+1
:‫السرعة‬ ‫معادلة‬ ‫في‬ ‫نعوض‬ ‫الزمن‬ ‫ويطلب‬ ‫معلومة‬ ‫السرعة‬ ‫ان‬ ‫بما‬
v(t) =
1
√2t+1
=
1
3
⟹ √2t + 1 = 3 ‫الطرفين‬ ‫تربيع‬
2t + 1 = 9 ⟹ 2t = 8 ⟹ t = 4 ‫ثانية‬
‫مثال‬10/‫ال‬ ‫وفق‬ ‫معطاة‬ ‫بازاحة‬ ‫االرض‬ ‫سطح‬ ‫عن‬ ‫االعلى‬ ‫نحو‬ ‫جسم‬ ‫قذف‬‫عالقة‬2
t16–96t=s(t)‫ان‬ ‫حيث‬s(t)
‫و‬ ‫باالمتار‬ ‫االزاحة‬t:‫احسب‬ , ‫بالثواني‬
1(.‫ثانيتين‬ ‫بعد‬ ‫الجسم‬ ‫سرعة‬‫)وزاري‬2011(‫اول‬ ‫دور‬
2(.‫صفرا‬ ‫سرعته‬ ‫تصبح‬ ‫متى‬
/‫الحل‬
1(:‫االزاحة‬ ‫دالة‬ ‫مشتقة‬ ‫تساوي‬ ‫السرعة‬ ‫دالة‬
v(t) = s̅ (t) = 96 – 32 t
:‫ثانيتين‬ ‫بعد‬ ‫السرعة‬
v(2) = 96 – 32 (2) = 96 – 64 = 32
‫متر‬
‫ثا‬
2(:‫صفر‬ ‫السرعة‬ ‫عند‬ ‫الزمن‬ ‫نحسب‬ ‫السرعة‬ ‫دالة‬ ‫من‬
v(t) = 96 – 32 t = 0 ⟹ 96 – 32 t = 0 ⟹ 32t = 96 ⟹ t =
96
32
= 3 ‫ثانية‬
‫مثال‬11/‫العالقة‬ ‫وفق‬ ‫الجسم‬ ‫تحرك‬ ‫اذا‬+ 18t + 122
6t–3
t=s(t)‫حيث‬s(t)‫و‬ ‫باالمتار‬t‫بالثان‬ ‫الزمن‬, ‫ية‬
.‫صفرا‬ ‫تعجيله‬ ‫يصبح‬ ‫عندما‬ ‫وسرعته‬ ‫الحركة‬ ‫بداية‬ ‫نقطة‬ ‫عن‬ ‫الجسم‬ ‫بعد‬ ‫احسب‬‫(وزاري‬2015‫دور‬3)
/‫الحل‬:‫االزاحة‬ ‫لدالة‬ ‫الثانية‬ ‫المشتقة‬ ‫تساوي‬ ‫التعجيل‬ ‫دالة‬
v(t) = s̅ (t) = 3t2
– 12t + 18
a(t) = v̅ (t) = 6t – 12
:‫صفر‬ ‫يساوي‬ ‫التعجيل‬ ‫عندما‬ ‫الزمن‬‫ثانية‬2=t⟹12=6t⟹0=12–6t=a(t)
‫عند‬t=2:‫الجسم‬ ‫بعد‬ ‫نحسب‬ ‫لذلك‬ ‫صفر‬ ‫يساوي‬ ‫التعجيل‬ ‫فان‬
s(t) = 23
– 6(2)2
+ 18(2) + 12 = 8 – 24 + 36 + 12 = 32 ‫متر‬
‫عندما‬ ‫الجسم‬ ‫سرعة‬t = 2:‫السرعة‬ ‫معادلة‬ ‫من‬
v(t) = 3(2)2
– 12(2) + 18 = 12 – 24 + 18 = 6
‫متر‬
‫ثا‬

55. ‫أدبي‬ ‫سادس‬‫المشتقة‬ ‫قواعد‬ ‫تطبيقات‬ ‫الثالث‬ ‫الفصل‬
/‫الشمري‬ ‫أحمد‬ :‫األستاذ‬0770451693755‫المرسل‬‫الطباعية‬ ‫للخدمات‬/07703458937
‫تط‬ ‫بعض‬:‫االقتصاد‬ ‫في‬ ‫المشتقة‬ ‫بيقات‬
x‫االنتاج‬ ‫حجم‬ ‫يمثل‬
‫الكلفة‬ ‫دالة‬)‫الكلية‬‫االنتاج‬ ‫حجم‬ ‫بداللة‬ ‫تكون‬ (c(x)
‫الحدية‬ ‫الكلفة‬ ‫دالة‬MC=c̅(x)
‫دالة‬‫الكلفة‬ ‫معدل‬(‫)الكلية‬Ac=
(‫الكلفة)الكلية‬ ‫دالة‬
x
‫دالة‬‫الحدية‬ ‫الكلفة‬ ‫معدل‬
d
dx
(Ac)=‫الكلفة‬ ‫معدل‬ ‫دالة‬ ‫مشتقة‬
‫مثال‬12/‫ما‬ ‫سلعة‬ ‫النتاج‬ ‫الكلية‬ ‫الكلفة‬ ‫دالة‬ ‫ان‬ ‫لنفرض‬c(x) = 3x2
– 60x + 1200:‫جد‬
a(.‫الحدية‬ ‫الكلفة‬ ‫دالة‬
b(.‫الكلفة‬ ‫معدل‬ ‫دالة‬
c(.‫الحدية‬ ‫الكلفة‬ ‫معدل‬ ‫دالة‬
d(.‫االنتاج‬ ‫ذلك‬ ‫عند‬ ‫الكلية‬ ‫والكلفة‬ ‫كلفة‬ ‫معدل‬ ‫اقل‬ ‫يعطي‬ ‫الذي‬ ‫االنتاج‬ ‫حجم‬
/‫الحل‬
a(:‫الحدية‬ ‫الكلفة‬ ‫دالة‬06–6x=(x)c̅=MC
b(:‫الكلفة‬ ‫معدل‬ ‫دالة‬Ac =
c(x)
x
=
3x2 – 60x + 1200
x
Ac = 3x – 60 +
1200
x
c(:‫الحدية‬ ‫الكلفة‬ ‫معدل‬ ‫دالة‬
d
dx
(Ac) = 3 −
1200
x2
d(‫كلفة‬ ‫معدل‬ ‫اقل‬ ‫يعطي‬ ‫الذي‬ ‫االنتاج‬ ‫حجم‬‫و‬‫الكلية‬ ‫الكلفة‬‫عند‬‫االنتاج‬ ‫ذلك‬.
/‫مالحظة‬‫عندما‬ ‫كلفة‬ ‫معدل‬ ‫اقل‬
𝐝
𝐝𝐱
(𝐀𝐂)‫قيمة‬ ‫نحسب‬ ‫حيث‬ ‫صفر‬ ‫تساوي‬x‫االنتاج‬ ‫حجم‬ ‫دالة‬ ‫ونعوضها‬c(x):
d
dx
(Ac) = 3 -
1200
x2 = 0 ⟹
1200
x2 = 3 ⟹ 1200 = 3x2
x2
=
1200
3
= 400 ⟹ x = ±20 ⟹ x = 20 unit ‫كلفة‬ ‫معدل‬ ‫اقل‬ ‫عند‬ ‫االنتاج‬ ‫حجم‬
‫االنتاج‬ ‫لحجم‬ ‫الكلية‬ ‫الكلفة‬20‫دالة‬ ‫من‬c(x):
c(x) = 3(20)2
– 60(20) + 1200 = 1200 – 1200 + 1200 = 1200
‫تمارين‬ ‫حلول‬3-3
1-‫المنحني‬ ‫مماس‬ ‫معادلة‬ ‫جد‬5+9x+x2
3-3
x=f(x)‫عند‬0=x.
/‫الحل‬
f̅(x) = 3x2
− 6x + 9 ⟹ f̅(0) = 3(0)2
− 6(0) + 9 = 9 = m
y1 = f(0) = 03
- 3(0)2
+ 9(0) + 5 = 5 (0,5) ‫النقطة‬ ‫احداثيات‬
: ‫المستقيم‬ ‫معادلة‬)1x–m ( x=1y–y
y − 5 = 9(x − 0) ⟹ y - 5 = 9x
y - 9x – 5 = 0 x = 0 ‫النقطة‬ ‫عند‬ ‫المماس‬ ‫معادلة‬

56. ‫أدبي‬ ‫سادس‬‫المشتقة‬ ‫قواعد‬ ‫تطبيقات‬ ‫الثالث‬ ‫الفصل‬
/‫الشمري‬ ‫أحمد‬ :‫األستاذ‬0770451693756‫المرسل‬‫الطباعية‬ ‫للخدمات‬/07703458937
2-‫للمنحـــــني‬ ‫المماس‬ ‫على‬ ‫والعمود‬ ‫المماس‬ ‫معادلة‬ ‫جد‬3
3)-(x=y‫عند‬2=x.
f̅(x) = 3(x − 3)2
⟹ f̅(2) = 3(2 − 3)2
= 3 = m /‫الحل‬
y1 = f(2) = (2-3)3
= -1 ( 2,-1) ‫النقطة‬ ‫احداثيات‬
: ‫المستقيم‬ ‫معادلة‬)1x–m ( x=1y–y
y − (−1) = 3(x − 2) ⟹ y + 1 = 3x - 6
y - 3x + 7 = 0 x = 2 ‫النقطة‬ ‫عند‬ ‫المماس‬ ‫معادلة‬
‫المماس‬ ‫على‬ ‫العمود‬ ‫ميل‬=
−1
3
y − (−1) =
−1
3
(x − 2) ⟹ 3y + 3 = -x + 2 ⟹ 3y + x + 1 = 0
‫معادلة‬‫على‬ ‫العمود‬‫النقطة‬ ‫عند‬ ‫المماس‬x = 2
3-‫للمنحني‬ ‫المماس‬ ‫معادلة‬ ‫جد‬
3
x2+2
+2x–3
x=f(x)‫عند‬1-=x.‫)وزاري‬2012(‫اول‬ ‫دور‬
f̅(x) = 3x2
− 2 +
−3(2x)
(x2
+2)
2 = 3x2
− 2 −
6x
(x2
+2)
2 /‫الحل‬
f̅(−1) = 3(−1)2
− 2 −
6(−1)
((−1)2
+2)
2 = 3 − 2— 6(1 + 2)2
= 3 − 2 +
6
9
= 1 +
2
3
=
5
3
y1 = f(-1) = (-1)3
– 2(-1) +
3
(−1)2+2
= -1 + 2 +
3
1+2
= 2 (-1,2) ‫النقطة‬ ‫احداثيات‬
:‫معرفة‬ ‫نقطة‬ ‫عند‬ ‫الدالة‬ ‫لمنحني‬ ‫المماس‬ ‫معادلة‬
y − 2 =
5
3
(x − (−1)) ⟹ 3y - 6 = 5x + 5 ⟹ 3y - 5x – 11 = 0 ‫المماس‬ ‫معادلة‬
4-‫المنحني‬ ‫على‬ ‫النقط‬ ‫جد‬9x + 4-x2
3-3
x=f(x).‫السينات‬ ‫لمحور‬ ‫موازيا‬ ‫المماس‬ ‫عندها‬ ‫يكون‬ ‫بحيث‬
/‫الحل‬‫(وزاري‬2015‫دور‬1)
f̅(x) = 3x2
− 6x − 9
‫ا‬ ‫المستقيم‬‫صفر‬ ‫يساوي‬ ‫ميله‬ ‫السينات‬ ‫لمحور‬ ‫لموازي‬
3x2
− 6x − 9 = 0 ⟹ 3(x2
− 2x − 3) = 0 3‫مشترك‬ ‫عامل‬
x2
− 2x − 3 = 0 ⟹ (x + 1)(x - 3) = 0 ⟹ x = -1 , x = 3
f(-1) = (-1)3
-3(-1)2
- 9(-1) + 4 = -1 -3 + 9 + 4 = 9
f(3) = (3)3
-3(3)2
- 9(3) + 4 = 27 – 27 – 27 + 4 = -23
‫النقطتين‬ ‫عند‬)23-,3) ‫و‬ (1,9-.‫السينات‬ ‫محور‬ ‫يوازي‬ ‫المماس‬ (
5-‫المنحني‬ ‫على‬ ‫نقطة‬ ‫جد‬f(x) = x2
- 4x + 5‫المستقيم‬ ‫يوازي‬ ‫المنحني‬ ‫مماس‬ ‫يكون‬ ‫عندما‬2x – y = 0.
/‫الحل‬‫(وزاري‬2015‫دور‬2)
m =
−2
−1
= 2 ‫المستق‬ ‫معادلة‬ ‫من‬‫الميل‬ ‫نستخرج‬ ‫يم‬
f̅(x) = 2x − 4 ‫الدالة‬ ‫مشتقة‬ ‫من‬ ‫المماس‬ ‫ميل‬
2x – 4 = 2 ⟹ 2x = 6 ⟹ x =
6
2
= 3 ‫المماس‬ ‫ميل‬=‫بالتوازي‬ ‫المستقيم‬ ‫ميل‬
f(3) = 32
– 4 . 3 + 5 = 9 – 12 + 5 = 2 (3,2) ‫النقطة‬ ‫احداثيات‬ ∴

57. ‫أدبي‬ ‫سادس‬‫المشتقة‬ ‫قواعد‬ ‫تطبيقات‬ ‫الثالث‬ ‫الفصل‬
/‫الشمري‬ ‫أحمد‬ :‫األستاذ‬0770451693757‫المرسل‬‫الطباعية‬ ‫للخدمات‬/07703458937
6-‫مستقي‬ ‫خط‬ ‫على‬ ‫يتحرك‬ ‫جسم‬‫بالعالقة‬ ‫معطى‬ ‫بالثواني‬ ‫والزمن‬ ‫باالمتار‬ ‫بعده‬ ‫ان‬ ‫بحيث‬ ‫م‬s(t) = √2t2 + 18
‫السرعة‬ ‫تصبح‬ ‫عندما‬ ‫بعده‬ ‫احسب‬1.‫بالثانية‬ ‫متر‬(‫تمهيدي‬2014))‫تمهيدي‬2016(
s(t) = (2t2
+ 18)
1
2 /‫الحل‬
v(t) = sˊ(t) =
1
2
(2t2
+ 18)
−1
2 . 4t = 2t
√2t2
+18
‫السرعة‬ ‫عند‬ ‫الزمن‬ ‫نحسب‬v(t) = 1:
1 =
2t
√2t2+18
⟹ 2t = √2t2 + 18 ‫الطرفين‬ ‫تربيع‬
4t2
= 2t2
+ 18 ⟹ 2t2
= 18 ⟹ t2
= 9 ⟹ t = ± 3
t = 3 sec ‫موجبة‬ ‫قيمة‬ ‫الزمن‬
‫الزمن‬ ‫عند‬ ‫االزاحة‬3:‫ثانية‬
s(3) = √2(3)2 + 18 = √18 + 18 = √36 = 6‫متر‬
7-‫العالقة‬ ‫وفق‬ ‫جسم‬ ‫تحرك‬ ‫اذا‬+ 9t + 72
6t-3
t=s(t)‫ان‬ ‫حيث‬s, ‫باالمتار‬ ‫بعده‬t:‫احسب‬ ‫بالثواني‬ ‫الزمن‬
‫)وزاري‬2013(‫اول‬ ‫دور‬
a(.‫صفرا‬ ‫سرعته‬ ‫تصبح‬ ‫عندما‬ ‫الحركة‬ ‫بداية‬ ‫نقطة‬ ‫من‬ ‫الجسم‬ ‫بعد‬
b(.‫صفرا‬ ‫التعجيل‬ ‫يصبح‬ ‫عندما‬ ‫الحركة‬ ‫بداية‬ ‫نقطة‬ ‫من‬ ‫الجسم‬ ‫بعد‬
/‫الحل‬a(:‫صفر‬ ‫تساوي‬ ‫السرعة‬ ‫عندما‬ ‫الزمن‬ ‫نحسب‬
v(t) = sˊ(t) = 3t2
- 12t + 9
3t2
- 12t + 9 = 0 ⟹ 3(t2
- 4t + 3) = 0 ‫مشترك‬ ‫عامل‬ 3
t2
- 4t + 3 = 0 ⟹ (t -1)(t – 3) = 0 ⟹ t = 1 ‫ثانية‬ , t = 3 ‫ثانية‬
s(1) = 13
- 6 .12
+ 9. 1 + 7 = 1 - 6 + 9 + 7 = 11 ‫متر‬ t = 1 ‫عند‬ ‫البعد‬
s(3) = 33
- 6 .32
+ 9. 3 + 7 = 27 - 54 + 27 + 7 = 7 ‫متر‬ t = 3 ‫عند‬ ‫البعد‬
‫السرعة‬ ‫عند‬v = 0‫الحركة‬ ‫بداية‬ ‫نقطة‬ ‫عن‬ ‫يبعد‬ ‫الجسم‬ ‫فان‬11‫و‬ ‫متر‬7‫متر‬
b(‫التعجيل‬ ‫عندما‬ ‫الزمن‬ ‫نحسب‬=0:
a(t) = vˊ(t) = 6t – 12 = 0 ⟹ 6t – 12 = 0 ⟹ 6t = 12 ⟹ t = 2 ‫ثانية‬
s(2) = 23
- 6 .22
+ 9. 2 + 7 = 8 - 24 + 18 + 7 = 9 ‫متر‬
‫عند‬‫التعجيل‬a = 0‫الحركة‬ ‫بداية‬ ‫نقطة‬ ‫عن‬ ‫يبعد‬ ‫الجسم‬ ‫فان‬9‫متر‬
8-‫لصنع‬ ‫الكلية‬ ‫الكلفة‬ ‫ان‬ ‫لنفرض‬x‫هي‬ ‫ما‬ ‫سلعة‬ ‫وحدات‬ ‫من‬c(x) = 1500 + 30x +
20
x
‫يكون‬ ‫عندما‬ ‫الحدية‬ ‫الكلفة‬ ‫جد‬
‫المصنوعة‬ ‫الوحدات‬ ‫عدد‬50.
/‫الحل‬‫الحدية‬ ‫الكلفة‬MC:
MC = c̅(x) = 30 +
−20
x2 = 30 -
20
x2
‫يساوي‬ ‫االنتاج‬ ‫عندما‬ ‫الحدية‬ ‫الكلفة‬50:
c̅(50) = 30 -
20
502 = 30 -
20
2500
= 30 −
1
125
=
3750−1
125
=
30 .125−1
125
=
3749
125
9-‫الكلية‬ ‫الكلفة‬ ‫دالة‬ ‫لتكن‬c(x) =
1
2
x2
– 2x + 5.‫الكلية‬ ‫الكلفة‬ ‫معدل‬ ‫دالة‬ , ‫الحدية‬ ‫الكلفة‬ ‫دالة‬ ‫جد‬)‫وزاري‬2013(‫تمهيدي‬
/‫الحل‬‫الحدية‬ ‫الكلفة‬ ‫دالة‬MC:2–x=x)(c̅=MC‫(وزاري‬4201‫دور‬1)
‫الكلفة‬ ‫معدل‬ ‫دالة‬AC:=
1
2
x – 2 +
5
x
1
2
x2 – 2x + 5
x
=
c(x)
x
=AC

58. ‫الص‬ ‫او‬ ‫العظمى‬ ‫النهايات‬ ‫الثالث‬ ‫الفصل‬ ‫أدبي‬ ‫سادس‬‫غرى‬
/‫الشمري‬ ‫أحمد‬ :‫األستاذ‬0770451693758‫المرسل‬‫الطباعية‬ ‫للخدمات‬/07703458937
‫الع‬ ‫النهايات‬‫ظ‬‫والصغرى‬ ‫مى‬‫الحرجة‬ ‫والنقاط‬:
‫العظم‬ ‫النهايات‬‫ى‬:‫النقا‬ ‫هي‬‫ويكون‬ ‫الدالة‬ ‫لمنحني‬ ‫تنتمي‬ ‫التي‬ ‫ط‬
‫للنقاط‬ ‫المماس‬ ‫وميل‬ ‫صفر‬ ‫يساوي‬ (‫)المشتقة‬ ‫المماس‬ ‫ميل‬ ‫فيها‬
:‫مبين‬ ‫كما‬ ‫سالب‬ ‫والالحقة‬ ‫موجب‬ ‫السابقة‬
‫الصغرى‬ ‫النهايات‬:‫ويكون‬ ‫الدالة‬ ‫لمنحني‬ ‫تنتمي‬ ‫التي‬ ‫النقاط‬ ‫هي‬
‫المماس‬ ‫وميل‬ ‫صفر‬ ‫يساوي‬ (‫)المشتقة‬ ‫المماس‬ ‫ميل‬ ‫فيها‬
‫و‬ ‫سالب‬ ‫السابقة‬ ‫للنقاط‬:‫مبين‬ ‫كما‬ ‫موجب‬ ‫الالحقة‬
: ‫الحرجة‬ ‫النقاط‬‫المنحني‬ ‫ميل‬ ‫فيها‬ ‫يتحول‬ ‫التي‬ ‫النقاط‬ ‫هي‬
.‫بالعكس‬ ‫او‬ ‫موجب‬ ‫الى‬ ‫سالب‬ ‫من‬
‫طريقة‬/‫الحل‬
1-.‫المنحني‬ ‫لدالة‬ ‫المشتقة‬ ‫ايجاد‬
2-‫قيم‬ ‫وحساب‬ ‫بالصفر‬ ‫المشتقة‬ ‫مساواة‬x
3-‫قيم‬ ‫نعوض‬x‫الدالة‬ ‫في‬f(x)‫لنحسب‬y.‫الحرجة‬ ‫النقاط‬ ‫لتحديد‬
4-‫اشارة‬ ‫تحديد‬(x)f̅.‫الحرجة‬ ‫النقاط‬ ‫وبعد‬ ‫قبل‬
5-.‫التناقص‬ ‫ومناطق‬ ‫التزايد‬ ‫مناطق‬ ‫تعريف‬
‫مثال‬1/:‫التالية‬ ‫للدوال‬ ‫التناقص‬ ‫ومناطق‬ ‫التزايد‬ ‫ومناطق‬ ‫الحرجة‬ ‫النقاط‬ ‫جد‬
a)f(x) = x2
– 4x + 3
f̅ (x) = 2x – 4 ⟹ 2x – 4 = 0 ‫الميل‬ ‫الحرجة‬ ‫النقاط‬ ‫عند‬=0
2x = 4 ⟹ x = 2
f(2) = 22
– 4. 2 + 3 = -1
) ‫حرجة‬ ‫نقطة‬1-,2(
:‫الفترة‬ ‫في‬ ‫متزايدة‬ ‫الدالة‬R , x >2}{x:x ∈
:‫الفترة‬ ‫في‬ ‫متناقصة‬ ‫الدالة‬R , x < 2}{x:x ∈
b) f(x) = x3
– 3x + 2
f̅ (x) = 3x2
– 3 ⟹ 3x2
– 3 = 0 ⟹ 3x2
= 3 ⟹ x2
= 1 ⟹ x = ±1
f(1) = 13
– 3 + 2 = 0
f(-1) = (-1)3
– 3(-1) + 2 = 4
) ‫الحرجة‬ ‫النقاط‬1,0) ‫و‬ (-1,4.(
:‫الفترتين‬ ‫في‬ ‫متزايدة‬ ‫الدالة‬
{x:x ∈ R , x < -1}
{x:x ∈ R , x > 1}
) ‫المفتوحة‬ ‫الفترة‬ ‫في‬ ‫متناقصة‬ ‫الدالة‬-1,1.(
c) f(x) = (2 – x)3
f̅ (x) = 3(2 – x)2
. (-1) = -3(2 - x)2
-3(2 - x)2
= 0 ⟹ (2 - x)2
= 0 ‫الطرفين‬ ‫جذر‬
2 - x = 0 ⟹ x = 2
f(2) = (2 – 2)3
= 0
2
---------- + + + + + + +
f̅(0) = 2(0) – 4 = - 4 f̅(3) = 2(3) – 4 = +2
‫اشارة‬(x)f̅
-------- + + + +
-1 1
+ + + +
‫اشارة‬f̅ (x)

59. ‫الص‬ ‫او‬ ‫العظمى‬ ‫النهايات‬ ‫الثالث‬ ‫الفصل‬ ‫أدبي‬ ‫سادس‬‫غرى‬
/‫الشمري‬ ‫أحمد‬ :‫األستاذ‬0770451693759‫المرسل‬‫الطباعية‬ ‫للخدمات‬/07703458937
) ‫الحرجة‬ ‫النقطة‬2,0(
:‫الفترتين‬ ‫في‬ ‫متناقصة‬ ‫الدالة‬
{x:x ∈R , x < 2}
{x:x ∈ R , x > 2}
) ‫النقطة‬0,2‫نهاية‬ ‫وليست‬ ‫حرجة‬ (
‫مثال‬2/‫كان‬ ‫اذا‬9x + 7–x2
3–3
x=f(x).‫وجدت‬ ‫ان‬ ‫والصغرى‬ ‫العظمى‬ ‫النهايات‬ ‫نقاط‬ ‫جد‬
/‫الحل‬
f̅ (x) = 6–x2
3 x – 9 ⟹ 6–x2
3 x – 9 = 0 ÷ 3
x2
– 2x – 3 = 0 ⟹ (x + 1)(x - 3) = 0 ⟹ x = -1 , x = 3
f(-1) = (-1)3
– 3(-1)2
– 9(-1) + 7 = -1 – 3 + 9 + 7 = 12
f(3) = (3)3
– 3(3)2
– 9(3) + 7 = 27 – 27 - 27 + 7 = -20
) : ‫الحرجة‬ ‫النقاط‬12,1-) ‫و‬ (20-,3(
‫ا‬ ‫في‬ ‫متزايدة‬ ‫الدالة‬:‫لفترتين‬
{x:x ∈ R , x < -1}
{x:x ∈ R , x > 3}
( ‫المفتوحة‬ ‫الفترة‬ ‫في‬ ‫متناقصة‬ ‫الدالة‬-1,3)
( ‫محلية‬ ‫عظمى‬ ‫نهاية‬ ‫نقطة‬12,-1)
( ‫محلية‬ ‫صغرى‬ ‫نهاية‬ ‫نقطة‬-20,3)
‫مثال‬3/‫كان‬ ‫اذا‬1+x2
2–4
x=f(x).‫وجدت‬ ‫ان‬ ‫والصغرى‬ ‫العظمى‬ ‫النهايات‬ ‫نقاط‬ ‫جد‬)2016‫دور‬2(
f̅ (x) = 4x3
– 4x ⟹ 4x3
– 4x = 0 ⟹ 4x(x2
– 1) = 0 4x ‫مشترك‬ ‫عامل‬
x(x2
– 1) = 0 ⟹ x (x – 1) (x + 1) = 0 ⟹ x = 0 , x = 1 , x = -1
) : ‫الحرجة‬ ‫النقاط‬1,0) ‫و‬ (0,1-) ‫و‬ (0,1(
f(0) = (0)4
– 2(0)2
+ 1 = 1
f(-1) = (-1)4
– 2(-1)2
+ 1 = 1 – 2 + 1 = 0
f(1) = (1)4
– 2(1)2
+ 1 = 1 – 2 + 1 = 0
‫الفترة‬ ‫في‬ ‫متزايدة‬ ‫الدالة‬R , x > 1}{x:x ∈( ‫المفتوحة‬ ‫الفترة‬ ‫وفي‬-1 , 0.)
‫الفترة‬ ‫في‬ ‫متناقصة‬ ‫الدالة‬R , x < -1}{x:x ∈‫المفتوح‬ ‫الفترة‬ ‫وفي‬( ‫ة‬0,1.)
( ‫محلية‬ ‫عظمى‬ ‫نهاية‬ ‫نقطة‬1,0)
( ‫محلية‬ ‫صغرى‬ ‫نهاية‬ ‫نقطة‬0,-1( ‫و‬ )0,1)
‫مثال‬4/‫لتكن‬4+x)-(3
x=f(x).‫وجدت‬ ‫ان‬ ‫والصغرى‬ ‫العظمى‬ ‫النهايات‬ ‫نقاط‬ ‫جد‬
f(x) = x3
(-4+x) = -4x3
+ x4
= x4
- 4x3
/‫الحل‬
f̅ (x) = 4x3
– 12x2
⟹ 4x3
– 12x2
= 0 ⟹ 4x2
(x – 3) = 0 ‫مشترك‬ ‫4عامل‬x2
x2
(x – 3) = 0 ⟹ x = 0 , x = 3
f(0) = 04
– 4(0)3
= 0
f(3) = 34
– 4(3)3
= 81 – 108 = -27
‫الحرج‬ ‫النقاط‬) : ‫ة‬0,0) ‫و‬ (72-,3(
:‫الفترة‬ ‫في‬ ‫متزايدة‬ ‫الدالة‬R , x > 3}{x:x ∈
‫الفترة‬ ‫في‬ ‫متناقصة‬ ‫الدالة‬:R , x < 0}{x:x ∈
( ‫المفتوحة‬ ‫والفترة‬0,3)
( ‫نهاية‬ ‫وليست‬ ‫حرجة‬ ‫نقطة‬0,0)
( ‫محلية‬ ‫صغرى‬ ‫نهاية‬ ‫نقطة‬-27,3)
‫ع‬ ‫نهاية‬ ‫نقطة‬ ‫تملك‬ ‫ال‬ ‫الدالة‬.‫ظمى‬
2
---------- ----------
‫اشارة‬f̅ (x)
-1 10
----- + + + ++ + + + -----
‫اشارة‬f̅ (x)
-------- + + + +
0 3
------
‫اشارة‬(x)f̅
-------- + + + +
-1 3
+ + + +
‫اشارة‬f̅ (x)

60. ‫الص‬ ‫او‬ ‫العظمى‬ ‫النهايات‬ ‫الثالث‬ ‫الفصل‬ ‫أدبي‬ ‫سادس‬‫غرى‬
/‫الشمري‬ ‫أحمد‬ :‫األستاذ‬0770451693760‫المرسل‬‫الطباعية‬ ‫للخدمات‬/07703458937
‫مثال‬5/‫كانت‬ ‫اذا‬+ ax + 53
x=f(x)‫عند‬ ‫محلية‬ ‫نهاية‬ ‫نقطة‬ ‫لها‬1=x‫قيمة‬ ‫جد‬a.‫النهاية‬ ‫نوع‬ ‫وبين‬
/‫الحل‬‫ان‬ ‫بما‬‫ل‬‫عند‬ ‫نهاية‬ ‫لدالة‬x = 1‫الميل‬ ‫فان‬‫يساوي‬0.
f̅ (x) = 3x2
+ a ⟹ f̅ (1) = 3.12
+ a = 3 + a = 0 ⟹ 3 + a = 0 ⟹ a = -3
:‫هي‬ ‫الدالة‬ ‫اذا‬3x + 5-3
x=f(x)
f̅ (x) = 3x2
– 3 ⟹ 3x2
– 3 = 0 ⟹ 3(x2
-1) = 0 3‫مشترك‬ ‫عامل‬
(x2
-1) = 0 ⟹ (x - 1) (x + 1) = 0 ⟹ x = 1 , x = -1
f(1)= 13
-3 . 1 + 5 = 3
f(-1)= (-1)3
- 3 . (-1) + 5 = -1 + 3 + 5 = 7
) :‫الحرجة‬ ‫النقاط‬1,3) ‫و‬ (-1,7(
‫الفتر‬ ‫في‬ ‫متزايدة‬ ‫الدالة‬‫تين‬:R , x < -1}{x:x ∈
‫و‬R , x > 1}{x:x ∈
) ‫المفتوحة‬ ‫الفترة‬ ‫في‬ ‫متناقصة‬ ‫الدالة‬-1,1(
) ‫محلية‬ ‫عظمى‬ ‫نهاية‬ ‫نقطة‬-1,7(
) ‫محلية‬ ‫صغرى‬ ‫نهاية‬ ‫نقطة‬1,3(
‫عند‬ ‫اذا‬1=x.‫محلية‬ ‫صغرى‬ ‫نهاية‬ ‫تكون‬
‫مثال‬6/‫كانت‬ ‫اذا‬+ bx3
ax=f(x)) ‫النقطة‬ ‫عند‬ ‫محلية‬ ‫نهاية‬ ‫تمتلك‬2-,1‫من‬ ‫كل‬ ‫قيمة‬ ‫فما‬ (R∈a , b‫هذه‬ ‫نوع‬ ‫وما‬
.‫النهاية‬
/‫الحل‬) ‫عند‬ ‫نهاية‬ ‫نقطة‬ ‫تملك‬ ‫الدالة‬ ‫ان‬ ‫السؤال‬ ‫في‬ ‫ذكر‬1,-2‫لذلك‬ (f(1) = -2:
f(1) = a. 13
+ b.1 = -2 ⟹ a + b = -2 ………………. 
‫عند‬ ‫نهاية‬ ‫تملك‬ ‫الدالة‬ ‫ان‬ ‫بما‬x = 1‫الميل‬ ‫فان‬=:‫صفر‬
f̅ (x) = 3ax2
+ b ⟹ f̅ (1) = 3a.12
+ b = 3a + b = 0 ⟹ 3a + b = 0 ………
‫المعادلة‬ ‫نطرح‬‫المعادلة‬ ‫من‬:
3a + b = 0
a + b = -2
2a + 0 = 2 ‫بالطرح‬
2a = 2 ⟹ a = 1
‫قيمة‬ ‫نعوض‬a‫معادلة‬ ‫في‬‫على‬ ‫لنحصل‬b:
a + b = -2 ⟹ 1 + b = -2 ⟹ b = -3
:‫هي‬ ‫الدالة‬ ‫اذا‬3x-3
x=f(x)
f̅ (x) = 3x2
- 3 ⟹ 3x2
– 3 = 0 ‫المشتقة‬ ‫النهايات‬ ‫عند‬=0
3(x2
-1) = 0 3‫مشترك‬ ‫عامل‬
(x - 1) (x + 1) = 0 ⟹ x = 1 , x = -1
f(1)= 13
-3 . 1 = -2
f(-1)= (-1)3
- 3 . (-1) = -1 + 3 = 2
) :‫الحرجة‬ ‫النقاط‬3-,1) ‫و‬ (1,2-(
:‫الفترتين‬ ‫في‬ ‫متزايدة‬ ‫الدالة‬R , x < -1}{x:x ∈
R , x > 1}{x:x ∈
‫الفترة‬ ‫في‬ ‫متناقصة‬ ‫الدالة‬R , -1 < x < 1}{x:x ∈
( ‫محلية‬ ‫عظمى‬ ‫نهاية‬ ‫نقطة‬-1,2)
( ‫محلية‬ ‫صغرى‬ ‫نهاية‬ ‫نقطة‬1,-2)
( ‫النقطة‬ ‫عند‬ ‫اذا‬1,-2.‫محلية‬ ‫صغرى‬ ‫نهاية‬ ‫تكون‬ )
-------- + + + +
-1 1
+ + + +
‫اشارة‬(x)f̅
-------- + + ++
-1 1
+ + + +
‫اشارة‬(x)f̅

61. ‫الص‬ ‫او‬ ‫العظمى‬ ‫النهايات‬ ‫الثالث‬ ‫الفصل‬ ‫أدبي‬ ‫سادس‬‫غرى‬
/‫الشمري‬ ‫أحمد‬ :‫األستاذ‬0770451693761‫المرسل‬‫الطباعية‬ ‫للخدمات‬/07703458937
‫تمارين‬ ‫حلول‬4-3
1)‫المحلي‬ ‫الصغرى‬ ‫او‬ ‫العظمى‬ ‫النهايات‬ ‫نقاط‬ ‫جد‬:‫التالية‬ ‫الدوال‬ ‫من‬ ‫ة‬
a) f(x) = x4
-1
f̅ (x) = 4x3
⟹ 4x3
= 0 ⟹ x = 0
f(0) = 04
-1 = -1
) : ‫الحرجة‬ ‫النقاط‬1-,0(
:‫الفترة‬ ‫في‬ ‫متزايدة‬ ‫الدالة‬R , x > 0}{x:x ∈
‫الفترة‬ ‫في‬ ‫متناقصة‬ ‫الدالة‬:R , x < 0}{x:x ∈
‫صغر‬ ‫نهاية‬ ‫نقطة‬( ‫محلية‬ ‫ى‬-1,0)
b) f(x) = x3
f̅ (x) = 3x2
⟹ 3x2
= 0 ⟹ x = 0
f(0) = 03
= 0
) : ‫الحرجة‬ ‫النقاط‬0,0(
‫الفتر‬ ‫في‬ ‫متزايدة‬ ‫الدالة‬‫تين‬:
R , x > 0}{x:x ∈
R , x < 0}{x:x ∈
(0,0‫حرجة‬ ‫نقطة‬ )‫نهاية‬ ‫وليست‬
c) f(x) =(x-1)3
f̅ (x) =3(x-1)2
⟹ 3(x-1)2
= 0 ⟹ (x-1)2
= 0 ⟹ x-1 = 0 ⟹ x = 1
f(1) = (1-1)3
= 0
) : ‫الحرجة‬ ‫النقاط‬0,1(
‫الفتر‬ ‫في‬ ‫متزايدة‬ ‫الدالة‬‫تين‬:R , x > 1}{x:x ∈
R , x < 1}{x:x ∈
)0,1(‫نهاية‬ ‫وليست‬ ‫حرجة‬ ‫نقطة‬
d) f(x) = x3
– 9x2
+ 24x(‫اول‬ ‫دور‬ 2011 ‫)وزاري‬
f̅ (x) = 0=6x + 8–x2
⟹0=18x + 24–x2
3⟹18x + 24–x2
3‫على‬ ‫بالقسمة‬3
(x-4)(x-2) = 0 ⟹ x = 4 , x = 2
f(4) = (4)3
– 9(4)2
+ 24(4) = 64 – 144 + 96 = 16
f(2) = (2)3
– 9(2)2
+ 24(2) = 8 – 36 + 48 = 20
) : ‫الحرجة‬ ‫النقاط‬20,2) ‫و‬ (16,4(
:‫الفترتين‬ ‫في‬ ‫متزايدة‬ ‫الدالة‬
R , x < 2}{x:x ∈
R , x > 4}{x:x ∈
( ‫المفتوحة‬ ‫الفترة‬ ‫في‬ ‫متناقصة‬ ‫الدالة‬2,4)
( ‫محلية‬ ‫عظمى‬ ‫نهاية‬ ‫نقطة‬20,2)
( ‫محلية‬ ‫صغرى‬ ‫نهاية‬ ‫نقطة‬16,4)
1
+ + + + + + + + + + + + + +
‫اشارة‬f̅(x)
0
---------- + + + + + + +
‫اشارة‬f̅ (x)
‫اشارة‬f̅(𝒙)0
+ + + + + + + + + + + + + +
-------- + + + +
2 4
+ + + +
‫اشارة‬f̅(𝒙)

62. ‫الص‬ ‫او‬ ‫العظمى‬ ‫النهايات‬ ‫الثالث‬ ‫الفصل‬ ‫أدبي‬ ‫سادس‬‫غرى‬
/‫الشمري‬ ‫أحمد‬ :‫األستاذ‬0770451693762‫المرسل‬‫الطباعية‬ ‫للخدمات‬/07703458937
e) f(x) = x4
– 2x2
- 3
f̅ (x) = 4x3
– 4x ⟹ 4x3
– 4x = 0 ⟹ 4x(x2
– 1) =0 ‫مشترك‬ ‫عامل‬ 4x
x(x–1)(x+1) =0 ⟹ x = 0 , x = 1 , x = -1
f(0) = 04
– 2(0)2
- 3 = -3
f(1) = 14
– 2(1)2
- 3 = -4
f(-1) = (-1)4
– 2(-1)2
- 3 = -4
) : ‫الحرجة‬ ‫النقاط‬3-,0) ‫و‬ (4-,1) ‫و‬ (4-,1-(
‫الفترة‬ ‫في‬ ‫متزايدة‬ ‫الدالة‬R , x > 1}{x:x ∈
‫المفتوحة‬ ‫الفترة‬ ‫في‬ ‫وكذلك‬(-1 , 0.)
‫الفترة‬ ‫في‬ ‫متناقصة‬ ‫الدالة‬R , x < -1}{x:x ∈
‫المفتوحة‬ ‫الفترة‬ ‫في‬ ‫وكذلك‬(0,1.)
( ‫محلية‬ ‫عظمى‬ ‫نهاية‬ ‫نقطة‬-3,0)
( ‫محلية‬ ‫صغرى‬ ‫نهاية‬ ‫نقطة‬-4,-1( ‫و‬ )-4,1)
f) f(x) = 5 + 4x3
– x4
f̅ (x) = 12x2
– 4x3
⟹ 12x2
– 4x3
= 0 ⟹ 4x2
(3 – x) =0 ‫مشترك‬ ‫عامل‬ 4x2
4x2
= 0 ⟹ x = 0 ⟹ f(0) = 5 + 4(0)3
– 04
= 5
3 - x =0 ⟹ x = 3 ⟹ f(3) = 5 + 4(3)3
– 34
= 5 + 108 - 81=32
) : ‫الحرجة‬ ‫النقاط‬5,0) ‫و‬ (32,3(
:‫الفترة‬ ‫في‬ ‫متزايدة‬ ‫الدالة‬R , x < 0}{x:x ∈
( ‫المفتوحة‬ ‫الفترة‬ ‫في‬ ‫وكذلك‬3,0)
‫الفترة‬ ‫في‬ ‫متناقصة‬ ‫الدالة‬R , x > 3}{x:x ∈
( ‫محلية‬ ‫عظمى‬ ‫نهاية‬ ‫نقطة‬32,3)
( ‫في‬ ‫حرجة‬ ‫نقطة‬5,0)
g) f(x) = 3x4
+ 4x3
f̅ (x) = 12x3
+ 12x2
⟹ 12x3
+ 12x2
= 0 ⟹ 12x2
(x + 1) =0 ‫مشترك‬ ‫عامل‬ 12x2
x = 0 , x = -1
f(0) = 3(0)4
+ 4(0)3
= 0
f(-1) = 3(-1)4
+ 4(-1)3
= -1
) : ‫الحرجة‬ ‫النقاط‬0,0) ‫و‬ (1-,1-(
‫الفترة‬ ‫في‬ ‫متناقصة‬ ‫الدالة‬R , x < -1}{x:x ∈
‫الفترة‬ ‫في‬ ‫متزايدة‬ ‫الدالة‬R , x > 0}{x:x ∈
‫المفتوحة‬ ‫الفترة‬ ‫في‬ ‫وكذلك‬(-1 , 0.)
( ‫محلية‬ ‫صغرى‬ ‫نهاية‬ ‫نقطة‬-1,-1)
( ‫حرجة‬ ‫نقطة‬0,0)
2)) ‫النقطة‬ ‫ان‬ ‫علمت‬ ‫اذا‬2,1‫للدالة‬ ‫المحلية‬ ‫الصغرى‬ ‫النهاية‬ ‫نقطة‬ ‫هي‬ (2
b)-a + (x=f(x)‫قيمة‬ ‫فجد‬∈ Ra , b.
‫)وزاري‬2013‫دور‬2((‫تمهيدي‬2015)‫)وزاري‬2016‫دور‬1(2016-3
/‫الحل‬‫عند‬) ‫النقطة‬2,1‫اذا‬ ‫صغرى‬ ‫نهاية‬ (f̅(2) = 0
f̅ (x) = 2(x - b) ⟹ f̅ (2) = 2(2 - b) = 0 ⟹ 2(2 - b) = 0 ⟹ 2 - b = 0 ⟹ b = 2
) ‫النقطة‬2,1‫الدالة‬ ‫لمنحني‬ ‫تنتمي‬ (‫ان‬ ‫اي‬f(2) = 1:
f(2) = a + (2 - 2)2
= 1 ⟹ a + 0 = 1 ⟹ a = 1
‫قيمة‬ ‫ايجاد‬ ‫هو‬ ‫المطلوب‬ ‫كون‬ ‫والتناقص‬ ‫التزايد‬ ‫مناطق‬ ‫اليجاد‬ ‫داعي‬ ‫ال‬ /‫مالحظة‬a‫و‬b.‫فقط‬
+ + + + + ------
0 3
+ + + +
‫اشارة‬f̅(𝒙)
-1 10
----- + + + ++ + + + -----
‫اشارة‬f̅(𝒙)
+ + + ++ + + + +
-1 0
------
‫اشارة‬f̅(𝒙)

63. ‫الص‬ ‫او‬ ‫العظمى‬ ‫النهايات‬ ‫الثالث‬ ‫الفصل‬ ‫أدبي‬ ‫سادس‬‫غرى‬
/‫الشمري‬ ‫أحمد‬ :‫األستاذ‬0770451693763‫المرسل‬‫الطباعية‬ ‫للخدمات‬/07703458937
3)) ‫النقطة‬ ‫كانت‬ ‫اذا‬1,4‫للدالة‬ ‫حرجة‬ ‫نقطة‬ (f(x) = 3 + ax + bx2
‫قيمة‬ ‫فما‬a , b ∈ R‫الحرجة؟‬ ‫النقطة‬ ‫نوع‬ ‫وما‬
‫)وزاري‬2012‫دور‬2(‫)وزاري‬2014‫دور‬1(‫)تمهيدي‬2016(
/‫الحل‬) ‫النقطة‬1,4‫اذا‬ ‫حرجة‬ (f̅(1)‫صفر‬ ‫تساوي‬
f̅ (x) = a + 2bx ⟹ f̅ (1) = a + 2b = 0 ⟹ a + 2b = 0 ………….❶
) ‫النقطة‬4,1‫الدالة‬ ‫لمنحني‬ ‫تنتمي‬ (f(1) = 4:
f(1) = 3 + a(1) + b(1)2
= 4 ⟹ a + b = 4 – 3 ⟹ a + b = 1 …………..❷
a + 2b = 0
a + b = 1
‫بالطرح‬
0 + b = -1
∴ b = -1
‫قيمة‬ ‫نعوض‬b‫معاد‬ ‫في‬‫لة‬❷
a + b = 1 ⟹ a - 1 = 1 ⟹ a = 1 + 1 ⟹ ∴ a = 2
∴ f(x) = 3 + 2x - x2
f̅ (x) = 2 - 2x ⟹ 2 - 2x = 0 ⟹ 2x = 2 ⟹ x = 1
) ‫الحرجة‬ ‫النقاط‬1,4(
‫الفترة‬ ‫في‬ ‫متزايدة‬ ‫الدالة‬R , x < 1}{x:x ∈
‫متناقص‬ ‫الدالة‬‫الفترة‬ ‫في‬ ‫ة‬R , x > 1}{x:x ∈
‫النق‬‫ط‬‫ة‬(1,4)‫محلية‬ ‫عظمى‬ ‫نهاية‬
1
+ + + + + + + ----------
‫اشارة‬f̅(𝐱)

64. ‫أدبي‬ ‫سادس‬‫االنقالب‬ ‫ونقاط‬ ‫والتحدب‬ ‫التقعر‬ ‫الثالث‬ ‫الفصل‬
/‫الشمري‬ ‫أحمد‬ :‫األستاذ‬0770451693764‫المرسل‬‫الطباعية‬ ‫للخدمات‬/07703458937
‫االنقالب‬ ‫ونقاط‬ ‫والتحدب‬ ‫التقعر‬:
‫محدب‬ ‫المنحني‬ ‫يكون‬‫المنطقة‬ ‫في‬‫الثانية‬ ‫المشتقة‬ ‫كانت‬ ‫اذا‬‫لكل‬
.‫صفر‬ ‫من‬ ‫اقل‬ ‫نقاطها‬
‫مقعر‬ ‫المنحني‬ ‫يكون‬‫المنطقة‬ ‫في‬‫لكل‬ ‫الثانية‬ ‫المشتقة‬ ‫كانت‬ ‫اذا‬
‫ص‬ ‫من‬ ‫اكبر‬ ‫نقاطها‬.‫فر‬
‫عندها‬ ‫الثانية‬ ‫المشتقة‬ ‫تكون‬ ‫االنقالب‬ ‫نقاط‬‫غير‬ ‫او‬ ‫صفر‬ ‫تساوي‬
.(‫سالبة‬ ‫لقيمة‬ ‫زوجي‬ ‫جذر‬ ‫او‬ ‫صفر‬ ‫على‬ ‫معرفة)قسمة‬
‫خطوات‬/‫الحل‬
1-.‫للدالة‬ ‫الثانية‬ ‫المشتقة‬ ‫ايجاد‬
2-‫قيم‬ ‫حساب‬x‫تساوي‬ ‫الثانية‬ ‫المشتقة‬ ‫عندما‬0.
3-‫قيم‬ ‫ايجاد‬y‫قيم‬ ‫لكل‬ ‫الدالة‬ ‫معادلة‬ ‫من‬x.
4-‫لتحدي‬ ‫االعداد‬ ‫خط‬ ‫استخدام‬.‫الثانية‬ ‫المشتقة‬ ‫اشارة‬ ‫د‬
‫مثال‬1/‫للدالة‬ ‫والتحدب‬ ‫التقعر‬ ‫ومناطق‬ ‫االنقالب‬ ‫نقاط‬ ‫جد‬f(x) = x2
- 4x + 2.‫وجدت‬ ‫ان‬(‫تمهيدي‬2014)
/‫الحل‬
f̅ (x) = 2x - 4
f̅̅ (x) = 2 > 0 ‫انقالب‬ ‫نقاط‬ ‫تحوي‬ ‫وال‬ ‫مجالها‬ ‫في‬ ‫مقعرة‬ ‫الدالة‬
‫مثال‬2/‫لتكن‬3x +2-3
x=f(x).‫وجدت‬ ‫ان‬ ‫والتحدب‬ ‫التقعر‬ ‫ومناطق‬ ‫االنقالب‬ ‫نقاط‬ ‫جد‬
/‫الحل‬
f̅ (x) = 3x2
– 3 ⟹ f̅̅ (x) = 6x ⟹ 6x = 0 ‫صفر‬ ‫تساوي‬ ‫الثانية‬ ‫المشتقة‬ ‫االنقالب‬ ‫نقاط‬ ‫عند‬
x = 0
f(0) = 03
-3(0) +2 = 2
‫التحدب‬ ‫منطقة‬R , x < 0}{x:x ∈
‫الت‬ ‫منطقة‬‫قعر‬R , x > 0}{x:x ∈
( ‫النقطة‬0,2.‫انقالب‬ ‫نقطة‬ ‫هي‬ )
‫التمارين‬ ‫حلول‬5-3
:‫والتحدب‬ ‫التقعر‬ ‫ومناطق‬ ‫االنقالب‬ ‫نقاط‬ ‫وجدت‬ ‫ان‬ ‫عين‬ ‫التالية‬ ‫الدوال‬ ‫من‬ ‫لكل‬
1) f(x) = 2x2
– 4x + 5
f̅ (x) = 4x - 4
f̅̅ (x) = 4 > 0 ‫مقعرة‬ ‫الدالة‬ ⟹
2) f(x) = 3x –x3
⟹ f̅ (x) = 3 - 3x2
⟹ f̅̅ (x) = -6x
-6x = 0 ⟹ x = 0 ‫صفر‬ ‫تساوي‬ ‫الثانية‬ ‫المشتقة‬ ‫االنقالب‬ ‫نقاط‬ ‫عند‬
f(0) = 3 . 0 - 03
= 0
‫التقعر‬ ‫منطقة‬R , x < 0}{x:x ∈
‫التحدب‬ ‫منطقة‬R , x > 0}{x:x ∈
( ‫النقطة‬0,0.‫انقالب‬ ‫نقطة‬ ‫هي‬ )
‫التقعر‬𝐟̅̅ (x) > 0
‫التحدب‬𝐟̅̅ (x) < 0
‫انقالب‬ ‫نقطة‬
‫اشارة‬f̅̅ (x)
0
---------- + + + + + + +
‫اشارة‬f̅̅ (x)
0
+ + + + + + + ----------
‫انقالب‬ ‫نقاط‬ ‫توجد‬ ‫ال‬
‫مجالها‬ ‫في‬ ‫مقعرة‬ ‫الدالة‬

65. ‫أدبي‬ ‫سادس‬‫االنقالب‬ ‫ونقاط‬ ‫والتحدب‬ ‫التقعر‬ ‫الثالث‬ ‫الفصل‬
/‫الشمري‬ ‫أحمد‬ :‫األستاذ‬0770451693765‫المرسل‬‫الطباعية‬ ‫للخدمات‬/07703458937
3) f(x) = x3
– 3x2
f̅ (x) = 3x2
- 6x ⟹ f̅̅ (x) = 6x - 6 = 0 ⟹ 6x - 6 = 0 ⟹ 6x = 6 ⟹ x =
1
f(1) = 13
– 3(1)2
= -2
‫التحدب‬ ‫منطقة‬R , x < 1}{x:x ∈
‫التقعر‬ ‫منطقة‬R , x > 1}{x:x ∈
( ‫النقطة‬1,-2.‫انقالب‬ ‫نقطة‬ ‫هي‬ )
4) f(x) = x5
f̅ (x) = 5x4
⟹ f̅̅ (x) = 20x3
⟹ 20x3
= 0 ⟹ x = 0
f(0) = 20(0)3
= 0
‫التحدب‬ ‫منطقة‬R , x < 0}{x:x ∈
‫التقعر‬ ‫منطقة‬R , x > 0}{x:x ∈
( ‫النقطة‬0,0.‫انقالب‬ ‫نقطة‬ ‫هي‬ )
5) f(x) = (x-2)3
+ 3 (3 ‫دور‬ 2012 ‫)وزاري‬
f̅ (x) = 3(x-2)2
⟹ f̅̅ (x) = 6(x-2)
:‫اذا‬ ‫صفر‬ ‫تساوي‬ ‫الثانية‬ ‫المشتقة‬ ‫االنقالب‬ ‫نقاط‬ ‫عند‬
6(x-2) = 0 ⟹ x - 2 = 0 ⟹ x = 2
f(2) = (2-2)3
+ 3 = 3
‫التحدب‬ ‫منطقة‬R , x < 2}{x:x ∈
‫التقعر‬ ‫منطقة‬R , x > 2}{x:x ∈
( ‫النقطة‬2,3.‫انقالب‬ ‫نقطة‬ ‫هي‬ )
6) f(x) =
1
4
x4
–
3
2
x2
f̅ (x) = x3
– 3x ⟹ f̅̅ (x) = 3x2
– 3 = 0 ⟹ 3x2
– 3 = 0 3 ‫على‬ ‫بالقسمة‬
(x2
– 1) = 0 ⟹ (x2
– 1) = 0 ⟹ (x - 1)(x + 1) = 0 ⟹ x = 1 , x = -1
f(1) =
1
4
(1)4
–
3
2
(1)2
=
1
4
–
3
2
=
1−6
4
=
−5
4
f(-1) =
1
4
(-1)4
–
3
2
(-1)2
=
1
4
–
3
2
=
1−6
4
=
−5
4
(‫المفتوحة‬ ‫الفترة‬ ‫في‬ ‫التحدب‬ ‫منطقة‬-1,1)
‫التقعر‬ ‫منطقة‬‫الفترتين‬ ‫في‬R , x > 1}{x:x ∈
R , x < -1}{x:x ∈
( ‫االنقالب‬ ‫نقاط‬1,
−𝟓
𝟒
( ‫و‬ )-1,
−𝟓
𝟒
.)
‫اشارة‬f̅̅ (x)
1
---------- + ++ + + + +
+ + + + + + + +
-1 1
------
‫اشارة‬f̅̅ (x)
‫اشارة‬f̅̅ (x)0
---------- + + + + + + +
‫اشارة‬f̅̅ (x) 2
---------- + + + + + + +

66. ‫أدبي‬ ‫سادس‬‫االنقالب‬ ‫ونقاط‬ ‫والتحدب‬ ‫التقعر‬ ‫الثالث‬ ‫الفصل‬
/‫الشمري‬ ‫أحمد‬ :‫األستاذ‬0770451693766‫المرسل‬‫الطباعية‬ ‫للخدمات‬/07703458937
7) f(x) = x3
+3x2
+3x +1 )2 ‫دور‬ 2015 ‫(وزاري‬ (2 ‫دور‬ 2013 ‫)وزاري‬
f̅ (x) = 3x2
+ 6x + 3 ⟹ f̅̅ (x) = 6x + 6
:‫اذا‬ ‫صفر‬ ‫تساوي‬ ‫الثانية‬ ‫المشتقة‬ ‫االنقالب‬ ‫نقاط‬ ‫عند‬
6x + 6 = 0 ⟹ 6(x + 1) = 0 ⟹ x + 1 = 0 ⟹ x = -1
f(-1) = (-1)3
+ 3(-1)2
+ 3 . (-1) + 1 = -1 + 3 - 3 + 1 = 0
‫التقعر‬ ‫منطقة‬R , x > -1}{x:x ∈
‫التحدب‬ ‫منطقة‬R , x < -1}{x:x ∈
( ‫االنقالب‬ ‫نقطة‬-1,0.)
‫اشارة‬f̅̅ (x)
---------- + + + + + + +
-1

67. ‫ر‬ ‫الثالث‬ ‫الفصل‬ ‫أدبي‬ ‫سادس‬‫س‬‫الدوال‬ ‫م‬
/‫الشمري‬ ‫أحمد‬ :‫األستاذ‬0770451693767‫المرسل‬‫الطباعية‬ ‫للخدمات‬/07703458937
:‫الدوال‬ ‫رسم‬‫اي‬ ‫منحني‬ ‫نرسم‬ ‫ان‬ ‫يمكننا‬ ‫والتحدب‬ ‫والتقعر‬ ‫والصغرى‬ ‫العظمى‬ ‫النهايات‬ ‫موضوعي‬ ‫في‬ ‫تعلمنا‬ ‫ما‬ ‫خالل‬ ‫من‬
‫دالة‬:‫التالية‬ ‫الخطوات‬ ‫خالل‬ ‫من‬ ‫تقريبية‬ ‫بصورة‬
1(‫نقط‬ ‫نجد‬‫ة‬‫محور‬ ‫مع‬ ‫التقاطع‬‫نعوض‬ ‫اي‬ ‫الصادات‬x = 0‫الدالة‬ ‫في‬f(x).
2(‫محور‬ ‫مع‬ ‫التقاطع‬ ‫نقاط‬ ‫نجد‬‫نعوض‬ ‫اي‬ ‫السينات‬f(x) = 0‫قيم‬ ‫ونحسب‬x.
3(‫والصغرى‬ ‫العظمى‬ ‫النهايات‬ ‫تعيين‬.
4(.‫االنقالب‬ ‫ونقاط‬ ‫والتحدب‬ ‫التقعر‬ ‫مناطق‬ ‫تعيين‬
5(‫اذ‬ ‫اخرى‬ ‫نقاط‬ ‫نجد‬.‫لها‬ ‫احتجنا‬ ‫ا‬
‫مثال‬1/‫الدالة‬ ‫منحني‬ ‫ارسم‬f(x) = x2
+ 4x + 3
/‫الحل‬‫)وزاري‬2013‫تمهيدي‬(
:‫المحورين‬ ‫مع‬ ‫التقاطع‬ ‫نقاط‬
f(0) = 02
+ 4 . 0 + 3 = 3
‫نقط‬‫ة‬) ‫هي‬ ‫الصادات‬ ‫محور‬ ‫مع‬ ‫التقاطع‬0,3(
f(x) = x2
+ 4x + 3 = 0 ⟹ x2
+ 4x + 3 = 0 ⟹ (x + 3)(x + 1) = 0
x = -3 , x = -1
‫محور‬ ‫مع‬ ‫التقاطع‬ ‫نقط‬‫السينات‬) ‫هي‬3,0-) ‫و‬ (1,0-(
:‫والصغرى‬ ‫العظمى‬ ‫النهايات‬
f̅ (x) = 2x + 4 ⟹ 2x + 4 = 0 ⟹ 2x = -4 ⟹ x = -2
f(-2) = (-2)2
+ 4 . (-2) + 3 = -1
) ‫حرجة‬ ‫نقطة‬1-,2-(
‫التزايد‬ ‫منطقة‬R , x > -2}{x:x ∈
‫التناقص‬ ‫منطقة‬R , x < -2}{x:x ∈
( ‫النقطة‬-2,-1.‫محلية‬ ‫صغرى‬ ‫نهاية‬ )
:‫االنقالب‬ ‫ونقاط‬ ‫والتحدب‬ ‫التقعر‬
f̅̅ (x) = 2 ‫مجالها‬ ‫في‬ ‫مقعرة‬ ‫والدالة‬ ‫انقالب‬ ‫نقاط‬ ‫توجد‬ ‫ال‬
‫مثال‬2/‫الدالة‬ ‫منحني‬ ‫ارسم‬3x–3
x=f(x).
:‫المحورين‬ ‫مع‬ ‫التقاطع‬ ‫نقاط‬
f(0) = 03
- 3 . 0 = 0
‫نقط‬‫ة‬) ‫هي‬ ‫الصادات‬ ‫محور‬ ‫مع‬ ‫التقاطع‬00,(
f(x) = x3
– 3x = 0 ⟹ x3
– 3x = 0 ⟹ x(x2
- 3) = 0
x(x - √3) (x + √3)= 0
x = 0 , x = √3 , x = −√3
‫السينات‬ ‫محور‬ ‫مع‬ ‫التقاطع‬ ‫نقط‬:)0,0(‫و‬)√30,(‫و‬)−√30,(
:‫والصغرى‬ ‫العظمى‬ ‫النهايات‬
f̅ (x) = 3x2
– 3 ⟹ 3x2
– 3= 0 ⟹ 3x2
= 3 ⟹ x2
= 1
x = 1 , x = -1
(0,3)
(-1,0)
(-3,0)
(-2,-1)
‫اشارة‬f̅(𝒙)
--------
-2
+ + + + + +

68. ‫ر‬ ‫الثالث‬ ‫الفصل‬ ‫أدبي‬ ‫سادس‬‫س‬‫الدوال‬ ‫م‬
/‫الشمري‬ ‫أحمد‬ :‫األستاذ‬0770451693768‫المرسل‬‫الطباعية‬ ‫للخدمات‬/07703458937
f(1) = (1)3
– 3.1 = -2
f(-1) = (-1)3
– 3 (-1) = 2
) ‫الحرجة‬ ‫النقاط‬2-.1) ‫و‬ (1,2-(
‫الدا‬:‫الفترتين‬ ‫في‬ ‫متزايدة‬ ‫لة‬R , x < -1}{x:x ∈
R , x > 1}{x:x ∈
‫الفترة‬ ‫في‬ ‫متناقصة‬ ‫الدالة‬R , -1 < x < 1}{x:x ∈
( ‫محلية‬ ‫عظمى‬ ‫نهاية‬ ‫نقطة‬-1,2)
( ‫محلية‬ ‫صغرى‬ ‫نهاية‬ ‫نقطة‬1,-2)
:‫االنقالب‬ ‫ونقاط‬ ‫والتحدب‬ ‫التقعر‬
f̅̅ (x) = 6x ⟹ 6x = 0 ⟹ x = 0
f(0) = 03
– 3(0) = 0
‫التحدب‬ ‫منطقة‬R , x < 0}{x:x ∈
‫التقعر‬ ‫منطقة‬R , x > 0}{x:x ∈
( ‫النقطة‬0,0.‫انقالب‬ ‫نقطة‬ ‫هي‬ )
‫مثال‬3/‫الدالة‬ ‫منحني‬ ‫ارسم‬1-3
(x+1)=f(x)‫)وزاري‬6201‫دور‬1(
/‫الحل‬‫التق‬ ‫نقاط‬:‫المحورين‬ ‫مع‬ ‫اطع‬
f(0) = (0+1)3
-1 = 0
‫نقط‬‫ة‬) ‫هي‬ ‫الصادات‬ ‫محور‬ ‫مع‬ ‫التقاطع‬00,(
f(x) = (x+1)3
-1= 0 ⟹ (x+1)3
-1= 0 ⟹ (x+1)3
= 1
x+1 = 1 ‫للطرفين‬ ‫التكعيبي‬ ‫الجذر‬
x = 1 – 1 = 0
‫السينات‬ ‫محور‬ ‫مع‬ ‫التقاطع‬ ‫نقط‬)0,0(
:‫والصغرى‬ ‫العظمى‬ ‫النهايات‬
f̅ (x) = 3(x+1)2
⟹ 3(x+1)2
= 0 ⟹ (x+1)2
= 0
x+1 = 0 ‫للطرفين‬ ‫التربيعي‬ ‫الجذر‬
x = -1
f(-1) = ((-1) +1)3
-1 = 0 -1 = -1
) ‫الحرجة‬ ‫النقاط‬-1,-1(
‫مجالها‬ ‫في‬ ‫متزايدة‬ ‫الدالة‬
( ‫النقطة‬-1,-1‫حرجة‬ ‫نقطة‬ )
-------- + + + +
-1 1
+ + + +
‫اشارة‬f̅(𝒙)
(-1,2)
(0,0)
(1,-2)
(−√𝟑,0)
(√𝟑,0)
‫اشارة‬f̅(𝒙)
+ + + + + + +
----------
+ + + + + + +
1-
‫اشارة‬f̅̅ (x)0
---------- + + + + + + +

69. ‫ر‬ ‫الثالث‬ ‫الفصل‬ ‫أدبي‬ ‫سادس‬‫س‬‫الدوال‬ ‫م‬
/‫الشمري‬ ‫أحمد‬ :‫األستاذ‬0770451693769‫المرسل‬‫الطباعية‬ ‫للخدمات‬/07703458937
:‫االنقالب‬ ‫ونقاط‬ ‫والتحدب‬ ‫التقعر‬
f̅̅ (x) = 6(x+1) ⟹ 6(x+1) = 0 ⟹ x+1 = 0 ⟹ x = -1
f(-1) = -1
‫التحدب‬ ‫منطقة‬R , x < -1}{x:x ∈
‫التقعر‬ ‫منطقة‬R , x > -1}{x:x ∈
(-1,-1.‫انقالب‬ ‫نقطة‬ )
‫كاف‬ ‫عدد‬ ‫على‬ ‫نحصل‬ ‫لم‬ ‫اننا‬ ‫بما‬ /‫مالحظة‬‫لـ‬ ‫تقريبية‬ ‫قيم‬ ‫اختيار‬ ‫خالل‬ ‫من‬ ‫نقاط‬ ‫اضافة‬ ‫فيمكننا‬ ‫الدالة‬ ‫لرسم‬ ‫النقاط‬ ‫من‬x
‫قيمة‬ ‫وحساب‬y:‫مبين‬ ‫كما‬ ‫الدالة‬ ‫من‬
‫التمارين‬ ‫حلول‬6-3
:‫التالية‬ ‫الدوال‬ ‫منحني‬ ‫ارسم‬ ‫بالتفاضل‬ ‫باالستعانة‬
1)f(x) = 4 – 6x – x2
‫)وزا‬‫ري‬3201(‫اول‬ ‫دور‬)‫تمهيدي‬6201(
f(0) = 4 – 6.0 – 02
= 4
‫نقط‬‫ة‬) ‫هي‬ ‫الصادات‬ ‫محور‬ ‫مع‬ ‫التقاطع‬40,(
f(x) = 4 – 6x – x2
= 0 ⟹ 4 – 6x – x2
= 0 .‫التجربة‬ ‫باستخدام‬ ‫حلها‬ ‫يمكن‬ ‫ال‬ ‫المعادلة‬
:‫والصغرى‬ ‫العظمى‬ ‫النهايات‬
f̅ (x) = -6 - 2x = 0 ‫ال‬ ‫في‬‫صفر‬ ‫تساوي‬ ‫المشتقة‬ ‫نهايات‬
-6 – 2x = 0 ⟹ 2x = -6 ⟹ x = -3
f(-3)=4 – 6(-3) – (-3)2
=4 + 18 - 9= 13
:‫الفترة‬ ‫في‬ ‫متزايدة‬ ‫الدالة‬R , x < -3}{x:x ∈
‫الفترة‬ ‫في‬ ‫متناقصة‬ ‫الدالة‬R , x > -3}{x:x ∈
‫محلية‬ ‫عظمى‬ ‫نهاية‬ ‫نقطة‬)13,3-(
‫االنقالب‬ ‫ونقاط‬ ‫والتحدب‬ ‫التقعر‬:
f̅̅ (x) = -2 < 0
‫الدالة‬ ‫اذا‬ ‫صفر‬ ‫من‬ ‫اقل‬ ‫الثانية‬ ‫المشتقة‬ ‫ان‬ ‫بما‬
.‫انقالب‬ ‫نقاط‬ ‫تحوي‬ ‫وال‬ ‫مجالها‬ ‫في‬ ‫محدبة‬
1-3(x+1)=yx
00
71
262
-1-1
-2-2
+ + + + + + + ----------
-3 ‫اشارة‬f̅(𝒙)
(0,0)
(-1,-1)
(1,7)
‫اشارة‬f̅̅ (x)
-1
---------- + + + + + + +
(-3,13)
(0,4)

70. ‫ر‬ ‫الثالث‬ ‫الفصل‬ ‫أدبي‬ ‫سادس‬‫س‬‫الدوال‬ ‫م‬
/‫الشمري‬ ‫أحمد‬ :‫األستاذ‬0770451693770‫المرسل‬‫الطباعية‬ ‫للخدمات‬/07703458937
2)f(x) = 3x – x3
(1 ‫دور‬ 2011 ‫و‬ 2 ‫دور‬ 2012)
f(0) = 3.0 – 03
= 0
) ‫هي‬ ‫الصادات‬ ‫محور‬ ‫مع‬ ‫التقاطع‬ ‫نقط‬00,(
f(x) = 3x – x3
= 0 ⟹ 3x – x3
= 0 ⟹ x (3 – x2
) = 0
3x (√3 – x) (√3 + x) = 0 ⟹ x = 0 , x = √3 , x = -√3
)‫هي‬ ‫التقاطع‬ ‫نقاط‬0,0) ‫و‬ (√3,0) ‫و‬ (-√3,0(
:‫والصغرى‬ ‫العظمى‬ ‫النهايات‬
f̅ (x) = 3 - 3x2
= 0 ‫صفر‬ ‫تساوي‬ ‫المشتقة‬ ‫النهايات‬ ‫في‬
3 - 3x2
= 0 ⟹ 1 - x2
= 0 3 ‫على‬ ‫نقسم‬
(1 – x) (1 + x) = 0 ⟹ x = 1 , x = -1
f(1) = 2
f(-1) = -2
) ‫الحرجة‬ ‫النقاط‬1,2) ‫و‬ (-1,-2(
‫الفترة‬ ‫في‬ ‫متزايدة‬ ‫الدالة‬) ‫المفتوحة‬-1,1(
‫الفترتين‬ ‫في‬ ‫متناقصة‬ ‫الدالة‬R , x > 1}{x:x ∈
{x:x ∈ R , x < -1}
) ‫محلية‬ ‫عظمى‬ ‫نهاية‬ ‫نقطة‬1,2(
‫نهاية‬ ‫نقطة‬‫صغرى‬) ‫محلية‬2-,1-(
‫االنقالب‬ ‫ونقاط‬ ‫والتحدب‬ ‫التقعر‬:‫صفر‬ ‫تساوي‬ ‫الثانية‬ ‫المشتقة‬ ‫االنقالب‬ ‫نقاط‬ ‫في‬
f̅̅ (x) = -6x ⟹ -6x = 0 ⟹ x = 0
f(0) = 3(0) – 03
= 0
‫التحدب‬ ‫منطقة‬R , x > 0}{x:x ∈
‫التقعر‬ ‫منطقة‬R , x < 0}{x:x ∈
)0,0.‫انقالب‬ ‫نقطة‬ (
3) f(x) = (x - 1)3
f(0) = (0 - 1)3
= -1
‫نقط‬‫ة‬) ‫هي‬ ‫الصادات‬ ‫محور‬ ‫مع‬ ‫التقاطع‬1-,0(
f(x) = (x - 1)3
= 0 ⟹ (x - 1)3
= 0 ⟹ x -1= 0 ⟹ x = 1
‫التقاطع‬ ‫نقاط‬‫السينات‬ ‫محور‬ ‫مع‬) ‫هي‬1,0(
:‫والصغرى‬ ‫العظمى‬ ‫النهايات‬
f̅ (x) = 3(x - 1)2
⟹ 3(x - 1) 2
= 0 ⟹ (x - 1) 2
= 0 3 ‫على‬ ‫الطرفين‬ ‫قسمة‬
x – 1 = 0 ‫للطرفين‬ ‫التربيعي‬ ‫الجذر‬
x = 1
+ + + + + ------
-1 1
------
‫اشارة‬f̅(𝒙)
(-1,-2)
(1,2)
(−√𝟑,0)
(√𝟑,0)
‫اشارة‬f̅̅ (x)0
+ + + + + + + ----------

71. ‫ر‬ ‫الثالث‬ ‫الفصل‬ ‫أدبي‬ ‫سادس‬‫س‬‫الدوال‬ ‫م‬
/‫الشمري‬ ‫أحمد‬ :‫األستاذ‬0770451693771‫المرسل‬‫الطباعية‬ ‫للخدمات‬/07703458937
f(1) = (1 - 1)3
= 0
‫متزايدة‬ ‫الدالة‬) ‫والنقطة‬ ‫مجالها‬ ‫في‬1,0‫حرجة‬ ‫نقطة‬ (
‫االنقالب‬ ‫ونقاط‬ ‫والتحدب‬ ‫التقعر‬:
f̅̅ (x) = 6(x - 1) ⟹ 6(x - 1) = 0 ⟹ x - 1 = 0 ⟹ x = 1
f(1) = 0
‫منط‬‫التحدب‬ ‫قة‬R , x < 1}{x:x ∈
‫التقعر‬ ‫منطقة‬R , x > 1}{x:x ∈
)1,0.‫انقالب‬ ‫نقطة‬ (
(1,0)(0,-1)
+ + + + + + + + + + + + + +
1
‫اشارة‬f̅(𝒙)
‫اشارة‬f̅̅ (x)1
---------- + + + + + ++

72. ‫ر‬ ‫الثالث‬ ‫الفصل‬ ‫أدبي‬ ‫سادس‬‫س‬‫الدوال‬ ‫م‬
/‫الشمري‬ ‫أحمد‬ :‫األستاذ‬0770451693772‫المرسل‬‫الطباعية‬ ‫للخدمات‬/07703458937
4) f(x) = x3
– 2 x2
+ 1
f(0) = 03
– 2 (0)2
+ 1= 1
‫نقط‬‫ة‬) ‫هي‬ ‫الصادات‬ ‫محور‬ ‫مع‬ ‫التقاطع‬10,(
f(x) = x3
– 2x2
+ 1= 0 ⟹ x3
– 2x2
+ 1= 0
.‫السينات‬ ‫محور‬ ‫مع‬ ‫التقاطع‬ ‫نقاط‬ ‫نهمل‬ ‫لذلك‬ ‫المعادلة‬ ‫تحليل‬ ‫يمكن‬ ‫ال‬
:‫والصغرى‬ ‫العظمى‬ ‫النهايات‬
f̅ (x) = 3x2
– 4x = 0 ‫صفر‬ ‫تساوي‬ ‫المشتقة‬ ‫النهايات‬ ‫في‬
3x2
– 4x = 0 ⟹ x (3x – 4) = 0 ⟹ x = 0
3x – 4 = 0 ⟹ 3x = 4 ⟹ x =
4
3
f(0) = 1
f(
4
3
) = (
4
3
)3
– 2 (
4
3
)2
+ 1 =
64
27
- 2
16
9
+ 1 =
64
27
-
32
9
+ 1 =
64 − 96 + 27
27
=
− 5
27
‫الفتر‬ ‫في‬ ‫متزايدة‬ ‫الدالة‬‫تين‬:R , x < 0}{x:x ∈
R , x >
4
3
}{x:x ∈
‫الفترة‬ ‫في‬ ‫متناقصة‬ ‫الدالة‬R ,0 < x <
4
3
}{x:x ∈
) ‫محلية‬ ‫عظمى‬ ‫نهاية‬ ‫نقطة‬0,1(
) ‫محلية‬ ‫صغرى‬ ‫نهاية‬ ‫نقطة‬
4
3
− 5
27
,(
‫االنقالب‬ ‫ونقاط‬ ‫والتحدب‬ ‫التقعر‬:
f̅̅ (x) = 6x – 4 = 0 ‫االنقالب‬ ‫نقاط‬ ‫في‬‫صفر‬ ‫تساوي‬ ‫الثانية‬ ‫المشتقة‬
6x – 4= 0 ⟹ 6x = 4 ⟹ x =
4
6
=
2
3
f(
2
3
) = (
2
3
)3
– 2 (
2
3
)2
+ 1 =
8
27
- 2
4
9
+ 1 =
8
27
-
8
9
+ 1 =
8 − 24 + 27
27
=
11
27
‫التحدب‬ ‫مناطق‬{x:x ∈ R , x <
2
3
}
‫التقعر‬ ‫مناطق‬{x:x ∈ R , x >
2
3
}
) ‫االنقالب‬ ‫نقطة‬
2
3
,
11
27
(
(0,1)
)
4
3
,
− 5
27
(
(
2
3
,
11
27
)
-------- + + + +
0
4
3
+ + + +
‫اشارة‬f̅(𝒙)
‫اشارة‬f̅̅ (x)
2
3
---------- + + + + + + +

73. ‫ادبي‬ ‫سادس‬‫ا‬‫الثالث‬ ‫لفصل‬‫االثرائية‬ ‫االمثلة‬
/‫الشمري‬ ‫أحمد‬ :‫األستاذ‬0770451693773‫المرسل‬‫الطباعية‬ ‫للخدمات‬/07703458937
:‫والصغرى‬ ‫العظمى‬ ‫النهايات‬ ‫على‬ ‫تطبيقات‬
1-.‫المتغيرات‬ ‫نعرف‬
2-.‫يمكن‬ ‫ما‬ ‫اقل‬ ‫او‬ ‫باكبر‬ ‫المطلوبة‬ ‫القيمة‬ ‫دالة‬ ‫نعرف‬
3-.‫واحد‬ ‫متغير‬ ‫بداللة‬ ‫المطلوبة‬ ‫القيمة‬ ‫دالة‬ ‫في‬ ‫المتغيرات‬ ‫نوحد‬
4-‫ن‬.‫القيمة‬ ‫دالة‬ ‫مشتقة‬ ‫ستخرج‬
5-)‫االعداد‬ ‫خط‬ ‫الى‬ ‫نذهب‬ ‫للمتغير‬ ‫قيمة‬ ‫من‬ ‫اكثر‬ ‫ظهرت‬ ‫(اذا‬ ‫المتغير‬ ‫قيمة‬ ‫الستخراج‬ ‫بالصفر‬ ‫المشتقة‬ ‫نساوي‬
6-.‫وجد‬ ‫ان‬ ‫االخر‬ ‫المتغير‬ ‫قيمة‬ ‫نحسب‬
7-‫القيمة‬ ‫دالة‬ ‫نحسب‬.
‫مثال‬1/‫محيطها‬ ‫مستطيله‬ ‫ارض‬ ‫لقطعة‬ ‫مساحة‬ ‫اكبر‬ ‫ابعاد‬ ‫جد‬60.‫متر‬
/‫الحل‬‫ابعاد‬ ‫نفرض‬‫قطعة‬‫اال‬‫رض‬a‫و‬b‫ومساحتها‬A
A = a . b
A = a . b = a . (30 – a) = 30a – a2
A̅ = 30 – 2a
A̅= 0 ‫النهايات‬ ‫عند‬ ‫صفر‬ ‫تساوي‬ ‫المشتقة‬
30 – 2a = 0 ⟹ 2a = 30 ⟹ a = 15 ‫متر‬
b = 30 – a = 30 – 15 ⟹ b = 15‫متر‬
‫مثال‬2/‫مجمو‬ ‫عددين‬ ‫جد‬‫يساوي‬ ‫عهما‬20:‫كان‬ ‫اذا‬
a(.‫يمكن‬ ‫ما‬ ‫اكبر‬ ‫ضربهما‬ ‫حاصل‬
b(.‫يمكن‬ ‫ما‬ ‫اصغر‬ ‫مربعيهما‬ ‫مجموع‬2016-3
/‫الحل‬
a(‫هو‬ ‫االول‬ ‫العدد‬ ‫نفرض‬x‫هو‬ ‫الثاني‬ ‫والعدد‬z‫هو‬ ‫العددين‬ ‫ضرب‬ ‫حاصل‬ ‫وان‬y:
y = x . z
x + z = 20 ‫يساوي‬ ‫العددين‬ ‫مجموع‬20
z = 20 –x
‫نعوض‬z‫دالة‬ ‫في‬y:
y = x . z = x . (20 –x) ⟹ y = 20x – x2
y̅ = 20 – 2x
y̅= 0 ⟹ 20 – 2x = 0 ⟹ 2x = 20 ⟹ x = 10
z = 20 – 10 ⟹ z = 10
b(‫هو‬ ‫االول‬ ‫العدد‬ ‫نفرض‬x‫هو‬ ‫الثاني‬ ‫والعدد‬z‫حاصل‬ ‫وان‬‫مربعي‬ ‫مجموع‬‫هو‬ ‫العددين‬y‫تكون‬ ‫بذلك‬‫دالة‬y:‫هي‬
y = x2
+ z2
‫يساوي‬ ‫العددين‬ ‫مجموع‬ ‫ان‬ ‫بما‬20:‫فان‬
x + z = 20
z = 20 –x
‫دالة‬ ‫في‬ ‫نعوض‬y:
y = x2
+ z2
= x2
+ (20 –x)2
= x2
+ 400 - 40x + x2
= 2x2
- 40x + 400
y̅ = 4x – 40 ⟹ y̅= 0 ⟹ 4x - 40= 0 ⟹ 4x = 40 ⟹ x = 10
z = 20 – 10 ⟹ z = 10
a
b
‫المستطيل‬ ‫محيط‬60
2(a + b) = 60
a + b = 30
b = 30 – a

74. ‫ادبي‬ ‫سادس‬‫ا‬‫الثالث‬ ‫لفصل‬‫االثرائية‬ ‫االمثلة‬
/‫الشمري‬ ‫أحمد‬ :‫األستاذ‬0770451693774‫المرسل‬‫الطباعية‬ ‫للخدمات‬/07703458937
‫مثال‬3/‫محيطه‬ ‫مستطيل‬ ‫اكبر‬ ‫ابعاد‬ ‫جد‬40.‫متر‬‫وزاري‬ (2011‫دور‬1)
/‫الحل‬‫المستطيل‬ ‫مساحة‬ ‫نفرض‬A‫وابعاده‬a‫و‬b:
A = a . b
A = a . b = a . (20 – a) = 20a – a2
A̅ = 20 – 2a
A̅= 0 ⟹ 20 – 2a = 0 ⟹ 2a = 20
a = 10 ‫متر‬
b = 20 – a = 20 – 10 ⟹ b = 10‫متر‬
‫مثال‬4/‫محيطه‬ ‫مستطيل‬ ‫من‬120‫الصغيرين‬ ‫الضلعين‬ ‫احد‬ ‫على‬ ‫قطرها‬ ‫ينطبق‬ ‫دائرة‬ ‫نصف‬ ‫شكل‬ ‫على‬ ‫منطقة‬ ‫قطعت‬ ‫سم‬
‫المساح‬ ‫تكون‬ ‫لكي‬ ‫المستطيل‬ ‫ذلك‬ ‫ابعاد‬ ‫جد‬ , ‫للمستطيل‬.‫يمكن‬ ‫ما‬ ‫اكبر‬ ‫القطع‬ ‫بعد‬ ‫منه‬ ‫المتبقية‬ ‫ة‬‫)وزاري‬2012‫دور‬2(
/‫الحل‬‫المستطيل‬ ‫ابعاد‬ ‫نفرض‬a‫و‬b‫القطع‬ ‫بعد‬ ‫ومساحته‬A:
A1 = a . b ‫القطع‬ ‫قبل‬ ‫الكلية‬ ‫المستطيل‬ ‫مساحة‬
A2 =
11 b2
28
b ‫قطرها‬ ‫دائرة‬ ‫نصف‬ ‫مساحة‬
A = A1 – A2 = a . b -
11 b2
28
= (60 – b) . b -
11 b2
28
A = 60b – b2
-
11 b2
28
= 60b -
39 b2
28
A̅ = 60 –
78b
28
= 60 –
39b
14
A̅= 0 ⟹ 60 –
39b
14
= 0 ⟹
39b
14
= 60
b =
14 . 60
39
=
14 . 20
13
=
𝟐𝟖𝟎
𝟏𝟑
‫متر‬ ‫الصغير‬ ‫الضلع‬ ‫طول‬
a = 60 – b = 60 -
280
13
=
780−280
13
=
𝟓𝟎𝟎
𝟏𝟑
‫متر‬ ‫الكبير‬ ‫الضلع‬ ‫طول‬
‫مثال‬5/.‫يمكن‬ ‫ما‬ ‫اكبر‬ ‫مكعبه‬ ‫على‬ ‫مربعه‬ ‫امثال‬ ‫ثالثة‬ ‫زيادة‬ ‫الذي‬ ‫العدد‬ ‫جد‬‫)وزاري‬2013‫تمهيدي‬(
/‫الحل‬‫العدد‬ ‫نفرض‬a‫مكعبه‬ ‫على‬ ‫مربعه‬ ‫امثال‬ ‫ثالثة‬ ‫وزيادة‬y
y = 3a2
- a3
‫هو‬ ‫واحد‬ ‫متغير‬ ‫تحوي‬ ‫المطلوبة‬ ‫القيمة‬ ‫دالة‬ ‫ان‬ ‫هنا‬ ‫نجد‬ /‫مالحظة‬a.‫مباشرة‬ ‫نشتق‬ ‫ان‬ ‫يمكننا‬ ‫اذا‬
y̅ = 6a - a2
3
y̅= 0 ⟹ 6a - 3a2
= 0 ⟹ 3a(2 - a) = 0 ⟹ a = 0 ‫تهمل‬
∴ a = 2
‫مثال‬6/‫امثا‬ ‫اربعة‬ ‫بين‬ ‫الفرق‬ ‫يكون‬ ‫الذي‬ ‫العدد‬ ‫جد‬.‫يمكن‬ ‫ما‬ ‫اكبر‬ ‫مربعه‬ ‫و‬ ‫له‬
/‫الحل‬‫هو‬ ‫العدد‬ ‫نفرض‬a‫هو‬ ‫ومربعه‬ ‫امثاله‬ ‫اربعة‬ ‫بين‬ ‫الفرق‬ ‫ونفرض‬y
y = 4a – a2
⟹ y̅ = 4 - 2a ⟹ y̅= 0 ⟹ 4 - 2a = 0
2a = 4 ⟹ a = 2
a
b
‫المستطيل‬ ‫محيط‬40
2(a + b) = 40
a + b = 20
b = 20 – a
a
b
‫يساوي‬ ‫المستطيل‬ ‫محيط‬120
2(a + b) = 120
a + b = 60
a = 60 - b

75. ‫ادبي‬ ‫سادس‬‫ا‬‫الثالث‬ ‫لفصل‬‫االثرائية‬ ‫االمثلة‬
/‫الشمري‬ ‫أحمد‬ :‫األستاذ‬0770451693775‫المرسل‬‫الطباعية‬ ‫للخدمات‬/07703458937
‫مثال‬7/‫مرب‬ ‫قاعدته‬ ‫غطاء‬ ‫بدون‬ ‫مستطيالت‬ ‫متوازي‬ ‫شكل‬ ‫على‬ ‫حوض‬ ‫صنع‬ ‫يراد‬‫وحجمه‬ ‫الشكل‬ ‫عة‬864‫متر‬‫مكعب‬‫اوجد‬
‫مساحة‬ ‫اقل‬.‫صنعه‬ ‫في‬ ‫تستخدم‬ ‫ان‬ ‫يمكن‬ ‫االلواح‬ ‫من‬
/‫الحل‬‫القاعدة‬ ‫ابعاد‬ ‫نفرض‬b‫واالرتفاع‬a‫ومساح‬‫هي‬ ‫االلواح‬ ‫ــــــة‬A:
:‫غطاء‬ ‫بدون‬ ‫النه‬ ‫القاعدة‬ ‫مساحة‬ ‫زائدا‬ ‫االربعة‬ ‫الجانبية‬ ‫االسطح‬ ‫مساحة‬ ‫تساوي‬ ‫االلواح‬ ‫مساحة‬
A = 4ab + b2
= 4(
864
b2 )b + b2
=
3456
b
+ b2
A̅ = -
3456
b2 + 2b = 0 ⟹ 2b =
3456
b2
b3
=
3456
2
= 1728 ⟹ b = 12 m
a =
864
122 =
864
144
= 6 m
‫قيمة‬ ‫نعوض‬a‫و‬b‫الدالة‬ ‫في‬A:
A = 4 . 12 . 6 + 122
A = 288 + 144
A = 432 m2
‫االلواح‬ ‫من‬ ‫مساحة‬ ‫اقل‬
‫مثال‬8/‫جد‬‫محيط‬ ‫اقل‬‫مساحته‬ ‫لمستطيل‬ ‫ممكن‬100‫سم‬2
.‫(وزاري‬4201‫دور‬1)
/‫الحل‬‫هي‬ ‫المستطيل‬ ‫ابعاد‬ ‫نفرض‬a‫و‬b‫ومحيطه‬S
S = 2(a + b) = 2(a +
100
a
)= 2a +
200
a
Sˊ = 2 –
200
a2
Sˊ = 0 ⟹ 2 –
200
a2 = 0 ⟹
200
a2 = 2
a2
= 100 ⇒ a = ± 10 ‫سالب‬ ‫بعد‬ ‫يوجد‬ ‫ال‬
∴ a = 10 cm2
b =
100
a
=
100
10
= 10 cm2
S = 2(a +b) = 2(10 + 10) ⟹ S = 40 cm ‫للمستطيل‬ ‫ممكن‬ ‫محيط‬ ‫اقل‬
‫مثال‬9/‫ا‬ ‫الكلفة‬ ‫دالة‬ ‫كانت‬ ‫اذا‬‫هي‬ ‫معينة‬ ‫سلعة‬ ‫النتاج‬ ‫لكلية‬c(x) =
1
9
x2
+ 6x + 100‫يكون‬ ‫عنده‬ ‫الذي‬ ‫االنتاج‬ ‫حجم‬ ‫جد‬
.‫يمكن‬ ‫ما‬ ‫اقل‬ ‫الكلفة‬ ‫معدل‬‫(وزاري‬2015‫دور‬3)
/‫الحل‬‫عند‬ ‫كلفة‬ ‫معدل‬ ‫اقل‬0=Ac̅:
Ac =
c(x)
x
=
1
9
x2+6x+100
x
=
1
9
x + 6 +
100
x
Ac̅̅̅ =
1
9
−
100
x2
Ac̅̅̅= 0 ⟹
1
9
−
100
x2 = 0 ⟹
100
x2 =
1
9
⟹ x2
= 900 ⟹ x = ±30
∴ x = 30
‫االنتاج‬ ‫حجم‬ ‫يكون‬ ‫عندما‬ ‫كلفة‬ ‫معدل‬ ‫اقل‬=30‫وحدة‬
a
b
b
‫الصندوق‬ ‫حجم‬ ‫من‬
V = ab2
= 864
a =
𝟖𝟔𝟒
𝐛 𝟐
2 1728
2 864
2 432
2 216
2 108
2 54
3 27
3 9
3 3
1
a
b
‫المستطيل‬ ‫مساحة‬100
a . b = 100
b =
100
a

76. ‫ادبي‬ ‫سادس‬‫ا‬‫الثالث‬ ‫لفصل‬‫االثرائية‬ ‫االمثلة‬
/‫الشمري‬ ‫أحمد‬ :‫األستاذ‬0770451693776‫المرسل‬‫الطباعية‬ ‫للخدمات‬/07703458937
‫التمارين‬ ‫حلول‬7-3
1-‫مجموعهما‬ ‫عددين‬ ‫جد‬15.‫يمكن‬ ‫ما‬ ‫اكبر‬ ‫االخر‬ ‫بمربع‬ ‫احدهما‬ ‫ضرب‬ ‫وحاصل‬‫)وزاري‬2013‫او‬ ‫دور‬(‫ل‬
/‫الحل‬‫االول‬ ‫العدد‬ ‫نفرض‬x‫الثاني‬ ‫والعدد‬z:
x + z = 15 ⟹ z = 15 – x
y = z . x2
= (15 – x) . x2
= 15x2
– x3
y̅ = 30x – 3x2
= 0 ⟹ 30x – 3x2
= 0 ⟹ 3x(10 – x) = 0 3x ‫مشترك‬ ‫عامل‬
x = 0 , x = 10 ⟹ ∴ x = 10
z = 15 – x = 15 – 10 = 5
2-.‫يمكن‬ ‫ما‬ ‫اكبر‬ ‫مربعه‬ ‫على‬ ‫زيادته‬ ‫الذي‬ ‫العدد‬ ‫ما‬(‫تمهيدي‬2014)
/‫الحل‬‫العدد‬ ‫نفرض‬x‫مربعه‬ ‫على‬ ‫وزيادته‬y:
y = x – x2
y̅ = 1 – 2x = 0 ⟹ 1 – 2x = 0 ⟹ 2x = 1 ⟹ ∴ x =
1
2
3-‫مجموعهما‬ ‫موجبين‬ ‫عددين‬ ‫جد‬15‫وحاص‬.‫يمكن‬ ‫ما‬ ‫اكبر‬ ‫االخر‬ ‫مكعب‬ ‫في‬ ‫احدهما‬ ‫مربع‬ ‫ضرب‬ ‫ل‬
/‫الحل‬‫االول‬ ‫العدد‬ ‫نفرض‬a‫الثاني‬ ‫والعدد‬b:
a + b = 15 ⇒ b = 15 - a
y = a3
. b2
= a3
. (15 – a)2
= a3
. (225 – 30a + a2
) = 225 a3
– 30 a4
+ a5
y̅ = 675a2
– 120 a3
+ 5a4
y̅ = 5a2
(135 – 24a + a2
) ‫مشترك‬ ‫عامل‬ 5a2
y̅ = 0 ⇒ 5a2
(135 – 24a + a2
)= 0
a = 0
a2
– 24a + 135 = 0
(a -15)(a - 9) = 0
a = 15 , a = 9
∴ a = 9
b = 15 – a = 15 – 9 = 6
4-‫مجموعهما‬ ‫عددين‬ ‫جد‬10‫ا‬ ‫مربع‬ ‫في‬ ‫احدهما‬ ‫مربع‬ ‫ضرب‬ ‫وحاصل‬.‫يمكن‬ ‫ما‬ ‫اكبر‬ ‫الخر‬‫)وزاري‬2012‫دور‬3(
‫الحل‬/‫االول‬ ‫العدد‬ ‫نفرض‬a‫الثاني‬ ‫والعدد‬b‫االخر‬ ‫مربع‬ ‫في‬ ‫احدهما‬ ‫مربع‬ ‫ضرب‬ ‫وحاصل‬y:
a + b = 10
b = 10 - a
y = a2
. b2
= a2
. (10 – a)2
= a2
. (100 – 20a + a2
) = 100a2
– 20 a3
+ a4
y̅ = 200a – 60 a3
+ a3
4
y̅ = 4a (50 – 15a + a2
) 4a ‫مشترك‬ ‫عامل‬
y̅ = 0 ⟹ 4a (50 – 15a + a2
) = 0 ⟹ a = 0
a2
– 15a + 50 = 0 ⟹ (a -5)(a - 10) = 0 ⟹ a = 5 , a = 10
∴ a = 5 ‫عظمى‬ ‫نهاية‬
b = 10 – a = 10 – 5 = 5
3 135
3 45
3 15
5 5
-------- + + +
++
9 15
+ + +
++
0
-------- + + +
++
5 10
++++
0
----

77. ‫ادبي‬ ‫سادس‬‫ا‬‫الثالث‬ ‫لفصل‬‫االثرائية‬ ‫االمثلة‬
/‫الشمري‬ ‫أحمد‬ :‫األستاذ‬0770451693777‫المرسل‬‫الطباعية‬ ‫للخدمات‬/07703458937
5-‫طوله‬ ‫بسياج‬ ‫تسييجها‬ ‫يمكن‬ ‫االرض‬ ‫من‬ ‫مساحة‬ ‫اكبر‬ ‫جد‬ ‫جهاتها‬ ‫احد‬ ‫من‬ ‫نهر‬ ‫يحدها‬ ‫الشكل‬ ‫مستطيله‬ ‫ارض‬ ‫قطعة‬100
.‫متر‬
/‫الحل‬‫هو‬ ‫االرض‬ ‫ومحيط‬ ‫بالرسم‬ ‫مبين‬ ‫كما‬ ‫االرض‬ ‫ابعاد‬ ‫نفرض‬S
:‫لسياج‬ ‫تحتاج‬ ‫ال‬ ‫نهر‬ ‫يحدها‬ ‫التي‬ ‫الجهة‬
A = a . b = a . (100 – 2a) = 100a – 2a2
A̅ = 100 – 4a
A̅ = 0 ⟹ 100 – 4a = 0
4a = 100 ⟹ a = 25 m
b = 100 – 2a = 100 – 2.25 = 50 m
A = a . b = 25 . 50 = 1250 m2
6-‫وحجمه‬ ‫مربعة‬ ‫قاعدته‬ ‫غطاء‬ ‫بدون‬ ‫مستطيالت‬ ‫متوازي‬ ‫شكل‬ ‫على‬ ‫حوض‬3
108m‫مساحة‬ ‫تكون‬ ‫بحيث‬ ‫ابعاده‬ ‫جد‬
‫صنعه‬ ‫في‬ ‫المستخدمة‬ ‫االلواح‬.‫يمكن‬ ‫ما‬ ‫اقل‬‫)وزاري‬2012(‫اول‬ ‫دور‬
/‫الحل‬‫القاعدة‬ ‫ضلع‬ ‫طول‬ ‫ليكن‬b‫واالرتفاع‬a
A = 4ab + b2
= 4(
108
b2 )b + b2
= 4
108
b
+ b2
A̅ = -4
108
b2 + 2b = 2(b -2
108
b2 )
A̅= 0 ⟹ 2(b - 2
108
b2 ) = 0
b - 2
108
b2 = 0 ⟹ b = 2
108
b2
b3
= 2 . 108 = 216
b = √23 . 333
= 2 . 3 ⟹ b = 6 m
a =
108
62 =
108
36
= 3 m
A = 4 . 6 . 3 + 62
= 72 + 36
A = 108 m2
‫االلواح‬ ‫من‬ ‫مساحة‬ ‫اقل‬
7-‫ارتفاعها‬ ‫وكان‬ ‫االعلى‬ ‫الى‬ ‫رصاصة‬ ‫اطلقت‬)m(‫نه‬ ‫في‬ ‫متر‬‫اية‬t‫بحيث‬ ‫الثواني‬ ‫من‬2
16t–224t=m‫اقصى‬ ‫احسب‬
.‫الرصاصة‬ ‫اليه‬ ‫تصل‬ ‫ارتفاع‬)2016‫دور‬2(
/‫الحل‬‫لـ‬ ‫قيمة‬ ‫اكبر‬ ‫حساب‬ ‫المطلوب‬m‫ت‬ ‫عندما‬ ‫وهي‬‫كون‬‫مشتقة‬m‫ت‬:‫صفر‬ ‫ساوي‬
m = 224t – 16t2
mˊ = 224 – 32t
‫نقطة‬ ‫اعلى‬ ‫عند‬(‫)نهاية‬‫المشتقة‬=‫صفر‬
m̅= 0 ⟹ 224 – 32t = 0 ⟹ 32t = 224 ⟹ t =
224
32
= 7‫ثانية‬
‫الزمن‬ ‫عند‬7‫ثانية‬‫صفر‬ ‫تساوي‬ ‫المشتقة‬‫اال‬ ‫نحسب‬ ‫اذا‬‫رتفاع‬m‫الزمن‬ ‫عند‬7‫ثانية‬:
m = 224 . 7 – 16(7)2
= 1568 – 784 = 784 ‫متر‬ ‫الرصاصة‬ ‫اليه‬ ‫تصل‬ ‫ارتفاع‬ ‫اعلى‬
2 216
2 108
2 54
3 27
3 9
33
1
a a
b
‫االرض‬ ‫محيط‬ ‫من‬
S = 2a + b = 100
b = 100 – 2a
a
b
b
‫الحجم‬ = ab2
= 108
a =
108
b2

78. ‫ادبي‬ ‫سادس‬‫ا‬‫الثالث‬ ‫لفصل‬‫االثرائية‬ ‫االمثلة‬
/‫الشمري‬ ‫أحمد‬ :‫األستاذ‬0770451693778‫المرسل‬‫الطباعية‬ ‫للخدمات‬/07703458937
8-‫قطر‬ ‫ينطبق‬ ‫بحيث‬ ‫دائرة‬ ‫نصف‬ ‫يعلوه‬ ‫مستطيل‬ ‫شكل‬ ‫على‬ ‫نافذة‬‫المستطيل‬ ‫محيط‬ ‫كان‬ ‫فاذا‬ ‫المستطيل‬ ‫ابعاد‬ ‫احد‬ ‫على‬ ‫ها‬8m
.‫يمكن‬ ‫ما‬ ‫اكبر‬ ‫النافذة‬ ‫مساحة‬ ‫تكون‬ ‫لكي‬ ‫المستطيل‬ ‫ابعاد‬ ‫جد‬)‫وزاري‬2013‫دور‬2()‫تمهيدي‬2016(
/‫الحل‬‫المستطيل‬ ‫ابعاد‬ ‫نفرض‬a‫و‬b‫النافذة‬ ‫ومساحة‬‫الكلية‬A
A = a . b +
11
28
a2
= a.( 4 – a) +
11
28
a
2
A = 4a – a2
+
11
28
a
2
= 4a +
11
28
a2
− a2
‫مشترك‬ ‫عامل‬ a2
A = 4a + a2
(
11
28
– 1) = 4a + a2
(
11
28
–
28
28
)
A = 4a + a2
(
−17
28
) = 4a -
17
28
a2
A̅ = 4 -
17
14
a = 0 ⟹ 4 -
17
14
a = 0 ⟹ 4 =
17
14
a
17a = 56 ⟹ a =
56
17
m
b = 4 – a = 4 -
56
17
=
68−56
17
=
12
17
m
9-‫جد‬ , ‫غطاء‬ ‫بدون‬ ‫الشكل‬ ‫مربعة‬ ‫قاعدته‬ ‫السطوح‬ ‫متوازي‬ ‫شكل‬ ‫على‬ ‫الخشب‬ ‫من‬ ‫صندوق‬ ‫صنع‬ ‫يراد‬ ‫للنجارة‬ ‫ورشة‬ ‫في‬
‫لكي‬ ‫الصندوق‬ ‫ابعاد‬‫وارتفاعه‬ ‫قاعدته‬ ‫محيط‬ ‫مجموع‬ ‫ان‬ ‫علما‬ ‫يمكن‬ ‫ما‬ ‫اكبر‬ ‫حجمه‬ ‫يكون‬90m.
/‫الحل‬‫هو‬ ‫القاعدة‬ ‫ضلع‬ ‫طول‬ ‫ان‬ ‫نفرض‬a‫هو‬ ‫الصندوق‬ ‫وارتفاع‬h:
V = a2
. h
V = a2
.(90 -4a) = 90a2
– 4a3
V̅ = 180a – 12a2
= 0 ⇒ 180a – 12a2
= 0
12a(15 – a) = 0
a = 0 ‫تهمل‬
a = 15 m
h = 90 – 4a = 90 – 4 . 15 = 90 – 60
h = 30m
10-‫هي‬ ‫ما‬ ‫سلعة‬ ‫النتاج‬ ‫الكلية‬ ‫الكلفة‬ ‫دالة‬ ‫كانت‬ ‫اذا‬c(x) =
1
2
x2 + x + 40‫معدل‬ ‫عنده‬ ‫يكون‬ ‫الذي‬ ‫االنتاج‬ ‫حجم‬ ‫جد‬
.‫يمكن‬ ‫ما‬ ‫اقل‬ ‫الكلفة‬
/‫الحل‬‫عند‬ ‫كلفة‬ ‫معدل‬ ‫اقل‬Ac̅̅̅ = 0:
Ac =
c(x)
x
=
1
2
x2
+ x + 40
x
Ac =
1
2
x + 1 +
40
x
Ac̅̅̅ =
1
2
−
40
x2 = 0 ⇒ 1
2
−
40
x2
= 0
40
x2 =
1
2
⇒ x2
= 80 ⇒ x = √80 = √16 . 5 = 4 √5 ‫االنتاج‬ ‫حجم‬
2 80
2 40
2 20
2 10
5 5
1
b
a
2(a + b) = 8
a + b = 4
b = 4 – a
h
a
a
‫وارتفاعه‬ ‫الصندوق‬ ‫قاعدة‬ ‫محيط‬ ‫مجموع‬90:‫متر‬
90 = 4a + h
h = 90 -4a

79. ‫ادبي‬ ‫سادس‬‫ا‬‫الثالث‬ ‫لفصل‬‫االثرائية‬ ‫االمثلة‬
/‫الشمري‬ ‫أحمد‬ :‫األستاذ‬0770451693779‫المرسل‬‫الطباعية‬ ‫للخدمات‬/07703458937
‫وا‬ ‫االثرائية‬ ‫األسئلة‬‫لوزارية‬
1(‫كانت‬ ‫اذا‬4
)3-x2
= (f(x)‫جد‬f̅(x)‫و‬f̅̅(x)‫عند‬x = 2.2013-‫ت‬2012-2
2)‫بازاحة‬ ‫االعلى‬ ‫نحو‬ ‫صلدة‬ ‫كرة‬ ‫العب‬ ‫رمى‬2
t16–s(t) = 224t‫نهاية‬ ‫في‬ ‫االمتار‬ ‫من‬t, ‫الثواني‬ ‫من‬
.‫الكرة‬ ‫تصله‬ ‫ارتفاع‬ ‫اقصى‬ ‫احسب‬2012-2
3(‫العالقة‬ ‫وفق‬ ‫جسم‬ ‫تحرك‬9t + 7+2
6t-3
s(t) = t‫حيث‬s‫و‬ ‫باالمتار‬t‫نقطة‬ ‫عن‬ ‫الجسم‬ ‫بعد‬ ‫جد‬ , ‫بالثواني‬
.‫صفرا‬ ‫التعجيل‬ ‫يصبح‬ ‫عندما‬ ‫وسرعته‬ ‫الحركة‬ ‫بداية‬2015-3
4(‫ارسم‬‫منحني‬‫الدالة‬‫باالستعانة‬‫بمعلوماتك‬‫بالتفاضل‬f(x) = x3
+ 3𝑥2
+ 1.2014-1
5(‫ارسم‬‫منحني‬‫الدالة‬‫باستخدام‬‫معلوماتك‬‫بالتفاضل‬f(x) = x3
− 3x2
+ 2.2015-3
6(‫استخدام‬‫معلوماتك‬‫بالتفاضل‬‫ل‬‫رسم‬‫منحني‬‫الدالة‬f(x) = x3(4 − x).
7(‫جد‬‫ان‬‫وجدت‬‫نقاط‬‫االنقالب‬‫ومناطق‬‫التقعر‬‫والتحدب‬‫للدالة‬f(x) = (x − 1)3
.2015-1
8(‫جد‬‫عددين‬‫مجموعهما‬9‫حيث‬‫ان‬‫حاصل‬‫ضرب‬‫مربع‬‫احدهما‬‫في‬‫ثالثة‬‫امثال‬‫االخر‬‫اكبر‬‫ما‬‫يمكن‬.2014-2
9(‫جد‬‫العددين‬‫اللذين‬‫مجموعهما‬8‫ومجموع‬‫مربعيهما‬‫اكبر‬‫ما‬‫يمكن‬.2015-1
10(‫جد‬
dy
dx
:‫يأتي‬ ‫لما‬
a. f(x) = (x3
+ 1)√(x3 + 1)
b. f(x) =
x2+1
x2−1
c. y = (2x -5)5
d. f(x) = (
2𝑥−1
x3+3
)
5
2015-1
e. f(x) = √x4 + 3x2 + 1 2015-1
f. f(x) = 6 . √3x2 + 4 2016-1
g. f(x) = (x2
+ 2x − 3)(2x + 1) 2016-1
11)‫كانت‬ ‫اذا‬f(x) =
4+5x
x2+x+1
,‫اوجد‬f̅(1)2014-2
12)‫كانت‬ ‫اذا‬f(x) = x3
+ 3x2
− 3,‫اوجد‬f̅(x),f̅(1)2015-2
13)‫جد‬y'‫للدالة‬y = (x3
+ 3x2
− 3)
3
2
‫عند‬ ,x = 22015-3
14)‫جسم‬‫يتحرك‬‫على‬‫خط‬‫مستقيم‬‫وفق‬‫المعادلة‬2-+ 3t2
f(t) = t‫جد‬‫سرعة‬‫الجسم‬‫بعد‬5‫ثواني‬‫من‬‫بدأ‬
‫الحركة‬‫علما‬‫ان‬‫االزاحة‬‫باالمتار‬2015-1
15)‫جد‬‫معادلة‬‫المماس‬‫والعمود‬‫على‬‫المماس‬‫لمنحني‬‫الدالة‬y = x3
− 3x2
+ 5‫عند‬x = 1.2015-3
16)‫المنحني‬ ‫الى‬ ‫تنتمي‬ ‫نقطة‬ ‫جد‬3x + 5+x2
=f(x)‫بحيث‬‫يكون‬‫الذي‬ ‫للمستقيم‬ ‫موازيا‬ ‫المماس‬ ‫عندها‬
‫معادلته‬3x + y + 4 =02016-1
17)‫طوله‬ ‫بسياج‬ ‫تسييجها‬ ‫يمكن‬ ‫االرض‬ ‫من‬ ‫مساحة‬ ‫اكبر‬ ‫جد‬ ‫جهاتها‬ ‫أحد‬ ‫من‬ ‫نهر‬ ‫يحدها‬ ‫الشكل‬ ‫مستطيله‬ ‫ارض‬ ‫قطعة‬
120.‫متر‬2016-1
18(‫جد‬f̅(x)‫و‬f̅̅(x):‫يأتي‬ ‫مما‬ ‫لكل‬2016-1
19(f(x) =
1
√2x−1
f(x) = (x2
− 3)4
20(‫الدالة‬ ‫كانت‬ ‫اذا‬f(x) = x2
+ ax + b) ‫انقالب‬ ‫نقطة‬ ‫تمتلك‬ ‫وكانت‬1,-2‫قيمة‬ ‫(جد‬a‫و‬b.2016-2
21(‫كانت‬ ‫اذا‬f(x) = (x2
− 4)4
‫جد‬f̅(1)‫و‬f̅̅(x).2016-2
22)‫كانت‬ ‫اذا‬f(x) = (x3
+ 3x2
− 3)
3
2
‫جد‬ ,f̅(2)2016-3

80. ‫ادبي‬ ‫سادس‬‫ا‬‫الثالث‬ ‫لفصل‬‫االثرائية‬ ‫االمثلة‬
/‫الشمري‬ ‫أحمد‬ :‫األستاذ‬0770451693780‫المرسل‬‫الطباعية‬ ‫للخدمات‬/07703458937
23(‫للدالة‬ ‫واالنقالب‬ ‫الحرجة‬ ‫النقاط‬ ‫جد‬4x + 2–3
f(x) = x.‫وجدت‬ ‫ان‬2016-3
24(‫العالقة‬ ‫وفق‬ ‫جسم‬ ‫تحرك‬ ‫اذا‬8t + 20-2
S(t) = t‫ان‬ ‫حيث‬s, ‫باالمتار‬ ‫بعده‬t‫احسب‬ ‫بالثواني‬ ‫الزمن‬
.‫صفرا‬ ‫سرعته‬ ‫تصبح‬ ‫عندما‬ ‫الحركة‬ ‫بداية‬ ‫نقطة‬ ‫من‬ ‫الجسم‬ ‫بعد‬2016-3

81. /‫الشمري‬ ‫أحمد‬ :‫األستاذ‬0770451693781/ ‫الطباعية‬ ‫للخدمات‬ ‫المرسل‬07703458937
‫األستاذ‬‫الشمري‬ ‫أحمد‬ :
07704516937
‫المرسل‬‫الطباعية‬ ‫للخدمات‬
‫المنصور‬–‫دراغ‬ ‫حي‬ ‫جامع‬ ‫مجاور‬
07703458937
‫ملزمة‬‫الرياضيات‬
‫االدبي‬ ‫السادس‬
2017-2016
‫الفصل‬‫الرابع‬
‫التكامل‬

82. ‫أدبي‬ ‫سادس‬‫الرابع‬ ‫الفصل‬‫المحدد‬ ‫غير‬ ‫التكامل‬
/‫الشمري‬ ‫أحمد‬ :‫األستاذ‬0770451693782/ ‫الطباعية‬ ‫للخدمات‬ ‫المرسل‬07703458937

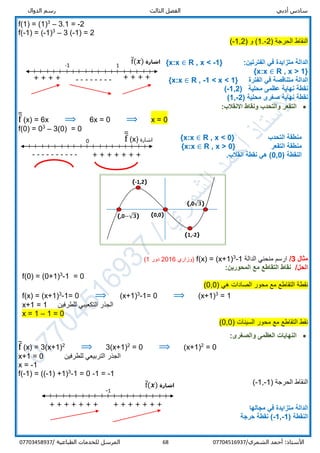
83. ‫أدبي‬ ‫سادس‬‫الرابع‬ ‫الفصل‬‫المحدد‬ ‫غير‬ ‫التكامل‬
/‫الشمري‬ ‫أحمد‬ :‫األستاذ‬0770451693783/ ‫الطباعية‬ ‫للخدمات‬ ‫المرسل‬07703458937
‫الفصل‬‫الرابع‬(‫التكامل‬:)‫االشتقاق‬ ‫عكس‬ ‫عملية‬ ‫وهو‬‫التكامل‬ ‫والثاني‬ ‫المحدد‬ ‫غير‬ ‫التكامل‬ ‫االول‬ ‫التكامل‬ ‫من‬ ‫نوعين‬ ‫وهناك‬
‫المحدد‬.
:‫المحدد‬ ‫غير‬ ‫التكامل‬‫منه‬ ‫الغرض‬‫مشتقتها‬ ‫خالل‬ ‫من‬ ‫الدالة‬ ‫استنتاج‬:‫له‬ ‫ويرمز‬
f(x) = ∫ f̅(x) . dx
‫بالدالة‬ ‫عنها‬ ‫يعبر‬ ‫المشتقة‬ ‫ان‬ ‫فرضنا‬ ‫اذا‬f̅(x) = xn‫ينتج‬ ‫تكاملها‬ ‫عملية‬ ‫فان‬f(x):‫مبين‬ ‫وكما‬
f(x) = ∫ xn.dx =
xn+1
n + 1
+ c
‫الرمز‬ ‫يمثل‬ ‫حيث‬c.‫اخرى‬ ‫معطيات‬ ‫خالل‬ ‫من‬ ‫استنتاجه‬ ‫يتم‬ ‫عددي‬ ‫ثابت‬
‫مثال‬1/‫الدالة‬ ‫كانت‬ ‫اذا‬f(x)( ‫بالنقطة‬ ‫تمر‬1,0‫ومشتقتها‬ )‫هي‬x3
) =x(f̅.‫الدالة‬ ‫تلك‬ ‫جد‬
/‫الحل‬
f(x) = ∫ f̅(x) . dx = ∫ x3
. dx =
x3+1
3+1
+ c ⟹ f(x) =
x4
4
+ c
‫بالنقطة‬ ‫تمر‬ ‫الدالة‬(1,0)‫اذا‬f(1) = 0:
f(1) =
14
4
+ c = 0 ⟹
1
4
+ c = 0 ⟹ c = −
1
4
:‫هي‬ ‫الدالة‬ ‫اذا‬
x4
4
−
1
4
=f(x)
‫مثال‬2/‫الدالة‬ ‫تكامل‬ ‫جد‬1=f(x).
/‫الحل‬‫المتغير‬ ‫يحوي‬ ‫ال‬ ‫الحدود‬ ‫احد‬ ‫كان‬ ‫اذا‬x‫المتغير‬ ‫ان‬ ‫يعني‬ ‫ذلك‬ ‫فان‬x:‫مبين‬ ‫كما‬ ‫صفر‬ ‫لالس‬ ‫مرفوع‬
f(x) = 1 = 1. x0
= x0
∫ x0
. dx =
x0+1
0+1
+ c = x + c
‫مثال‬3/:‫التالية‬ ‫التكامالت‬ ‫من‬ ‫كل‬ ‫جد‬
1) ∫(3x2
+ 5). dx = 3∫ x2
. dx + 5 ∫ x0
. dx = 3
x3
3
+ 5
x1
1
+ c = x3
+ 5x + c
2)∫(x2
+ 1)(2x − 3). dx
:‫االقواس‬ ‫نفتح‬ ‫االول‬ ‫القوس‬ ‫داخل‬ ‫مشتقة‬ ‫يمثل‬ ‫ال‬ ‫الثاني‬ ‫القوس‬ ‫ان‬ ‫مالحظة/بما‬
= ∫(x2
+ 1)(2x − 3). dx = ∫(2x3
+ 2x − 3x2
− 3). dx
:‫المحدد‬ ‫التكامل‬ ‫قواعد‬
1-:‫الدالة‬ ‫تكامل‬ ‫في‬ ‫الثابت‬ ‫يساوي‬ ‫ثابت‬ ‫في‬ ‫دالة‬ ‫تكامل‬
∫[a ∗ f̅(x)] . dx = a ∗ ∫ f̅(x) . dx
2-‫طرح‬ ‫او‬ ‫مجموع‬ ‫يساوي‬ ‫دالتين‬ ‫طرح‬ ‫او‬ ‫مجموع‬ ‫تكامل‬:‫دالة‬ ‫كل‬ ‫تكامل‬
∫[f(x) ± g(x)] dx = ∫ f(x)dx ± ∫ g(x)dx
3-‫للقوة‬ ‫مرفوعة‬ ‫دالة‬ ‫تكامل‬n‫لالس‬ ‫مرفوعة‬ ‫الدالة‬ ‫تساوي‬ ‫القوس‬ ‫داخل‬ ‫مشتقة‬ ‫في‬n+1‫على‬ ‫مقسومة‬n+1:
∫[f(x)]n
. f̅(x) . dx =
[f(x)]n+1
n+1
+ c

84. ‫أدبي‬ ‫سادس‬‫الرابع‬ ‫الفصل‬‫المحدد‬ ‫غير‬ ‫التكامل‬
/‫الشمري‬ ‫أحمد‬ :‫األستاذ‬0770451693784/ ‫الطباعية‬ ‫للخدمات‬ ‫المرسل‬07703458937
= 2
x4
4
+ 2
x2
2
− 3
x3
3
− 3x + c =
x4
2
+ x2
− x3
− 3x + c
3) ∫ (√x −
3
√x23 − 1) . dx = ∫ (x
1
2 − 3 (x)
−2
3 − 1) . dx
=
x
3
2
3
2
− 3
x
1
3
1
3
– x + c =
2
3
x
3
2 − 9 x
1
3 – x + c
=
2
3
√x3
− 9 √x
3
– x + c
4) ∫
x4−8x
x−2
dx = ∫
x(x3−8)
x−2
dx = ∫
x(x−2)(x2+2x+4)
x−2
dx
= ∫ x(x2
+ 2x + 4)dx = ∫(x3
+ 2x2
+ 4x)dx =
x4
4
+
2x3
3
+
4x2
2
+ c
=
x4
4
+
2x3
3
+ 2x2
+ c
5)∫(x3
+ 7)5
. x2
. dx
‫هي‬ ‫االول‬ ‫القوس‬ ‫داخل‬ ‫مشتقة‬23x‫ان‬ ‫وبما‬2x‫بـ‬ ‫الدالة‬ ‫نضرب‬ ‫القوس‬ ‫خارج‬ ‫موجود‬
𝟑
𝟑
:‫مبين‬ ‫كما‬
=
3
3
∫(x3
+ 7)
5
. x2 .dx =
1
3
∫(x3
+ 7)5
. 3x2
. dx
‫دالة‬ ‫لدينا‬(𝐱 𝟑
+ 𝟕) 𝟓
:‫الثالثة‬ ‫القاعدة‬ ‫نطبق‬ ‫اذا‬ ‫القوس‬ ‫داخل‬ ‫بمشتقة‬ ‫مضروبة‬
=
1
3
.
(x3+7)6
6
+ c=
(x3+7)6
18
+ c
6) ∫
x−2
(x2−4x+5)2 dx = ∫(x2
− 4x + 5)
−2
. (x − 2)dx ‫(وزاري‬5201‫دور‬2)
:‫هي‬ ‫االول‬ ‫القوس‬ ‫داخل‬ ‫مشتقة‬ /‫مالحظة‬(2x-4) = 2(x-2)
‫ان‬ ‫وبما‬(x-2)‫بـ‬ ‫التكامل‬ ‫نضرب‬ ‫ان‬ ‫بعد‬ ‫الثالثة‬ ‫القاعدة‬ ‫نطبق‬ ‫فاننا‬ ‫القوس‬ ‫خارج‬ ‫موجودة‬
𝟐
𝟐
=
2
2
∫(x2
− 4x + 5)
−2
. (x − 2)dx =
1
2
∫(x2
− 4x + 5)
−2
. 2(x − 2)dx
=
1
2
.
(x2
−4x+5)
−1
−1
+ c =
−1
2(x2
−4x+5)
+ c
7)∫
x3
√5−x45 dx = ∫(5 − x4
)
−1
5 . x3
dx
‫بـ‬ ‫نضرب‬ ‫القوس‬ ‫داخل‬ ‫مشتقة‬ ‫على‬ ‫لنحصل‬
−𝟒
−𝟒
:‫مبين‬ ‫كما‬
=
−4
−4
∫(5 − x4
)
−1
5 . x3
dx =
1
−4
∫(5 − x4
)
−1
5 . (−4x3
) dx
=
1
−4
.
(5−x4)
4
5
4
5
+ c=
1
−4
.
5
4
(5 − x4
)
4
5 + c=
−5
16
√(5 − x4)45
+ c
8)∫ √3x3 − 5x53
. dx 2016-2

85. ‫أدبي‬ ‫سادس‬‫الرابع‬ ‫الفصل‬‫المحدد‬ ‫غير‬ ‫التكامل‬
/‫الشمري‬ ‫أحمد‬ :‫األستاذ‬0770451693785/ ‫الطباعية‬ ‫للخدمات‬ ‫المرسل‬07703458937
(‫تمهيدي‬ 𝟐𝟎𝟏𝟑 ‫وزاري‬ )(2016‫دور‬2)
= ∫ √x3(3 − 5x2)
3
. dx x3‫مشترك‬ ‫عامل‬
= ∫ x . √(3 − 5x2)
3
. dx = ∫ x . (3 − 5x2
)
1
3. dx
‫القوس‬ ‫داخل‬ ‫مشتقة‬-10x‫نضرب‬ ‫اذا‬‫بـ‬
− 𝟏𝟎
−𝟏𝟎
=
−𝟏𝟎
−𝟏𝟎
∫ x . (3 − 5x2)
1
3
. dx =
𝟏
−𝟏𝟎
∫(−10x) (3 − 5x2
)
1
3. dx
:‫الثالثة‬ ‫القاعدة‬ ‫نطبق‬
=
1
−10
.
(3−5x2)
4
3
4
3
+ c =
−3
40
. √(3 − 5x2)43
+ c
9) ∫
dx
√x2−14x+49
5 = ∫(x2
− 14x + 49)
−1
5 . dx = ∫((x − 7)(x − 7))
−1
5
. dx
= ∫((x − 7)2)
−1
5 . dx = ∫(x − 7)
−2
5 . dx ‫(وزاري‬6201‫دور‬1)
‫القوس‬ ‫داخل‬ ‫مشتقة‬1:‫الثالثة‬ ‫القاعدة‬ ‫نطبق‬ ‫اذا‬ ‫القوس‬ ‫خارج‬ ‫ضمنيا‬ ‫موجود‬ ‫وهو‬
=
(x−7)
3
5
3
5
+ c =
5
3
. √(x − 7)35
+ c
10) ∫
(3x2−4)2− 16
x2 dx 2016-3
:‫مربعين‬ ‫بين‬ ‫فرق‬ ‫البسط‬ ‫نحلل‬
= ∫
((3x2−4)−4)((3x2−4)+4)
x2 dx = ∫
(3x2−8)(3x2)
x2 dx = ∫ 3 . (3x2
− 8) . dx
= 3 ∫(3x2
− 8) . dx = 3(
3x3
3
− 8x )+ c = 3x3
− 24x + c
11) ∫ √z2 + 3z + 2 . dx
‫بداللة‬ ‫التكامل‬ ‫ان‬ ‫بما‬ /‫مهمة‬ ‫مالحظة‬dx‫رمز‬ ‫اي‬ ‫ان‬ ‫اي‬‫عدا‬‫الـ‬x‫الرمز‬ ‫فان‬ ‫المثال‬ ‫هذا‬ ‫وفي‬ ‫ثابت‬ ‫عدد‬ ‫يعتبر‬z‫ان‬ ‫يمكننا‬ ‫لذلك‬ ‫ثابت‬ ‫عدد‬ ‫يمثل‬
:‫االولى‬ ‫القاعدة‬ ‫حسب‬ ‫التكامل‬ ‫عملية‬ ‫من‬ ‫نخرجه‬
= √z2 + 3z + 2 . ∫ x0
. dx = (√z2 + 3z + 2 ). x + c
4-1 ‫التمارين‬ ‫حلول‬
:‫يأتي‬ ‫مما‬ ‫كل‬ ‫تكامالت‬ ‫جد‬
1) ∫(6x2
− 4x + 3)dx ‫(وزاري‬2013‫دور‬1)
=
6x3
3
−
4x2
2
+ 3x + c = 2x3
− 2x2
+ 3x + c
2) ∫(3x − 1)(x + 5)dx ‫(وزاري‬1201‫دور‬1)
= ∫(3x2
− x + 15x − 5)dx = ∫(3x2
+ 14x − 5)dx

86. ‫أدبي‬ ‫سادس‬‫الرابع‬ ‫الفصل‬‫المحدد‬ ‫غير‬ ‫التكامل‬
/‫الشمري‬ ‫أحمد‬ :‫األستاذ‬0770451693786/ ‫الطباعية‬ ‫للخدمات‬ ‫المرسل‬07703458937
= 3
x3
3
+ 14
x2
2
− 5x + c = x3
+ 7x2
− 5x + c
3) ∫ √x (√x + 1)2
dx
= ∫ x
1
2 (x + 2√x + 1)dx = ∫ x
1
2 (x + 2x
1
2 + 1)dx = ∫ (x
3
2 + 2x + x
1
2)dx
=
x
5
2
5
2
+
2x2
2
+
x
3
2
3
2
+ c =
2
5
x
5
2 + x2
+
2
3
x
3
2 + c =
2
5
√x5 + x2
+
2
3
√x3
+ c
4) ∫
x3+27
x+3
dx (2016‫دور‬2)
= ∫
(x+3)(x2−3x+9)
x+3
dx = ∫(x2
− 3x + 9) dx =
x3
3
−
3x2
2
+ 9x + c
5)∫
x3−2x2 +1
5x5 dx =
1
5
∫ (
x3
x5 −
2x2
x5 +
1
x5) dx ‫(وزاري‬5201‫دور‬1)
=
1
5
∫(x−2
− 2x−3
+ x−5) dx =
1
5
(
x−1
−1
−
2x−2
−2
+
x−4
−4
) + c
=
1
5
(
−1
x
−
−1
x2
+
−1
4x4
) + c =
1
5
( −
1
x
+
1
x2
−
1
4x4
) + c
6) ∫
x2+2
√x3+6x+1
3 dx = ∫(x3
+ 6x + 1)
−1
3
. (x2
+ 2) dx
( ‫القوس‬ ‫داخل‬ ‫مشتقة‬𝟑𝐱 𝟐
+ 𝟔‫بـ‬ ‫نضرب‬ ‫اذا‬ )
𝟑
𝟑
:
=
3
3
∫(x3
+ 6x + 1)
−1
3 . (x2
+ 2) dx =
1
3
∫(x3
+ 6x + 1)
−1
3 . (3x2
+ 6) dx
=
1
3
(x3+6x+1)
2
3
2
3
+ c=
1
3
.
3
2
√(x3 + 6x + 1)23
+ c =
1
2
√(x3 + 6x + 1)23
+ c
7) ∫
√x23
+2
√x
3 dx= ∫ (x
2
3 + 2) . x
−1
3 dx ‫(وزاري‬5201‫دور‬3)
( ‫القوس‬ ‫داخل‬ ‫مشتقة‬
𝟐
𝟑
𝐱
−𝟏
𝟑‫نضرب‬ ‫اذا‬ )
𝟐
𝟑
.
𝟑
𝟐
:
=
2
3
.
3
2
∫ (x
2
3 + 2) . x
−1
3 dx=
3
2
∫ (x
2
3 + 2) . (
2
3
x
−1
3 ) dx =
3
2
.
(x
2
3+2)2
2
+ c
=
3
4
. (√x23
+ 2)2
+ c
:‫للحل‬ ‫ثانية‬ ‫طريقة‬
= ∫
√x23
+2
√x
3 dx = ∫(
√x23
√x
3 +
2
√x
3 ) dx = ∫(
x
2
3
x
1
3
+
2
x
1
3
) dx
= ∫(x
2
3 . x−1
3 + 2x
−1
3 ) dx = ∫( x
1
3 + 2x
−1
3 ) dx

87. ‫أدبي‬ ‫سادس‬‫الرابع‬ ‫الفصل‬‫المحدد‬ ‫غير‬ ‫التكامل‬
/‫الشمري‬ ‫أحمد‬ :‫األستاذ‬0770451693787/ ‫الطباعية‬ ‫للخدمات‬ ‫المرسل‬07703458937
=
x
4
3
4
3
+
2x
2
3
2
3
+ c =
3
4
√x43
+ 3 √x23
+ c
8) ∫
dx
√x2+16x+64
5 = ∫
dx
√(x+8)(x+8)
5
= ∫
]dx
√(x+8)
25
= ∫(x + 8)
−2
5 dx
‫تساوي‬ ‫القوس‬ ‫داخل‬ ‫مشتقة‬1:
=
(x+8)
3
5
3
5
+ c =
5
3
√(x + 8)35
+ c
9) ∫ √2x9 − 3x77
dx = ∫ √x7(2x2 − 3)
7
dx ‫مشترك‬ ‫عامل‬ x7
= ∫ x √2x2 − 3
7
dx
= ∫ x (2x2
− 3)
1
7dx
‫القوس‬ ‫داخل‬ ‫مشتقة‬4x‫اذا‬‫ب‬ ‫نضرب‬‫ـ‬
𝟒
𝟒
:
=
1
4
∫ 4x (2x2
− 3)
1
7dx =
1
4
.
(2x2− 3)
8
7
8
7
+c=
7
32
√(2x2 − 3)87
+ c
10)∫(3x2
+
1
√x
)dx = ∫(3x2 + x
−1
2 )dx
=
3x3
3
+
x
1
2
1
2
+ c = x3
+ 2√x + c
11) ∫
y dx
(19−2y2)
1
3
‫للمتغير‬ ‫التكامل‬ ‫هو‬ ‫المطلوب‬ ‫ان‬ ‫بما‬x‫الرمز‬ ‫وضع‬ ‫كونه‬dx‫الرمز‬ ‫يعامل‬ ‫اذا‬y:‫مبين‬ ‫كما‬ ‫التكامل‬ ‫يكون‬ ‫وبذلك‬ ‫ثابت‬ ‫انه‬ ‫على‬
=
y
(19−2y2)
1
3
∫ dx =
y
(19−2y2)
1
3
(x + c) =
y . x
(19−2y2)
1
3
+ c
‫المقدار‬ ‫ان‬
𝐲
(𝟏𝟗−𝟐𝐲 𝟐)
𝟏
𝟑
‫بالثابت‬ ‫ضربناه‬ ‫واذا‬ ‫ثابتة‬ ‫قيمة‬ ‫يمثل‬c‫نعتبره‬ ‫ان‬ ‫يمكننا‬ ‫جديد‬ ‫ثابت‬ ‫سيكون‬ ‫الناتج‬ ‫فان‬c.
12) ∫
x4−16
x+2
dx ‫(وزاري‬2013‫دور‬2)
= ∫
(x2
− 4)(x2
+ 4)
x + 2
dx = ∫
(x − 2)(x + 2)(x2
+ 4)
x + 2
dx
= ∫(x − 2)(x2
+ 4) dx = ∫(x3
+ 4x − 2x2
− 8) dx
=
x4
4
+
4x2
2
−
2x3
3
− 8x + c =
x4
4
+ 2x2
−
2
3
x3
− 8x + c

88. ‫أدبي‬ ‫سادس‬‫الرابع‬ ‫الفصل‬‫المحدد‬ ‫غير‬ ‫التكامل‬
/‫الشمري‬ ‫أحمد‬ :‫األستاذ‬0770451693788/ ‫الطباعية‬ ‫للخدمات‬ ‫المرسل‬07703458937
13) ∫(√x
3
−
1
√x
3 ) dx
= ∫(x
1
3 − x−1
3 ) dx=
x
4
3
4
3
−
x
2
3
2
3
+ c =
3
4
x
4
3 −
3
2
x
2
3 + c
=
3
4
√x43
−
3
2
√x23
+ c
14) ∫ √(1 − 3x)25
dx = ∫(1 − 3x)
2
5 dx (‫تمهيدي‬4201)
‫القوس‬ ‫داخل‬ ‫مشتقة‬-3‫ب‬ ‫نضرب‬ ‫اذا‬
−𝟑
−𝟑
:
=
𝟏
−𝟑
∫(1 − 3x)
2
5 (−𝟑) dx = 𝟏
−𝟑
.
(1−3x)
7
5
7
5
+ c
=
𝟏
−𝟑
.
5
7
. √(1 − 3x)75
+ c= −
𝟓
𝟐𝟏
. √(1 − 3x)75
+ c
15) ∫ x2
. √x3 + 4 dx = ∫ x2
. (x3
+ 4)
1
2 dx
‫القوس‬ ‫داخل‬ ‫مشتقة‬23x‫ب‬ ‫نضرب‬ ‫اذا‬
𝟑
𝟑
:
=
𝟏
𝟑
∫ 3x2
. (x3
+ 4)
1
2 dx =
𝟏
𝟑
(x3+4)
3
2
3
2
+ c=
𝟏
𝟑
.
2
3
. √(x3 + 4)3
+ c
=
𝟐
𝟗
. √(x3 + 4)3
+ c
16) ∫ x (√x3 + 4) dx = ∫(x. √x3 + 4x) dx = ∫(x. x
3
2 + 4x) dx = ∫(x
5
2 + 4x) dx
=
x
7
2
7
2
+
4x2
2
+ c =
2
7
√x7
+ 2x2
+ c
‫ال‬‫تطبيقات‬‫ل‬ ‫الهندسية‬:‫المحدد‬ ‫غير‬ ‫لتكامل‬
:‫التالية‬ ‫الخطوات‬ ‫نتبع‬ ‫فاننا‬ ‫االولى‬ ‫مشتقتها‬ ‫خالل‬ ‫من‬ ‫دالة‬ ‫ايجاد‬ ‫اردنا‬ ‫اذا‬
1-‫الثابت‬ ‫ونضيف‬ ‫الدالة‬ ‫نكامل‬c.
2-‫نقطة‬ ‫عن‬ ‫نبحث‬(x,y)‫الثابت‬ ‫قيمة‬ ‫لنحسب‬ ‫ونعوضها‬ ‫الدالة‬ ‫لمنحني‬ ‫تنتمي‬c.
‫اذا‬:‫التالية‬ ‫الخطوات‬ ‫نتبع‬ ‫فاننا‬ ‫ونقطة‬ ‫ميل‬ ‫بمعلومية‬ ‫الثانية‬ ‫مشتقتها‬ ‫خالل‬ ‫من‬ ‫دالة‬ ‫ايجاد‬ ‫اردنا‬
1-‫على‬ ‫لنحصل‬ ‫الدالة‬ ‫نكامل‬f̅(x)‫تكامل‬ ‫ثابت‬ ‫ونضيف‬k.
2-‫االحداثي‬ ‫فيها‬ ‫نقطة‬ ‫عن‬ ‫نبحث‬x‫معلوم‬ ‫المماس‬ ‫وميل‬ ‫معلوم‬
‫الميل‬ ‫الحرجة‬ ‫والنقاط‬ ‫النهايات‬ ‫(عند‬=0)
3-‫من‬ ‫بدل‬ ‫الميل‬ ‫قيمة‬ ‫نعوض‬f̅(x)‫وقيمة‬x‫قيمة‬ ‫لنجد‬ ‫الدالة‬ ‫في‬k.
4-‫نكامل‬f̅(x)‫على‬ ‫لنحصل‬f(x)‫التكامل‬ ‫ثابت‬ ‫ونضيف‬c.
5-‫المعلومة‬ ‫النقطة‬ ‫نعوض‬(x,y)‫التكامل‬ ‫ثابت‬ ‫قيمة‬ ‫لنجد‬c.
:‫التالية‬ ‫الخطوات‬ ‫نتبع‬ ‫فاننا‬ ‫للدالة‬ ‫تنتميان‬ ‫نقطتين‬ ‫بمعلومية‬ ‫الثانية‬ ‫مشتقتها‬ ‫خالل‬ ‫من‬ ‫دالة‬ ‫ايجاد‬ ‫اردنا‬ ‫اذا‬
1-‫الدالة‬ ‫نكامل‬‫على‬ ‫لنحصل‬f̅(x)‫تكامل‬ ‫ثابت‬ ‫ونضيف‬k.
2-‫نكامل‬f̅(x)‫على‬ ‫لنحصل‬f(x)‫التكامل‬ ‫ثابت‬ ‫ونضيف‬c.
3-‫بمجهولين‬ ‫معادلتين‬ ‫على‬ ‫لنحصل‬ ‫المعلومتين‬ ‫النقطتين‬ ‫نعوض‬k,c.
4-‫قيمة‬ ‫لنجد‬ ‫المعادالت‬ ‫نحل‬k , c.

89. ‫أدبي‬ ‫سادس‬‫الرابع‬ ‫الفصل‬‫المحدد‬ ‫غير‬ ‫التكامل‬
/‫الشمري‬ ‫أحمد‬ :‫األستاذ‬0770451693789/ ‫الطباعية‬ ‫للخدمات‬ ‫المرسل‬07703458937
‫مثال‬1/( ‫نقطة‬ ‫كل‬ ‫عند‬ ‫المنحني‬ ‫ميل‬ ‫كان‬ ‫اذا‬x,y‫هو‬ ‫نقاطه‬ ‫من‬ )2x + 1–2
3x‫بالنقطة‬ ‫يمر‬ ‫الذي‬ ‫المنحني‬ ‫معادلة‬ ‫جد‬
(2,3.)‫(وزاري‬2014‫دور‬1)
/‫الحل‬:‫اذا‬ ‫نقطة‬ ‫اي‬ ‫عند‬ ‫المماس‬ ‫ميل‬ ‫تمثل‬ ‫الدالة‬ ‫مشتقة‬ ‫ان‬ ‫بما‬
f̅(x)= 3x2
– 2x + 1
f(x) = ∫(3x2
– 2x + 1) dx =
3x3
3
–
2x2
2
+ x + c = x3
– x2
+ x + c
( ‫بالنقطة‬ ‫تمر‬ ‫الدالة‬2,3‫اذا‬ )f(2) = 3:
f(2) = 23
– 22
+ 2 + c = 3 ⟹ 8 – 4 + 2 + c = 3
6 + c = 3 ⟹ c = 3 – 6 = -3 ⟹ ∴ f(x) = x3
– x2
+ x − 3
‫مثال‬2/( ‫نقطة‬ ‫كل‬ ‫عند‬ ‫ميله‬ ‫منحني‬x,y‫يساوي‬ )x √x2 + 9‫بالنقطة‬ ‫يمر‬ ‫كان‬ ‫اذا‬ ‫معادلته‬ ‫جد‬(0,7).
/‫الحل‬‫(وزاري‬2012‫دور‬2)
f̅(x)= x √x2 + 9
f(x) = ∫ x √x2 + 9 dx = ∫ x (x2
+ 9)
1
2 dx =
1
2
∫ 2x (x2
+ 9)
1
2 dx
2
2
‫بـ‬ ‫نضرب‬
=
1
2
.
(x2+9)
3
2
3
2
+ c =
1
2
.
2
3
(x2
+ 9)
3
2 + c =
1
3
√(x2 + 9)
3
+ c
( ‫بالنقطة‬ ‫تمر‬ ‫الدالة‬0,7‫اذا‬ )f(0) = 7:
f(0) =
1
3
√(02 + 9)3
+ c = 7
1
3
√93 + c = 7 ⟹
1
3
(√9 )3
+ c = 7 ⟹
1
3
(3)3
+ c = 7 ⟹ 9 + c = 7
c = 7 – 9 = -2 ⟹ ∴ f(x) =
1
3
√(x2 + 9)3
-2
‫مثال‬3/( ‫نقطة‬ ‫اية‬ ‫عند‬ ‫ميله‬ ‫الذي‬ ‫المنحني‬ ‫معادلة‬ ‫جد‬x,y‫هو‬ ‫نقاطه‬ ‫من‬ )2x - 4( ‫قيمتها‬ ‫صغرى‬ ‫نهاية‬ ‫للمنحني‬ ‫وكان‬-3.)
/‫الحل‬:‫الدالة‬ ‫مشتقة‬ ‫هي‬ ‫المماس‬ ‫ميل‬
f̅(x)= 2x -4
f(x) = ∫(2x − 4) dx =
2x2
2
– 4x + c = x2
– 4x + c
‫االحداثي‬ ‫تمثل‬ ‫النهاية‬ ‫مالحظة/قيمة‬y‫قيمة‬ ‫نحسب‬ ‫لذلك‬ , ‫الدالة‬ ‫لمنحني‬ ‫تنتمي‬ ‫التي‬ ‫النهاية‬ ‫لنقطة‬x‫ميل‬ ‫ان‬ ‫وبما‬ ‫للمنحني‬ ‫الصغرى‬ ‫النهاية‬ ‫عند‬
:‫اذا‬ ‫صفر‬ ‫تساوي‬ ‫النهاية‬ ‫عند‬ ‫المشتقة‬ ‫اي‬ ‫صفر‬ ‫يساوي‬ ‫النهاية‬ ‫هذه‬ ‫عند‬ ‫المماس‬
f̅(x)= 2x -4 = 0 ⟹ 2x = 4 ⟹ ∴ x = 2
( ‫النقطة‬2,-3‫للدالة‬ ‫تنتمي‬ ‫انها‬ ‫اي‬ ‫للدالة‬ ‫صغرى‬ ‫نهاية‬ )‫اذا‬f(2) = -3:
f(2) = 22
– 4 . 2 + c = -3 ⟹ 4 – 8 + c = -3 ⟹ c = 4 – 3 = 1
∴ f(x) = x2
− 4x + 1

90. ‫أدبي‬ ‫سادس‬‫الرابع‬ ‫الفصل‬‫المحدد‬ ‫غير‬ ‫التكامل‬
/‫الشمري‬ ‫أحمد‬ :‫األستاذ‬0770451693790/ ‫الطباعية‬ ‫للخدمات‬ ‫المرسل‬07703458937
‫مثال‬4/‫نقطة‬ ‫اي‬ ‫عند‬ ‫ميله‬ ‫الذي‬ ‫المنحني‬ ‫معادلة‬ ‫جد‬(x,y‫هو‬ ‫نقطه‬ ‫من‬ )2-x–2
x‫تنتمي‬ ‫عظمى‬ ‫نهاية‬ ‫للمنحني‬ ‫وكان‬
.‫السينات‬ ‫لمحور‬‫(وزاري‬2015‫دور‬1)‫(وزاري‬2016‫دور‬1)
/‫الحل‬:‫الدالة‬ ‫مشتقة‬ ‫هو‬ ‫المماس‬ ‫ميل‬
f̅(x)= x2
–x -2
f(x)= ∫(x2–x − 2) dx=
x3
3
–
x2
2
- 2x + c
‫قيمة‬ ‫اذا‬ ‫السينات‬ ‫لمحور‬ ‫تنتمي‬ ‫العظمى‬ ‫النهاية‬ ‫ان‬ ‫بما‬y‫تساوي‬ ‫عندها‬0.
‫عند‬ ‫المشتقة‬: ‫صفر‬ ‫تساوي‬ ‫النهايات‬
f̅(x)= x2
–x -2 = 0 ⟹ x2
–x -2 = 0 ⟹ (x – 2)(x +1) =0
x = 2 , x = -1
:‫العظمى‬ ‫النهاية‬ ‫لتحديد‬ ‫المشتقة‬ ‫اشارة‬ ‫بفحص‬ ‫نقوم‬ ‫الدالة‬ ‫لمنحني‬ ‫نهايتين‬ ‫توجد‬
‫عند‬x = -1.‫عظمى‬ ‫نهاية‬
( ‫النقطة‬-1 , 0‫اذا‬ ‫الدالة‬ ‫لمنحني‬ ‫تنتمي‬ )f(-1) = 0:
f(-1) =
(−1)3
3
–
(−1)2
2
− 2(−1) + c = 0
−1
3
–
1
2
+ 2 + c = 0 ⟹ c =
1
3
+
1
2
− 2 =
2+3−12
6
=
−7
6
∴ f(x) =
x3
3
–
x2
2
− 2x −
7
6
‫مثال‬5/‫تحقق‬ ‫التي‬ ‫الدالة‬ ‫جد‬
d2y
d2x
= 12x2
− 2,
dy
dx
= 5( ‫النقطة‬ ‫عند‬1,2.)
/‫الحل‬:‫الدالة‬ ‫على‬ ‫لنحصل‬ ‫مرتين‬ ‫نكامل‬ ‫الثانية‬ ‫المشتقة‬ ‫خالل‬ ‫من‬
d2
y
dx2
= 12x2
− 2
dy
dx
= ∫(12x2
− 2) dx = 4x3
– 2x + k
( ‫النقطة‬ ‫عند‬1,2‫فان‬ )
dy
dx
= 5:
4(1)3
– 2(1) + k = 5 ⟹ 4 – 2+ k = 5 ⟹ k = 5 – 2 = 3
∴
dy
dx
= 4x3
– 2x + 3
y = ∫(4x3
– 2x + 3) dx = x4
– x2
+ 3x + c
( ‫النقطة‬1,2:‫الدالة‬ ‫لمنحني‬ ‫تنتمي‬ )
2 = 14
– 12
+ 3 + c ⟹ 2 = 1 – 1 + 3 + c
c = 2 - 3 = -1 ⟹ ∴ y = x4
– x2
+ 3x − 1
‫مثال‬6/( ‫الثانية‬ ‫مشتقته‬ ‫الذي‬ ‫المنحني‬ ‫معادلة‬ ‫جد‬6x( ‫بالنقطتين‬ ‫ويمر‬ )1,6(, )-1,6.)
/‫الحل‬
y̅̅ = 6x
y̅ = ∫(6x) dx = 3x2
+ k
y = ∫(3x2
+ c1) dx = x3
+ k x + c
-------- + + + +
-1 2
+ + + +

91. ‫أدبي‬ ‫سادس‬‫الرابع‬ ‫الفصل‬‫المحدد‬ ‫غير‬ ‫التكامل‬
/‫الشمري‬ ‫أحمد‬ :‫األستاذ‬0770451693791/ ‫الطباعية‬ ‫للخدمات‬ ‫المرسل‬07703458937
‫النقطة‬ ‫نعوض‬(1,6):‫الدالة‬ ‫في‬
1 + k + c = 6 ⟹ k + c = 6-1 ⟹ k + c = 5 ……………….❶
‫النقطة‬ ‫نعوض‬(1,6-):‫الدالة‬ ‫في‬
-1 – k + c = 6 ⟹ – k + c = 6 + 1 ⟹ – k + c = 7 ………❷
‫بين‬ ‫بالجمع‬❶‫و‬❷:
k + c = 5
– k + c = 7
‫بالجمع‬
0 + 2 c = 12
c = 6
‫معادلة‬ ‫في‬ ‫نعوض‬❶‫على‬ ‫لنحصل‬k:
k = 5 – c ⟹ k= 5 – 6 ⟹ k = -1 ⟹ ∴ y = x3
- x + 6
‫مثال‬7/( ‫عند‬ ‫منحني‬ ‫ميل‬ ‫كان‬ ‫اذا‬x,y‫هو‬ )2
3x–ax‫المستقيم‬ ‫وكان‬0=4-y–9x( ‫عند‬ ‫مماسا‬1,5.‫معادلته‬ ‫جد‬ , )
/‫الحل‬( ‫عند‬ ‫منحني‬ ‫ميل‬x,y:‫الدالة‬ ‫مشتقة‬ ‫هو‬ )(‫تمهيدي‬2014)
y̅ = ax – 3x2
‫الثابت‬ ‫تحوي‬ ‫المشتقة‬ ‫ان‬ ‫بما‬ /‫مالحظة‬a. ‫اوال‬ ‫قيمته‬ ‫بتعريف‬ ‫نقوم‬ ‫فاننا‬
m =
−9
−1
= 9 ‫المماس‬ ‫ميل‬
‫معامل‬ ‫سالب‬ ‫يساوي‬ ‫المعادلة‬ ‫من‬ ‫المستقيم‬ ‫ميل‬ /‫مالحظة‬x‫معامل‬ ‫على‬y.
( ‫النقطة‬ ‫عند‬ ‫المماس‬ ‫ميل‬1,5: ‫النقطة‬ ‫تلك‬ ‫عند‬ ‫الدالة‬ ‫مشتقة‬ ‫يساوي‬ )
y̅ = ax – 3x2
⟹ 9 = a(1) – 3(1)2
⟹ 9 = a – 3 ⟹ a = 9 + 3 = 12
∴ y̅ = 12x – 3x2
y = ∫(12x – 3x2
) dx = 6x2
– x3
+ c
( ‫النقطة‬1,5:‫الدالة‬ ‫لمنحني‬ ‫تنتمي‬ )
5 = 6(1)2
– (1)3
+ c ⟹ 5 = 6– 1 + c ⟹ c = 0
∴ y = 6x2
– x3
‫مثال‬8/( ‫هو‬ ‫نقطة‬ ‫اي‬ ‫عند‬ ‫ميله‬ ‫الذي‬ ‫المنحني‬ ‫معادلة‬ ‫جد‬9-6x-2
ax( ‫انقالب‬ ‫نقطة‬ ‫وللمنحني‬ )6-,1.)(5201‫دور‬3)
/‫الحل‬:‫الدالة‬ ‫مشتقة‬ ‫يساوي‬ ‫المماس‬ ‫ميل‬
y̅ = ax2
-6x -9
( ‫االنقالب‬ ‫نقاط‬ ‫عند‬1,-6):‫صفر‬ ‫تساوي‬ ‫للدالة‬ ‫الثانية‬ ‫المشتقة‬
y̅̅ = 2a(1) – 6 = 0
2a – 6 = 0 ⟹ 2a = 6 ⟹ a = 3 ⟹ ∴ yˊ = 3x2
– 6x -9
y = ∫(3x2
− 6x − 9) dx = x3
− 3x2
− 9x + c
( ‫النقطة‬1,-6‫لمنحني‬ ‫تنمي‬ ):‫الدالة‬
-6 = 13
− 3(1)2
− 9(1) + c ⟹ -6 = 1 − 3 − 9 + c ⟹ c = 11 – 6 = 5
∴ y = x3
− 3x2
− 9x + 5

92. ‫أدبي‬ ‫سادس‬‫الرابع‬ ‫الفصل‬‫المحدد‬ ‫غير‬ ‫التكامل‬
/‫الشمري‬ ‫أحمد‬ :‫األستاذ‬0770451693792/ ‫الطباعية‬ ‫للخدمات‬ ‫المرسل‬07703458937
:‫المحدد‬ ‫غير‬ ‫للتكامل‬ ‫االقتصادي‬ ‫التطبيق‬
‫الكلي‬ ‫االيراد‬ ‫دالة‬M(v)‫حيث‬v‫يمثل‬‫االنتاج‬ ‫حجم‬.
‫الحدي‬ ‫االيراد‬ ‫دالة‬=𝐌̅(𝐯).
‫السعر‬ ‫دالة‬=
𝐌(𝐯)
‫المباعة‬ ‫الكمي‬‫ة‬
‫المباعة‬ ‫الكمية‬ ‫فان‬ ‫يباع‬ ‫االنتاج‬ ‫كل‬ ‫اذا‬‫تساوي‬.‫االنتاج‬ ‫حجم‬
‫اذا‬‫االنتاج‬ ‫حجم‬‫يساوي‬0‫الكلي‬ ‫االيراد‬ ‫فان‬‫يساوي‬0.
‫االنتاج‬ ‫عندما‬ ‫التكلفة‬ ‫هي‬ ‫الثابتة‬ ‫التكلفة‬‫يساوي‬0.
‫مثال‬9/‫هي‬ ‫الحدي‬ ‫االيراد‬ ‫دالة‬ ‫كانت‬ ‫اذا‬:M̅ = 8 − 6v − 2v2
‫حيث‬v‫االنتاج‬ ‫حجم‬‫الكلي‬ ‫االيراد‬ ‫دالة‬ ‫جد‬ ,
.‫السعر‬ ‫ودالة‬
/‫الحل‬:‫الحدي‬ ‫االيراد‬ ‫دالة‬ ‫تكامل‬ ‫تساوي‬ ‫االيراد‬ ‫دالة‬
M(v) = ∫(8 − 6v − 2v2
) dv = 8v − 3v2
−
2v3
3
+ c
‫عندما‬‫االنتاج‬ ‫حجم‬v=0‫الكلي‬ ‫االيراد‬ ‫فان‬M(v)=0:
M(0) = 8(0) − 3(0)2
−
2(0)3
3
+ c = 0 ⟹ ∴ c = 0
∴ M = 8v − 3v2
−
2v3
3
‫المباعة‬ ‫الكمية‬ ‫ان‬ ‫اي‬ ‫يباع‬ ‫ينتج‬ ‫ما‬ ‫كل‬ ‫ان‬ ‫نفرض‬=v
‫السعر‬ ‫دالة‬ =
M(v)
‫المباعة‬ ‫الكمية‬
=
8v−3v2−
2v3
3
v
= 8 – 3v -
2v2
3
‫مثال‬10/‫الحدية‬ ‫التكلفة‬ ‫دالة‬ ‫كانت‬ ‫اذا‬ˊT‫هي‬25v–2 + 60v=ˊT‫حيث‬v‫الكلية‬ ‫التكلفة‬ ‫دالة‬ ‫جد‬ , ‫االنتاج‬ ‫حجم‬
‫ان‬ ‫علما‬T = 65‫االنتاج‬ ‫عندما‬.‫صفر‬ ‫يساوي‬(2013‫دور‬1)
/‫الحل‬
T = ∫(2 + 60v– 5v2
) dv = 2v + 30v2
–
5v3
3
+ c
‫االنتاج‬ ‫عند‬=‫فان‬ ‫صفر‬T = 65:
65 = 2(0) + 30(0)2
–
5(0)3
3
+ c ⟹ c = 65
∴ T = 2v + 30v2
–
5v3
3
+ 65
‫تمارين‬ ‫حلول‬2-4
1-( ‫عند‬ ‫ميله‬ ‫الذي‬ ‫المنحني‬ ‫معادلة‬ ‫جد‬x,y‫يساوي‬ )
−2
x3( ‫بالنقطة‬ ‫يمر‬ ‫المنحني‬ ‫وكان‬1,3.)(2011‫دور‬1)
/‫الحل‬:‫المشتقة‬ ‫يساوي‬ ‫المماس‬ ‫ميل‬
y̅ =
−2
x3
⟹ y = ∫ (
−2
x3 ) dx = −2 ∫(x−3)dx = -2
x−2
−2
+c =
1
x2 + c
( ‫النقطة‬1,3):‫الدالة‬ ‫لمنحني‬ ‫تنتمي‬
3 =
1
12 + c ⟹ c = 3 -1 = 2 ⟹ ∴ y =
1
x2 + 2

93. ‫أدبي‬ ‫سادس‬‫الرابع‬ ‫الفصل‬‫المحدد‬ ‫غير‬ ‫التكامل‬
/‫الشمري‬ ‫أحمد‬ :‫األستاذ‬0770451693793/ ‫الطباعية‬ ‫للخدمات‬ ‫المرسل‬07703458937
2-‫معادلة‬ ‫جد‬( ‫عند‬ ‫ميله‬ ‫الذي‬ ‫المنحني‬x,y‫هو‬ ‫نقاطه‬ ‫من‬ )9-6x–2
3x‫قيمتها‬ ‫عظمى‬ ‫نهاية‬ ‫للمنحني‬ ‫وكان‬10.
/‫الحل‬:‫المشتقة‬ ‫يساوي‬ ‫المماس‬ ‫ميل‬‫(وزاري‬2015‫دور‬2)
y̅ = 3x2
– 6x - 9
y = ∫(3x2
– 6x − 9)dx = x3
– 3x2
− 9x + c
‫العظمى‬ ‫النهاية‬ ‫عند‬y = 10:‫صفر‬ ‫يساوي‬ ‫المماس‬ ‫وميل‬
3x2
– 6x – 9 = 0 ⟹ 3)x2
– 2x – 3) = 0 ⟹ 3 (x - 3)(x + 1) = 0
x = 3 , x = -1
( ‫النقطة‬ ‫عند‬ ‫العظمى‬ ‫النهاية‬-1 , 10)
10 = (−1)3
– 3(−1)2
− 9(−1) + c ⟹ 10 = −1– 3 + 9 + c ⟹ c = 5
∴ y = x3
– 3x2
− 9x + 5
3-‫الثانية‬ ‫مشتقته‬ ‫الذي‬ ‫المنحني‬ ‫معادلة‬ ‫جد‬6x -2‫ا‬ ‫عند‬ ‫ميله‬ ‫وكان‬( ‫لنقطة‬2,5( ‫يساوي‬ )-1.)
‫(وزاري‬2013‫تمهيدي‬‫و‬2013‫دور‬2)
/‫الحل‬
y̅̅ = 6x -2
y̅ = ∫(6x − 2) dxˊ = 3x2
− 2x + c
‫ا‬ ‫عند‬ ‫المماس‬ ‫ميل‬( ‫لنقطة‬2,5( ‫يساوي‬ )-1:)
-1 = 3(2)2
- 2(2) + c ⟹ -1 = 12 - 4 + c ⟹ c = -9 ⟹
∴ yˊ = 3x2
-2x -9
y = ∫(3x2
− 2x − 9) dx = x3
− x2
− 9x + c
‫ا‬( ‫لنقطة‬2,5):‫الدالة‬ ‫لمنحني‬ ‫تنتمي‬
5 = 23
− 22
− 9(2) + c ⟹ 5 = 8 − 4 − 18 + c ⟹ c = 19
∴ y = x3
− x2
− 9x + 19
4-( ‫بالنقطتين‬ ‫يمر‬ ‫منحني‬2,-3( , )-1,9)( ‫عند‬ ‫وميله‬x,y‫يساوي‬ )ax-5.‫معادلته‬ ‫جد‬2012-32016-3
/‫الحل‬:‫المشتقة‬ ‫يساوي‬ ‫المماس‬ ‫ميل‬
y̅ = ax - 5
y = ∫(ax − 5)dx =
ax2
2
− 5x + c
‫النقطة‬(2,-3:‫المنحني‬ ‫على‬ ‫تقع‬ )
-3 =
a(2)2
2
- 5(2) + c ⟹ -3 = 2a − 10 + c ⟹ -2a - c = - 10 + 3
-2a - c = -7 ……………❶
‫النقطة‬(-1,9:‫المنحني‬ ‫على‬ ‫تقع‬ )
9 =
a(−1)2
2
− 5(−1) + c ⟹ 9 =
a
2
+ 5 + c ⟹
a
2
+ c = 9 + 5
a
2
+ c = 4 ‫بـ‬ ‫الطرفين‬ ‫نضرب‬4
-------- + + + +
-1 3
+ + + +

94. ‫أدبي‬ ‫سادس‬‫الرابع‬ ‫الفصل‬‫المحدد‬ ‫غير‬ ‫التكامل‬
/‫الشمري‬ ‫أحمد‬ :‫األستاذ‬0770451693794/ ‫الطباعية‬ ‫للخدمات‬ ‫المرسل‬07703458937
2a + 4c = 16 ……………….❷
‫بين‬ ‫بالجمع‬❶‫و‬❷:
-2a - c = -7
2a + 4c = 16
‫بالجمع‬
0 + 3c = 9
3c = 9 ⟹ c = 3
‫معادلة‬ ‫من‬❶‫قيم‬ ‫نستخرج‬‫ة‬a:
-2a - c = -7 ⟹ −2a − 3 = −7 ⟹ -2a = -7 + 3 = -4 ⟹ a = 2
∴ y = x2
− 5x + 3
5-‫هي‬ ‫الحدي‬ ‫االيراد‬ ‫دالة‬ ‫كانت‬ ‫اذا‬2
8v + v-12=M̅)‫(السعر‬ ‫الطلب‬ ‫ودالة‬ ‫الكلي‬ ‫االيراد‬ ‫دالة‬ ‫فأوجد‬‫ان‬ ‫بفرض‬
.‫يباع‬ ‫ينتج‬ ‫ما‬‫(وزاري‬2013‫دور‬1)(2016)‫تمهيدي‬
/‫الحل‬
M(v) = ∫(12 − 8v + v2
) dv = 12v − 4v2
−
v3
3
+ c
‫االنتاج‬ ‫حجم‬ ‫كان‬ ‫اذا‬v:‫صفر‬ ‫يساوي‬ ‫االيراد‬ ‫فان‬ ‫صفر‬ ‫يساوي‬
0 = 12(0) − 4(0)2
−
(0)3
3
+ c ⟹ c = 0
∴ M = 12v − 4v2
−
v3
3
‫يباع‬ ‫ينتج‬ ‫ما‬ ‫كل‬ ‫ان‬ ‫بما‬:‫السعر‬ ‫دالة‬=
12v−4v2−
v3
3
v
=
v2
3-4v–12
6-‫هي‬ ‫الحدية‬ ‫التكلفة‬ ‫دالة‬ ‫كانت‬ ‫اذا‬5v-1000=ˊT‫حيث‬v‫ان‬ ‫العلم‬ ‫مع‬ ‫الكلية‬ ‫التكلفة‬ ‫دالة‬ ‫فاوجد‬ , ‫االنتاج‬ ‫حجم‬
‫الثابتة‬ ‫التكلفة‬=150.
/‫الحل‬
T = ∫(1000 − 5v) dv = 1000v −
5v2
2
+ c
‫االنتاج‬ ‫عند‬=‫فان‬ ‫صفر‬T = 150:
150 = 1000(0)–
5(0)2
2
+ c ⟹ c = 150
∴ T = 1000v −
5v2
2
+ 150

95. ‫أدبي‬ ‫سادس‬‫الرابع‬ ‫الفصل‬‫المحدد‬ ‫التكامل‬
/‫الشمري‬ ‫أحمد‬ :‫األستاذ‬0770451693795/ ‫الطباعية‬ ‫للخدمات‬ ‫المرسل‬07703458937
:‫المحدد‬ ‫التكامل‬‫محدد‬ ‫الغير‬ ‫التكامل‬ ‫قواعد‬ ‫نفس‬ ‫نستخدم‬ ‫وفيه‬ ‫المنحنيات‬ ‫بين‬ ‫المساحة‬ ‫حساب‬ ‫في‬ ‫المحدد‬ ‫التكامل‬ ‫يستخدم‬
‫الثابت‬ ‫نضيف‬ ‫ال‬ ‫ولكننا‬c:‫بـ‬ ‫المحدد‬ ‫للتكامل‬ ‫ويرمز‬ ‫التكامل‬ ‫لناتج‬
A = ∫ f(x)dx
b
a
‫على‬ ‫نطلق‬ ‫حيث‬a‫وعلى‬ ‫االسفل‬ ‫الحد‬b.‫للتكامل‬ ‫االعلى‬ ‫الحد‬
‫الدالة‬ ‫ان‬ ‫فرضنا‬ ‫اذا‬g(x)‫الدالة‬ ‫مشتقة‬ ‫هي‬f(x):‫التالي‬ ‫القانون‬ ‫طريق‬ ‫عن‬ ‫تتم‬ ‫المحدد‬ ‫التكامل‬ ‫قيمة‬ ‫حساب‬ ‫عملية‬ ‫فان‬
∫ g(x)dx
b
a
= f(b) – f(a)
‫للدالة‬ ‫المحدد‬ ‫التكامل‬ ‫ان‬ ‫اي‬g(x)‫من‬a‫الى‬b‫الدالة‬ ‫قيمة‬ ‫طرح‬ ‫ناتج‬ ‫يساوي‬f(a)‫الدالة‬ ‫قيمة‬ ‫من‬f(b).
‫مثال‬1/:‫التالية‬ ‫التكامالت‬ ‫قيمة‬ ‫جد‬
1) ∫ (3x2
+ 2x − 2)dx
2
1
= [x3
+ x2
− 2x] 2
1
c ‫للدالة‬ ‫التكامل‬ ‫بحساب‬ ‫اوال‬ ‫نقوم‬‫الثابت‬ ‫نظيف‬ ‫وال‬
‫للتكامل‬ ‫االعلى‬ ‫الحد‬ ‫بتعويض‬ ‫نقوم‬2‫الحد‬ ‫نعوض‬ ‫وبعده‬ ‫الطرح‬ ‫اشارة‬ ‫ثم‬ ‫ومن‬‫للتكامل‬ ‫االسفل‬1:
= [23
+ 22
− 2(2)] − [13
+ 12
− 2(1)] = [8 + 4 − 4] − [1 + 1 − 2] = 8 − 0 = 8
.‫الصادات‬ ‫او‬ ‫السينات‬ ‫ومحور‬ ‫بتكاملها‬ ‫قمنا‬ ‫التي‬ ‫الدالة‬ ‫منحني‬ ‫بين‬ ‫المساحة‬ ‫يمثل‬ ‫كونه‬ ‫عددية‬ ‫قيمة‬ ‫يكون‬ ‫دائما‬ ‫المحدد‬ ‫التكامل‬ ‫ناتج‬
2) ∫
2x
√x2+16
dx
3
0
= ∫ 2x . (x2
+ 16)−
1
2 . dx
3
0
= [
(x2+16)
1
2
1
2
]
3
0
= [2√ x2 + 16 ]
3
0
= [2√ 32
+ 16 ] − [2√ 02
+ 16 ] = [2√25 ] − [2√16 ] = 2 .5 − 2 .4 = 2 )‫تمهيدي‬ 2014()3 ‫دور‬ 2015(
3) ∫ x(x − 1)(x − 2)dx
0
4
= ∫ (x2
− 2x)(x − 1)dx
0
4
‫االول‬ ‫القوس‬ ‫داخل‬ ‫مشتقة‬2x-2‫بـ‬ ‫نضرب‬ ‫اذا‬
𝟐
𝟐
:
=
1
2
∫ (x2
− 2x) . 2(x − 1)dx
0
4
=
1
2
∫ (x2
− 2x) . (2x − 2)dx
0
4
=
1
2
[
(x2−2x)2
2
]
0
4
=
1
2
[
(02−2(0))2
2
]-
1
2
[
(42−2(4))2
2
] = 0 -
(16−8)2
4
= -
(8)2
4
= -
64
4
= -16
4) ∫ (
√ √x
3
− 1
√x23 )dx
125
1
= ∫ (
√x
1
3− 1
x
2
3
)dx
125
1
= ∫ (x
1
3 − 1)
1
2 . x−
2
3 . dx
125
1
‫القوس‬ ‫داخل‬ ‫مشتقة‬
𝐱
−
𝟐
𝟑
𝟑
‫بـ‬ ‫نضرب‬ ‫اذا‬
𝟑
𝟑
:(2014‫دور‬1)
= 3 ∫ (x
1
3 − 1)
1
2 .
x
−
2
3
3
. dx
125
1
= 3[
(x
1
3− 1)
3
2
3
2
]
125
1
= [2√(√x
3
− 1)3]
125
1
= [2√(√125
3
− 1)3 ]- [2√(√1
3
− 1)3 ] = [2√(5 − 1)3 ]- [2√(0)3 ]
= 2√(4)3 = 2√16 . 4 = 2 . 4 . 2 = 16

96. ‫أدبي‬ ‫سادس‬‫الرابع‬ ‫الفصل‬‫المحدد‬ ‫التكامل‬
/‫الشمري‬ ‫أحمد‬ :‫األستاذ‬0770451693796/ ‫الطباعية‬ ‫للخدمات‬ ‫المرسل‬07703458937
5) ∫ (
1
√x
+ √x)dx
4
1
= ∫ (x−
1
2 + x
1
2)dx
4
1
= [2x
1
2 +
2
3
x
3
2]1
4
= [2√x +
2
3
√x3
] 1
1
41
= [2√4 +
2
3
√43
] - [2√1 +
2
3
√13
] = [4 +
2
3
8] - [2 +
2
3
]
= 4 +
16
3
– 2 −
2
3
= 2 +
14
3
=
6
3
+
14
3
=
20
3
6)‫قيمة‬ ‫جد‬a∈ R‫ان‬ ‫علمت‬ ‫اذا‬:∫ (𝟐𝐱 − 𝟏)𝐝𝐱 = 𝟒𝟐
𝐚
𝟎
/‫الحل‬
∫ (2x − 1)dx
a
0
= [x2
− x] 1
0
a1
= [a2
− a] - [02
− 0] = a2
− a
∴ a2
− a = 42
a2
− a − 42 = 0 ⟹ (a - 7)(a + 6) = 0 ⟹ a = 7 or a = -6
7) ∫ √x2 + 12x + 36
3
. dx
−5
−6
= ∫ √(x + 6)(x + 6)
3
. dx
−5
−6
= ∫ √(x + 6)23
. dx
−5
−6
= ∫ (x + 6)
2
3 . dx
−5
−6
= [
3
5
(x + 6)
5
3]−6
−5
= [
3
5
√(x + 6)53
] 1
−6
−51
= [
3
5
√(−5 + 6)53
] – [
3
5
√(−6 + 6)53
] =
3
5
8)‫قيمة‬ ‫جد‬a∈ R‫ان‬ ‫علمت‬ ‫اذا‬∫ (3 + 2x)dx = 6
2
a
/‫الحل‬
∫ (3 + 2x)dx
2
a
= [3x + x2]1
a
21
= [3(2) + 22
] - [3a + a2
]
= 6 + 4 - 3a − a2
= 10 - 3a − a2
= 6
10 - 3a − a2
– 6 = 0 -1 ‫بـ‬ ‫نضرب‬
a2
+ 3a – 4 = 0 ⟹ (a + 4)(a - 1) = 0 ⟹ a = -4 or a = 1
‫التمارين‬ ‫حلول‬3-4
:‫يأتي‬ ‫مما‬ ‫كال‬ ‫تكامالت‬ ‫جد‬
1) ∫(2x + 5)(x + 1)dx = ∫(2x2
+ 2x + 5x + 5)dx = ∫(2x2
+ 7x + 5)dx
=
2x3
3
+
7x2
2
+ 5x + c
2) ∫ (x + 3)(x − 2)dx
1
−1
= ∫ (x2
− 2x + 3x − 6)dx
1
−1
= ∫ (x2
+ x − 6)dx
1
−1
= [
x3
3
+
x2
2
− 6x] 1
−1
11
= [
13
3
+
12
2
− 6] − [
−13
3
+
−12
2
+ 6]
=
1
3
+
1
2
− 6 −
−1
3
−
1
2
− 6 =
1
3
+
1
2
− 6 +
1
3
−
1
2
− 6 =
2
3
− 12 =
−34
3
3) ∫ √x(√x + 5)dx (2012‫دور‬1‫ودور‬3)
= ∫(x + 5√x)dx = ∫(x + 5x
1
2)dx =
x2
2
+
10
3
x
3
2 + c =
1
2
x2
+
10
3
√x3
+ c

97. ‫أدبي‬ ‫سادس‬‫الرابع‬ ‫الفصل‬‫المحدد‬ ‫التكامل‬
/‫الشمري‬ ‫أحمد‬ :‫األستاذ‬0770451693797/ ‫الطباعية‬ ‫للخدمات‬ ‫المرسل‬07703458937
4) ∫ √x(x + 1)2
dx
4
0
‫(وزاري‬2011‫دور‬1)
= ∫ √x(x2
+ 2x + 1)dx
4
0
= ∫ (x
5
2 + 2x
3
2 + x
1
2)dx
4
0
= [
2
7
x
7
2 +
4
5
x
5
2 +
2
3
x
3
2] 1
0
41
= [
2
7
4
7
2 +
4
5
4
5
2 +
2
3
4
3
2] − [
2
7
0
7
2 +
4
5
0
5
2 +
2
3
0
3
2] = [
2
7
27
+
4
5
25
+
2
3
23
]
= [
2
7
128 +
4
5
32 +
2
3
8] =
256
7
+
128
5
+
16
3
=
3840+ 2688+ 560
105
=
7088
105
5) ∫ √x(√x + 2)
2
dx
= ∫ √x(x + 4√x + 4)dx = ∫ x
1
2(x + 4x
1
2 + 4)dx = ∫(x
3
2 + 4x + 4x
1
2)dx
=
2
5
x
5
2 + 2x2
+ 8x
3
2 + c =
2
5
√x5
+ 2x2
+ 8√x3
+ c
6) ∫
x3−27
x−3
dx
0
−1
= ∫
(x−3)(x2+3x+9)
x−3
dx
0
−1
= ∫ (x2
+ 3x + 9)dx
0
−1
= [
1
3
x3
+
3
2
x2
+ 9x] 1
−1
01
= [
1
3
03
+
3
2
02
+ 9 . 0] − [
1
3
(−1)3
+
3
2
(−1)2
+ 9(−1)]
= − [−
1
3
+
3
2
− 9] =
1
3
−
3
2
+ 9 =
2−9+54
6
=
47
6
7) ∫
x4−1
x−1
dx = ∫
(x2−1)(x2+1)
x−1
dx = ∫
(x−1)(x+1)(x2+1)
x−1
dx
= ∫(x + 1)(x2
+ 1)dx = ∫(x3
+ x + x2
+ 1)dx =
x4
4
+
x2
2
+
x3
3
+ x +
c
8) ∫
x dx
√x2+1
1
0
‫(وزاري‬2013‫دور‬1‫تمهيدي‬ ‫و‬)(5201‫دور‬1)
= ∫ x (x2
+ 1)
−1
2 dx
1
0
=
1
2
∫ 2x (x2
+ 1)
−1
2 dx
1
0
= [2(x2
+ 1)
1
2] 1
0
11
= [2(12
+ 1)
1
2] − [2(02
+ 1)
1
2] = [2(2)
1
2] − [2] = 2√2 – 2
9) ∫
x2+1
√x3+3x+1
3 dx = ∫(x2
+ 1)(x3
+ 3x + 1)
−1
3 dx
=
1
3
∫ 3(x2
+ 1)(x3
+ 3x + 1)
−1
3 dx =
1
3
.
3
2
(x3
+ 3x + 1)
2
3 + c
=
1
2
√(x3 + 3x + 1)23
+ c

98. ‫أدبي‬ ‫سادس‬‫الرابع‬ ‫الفصل‬‫المحدد‬ ‫التكامل‬
/‫الشمري‬ ‫أحمد‬ :‫األستاذ‬0770451693798/ ‫الطباعية‬ ‫للخدمات‬ ‫المرسل‬07703458937
10) ∫ √(3x − 1)233
0
dx =
1
3
∫ 3. (3x − 1)
2
3
3
0
dx (4201‫دور‬2)
=
1
3
[
3
5
(3x − 1)
5
3]0
3
=
1
5
[(3x − 1)
5
3] 1
0
31
= [
1
5
(3 . 3 − 1)
5
3] − [
1
5
(3 . 0 − 1)
5
3]
= [
1
5
(8)
5
3] − [
1
5
(−1)
5
3] = [
1
5
(2)5
] − [
1
5
(−1)5
] =
1
5
. 32 +
1
5
=
33
5
11) ∫
√x
3
+1
√x23 dx = ∫ x
−2
3 (x
1
3 + 1)dx = ∫(x
−1
3 + x
−2
3 )dx
=
3
2
x
2
3 + 3x
1
3 + c =
3
2
√x23
+ 3√x
3
+ c
12) ∫
√√x−1
3
√x
dx = ∫
√√x−1
3
√x
dx = ∫ x
−1
2 (x
1
2 − 1)
1
3
dx
= 2∫
x
−1
2
2
(x
1
2 − 1)
1
3
dx = 2 .
3
4
(x
1
2 − 1)
4
3
+ c =
3
2
. √(√x − 1)
43
+ c
13) ∫
x4
√a2x5+ b25 dx = ∫ x4 (a2
x5
+ b2)
−1
5 dx =
1
5a2 ∫ 5a2
x4 (a2
x5
+
b2)
−1
5 dx
=
1
5a2 .
5
4
(a2
x5
+ b2)
4
5 =
1
4a2
√(a2x5 + b2)45
+ c
14) ∫ √x2 − 14x + 49
8
0
dx ‫(وزاري‬2013‫دور‬3)
= ∫ √(x − 7)(x − 7)
8
0
dx= ∫ √(x − 7)28
0
dx = ∫ ǀx − 7
8
0
ǀ dx
‫تتكون‬ ‫المطلقة‬ ‫الدالة‬‫عندما‬ ‫يتصالن‬ ‫مجال‬ ‫منها‬ ‫لكل‬ ‫دالتين‬ ‫من‬y = 0:
x-7 = 0 ⟹ x = 7
ǀx - 7ǀ = {
x − 7 x ≥ 7
7 − x x < 7
‫من‬ ‫التكامل‬ ‫تقسيم‬ ‫يتم‬0‫الى‬7‫للدالة‬(7-x)‫ومن‬7‫الى‬8‫للدالة‬(x-7):‫مبين‬ ‫كما‬
= ∫ (7 − x)
7
0
dx + ∫ (x − 7)
8
7
dx
= [7x −
x2
2
]0
7
+ [
x2
2
− 7x] 1
7
81
= [[7 . 7 −
72
2
] − 0 ] + [[
82
2
− 7 . 8] − [
72
2
− 7 . 7]]
= [49 −
49
2
] + [[
64
2
− 56] − [
49
2
− 49]] = [
49
2
] + [[ 32 − 56] + [
49
2
]]
=
49
2
+ [−24 +
49
2
] =
49
2
− 24 +
49
2
= 25
15) ∫
dx
4x2−12x+9
= ∫
dx
(2x−3)(2x−3)
= ∫
dx
(2x−3)2 = ∫(2x − 3)−2
dx
=
1
2
∫ 2. (2x − 3)−2
dx =
1
2
(2x−3)−1
−1
+ c =
−1
2(2x−3)
+ c

99. ‫أدبي‬ ‫سادس‬‫الرابع‬ ‫الفصل‬‫المحدد‬ ‫التكامل‬
/‫الشمري‬ ‫أحمد‬ :‫األستاذ‬0770451693799/ ‫الطباعية‬ ‫للخدمات‬ ‫المرسل‬07703458937
16) ∫ √3x5 − 2x751
−1
dx = ∫ √x5(3 − 2x2)
51
−1
dx = ∫ x . √(3 − 2x2)
51
−1
dx
= ∫ x. (3 − 2x2
)
1
5
1
−1
dx =
1
−4
∫ (−4x). (3 − 2x2
)
1
5
1
−1
dx
=
1
−4
[
5
6
(3 − 2x2
)
6
5 ] 1
−1
11
=
1
−4
([
5
6
(3 − 2)
6
5 ]- [
5
6
(3 − 2)
6
5 ]) =
1
−4
(0) = 0
17) ∫ √2x5 − 7x33
dx = ∫ √x3(2x2 − 7)
3
dx = ∫ x. √2x2 − 7
3
dx
= ∫ x. (2x2
− 7)
1
3 dx =
1
4
∫ 4x. (2x2
− 7)
1
3 dx =
1
4
.
3
4
(2x2
− 7)
4
3 + c
=
3
16
√(2x2 − 7)43
+ c
18)‫قيمة‬ ‫جد‬b ∈R‫ان‬ ‫علمت‬ ‫اذا‬:
∫ (13 − 4x)dx
b
1
= 9
/‫الحل‬
∫ (13 − 4x)dx
b
1
= [(13x − 2x2)] 1
1
b1
= [(13b − 2b2)]- [(13 − 2)] = 13b − 2b2
- 11 = 9
13b − 2b2
- 11 – 9 = 0 ⟹ 13b − 2b2
- 20 = 0 ‫الحدود‬ ‫ونرتب‬ -1 ‫بـ‬ ‫نضرب‬
2b2
− 13b + 20 = 0 ⟹ (2b - 5)(b - 4) = 0
b = 4 or 2b = 5 ⇒ b =
5
2

100. ‫ادبي‬ ‫سادس‬‫الرابع‬ ‫الفصل‬‫المنحني‬ ‫تحت‬ ‫المساحة‬
/‫الشمري‬ ‫أحمد‬ :‫األستاذ‬07704516937100/ ‫الطباعية‬ ‫للخدمات‬ ‫المرسل‬07703458937
‫تحت‬ ‫المساحة‬‫المنحني‬:
‫من‬ ‫للفترة‬ ‫السينات‬ ‫ومحور‬ ‫المنحني‬ ‫بين‬ ‫المساحة‬a‫الى‬b:
1-‫السينات‬ ‫محور‬ ‫فوق‬ ‫المنطقة‬ ‫كانت‬ ‫اذا‬f(x)>0:‫تساوي‬ ‫المساحة‬ ‫فان‬A = ∫ f(x)dx
b
a
2-‫السينات‬ ‫محور‬ ‫اسفل‬ ‫المنطقة‬ ‫كانت‬ ‫اذا‬f(x)<0:‫تساوي‬ ‫المساحة‬ ‫فان‬A = − ∫ f(x)dx
b
a
‫مثال‬1/‫الدالة‬ ‫بمنحني‬ ‫المحددة‬ ‫المساحة‬ ‫جد‬2–x+2x=f(x)=y‫الفترة‬ ‫وعلى‬ ‫السينات‬ ‫ومحور‬]1,3-[.
/‫الحل‬‫من‬ ‫المعطاة‬ ‫الفترة‬-1‫الى‬3
1-‫عندما‬ ‫السينات‬ ‫محور‬ ‫مع‬ ‫التقاطع‬ ‫نقاط‬ ‫نحدد‬y= 0:
x2 + x - 2 = 0 ⟹ (x + 2) (x - 1) = 0 ⟹ x = -2 , x = 1
2-‫اشارة‬ ‫نحدد‬f(x):
‫سالب‬ ‫جزء‬ ‫تحوي‬ ‫المنطقة‬‫من‬ ‫للفترة‬-1‫الى‬1‫من‬ ‫للفترة‬ ‫موجب‬ ‫وجزء‬1‫الى‬3:‫اذا‬
A1 = ∫ (x2 + x − 2)
3
1
‫الموجبة‬ ‫المنطقة‬
A1 = [
x3
3
+
x2
2
− 2x]1
3
1 = [
33
3
+
32
2
− 2 . 3] − [
(1)3
3
+
(1)2
2
− 2(1)]
A1 = [9 +
9
2
− 6] − [
1
3
+
1
2
− 2] =
15
2
+
7
6
=
90+14
12
=
104
12
=
26
3
unit2
A2 = −∫ (x2 + x − 2)1
−1 dx ‫السالبة‬ ‫المنطقة‬
A2 = −[
x3
3
+
x2
2
− 2x] 1
−1
11
= − [
13
3
+
12
2
− 2 . 1] + [
(−1)3
3
+
(−1)2
2
− 2(−1)]
A2 = − [
1
3
+
1
2
− 2] + [
−1
3
+
1
2
+ 2] = −
1
3
−
1
2
+ 2 −
1
3
+
1
2
+ 2
A2 = −
2
3
+ 4 =
−2+12
3
=
10
3
unit2
A = A1 + A2 =
26
3
+
10
3
=
36
3
= 12 unit2
‫مثال‬2/‫الدالة‬ ‫بمنحني‬ ‫المحددة‬ ‫المساحة‬ ‫جد‬3-2x-2x=f(x)=y‫والمستقيمين‬ ‫السينات‬ ‫محور‬3=x‫و‬1-=x.
/‫الحل‬/‫(وزاري‬2011‫دور‬1)
x2 - 2x -3 = 0 ⟹ (x - 3) (x + 1) = 0 ⟹ x = 3 , x = -1
:‫اذا‬ ‫السينات‬ ‫محور‬ ‫اسفل‬ ‫بالكامل‬ ‫تقع‬ ‫المنطقة‬
A = − ∫ f(x)
b
a
= − ∫ (x2
− 2x − 3 )
3
−1
dx = −[
x3
3
− x2
− 3x] 1
−1
31
A = − [
33
3
− 32
− 3 . 3] + [
(−1)3
3
− (−1)2
− 3(−1)]
A = −[9 − 9 − 9] + [
−1
3
− 1 + 3] = 9 + 2 −
1
3
= 11 −
1
3
=
33−1
3
=
32
3
unit2
-1 3
------
1-2
+ ++ +‫أشارة‬f(x)
f(0) = -2 f(2) = +4
-1 3
-----------
‫اشارة‬f(x)
f(0) = -3

101. ‫ادبي‬ ‫سادس‬‫الرابع‬ ‫الفصل‬‫المنحني‬ ‫تحت‬ ‫المساحة‬
/‫الشمري‬ ‫أحمد‬ :‫األستاذ‬07704516937101/ ‫الطباعية‬ ‫للخدمات‬ ‫المرسل‬07703458937
‫مثال‬3/‫الدالة‬ ‫بمنحني‬ ‫المحددة‬ ‫المساحة‬ ‫جد‬3–23x=f(x)=y‫الفترة‬ ‫وعلى‬ ‫السينات‬ ‫ومحور‬]32,-[.
/‫الحل‬
3x2 - 3= 0 ⟹ 3(x2 – 1)= 0 ⟹ (x2 – 1)= 0
(x - 1) (x + 1) = 0 ⟹ x = 1 , x = -1
A1 = ∫ (3x2
− 3)
−1
−2
dx ‫الموجبة‬ ‫المنطقة‬
A1 = [x3
− 3x] 1
−2
−11
= [(−1)3
− 3(−1)] -[(−2)3
− 3(−2)] = −1 + 3 + 8 − 6 = 4 unit2
A2 = −∫ (3x
2
− 3)1
−1 dx ‫السالبة‬ ‫المنطقة‬
A2 = −[x3
− 3x]−1
1
= −[(1)3
− 3(1)] +[(−1)3
− 3(−1)] = −1 + 3 − 1 + 3 = 4 unit2
A3 = ∫ (3x2
− 3)
3
1
dx ‫الموجبة‬ ‫المنطقة‬
A3 = [x3
− 3x] 1
1
31
= [(3)3
− 3(3)] -[(1)3
− 3(1)] = 27 − 9 − 1 + 3 = 20 unit2
A = A1 + A2 + A3 =4 + 4 + 20= 28 unit2
‫مثال‬4/‫الدالة‬ ‫بمنحني‬ ‫المحددة‬ ‫المساحة‬ ‫جد‬x-3x=f(x)=y‫ومحور‬. ‫السينات‬(4201‫تمهيدي‬)(5201‫دور‬2)
‫الحل‬/.‫السينات‬ ‫محور‬ ‫مع‬ ‫التقاطع‬ ‫لنقاط‬ ‫نحسب‬ ‫اذا‬ ‫الفترة‬ ‫يحدد‬ ‫لم‬ ‫انه‬ ‫بما‬
x3 - x = 0 ⟹ x(x2 - 1) = 0 ⟹ x = 0 , x = 1 , x = -1
A1 = ∫ (x3
− x)
0
−1
dx ‫الموجبة‬ ‫المنطقة‬
A1 = [
x4
4
−
x2
2
] 1
−1
01
= [
04
4
−
02
2
] − [
(−1)4
4
−
(−1)2
2
]
A1 = 0 − [
1
4
−
1
2
] =
1
4
unit2
A2 = − ∫ (x3 − x)
1
0
dx ‫السالبة‬ ‫المنطقة‬
A2 =- [
x4
4
−]
x2
2
] 1
0
11
= − [
14
4
−
12
2
] + [
(0)4
4
−
(0)2
2
] = − [
1
4
−
1
2
] + 0 =
1
4
unit2
A = A1 + A2 =
1
4
+
1
4
=
1
2
unit2
‫مثال‬5/‫الدالة‬ ‫بمنحني‬ ‫المحددة‬ ‫المساحة‬ ‫جد‬y = f(x) = √x + 1‫والمستقيمين‬ ‫السينات‬ ‫ومحور‬x = 3‫و‬x = 0.
/‫الحل‬‫(وزاري‬2013‫تمهيدي‬)(2015‫دور‬1)
√x + 1 = 0 ⟹ x + 1 = 0 ‫الطرفين‬ ‫تربيع‬
x = -1
A = ∫ √x + 1
3
0
dx = ∫ (x + 1)
1
2
3
0
dx
A =[
2
3
(x + 1)
3
2] 1
0
31
= [
2
3
(3 + 1)
3
2] − [
2
3
(0 + 1)
3
2]
A = [
2
3
(2)3
] − [
2
3
(1)3
] =
16
3
−
2
3
=
14
3
unit2
-1 3
-----
1-2
+ + + + + +
‫أشارة‬f(x)
+ + + + + +
f(-3) = + f(0) = - f(2) = +
f(
1
2
) = -
-1 1
-----
‫اشارة‬f(x) 0
+ + + +
f(
−1
2
) = +
f(0) = +
-1
+ + + + ++ + + + ++
‫اشارة‬f(x)
-------
f(-2) = -
0 3

102. ‫ادبي‬ ‫سادس‬‫الرابع‬ ‫الفصل‬‫المنحني‬ ‫تحت‬ ‫المساحة‬
/‫الشمري‬ ‫أحمد‬ :‫األستاذ‬07704516937102/ ‫الطباعية‬ ‫للخدمات‬ ‫المرسل‬07703458937
:‫دالتين‬ ‫منحني‬ ‫بين‬ ‫المساحة‬‫دالتين‬ ‫لدينا‬ ‫كان‬ ‫اذا‬f(x)‫و‬g(x)‫من‬ ‫للفترة‬ ‫الدالتين‬ ‫منحني‬ ‫بين‬ ‫المساحة‬ ‫حساب‬ ‫واردنا‬a
‫الى‬b:
1-‫لتكن‬:R(x) = f(x) – g(x)
2-‫التقاطع‬ ‫نقاط‬ ‫نحدد‬‫عندما‬ ‫الدالتين‬ ‫بين‬R(x)= 0.
3-‫اشارة‬ ‫نحدد‬R(x).‫االعداد‬ ‫خط‬ ‫على‬
4-‫كانت‬ ‫اذا‬:‫فان‬ ‫صفر‬ ‫من‬ ‫اكبر‬
A = ∫ R(x)
b
a
dx
5-‫كانت‬ ‫اذا‬R(x):‫فان‬ ‫صفر‬ ‫من‬ ‫اقل‬
A = -∫ R(x)
b
a
dx
‫مثال‬1/‫الدالتين‬ ‫منحني‬ ‫بين‬ ‫المحددة‬ ‫المساحة‬ ‫جد‬x=f(x)=y,3x=g(x)=y
/‫الحل‬‫(وزاري‬2013‫دور‬2‫و‬1)
1-‫لتكن‬:R(x) = f(x) – g(x)
R(x) = x – x3=0 ⟹ x – x3 = 0 ⟹ x(1-x2) = 0
x(1-x)(1+x) = 0 ⟹ x = 0 , x = -1 , x = 1
2-‫اشارة‬ ‫نحدد‬R(x):
:‫بعضهما‬ ‫مع‬ ‫الدالتين‬ ‫تقاطع‬ ‫نقاط‬ ‫بين‬ ‫محصورة‬ ‫مساحتها‬ ‫حساب‬ ‫المراد‬ ‫الفترة‬ ‫ان‬ /‫مالحظة‬
A1 = − ∫ (x − x3
)
0
−1
dx
A1 = ∫ (x3
− x
0
−1
)dx ‫التكامل‬ ‫الى‬ ‫السالب‬ ‫اشارة‬ ‫ندخل‬
A1 = ∫ (x3
− x
0
−1
)dx = [
x4
4
−
x2
2
] 1
−1
01
1 = [
04
4
−
02
2
] − [
(−1)4
4
−
(−1)2
2
]
A1 = 0 − [
1
4
−
1
2
] =
1
4
unit2
A2 = ∫ (x − x3
)
1
0
dx = ∫ (x−x31
0
)dx = [
x2
2
−
x4
4
] 1
0
11
= [
12
2
− 14
4
] − [
02
2
− 04
4
]
A2 = [
1
2
−
1
4
] − 0 =
1
4
unit2
A = A1 + A2 =
1
4
+
1
4
=
1
2
unit2
‫مثال‬2/‫لتكن‬x=f(x)=y‫الفترة‬ ‫وعلى‬]1,1-[‫ولتكن‬= √x3
g(x)=y‫الفترة‬ ‫وعلى‬]1,1-[‫المساحة‬ ‫جد‬
.‫الدالتين‬ ‫منحني‬ ‫بين‬ ‫المحددة‬(2012‫دور‬2)(2016‫دور‬2)
/‫الحل‬
‫لتكن‬:R(x) = f(x) – g(x)
R(x) = x – √x
3
⟹ x – √x
3
= 0 ⟹ x = √x
3
‫الطرفين‬ ‫تكعيب‬
x3 = x ⟹ x3 – x = 0 ⟹ x(x2-1) = 0
x(x-1)(x+1) = 0 ⟹ x = 0 , x = -1 , x = 1
‫من‬ ‫الدالتين‬ ‫فترتي‬ ‫ان‬ ‫بما‬-1‫الى‬1‫من‬ ‫المساحات‬ ‫نحسب‬ ‫فاننا‬ ‫الدالتين‬ ‫منطقتي‬ ‫ضمن‬ ‫كلها‬ ‫تقع‬-1‫الى‬1:
A1 = ∫ (x − x
1
31
0
−1
)dx ‫الموجبة‬ ‫المنطقة‬
‫اشارة‬R(x) -1
----- ++ ++
0 1
‫اشارة‬R(x) -1
+ + + + + ----
-
0 1

103. ‫ادبي‬ ‫سادس‬‫الرابع‬ ‫الفصل‬‫المنحني‬ ‫تحت‬ ‫المساحة‬
/‫الشمري‬ ‫أحمد‬ :‫األستاذ‬07704516937103/ ‫الطباعية‬ ‫للخدمات‬ ‫المرسل‬07703458937
A1= [
x2
2
−
3
4
x
4
31
] 1
−1
01
= [
02
2
−
3
4
(0
4
31
)] − [
(−1)2
2
−
3
4
(−1)
4
31
] = 0 − [
1
2
−
3
4
] =
1
4
unit2
A2 = − ∫ (x − x
1
31
)
1
0
dx ‫السالبة‬ ‫المنطقة‬
A2 = ∫ (x
1
31
− x
1
0
)dx = [
3
4
x
4
31
−
x2
2
] 1
0
11
A2 = [
3
4
(1
4
31
) −
12
2
] − [
3
4
(0
4
31
) −
02
2
]
A2 = [
3
4
−
1
2
] − 0 =
1
4
unit2
A = A1 + A2 =
1
4
+
1
4
=
1
2
unit2
‫ح‬‫التمارين‬ ‫لول‬4-4
1-‫الدالة‬ ‫منحني‬ ‫بين‬ ‫المساحة‬ ‫جد‬f(x)‫والمستقيمين‬ ‫السينات‬ ‫ومحور‬2=x‫و‬2-=x‫حيث‬x4-3x=f(x)=y
/‫الحل‬‫(وزاري‬2012‫دور‬3)‫(وزاري‬2016‫دور‬1)
x3 - 4x = 0 ⟹ x(x2 - 4) = 0 ⟹ x(x - 2)(x+2) = 0
x = 0 , x = 2 , x = -2
A1 = ∫ (x3
− 4x)
0
−2
dx ‫الموجبة‬ ‫المنطقة‬
A1 = [
x4
4
− 2x2
] 1
−2
01
= [
04
4
− 2(02
)] − [
(−2)4
4
− 2(−2)2
] = 0 − [4 − 8] = 4 unit2
A2 = − ∫ (x3
− 4x)
2
0
dx ‫السالبة‬ ‫المنطقة‬
A2 = −[
x4
4
− 2x2
] 1
0
21
= − [
24
4
− 2(22
)] + [
(0)4
4
− 2(02
)] = −[4 − 8] + 0 = 4 unit2
A = A1 + A2 = 4 + 4 = 8 unit2
2-‫ج‬‫الدالة‬ ‫بمنحني‬ ‫المحددة‬ ‫المساحة‬ ‫د‬2x-4x=f(x)=y‫الفترة‬ ‫وعلى‬ ‫السينات‬ ‫ومحور‬]1,1-[
/‫الحل‬(2014‫دور‬1)
x4 - x2
= 0 ⟹ x2(x2 - 1) = 0 ⟹ x2(x - 1)(x+1) = 0
x = 0 , x = 1 , x = -1
A = − ∫ (x4
− x2
)
1
−1
dx
A = −[
x5
5
−
x3
3
] 1
−1
11
= − [
15
5
−
13
3
] + [
(−1)5
5
−
(−1)3
3
]
A = − [
1
5
−
1
3
]+ [
−1
5
−
−1
3
] =
−1
5
+
1
3
−
1
5
+
1
3
= −
2
5
+
2
3
=
4
15
unit2
f(1) = -
-2 2
-----
‫اشارة‬f(x) 0
+ + + +
f(-1) = +
f(
1
2
) = -
-1 1
------
‫اشارة‬f(x) 0
------
f(
−1
2
) = -

104. ‫ادبي‬ ‫سادس‬‫الرابع‬ ‫الفصل‬‫المنحني‬ ‫تحت‬ ‫المساحة‬
/‫الشمري‬ ‫أحمد‬ :‫األستاذ‬07704516937104/ ‫الطباعية‬ ‫للخدمات‬ ‫المرسل‬07703458937
3-‫بالدالة‬ ‫المحددة‬ ‫المساحة‬ ‫جد‬+2x23x-3x=f(x)=y.‫السينات‬ ‫ومحور‬
/‫الحل‬
x3 -3x2+2x = 0 ⟹ x(x2 – 3x + 2) = 0 ⟹ x(x - 2)(x -1) = 0
x = 0 , x = 2 , x = 1
A1 = − ∫ (x3
− 3x2
+ 2x )
2
1
dx
A1 = −[
x4
4
− x3
+ x2
] 1
1
21
A1 = − [
24
4
− 23
+ 22
] + [
14
4
− 13
+ 12
] = −4 + 8 − 4 +
1
4
− 1 + 1 =
1
4
unit2
A2 = ∫ (x3
− 3x2
+ 2x )
1
0
dx = [
x4
4
− x3
+ x2
] 1
0
11
A2 = [
14
4
− 13
+ 12
] − [
04
4
− 03
+ 02
] =
1
4
− 1 + 1 =
1
4
unit2
A = A1 + A2 =
1
4
+
1
4
=
1
2
unit2
4-‫الد‬ ‫بمنحني‬ ‫المحددة‬ ‫المساحة‬ ‫جد‬‫التين‬f(x) = √x − 1,g(x) =
1
2
x‫والمستقيمين‬x = 5,x =2.
/‫الحل‬‫لتكن‬:R(x) = f(x) – g(x)
R(x) = √x − 1 –
1
2
x ⟹ √x − 1 –
1
2
x = 0 ⟹ √x − 1 =
1
2
x
x - 1 =
1
4
x2
‫الطرفين‬ ‫تربيع‬
4x - 4 = x2
⟹ x2
– 4x + 4 =0 ⟹ (x-2)(x-2) = 0 ⟹ x = 2
A = − ∫ (√x − 1 –
1
2
x)
5
2
dx
A= ∫ (
1
2
x − √x − 1)
5
2
dx ‫السالب‬ ‫من‬ ‫نتخلص‬
A= ∫ (
1
2
x − (x − 1)
1
21
)
5
2
dx = [
x2
4
−
2
3
(x − 1)
3
21
] 1
2
5
1
A = [
52
4
−
2
3
(5 − 1)
3
21
] − [
22
4
−
2
3
(2 − 1)
3
21
] =
25
4
− 8(
2
3
) − [
4
4
−
2
3
]
A =
25
4
−
16
3
−
4
4
+
2
3
=
21
4
−
14
3
=
63−56
12
=
7
12
unit2
5-‫جد‬‫الدالتين‬ ‫بمنحني‬ ‫المحددة‬ ‫المساحة‬y = x4
− 12,y = x2
.‫(وزاري‬2012‫دور‬1)(2015‫دور‬3)
/‫الحل‬: ‫لتكن‬f(x) = x4
− 12‫و‬g(x) = x2
‫و‬R(x) = f(x) – g(x)
R(x) = [(x4
− 12)− x2
]
x4
− 12 − x2
= 0 ⟹ x4
− x2
− 12 = 0 ⟹ (x2
− 4)(x2
+ 3 ) =
0
x2
− 4 = 0 ⟹ (x-2)(x +2) = 0 ⟹ x = 2 , x = -2
x2
+ 3 = 0 ⟹ x2
= −3 ‫سالب‬ ‫مربعه‬ ‫حقيقي‬ ‫عدد‬ ‫وجود‬ ‫لعدم‬ ‫تهمل‬
f(
3
2
) = -
0 2
-----
‫اشارة‬f(x) 1
+ + + +
f(
1
2
) =+
‫اشارة‬R(x) 2
---------
--
5

105. ‫ادبي‬ ‫سادس‬‫الرابع‬ ‫الفصل‬‫المنحني‬ ‫تحت‬ ‫المساحة‬
/‫الشمري‬ ‫أحمد‬ :‫األستاذ‬07704516937105/ ‫الطباعية‬ ‫للخدمات‬ ‫المرسل‬07703458937
A = − ∫ [(x4
− 12)− x2
]
2
−2
dx
A= ∫ [ x2
− (x4
− 12)]
2
−2
dx = ∫ ( x2
− x4
+ 12)
2
−2
dx
A= [
x3
3
−
x5
5
+ 12x] 1
−2
21
= [
23
3
−
25
5
+ 12 (2)] − [
(−2)
3
3
−
(−2)5
5
+ 12(−2)]
A =
8
3
−
32
5
+ 24 − [
−8
3
−
−32
5
− 24 ] =
8
3
−
32
5
+ 24 +
8
3
−
32
5
+ 24
A =
16
3
−
64
5
+ 48 =
80−192+720
15
=
608
15
unit2
‫اشارة‬R(x) -2
----------
--
2

106. ‫ادبي‬ ‫سادس‬‫الرابع‬ ‫الفصل‬‫المنحني‬ ‫تحت‬ ‫المساحة‬
/‫الشمري‬ ‫أحمد‬ :‫األستاذ‬07704516937106/ ‫الطباعية‬ ‫للخدمات‬ ‫المرسل‬07703458937
‫الوزارية‬ ‫االسئلة‬
1):‫التكامل‬ ‫ناتج‬ ‫جد‬
a) ∫
𝑑𝑥
√𝑥2−16𝑥+64
5 ‫(وزاري‬2013‫دور‬2) , ∫
𝑥3+3𝑥2
𝑥+3
𝑑𝑥 ‫(وزاري‬2011‫دور‬1)
b) ∫ (𝑥4
+
1
2𝑥2 + 3) 𝑑𝑥 ‫(وزاري‬2014‫دور‬1) , ∫ √𝑥2 − 8𝑥 + 16
5
. 𝑑𝑥 ‫(وزاري‬2014‫دور‬2)
c) ∫
𝑥2+1
√2𝑥3+6𝑥+5
3 𝑑𝑥 ‫(وزاري‬2005)‫تمهيدي‬ , ∫(5𝑥 +
2
𝑥2) 𝑑𝑥 ‫(وزاري‬2005)‫تمهيدي‬
d) ∫
𝑎𝑥2+1
√𝑎𝑥3+3𝑥+1
3 𝑑𝑥 ‫(وزاري‬2012‫دور‬2) , ∫
2𝑥
√𝑥2+16
𝑑𝑥
2
0
‫(وزاري‬2012‫دور‬1)
e) ∫ 𝑥( 𝑥 − 1)( 𝑥 − 2) 𝑑𝑥
0
4
‫(وزاري‬2015‫دور‬2) , ∫
𝑥3+8
𝑥+2
𝑑𝑥 (2016)‫تمهيدي‬
f) ∫ √𝑥2 − 1
3
. 𝑥 𝑑𝑥 (2016)‫تمهيدي‬ , ∫(𝑥2
+ 3)(𝑥 + 2). 𝑑𝑥 ‫(وزاري‬2016‫دور‬1)
g) ∫ √3𝑥5 − 2𝑥751
−1
𝑑𝑥 2016-3
2)‫اذا‬‫كانت‬‫دالة‬‫التكلفة‬‫الحدية‬T̅‫هي‬2
5v-40v+2=T̅‫حيث‬v‫حجم‬‫االنتاج‬,‫جد‬‫دالة‬‫التكلفة‬‫الكلية‬‫ان‬ ‫علما‬
T = 65‫عندما‬v=0.‫(وزاري‬2014‫دور‬2)
3)‫جد‬‫المساحة‬‫المحددة‬‫بمنحني‬‫الدالتين‬y =x2
, y =2x‫(وزاري‬2014‫دور‬2)
4)‫جد‬‫المساحة‬‫المحددة‬‫بمنحني‬‫الدالة‬f(x) = x3
- 3x2
‫السينات‬ ‫ومحور‬(2016)‫تمهيدي‬
5)‫عند‬ ‫ميله‬ ‫الذي‬ ‫المنحني‬ ‫معادلة‬ ‫جد‬( ‫النقطة‬x,y‫يساوي‬ )8 + 6x( ‫بالنقطة‬ ‫يمر‬ ‫المنحني‬ ‫وكان‬1,11.)(2016‫تمهيدي‬)
6)( ‫نقطة‬ ‫اي‬ ‫عند‬ ‫ميله‬ ‫الذي‬ ‫المنحني‬ ‫معادلة‬ ‫جد‬4x + 1( ‫بالنقطة‬ ‫ويمر‬ )-1,3.)2005‫تمهيدي‬
7)‫الحدية‬ ‫التكلفة‬ ‫دالة‬ ‫كانت‬ ‫اذا‬T̅‫هي‬25v–60v+2=T̅‫حيث‬v‫علما‬ ‫الكلية‬ ‫التكلفة‬ ‫دالة‬ ‫جد‬ , ‫االنتاج‬ ‫حجم‬
‫ان‬T = 45.(2016‫دور‬2)
8)‫ان‬ ‫اثبت‬∫ (
√ √x
3
− 1
√x23 )dx
125
1
= 16(2016‫دور‬2)
9)‫اذا‬‫كانت‬‫دالة‬‫التكلفة‬‫الحدية‬T̅‫هي‬2
5v-60v+2=T̅‫حيث‬v‫حجم‬‫االنتاج‬,‫جد‬‫دالة‬‫التكلفة‬‫الكلية‬‫ان‬ ‫علما‬
T = 45.2016-2
10)‫تحقق‬ ‫التي‬ ‫الدالة‬ ‫جد‬y̅ = 𝟓,y̅̅ = 12x2
− 2‫النقطة‬ ‫عند‬(1,2).2016-3
11)‫جد‬‫المساحة‬‫المحددة‬‫بمنحني‬‫الدالة‬f(x) = x2
– 5x‫السينات‬ ‫ومحور‬2016-3