يتناول الكتاب المعادلات التفاضلية من حيث نظريتها وتطبيقاتها، حيث يقدّم مؤلفوه د. بخيت نفيع المطرفي ود. عبد الله عبد الله موسى محتوى علمياً شاملاً يستهدف طلبة العلوم والهندسة. يتضمن الكتاب تفسيراً مفصلاً للمعادلات التفاضلية، ويتناول طرق الحلول المختلفة، بما في ذلك الحلول التحليلية والعددية، بالإضافة إلى تمارين متنوعة لتعزيز الفهم.




















































![الباب السادس
)83.6( --------------------------- 0 y 4
ادط مل رت خطم ح ا طرق رت حل طتق (53.6-83.6) حلا طرق
ماال احطتحاط أ حلنع حلحطل
1 0 0 00 y1
202300.0 0.0016 6100.0 y 9.375 10 4
0 2
0 6100.0 0.003202 0.0016 y 3 9.375 10 4
0 0 0 01 y 4
تط حخرحك MATLABااط مأ تعل حأع حلا طرق
202300.0- 6100.0 0 ;0 6100.0 202300.0- 6100.0; 0 0 0 1 [=a
]1 0 0 0 ;6100.0
;']0 4-^01*573.9 4-^01*573.9 0[=b
y=inv(a)*b
نعصل أ
0 y1
y
2 0.5852
y 3 0.5852
0 y 4
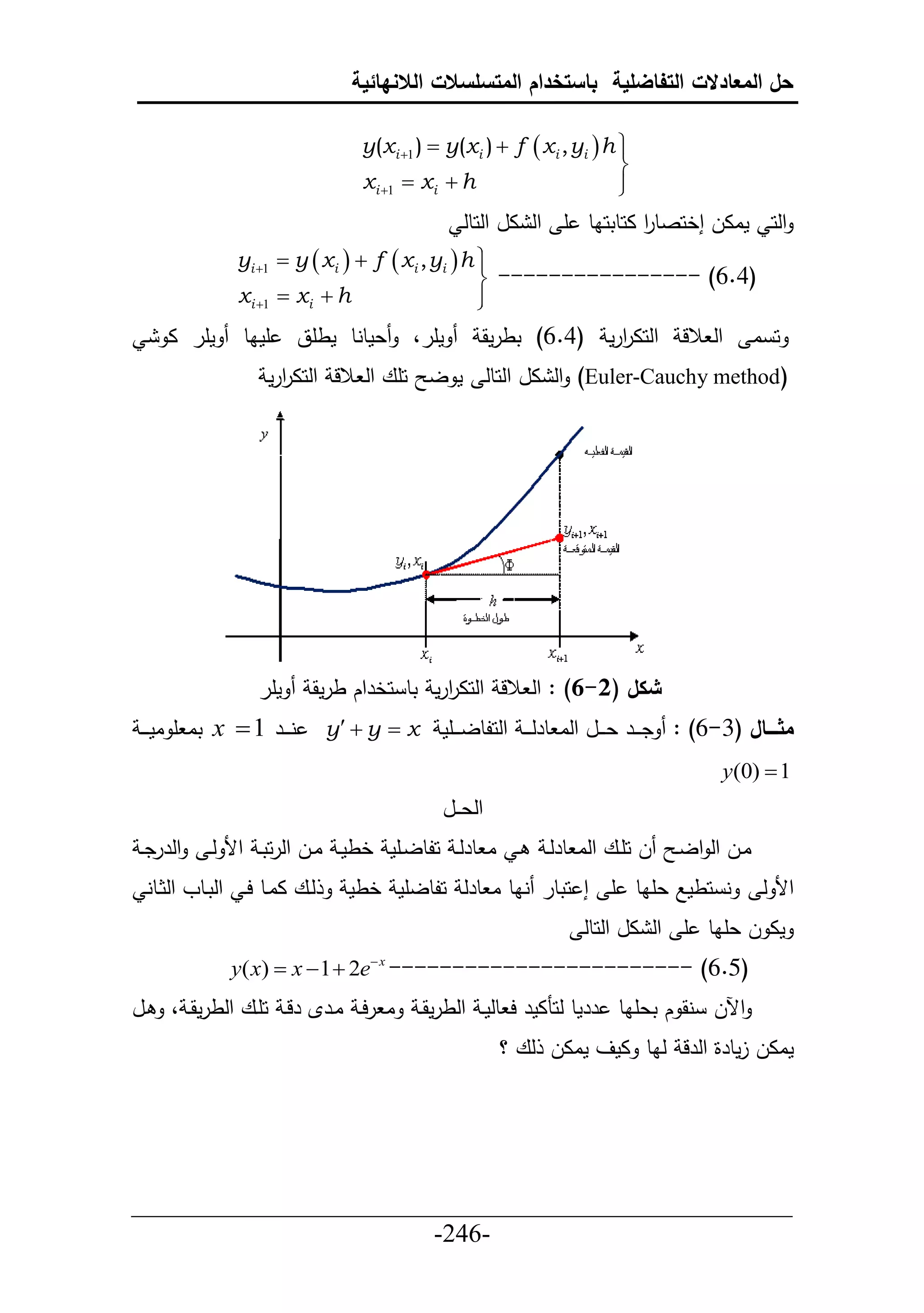
لما ) 2 y (xتا ن ما ل حقنع حف نر "05 x
ر
"2585.0y(50) y( x2 ) y 2
2 y y x 2 اييال حل أييك ل ديير عييل ا يينل حلقييمك حلعر رم ي مثاااال (51-6) :
1- )1( y(0) 0, y(1) coshتط ي ييحخرحك ط ي ي ل خط ي ي ة اقي ييرحر ط 52.0 h تط ي ييحخرحك
حلحقرمو حللرل حلاق ك حق ط .
حلعل
d2y
تط يحخرحك ()Central Divided Difference Approximation تحقرمو حلا حق حلثطنمي
2 dx
نر حل قرم iااط ح (33.6)
___________________________________________________
-382-](https://image.slidesharecdn.com/random-130131153230-phpapp01/75/slide-60-2048.jpg)

![الباب السادس
y 5 2y 4 y 3
2
y 4 x 4 1
2
(0.25)
y5 2 y4 y3
y4 (0.75)2 1 y3 2.0625 y4 y5 0.1094 --(6.43)
(0.25)2
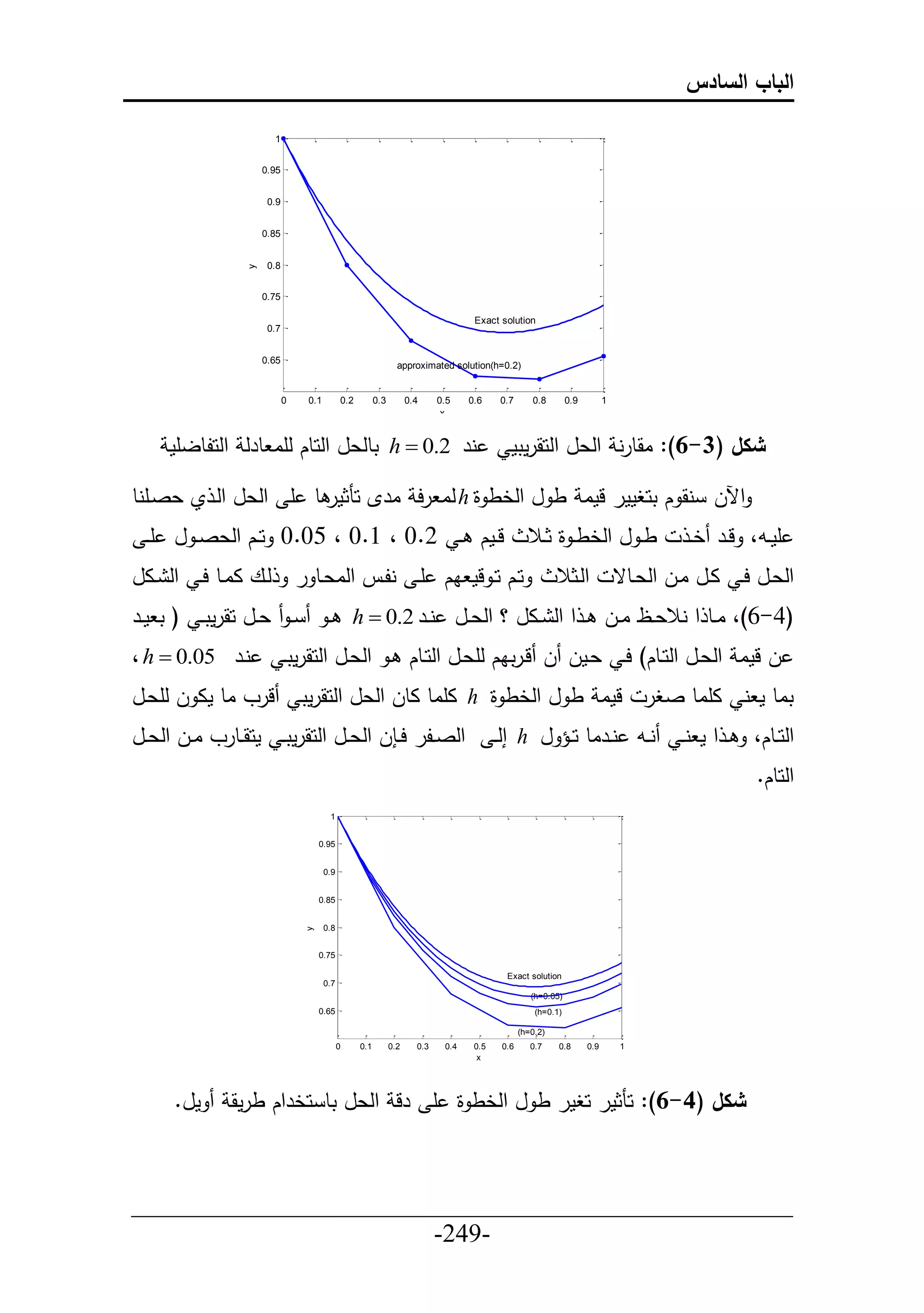
نعصل أy(1) cosh(1) 1 : عم حل قرم حلخطا
y5 cosh(1) 1 ------------------- (6.44)
خطم ي ح ي خا ي ادط مييل حل ييطتق (04.6-44.6) ي خايين ا ييطرق حلا ييطرق
أ حلنع حلحطل ماال احطتحاط أ ص ة اصل ح
ر
1 0 0 0 0 y1 0
1 2.0625 1 0 y 0.2344
0 2
0 1 2.0625 1 0 y3 0.1875
0 0 1 2.0625 1 y4 0.1094
0
0 0 0 1 y5 cosh(1) 1
ااط مأMATLAB تط حخرحك ترنطاج تعل حأع حلا طرق
a=[ 1 0 0 0 0 ;1 -2.0625 1 0 0;0 1 -2.0625 1 0;0 0 1 -2.0625 1; 0 0 0 0
1];
b=[0 -0.2344 -0.1875 -0.1094 cosh(1)-1]';
y=inv(a)*b
نعصل أ
y1 0
y 0.3876
2
y3 0.05651
y4 0.5903
y5 0.5431
___________________________________________________
-285-](https://image.slidesharecdn.com/random-130131153230-phpapp01/75/slide-62-2048.jpg)


