Download to read offline
Uploaded byAgung Anggoro
Sisi Lain Distribusi Binomial dan Normal
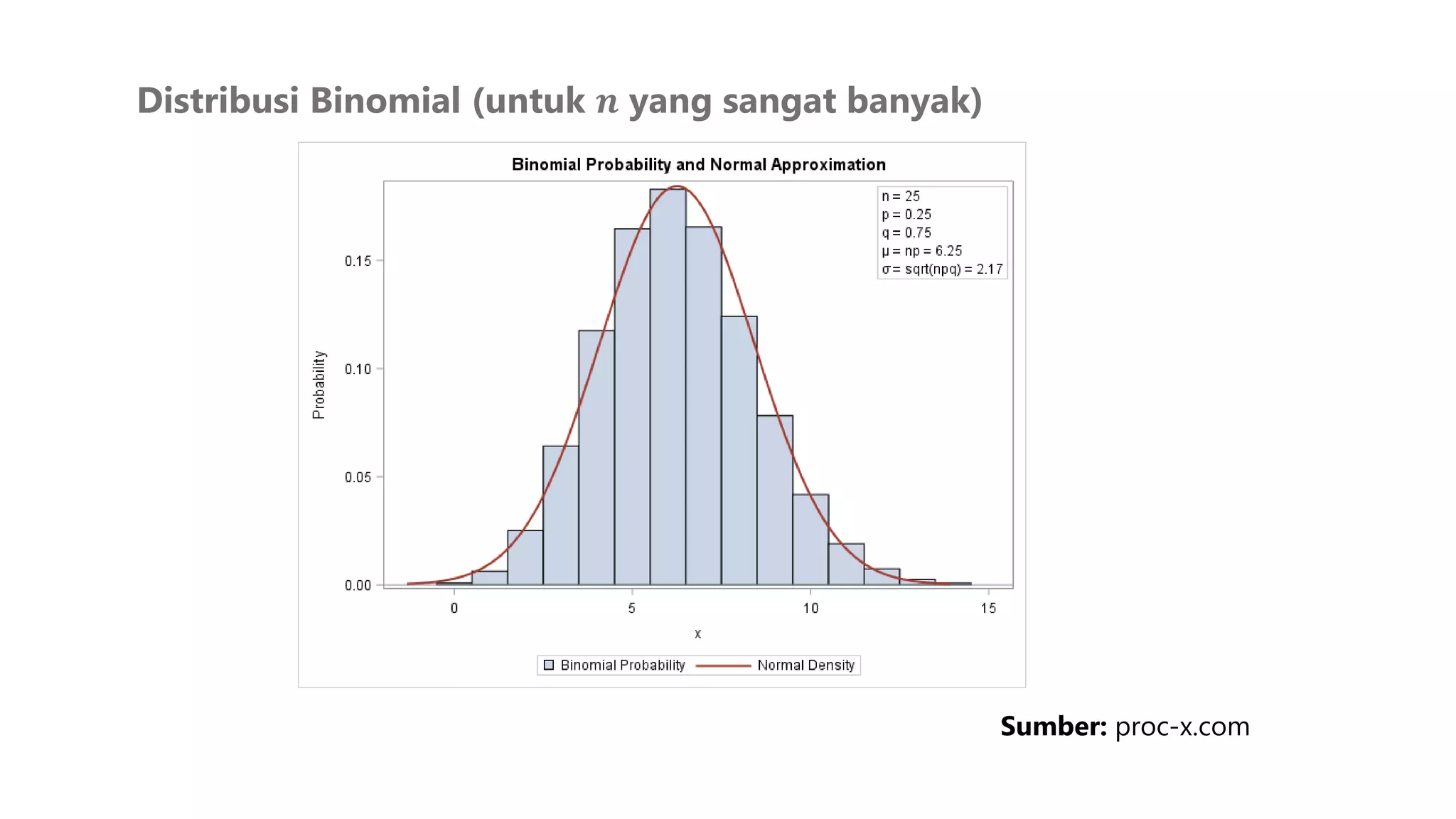
Dokumen ini membahas konsep distribusi probabilitas, termasuk distribusi binomial dan normal, serta cara menghitung ekspektasi dan variansi. Diterangkan secara rinci tentang fungsi peluang dan densitas, serta teknik integrasi untuk menghitung luas di bawah kurva distribusi. Contoh aplikasi distribusi normal untuk mendekati distribusi binomial juga disediakan.
More Related Content
Similar to Sisi Lain Distribusi Binomial dan Normal
Sisi Lain Distribusi Binomial dan Normal
- 1. Distribusi Binomial & Normal Darimana muncul 𝟐𝝅 ? Agung Anggoro
- 2. Variabel Acak Diskrit 𝑎 𝑏 𝑐 Kontinu ___________ 𝑎𝑏 Fungsi Peluang Fungsi Densitas Distribusi Distribusi Bernoulli Binomial 𝑛 percobaan Normal Normal Baku 𝑧 = 𝑥 − 𝜇 𝜎 ▪ 𝑝 𝑥 ≥ 0 ▪ σ 𝑥 𝑝 𝑥 = 1 ▪ 𝑓 𝑥 ≥ 0 ▪ −∞ ∞ 𝑓(𝑥) 𝑑𝑥 = 1 ▪ 𝑃 𝑎 ≤ 𝑋 ≤ 𝑏 = 𝑎 𝑏 𝑓(𝑥) 𝑑𝑥
- 3. Nilai Ekspektasi 𝑬𝑿 Misalnya 𝑋 adalah peubah acak. Dapat didefinisikan sebuah besaran 𝐸 𝑋 , yaitu: Diskrit Kontinu 𝐸 𝑋 = 𝑥 𝑥 ⋅ 𝑝 𝑥 dengan 𝑝 𝑥 adalah fungsi peluang dari 𝑋. 𝐸 𝑋 = න −∞ ∞ 𝑥 ⋅ 𝑓(𝑥) 𝑑𝑥 dengan 𝑓 𝑥 adalah fungsi densitas dari 𝑋.
- 4. Nilai Variansi 𝑽𝒂𝒓𝑿 Misalnya 𝑋 adalah peubah acak. Dapat didefinisikan sebuah besaran 𝑉𝑎𝑟 𝑋 , yaitu: 𝑉𝑎𝑟 𝑋 = 𝐸 𝑋 − 𝐸 𝑋 2
- 5. Distribusi Bernoulli ▪ Misalnyasebuah percobaan acak dimana ruang sampelnya adalah 𝑆. Fungsi peluang ▪ Untuk setiap 𝑎 ∈ 𝑆 hanya berlaku salah satu dari 𝑋 𝑎 = 0 atau 𝑋 𝑎 = 1, dengan 𝑋 adalah variabel acak. ▪ Percobaan acak dilakukan hanya satu kali. 𝑝 𝑥 = 𝑡 𝑥 1 − 𝑡 1−𝑥 dengan 𝑡 = 𝑃 𝑋 = 1 𝑥 = 0, 1 Ekspektasi 𝜇 = 𝑡 Variansi 𝜎2 = 𝑡(1 − 𝑡)
- 6. Distribusi Binomial ▪ Sebuahpercobaan acak diulang secara bebas sebanyak 𝒏 kali. Fungsi peluang ▪ Terdapat dua kemungkinan hasil pada setiap percobaannya yaitu A dan B, dimana peluang terjadinya A adalah 𝑡. ▪ Definisikan 𝑋 = banyaknya percobaan dengan hasil A. 𝑃 𝑋 = 𝑥 = 𝑝 𝑥 = 𝑛 𝑥 𝑡 𝑥 1 − 𝑡 1−𝑥 dengan 𝑥 = 0, 1, 2, … , 𝑛 Ekspektasi 𝜇 = 𝑛𝑡 Variansi 𝜎2 = 𝑛𝑡(1 − 𝑡)
- 7. Distribusi Binomial (untuk𝒏 yang sangat banyak) Sumber: dummies.com
- 8. Distribusi Binomial (untuk𝒏 yang sangat banyak) Sumber: proc-x.com
- 9. Distribusi Binomial (untuk𝒏 yang sangat banyak) Sumber: stackoverflow.com
- 10. 𝑋 𝜇 + 𝜎𝜇− 𝜎 𝜇 Karakteristik Model untuk Peubah Acak Kontinu ▪ Simetris di 𝑥 = 𝜇. ▪ Titik infleksi di 𝑥 = 𝜇 ∓ 𝜎 Bentuk Model adalah 𝑓 𝑥 = 𝑘𝑒−𝑝 𝑥−𝜇 2
- 11. Karakteristik Model untuk PeubahAcak Kontinu Bentuk Model adalah 𝑓 𝑥 = 𝑘𝑒−𝑝 𝑥−𝜇 2 𝑓′′ (𝑥) = −2𝑝𝑘𝑒− 𝑥−𝜇 2 𝑝 1 − 𝑥 − 𝜇 2𝑝 1 + 𝑥 − 𝜇 2𝑝 Kurva mengalami infleksi di 𝑥 = 𝜇 ∓ 𝜎, maka 𝑓′′ 𝜇 − 𝜎 = 0 dan 𝑓′′ 𝜇 + 𝜎 = 0 𝑓′′ 𝜇 − 𝜎 = 0 1 − 𝜇 − 𝜎 − 𝜇 2𝑝 = 0 1 + 𝜇 − 𝜎 − 𝜇 2𝑝 = 0 atau 2𝑝 = − 1 𝜎 𝑝 = 1 2𝜎2 (tidak memenuhi)
- 12. Karakteristik Model untuk PeubahAcak Kontinu Sampai disini, kita memeroleh: 𝑓(𝑥) = 𝑘𝑒 − 1 2𝜎2 𝑥−𝜇 2
- 13. Syarat 𝒇(𝒙) sebagaiFungsi Densitas න −∞ ∞ 𝑓(𝑥) 𝑑𝑥 = න −∞ ∞ 𝑘𝑒 − 1 2𝜎2 𝑥−𝜇 2 𝑑𝑥 = 1 Dengan demikian: ▪ Luasan di bawah kurva harus tetap, sehingga ketika 𝜎 berubah-rubah (kurva melebar-menyempit) harus diimbangi dengan perubahan ketinggian kurva yang bergantung pada 𝜎. ▪ Harus dicari nilai 𝑘 sedemikian sehingga 𝑓(𝑥) merupakan fungsi densitas yang valid.
- 14. Syarat 𝒇(𝒙) sebagaiFungsi Densitas 𝑓 𝑥 = 𝑐 𝜎 𝑒 − 1 2𝜎2 𝑥−𝜇 2 Sampai sini kita menggunakan 𝑘 = 𝑐/𝜎 : Bentuk ini ternyata bisa memudahkan kita melakukan integrasi nantinya.
- 15. 𝜇 + 𝜎𝜇− 𝜎 𝜇 𝑋 𝟎 𝟏−𝟏 𝑥1 = 𝜇 + 𝒛 𝟏 𝜎 𝑥2 = 𝜇 + 𝒛 𝟐 𝜎 𝒛 𝟏 𝒛 𝟐 න 𝑥1 𝑥2 𝑐 𝜎 𝑒 − 1 2𝜎2 𝑥−𝜇 2 𝑑𝑥
- 16. Kita akan menghitung Luasanyang Sama Dengan memisalkan 𝑧 = 𝑥−𝜇 𝜎 diperoleh 𝜎𝑑𝑧 = 𝑑𝑥, sehingga: න 𝑥1 𝑥2 𝑐 𝜎 𝑒 − 1 2𝜎2 𝑥−𝜇 2 𝑑𝑥 = න 𝑧1 𝑧2 𝑐 𝜎 𝑒− 1 2 𝑧2 𝜎𝑑𝑧 = න 𝑧1 𝑧2 𝑐𝑒− 1 2 𝑧2 𝑑𝑧 Untuk selanjutnya kita bisa menggunakan fungsi 𝑓 𝑥 = 𝑐𝑒− 1 2 𝑥2 න 𝑥1 𝑥2 𝑐 𝜎 𝑒 − 1 2𝜎2 𝑥−𝜇 2 𝑑𝑥
- 17. Mencari konstanta Kita akanmenghitung න −∞ ∞ 𝑒− 1 2 𝑥2 𝑑𝑥 Misal න −∞ ∞ 𝑒− 1 2 𝑥2 𝑑𝑥 = 𝐼, maka lim 𝑏→∞ න −𝑏 𝑏 𝑒− 1 2 𝑥2 𝑑𝑥 = 𝐼
- 18. Mencari konstanta Kita bisamenentukan volume di bawah permukaan 𝑧 = 𝑒− 1 2 𝑥2+𝑦2 dan di atas persegi dengan titik-titik sudut (±𝑏, ±𝑏) dan (±𝑏, ∓𝑏) 𝑉𝑏 = න −𝑏 𝑏 න −𝑏 𝑏 𝑒− 1 2 𝑥2+𝑦2 𝑑𝑦𝑑𝑥 = න −𝑏 𝑏 න −𝑏 𝑏 𝑒− 1 2 𝑥2 𝑒− 1 2 𝑦2 𝑑𝑦𝑑𝑥 = න −𝑏 𝑏 𝑒− 1 2 𝑥2 න −𝑏 𝑏 𝑒− 1 2 𝑦2 𝑑𝑦 𝑑𝑥 = න −𝑏 𝑏 𝑒− 1 2 𝑦2 𝑑𝑦 න −𝑏 𝑏 𝑒− 1 2 𝑥2 𝑑𝑥 lim 𝑏→∞ 𝑉𝑏 = 𝐼2 Sehingga Sumber: Purcell, dkk.
- 19. Mencari konstanta Disisi lain,dengan memanfaatkan koordinat polar, kita dapat menentukan volume di bawah permukaan 𝑧 = 𝑒− 1 2 𝑥2+𝑦2 dan di atas lingkaran berjari-jari 𝑎 melalui 𝑉𝑎 = න 0 2𝜋 න 0 𝑎 𝑒− 1 2 𝑟2 𝑟𝑑𝑟𝑑𝜃 = 2𝜋 1 − 1 𝑒 1 2 𝑎2 2𝜋 = 𝐼2 ⇔ 𝐼 = 2𝜋 SehinggaDalam ketakhinggaan, lim 𝑎→∞ 𝑉𝑎 = lim 𝑏→∞ 𝑉𝑏 = 𝐼2.
- 20. Mencari konstanta Sampai disinikita peroleh: න −∞ ∞ 𝑒− 1 2 𝑥2 𝑑𝑥 = 𝐼 = 2𝜋 Sebelumnya kita sedang mencari 𝑐 dimana න −∞ ∞ 𝑐𝑒− 1 2 𝑥2 𝑑𝑥 = 𝑐 න −∞ ∞ 𝑒− 1 2 𝑥2 𝑑𝑥 = 1 dan akhirnya 𝑐 = 1 2𝜋
- 21. Distribusi Normal Umumdan Normal Baku Distribusi Normal (Umum) Distribusi Baku Fungsi densitas 𝑬(𝑿) 𝑽𝒂𝒓(𝑿) 𝑓 𝑥 = 1 𝜎 2𝜋 𝑒 − 1 2𝜎2(𝑥−𝜇)2 𝑓 𝑥 = 1 2𝜋 𝑒− 1 2 𝑥2 𝜇 𝜎2 0 1 𝑧 = 𝑥 − 𝜇 𝜎 (dibuat tabel)(tidak mungkin dibuat tabel berbeda untuk setiap nilai 𝝁 dan 𝝈)
- 22. 0 1 𝑋 Mengintegralkan SecaraNumerik න 0 1 1 2𝜋 𝑒− 1 2 𝑥2 𝑑𝑥 𝑃 0 ≤ 𝑍 ≤ 1 = න 0 1 1 2𝜋 𝑒− 1 2 𝑥2 𝑑𝑥 dicari menggunakan metoda trapesium.
- 23. Mengintegralkan Secara Numerik න 0 1 1 2𝜋 𝑒− 1 2 𝑥2 𝑑𝑥dicari menggunakan metoda trapesium. න 0 1 1 2𝜋 𝑒− 1 2 𝑥2 𝑑𝑥 = 1 2𝑛 2𝜋 exp − 02 2 + 2 exp − 1 𝑛 2 2 + ⋯ + exp − 𝑛 − 1 𝑛 2 2 + exp − 12 2 0 11 𝑛
- 24. Mengintegralkan Secara Numerik 𝒏Estimasi untuk 𝑷(𝟎 ≤ 𝒁 ≤ 𝟏) 10 0,341143037 50 0,341336680 100 0,341342730 150 0,341343850 190 0,341344188 200 0,341344242 1100 0,341344729 0 1 𝑋 0,341344746068543 (by Excell)
- 25. Aproksimasi Normal untuk Binomial Sumber:Rinaldi Munir (Slide kuliah). ▪ Distribusi dapat digunakan untuk menghampiri distribusi binomial untuk 𝑛 yang cukup besar. ▪ Jika 𝑋~ 𝑥; 𝑛, 𝑝 dan 𝑍 = lim 𝑋−𝑛𝑝 𝑛𝑝 1−𝑝 , maka 𝑍~𝑁(𝑧; 0,1).
- 26. Contoh Soal Peluang seorangpenderita sembuh dari suatu penyakit adalah 0,45. Bila ada 100 orang yang terkena penyakit tersebut, tentukan peluang dari: a) 30 orang sembuh. b) kurang dari 30 orang yang sembuh.