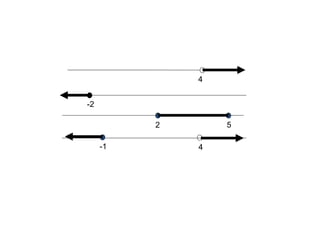
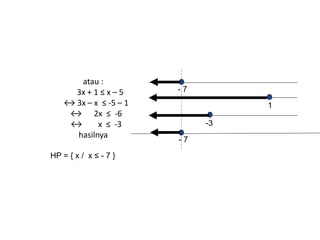
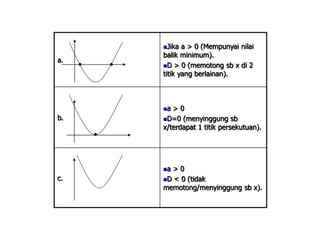
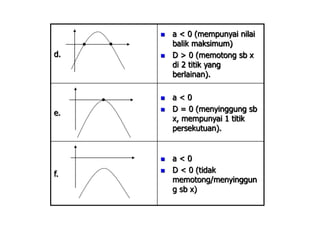
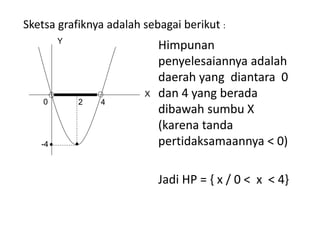
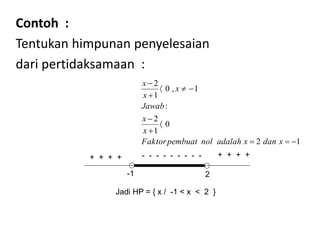
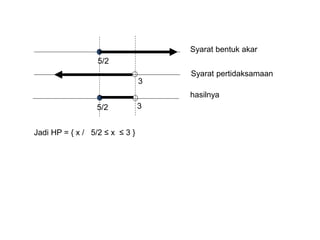
Dokumen tersebut membahas tentang pertidaksamaan, yang didefinisikan sebagai kalimat terbuka yang dihubungkan dengan notasi <, >, ≤ atau ≥. Pertidaksamaan dibedakan menjadi beberapa jenis seperti pertidaksamaan linier, kuadrat, tingkat tinggi, dan bentuk pecahan. Setiap jenis pertidaksamaan memiliki cara penyelesaian tersendiri seperti menggunakan garis bilangan, sketsa grafik, atau kuadrat

1. PERTIDAKSAMAAN
Oleh : Sherli Pitrah Dewi
SMA NEGERI 1 BANGKINANG KOTA

2. 1. Pengertian Pertidaksamaan
Pertidaksamaan didefinisikan sebagai kalimat terbuka yang
dihubungkan dengan notasi / lambang <, >, ≤ atau ≥.
Contoh :
a. x + 5 < 12 c. 2x2 – 3x + 5 ≥ 0
b. (x – 2)(x + 3)2(x + 4) ≤ 0 d. √(10 – 2x) > x + 5
Sebelum kita bahas lebih jauh tentang pertidaksamaan, masih
ingatkah kamu tentang pengertian interval / selang ?
Contoh :
Nyatakan suatu himpunan penyelesaian yang merupakan himpunan
bilangan real yang memenuhi :
a. x > 4 c. 2 ≤ x ≤ 5
b. x ≤ -2 d. x ≤ -1 atau x > 4

3. 4
-1
-2
2 5
4

4. Sifat-sifat Pertidaksamaan
1. Tanda pertidaksamaan tidak berubah jika penambahan
atau pengurangan suatu bilangan yang sma dilakukan
pada kedua ruas pertidaksamaan tersebut.
Misal :
x + 3 < 5
↔x + 3 – 3 < 5 – 3
↔ x < 2
2. Tanda pertidaksamaan tidak berubah jika perkalian atau
pembagian suatu bilangan positif dilakukan pada kedua
ruas pertidaksamaan tersebut
Misal :
2x ≥ 18
↔ 2x . ½ ≥ 18 . ½
↔ x ≥ 9

5. 3. Tanda pertidaksamaan akan berubah jika
perkalian atau pembagian suatu bilangan negatif
dilakukan pada kedua ruas pertidaksamaan
tersebut.
Bukti :
Misalnya : a < b dan k < 0
karena a < b maka a – b = n , dimana n < 0
sehingga : k ( a – b ) = kn
↔ ka - kb = kn > 0
↔ ka > kb
Contoh :
- 4x < 12
↔ - 4x . – ¼ > 12 . - ¼
↔ x > -3

6. Pertidaksamaan Linier
Pertidaksamaan linier adalah pertidaksamaan yang
memuat variabel dengan pangkat tertinggi adalah satu
Contoh :
Tentukan HP dari pertidaksamaan berikut ini :
a. 2x – 5 < 13
b. 3x + 2 ≥ 5x – 22
c. 3 < x + 4 < 7
d. 3x + 1 ≤ 2x – 6 ≤ x – 5
Jawab :
a. 2x – 5 < 13
↔2x < 13 + 5
18
↔ x < 18
HP = { x / x < 18 }

7. b. 3x + 2 ≥ 5x – 22
↔ 3x – 5x ≥ - 22 – 2
↔ - 2x ≥ -24
↔ x ≤ 12
HP = { x / x ≤ 12 }
c. 3 < x + 4 < 7
↔ 3 – 4 < x < 7 – 4
↔ - 1 < x < 3
HP = { x / -1 < x < 3 }
d. 3x + 1 ≤ 2x – 6 ≤ x – 5
↔ 3x + 1 ≤ 2x – 6
↔ 3x – 2x ≤ -6 - 1
↔ x ≤ - 7
atau :
2x – 6 ≤ x – 5
↔ 2x – x ≤ -5 + 6
↔ x ≤ 1
12
- 1 3

8. atau :
3x + 1 ≤ x – 5
↔ 3x – x ≤ -5 – 1
↔ 2x ≤ -6
↔ x ≤ -3
hasilnya
- 7
-3
1
- 7
HP = { x / x ≤ - 7 }

9. Pertidaksamaan Kuadrat
Pertidaksamaan kuadrat adalah pertidaksamaan
yang memuat variabel dengan pangkat tertinggi
adalah dua.
Ada 2 cara menyelesaiakan pertidaksamaan kuadrat
yaitu :
a. dengan metode garis bilangan
b. dengan metode sketsa grafik

10. Penyelesaian
1. Ruas kanan dibuat menjadi nol.
2. Faktorkan.
3. Tentukan harga nol, yaitu nilai variabel yang
menyebabkan nilai faktor sama dengan nol.
4. Gambar garis bilangannya
• Jika tanda pertidaksamaan ≥ atau ≤, maka
harga nol ditandai dengan titik hitam •
• Jika tanda pertidaksamaan > atau <, maka
harga nol ditandai dengan titik putih °

11. 5. Tentukan tanda (+) atau (–) pada masing-masing
interval di garis bilangan. Caranya adalah dengan
memasukkan salah satu bilangan pada interval
tersebut pada persamaan di ruas kiri.
Tanda pada garis bilangan berselang-seling, kecuali jika
ada batas rangkap (harga nol yang muncul 2 kali atau
sebanyak bilangan genap untuk pertidaksamaan
tingkat tinggi), batas rangkap tidak merubah tanda.
6. Tentukan himpunan penyelesaian
→ jika tanda pertidaksamaan > 0 berarti daerah pada
garis bilangan yang diarsir adalah yang bertanda (+)
→ jika tanda pertidaksamaan < 0 berarti daerah pada
garis bilangan yang diarsir adalah yang bertanda (–)

12. Contoh:
(2x – 1)2 ≥ (5x – 3).(x – 1) – 7
4x2 – 4x + 1 ≥ 5x2 – 5x – 3x + 3 – 7
4x2 – 4x + 1 – 5x2 + 5x + 3x – 3 + 7 ≥ 0
–x2 + 4x + 5 ≥ 0
–(x2 – 4x – 5) ≥ 0
–(x – 5).(x + 1) ≥ 0
Harga nol: x – 5 = 0 atau x + 1 = 0
x = 5 atau x = –1
Garis bilangan :
• menggunakan titik hitam karena tanda
pertidaksamaan ≥
• jika dimasukkan x = 0 hasilnya positif

13. • karena 0 berada di antara –1 dan 5, maka
daerah tersebut bernilai positif, di kiri dan
kanannya bernilai negatif
• karena tanda pertidaksamaan ≥ 0, maka yang
diarsir adalah yang positif
Jadi penyelesaiannya: {x | –1 ≤ x ≤ 5}

14. Metode sketsa grafik
Menyelesaikan pertidaksamaan kuadrat
dengan menggunakan metode sketsa grafik
fungsi kuadrat seperti yang telah kita pelajari
pada kompetensi dasar grafik fungsi kuadrat yang
lalu. Grafik fungsi kuadrat berbentuk parabola.
Hal yang perlu diperhatikan sebelum kita
menggambar parabola y = ax2 + bx + c adalah a
dan D (diskriminan = b2 – 4ac) . Perhatikanlah hal
yang berikut ini :

15. a.
Jika a > 0 (Mempunyai nilai
balik minimum).
D > 0 (memotong sb x di 2
titik yang berlainan).
b.
a > 0
D=0 (menyinggung sb
x/terdapat 1 titik persekutuan).
c.
a > 0
D < 0 (tidak
memotong/menyinggung sb x).

16. d.
 a < 0 (mempunyai nilai
balik maksimum)
 D > 0 (memotong sb x
di 2 titik yang
berlainan).
e.
 a < 0
 D = 0 (menyinggung sb
x, mempunyai 1 titik
persekutuan).
f.
 a < 0
 D < 0 (tidak
memotong/menyinggun
g sb x)

17. Hal yang perlu diperhatikan dalam menggambar sketsa
grafik fungsi kuadrat yaitu :
a. Titik potong dengan sumbu X syaratnya y = 0
b. Titik potong dengan sumbu Y syartanya x = 0
c. Sumbu simetri yaitu x = -b/2a
d. Titik Puncak yaitu P( -b/2a , -D/4a)
Contoh 5 :
Tentukan HP dari pertidaksamaan kuadrat x2 – x < 3x
dengan menggunakan sketsa grafik.
Jawab :
x2 – x < 3x
↔ x2 – x - 3x < 0
↔ x2 – 4x < 0
Kita harus menggambar grafik fungsi kuadrat y = x2 – 4x
dan setelah itu kita tentukan daerah penyelesaiannya yang
berada dibawah sumbu X.

18. a. Titik potong dengan sumbu X syaratnya y – 0
y = x2 – 4x
0 = x2 – 4x
0 = x ( x – 4)
x = 0 atau x = 4
b. Titik potong dengan sumbu Y syaratnya x = 0
y = 3
Jadi titik potong dengan sumbu Y adalah (3,0)
c. Sumbu simetri x = -b/2a
x = - (-4) / 2.1
x = 2
d. Puncak P(-b/2a , -D/4a)
P ( 2, -(b2 – 4ac) /4a )
P ( 2, -((-4)2-4.1.0 / 4.1)
P ( 2, -16/4)
P (2 , -4)

19. Sketsa grafiknya adalah sebagai berikut :
0 2
-4
4
Y
X
Himpunan
penyelesaiannya adalah
daerah yang diantara 0
dan 4 yang berada
dibawah sumbu X
(karena tanda
pertidaksamaannya < 0)
Jadi HP = { x / 0 < x < 4}

20. Pertidaksamaan Bentuk Pecahan
Pertidaksamaan bentuk pecahan adalah
pertidaksamaan yang terdiri atas pembilang
dan penyebut dimana bagian penyebut
terdapat variabel.

21. Penyelesaian
• Ruas kanan dijadikan nol
• Samakan penyebut di ruas kiri
• Faktorkan pembilang dan penyebut (jika bisa)
• Cari nilai-nilai variabel yang menyebabkan pembilang
dan penyebutnya sama dengan nol (harga nol untuk
pembilang dan penyebut)
• Gambar garis bilangan yang memuat semua nilai yang
didapatkan pada langkah 4
• Apapun tanda pertidaksamaannya, harga nol untuk
penyebut selalu digambar dengan titik putih (penyebut
suatu pecahan tidak boleh sama dengan 0 agar
pecahan tersebut mempunyai nilai)
• Tentukan tanda (+) atau (–) pada masing-masing
interval

22. Contoh :
Tentukan himpunan penyelesaian
dari pertidaksamaan :
2 1
x
0 , 1
0
2
x
x
Jawab
2
1
:
1
  




  

x
x
Faktor pembuat nol adalah x dan x
+ + + + - - - - - - - - - + + + +
-1 2
Jadi HP = { x / -1 < x < 2 }

23. Pertidaksamaan Bentuk Akar
Pertidaksamaan yang mengandung bentuk akar
diselesaikan dengan mengkuadratkan kedua ruas. Akan
tetapi harus dijamin bahwa setiap yang berada dalam akar
dan hasil penarikam akar harus ≥ 0
Penyelesaian:
• Kuadratkan kedua ruas
• Jadikan ruas kanan sama dengan nol
• Selesaikan seperti menyelesaikan pertidaksamaan
linear/kuadrat
• Syarat tambahan: yang berada di dalam setiap tanda akar
harus ≥ 0

24. Contoh
Tentukan penyelesaian dari pertidaksamaan
bentuk akar berikut :
2x 5  1
syarat pertidaksamaan
 
x syarat bentuk akar
(2 5) 1 :
x x
2  6 2  5 
0
x x
 
3 2 5
5
2
( 2 5) (1)
:
2 2

 
x
x

25. 5/2
5/2
3
3
Syarat bentuk akar
Syarat pertidaksamaan
hasilnya
Jadi HP = { x / 5/2 ≤ x ≤ 3 }

26. Pertidaksamaan Tingkat Tinggi
Variabel berpangkat lebih dari 2
Penyelesaian sama dengan pertidaksamaan kuadrat
Contoh:
(2x + 1)2.(x2 – 5x + 6) < 0
(2x + 1)2.(x – 2).(x – 3) < 0
Harga nol: 2x + 1 = 0 atau x – 2 = 0 atau x – 3 = 0
x = –1/2 atau x = 2 atau x = 3
Garis bilangan:
• menggunakan titik putih karena tanda pertidaksamaan <
• jika dimasukkan x = 0 hasilnya positif

27. • karena 0 berada di antara –1/2 dan 2, maka
daerah tersebut bernilai positif
• karena –1/2 adalah batas rangkap (–1/2 muncul
sebanyak 2 kali sebagai harga nol, jadi –1/2
merupakan batas rangkap), maka di sebelah kiri –
1/2 juga bernilai positif
• selain daerah yang dibatasi oleh batas rangkap,
tanda positif dan negatif berselang-seling
• karena tanda pertidaksamaan ³ 0, maka yang
diarsir adalah yang positif
Jadi penyelesaiannya: {x | 2 < x < 3}

28. Pertidaksamaan Bentuk Harga Mutlak
variabelnya berada di dalam tanda mutlak
|…..|
(tanda mutlak selalu menghasilkan hasil yang
positif, contoh: |3| = 3; |–3| = 3)
Pengertian nilai mutlak:

29. Contoh 1:
|2x – 3| ≤ 5
berarti:
–5 ≤ 2x – 3 ≤ 5
–5 + 3 ≤ 2x ≤ 5 + 3
–2 ≤ 2x ≤ 8
Semua dibagi 2:
–1 ≤ x ≤ 4
Contoh 2:
|3x + 7| > 2
berarti:
3x + 7 < –2 atau 3x + 7 > 2
3x < –2 – 7 atau 3x > 2 – 7
x < –3 atau x > –5/3

30. Contoh 3:
|x – 2|2 – |x – 2| < 2
Misalkan |x – 2| = y
y2 – y < 2
y2 – y – 2 < 0
(y – 2).(y + 1) < 0
Harga nol: y – 2 = 0 atau y + 1 = 0
y = 2 atau y = –1
Garis bilangan:
Artinya:
–1 < y < 2
–1 < |x – 2| < 2
Karena nilai mutlak pasti bernilai positif, maka batas kiri tidak berlaku
|x – 2| < 2
Sehingga:
–2 < x – 2 < 2
–2 + 2 < x < 2 + 2
0 < x < 4