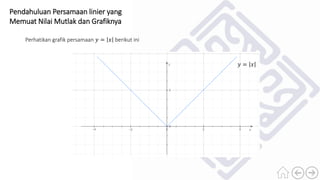
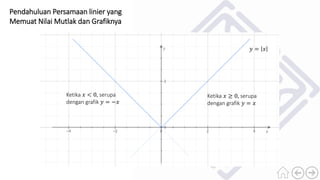
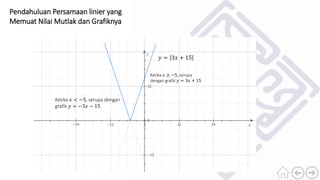
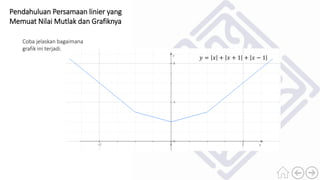
Dokumen ini membahas konsep nilai mutlak dari bilangan real, termasuk definisi nilai mutlak dan cara menuliskan bentuk aljabar dengan nilai mutlak. Terdapat contoh-contoh untuk ilustrasi, serta penjelasan mengenai jarak dalam garis bilangan yang dinyatakan sebagai nilai mutlak. Selain itu, dokumen juga menyertakan sifat-sifat nilai mutlak dan soal latihan untuk memperdalam pemahaman.