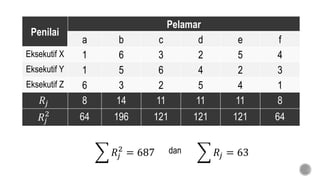
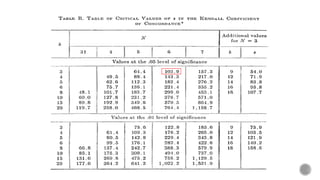
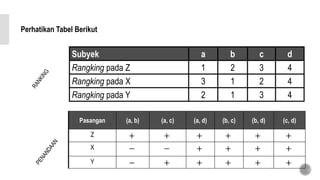
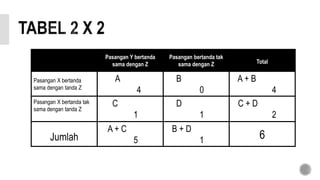
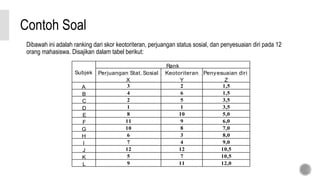
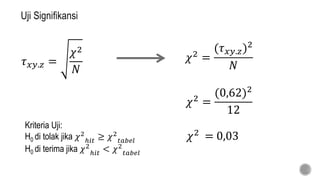
Dokumen ini membahas metode analisis korelasi dan koefisien korelasi ranking Kendall, serta prosedur untuk menguji signifikansi hubungan antara variabel. Terdapat penjelasan mengenai perhitungan korelasi parsial, serta contoh aplikasi menggunakan data mahasiswa dalam konteks hubungan antara perjuangan sosial, keotoriteran, dan penyesuaian diri. Selain itu, dijelaskan juga tentang pengujian signifikansi menggunakan uji chi-square dan perhitungan koefisien konkordansi Kendall.

1. Disusun Oleh :
1. Agung Anggoro
2. Agus Ahmad D
3. Hibatul Azizi
4. M. Rizki Fauzi
5. Riksa Rishanif
𝜏
𝑊

2. 𝜏

3. KOEFISIEN KORELASI RANKING
PARSIAL KENDALL : 𝜏 𝑥𝑦.𝑧
 Korelasi adalah pengukuran keeratan hubungan antar dua variabel.
 Korelasi parsial mengukur korelasi antara dua buah variabel seperti
perhitungan korelasi pada umumnya, namun dengan menganggap sebuah
variabel (ketiga) yang dibuat konstan.
 Perhitungan korelasi secara per bagian ini (parsial) bertujuan untuk
mengukur pengaruh ‘efek ketiga’ pada keeratan hubungan dua variabel yang
dikorelasi.
 Keeratan hubungan antara dua variabel yang diperoleh adalah murni dan
langsung.
 Data yang digunakan ‘sekurang-kurangnya’ berskala ordinal.

4. Perhatikan Tabel Berikut
Subyek a b c d
Rangking pada Z 1 2 3 4
Rangking pada X 3 1 2 4
Rangking pada Y 2 1 3 4
Pasangan (a, b) (a, c) (a, d) (b, c) (b, d) (c, d)
Z + + + + + +
X − − + + + +
Y − + + + + +

5. Pasangan Y bertanda
sama dengan Z
Pasangan bertanda tak
sama dengan Z Total
Pasangan X bertanda
sama dengan tanda Z
A
4
B
0
A + B
4
Pasangan X bertanda tak
sama dengan tanda Z
C
1
D
1
C + D
2
Jumlah
A + C
5
B + D
1 6

6. 𝜏 𝑥𝑦.𝑧 =
𝐴𝐷 − 𝐵𝐶
(𝐴 + 𝐵)(𝐶 + 𝐷)(𝐴 + 𝐶)(𝐵 + 𝐷)
𝜏 𝑥𝑦.𝑧 =
(4)(1) − (0)(1)
4 2 5 (1)
= 0,63 (Dari Tabel 2 X 2)

7. Bila terdapat angka yang sama Bila tidak terdapat angka yang tidak sama
𝜏 =
𝑆
1
2
𝑁 (𝑁 − 1)
𝜏 =
𝑆
1
2
𝑁 𝑁 − 1 − 𝑇𝑥
1
2
𝑁 𝑁 − 1 − 𝑇𝑦
𝑇𝑥 =
1
2
𝑥
𝑡(𝑡 − 1) 𝑇𝑦 =
1
2
𝑦
𝑡(𝑡 − 1)
𝝉 𝒙𝒚.𝒛 =
𝝉 𝒙𝒚 − 𝝉 𝒛𝒚 𝝉 𝒛𝒙
𝟏 − 𝝉 𝒙𝒛
𝟐 )(𝟏 − 𝝉 𝒚𝒛
𝟐
Rumus Korelasi Parsial Ranking
Kendall

8. Uji Signifikansi
𝐻0: Tidak terdapat hubungan yang signifikan antara variabel X dan Y dengan
variabel Z yang konstan
𝐻 𝑎: Terdapat hubungan yang signifikan antara variabel X dan Y dengan variabel Z
yang konstan
𝐻0 ∶ 𝜏 𝑥𝑦.𝑧 = 0
𝐻 𝑎 ∶ 𝜏 𝑥𝑦.𝑧 ≠ 0
Hipotesis

9. Uji Signifikansi Korelasi Partial kendal dapat dilakukan dengan uji Chi-Square
𝜏 𝑥𝑦.𝑧 =
𝜒2
𝑁
𝜒2
=
(𝜏 𝑥𝑦.𝑧)2
𝑁
Kriteria Uji :
H0 di tolak jika 𝜒2
ℎ𝑖𝑡 ≥ 𝜒2
𝑡𝑎𝑏𝑒𝑙
H0 di terima jika 𝜒2
ℎ𝑖𝑡 < 𝜒2
𝑡𝑎𝑏𝑒𝑙

10. IKHTISAR PROSEDUR
1. Misalkan X dan Y adalah dua variabel yang hubungannya akan kita tentukan,
dan Z adalah variabel yang efeknya terhadap X dan Y yang diparsialkan, atau
dianggap konstan.
2. Memberi ranking pada variabel X, Y, dan Z dari 1 hingga n.
3. Menentukan harga-harga observasi 𝜏 𝑥𝑦, 𝜏 𝑦𝑧, 𝑑𝑎𝑛 𝜏 𝑥𝑧.
4. Menghitung 𝜏 𝑥𝑦.𝑧
5. Uji Signifikansi
6. Kesimpulan

11. Contoh Soal
Dibawah ini adalah ranking dari skor keotoriteran, perjuangan status sosial, dan penyesuaian diri pada 12
orang mahasiswa. Disajikan dalam tabel berikut:
Perjuangan Stat. Sosial Keotoriteran Penyesuaian diri
X Y Z
A 3 2 1,5
B 4 6 1,5
C 2 5 3,5
D 1 1 3,5
E 8 10 5,0
F 11 9 6,0
G 10 8 7,0
H 6 3 8,0
I 7 4 9,0
J 12 12 10,5
K 5 7 10,5
L 9 11 12,0
Subjek
Rank

12. HIPOTESIS
𝐻0 ∶ Tidak terdapat hubungan yang signifikan antara perjuangan status
sosial dan keotoriteran dengan penyesuaian diri “yang konstan”
𝐻 𝑎 ∶ Tidak terdapat hubungan yang signifikan antara perjuangan status
sosial dan keotoriteran dengan penyesuaian diri "yang konstan"
Taraf signifikansi 𝛼 = 5% = 0,05

13. Setelah dihitung untuk 𝜏 𝑥𝑦, 𝜏 𝑦𝑧, 𝑑𝑎𝑛 𝜏 𝑥𝑧 adalah sebagai berikut:
𝝉 𝒙𝒚 = 𝟎, 𝟔𝟕
𝝉 𝒚𝒛 = 𝟎, 𝟑𝟔
𝝉 𝒙𝒛 = 𝟎, 𝟑𝟗
𝝉 𝒙𝒚.𝒛 =
𝝉 𝒙𝒚 − 𝝉 𝒚𝒛 𝝉 𝒙𝒛
(𝟏 − 𝝉 𝒚𝒛
𝟐)(𝟏 − 𝝉 𝒙𝒛
𝟐)
=
𝟎, 𝟔𝟕 − (𝟎, 𝟑𝟔)(𝟎, 𝟑𝟗)
(𝟏 − (𝟎, 𝟑𝟔) 𝟐)(𝟏 − (𝟎, 𝟑𝟗) 𝟐)
= 0,62
Setelah dihitung untuk 𝜏 𝑥𝑦, 𝜏 𝑦𝑧, dan 𝜏 𝑥𝑧adalah sebagai berikut:
𝜏 𝑥𝑦 = 0,67
𝜏 𝑦𝑧 = 0,36
𝜏 𝑥𝑧 = 0,39
𝜏 𝑥𝑦.𝑧 =
𝜏 𝑥𝑦 − 𝜏 𝑦𝑧 𝜏 𝑥𝑧
(1 − 𝜏 𝑦𝑧
2)(1 − 𝜏 𝑥𝑧
2)
=
0,67 − (0,36)(0,39)
(1 − (0,36)2)(1 − (0,39)2)
= 0,62

14. Uji Signifikansi
𝜏 𝑥𝑦.𝑧 =
𝜒2
𝑁
𝜒2
=
(𝜏 𝑥𝑦.𝑧)2
𝑁
Kriteria Uji:
H0 di tolak jika 𝜒2
ℎ𝑖𝑡 ≥ 𝜒2
𝑡𝑎𝑏𝑒𝑙
H0 di terima jika 𝜒2
ℎ𝑖𝑡 < 𝜒2
𝑡𝑎𝑏𝑒𝑙
𝜒2
=
(0,62)2
12
𝜒2
= 0,03

15. Taraf signifikansi α = 5% = 0,05
df = 12-1 =11
Diperoleh :
𝜒2
(0,05 , 11) = 19,68
Kesimpulan
H0 di terima karena 𝜒2
ℎ𝑖𝑡 < 𝜒2
𝑡𝑎𝑏𝑒𝑙
Yaitu, Tidak terdapat hubungan yang signifikan antara perjuangan status sosial
dan keotoriteran dengan penyesuaian diri “yang konstan”

16. 𝑊

17. Koefisien konkordansi kendall: 𝑊
 Mengukur derajat asosiasi dari k buah variabel (> 2)
 Dalam praktek,sering dipakai untuk menilai tingkat
kesepakatan/kecocokan/korelasi antara beberapa 𝑘 pengamat dalam
memberikan peringkat pada suatu set obyek.
 Data berskala ordinal,interval atau rasio.

18. Prosedur
 Menentukan rangking terlebih dahulu pada masing masing variabel
 Menghitung jumlah rangking untuk setiap obyek
 Hitung nilai koefisien Konkordansi Kendall:W

19. Kecocokan Sempurna
Misalkan 𝑘 orang juri memberikan penilaian terhadap 𝑛 kontestan lomba
berupa ranking versi masing-masing juri. Pertanyaan yang muncul
adalah, bagaimanakah bentuk matriks penilaian yang ditampilkan jika
tidak terdapat atau hanya terdapat sedikit sekali kecocokan penilaian
diantara 𝑘 juri tersebut ? serta, bagaimanakah jika terjadi kecocokan
yang sempurna dalam penilaian tersebut ?

20. Kecocokan Sempurna
Juri
Ranking Kontestan
𝐴1 𝐴2 ... 𝐴 𝑁
𝐽1 𝑥11 𝑥12 ... 𝑥1𝑁
𝐽2 𝑥21 𝑥21 ... 𝑥2𝑁
... ... ... ... ...
𝐽 𝑘 𝑥 𝑘1 𝑥 𝑘2 ... 𝑥 𝑘𝑁
𝑅𝑗
𝑗 = 1,2, … , 𝑁
𝑖=1
𝑘
𝑥𝑖1
𝑖=1
𝑘
𝑥𝑖2
...
𝑖=1
𝑘
𝑥𝑖𝑁

21. Kecocokan Sempurna
Kecocokan sempurna akan terjadi jika tiap juri memberikan ranking dengan
urutan yang sama pada 𝑛 kontestan. Dimana baris terakhir berupa
penjumlahan ranking pada tiap kontestan (𝑅𝑗) akan bernilai berbeda-beda
dengan kemungkinan-kemungkinan nilai hanyalah 𝑘, 2𝑘, 3𝑘, … , 𝑛𝑘. Matriks
data seperti demikian akan menghasilkan 𝑊 = 1.

22. Kalkulasi 𝑾
𝑊 dihitung dengan rumus berikut
𝑊 =
𝑠
1
12
𝑘2 𝑁3 − 𝑁
dimana 𝑠 adalah jumlah kuadrat deviasi observasi dari rataan 𝑅𝑗, yaitu (3)
𝑠 =
𝑗=1
𝑁
𝑅𝑗 −
𝑗=1
𝑁
𝑅𝑗
2
=
𝑗=1
𝑁
𝑅𝑗
2
−
𝑗=1
𝑁
𝑅𝑗
2
𝑁

23. Kalkulasi 𝑾
Apabila terdapat objek-objek dengan ranking sama pada sebuah variabel atau
lebih, maka perhitungan disesuaikan dengan rumus
𝑊 =
𝑠
1
12
𝑘2 𝑁3 − 𝑁 − 𝑘 𝑗=1
𝑘
𝑇𝑗
𝑇𝑗 adalah hasil penjumlahan dari (𝑡3
− 𝑡)/12 dimana 𝑡 adalah banyaknya
sebuah angka ranking muncul dalam perankingan oleh variabel ke 𝑗.

24. Uji Signifikansi 𝑾
𝐻0 : 𝑘 himpunan Ranking independen
𝐻 𝐴 : 𝑘 himpunan Ranking dependen

25. Metode untuk menentukan apakah harga 𝑊 observasi signifikan berbeda
bergantung pada ukuran 𝑁 ,sbb:
 Jika N dari 3-7 dan k antara 3-20
𝐻0 ditolak jika 𝑠ℎ𝑖𝑡 ≥ 𝑠𝑡𝑎𝑏𝑒𝑙
𝐻0 diterima jika 𝑠ℎ𝑖𝑡 < 𝑠𝑡𝑎𝑏𝑒𝑙
𝑠𝑡𝑎𝑏𝑒𝑙 dapat dilihat pada tabel R (Siegel, 1986: 338)
 Jika N lebih besar dari 7, menggunakan rumus:
𝜒2
= 𝑘 𝑁 − 1 𝑊
Uji Signifikansi 𝑾

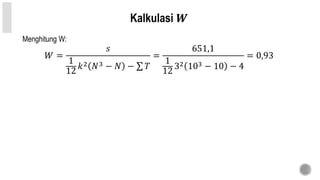
26. Uji Signifikansi 𝑾
[Sampel Besar]
Statistik Uji:
𝜒2
= 𝑘 𝑁 − 1 𝑊
Kriteria Uji:
H0 di tolak jika 𝜒2
ℎ𝑖𝑡 ≥ 𝜒2
𝑡𝑎𝑏𝑒𝑙
H0 di terima jika 𝜒2
ℎ𝑖𝑡 < 𝜒2
𝑡𝑎𝑏𝑒𝑙
Untuk 𝜒2
𝑡𝑎𝑏𝑒𝑙 dapat dilihat dari tabel harga-harga kritis Chi-Kuadrat. Dengan:
𝑑𝑓 = 𝑁 − 1

27. Contoh Soal
Ranking diberikan kepada 6 pelamar pekerjaan oleh tiga eksekutif
perusahaan. Kemudian ingin diketahui apakah ada hubungan
antara ranking yang diberikan oleh tiga eksekutif perusahaan
tersebut. (𝛼 = 5%)
Kasus Sampel Kecil dan Tidak Ada Ranking Sama

28. Penilai
Pelamar
a b c d e f
Eksekutif X 1 6 3 2 5 4
Eksekutif Y 1 5 6 4 2 3
Eksekutif Z 6 3 2 5 4 1
𝑅𝑗 8 14 11 11 11 8
𝑅𝑗
2
64 196 121 121 121 64
𝑅𝑗
2
= 687 𝑅𝑗 = 63dan

29. Kalkulasi Nilai 𝑾
𝑠 =
𝑗=1
6
𝑅𝑗
2
−
𝑗=1
6
𝑅𝑗
2
𝑁
=687−
632
6
= 25,5
𝑊 =
𝑠
1
12
𝑘2(𝑁3 − 𝑁)
=
25,5
1
12
(3)2(63 − 6)
= 0,16

30. Uji Signifikansi
Statistik uji :
Karena 𝑁 < 7, maka kita menggunakan harga s sebagai statistik uji.
Kriteria :
𝐻0 ditolak jika 𝑠ℎ𝑖𝑡 ≥ 𝑠𝑡𝑎𝑏𝑒𝑙
𝐻0 diterima jika 𝑠ℎ𝑖𝑡 < 𝑠𝑡𝑎𝑏𝑒𝑙 𝛼 = 0,05
Keputusan
Karena 𝑠ℎ𝑖𝑡 = 25,5 < 𝑠𝑡𝑎𝑏𝑒𝑙 = 103,9 , maka 𝐻0 diterima
Kesimpulan : Dengan tingkat keyakinan 95% kita dapat menyimpulkan bahwa Tidak
terdapat kecocokan yang signifikan pada pemberian rangking oleh eksekutif X, Y, dan Z,
yang artinya kecocokan yang terjadi merupakan kebetulan semata.

32. Contoh Soal
Sepuluh siswa diberi ranking berdasarkan kemampuan matematika
dalam topik trigonometri oleh tiga guru yang berbeda X, Y, dan Z.
Dengan 𝛼=0.05 selidikilah kecocokan ketiga guru tersebut dalam
memberikan ranking kepada siswa.
Kasus Sampel Besar dan Angka sama

33. dan
Siswa
A B C D E F G H I J
Guru X
3 4,5 4,5 2 1 7 7 7 9 10
Guru Y
3,5 3,5 5 1 2 6 7,5 7,5 10 9
Guru Z
3 2 5 4 1 7,5 6 9 7,5 10
𝑅𝑗 9,5 10 14,5 7 4 20,5 20,5 23,5 26,5 29
𝑅𝑗
2
90,25 100 210,25 49 16 420,25 420,25 552,25 702,25 841
𝑅𝑗
2
= 3275,5 𝑅𝑗 = 162

34. Statistik Uji
Karena N = 10 dan k = 3 maka kita menggunakan uji Konkordansi Kendall W untuk sampel
besar.
Mencari s terlebih dahulu:
𝑠 = 𝑅𝑗 −
𝑅𝑗
𝑁
2
= 651,1
Menghitung angka yang sama:
𝑇𝑋 =
𝑡3
− 𝑡
12
=
23
− 2 + 33
− 3
12
= 2,5
𝑇𝑌 =
𝑡3 − 𝑡
12
=
23 − 2 + 23 − 2
12
= 1
𝑇𝑍 =
𝑡3 − 𝑡
12
=
23 − 2
12
= 0,5

35. Kalkulasi 𝑾
Menghitung W:
𝑊 =
𝑠
1
12
𝑘2 𝑁3 − 𝑁 − 𝑇
=
651,1
1
12
32 103 − 10 − 4
= 0,93

36. Menghitung 𝜒2
𝜒2
= 𝑘 𝑁 − 1 𝑊 = 3 10 − 1 0,93 = 25,09
Keputusan:
Karena 𝜒2
ℎ𝑖𝑡 = 25,09 > 𝜒2
𝑡𝑎𝑏𝑒𝑙 = 16,92, maka 𝐻0 ditolak.
Kesimpulan:Terdapat kecocokan yang signifikan pada pemberian
ranking oleh guru X, Y, dan Z.
Uji Signifikansi

37. Hipotesis
𝐻0: Tidak terdapat kecocokan yang signifikan pada pemberian
rangking oleh guru X, Y, dan Z.
𝐻 𝑎: Terdapat kecocokan yang signifikan pada pemberian
rangking oleh guru X, Y, dan Z.
Taraf Signifikan:
𝛼 = 0,05 𝑑𝑎𝑛 𝑑𝑓 = 9 → 𝝌 𝟐
𝜶, 𝒅𝒇 = 𝟏𝟔, 𝟗𝟐
Daerah Penolakan 𝐻0
H0 di tolak jika 𝝌 𝟐
𝒉𝒊𝒕 ≥ 𝝌 𝟐
𝒕𝒂𝒃𝒆𝒍

38. Terima Kasih