Downloaded 366 times
![Example
Lets look for a solution to the equation x3
-2x-3=0.
We consider the function f(x)=x3
-2x-3
On the interval [0,2] the function is negative at 0 and positive at 2. This
means that a=0 and b=2 (i.e. f(0)f(2)=(-3)(1)=-3<0, this means we can
apply the algorithm).
( )
2
3
4
6
31
)2(3
)0()2(
02)0(
0 =
−
−=
−−
−
−=
−
−
−=
ff
f
xrfp
8
21
2
3
)(
−
=
= fxf rfp
This is negative and we will make the a
=3/2 and b is the same and apply the
same thing to the interval [3/2,2].
( )( )
( )
( )
29
54
58
21
2
3
12
3
)2(
2
2
3
8
21
2
1
8
21
2
3
2
3
2
3
=+=
−
−=
−
−
−= −
−
ff
f
xrfp
267785.0
29
54
)( −=
= fxf rfp
This is negative and we will make the a
=54/29 and b is the same and apply the
same thing to the interval [54/29,2].](https://image.slidesharecdn.com/regulafalsi1603216026-150426045300-conversion-gate01/85/Regulafalsi_bydinesh-9-320.jpg)
Uploaded byDinesh Kumar
Regulafalsi_bydinesh
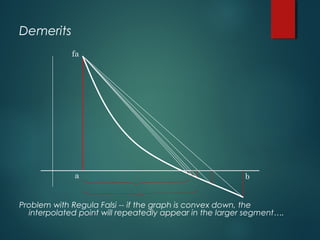
This document describes the False Position Method for finding the roots of equations. The method uses linear interpolation to estimate the root between two initial guesses that bracket it. It improves on the bisection method by choosing a "false position" where the line between the guesses crosses the x-axis, rather than the midpoint. The false position formula is derived using similar triangles. An example applying the method to find a root of x^3 - 2x - 3 = 0 is shown. The merits of the false position method are faster convergence compared to bisection, while the demirits are possible non-monotonic convergence and lack of precision guarantee.
More Related Content
Similar to Regulafalsi_bydinesh
Regulafalsi_bydinesh
- 1. FALSE POSITION METHOD Name–Dinesh Kumar and Himanshu Sharma Roll No. – 16032 and 16026 respectively Submitted To : - Mr. Jitendra Singh
- 2. Finding roots /solving equations The given quadratic formula provides a quick answer to all quadratic equations: Easy But, not easy No exact general solution (formula) exists for equations with exponents greater than 4. a acbb xcbxax 2 4 0 2 2 −− =⇒=++ ?02345 =⇒=+++++ xfexdxcxbxax
- 3. Finding roots… Forthis reason, we have to find out the root to solve the equation. However we can say how accurate our solution is as compared to the “exact” solution. One of the method is FALSE POSITION.
- 4. The False-Position Method(Regula-Falsi) To refine the bisection method, we can choose a ‘false- position’ instead of the midpoint. The false-position is defined as the x position where a line connecting the two boundary points crosses the axis.
- 5. Regula Falsi Forexample, if f(xlow) is much closer to zero than f(xup), it is likely that the root is closer to xlow than to xup. False position method is an alternative approach where f(xlow) and f(xup) are joined by a straight line; the intersection of which with the x-axis represents and improved estimate of the root. The intersection of this line with the x axis represents an improved estimate of the root.
- 6. Linear Interpolation Method Thefact that the replacement of the curve by a straight line gives the false position of the root is the origin of the name, method of false position, or in Latin, Regula Falsi. It is also called the Linear Interpolation Method.
- 7. False Position formulae Using similar triangles, the intersection of the straight line with the x axis can be estimated as This is the False Position formulae. The value of x then replaces whichever of the two initial guesses, low x or up x , yields a function value with the same sign as f (x) . )()( ))(( )()( ul ulu u u u l l xfxf xxxf xx xx xf xx xf − − −= − = −
- 8. Algorithm Given two guessesxlow, xup that bracket the root, Repeat Set If f(xup) is of opposite sign to f(xlow) then Set xlow = xup Else Set xlow = x End If Until y< tolerance value. ( )( ) ( ) ( )ul ulu u xfxf xxxf xx − − −=
- 9. Example Lets look fora solution to the equation x3 -2x-3=0. We consider the function f(x)=x3 -2x-3 On the interval [0,2] the function is negative at 0 and positive at 2. This means that a=0 and b=2 (i.e. f(0)f(2)=(-3)(1)=-3<0, this means we can apply the algorithm). ( ) 2 3 4 6 31 )2(3 )0()2( 02)0( 0 = − −= −− − −= − − −= ff f xrfp 8 21 2 3 )( − = = fxf rfp This is negative and we will make the a =3/2 and b is the same and apply the same thing to the interval [3/2,2]. ( )( ) ( ) ( ) 29 54 58 21 2 3 12 3 )2( 2 2 3 8 21 2 1 8 21 2 3 2 3 2 3 =+= − −= − − −= − − ff f xrfp 267785.0 29 54 )( −= = fxf rfp This is negative and we will make the a =54/29 and b is the same and apply the same thing to the interval [54/29,2].
- 10. Merits & Demerits Merits As the interval becomes small, the interior point generally becomes much closer to root. Faster convergence than bisection. Often superior to bisection.
- 11. Demerits Problem with RegulaFalsi -- if the graph is convex down, the interpolated point will repeatedly appear in the larger segment…. a b fa
- 12. Demerits Demerits It can’tpredict number of iterations to reach a give precision. It can be less precise than bisection – no strict precision guarantee.
- 13. Though thedifference between Bisection and False Position Method is little but for some cases False Position Method is useful and for some problems Bisection method is effective…. In fact they both are necessary to solve any equation by ‘Bracketing method’.
- 14.