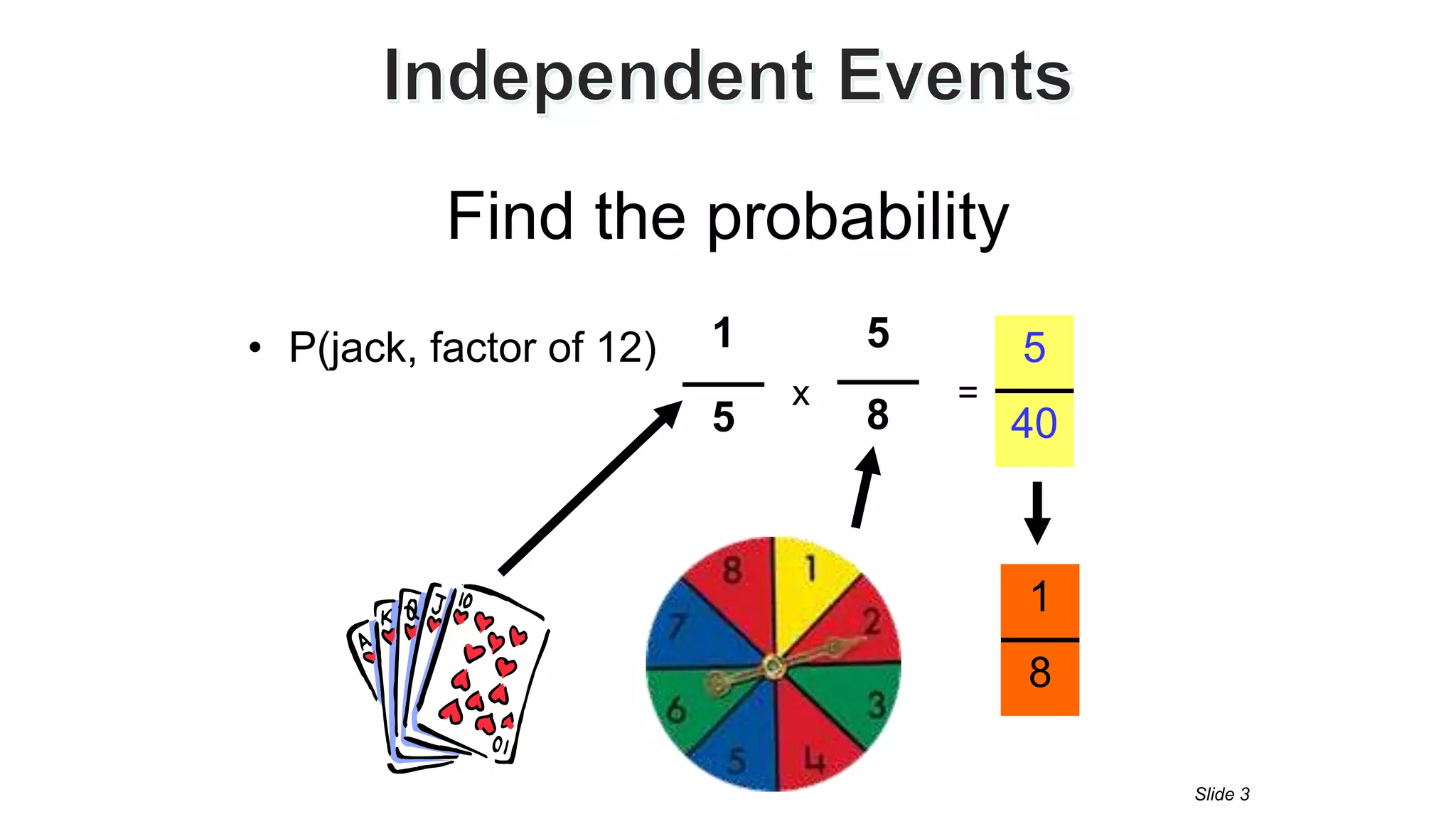
This document discusses independent events and how to calculate the probability of multiple independent events occurring. It defines independent events as those where the outcome of one event does not affect the outcome of the next event. It provides examples of independent events, such as spinning spinners or rolling dice, where replacing or leaving the item unchanged does not change the probabilities. The document states that the probability of two independent events A and B occurring is equal to the probability of A multiplied by the probability of B. It provides an example calculation of the probability of spinning an even number and a vowel.

2. Independent Events
Whatever happens in one event has absolutely nothing to do
with what will happen next because:
1. The two events are unrelated
OR
2. You repeat an event with an item whose numbers will not
change (eg.: spinners or dice)
OR
3. You repeat the same activity, but you REPLACE the item that
was removed.
The probability of two independent events, A and B, is equal to the
probability of event A times the probability of event B.
P(A, B) = P(A) P(B) Slide 2

3. Find the probability
• P(jack, factor of 12) 1
5
5
8
x =
5
40
1
8
Slide 3

4. Find the probability
• P(6, not 5)
1
6
5
6
x =
5
36
Slide 4

5. 1
2
1
5
1 1 1
2 5 10
 
S
T
R
O
P1
2
3
6
5
4
Example: Suppose you spin each of these two spinners. What
is the probability of spinning an even number and a vowel?
P(even) = (3 evens out of 6 outcomes)
(1 vowel out of 5 outcomes)P(vowel) =
P(even, vowel) =
Independent Events
Slide 5

6. Examples:
1. Removing (selecting randomly) three red marbles without
replacement from a bag that contains six red and nine blue marbles.
2. Selecting a red card from a deck of cards, returning the card to the
deck, shuffling the card, and selecting a second red card.
3. Rolling two dice.
4. The weather and how likely you are to go visiting. You have decided
that there is a 50% chance that you will visit your friend if it does
not snow, and a 10% chance if it does snow.
DEPENDENT
INDEPENDENT
INDEPENDENT
DEPENDENT