This document outlines the course on functions of several variables taught by Dr. Kamel Attar at the Lebanese University. It covers definitions, domains, ranges, limits, partial derivatives, and graphs of functions in one, two, and three variables, along with various examples and exercises. The content is designed for the academic year 2020-2021 and serves as a comprehensive resource for understanding multivariable calculus.




![6Ú74
Functions of one variable
Functions of SeveraL VariabLes
Limits for Functions of Two Variables
Partial Derivatives of a Function of Two Variables
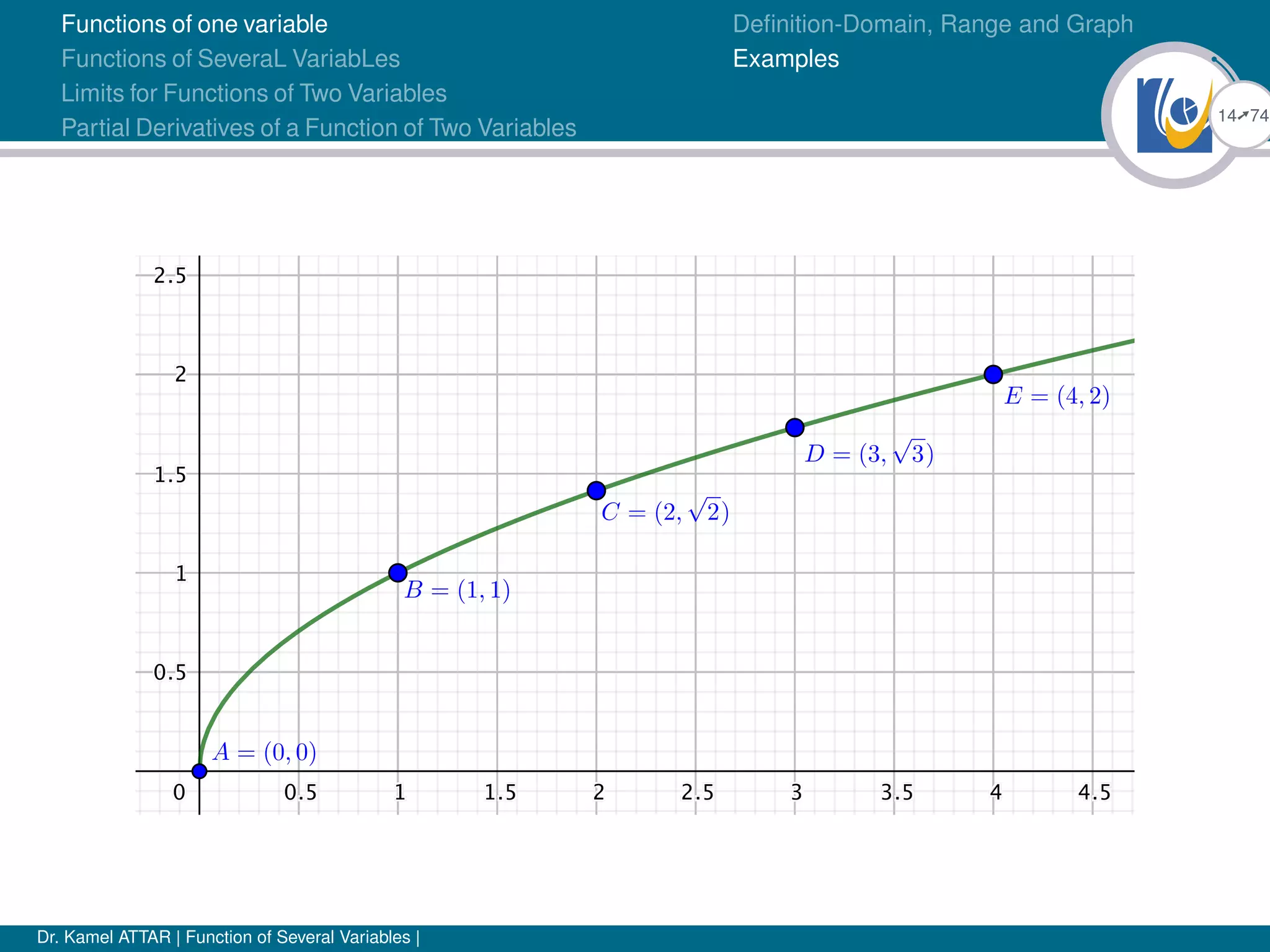
Definition-Domain, Range and Graph
Examples
Example
Function Domain Range
y = x + 2 R =] − ∞, ∞[ R =] − ∞, ∞[
y = 3x2
− 7 R [−7, +∞[
y = sin x R [−1, 1]
y =
1
x
] − ∞, 0[∪]0, +∞[ ] − ∞, 0[∪]0, +∞[
y =
√
x [0, +∞[ [0, +∞[
y = ln x ]0, +∞[ ] − ∞, +∞[
Dr. Kamel ATTAR | Function of Several Variables |](https://image.slidesharecdn.com/functionofseveralvariables-210413093505/75/Function-of-several-variables-6-2048.jpg)


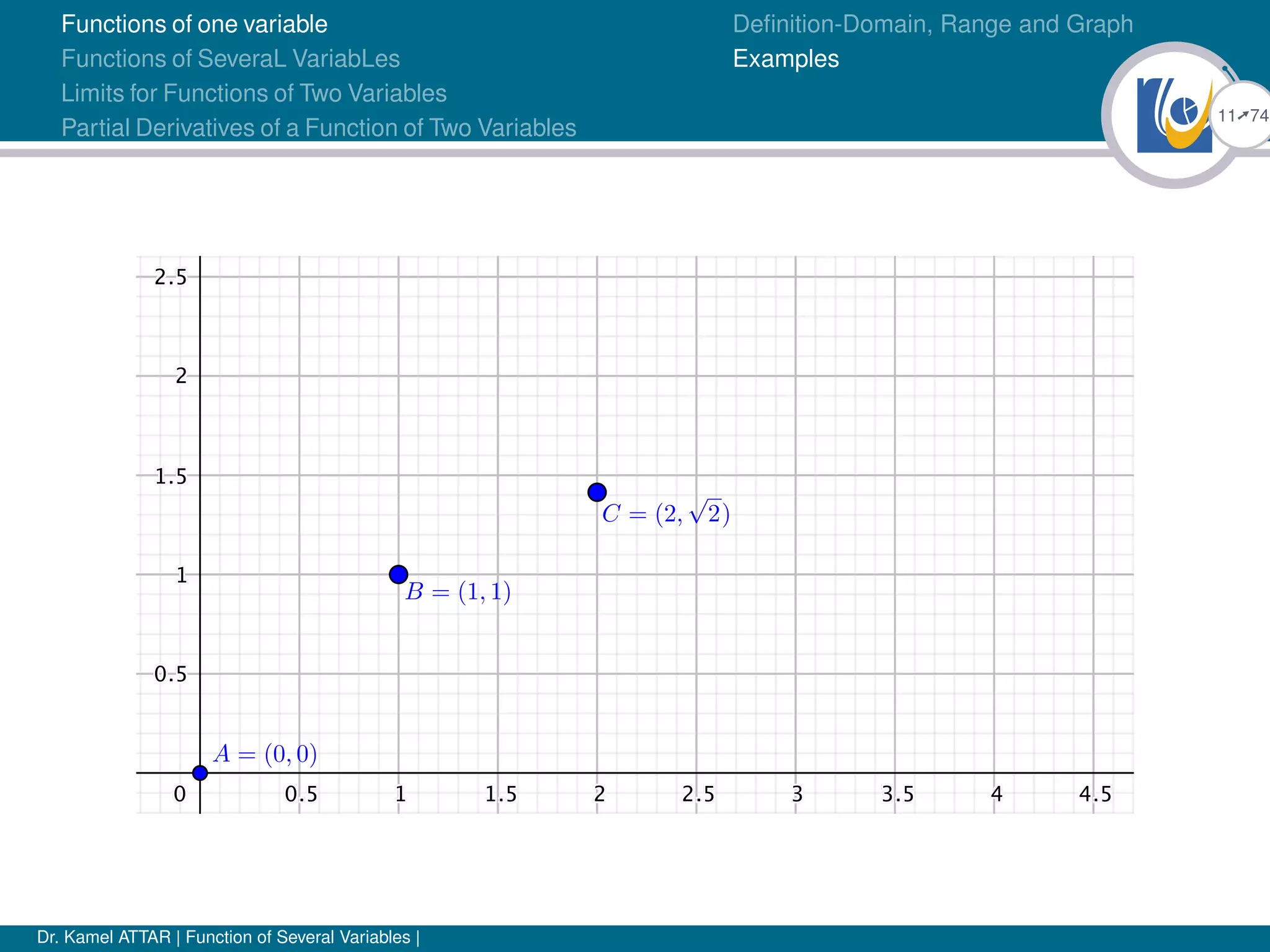
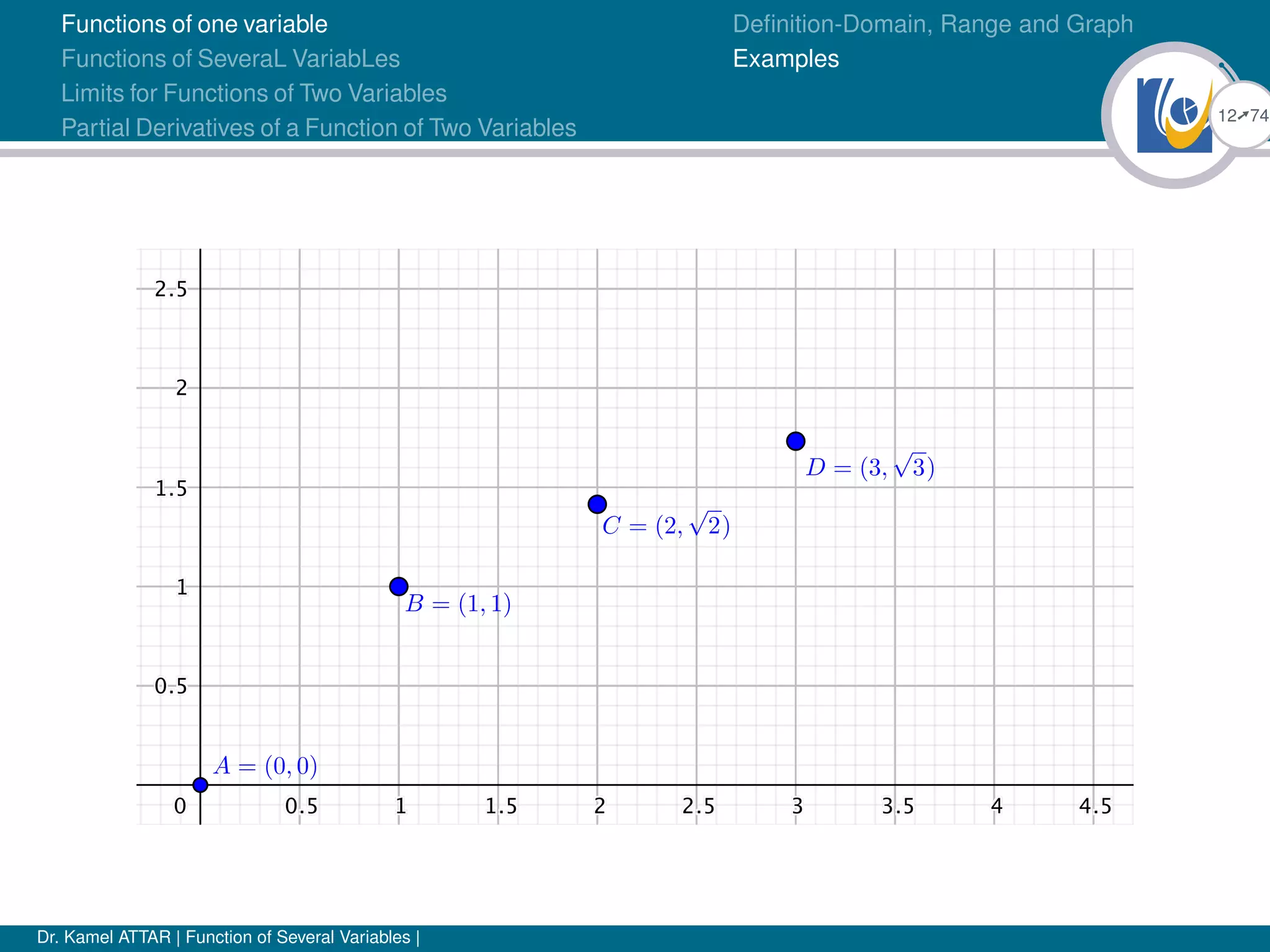





![22Ú74
Functions of one variable
Functions of SeveraL VariabLes
Limits for Functions of Two Variables
Partial Derivatives of a Function of Two Variables
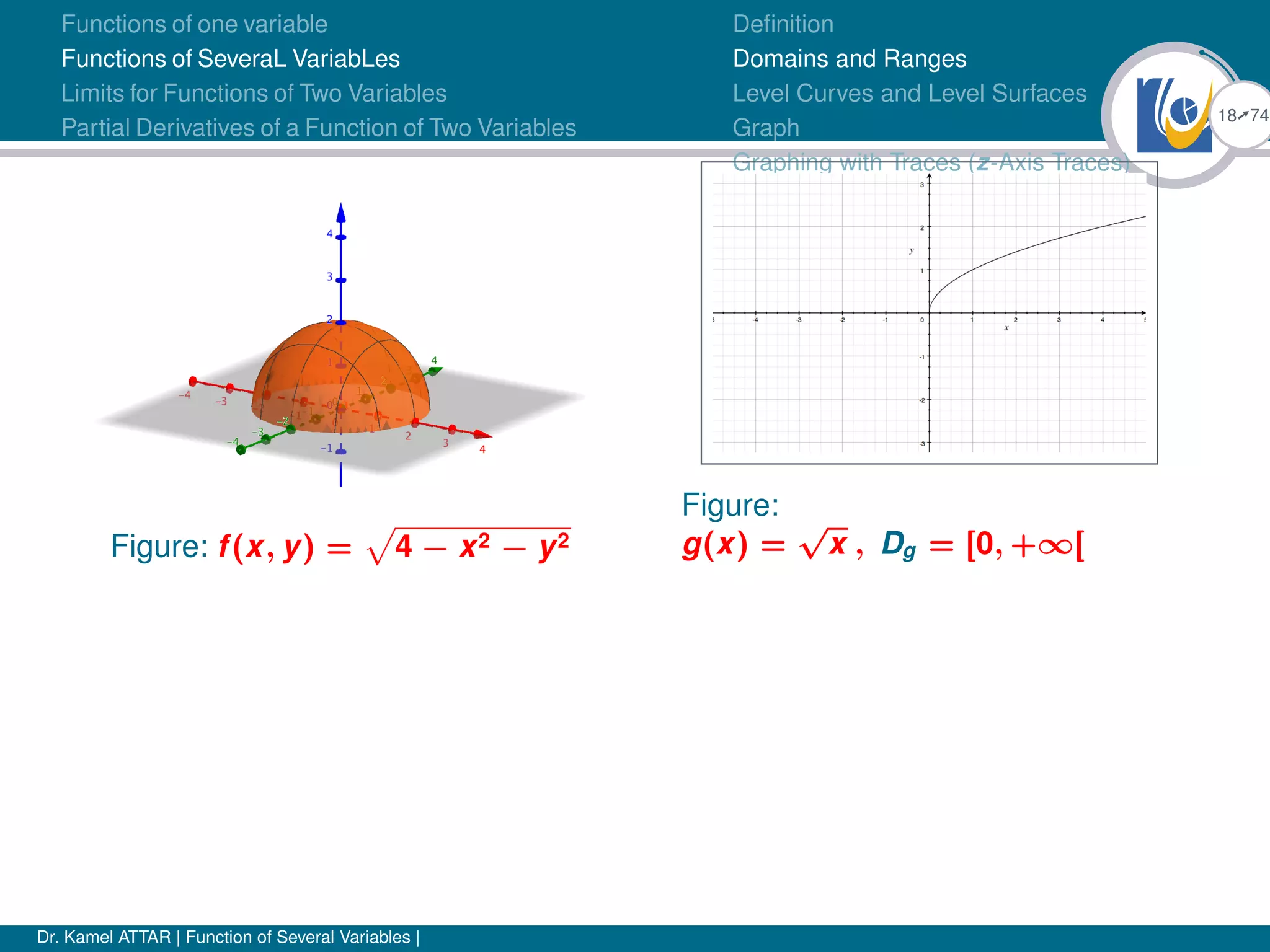
Definition
Domains and Ranges
Level Curves and Level Surfaces
Graph
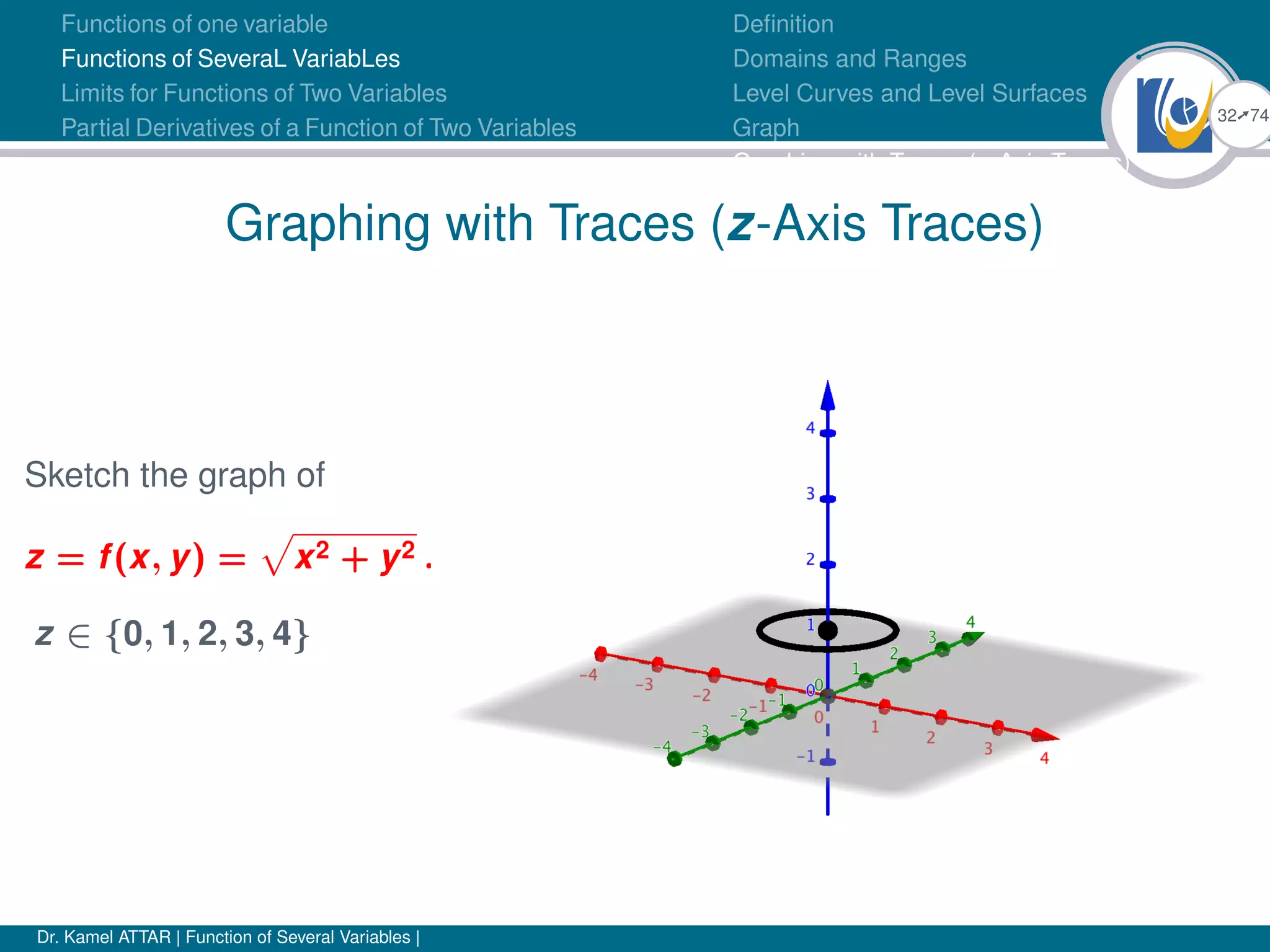
Graphing with Traces (z-Axis Traces)
Figure: f(x, y) = ln(1 − x − y)
Figure:
g(x) = ln(x) , Dg =]0, +∞[
Dr. Kamel ATTAR | Function of Several Variables |](https://image.slidesharecdn.com/functionofseveralvariables-210413093505/75/Function-of-several-variables-22-2048.jpg)
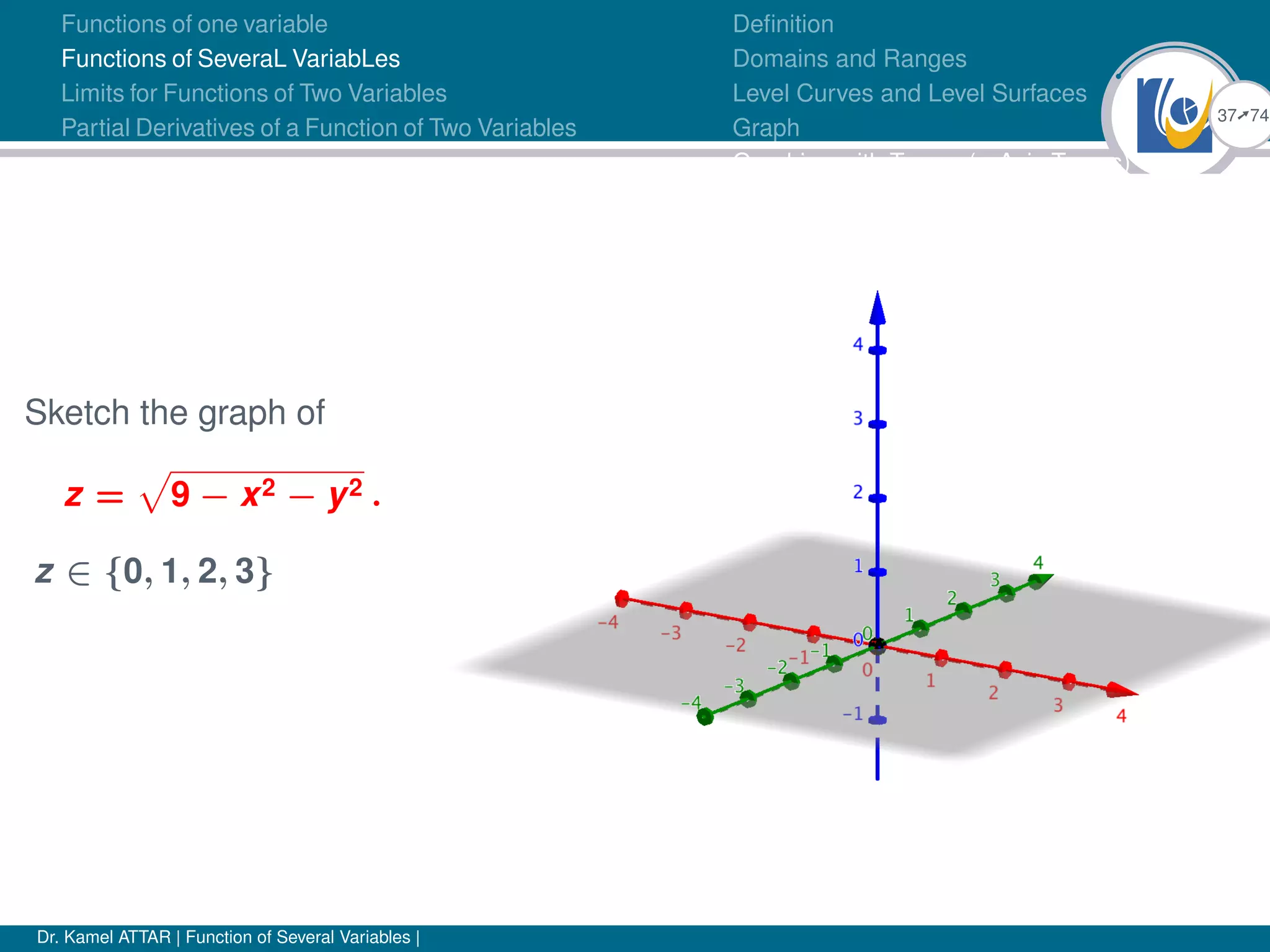
![23Ú74
Functions of one variable
Functions of SeveraL VariabLes
Limits for Functions of Two Variables
Partial Derivatives of a Function of Two Variables
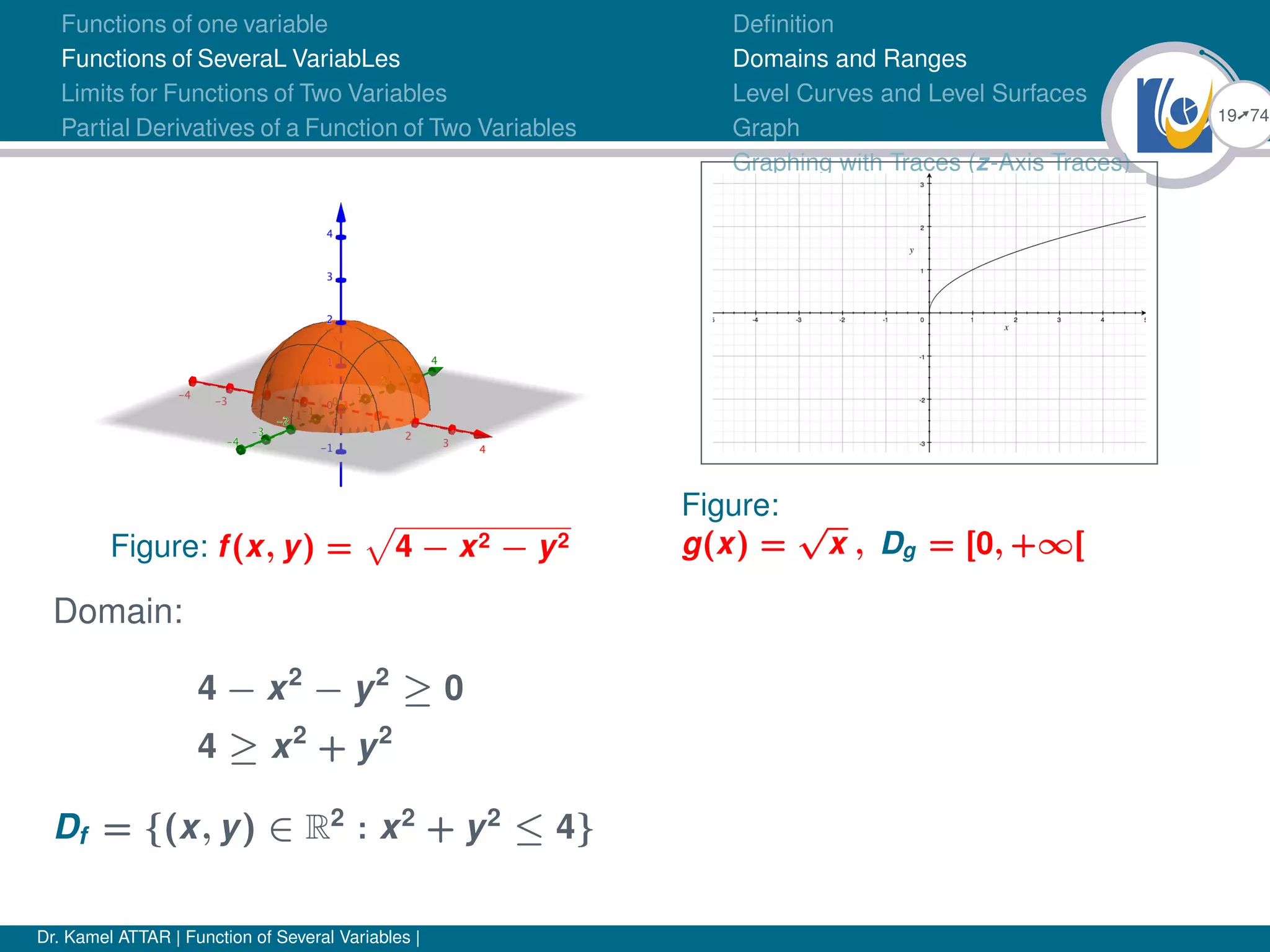
Definition
Domains and Ranges
Level Curves and Level Surfaces
Graph
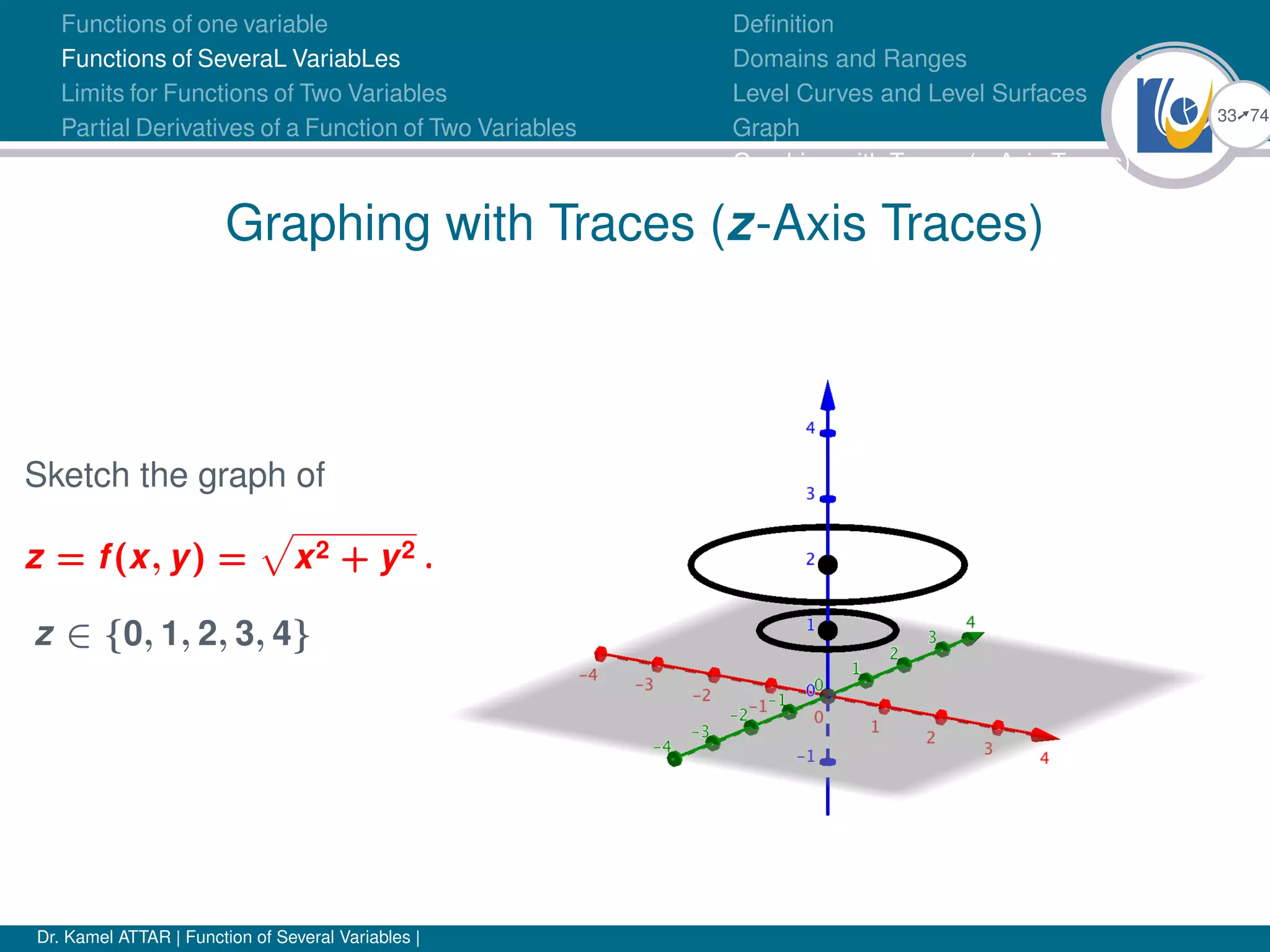
Graphing with Traces (z-Axis Traces)
Figure: f(x, y) = ln(1 − x − y)
Figure:
g(x) = ln(x) , Dg =]0, +∞[
Domain:
1 − x − y > 0
1 > x + y
Df = {(x, y) ∈ R2
: x+y < 1}
Dr. Kamel ATTAR | Function of Several Variables |](https://image.slidesharecdn.com/functionofseveralvariables-210413093505/75/Function-of-several-variables-23-2048.jpg)
![24Ú74
Functions of one variable
Functions of SeveraL VariabLes
Limits for Functions of Two Variables
Partial Derivatives of a Function of Two Variables
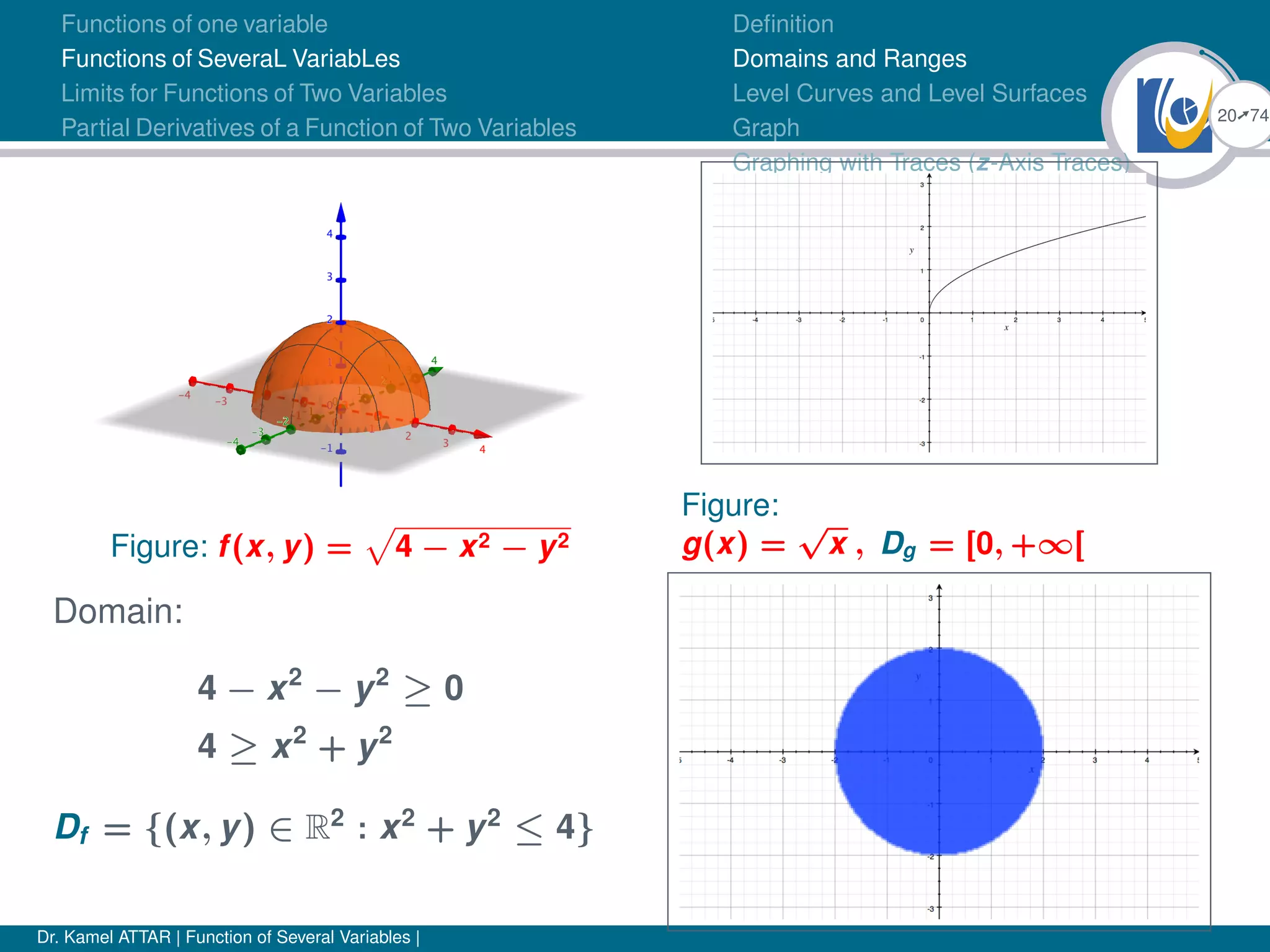
Definition
Domains and Ranges
Level Curves and Level Surfaces
Graph
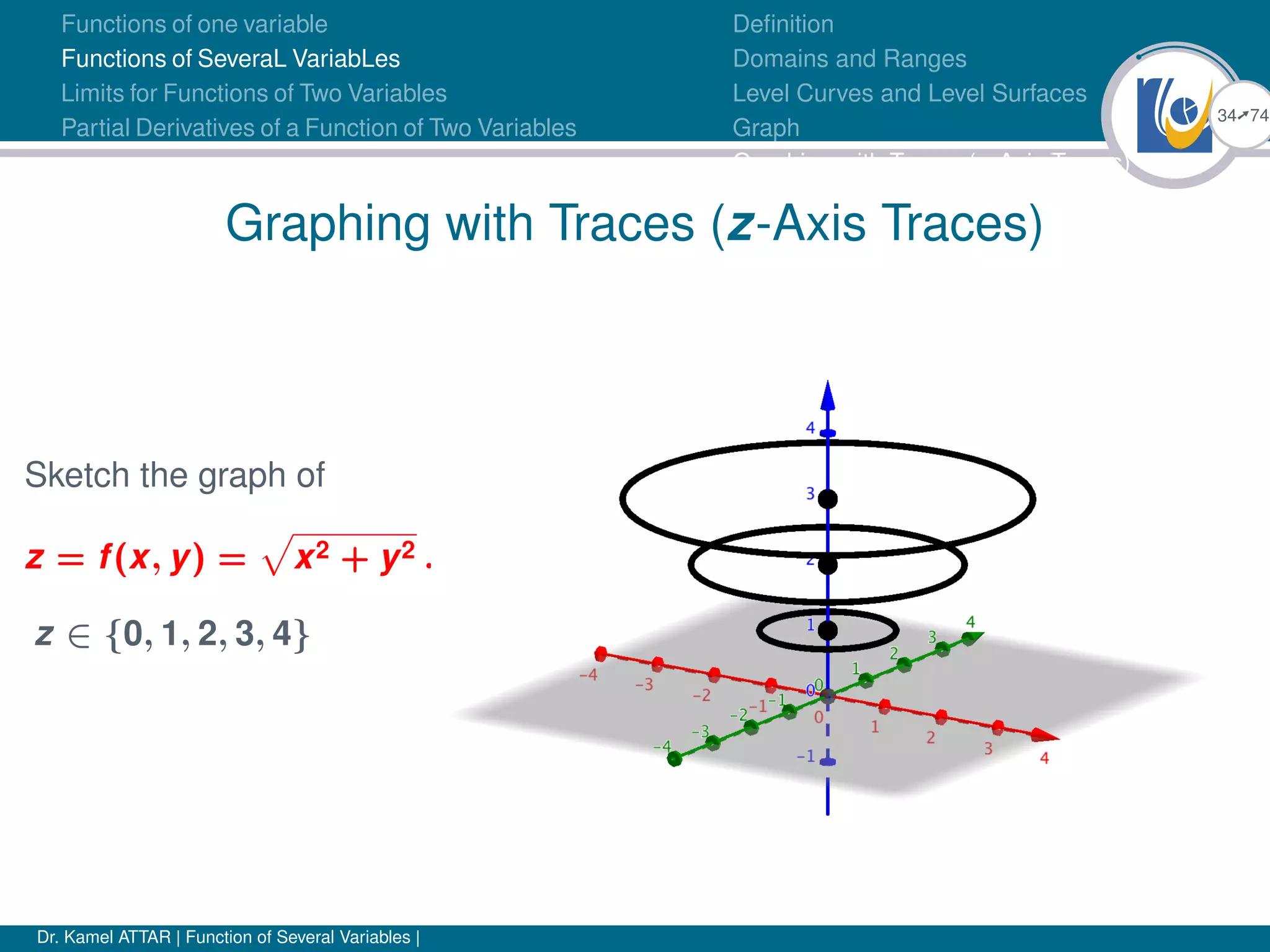
Graphing with Traces (z-Axis Traces)
Figure: f(x, y) = ln(1 − x − y)
Figure:
g(x) = ln(x) , Dg =]0, +∞[
Domain:
1 − x − y > 0
1 > x + y
Df = {(x, y) ∈ R2
: x+y < 1}
Dr. Kamel ATTAR | Function of Several Variables |](https://image.slidesharecdn.com/functionofseveralvariables-210413093505/75/Function-of-several-variables-24-2048.jpg)
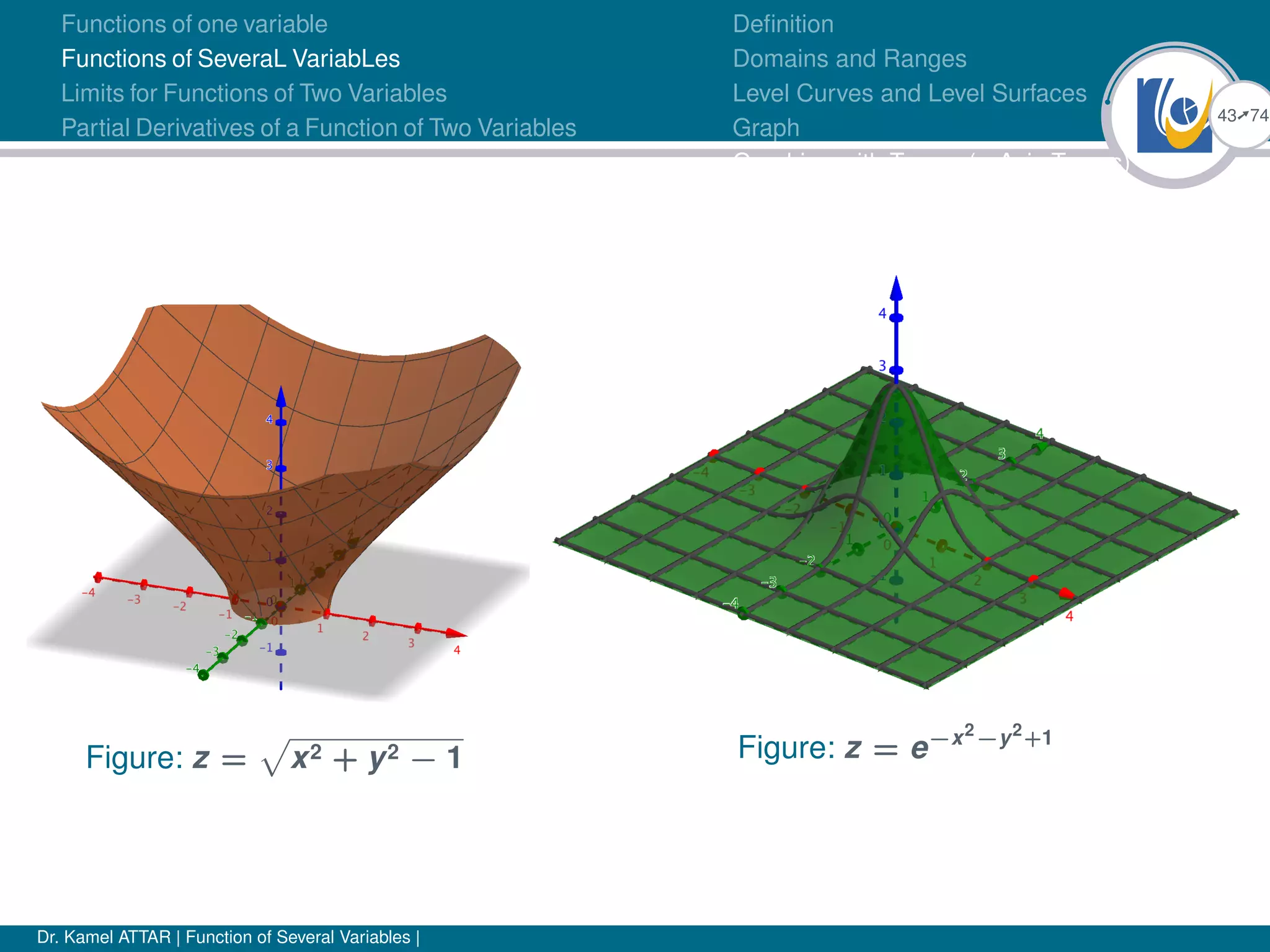
![25Ú74
Functions of one variable
Functions of SeveraL VariabLes
Limits for Functions of Two Variables
Partial Derivatives of a Function of Two Variables
Definition
Domains and Ranges
Level Curves and Level Surfaces
Graph
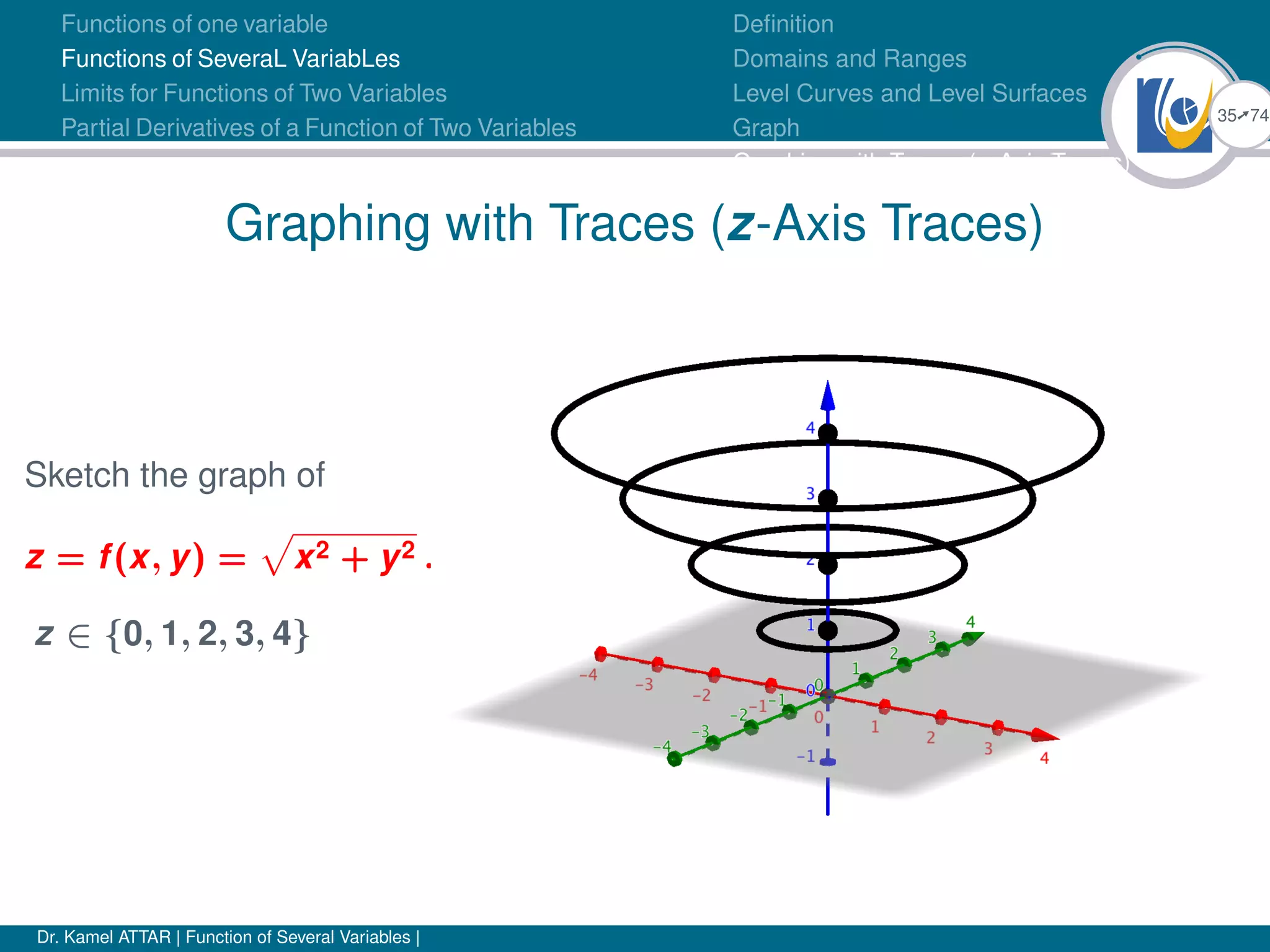
Graphing with Traces (z-Axis Traces)
Example (Functions of two variables)
Function Domain Range
z = ex
cos y R2
Entire plane ] − ∞, ∞[
z =
p
y − x2 y ≥ x2
[0, ∞[
z =
1
xy
xy 6= 0 ] − ∞, 0[∪]0, ∞[
z = sin xy R2
Entire plane [−1, 1]
Example
Find the domain of the function f(x, y) =
ln(x − 3)
p
y + 2
x2 − 4
.
Dr. Kamel ATTAR | Function of Several Variables |](https://image.slidesharecdn.com/functionofseveralvariables-210413093505/75/Function-of-several-variables-25-2048.jpg)
![26Ú74
Functions of one variable
Functions of SeveraL VariabLes
Limits for Functions of Two Variables
Partial Derivatives of a Function of Two Variables
Definition
Domains and Ranges
Level Curves and Level Surfaces
Graph
Graphing with Traces (z-Axis Traces)
Example (Functions of three variables)
Function Domain Range
w = x2
cos y sin z R3
Entire space ] − ∞, ∞[
w =
p
x2 + y2 + z2 R3
Entire space [0, ∞[
w =
1
x2 + y2 + z2
(x, y, z) 6= (0, 0, 0) ]0, ∞[
w = xy ln z R2
∪ R∗
+ Half-space z > 0 ] − ∞, ∞[
Dr. Kamel ATTAR | Function of Several Variables |](https://image.slidesharecdn.com/functionofseveralvariables-210413093505/75/Function-of-several-variables-26-2048.jpg)