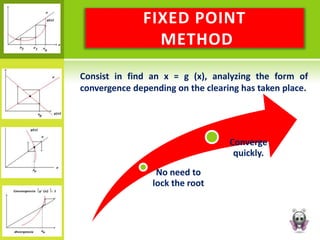
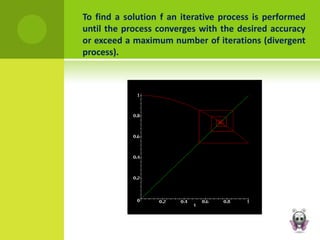
This document discusses various graphical and numerical methods for finding the roots or zeros of equations, including interval methods like bisection, the false position method, open methods like Newton-Raphson and secant methods, and fixed point methods. Interval methods use initial lower and upper bounds to repeatedly narrow the range containing the root. Open methods take initial values and generate successive approximations converging on the root through techniques like drawing tangents or divided differences. Fixed point methods analyze convergence based on the form of iteration used to find a solution.

1. ROOTS OF EQUATIONS

2. GRAPHICAL METHODS In these methods, what is sought is to plot the graph of y = f (x). The point where cutting the abscissa (x) is the root. These methods although very general, have their drawbacks.

3. INTERVAL METHODS

4. It is a simple, time-consuming and has linear convergence, and is performed as follows:1. Choose the initial values lower Xi and upper Xs.2. The first approximation to the root Xr is determined as:𝑿𝒓= 𝑿𝒔−𝑿𝒊𝟐3. Calculate F (Xi), F (Xr) to determine in which subinterval the root lies. BISECTION METHODS

5. 4.Then:a) If F (Xi) * F (Xr) <0, the root is in the lower subinterval then:Xr= Xsb) If F (Xi) * F (Xr)> 0, the root is in the upper subinterval, then:Xr= Xi5.Then, repeat the pointtwo y when Error <0.001, the calculation ends.

6. THE FALSE POSITION METHODThe method of false position is intended to combine the security of the bisection method with the speed of the secant method. This method, as with the bisection method stems from two points surrounding the root f (x) = 0. However, the method of false position has a very slow convergence towards the solution.

7. Usingthetwo-pointform of theline:with, using , and solvingforthereforegivestheiteration.

8. OPEN METHODS

9. RHAPSON-NEWTON METHODIt involves taking an initial value and from the same draw tangents to approach the value of the root.

10. SECANT METHODIt is similar to Newton's method, but the derivative is replaced by a divided difference. The method requires two points to start iterate.

11. FIXED POINT METHODConsist in find an x = g (x), analyzing the form of convergence depending on the clearing has taken place.

12. To find a solution f an iterative process is performed until the process converges with the desired accuracy or exceed a maximum number of iterations (divergent process).

13. BIBLIOGRAPHYhttp://html.rincondelvago.com/0003061310.pnghttp://www.uv.mx/anmarin/images/puntofijo.gif