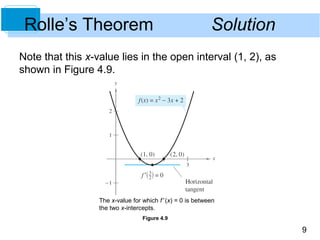
This document discusses Rolle's Theorem from calculus. Rolle's Theorem states that if a function f is continuous on a closed interval [a,b] and differentiable on the open interval (a,b), and if f(a) = f(b), then there exists at least one value c in the interval (a,b) where the derivative of f is equal to 0. The document provides an example of applying Rolle's Theorem to show that the derivative of the function f(x) = x^2 - 3x + 2 is equal to 0 at some point between the two x-intercepts of the function.

1. 1

2. 2
Name: Rima akteR
DepaRtmeNt: CSe
StuDeNt iD: 171015003
CouRSe CoDe: math-101
CouRSe title: DiffeReNtial CalCuluS

3. 3
Rolle’s Theorem
The Extreme Value Theorem states that a continuous
function on a closed interval [a, b] must have both a
minimum and a maximum on the interval.
 Both of these values, however, can occur at the
endpoints. Rolle’s Theorem, named after the French
mathematician Michel Rolle’s, gives conditions that
guarantee the existence of an extreme value in the interior
of a closed interval.

4. 4
Rolle’s Theorem

5. 5
Rolle’s Theorem
From Rolle’s Theorem, you can see that if a function f is
continuous on [a, b] and differentiable on (a, b), and if
f(a) = f(b), then there must be at least one x-value between
a and b at which the graph of f has a horizontal tangent, as
shown in Figure 4.8(a).
f is continuous on [a, b] and differentiable on (a, b).
Figure 4.8(a)

6. 6
Rolle’s Theorem
If the differentiability requirement is dropped from Rolle’s
Theorem, f will still have a critical number in (a, b), but it
may not yield a horizontal tangent. Such a case is shown in
Figure 4.8(b).
f is continuous on [a,
b]. Figure 4.8(b)

7. 7
Rolle’s Theorem Example
Find the two x-intercepts of f(x) = x2
– 3x + 2
and show that f′(x) = 0 at some point between the two x-
intercepts.
Solution:
Note that f is differentiable on the entire real number line. Setting f(x)
equal to 0 produces
x2
– 3x + 2 = 0
(x – 1)(x – 2) = 0.

8. 8
Rolle’s Theorem Solution
So, f(1) = f(2) = 0, and from Rolle’s Theorem you know that
there exists at least one c in the interval (1, 2) such that
f′(c) = 0.
To find such a c, you can solve the equation
f′(x) = 2x – 3 = 0
and determine that f′(x) = 0 when
Set f′(x) equal to 0.

9. 9
Rolle’s Theorem Solution
Note that this x-value lies in the open interval (1, 2), as
shown in Figure 4.9.
The x-value for which f ′(x) = 0 is between
the two x-intercepts.
Figure 4.9

10. 10
Rolle’s Theorem
Rolle’s Theorem states that if f satisfies the conditions of
the theorem, there must be at least one point between
a and b at which the derivative is 0.

11. 11
Rolle’s Theorem