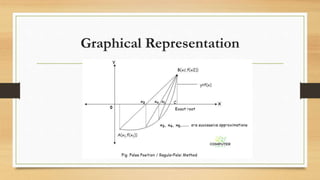
The regula falsi method is a numerical technique for finding roots of polynomials by using linear interpolation between two points where the function changes sign. The method iteratively improves the approximation of the root without requiring derivatives, although it can experience slower convergence in certain scenarios. An example application and MATLAB code are provided to illustrate the method's use and advantages.

1. Numerical Computing
Lecture # 11
Regula Falsi Method
By Nasima Akhtar

2. Working Rule
• The Regula–Falsi Method is a numerical method for estimating the roots of a
polynomial f(x). A value x replaces the midpoint in the Bisection Method and serves as
the new approximation of a root of f(x). The objective is to make convergence
faster. Assume that f(x) is continuous.
• This method also known as CHORD METHOD ,, LINEAR INTERPOLATION and
method is one of the bracketing methods and based on intermediate value theorem

3. Graphical Representation

4. Derivation
• Equation Of line gives us:
•
𝑦 − 𝑦1
𝑥 − 𝑥1
=
𝑦2− 𝑦1
𝑥2− 𝑥1
• 𝑦 − 𝑦1 =
𝑦2− 𝑦1
𝑥2− 𝑥1
(𝑥 − 𝑥1)
• (𝑥1, 𝑦1)=(a,f(a)), (𝑥2, 𝑦2)=(b,f(b)), (𝑥 , 𝑦 )=(𝑥0, 𝑦0)
• y- f(a) =
f(b)−f(a)
b− 𝑎
(𝑥 −a)
• 0- f(a) =
f(b)−f(a)
b− 𝑎
(𝑥 −a) at x-axis y=0
• 0- f(a) =
f(b)−f(a)
b− 𝑎
(𝑥 −a)
•
(b− 𝑎)(− f(a) )
f(b)−f(a)
=x-a
• a +
(b− 𝑎)(− f(a) )
f(b)−f(a)
=x
•
𝑎(f(b)−f(a))+(b− 𝑎)(− f(a) )
f(b)−f(a)
=x `
•
𝑎(f(b))−a(f(a))−b(f(a) )+a(f(a) )
f(b)−f(a)
=x `
•
𝑎(f(b)) −b(f(a) )
f(b)−f(a)
=x `
• X=
𝑎(f(b)) −b(f(a) )
f(b)−f(a)
`

5. Algorithm
1.Find points a and b such that a < b and f(a) * f(b) < 0.
2.Take the interval [a, b] and determine the next value of x1.
3.If f(x1) = 0 then x1 is an exact root, else if f(x1) * f(b) < 0 then let a = x1,
else if f(a) * f(x1) < 0 then let b = x1.
4.Repeat steps 2 & 3 until f(xi) = 0 or |f(xi)|  tolerance

6. Example Numerical
• Find Approximate root using Regula Falsi method of the equation
𝑥3-4x+1
Putting values in
x=
𝑎(f(b)) −b(f(a) )
f(b)−f(a)
`
X F(x)
a=0 1
b=1 -2
𝑥0=0.3333 F(𝑥0)= -0.2963
𝑥1=0.25714 F(𝑥1)= -0.0115
𝑥2=0.2542 F(𝑥2)= -0.0003
𝑥3=0.2541 F(𝑥3)= -0.00001
𝑥4=0.2541

7. Pros and Cons
Advantages
• 1. It always converges.
• 2. It does not require the derivative.
• 3. It is a quick method.
Disadvantages
• 1. One of the interval definitions can get stuck.
• 2. It may slowdown in unfavourable situations.

8. Matlab Code
f=@(x)(x^3+3*x-5);
x1=1;
x2 = 2;
i = 0;
val = f(x2);
val1 = f(x1);
if val*val1 >= 0
i = 99;
end
while i <= 4
val = f(x2);
val1 = f(x1);24
temp = x2 - x1;
temp1 = val - val1;
nVal = temp/temp1;
nVal = nVal * val;
nVal = x2 - nVal;
if (f(x2)*nVal <= 0)
x1 = x2;
x2 = nVal;
else
if (f(x1)*nVal <= 0)
x2 = nVal;
end
end
i = i+1;
end
fprintf('Point is %fn',x2)
fprintf('At This Point Value is %fn',f(x2))