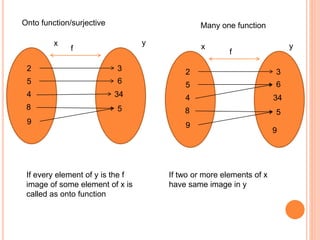
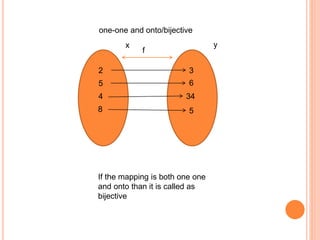
A function is a relation between a set of inputs (domain) and set of outputs (codomain) where each input is mapped to exactly one output. There are different types of functions such as one-to-one, onto, bijective, many-to-one, and inverse functions. Functions can be represented graphically or using function notation such as f(x). Common functions include polynomial, trigonometric, exponential, logarithmic, and composite functions which are the composition of two simpler functions.

1. FUNCTIONS
Submitted to:
Prof. Shubha Agarwal
Submitted by:
Ankit Bhandari
II year, IV Sem
IT

2. WHAT ARE FUNCTIONS?
a function is a relation between a set of inputs and a set of
permissible outputs with the property that each input is
related to exactly one output. Set of input is known as
domain, while the set of permissible outputs is called the
codomain and the set of all output values of a function.
2
8
7
5
3
6
9
12
15
DOMAIN={2,8,7,5}
RANGE={2,6,12}
CO-
DOMAIN={3,6,9,12,
15}
Y=F(x)x y

3. 2
4
5
8
9
3
34
6
5
The function here y=f(x)
is not a function because
domain of this function
has a member that has
two image of it in the co
domain i.e. 8 has two
images, 34 and 5
x yY=f(x)
Function notation is done as f:x->y
Or y=F(x)

4. GRAPHICAL REPRESENTATION OF SET
Let F(x)=x+8 be a function, from x->y, then its graph
F(x)=x+8

5. The graph of y=sin-1 (x) is not a function as the graph of it
is intersected by line drawn parallel to y axis more than 1
time

6. TYPES OF FUNCTION MAPPING
1) one-one or injective or monomorphism
2) Onto or Surjective
3) one-one and onto or bijection
4) Many one
One One/injective
function
2
4
5
8
9
3
34
6
5
x y
f
Different elements
of x have different
images in y

7. Onto function/surjective
2
4
5
8
9
3
34
6
5
x y
f
Many one function
2
4
5
8
9
3
34
6
5
x y
f
9
If every element of y is the f
image of some element of x is
called as onto function
If two or more elements of x
have same image in y

8. 2
4
5
8
3
34
6
5
x y
f
If the mapping is both one one
and onto than it is called as
bijective
one-one and onto/bijective

9. INVERSE FUNCTION
An inverse function for f, denoted by f−1, is a function
in the opposite direction, from Y to X
And F:y->x
For eg: f(c)=9/5c+32
f-1 (F)=5/9(F-32)
As a simple example, if f converts a temperature in degrees Celsius
C to degrees Fahrenheit F, the function converting degrees
Fahrenheit to degrees Celsius would be a suitable f−1.
Such an inverse function exists if and only if f is bijective
With this analogy, identity functions are like the multiplicative identity,
1, and inverse functions are like reciprocals

10. IDENTITY FUNCTION
Function of the type f(x)=c where c is a constant
They have a line parallel
to x axis

11. POLYNOMIAL FUNCTION
Functions of the type
F(x)=a0+ a1x+ a2x2…………+ anxn-1

12. TRIGNOMETRIC FUNCTIONS
Functions like f(x)=sin(x) or f(x)=cos(x)

13. EXPONENTIAL FUNCTION
Functions of the type f(x)=ex
The graph of
these type of
function
either remain
constant or
increase,
they never
decrease

14. LOGARITHMIC FUNCTIONS
These functions are inverse of exponential functions
and are of form f(x)=loge(x)

15. COMPOSITE FUNCTIONS
function composition is the application of one function
to the results of another. For instance, the functions f:
X → Y and g: Y → Z can be composed by computing
the output of g when it has an argument of f(x)
instead of x. Intuitively, if z is a function g of y and y is
a function f of x, then z is a function of x.
Thus one obtains a composite function g ∘ f: X → Z
defined by (g ∘ f )(x) = g(f(x)) for all x in X. The
notation g ∘ f is read as "g circle f ", or "g round f ", or
"g composed with f ", "g after f ", "g following f ", or just
"g of f ".

16. G(f(x))
For x=1,
G(f(1))=5
For x=2,
G(f(2))=6