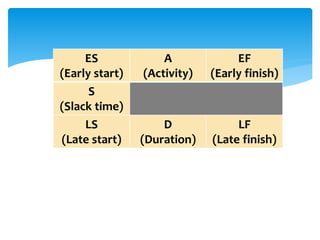
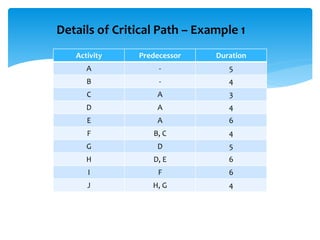
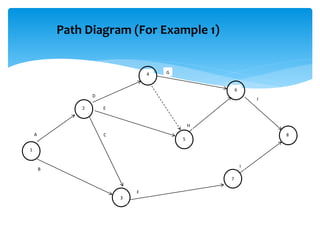
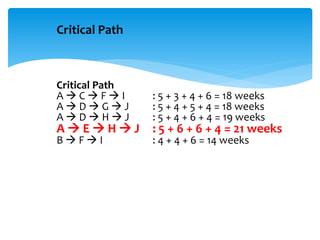
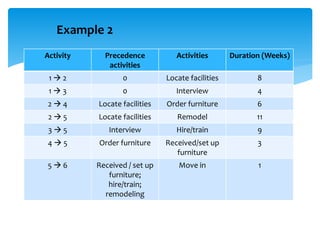
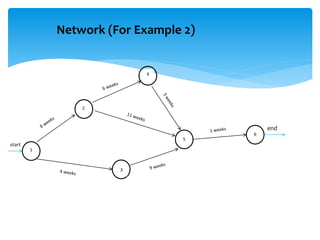
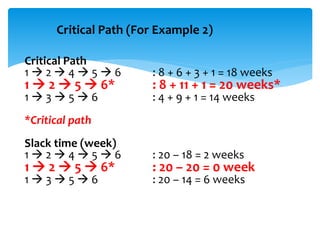
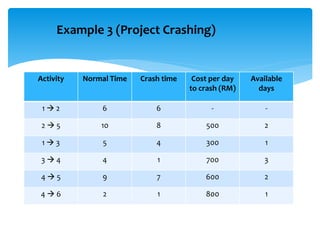
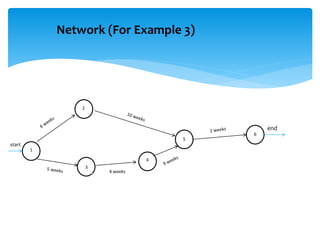
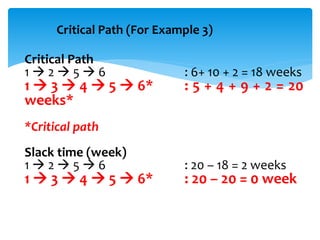
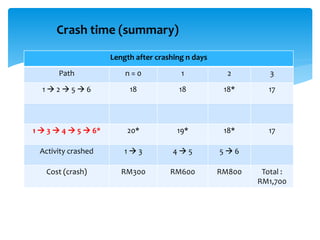
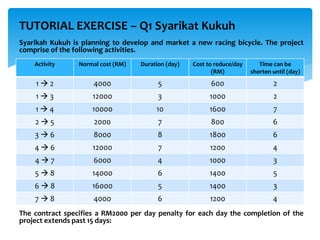
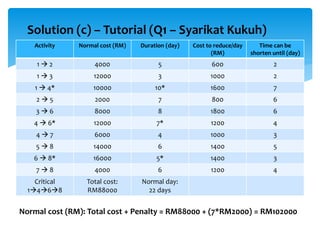
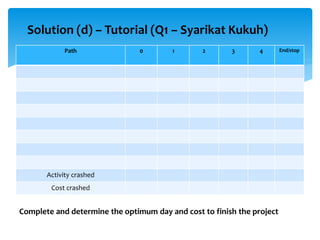
CPM involves drawing a network diagram of activities and their relationships, analyzing paths and determining earliest and latest start/finish times to identify the critical path and calculate slack. Project crashing involves shortening activity durations by incurring costs to potentially reduce the project duration below that of the critical path. An example outlines crashing the critical

1. PERT & CPM
…are the two most widely use techniques for
planning and coordinating large-scale projects…
…by using PERT or CPM, managers are able to
obtain:
1. A graphical display of projects activities.
2. An estimate of how long the project will
take.
3. An indication of which activities are the most
critical to timely completion of the project.
4. An indication of how long any activity can be
delayed without lengthening the project.

2. PERT & CPM
The network diagram:
• The arrows represent the project
activities
• The nodes represent both
beginnings and endings of
activities

3. CPM Terminology
 Activity
 A task or a certain amount of work required in the
project
 Requires time to complete
 Represented by an arrow
 Dummy Activity
 Indicates only precedence relationships
 Does not require any time of effort

4. CPM Terminology
 Event
 Signals the beginning or ending of an activity
 Designates a point in time
 Represented by a circle (node)
 Network
 Shows the sequential relationships among activities
using nodes and arrows

5. CPM Terminology
 Path
 A connected sequence of activities leading from the
starting event to the ending event
 Critical Path
 The longest path (time); determines the project
duration
 Critical Activities
 All of the activities that make up the critical path

6. CPM Terminology
 Earliest Start (ES)
 The earliest that an activity can begin; assumes all
preceding activities have been completed
 Earliest Finish (EF)
 ES + activity time
 Latest Finish (LF)
 The latest that an activity can finish and not change the
project completion time
 Latest Start (LS)
 LF - activity time

7. Steps in CPM Analysis
 Draw the CPM network
 A graphic view of the relationships among the required
activities
 Analyze the paths through the network
 Determine the length of each path (time required to
complete each path)
 Starting at the beginning of the network and working
toward the end (from left to right), determine the ES and EF
for each activity
 . . . more

8. Steps in CPM Analysis
 Path analysis (continued)
 Identify the critical path(s) (the longest path[s]
through the network)
 The critical path(s) determines how long the project
will take
 . . . more

9. Steps in CPM Analysis
 Determine the slack for each activity
 Working from the end of the project network (from
right to left), find the LF and the LS for each activity
 Compute the activity’s slack
slack = LS - ES = LF - EF
 Slack is the maximum amount of time that this activity
can be delay in its completion before it becomes a
critical activity, i.e., delays completion of the project

10. PERT Analysis
Critical Path Method
…is one of two ways or tools to identify
the path through your project…

11. Critical Path
Uses one time estimate
Where as
PERT
Uses three time estimate

12. Critical path is for those times when
you are pretty sure about the
duration of each task.

13. PERT is used in more uncertain
situations.

14. ES
(Early start)
A
(Activity)
EF
(Early finish)
S
(Slack time)
LS
(Late start)
D
(Duration)
LF
(Late finish)

15. Details of Critical Path – Example 1
Activity Predecessor Duration
A - 5
B - 4
C A 3
D A 4
E A 6
F B, C 4
G D 5
H D, E 6
I F 6
J H, G 4

16. Path Diagram (For Example 1)
1
2
3
4
5
6
7
8A
B
C
D
E
F
G
H
I
J

17. Critical Path
Critical Path
A  C  F  I : 5 + 3 + 4 + 6 = 18 weeks
A  D  G  J : 5 + 4 + 5 + 4 = 18 weeks
A  D  H  J : 5 + 4 + 6 + 4 = 19 weeks
A  E  H  J : 5 + 6 + 6 + 4 = 21 weeks
B  F  I : 4 + 4 + 6 = 14 weeks

18. Example 2
Activity Precedence
activities
Activities Duration (Weeks)
1  2 0 Locate facilities 8
1  3 0 Interview 4
2  4 Locate facilities Order furniture 6
2  5 Locate facilities Remodel 11
3  5 Interview Hire/train 9
4  5 Order furniture Received/set up
furniture
3
5  6 Received / set up
furniture;
hire/train;
remodeling
Move in 1

19. Network (For Example 2)
1
2
3
4
5
6
start
end

20. Critical Path (For Example 2)
Critical Path
1  2  4  5  6 : 8 + 6 + 3 + 1 = 18 weeks
1  2  5  6* : 8 + 11 + 1 = 20 weeks*
1  3  5  6 : 4 + 9 + 1 = 14 weeks
*Critical path
Slack time (week)
1  2  4  5  6 : 20 – 18 = 2 weeks
1  2  5  6* : 20 – 20 = 0 week
1  3  5  6 : 20 – 14 = 6 weeks

21. Practicing draw a network
See Example on page 102 – 103 (Notes)

22. Example 3 (Project Crashing)
Activity Normal Time Crash time Cost per day
to crash (RM)
Available
days
1  2 6 6 - -
2  5 10 8 500 2
1  3 5 4 300 1
3  4 4 1 700 3
4  5 9 7 600 2
4  6 2 1 800 1

23. Network (For Example 3)
1
2
3
4
5
6
4 weeks
start
end

24. Critical Path (For Example 3)
Critical Path
1  2  5  6 : 6+ 10 + 2 = 18 weeks
1  3  4  5  6* : 5 + 4 + 9 + 2 = 20
weeks*
*Critical path
Slack time (week)
1  2  5  6 : 20 – 18 = 2 weeks
1  3  4  5  6* : 20 – 20 = 0 week

25. Crash time (summary)
Length after crashing n days
Path n = 0 1 2 3
1  2  5  6 18 18 18* 17
1  3  4  5  6* 20* 19* 18* 17
Activity crashed 1  3 4  5 5  6
Cost (crash) RM300 RM600 RM800 Total :
RM1,700

26. TUTORIAL EXERCISE – Q1 Syarikat Kukuh
Syarikah Kukuh is planning to develop and market a new racing bicycle. The project
comprise of the following activities.
Activity Normal cost (RM) Duration (day) Cost to reduce/day
(RM)
Time can be
shorten until (day)
1  2 4000 5 600 2
1  3 12000 3 1000 2
1  4 10000 10 1600 7
2  5 2000 7 800 6
3  6 8000 8 1800 6
4  6 12000 7 1200 4
4  7 6000 4 1000 3
5  8 14000 6 1400 5
6  8 16000 5 1400 3
7  8 4000 6 1200 4
The contract specifies a RM2000 per day penalty for each day the completion of the
project extends past 15 days:

27. Required to:
a) Draw the network diagram
b) Determine the critical path
c) Determine the normal time (day) and cost
(RM) to finish the project
d) Determine the optimum time (day) and
cost (RM) to finish the project

28. Solution (a) – Tutorial (Q1 – Syarikat Kukuh)
Please draw the network

29. Solution (b) – Tutorial (Q1 – Syarikat Kukuh)
Please determine the critical path

30. Solution (c) – Tutorial (Q1 – Syarikat Kukuh)
Activity Normal cost (RM) Duration (day) Cost to reduce/day
(RM)
Time can be
shorten until (day)
1  2 4000 5 600 2
1  3 12000 3 1000 2
1  4* 10000 10* 1600 7
2  5 2000 7 800 6
3  6 8000 8 1800 6
4  6* 12000 7* 1200 4
4  7 6000 4 1000 3
5  8 14000 6 1400 5
6  8* 16000 5* 1400 3
7  8 4000 6 1200 4
Critical
1468
Total cost:
RM88000
Normal day:
22 days
Normal cost (RM): Total cost + Penalty = RM88000 + (7*RM2000) = RM102000

31. Solution (d) – Tutorial (Q1 – Syarikat Kukuh)
Path 0 1 2 3 4 End/stop
Activity crashed
Cost crashed
Complete and determine the optimum day and cost to finish the project

32. Task to complete
Complete all Questions in Workbook:
Question 2 – Harmony (F1001 F1023; F1091 F1037 F1042)
Question 3 – Syarikat Ramadhani (F1009 F1026; F1010 F1045)
Question 4 – Syarikat TT (F1012 F1025; F1013 F1028)
Question 5 – Hitech (F1015 F1035; F1017 F1024)
Question 6 – A Farm (F1018 F1052; F1039 F1044)
Question 7 – Rainbow (F1041 F1047; F1048 F1049; F1050 F1051)