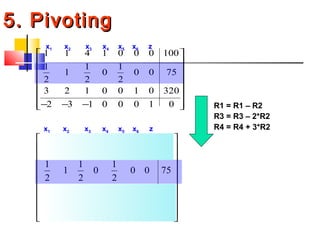
The Simplex Method is an algorithm for solving linear programming problems. It involves setting up the problem in standard form, constructing an initial simplex tableau, and then iteratively selecting pivot columns and performing row operations until an optimal solution is found. The method terminates when all indicators in the tableau are positive or zero, at which point the basic and non-basic variables can be identified to read the optimal solution.

1. SIMPLEX
METHOD

2. SIMPLEX METHOD
 1. INTRODUCTION
 The graphical method is
usually inefficient or
impossible
  The Simplex method used.
 All constrains must be
expressed in the linear form:

3. SIMPLEX METHOD
2. Standard Maximum Form
The objective function is to be
maximized
All variables are nonnegative
(xi ≥ 0,i = 1, 2, 3 …)
All constraints involve ≤
The constants on the right side in the
constraints are all nonnegative (b ≥ 0)

4. SIMPLEX METHOD
3. Setting Up Problem3. Setting Up Problem
Convert x1+x2 10 in to
x1+x2+x3=10
x3 : slack variable

5. 1 2 3
1 2 3
1 2 3
1 2 3
1 2 3
: 2 3
4 100
2 150
3 2 320
0, 0, 0
Maximize z x x x
subject to x x x
x x x
x x x
with x x x
= + +
+ + ≤
+ + ≤
+ + ≤
≥ ≥ ≥
 Example:
1 2 3
1 2 3 4
1 2 3 5
1 2 3 6
1 2 3 4 5 6
: 2 3
4 100
2 150
3 2 320
0, 0, 0, 0, 0, 0
Maximize z x x x
subject to x x x x
x x x x
x x x x
with x x x x x x
= + +
+ + + =
+ + + =
+ + + =
≥ ≥ ≥ ≥ ≥ ≥
Slack variables
3. Setting Up Problem3. Setting Up Problem Restate the
following
linear
programming
by
introducing
slack vars

6. 1 2 3
1 2 3 4
1 2 3 5
1 2 3 6
1 2 3 4 5 6
: 2 3
4 100
2 150
3 2 320
0, 0, 0, 0, 0, 0
Maximize z x x x
subject to x x x x
x x x x
x x x x
with x x x x x x
= + +
+ + + =
+ + + =
+ + + =
≥ ≥ ≥ ≥ ≥ ≥
1 1 4 1 0 0 0 100
1 2 1 0 1 0 0 150
3 2 1 0 0 1 0 320
2 3 1 0 0 0 1 0
 
 
 
 
 
− − − 
x1 x2 x3 x4 x5 x6 z
Constraint 1
Constraint 2
Constraint 3
Objective Function
Indicators
1 2 32 3 0x x x z− − − + =
3. Setting Up Problem3. Setting Up Problem

7. 3. Setting Up Problem3. Setting Up Problem
Make the initial simplex tableau
Indicators: the number in the bottom row of
the initial simplex tableau, except for the
last element (1) and 0 on the right
Goal: To find a solution in which all the
variables are nonnegative and z is as
larger as possible.

8. Quotients
1 1 4 1 0 0 0 100
1 2 1 0 1 0 0 150
3 2 1 0 0 1 0 320
2 3 1 0 0 0 1 0
 
 
 
 
 
− − − 
x1 x2 x3 x4 x5 x6 z
Most negative
indicator
100 /1 100=
150 / 2 75=
320 / 2 160=
Smallest
1 1 4 1 0 0 0 100
1 1 1
1 0 0 0 75
2 2 2
3 2 1 0 0 1 0 320
2 3 1 0 0 0 1 0
 
 
 
 
 
 
− − −  
x1 x2 x3 x4 x5 x6 z
4. Selecting the Pivot4. Selecting the Pivot

9. 4. Selecting the Pivot4. Selecting the Pivot
 Change a particular nonzore to 1, then all
other elements in that column are
changed to 0
 In example 2: select the most negative
one. The column contains that number is
pivot column












−−−
−
01000132
3200100123
1500010121
1000001411

10. 5. Pivoting5. Pivoting
1 1 4 1 0 0 0 100
1 1 1
1 0 0 0 75
2 2 2
3 2 1 0 0 1 0 320
2 3 1 0 0 0 1 0
 
 
 
 
 
 
− − −  
x1 x2 x3 x4 x5 x6 z
1 7 1
0 1 0 0 25
2 2 2
1 1 1
1 0 0 0 75
2 2 2
2 0 0 0 1 1 0 170
1 1 3
0 0 0 1 225
2 2 2
 
− 
 
 
 
 − 
 
− 
 
x1 x2 x3 x4 x5 x6 z
R1 = R1 – R2
R3 = R3 – 2*R2
R4 = R4 + 3*R2

11. Selecting the new Pivot
1 7 1
0 1 0 0 25
2 2 2
1 1 1
1 0 0 0 75
2 2 2
2 0 0 0 1 1 0 170
1 1 3
0 0 0 1 225
2 2 2
 
− 
 
 
 
 − 
 
− 
 
x1 x2 x3 x4 x5 x6 z
Most negative indicator: Pivot
column
Quotients
25 / 0.5 50=
75 / 0.5 150=
170 / 2 85=
Smallest
Pivot
row
1 0 7 2 1 0 0 50
1 1 1
1 0 0 0 75
2 2 2
2 0 0 0 1 1 0 170
1 1 3
0 0 0 1 225
2 2 2
− 
 
 
 
 −
 
 −  
x1 x2 x3 x4 x5 x6 z

12. Pivoting again
1 0 7 2 1 0 0 50
1 1 1
1 0 0 0 75
2 2 2
2 0 0 0 1 1 0 170
1 1 3
0 0 0 1 225
2 2 2
− 
 
 
 
 −
 
 −  
x1 x2 x3 x4 x5 x6 z
1 0 7 2 1 0 0 50
0 1 3 1 1 0 0 50
0 0 14 4 1 1 0 70
0 0 4 1 1 0 1 250
− 
 − − 
 − −
 
 
x1 x2 x3 x4 x5 x6 z
R2 = R2 – 0.5*R1
R3 = R3 – 2*R1
R4 = R4 + 0.5*R2
No negative indicator:
Stop!!!!!
The final simplex tableau

13. 6. Reading solution6. Reading solution
Solution:
The maximum value of z is 250,
where x1=50, x2=50 and x3=0
1 0 7 2 1 0 0 50
0 1 3 1 1 0 0 50
0 0 14 4 1 1 0 70
0 0 4 1 1 0 1 250
− 
 − − 
 − −
 
 
x1 x2 x3 x4 x5 x6 z
3 4 54 250x x x z+ + + = 3 4 5250 4z x x x⇔ = − − −
3 4 50, 0 0x x and x= = =
Maximize value of z
1 50x =
2 50x =
6 70x =
Basic variables Non-basic
variables

14. 6. Reading solution (cont)6. Reading solution (cont)
 In any simplex tableau:
 Basic variables: The variables corresponding
to the column one element is 1
 Non-basic variables: the variables
corresponding other columns.












−−
−−
−
2501011400
7001141400
500011310
500012701

15. 7. Simplex Method7. Simplex Method
1. Determine the objective function.
2. Write all necessary constraints.
3. Convert each constraint into an
equation by adding slack
variables.
4. Set up the initial simplex tableau.
5. Locate the most negative
indicator. If there are two such
indicators, choose one. This
indicator determines the pivot
column.

16. 7. Simplex Method (cont)7. Simplex Method (cont)
6. Use The Positive Entries In The
Pivot Column To Form The
Quotients Necessary For
Determining The Pivot. If There Are
No Positive Entries In The Pivot
Column, No Maximum Solution
Exists. If 2 quotients are equally the
smallest, let either determines the
pivot.

17. .Simplex Method (cont).Simplex Method (cont)
7. Multiply every entry in the pivot row
by the reciprocal of the pivot to
change the pivot to 1. The use row
operations to change all other
entries in the pivot column to 0 by
adding suitable multiplies of the
pivot to the other rows.

18. 7. Simplex Method (cont)7. Simplex Method (cont)
8. If the indicators are all positive or 0,
this is the final tableau. If not, go back
to step 5 above and repeat the process
until a tableau with no negative
indicators is obtained.
9. Determine the basic and non-basic
variables and read the solution from
the final tableau. The maximum value
of the objective function is the number
in the lower right corner of the final