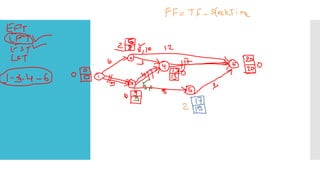
The document discusses the Critical Path Method (CPM), a project management technique used for scheduling activities based on mathematical calculations. Developed in 1959, CPM identifies the longest sequence of dependent activities to determine the minimum project duration. The document also outlines the steps for calculating early and late start/finish times, as well as concepts such as float time and various terminologies used in CPM.

1. Critical Path Method
Puneet Mathur
Assistant Professor
Marwadi University, Rajkot

2. Project
M a n a g e m e n t

Managers have been planning, scheduling, monitoring, and
controlling large scale projects for hundred years, but it has
only been in the last 50 years that management science
techniques have been applied to major projects.

They are two
types:
1. Critical Path Method(CPM)
2. Project Evaluation and Review Technique(PERT)

3. I n t r o d uc t i o n - CPM   Defination:-
 Critical path is a sequence of activity between a project’s start
and finish that takes the longest time to complete.
  Critical path method is based on mathematical calculations and
it is used for scheduling project activities.

In 1959, Critical path method(CPM) was developed by Kelly and
Walker to assist in building and maintains of chemical plants.
 The initial critical path method was used for managing plant
maintenance projects.

4. Critical path is the sequential activities from start to the end of a project.
Although many projects have only one critical path, some projects may have
more than one critical paths depending on the flow logic used in the project
 The essential technique for using CPM is to construct a model of the project
that includes the following:
 A list of all activities required to complete the project (typically categorized
within a work breakdown structure
The time (duration) that each activity will take to completion,
The dependencies between the activities


.

5. Te r m i n o l o g i e s
u s e d i n C P M
Inordertoexplainthepurpose,structureandoperationofCPM, itishelpfulto definethefollowing
terms:
Activity: An activity carries the arrow symbol.This represent a task or
subproject that uses time or resources
Event:- Anode (an event), denotedby a circle , marks the start and
completion of an activity, which contain a number that helps to identify its
location. For example activity A can be drawn as:
Dummy Activity: Anactivity
,whichisusedtomaintainthepre-defined precedencerelationshiponlyduringthe
constructionoftheprojectnetwork,is calledadummy activity
.Dummyactivityisrepresentedbyadottedarrow anddoes
notconsumeanytimeand resource
2
1
A

6.  Parallel activity: There are two activity which being at same
event and end at same event.this activities are called parallel
activity.
Not allowed…..
 Path: A path is a series of adjacent activities leading from one
event to another.
Critical path: A critical path is the sequence of critical activities
that forms a continuous path between the start of a project and
its completion.

7. A
Situations
in
network
diagram
B
A must finish before either B or
C
can start, it called burst
event.
C
A
B
C both A and B must finish before
C
can start, it called merge
event.
Dangling events is not
allow.
A
C
B
D
Dummy
A must finish before B can start
both A and C must finish before
D can start, it’s called dummy
activity.
A
B
C

8. Forward pass:
The Early Start and Early Finish Time
Calculated by moving Forward Through
the Network.
Consider Maximum.

9. Backward pass: The Latest Start and Latest Finish
Time Calculated by moving Backward
Through the Network.
Consider Minimum

10. Float activity: Float activity For an Activity is The
Difference between its Earliest and
Latest Start Time or Earliest and
Latest Finish Time .

11. Steps inCritical
P a t h Method
 Step 1: Make a forward pass through the
network as For each activity i beginnin g at the
Sta rt node, compute:
Earliest Start Time (ES) = the maximum of the earliest
finish times of all activities immediately preceding
activity i. (This is 0 for an activity with no
predecessors.). This is the earliest time an activity
can begin without violation of immediate predecessor
requirements.
Earliest Finish Time (Ef) = (Earliest Start Time) + (Time
to complete activity i. This repreactivity can end.The
project completion time is the maximum of the Earliest
Finish Times at the Finish node.sent the earliest time
at which an

12. Continue..........
 Step 2: Make a backwards pass through the network as
follows: Move sequentially backwards from the Finish
node to the Start node. At a given node, j, consider all
activities ending at node j. For each of these activities,
(i,j), compute:
Latest Finish Time (LF) = the minimum of the
latest start times beginning at node j. (For node N,
this is the project
completion time.). This is the latest time an activity can
end without delaying the entire project.
Latest Start Time (LS) = (Latest Finish Time) -
(Time to complete activity (i,j)). This is the latest time
an activity can begin without delaying the entire
project.

13. Continue..........
 Step 3: Calculate the float time for each activity
by:
float = (Latest Start) - (Earliest
Start), or
= (Latest Finish)-(EarliesFinish).
A critical path is a path of activities, from the Start
node to the Finish node, with 0 float times.

14. Example
Activity Duration
1-2 6
1-3 9
2-4 3
3-4 4
3-5 8
2-6 12
4-6 7
5-6 1
Construct the CPM Network using the details below and
determine the critical path

16. Activ
ity
Dura
tion
EST EFT LST LFT Float
1-2 6
1-3 9
2-4 3
3-4 4
3-5 8
2-6 12
4-6 7
5-6 1

17. Numeric
al-II
 A Project schedule has following characteristics:
 Draw the network diagram and trace the critical path
of the network. What are the various time estimates
and total duration of project?
Description Activity Duration
Start earth work A (1-2) 3
Vendor Selection B(1-4) 2
Start handling C(1-7) 1
Continue earth work D(2-3) 3
Finish earth work E(3-6) 2
Ordering raw
material
F(4-5) 4
Excavation for drains G(4-8) 6
Receiving raw
materials
H(5-6) 5

18. Step-1
(Construct
the Network
Diagram)

19. Activi
ty
Durat
ion
EST EFT LST LFT Float

20. Numeric
al -III
A) Construct the CPM Network
B) Determine the critical path and project completion time
C) Compute total floats for non critical activities
Activity
Immediate
Predecessor
Duration
(Months)
A. - 2
B. - 5
C. - 4
D. B 5
E. A 7
F. A 3
G. B 3
H. C,D 6
I. C,D 2
J. E 5
K. F,G,H 4
L. F,G,H 3
M. I 12
N. J,K 8
Consider the details of a project

21. Activi
ty
Durat
ion
EST EFT LST LFT Float

22. Benefits of CPMUseful at many stages of project management
Mathematically simple
Give critical path and float time
Provide project documentation
Useful in monitoring costs
Visual representation

23. Limitations
to CPM
Specified precedence relationship
Activity time estimates are subjective and depend on
judgment
Can bemore difficult understand ten grant charts
The time needed for tasks is not as clear as with grant charts

24.  The following table give the duration in days and the predecessor for the
various tasks.
Numeric
al
Tasks A B C D E F G H I
Time
(days)
8 10 8 10 16 17 18 14 9
Prede
cessor
- - - A A B,D C C F,G
Draw the EON Diagram and find the minimum time for completion of the
project.

26. Activ
ity
Dura
tion
EST EFT LST LFT Total
float
1-2 8
1-3 10
1-4 8
2-3 10
2-6 16
3-5 17
4-5 18
4-6 14
5-6 9

27. Numerical-5
 The details of activity and duration are shown
below:
Activit
y
A B C D E F G
Prede
cessor
- A A A B,C C,D E,F
Durati
on
(Days)
10 5 4 7 6 4 7
i) Find a Network ii) Find the critical Path iii) Project duration

28. Numerical
-6
 Determine the critical path for given activities
and find out floats
Activity Duration
1-2 5
1-3 6
2-6 8
3-4 1
3-5 1
4-6 1
5-7 2
6-8 3
7-8 1
7-9 4
2-9 9

29. Numerical
-6
 Determine the critical path for given activities
and find out floats
Activ
ity
Dura
tion
EST EFT LST LFT Total
float
1-2 6
1-3 9
2-4 3
3-4 4
3-5 8
2-6 12
4-6 7
5-6 1