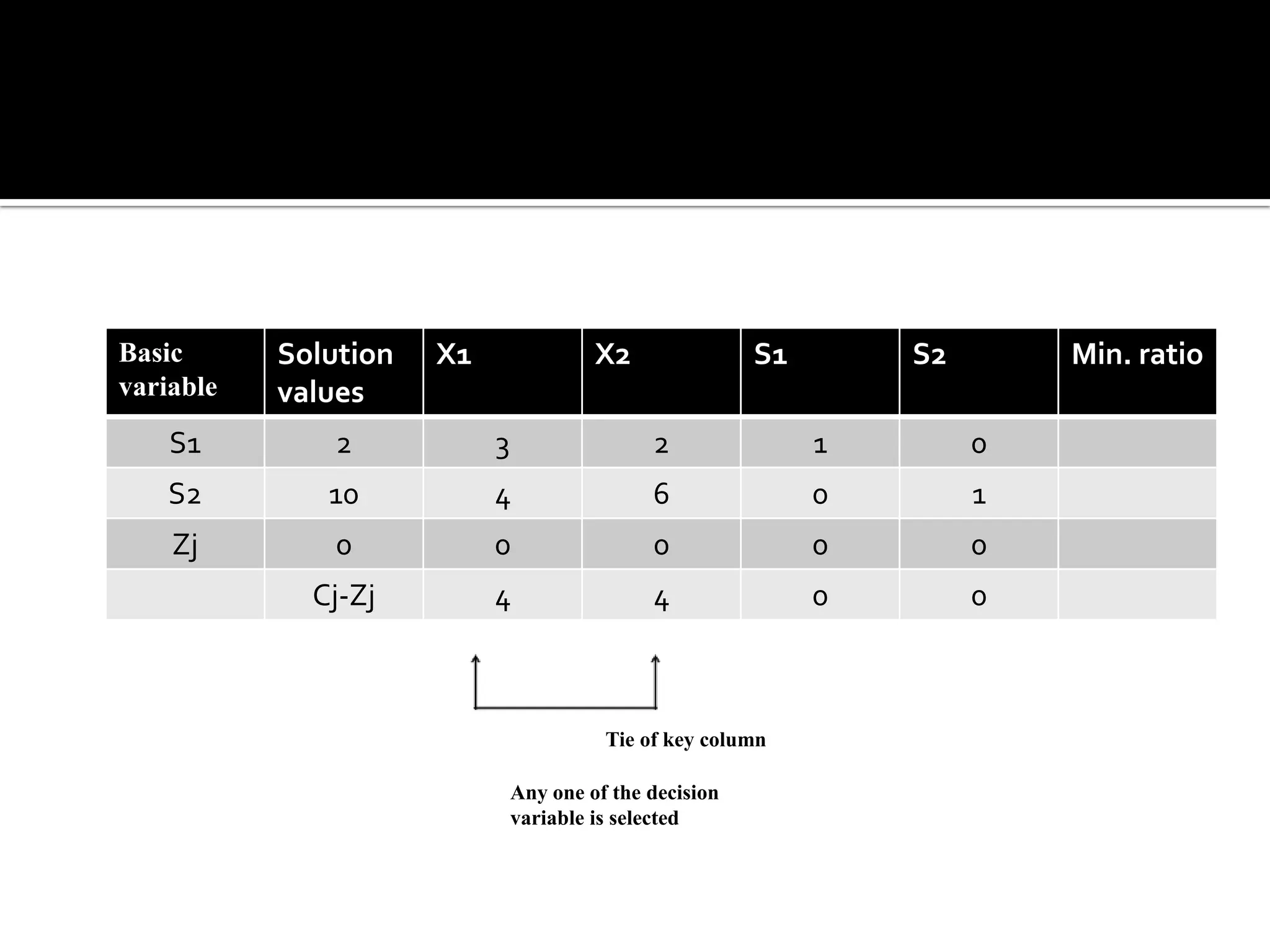
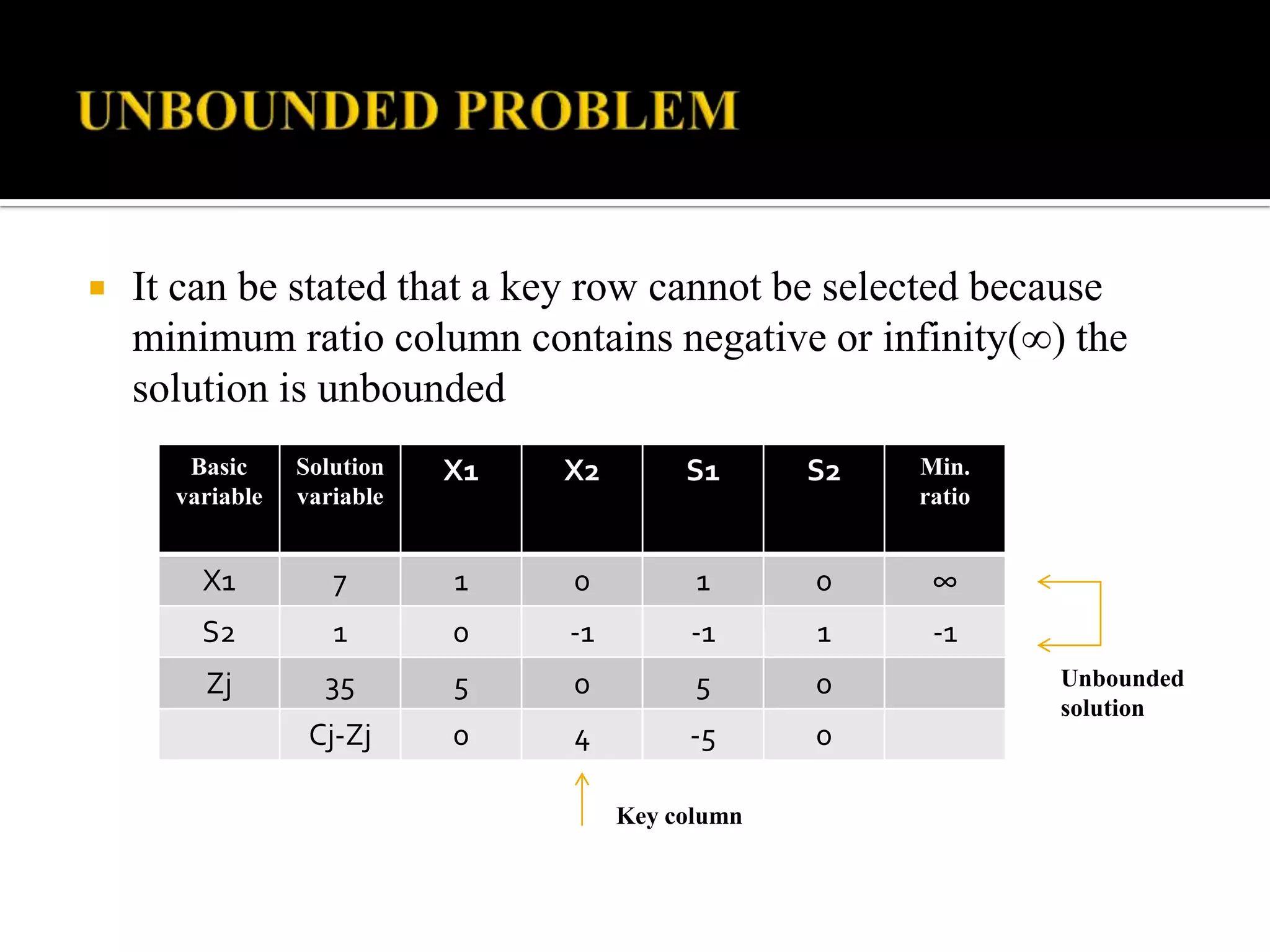
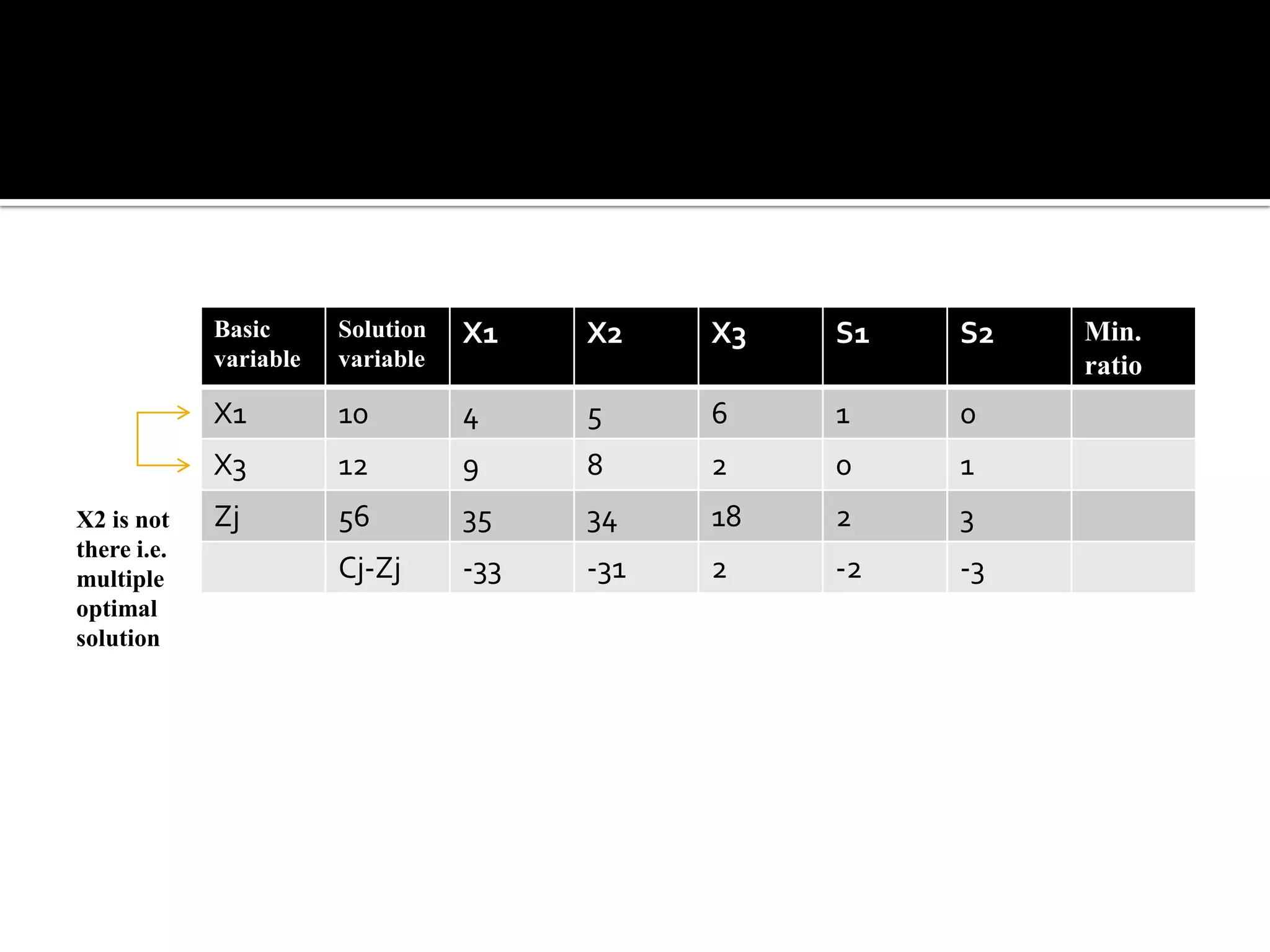
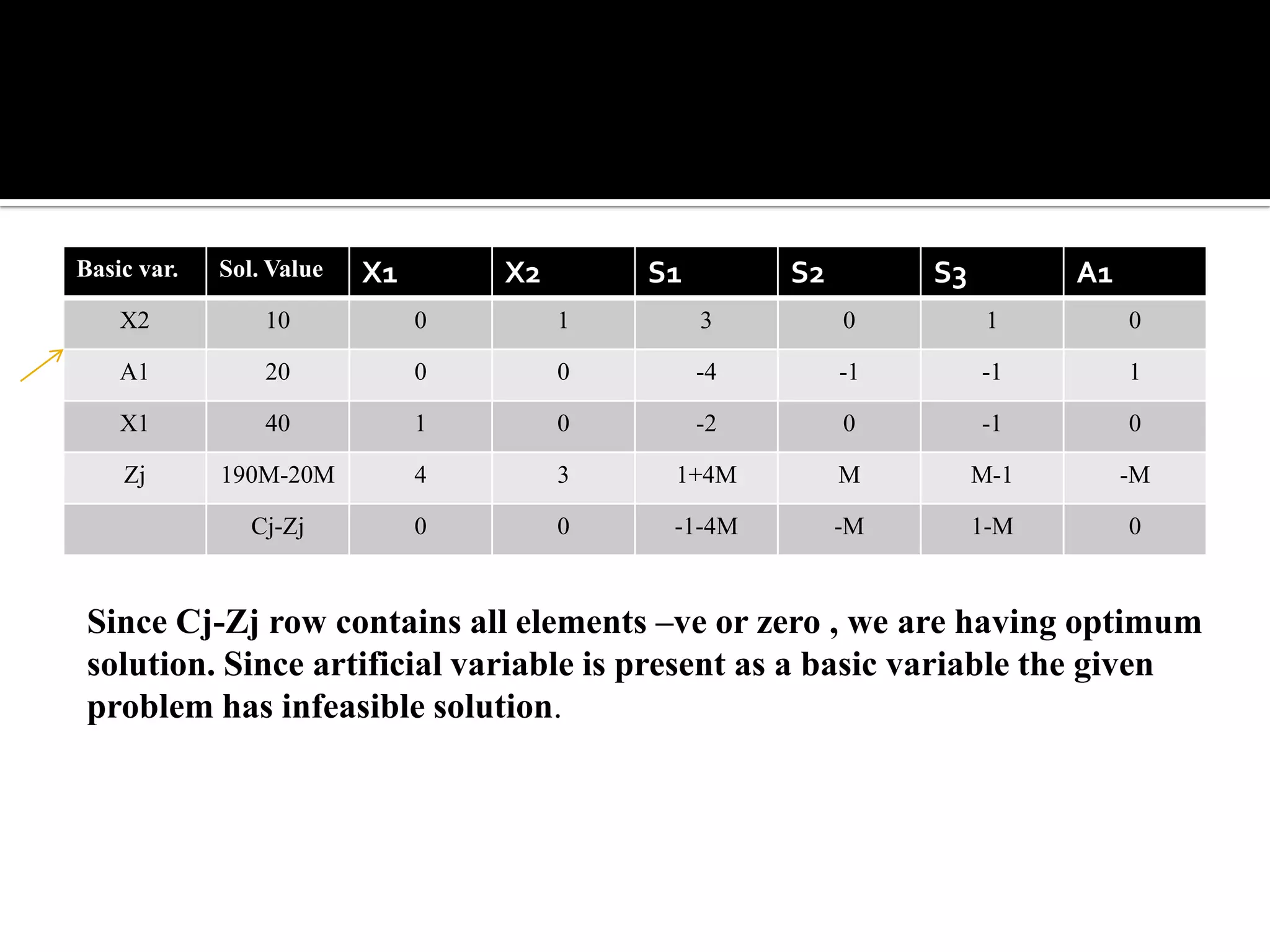
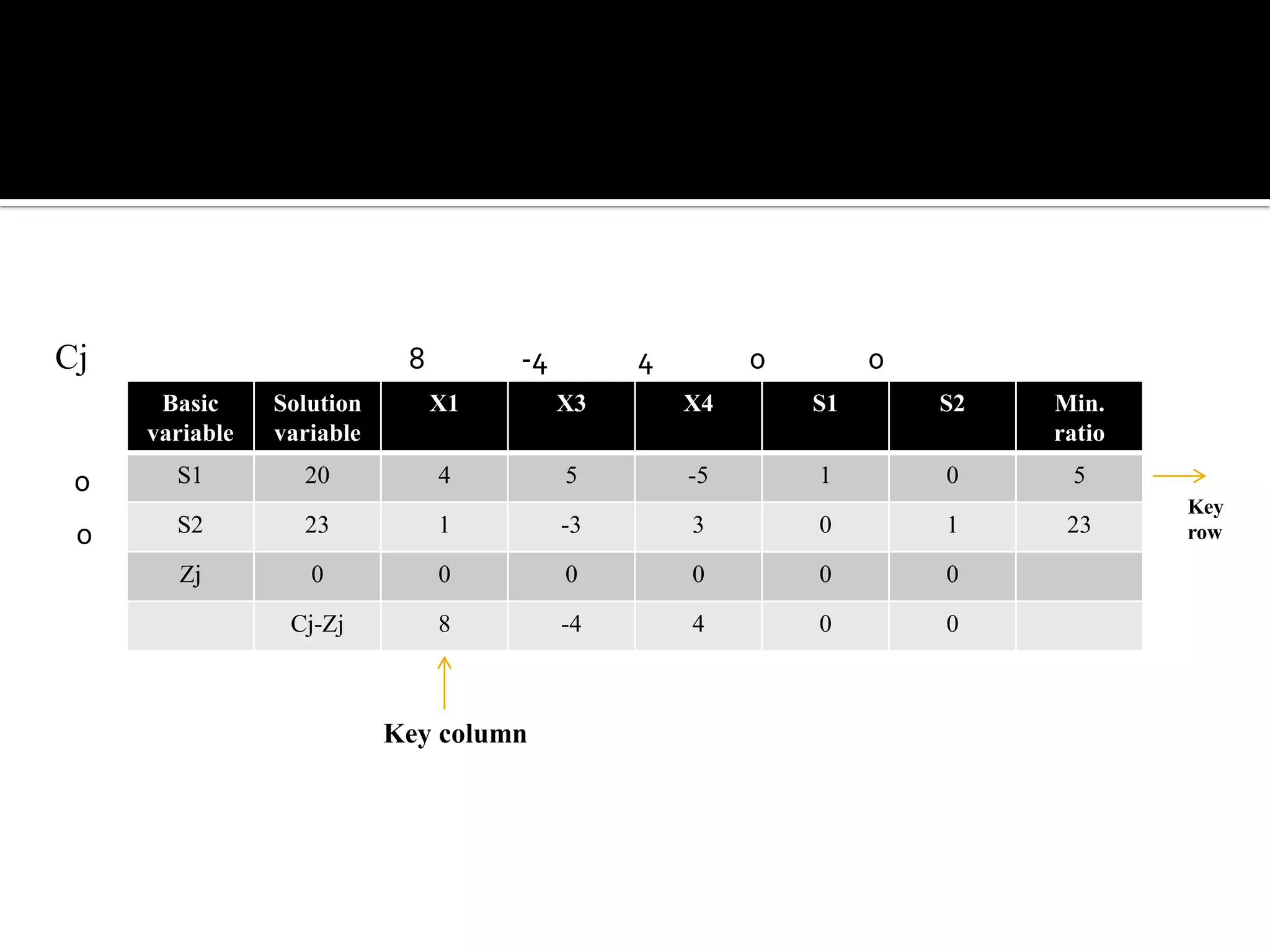
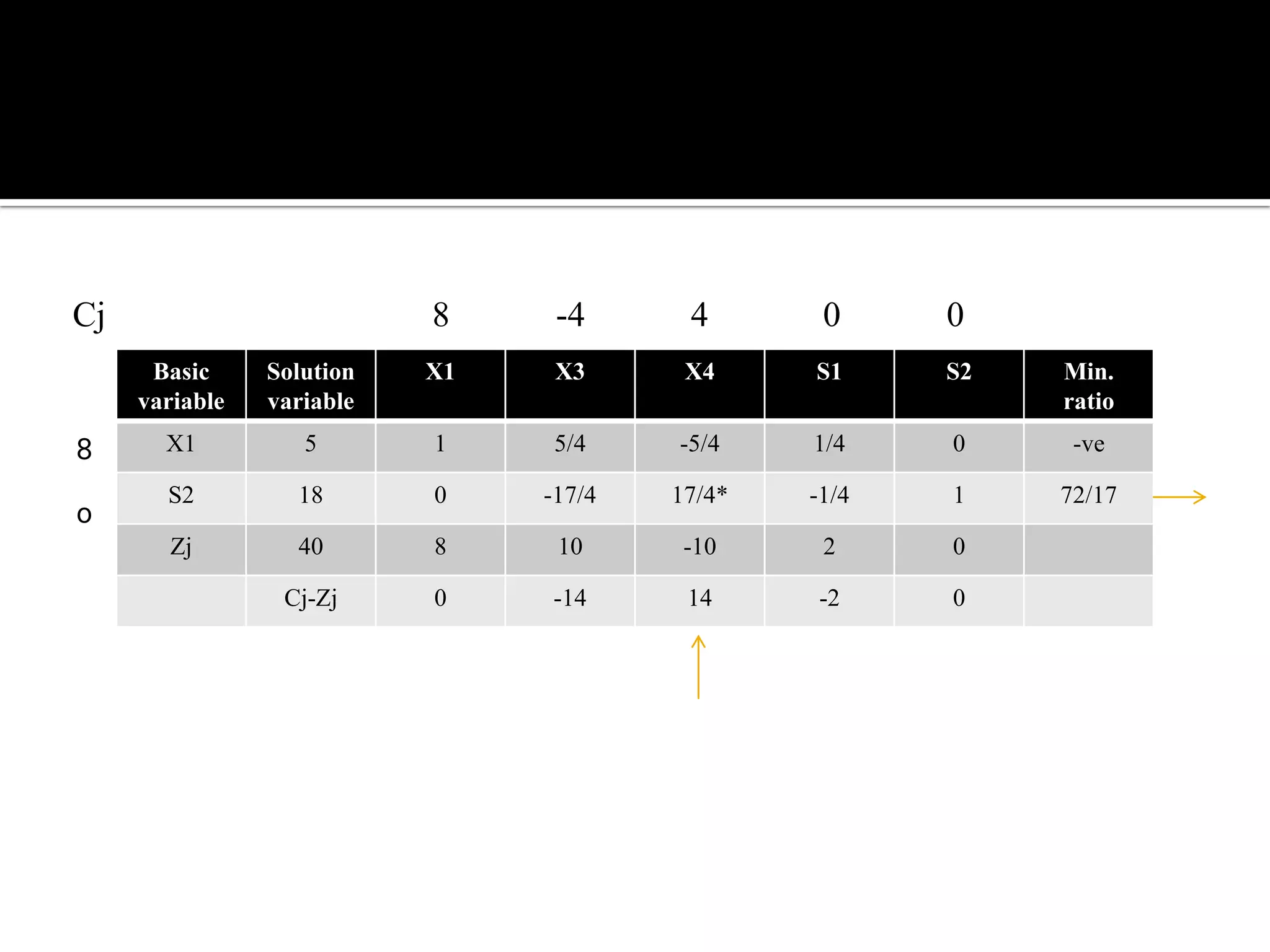
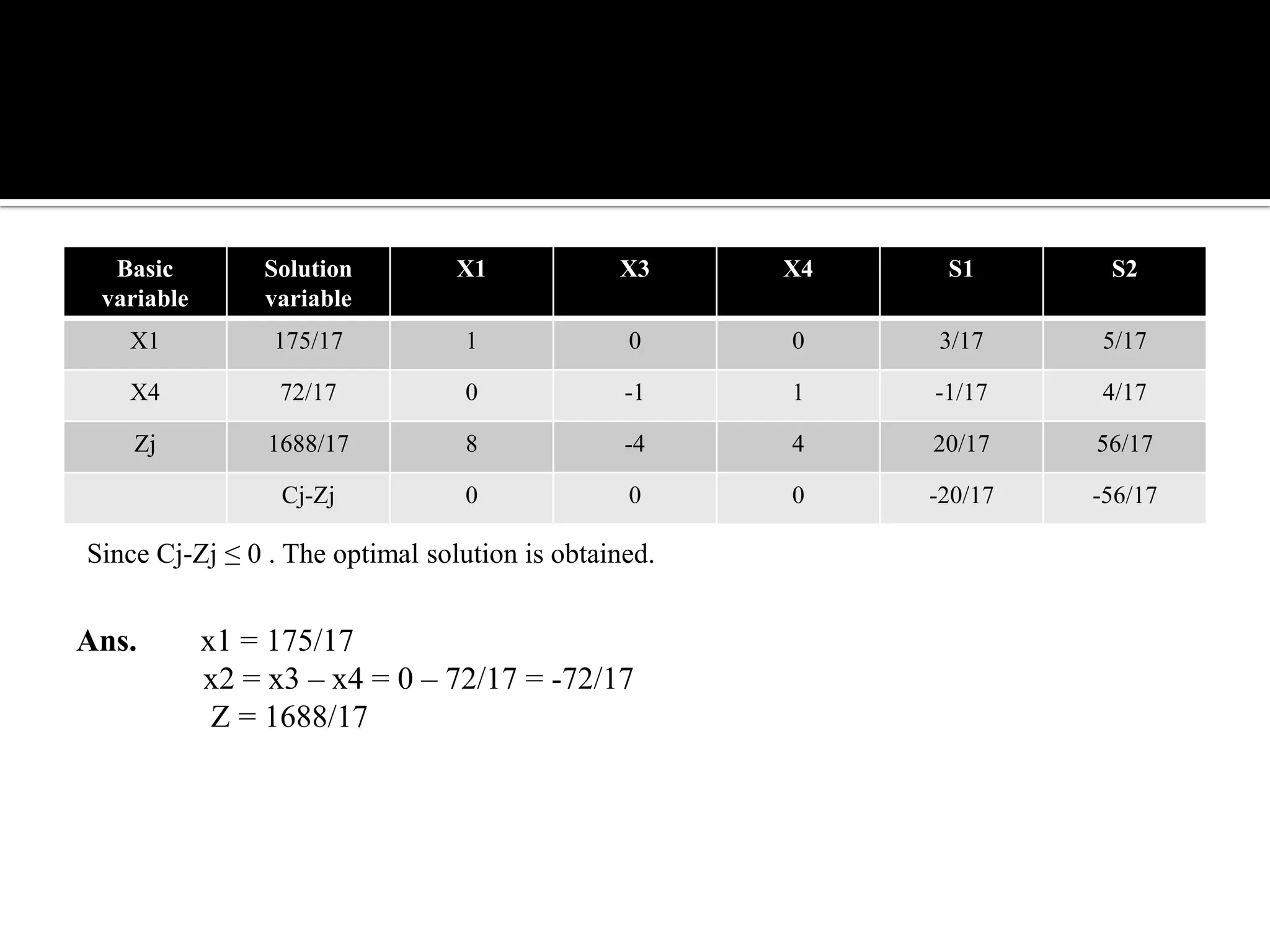
This document discusses several types of complications that can occur when solving linear programming problems (LPP), including degeneracy, unbounded problems, multiple optimal solutions, infeasible problems, and redundant or unrestricted variables. It provides examples and explanations of how to identify each type of complication and the appropriate steps to resolve it such as introducing slack or artificial variables, breaking ties, or setting unrestricted variables equal to the difference of two non-negative variables.

2. Several complications can occur while solving the LPP. Such
problems are:
 Tie for the key row(degeneracy)
 Tie for the key column
 Unbounded problems
 Multiple optimal solutions
 Infeasible problems
 Redundant constraints
 Unrestricted Variables

3.  Degeneracy occurs when there is tie for the minimum
ratio(MR) for choosing the departing variable
Basic Solution X1 X2 S1 S2 Min.
variables variables ratio
S1 20 4 9 1 0 5
S2 10 2 7 0 1 5
Zj 0 0 0 0 0
Tie of key
Cj-Zj 5 3 0 0 row
Key column

4.  Find the coefficient of the slack variables and divide each
coefficient by the corresponding positive numbers of the key
column in the row, starting from left to right in order to break
the tie X1 is replaced by S1
S1 S2
Lowest element 1/4= 0.25 0/4= 0
and S1 row is a
key row 0/2= 0 1/2= 0.5

5.  If the ratio do not break the tie, find the similar ratio for the
coefficient of decision variables
 Compare the resulting ratio, column by column
 Select the row which contains smallest ratio.This row
becomes the key row
 After resolving of this tie, simplex method is applied to obtain
the optimum solution

6.  This problem can arise in case of tie between identical Cj-Zj
values
 In such a situation selection for key column can be made
arbitrarily
 There is no wrong choice, although selection of one variable
may result in more iteration
 Regardless of which variable column is chosen the optimal
solution will eventually be found

7. Basic Solution X1 X2 S1 S2 Min. ratio
variable values
S1 2 3 2 1 0
S2 10 4 6 0 1
Zj 0 0 0 0 0
Cj-Zj 4 4 0 0
Tie of key column
Any one of the decision
variable is selected

8.  It can be stated that a key row cannot be selected because
minimum ratio column contains negative or infinity(∞) the
solution is unbounded
Basic Solution X1 X2 S1 S2 Min.
variable variable ratio
X1 7 1 0 1 0 ∞
S2 1 0 -1 -1 1 -1
Zj 35 5 0 5 0 Unbounded
solution
Cj-Zj 0 4 -5 0
Key column

9.  If the index row indicates the value of Cj-Zj for a non basic
variable to be zero, there exists an alternative optimum
solution.
 To find the alternative optimal solution, the non basic variable
with the Cj-Zj value of zero, should be selected as an entering
variable and the simplex steps continued.

10. Basic Solution X1 X2 X3 S1 S2 Min.
variable variable ratio
X1 10 4 5 6 1 0
X3 12 9 8 2 0 1
X2 is not Zj 56 35 34 18 2 3
there i.e.
multiple Cj-Zj -33 -31 2 -2 -3
optimal
solution

11.  This condition occurs when the problem has incompatible
constraints
 In final simplex table, all Cj-Zj elements +ve or zero in case
of minimization and –ve or zero in case of maximization
 And if the basic variable include artificial variable, then LPP
got an infeasible solution

12. Basic var. Sol. Value X1 X2 S1 S2 S3 A1
X2 10 0 1 3 0 1 0
A1 20 0 0 -4 -1 -1 1
X1 40 1 0 -2 0 -1 0
Zj 190M-20M 4 3 1+4M M M-1 -M
Cj-Zj 0 0 -1-4M -M 1-M 0
Since Cj-Zj row contains all elements –ve or zero , we are having optimum
solution. Since artificial variable is present as a basic variable the given
problem has infeasible solution.

13. Consider the constraints,
3X1 + 4X2 < 7
neglected
3X1 + 4X2 < 15
The second constraint is less restrictive(because both the
constraints have same co-efficient and variable) than first one,
and is not required. Normally redundant constraint does not pose
any problem except the computational work is unnecessarily
increased

14.  It is that decision variable which does not carry any value.
 To solve this problem, the variable can take two values i.e.
one +ve & one –ve because difference between these two
same +ve and –ve value is zero
 All variables become non-negative in the system and problem
is solved.

15.  Example:
Max Z = 8x1 – 4x2
4x1 + 5x2 ≤ 20
-x1 + 3x2 ≥ -23
when x1 ≥ 0 , x2 is unrestricted in sign
Solution :
Firstly replace the unrestricted variable x2
x2 = x3 – x4

16.  After replacing the x2 ,
Max Z = 8x1 – 4x3 + 4x4
4x1 + 5x3 – 5x4 ≤ 20
x1 – 3x3 + 3x4 ≤ 23; x1,x3,x4 ≥ 0
 After that slack variables are added to the constraints ,
Max Z = 8x1 – 4x3 + 4x4 + 0S1 + 0S2
4x1 + 5x3 – 5x4 + S1 + 0S2 = 20
x1 – 3x3 + 3x4 + 0S1 + S2 = 23;
x1,x3,x4,S1,S2 ≥ 0

17. Cj 8 -4 4 0 0
Basic Solution X1 X3 X4 S1 S2 Min.
variable variable ratio
0 S1 20 4 5 -5 1 0 5
Key
0 S2 23 1 -3 3 0 1 23 row
Zj 0 0 0 0 0 0
Cj-Zj 8 -4 4 0 0
Key column

18. Cj 8 -4 4 0 0
Basic Solution X1 X3 X4 S1 S2 Min.
variable variable ratio
8 X1 5 1 5/4 -5/4 1/4 0 -ve
S2 18 0 -17/4 17/4* -1/4 1 72/17
0
Zj 40 8 10 -10 2 0
Cj-Zj 0 -14 14 -2 0

19. Basic Solution X1 X3 X4 S1 S2
variable variable
X1 175/17 1 0 0 3/17 5/17
X4 72/17 0 -1 1 -1/17 4/17
Zj 1688/17 8 -4 4 20/17 56/17
Cj-Zj 0 0 0 -20/17 -56/17
Since Cj-Zj ≤ 0 . The optimal solution is obtained.
Ans. x1 = 175/17
x2 = x3 – x4 = 0 – 72/17 = -72/17
Z = 1688/17

20. Presented by:-
Astha
Harpreet Singh
Shivani
Shweta