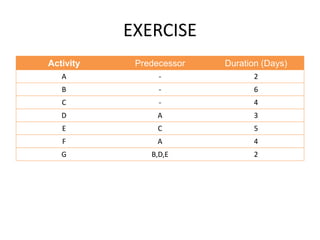
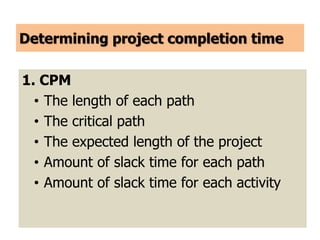
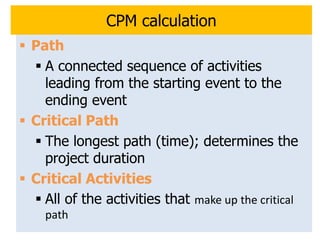
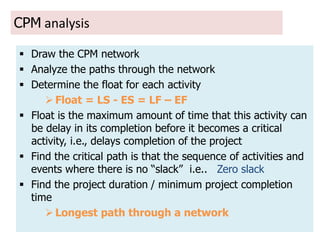
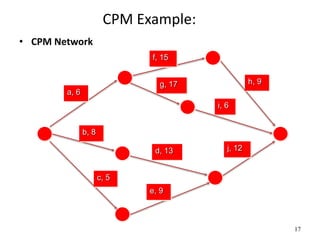
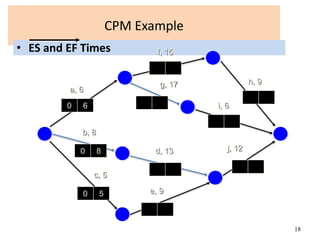
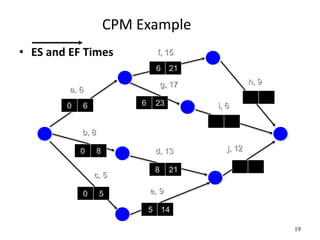
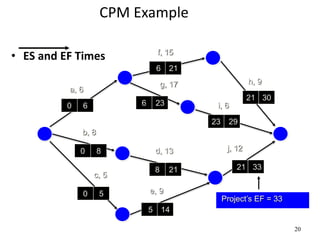
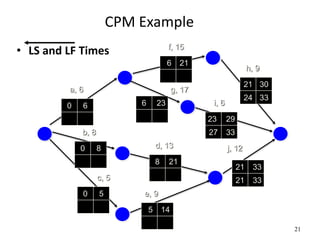
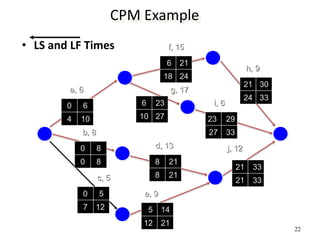
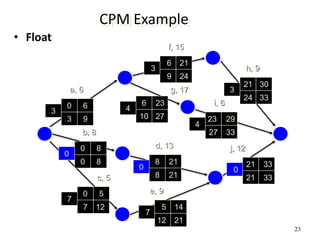
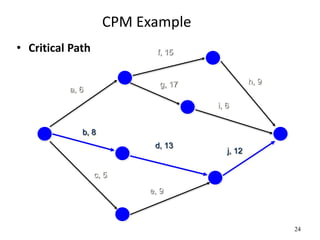
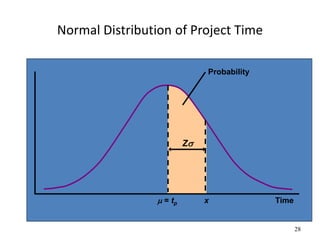
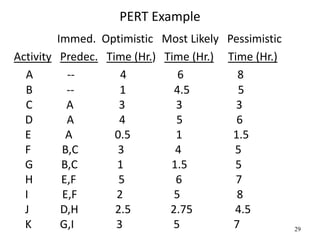
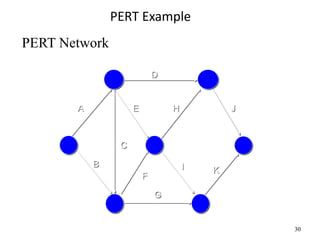
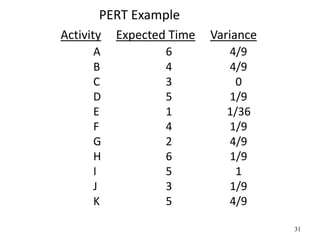
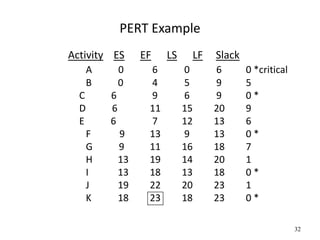
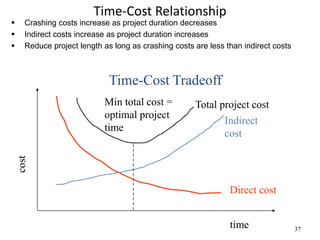
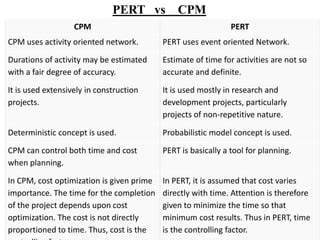
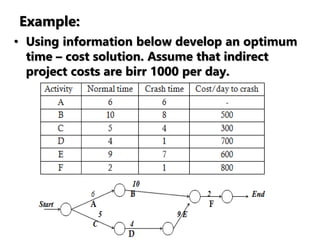
The document discusses network models like CPM and PERT that are used for project management. CPM uses deterministic activity times to create a network and identify the critical path, while PERT uses probabilistic estimates. Both techniques can determine the project duration, start/finish dates, critical activities, float, and the effects of delays. The document also covers crashing the critical path to shorten a project's duration, including calculating activity costs and finding the minimum total project cost.

1. Chapter Six
Network Models and
Project Management

2. Introduction
• A project is a series of activities designed to
achieve a specific objective, and which has a
definite beginning and a definite end.
• Project life cycle:
• Concept
• Feasibility analysis
• Planning
• Execution
• Termination

3. PERT AND CPM
• Used techniques for planning and
coordinating large scale projects
 Using PERT and CPM, it is possible to:
• Graphically displays project activities
• Estimates how long the project will take
• Indicates most critical activities
• Show where delays will not affect project

4. PERT/CPM
• Project managers rely on PERT/CPM to help them answer
questions such as:
 What is the total time to complete the project?
 What are the scheduled start and finish dates for each specific
activity?
 Which activities are critical and must be completed exactly as
scheduled to keep the project on schedule?
 How long can noncritical activities be delayed before they
cause an increase in the project completion time?
 If activity times are uncertain (i.e., they are random variables),
what is the probability that the project will be finished in any
given time-frame?
 If there is a cost associated with “crashing” each activity, what
is the extra cost of completing the project at a time earlier than
the normal time?

5. 5
Difference
 Critical Path Method (CPM)
• Deterministic task times
• Activity-on-node network construction
• Repetitive nature of jobs
 Project Evaluation and Review Technique
(PERT)
• Multiple task time estimates (probabilistic nature)
• Activity-on-arrow network construction
• Non-repetitive jobs (R & D work)

6. The Network Diagram
 Network diagram is diagram of project activities
that shows sequential relationships by use of
arrows and nodes.
Arrows: Indicate Activity, a time consuming
effort that is required to perform a part of
the work.
Nodes : are represented by a circle
- Indicate Event, a point in time where one or
more activities start and/or finish.

7. 1
2
3
4
5 6
Locate
facilities
Order
furniture
Furniture
setup
Interview
Hire and
train
Remodel
Move in

8. 1
2
3
5
6
Locate
facilities
Order
furniture
Furniture
setup
Interview
Remodel
Move in
4
Hire and
train
7
S

9. Terms
 Preceding activities: activities which must be
accomplished before a given event can occur
 Succeeding activities: activities which cannot
be accomplished until any event has occurred
 Concurrent activities: activities that can be
accomplished concurrently
 Dummy activities are neither consume time
nor resources
 Merge events
 Burst events

10. Example: Draw a network diagram
Activity Immediate
Expected time
Predecessor
A -
4
B -
6
C A

11. EXERCISE
Activity Predecessor Duration (Days)
A - 2
B - 6
C - 4
D A 3
E C 5
F A 4
G B,D,E 2

12. Determining project completion time
1. CPM
• The length of each path
• The critical path
• The expected length of the project
• Amount of slack time for each path
• Amount of slack time for each activity

13. 13
CPM calculation
 Path
 A connected sequence of activities
leading from the starting event to the
ending event
 Critical Path
 The longest path (time); determines the
project duration
 Critical Activities
 All of the activities that make up the critical
path

14. 14
CPM analysis
 Draw the CPM network
 Analyze the paths through the network
 Determine the float for each activity
 Float = LS - ES = LF – EF
 Float is the maximum amount of time that this activity can
be delay in its completion before it becomes a critical
activity, i.e., delays completion of the project
 Find the critical path is that the sequence of activities and
events where there is no “slack” i.e.. Zero slack
 Find the project duration / minimum project completion
time
 Longest path through a network

15. 15
Forward Pass
 Earliest Start Time (ES)
 Earliest time an activity can start
 ES = maximum EF of immediate predecessors
 Earliest finish time (EF)
 Earliest time an activity can finish
 Earliest start time plus activity time
 EF= ES + t
 Latest Start Time (LS)
 Latest time an activity can start without delaying critical
path time
 LS= LF - t
 Latest finish time (LF)
 latest time an activity can be completed without delaying
critical path time
Backward Pass

16. Consider below table summarizing the details of a project involving 10
activities
Activity Immediate precedence duration
a - 6
b - 8
c - 5
d b 13
e c 9
f a 15
g a 17
h f 9
i g 6
j d, e 12
Construct the CPM network. Determine the critical path and project
completion time .Also compute total float and free floats for the non-
critical activities
16

17. 17
CPM Example:
• CPM Network
a, 6
f, 15
b, 8
c, 5
e, 9
d, 13
g, 17 h, 9
i, 6
j, 12

18. 18
CPM Example
• ES and EF Times
a, 6
f, 15
b, 8
c, 5
e, 9
d, 13
g, 17 h, 9
i, 6
j, 12
0 6
0 8
0 5

19. 19
CPM Example
• ES and EF Times
a, 6
f, 15
b, 8
c, 5
e, 9
d, 13
g, 17 h, 9
i, 6
j, 12
0 6
0 8
0 5
5 14
8 21
6 23
6 21

20. 20
CPM Example
• ES and EF Times
a, 6
f, 15
b, 8
c, 5
e, 9
d, 13
g, 17 h, 9
i, 6
j, 12
0 6
0 8
0 5
5 14
8 21 21 33
6 23
21 30
23 29
6 21
Project’s EF = 33

21. 21
CPM Example
• LS and LF Times
a, 6
f, 15
b, 8
c, 5
e, 9
d, 13
g, 17
h, 9
i, 6
j, 12
0 6
0 8
0 5
5 14
8 21
21 33
6 23
21 30
23 29
6 21
21 33
27 33
24 33

22. 22
CPM Example
• LS and LF Times
a, 6
f, 15
b, 8
c, 5
e, 9
d, 13
g, 17
h, 9
i, 6
j, 12
0 6
0 8
0 5
5 14
8 21
21 33
6 23
21 30
23 29
6 21
4 10
0 8
7 12
12 21
21 33
27 33
8 21
10 27
24 33
18 24

23. 23
CPM Example
• Float
a, 6
f, 15
b, 8
c, 5
e, 9
d, 13
g, 17
h, 9
i, 6
j, 12
0 6
0 8
0 5
5 14
8 21 21 33
6 23
21 30
23 29
6 21
3 9
0 8
7 12
12 21
21 33
27 33
8 21
10 27
24 33
9 24
3 4
3
3
4
0
0
7
7
0

24. 24
CPM Example
• Critical Path
a, 6
f, 15
b, 8
c, 5
e, 9
d, 13
g, 17 h, 9
i, 6
j, 12

25. darla/smbs/vit 25
PERT
• PERT is based on the assumption that an activity’s duration
follows a probability distribution instead of being a single value
• Three time estimates are required to compute the parameters
of an activity’s duration distribution:
– pessimistic time (tp ) - the time the activity would take if
things did not go well
– most likely time (tm ) - the consensus best estimate of the
activity’s duration
– optimistic time (to ) - the time the activity would take if
things did go well
Mean (expected time): te =
tp + 4 tm + to
6
Variance: Vt = 2 =
tp - to
6
2

26. 26
PERT analysis
• Draw the network.
• Analyze the paths through the network and find the critical path.
• The length of the critical path is the mean of the project duration
probability distribution which is assumed to be normal
• The standard deviation of the project duration probability
distribution is computed by adding the variances of the critical
activities (all of the activities that make up the critical path) and
taking the square root of that sum
• Probability computations can now be made using the normal
distribution table.

27. 27
Probability computation
Determine probability that project is completed within specified time
Z =
x - 

where  = tp = project mean time
 = project standard mean time
x = (proposed ) specified time

28. 28
Normal Distribution of Project Time
 = tp Time
x
Z
Probability

29. 29
PERT Example
Immed. Optimistic Most Likely Pessimistic
Activity Predec. Time (Hr.) Time (Hr.) Time (Hr.)
A -- 4 6 8
B -- 1 4.5 5
C A 3 3 3
D A 4 5 6
E A 0.5 1 1.5
F B,C 3 4 5
G B,C 1 1.5 5
H E,F 5 6 7
I E,F 2 5 8
J D,H 2.5 2.75 4.5
K G,I 3 5 7

30. 30
PERT Example
A
D
C
B
F
E
G
I
H
K
J
PERT Network

31. 31
PERT Example
Activity Expected Time Variance
A 6 4/9
B 4 4/9
C 3 0
D 5 1/9
E 1 1/36
F 4 1/9
G 2 4/9
H 6 1/9
I 5 1
J 3 1/9
K 5 4/9

32. 32
PERT Example
Activity ES EF LS LF Slack
A 0 6 0 6 0 *critical
B 0 4 5 9 5
C 6 9 6 9 0 *
D 6 11 15 20 9
E 6 7 12 13 6
F 9 13 9 13 0 *
G 9 11 16 18 7
H 13 19 14 20 1
I 13 18 13 18 0 *
J 19 22 20 23 1
K 18 23 18 23 0 *

33. 33
PERT Example
Vpath = VA + VC + VF + VI + VK
= 4/9 + 0 + 1/9 + 1 + 4/9
= 2
path = 1.414
z = (24 - 23)/(24-23)/1.414 = .71
From the Standard Normal Distribution table:
P(z < .71) = .5 + .2612 = .7612

34. PROJECT COST

35. 35
Cost consideration in project
• Project managers may have the option or requirement to crash
the project, or accelerate the completion of the project.
• This is accomplished by reducing the length of the critical path(s).
• The length of the critical path is reduced by reducing the
duration of the activities on the critical path.
• If each activity requires the expenditure of an amount of money
to reduce its duration by one unit of time, then the project
manager selects the least cost critical activity, reduces it by one
time unit, and traces that change through the remainder of the
network.
• As a result of a reduction in an activity’s time, a new critical path
may be created.
• When there is more than one critical path, each of the critical
paths must be reduced.
• If the length of the project needs to be reduced further, the
process is repeated.

36. 36
Project Crashing
• Crashing
– reducing project time by expending additional resources
• Crash time
– an amount of time an activity is reduced
• Crash cost
– cost of reducing activity time
• Goal
– reduce project duration at minimum cost

37. 37
Time-Cost Relationship
 Crashing costs increase as project duration decreases
 Indirect costs increase as project duration increases
 Reduce project length as long as crashing costs are less than indirect costs
Time-Cost Tradeoff
time
Direct cost
Indirect
cost
Total project cost
Min total cost =
optimal project
time

38. 38
Benefits of CPM/PERT
• Useful at many stages of project management
• Mathematically simple
• Give critical path and slack time
• Provide project documentation
• Useful in monitoring costs
•How long will the entire project take to be completed? What are the risks involved?
•Which are the critical activities or tasks in the project which could delay the entire
project if they were not completed on time?
•Is the project on schedule, behind schedule or ahead of schedule?
•If the project has to be finished earlier than planned, what is the best way to do this
at the least cost?
CPM/PERT can answer the following important
questions:

39. 39
Limitations to CPM/PERT
• Clearly defined, independent and stable activities
• Specified precedence relationships
• Over emphasis on critical paths
• Deterministic CPM model
• Activity time estimates are subjective and depend on judgment
• PERT assumes a beta distribution for these time estimates, but
the actual distribution may be different
• PERT consistently underestimates the expected project
completion time due to alternate paths becoming critical
To overcome the limitation, Monte Carlo simulations can be
performed on the network to eliminate the optimistic bias

40. 40
CPM PERT
CPM uses activity oriented network. PERT uses event oriented Network.
Durations of activity may be estimated
with a fair degree of accuracy.
Estimate of time for activities are not so
accurate and definite.
It is used extensively in construction
projects.
It is used mostly in research and
development projects, particularly
projects of non-repetitive nature.
Deterministic concept is used. Probabilistic model concept is used.
CPM can control both time and cost
when planning.
PERT is basically a tool for planning.
In CPM, cost optimization is given prime
importance. The time for the completion
of the project depends upon cost
optimization. The cost is not directly
proportioned to time. Thus, cost is the
In PERT, it is assumed that cost varies
directly with time. Attention is therefore
given to minimize the time so that
minimum cost results. Thus in PERT, time
is the controlling factor.
PERT vs CPM

41. Time-Cost Trade Offs: Crashing
• It is possible to reduce the length of a project by
injecting additional resources
• A project manager may be able to shorten a
project: by realizing a savings on indirect project
costs by increasing direct expenses to speed up
the project.
• The objective of project crash cost analysis is to
reduce the total projected completion time
while minimizing the cost of crashing.
• A manager needs the following information:
• Regular time and crash time estimates
• Regular (normal) cost and crash cost estimates
• A list of activates that are on the critical path

42. Example:
• Using information below develop an optimum
time – cost solution. Assume that indirect
project costs are birr 1000 per day.

43. End of
Chapter Six