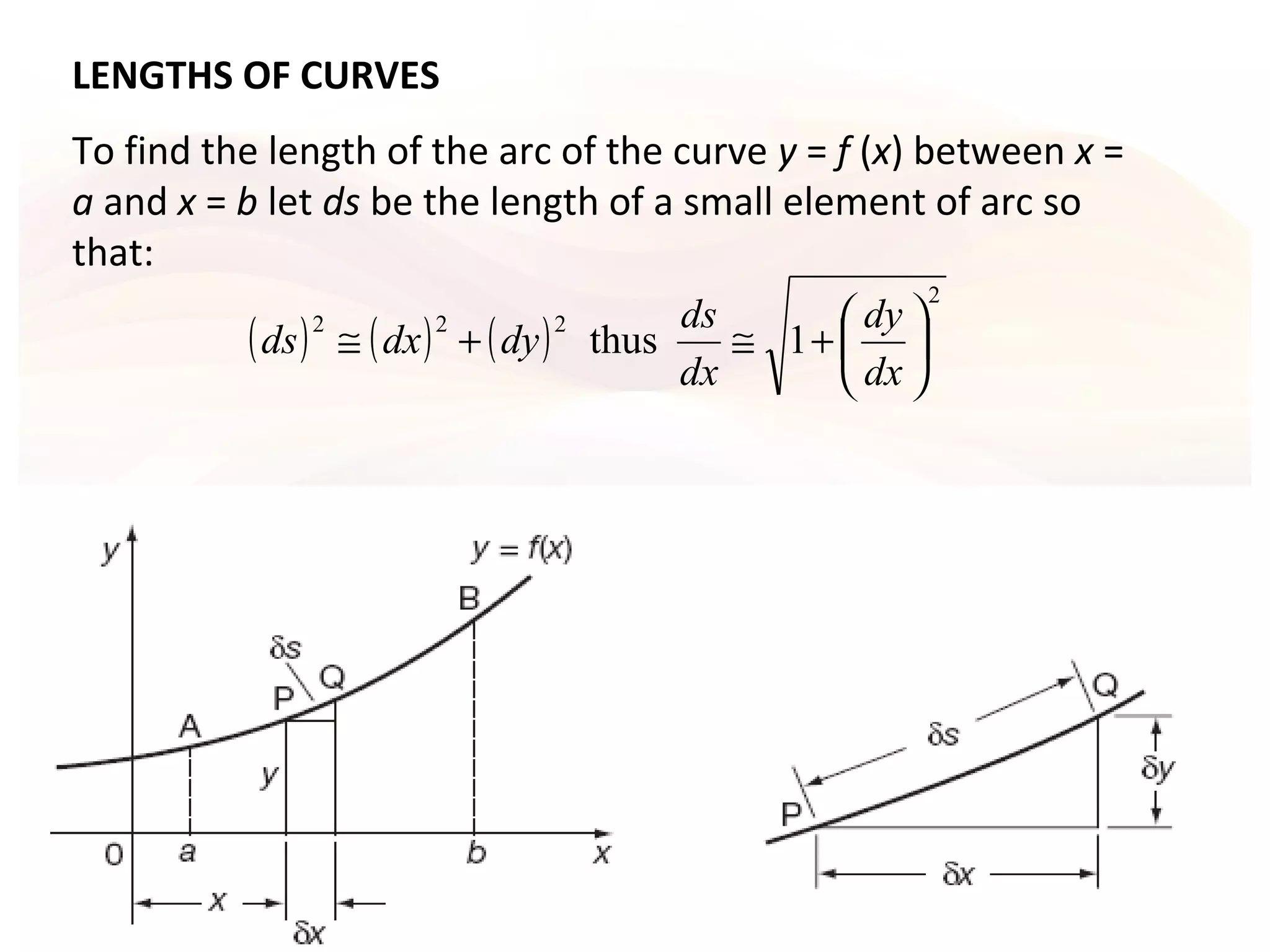
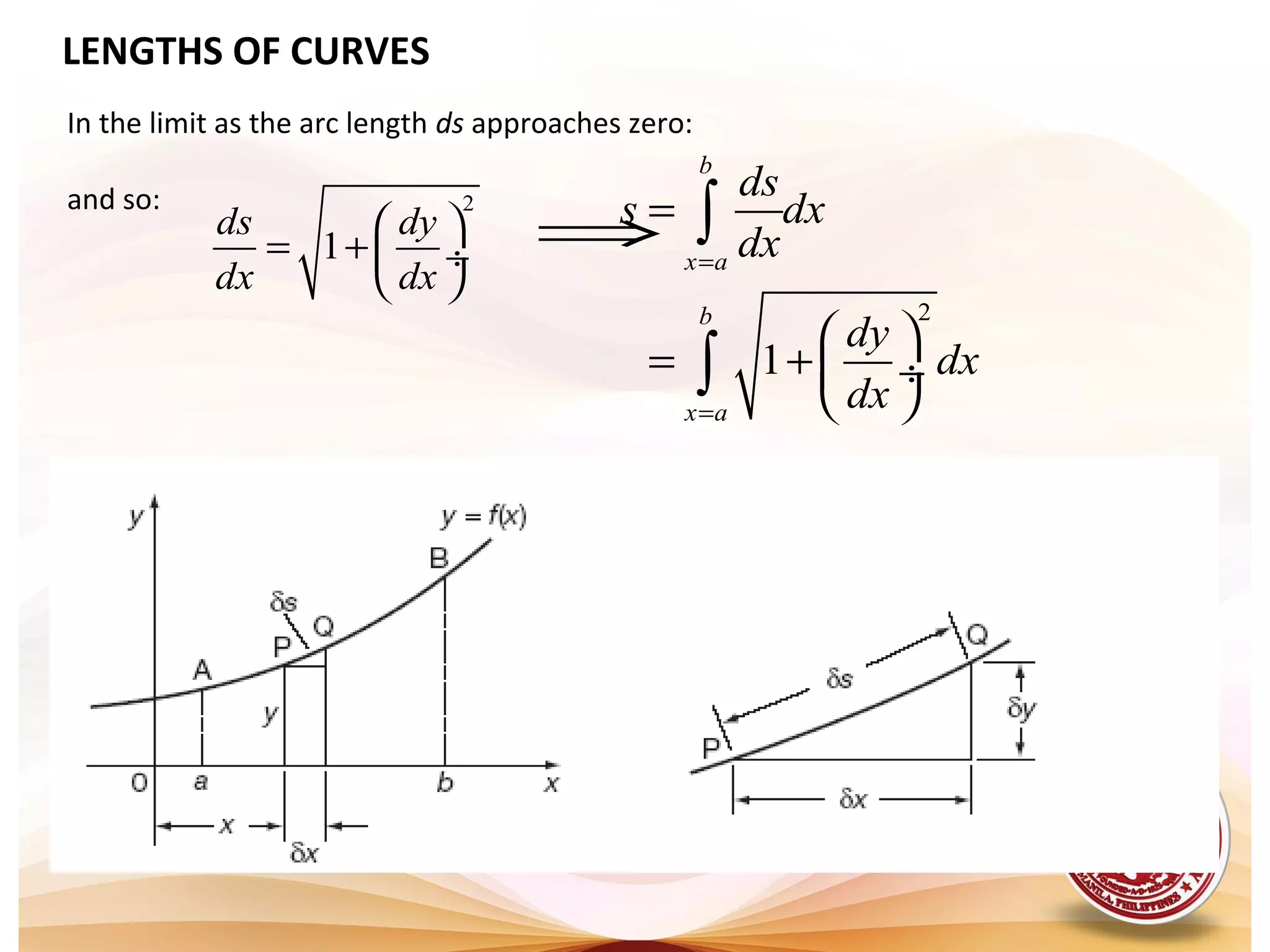
1. This document discusses methods for calculating the length of an arc of a curve and the surface area of revolution. It provides formulas for finding arc length and surface area when curves are defined by rectangular coordinates, parametric equations, or polar coordinates. 2. Several examples are given of applying the formulas to find the arc length of curves and the surface area when graphs are revolved about axes. This includes revolving curves like y=x^3, y=x^2, and xy=2 about the x-axis and y-axis. 3. The key formulas presented are that arc length can be found using an integral of the form ∫√(dx/dy)^2 + 1 dy or

1. TOPIC
LENGTH OF AN ARC
and
AREA OF SURFACE OF REVOLUTION

2. LENGTHS OF CURVES
To find the length of the arc of the curve y = f (x) between x =
a and x = b let ds be the length of a small element of arc so
that:
( ) ( ) ( )
2
222
1thus 





+≅+≅
dx
dy
dx
ds
dydxds

3. LENGTHS OF CURVES
In the limit as the arc length ds approaches zero:
and so: 2
1
ds dy
dx dx
 
= + ÷
 
2
1
b
x a
b
x a
ds
s dx
dx
dy
dx
dx
=
=
=
 
= + ÷
 
∫
∫
⇒

4. LENGTHS OF CURVES – PARAMETRIC EQUATIONS
Instead of changing the variable of the integral as before when
the curve is defined in terms of parametric equations, a special
form of the result can be established which saves a deal of
working when it is used.
Let: ( ) ( ) ( ) ( ) ( )
dt
dt
dy
dt
dx
sand
dt
dy
dt
dx
dt
ds
0dtasso
dt
dy
dt
dx
dt
ds
so
dydxdsbeforeAs.tFxandtfy
t
tt 1
∫
=






+





=





+





=
→





+





=





+≅==
2 2222
222
222

5. LENGTH OF AN ARC
A. Rectangular Coordinates
f(x)y,1
2
=





+= dx
dx
dy
ds g(y)x,dy
dy
dx
1ds
2
=





+=
B. Parametric Form
dt
dt
dy
dt
dx
ds
22






+





= when x=x(t), y=y(t); where t is a parameter
1. 2.
C. Polar Coordinates
f(r),dr
dr
d
r1ds
2
2
=θ




 θ
+= )g(r,d
d
dr
rds
2
2
θ=θ





θ
+=2.1.

6. EXAMPLE
Find the length of the arc of each of the following:
2
3
3
3
ty
ttx
=
−=1.
from t=o to t=1
2.
tsiney
tcosex
t
t
=
=
from t=o to t=4
5. Length of the arc of the semicircle
222
ayx =+
2xto1xfrom
e
e
lny x
x
==
+
−
=
1
1
3.
4.
),(to),(from
xy
2100
8 23
=

7. AREA OF SURFACE OF REVOLUTION
• DEFINITION:
Let y = f(x) have a continuous derivative on the interval [a, b].
The area S of the surface of revolution formed by revolving
the graph of f about a horizontal or vertical axis is
where r(x) is the distance between the graph of f and the axis
of revolution.
[ ] xoffunctionaisydx)x('f)x(rS
b
a
→+π= ∫
2
12

8. If x = g(y) on the interval [c, d], then the surface area is
where r(y) is the distance between the graph of g and the axis of
revolution.
[ ] yoffunctionaisxdy)y('g)y(rS
d
c
→+π= ∫
2
12

9. EXAMPLE
1. Find the area formed by revolving the graph of f(x) = x3
on
the interval [0,1] about the x-axis.
2. Find the area formed by revolving the graph of f(x) = x2
on
the interval [0, ] about the y – axis.
3. Find the area of the surface generated by revolving the
curve
, 1 ≤ x ≤ 2 about the x – axis.
4. The line segment x = 1 – y, 0 ≤ y ≤ 1, is revolved about the y
– axis to generate the cone. Find its lateral surface area.
2
xy 2=

10. EXAMPLE
1. Find the area formed by revolving the graph of f(x) = x3
on
the interval [0,1] about the x-axis.
2. Find the area formed by revolving the graph of f(x) = x2
on
the interval [0, ] about the y – axis.
3. Find the area of the surface generated by revolving the
curve
, 1 ≤ x ≤ 2 about the x – axis.
4. The line segment x = 1 – y, 0 ≤ y ≤ 1, is revolved about the y
– axis to generate the cone. Find its lateral surface area.
2
xy 2=