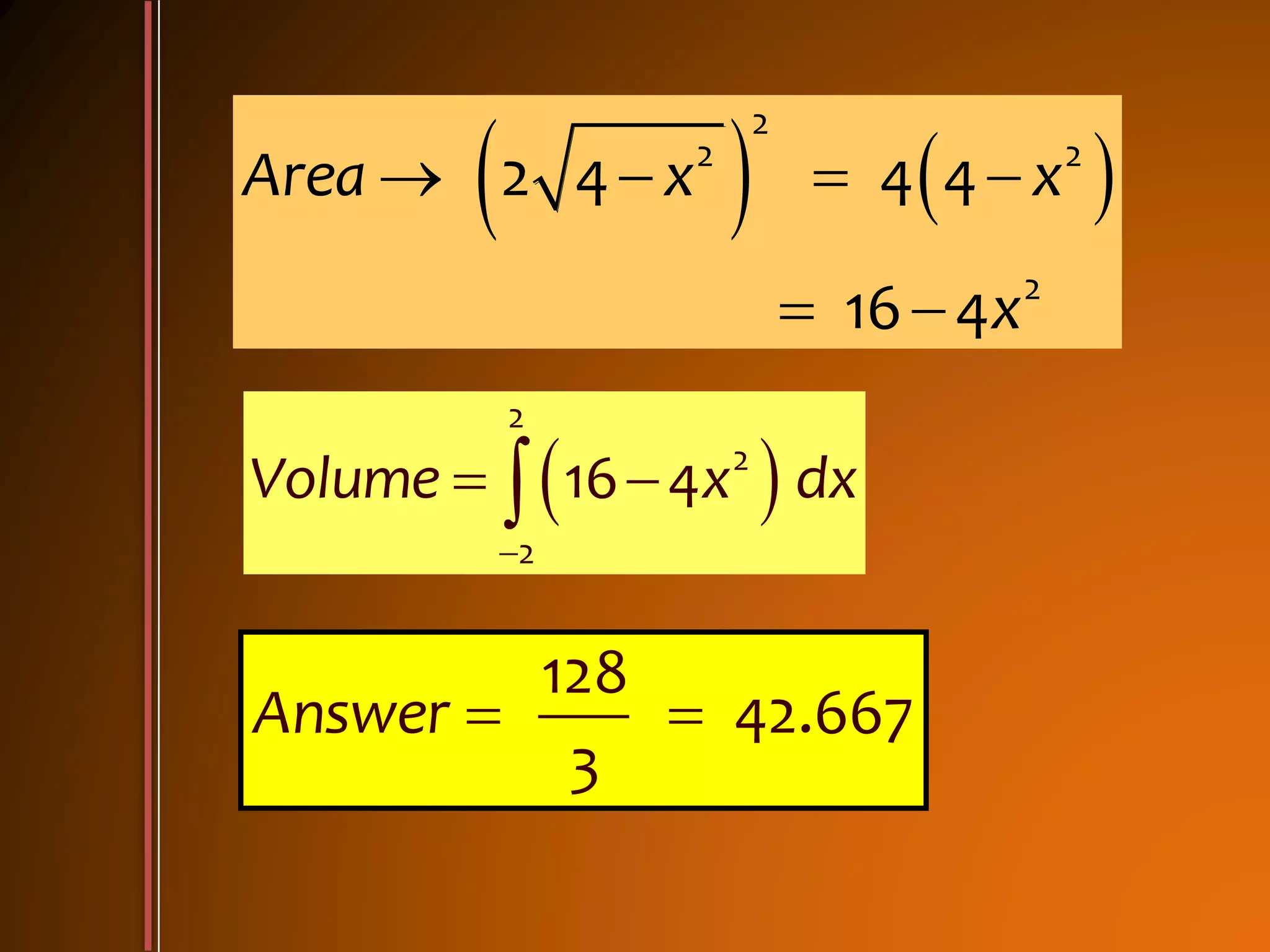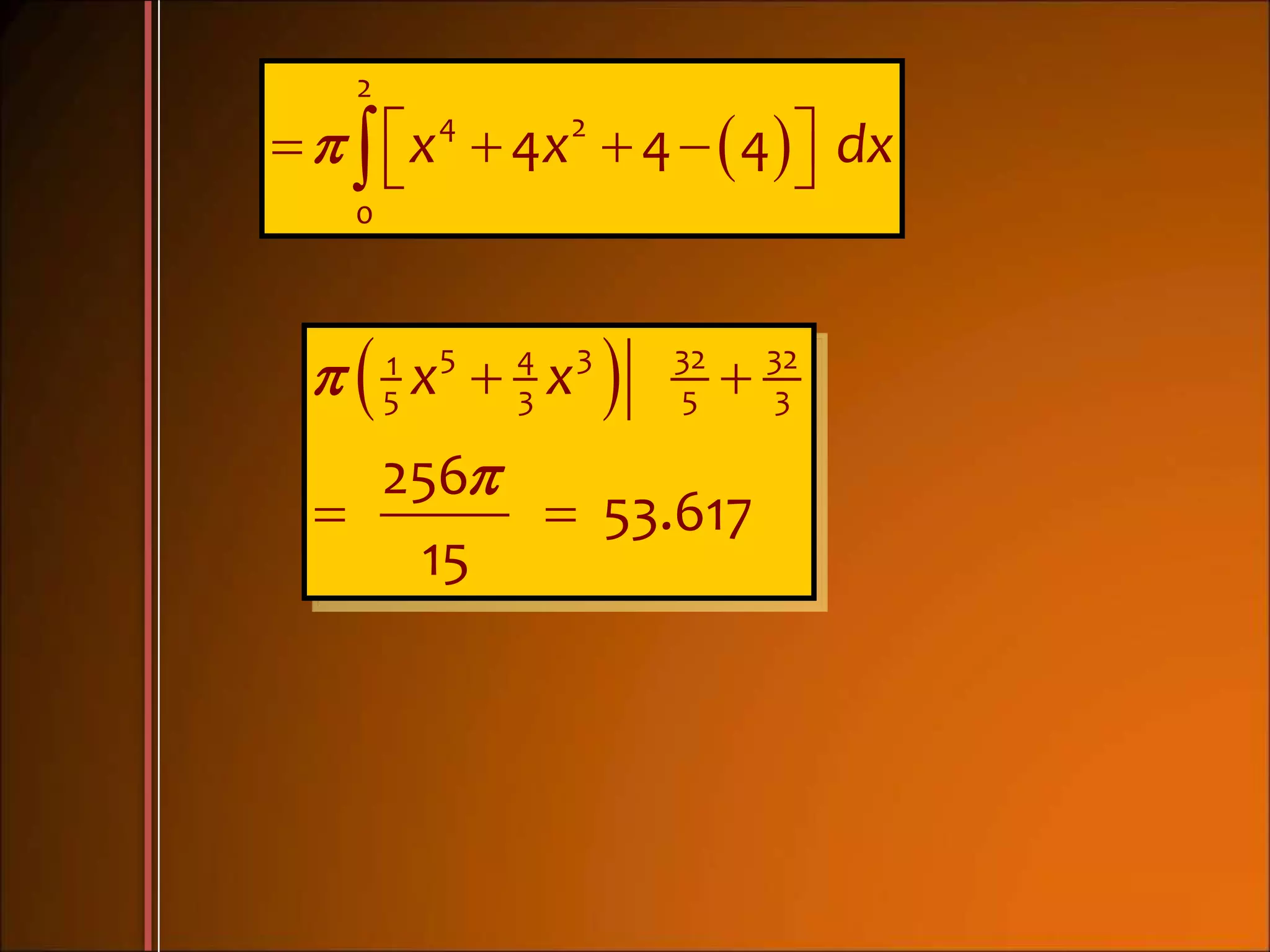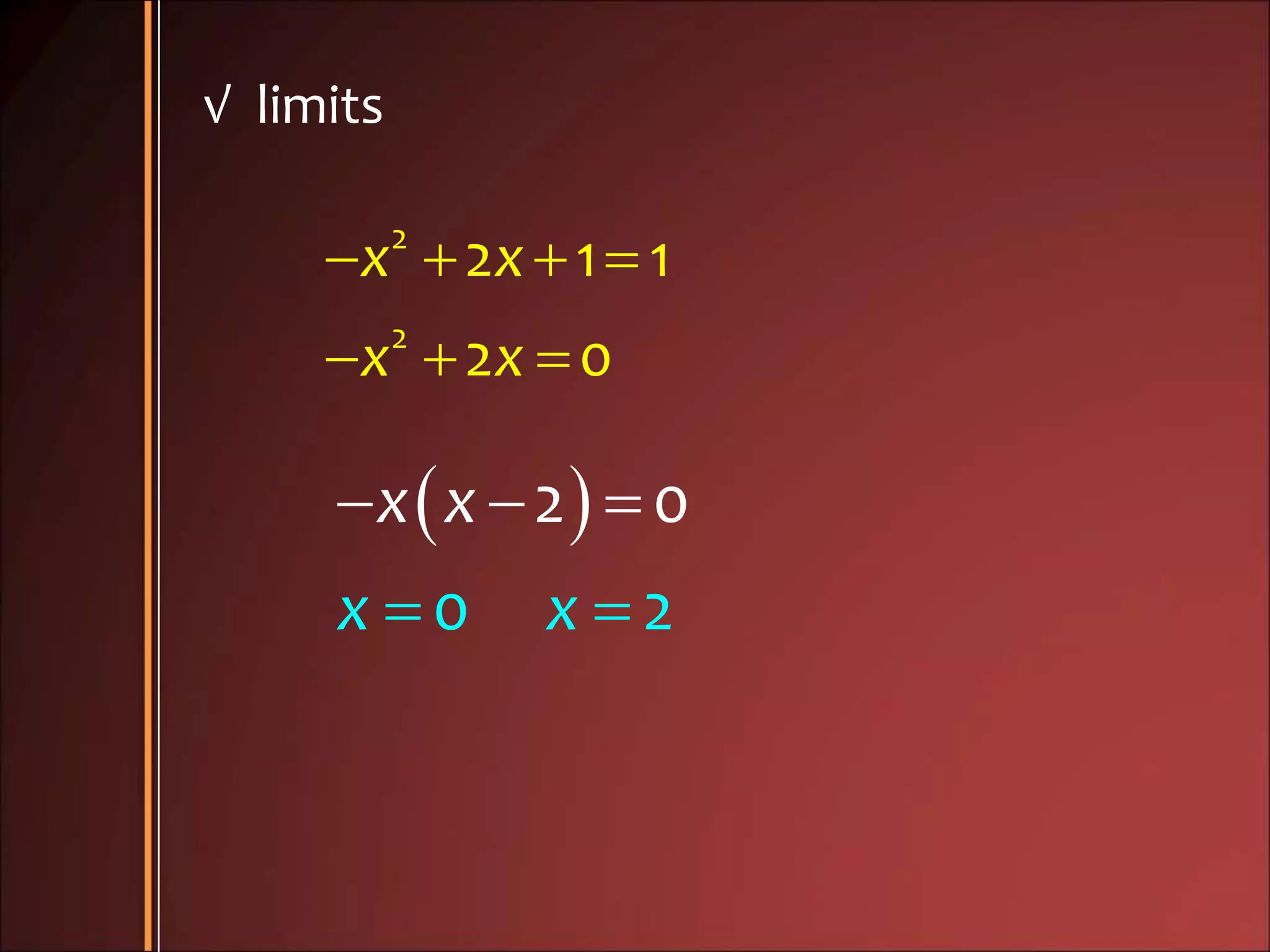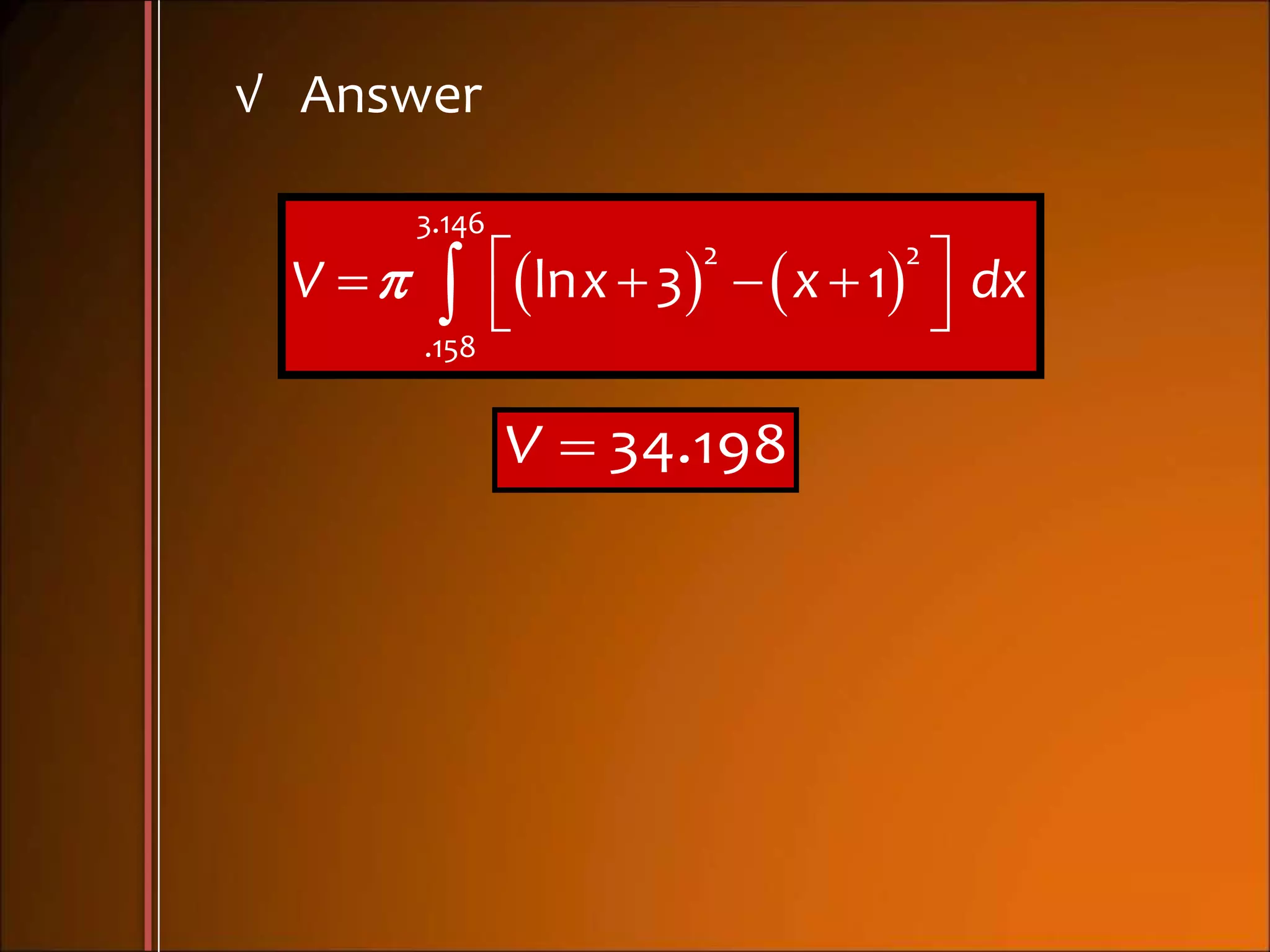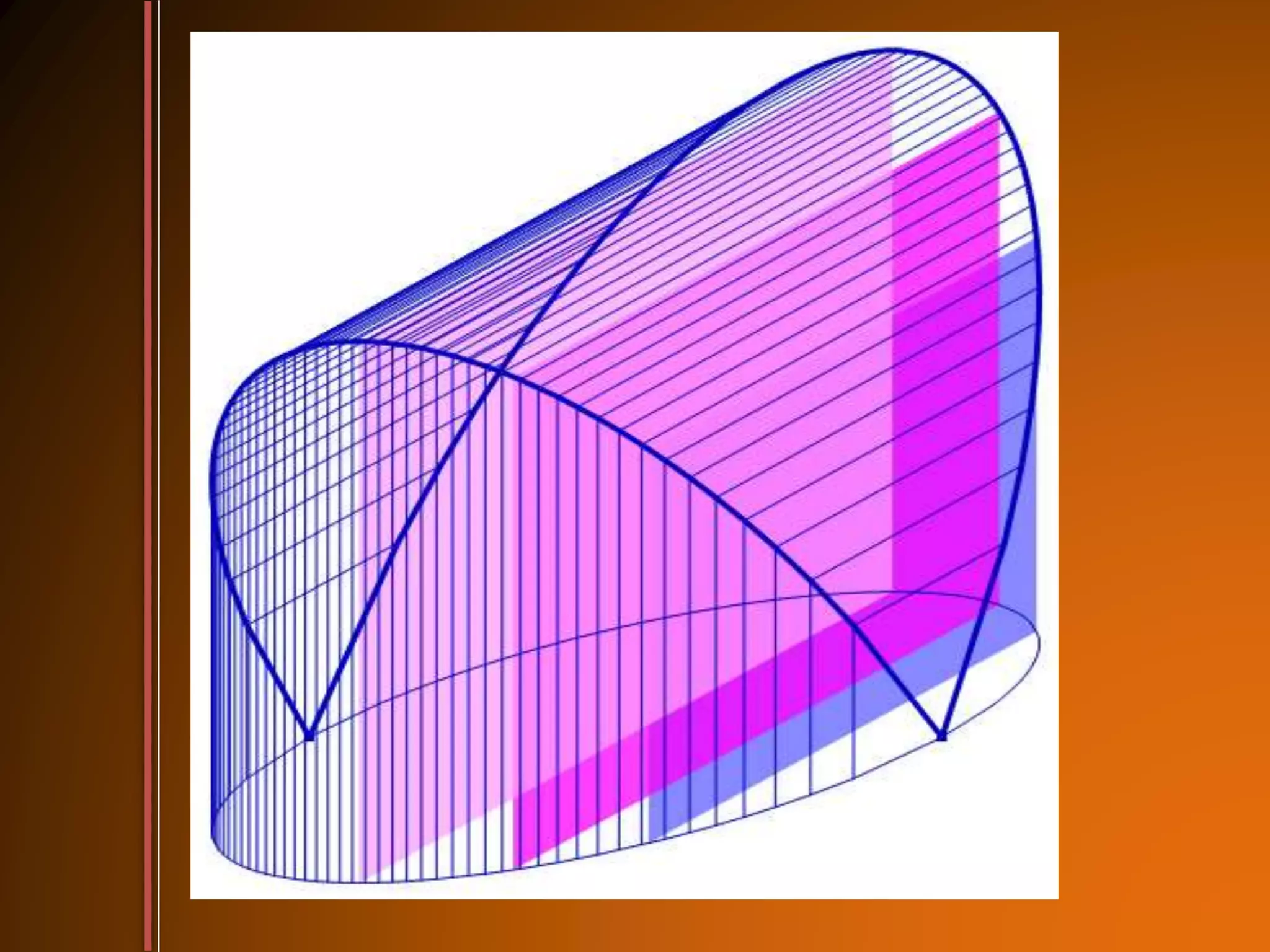
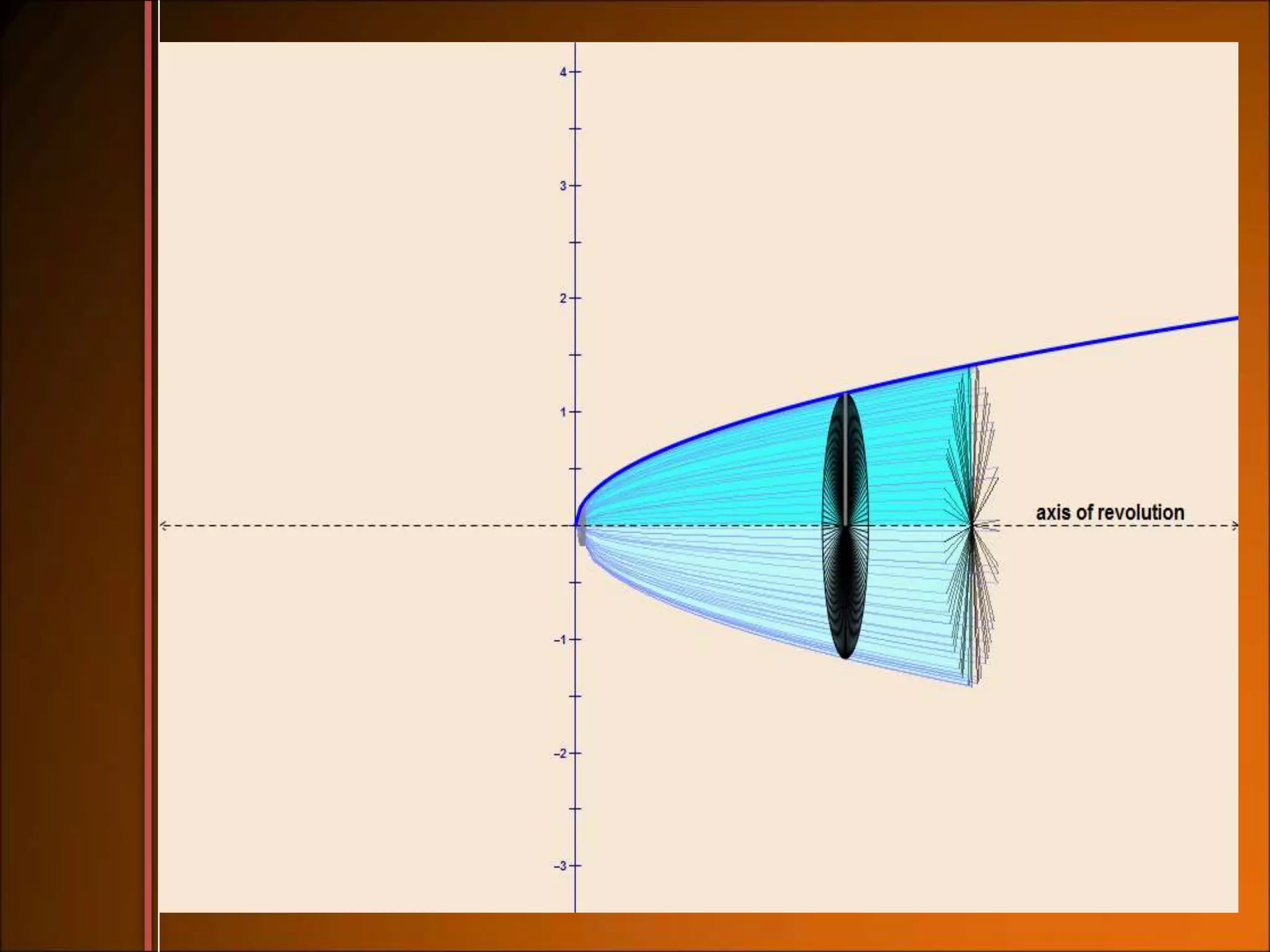
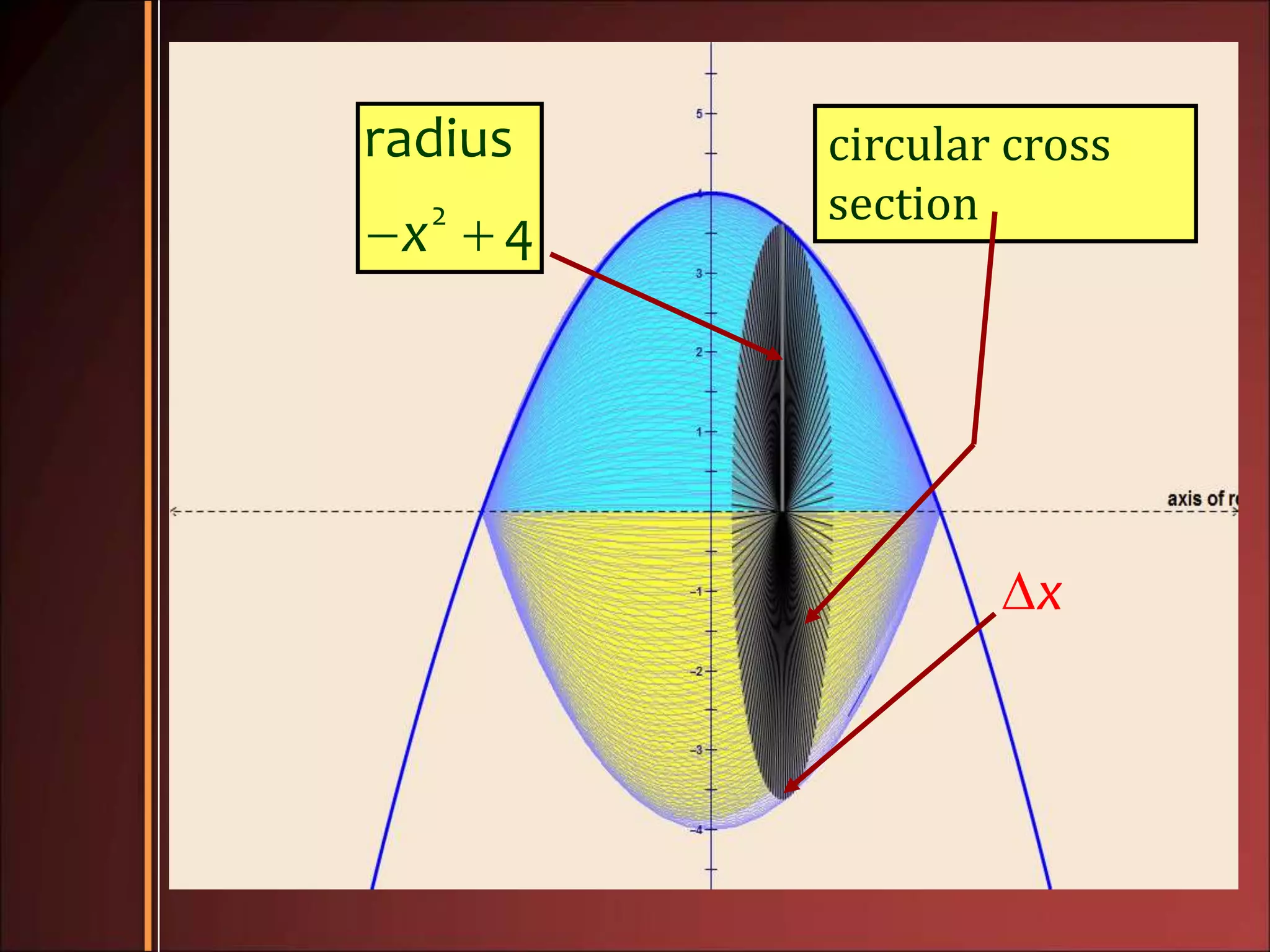
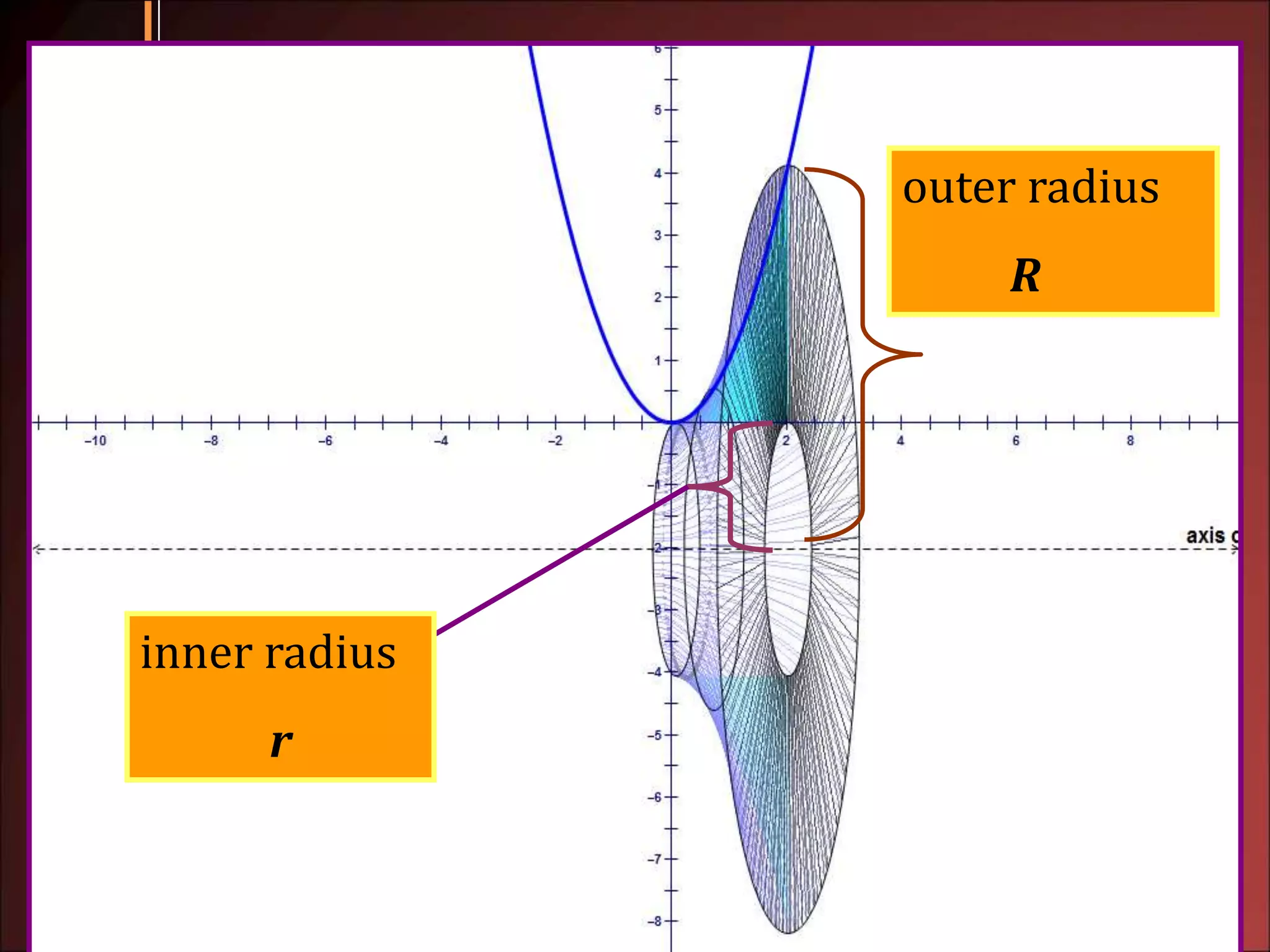
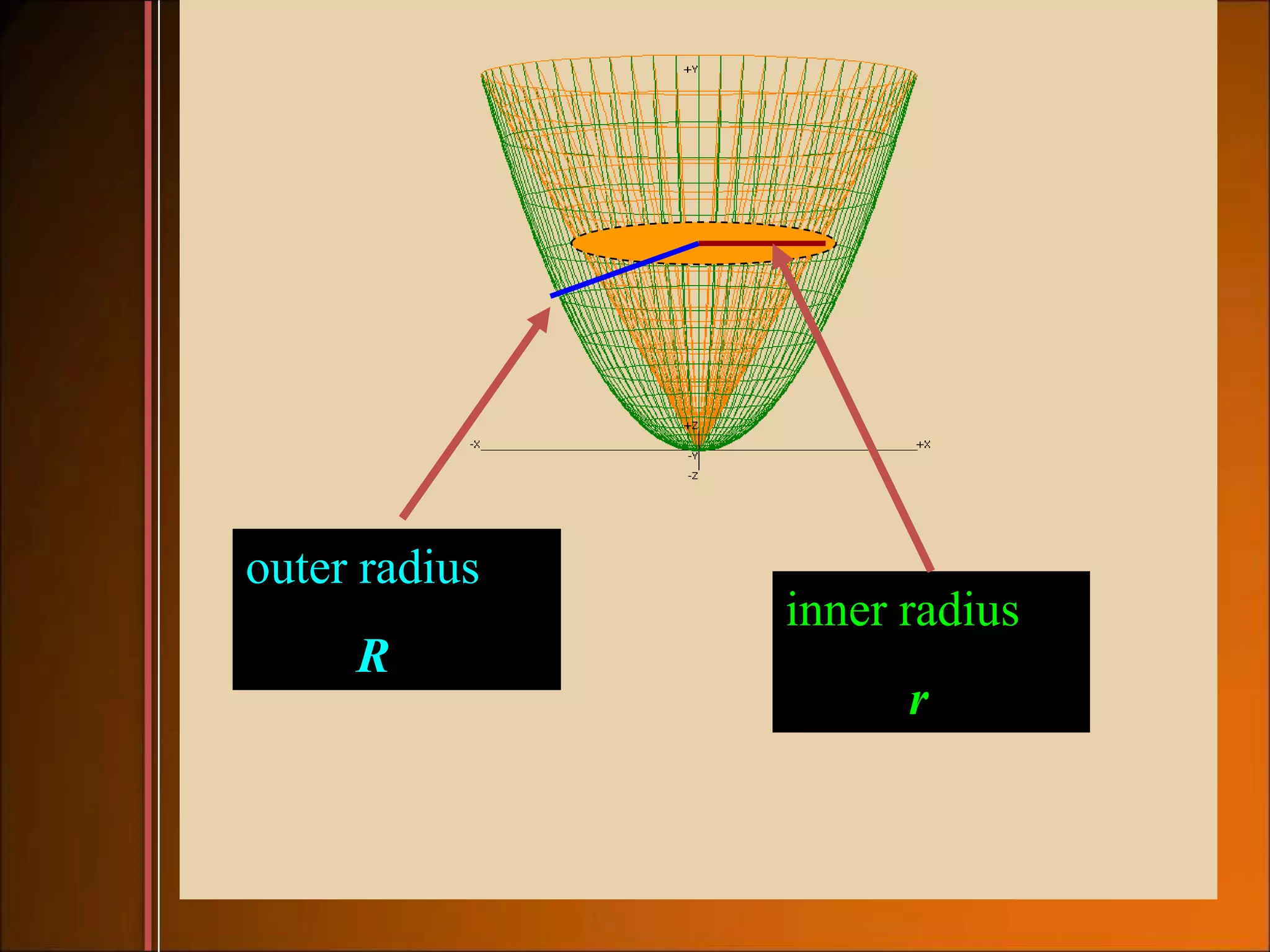
1. The document discusses several methods for calculating the volume of solids of revolution, including slicing, disk, washer, and specific examples of their use. 2. The slicing method is used when the cross sections are all the same regular shape. The disk and washer methods are used when revolving an area about an axis, with disk for solids without hollow parts and washer for solids with hollow parts. 3. Examples show how to set up the integrals to calculate volume using the appropriate method, finding radii of cross sections and limits of integration.

1. Volume
Application of
Integrals

2. Volume by Slicing
Use when given an object where you know
the shape of the base and where
perpendicular cross sections are all the same,
regular, planar geometric shape.

3. Volume of a Solid …
of known integrable cross section -
area A(x) – from a to b, defined as
 
b
a
V A x dx 

4. Procedure: volume by slicing
o sketch the solid and a typical cross
section
o find a formula for the area, A(x), of the
cross section
o find limits of integration
o integrate A(x) to get volume

5. Example
Find the volume of a solid whose
base is the circle and
where cross sections perpendicular to
the x-axis are all squares whose sides
lie on the base of the circle.
2 2
4x y 

7. First, find the length of a side of the square
the distance from the curve to the x-axis
is half the length of the side of the
square … solve for y
2 2
2 2
2
4
4
4
x y
y x
y x
 
 
 
length of a side is : 2
2 4 x

8.    
2
2 2
2
2 4 4 4
16 4
Area x x
x
   
 
 
2
2
2
16 4Volume x dx

 
128
42.667
3
Answer  

9. Example
A solid has a circular base. Find the
volume of the solid if every plane cross
section is an equilateral triangle,
perpendicular to the x-axis, given the
equation of the circle to be …
2 2
9x y 

10. Solution
2
2 9s x 
2
27 3h x 
    2 21
2 2 9 3 9A x x x   
length of a side:
height of triangle … found using
Pythagorean Theorem:
Area:
Volume:  
3
2
3
3 9 36 3 62.354V x dx

   

11. Volume of a Solid of
Revolution
A solid of revolution may be generated by
revolving the area under the graph of a
continuous, non-negative function y = f(x)
from a to b, about the x-axis
Common Examples
cone … generated by revolving the area
under a line that passes through the
origin, from 0 to k, about the x-axis

13. cylinder … generated by revolving the area
under a horizontal line of positive height
from a to b, about the x-axis

14. Example
Look at the region between the curve
and the x-axis, from x = 0 to
x = 2, and revolve it about the x-axis
y x

15. If we slice the resulting solid
perpendicular to the x-axis, each cross
section is a circle, or disk
The radius of the circle is the distance
from the curve to the axis of rotation
Area of a cross section (circle)
   
2
2
/ radiuscircleA r x
A x xx


 
 

17. The thickness of each disk is infinitely
small, so it is represented as dx. By
adding the area of all these circles, from
x=0 to x=2, we would get the volume of
the solid.
 
2
0
21
2
...
2 0
2
V A x dx V x dx
x





 

 

18. Disk Method
2
r
radius is always perpendicular to the
rotational axis
rotational solid with no hollow parts
will always have a circular cross
section, with area
use as long as there is NO hollow
space
Formula:  
2
b
a
V f x dx   

19. Example: Disk Method
Rotate the area bounded by
and the x-axis, about the x-axis; then
calculate the volume
  2
4f x x  
Calculus Applet
Volumes of Revolution

20. x
circular cross
section2
radius
4x 

21. Solution
  
2
4 0
2 2 0
2 2
x
x x
x x
  
  
  
√ Find limits of integration
√ Find radius of cross section
2
4r x  

22. √ Volume
 
2
22
2
4V x dx

  
512
107.233
15

 

23. Example: Disk Method
Find the volume generated by rotating
the area in the first quadrant bounded by
the curve, the y-axis, and the line y = 9,
around the y-axis.
  2
curve: f x x
Use y as variable of integration
Calc Applets Volumes of Revolution

24. circular cross
section
radius
y

25. Solution
x y
    
9
2
0
V y dy
√ limits
from y = 0 to y = 9
√ radius
√ Answer


81
2

26. Washer Method
used when solid has hollow parts
radius of rotation – perpendicular to
the axis of rotation
two radii - outer and inner
Formula
R » outer radius r » inner radius
        
 
2 2
b
a
V R x r x dx

27. Example: Washer
Method
Find the volume of the solid when
is rotated about the line y = -2, from
x=0 to x=2
 2
y x

28. outer radius
R
inner radius
r

29. Solution
Find outer and inner radii
outer - curve furthest away from
the axis of rotation; subtract
from this, the axis of rotation
  
 
2
2
2
2
x
x

30. inner - inside curve, forms the
hollow wall of the solid
   
 

0 2
0 2
2
r
       
  
2
2 22
0
2 2V x dx

31.        
2
4 2
0
4 4 4x x dx
 

 
 
5 3 32 3241
5 3 5 3
256
53.617
15
x x

32. Example: Washer
Method
Find the volume of the solid of
revolution generated by revolving about
the y-axis, the area enclosed by the
graphs of   2
2 andy x y x

33. outer radius
R
inner radius
r

34. Solution

 
2
2
2
2 0
x x
x x
√ solve for limits
 
   
 
 
ordered pa
2 0
0 an
irs: 0,0
d
and 2,
2
4
x x
x x

35. √ to revolve about the y-axis, need to
solve each equation for x
 
1
and
2
x y x y
√ radii - in relation to the y-axis, the
outer radius is and the inner
radius is
x y

1
2
x y

36.    

  
  


4
2 21
2
0
8
3
V y y dy

37. Example: Washer Method
Consider the area captured between the
graphs of     2
2 1 and 1y x x y
What volume is generated if this area is
rotated about the x-axis ?

39. √ limits
   
  
2
2
2 1 1
2 0
x x
x x
 

 
0
2 0
2x
x
x
x

40. √ radii
    2
2 1 1R x x r
√ answer
         
  
2
2 22
0
2 1 1V x x dx

 
56
11.729
15

41. Example: Washer Method
Find the volume of the solid generated
when the region bounded by
  ln and 2y x y x
is rotated about the line y = -3

43. √ limits
Only way is to obtain from graphing
calculator …
   3.146, 1.146 .158, 1.841
√ radii
 
 
    
     
ln 3 ln 3
2 3 1
R x x
r x x

44. √ Answer
        
 
3.146
2 2
.158
ln 3 1V x x dx
 34.198V