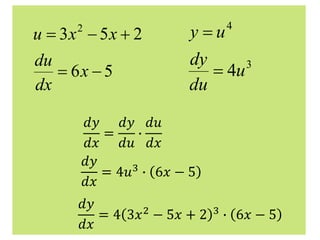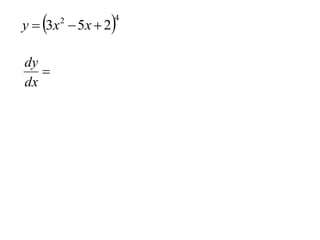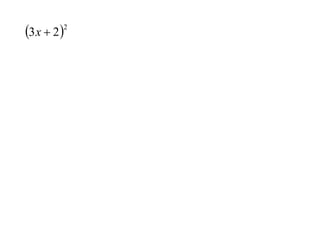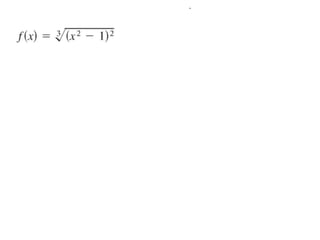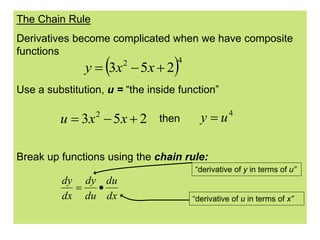
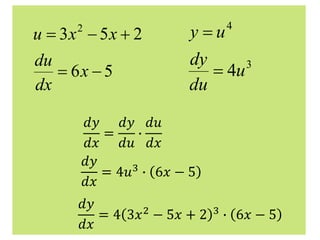
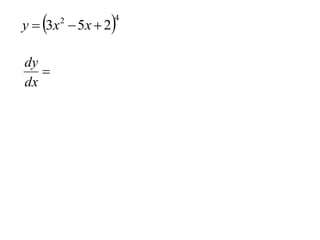
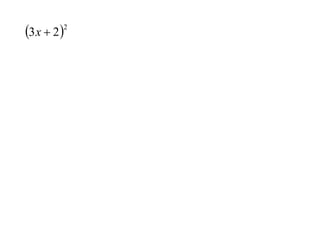
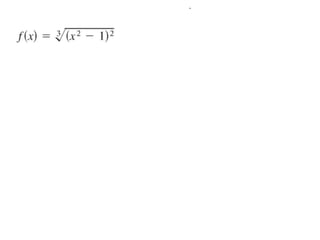
The document discusses the chain rule for taking derivatives of composite functions. It explains that the chain rule allows you to break down composite functions into their constituent parts. The chain rule states that the derivative of the outside function is the derivative of the inside function multiplied by the derivative of the inside with respect to the outside. The document provides an example of using the chain rule to take the derivative of a polynomial function composed of simpler functions. It also notes that the general power rule can be used to take derivatives when the outside function is a power and the inside is a differentiable function.

1. Warm-up
Find the derivative of the following:
1)
2)
3)
13
2
x
 2
23 x
x2
sin

2. Lesson 4.1
The Chain
Rule

3. The Chain Rule
Derivatives become complicated when we have composite
functions
Use a substitution, u = “the inside function”
then
Break up functions using the chain rule:
253 2
 xxu
dx
du
du
dy
dx
dy

“derivative of y in terms of u”
“derivative of u in terms of x”
 42
253  xxy
4
uy 

4. 56
253 2


x
dx
du
xxu
3
4
4u
du
dy
uy


𝑑𝑦
𝑑𝑥
=
𝑑𝑦
𝑑𝑢
∙
𝑑𝑢
𝑑𝑥
𝑑𝑦
𝑑𝑥
= 4𝑢3
∙ 6𝑥 − 5
𝑑𝑦
𝑑𝑥
= 4 3𝑥2
− 5𝑥 + 2 3
∙ 6𝑥 − 5

5. Steps:
1) Set u equal to an “inner” function
2) Rewrite original function in terms of u
3) Derive u in terms of x and y in terms of u
4) Plug derivatives into chain rule
5) Simplify
Function form:
        xgxgfxgf
dx
d


6.  42
253  xxy

dx
dy

7. Example 1 Find the derivatives of the warm-ups using the chain rule
13
2
x

8.  2
23 x

9. x2
sin

11. Since polynomials are prevalent we come up with a
general power rule:
derivative of outside function times derivative of
inside function

dx
dy

12. Example 1 Find the derivative

14. Copyright © 2007 Pearson Education, Inc. Publishing as Pearson Prentice Hall
Slopes of Parametrized Curves
    A parametrized curve , is if
and are differentiable at .
x t y t differentiable at t
x y t

15. Copyright © 2007 Pearson Education, Inc. Publishing as Pearson Prentice Hall Slide 3- 15
Finding dy/dx Parametrically
If all three derivatives exist and 0,
dx
dt
dy
dy dt
dxdx
dt

