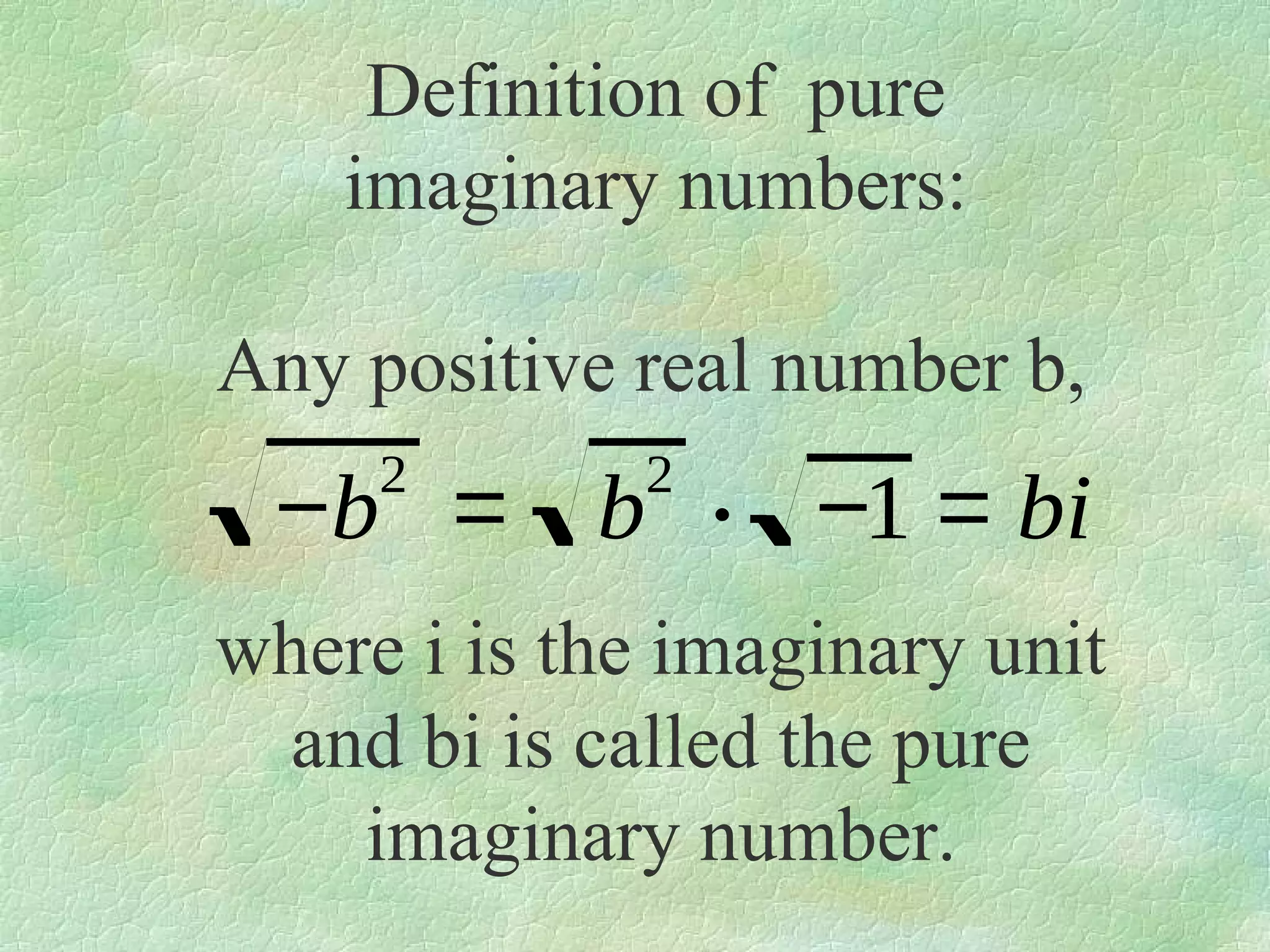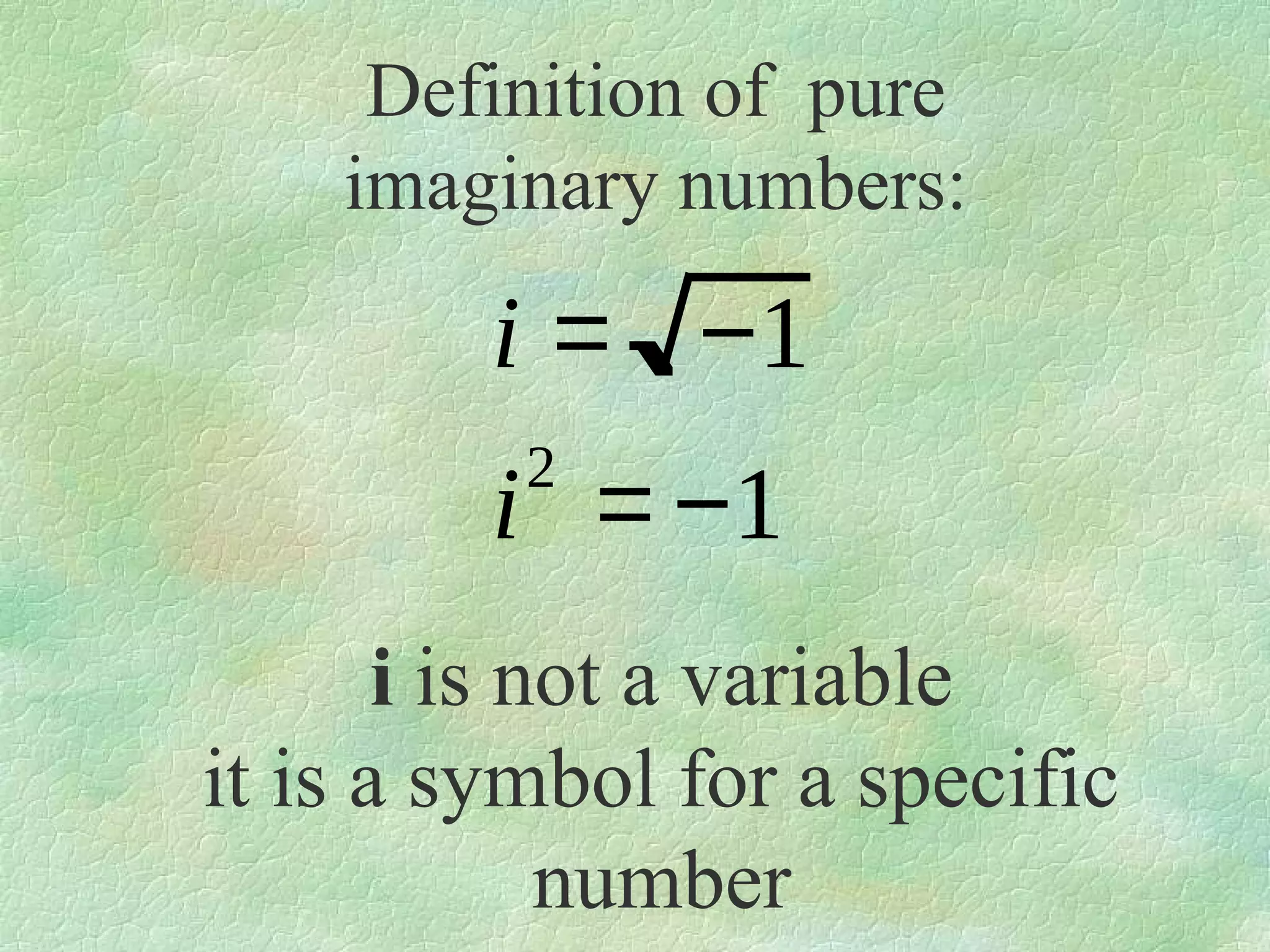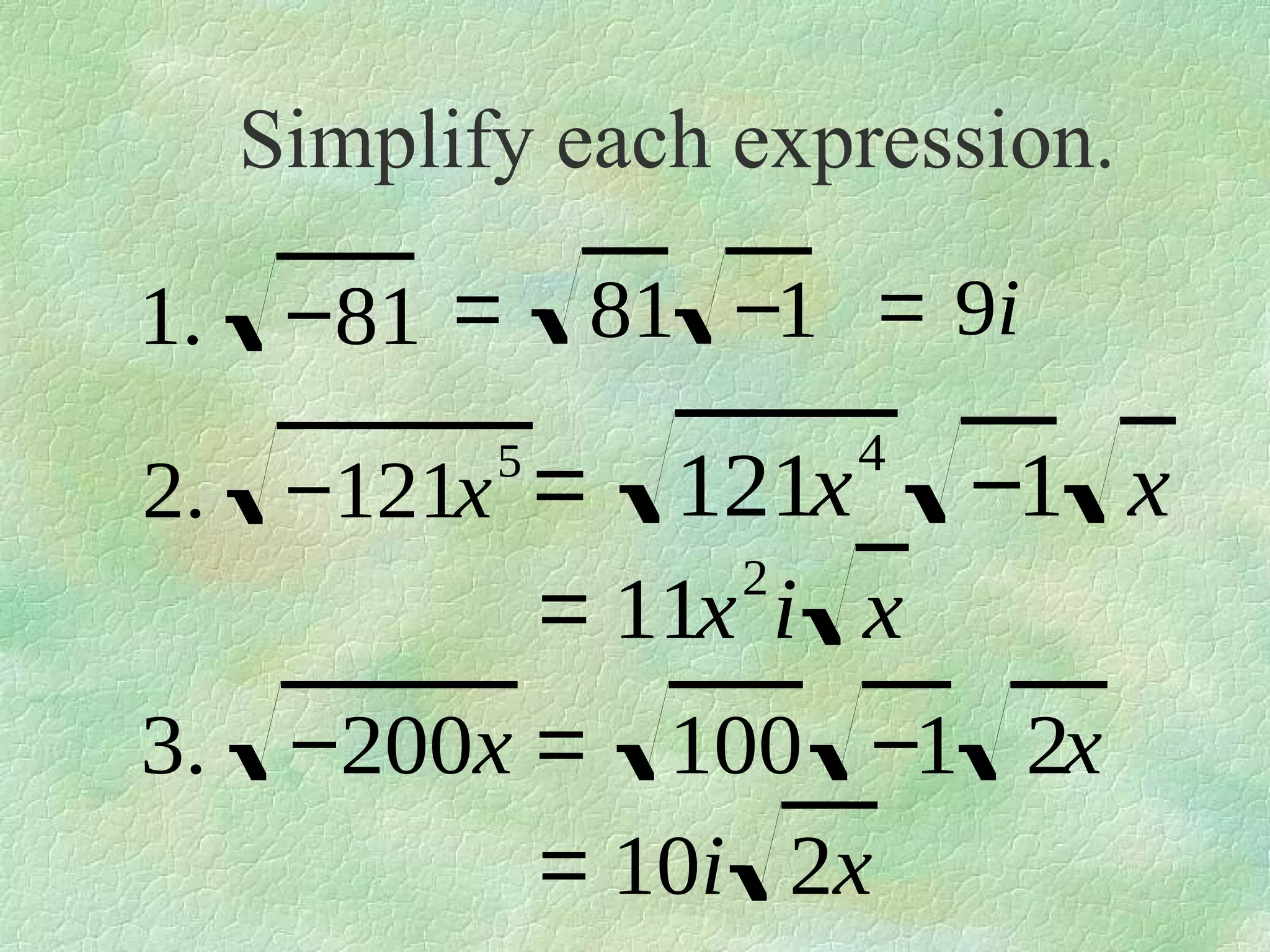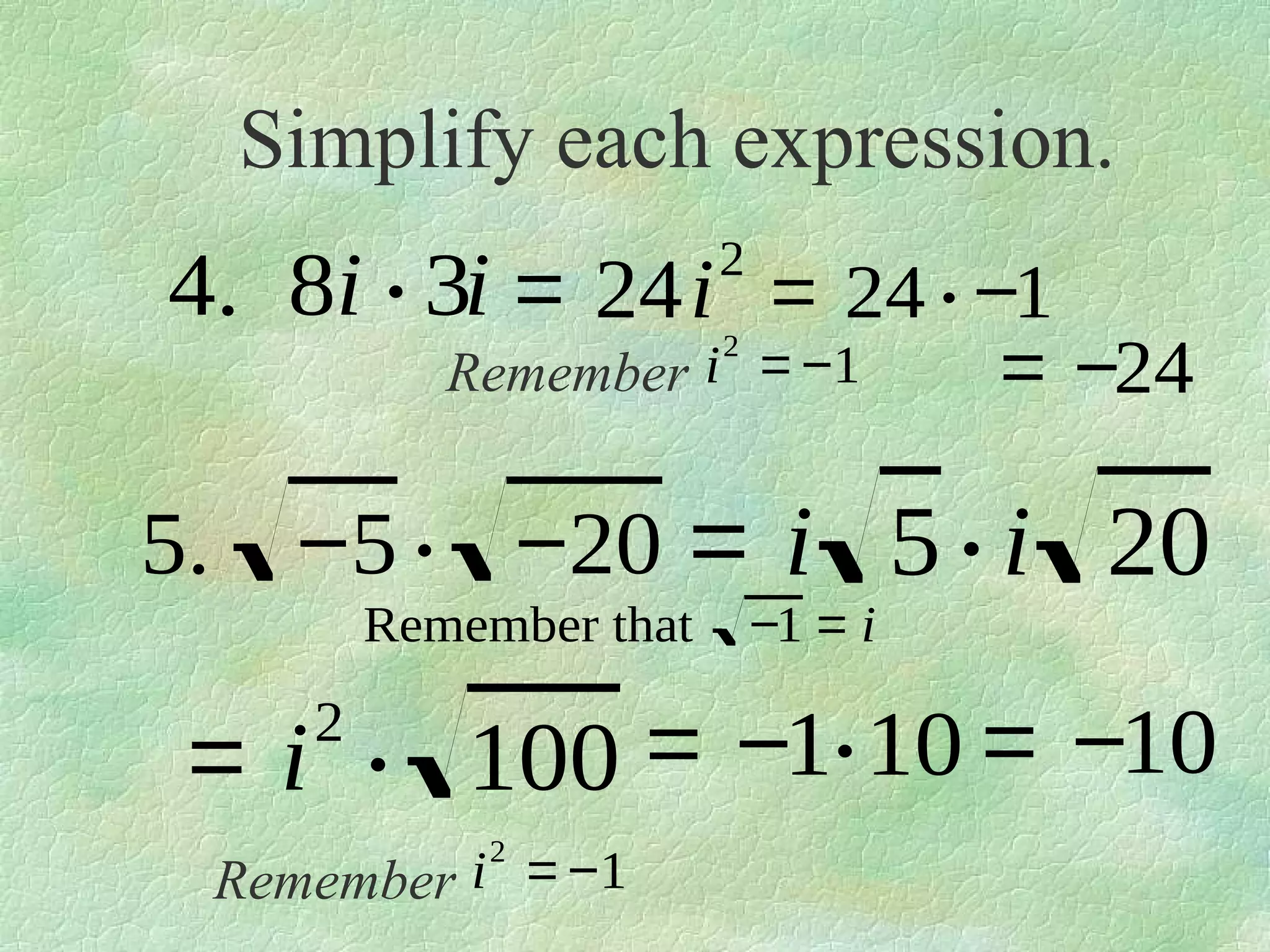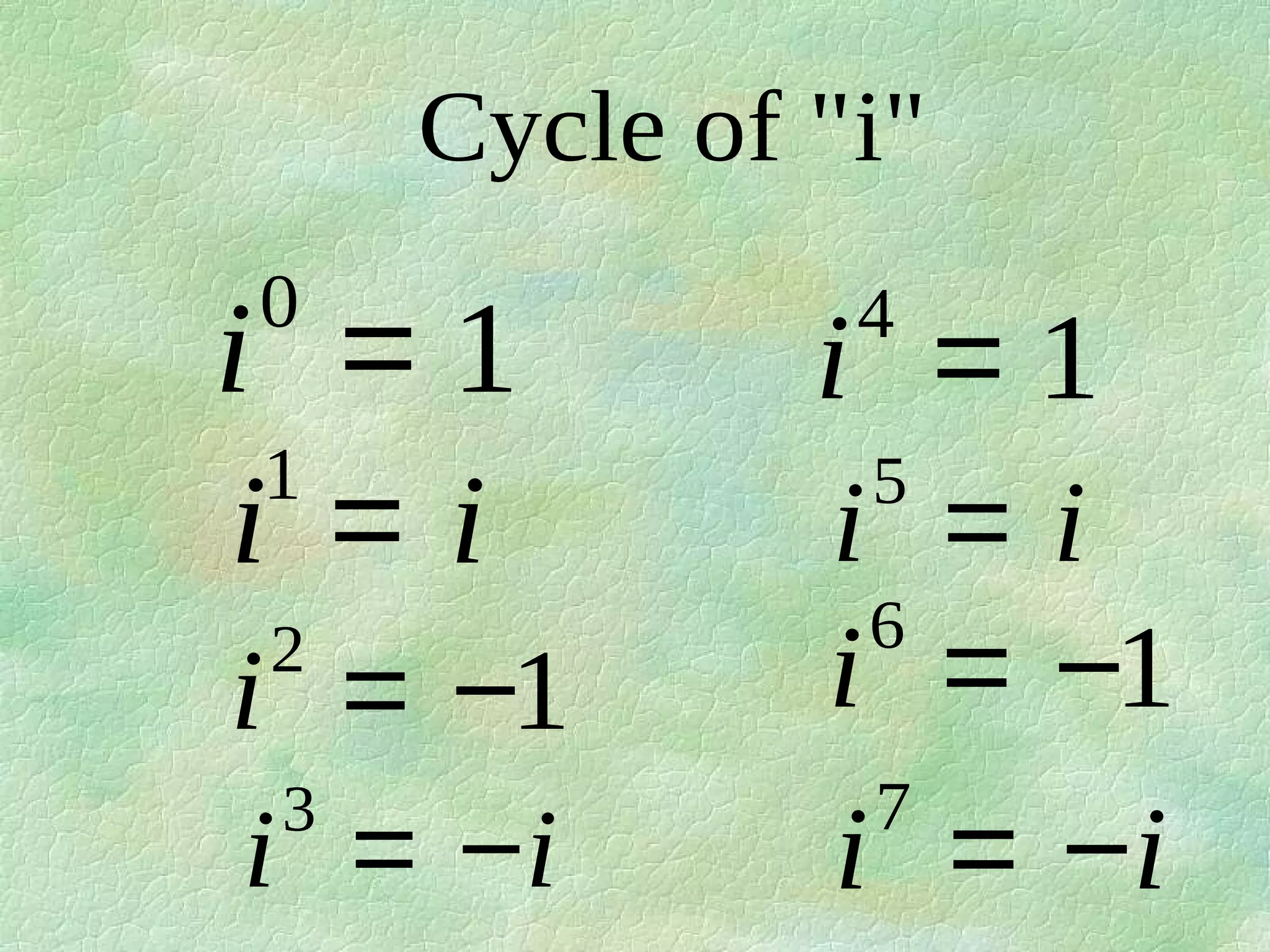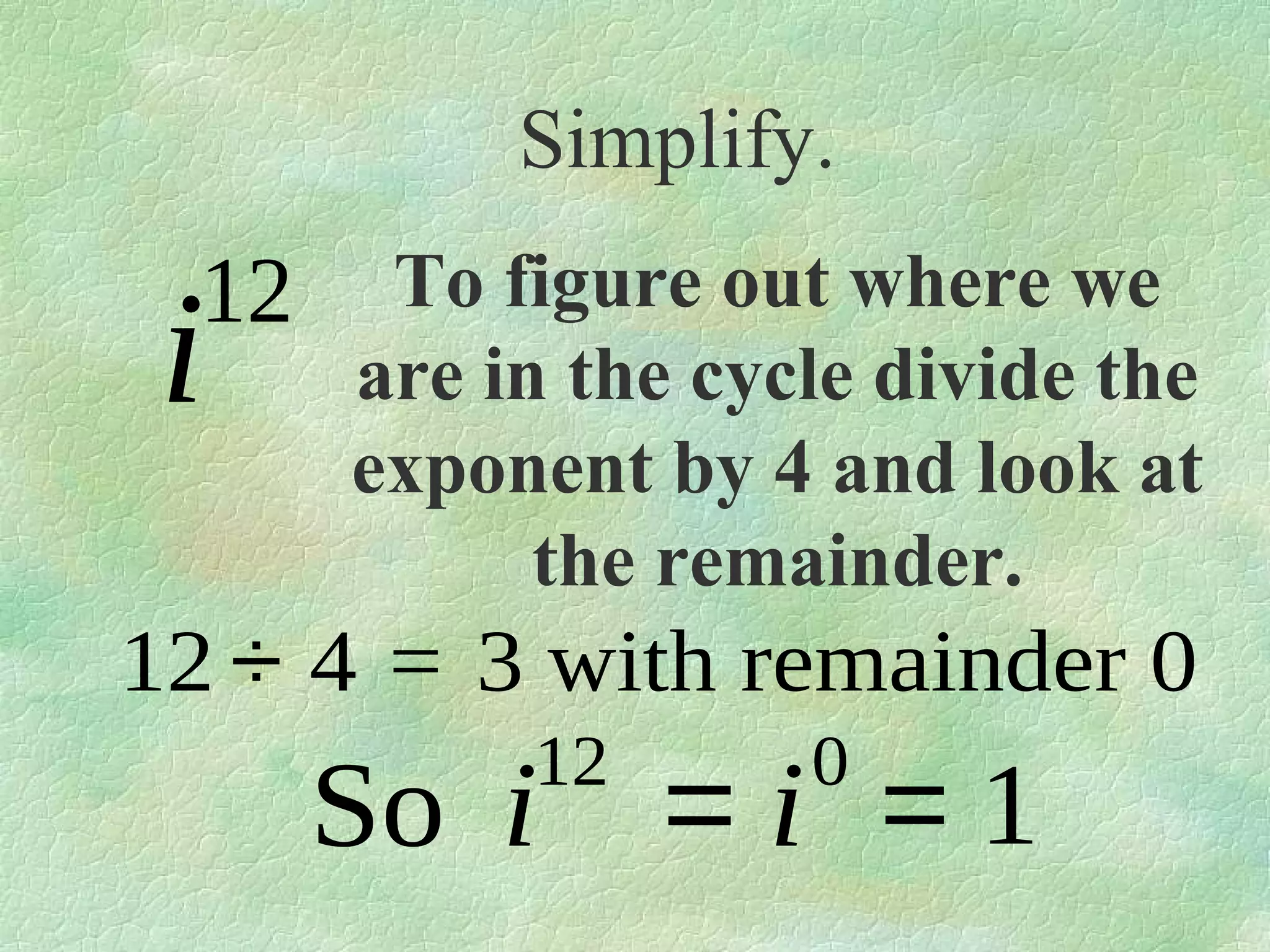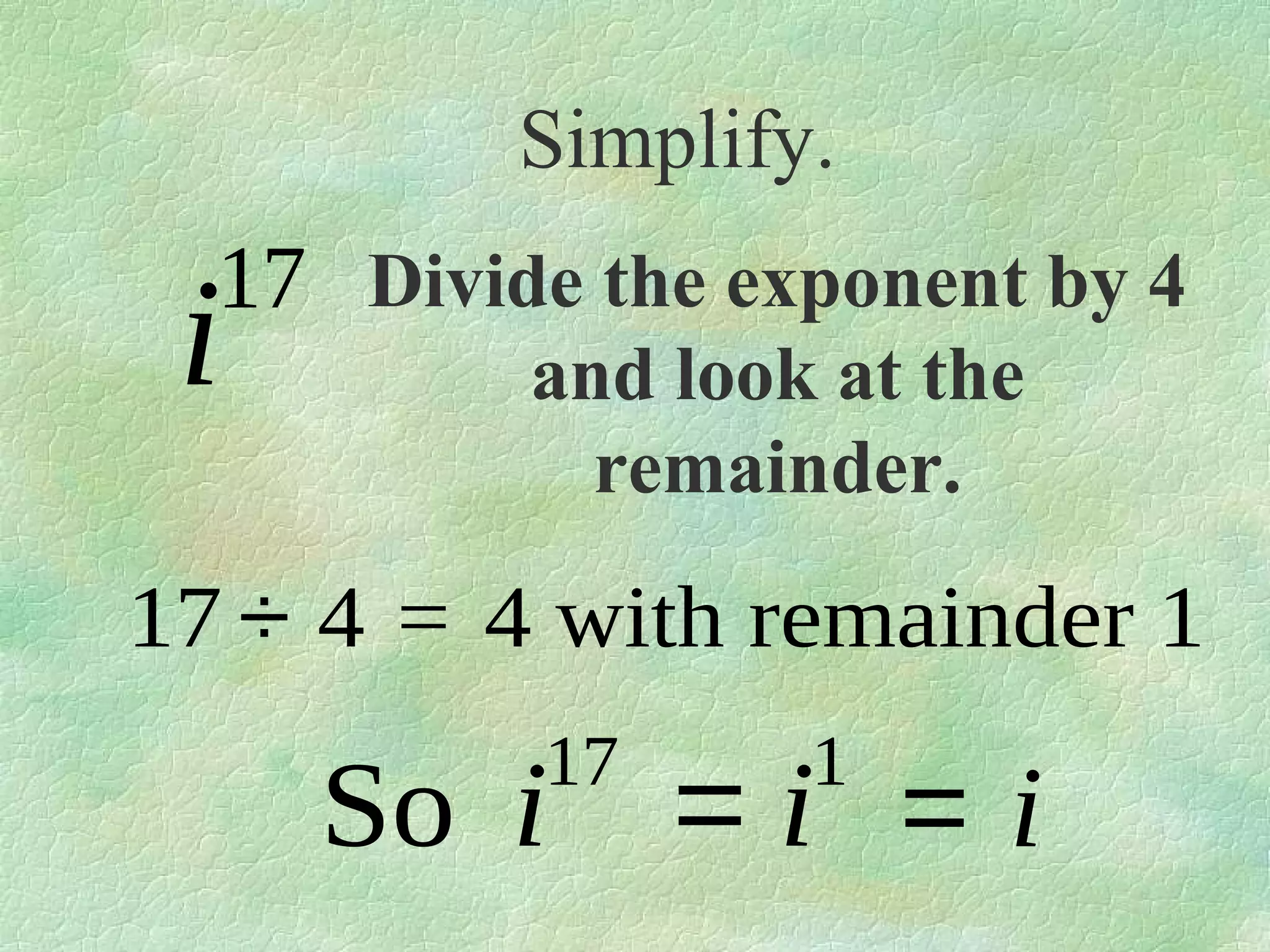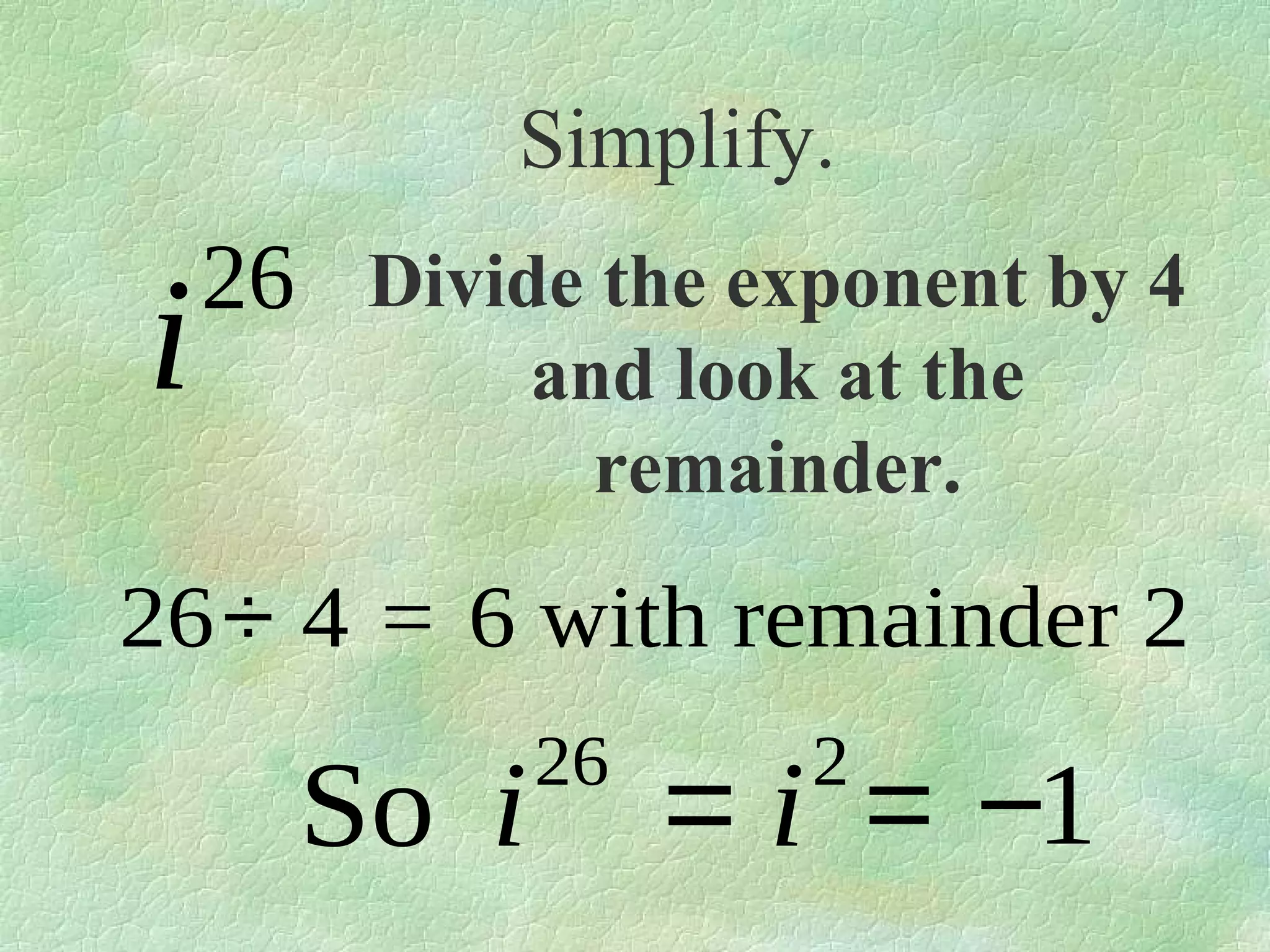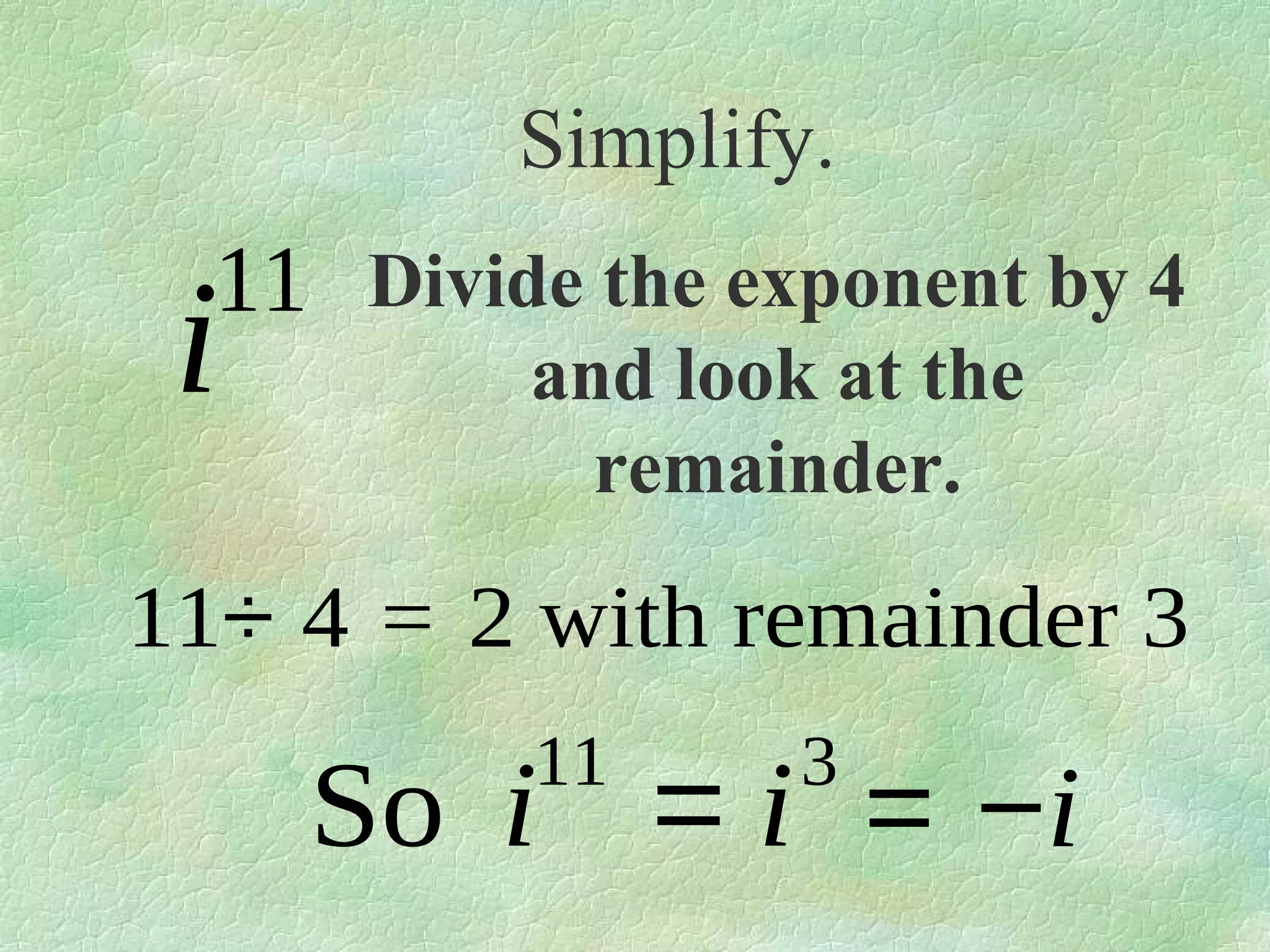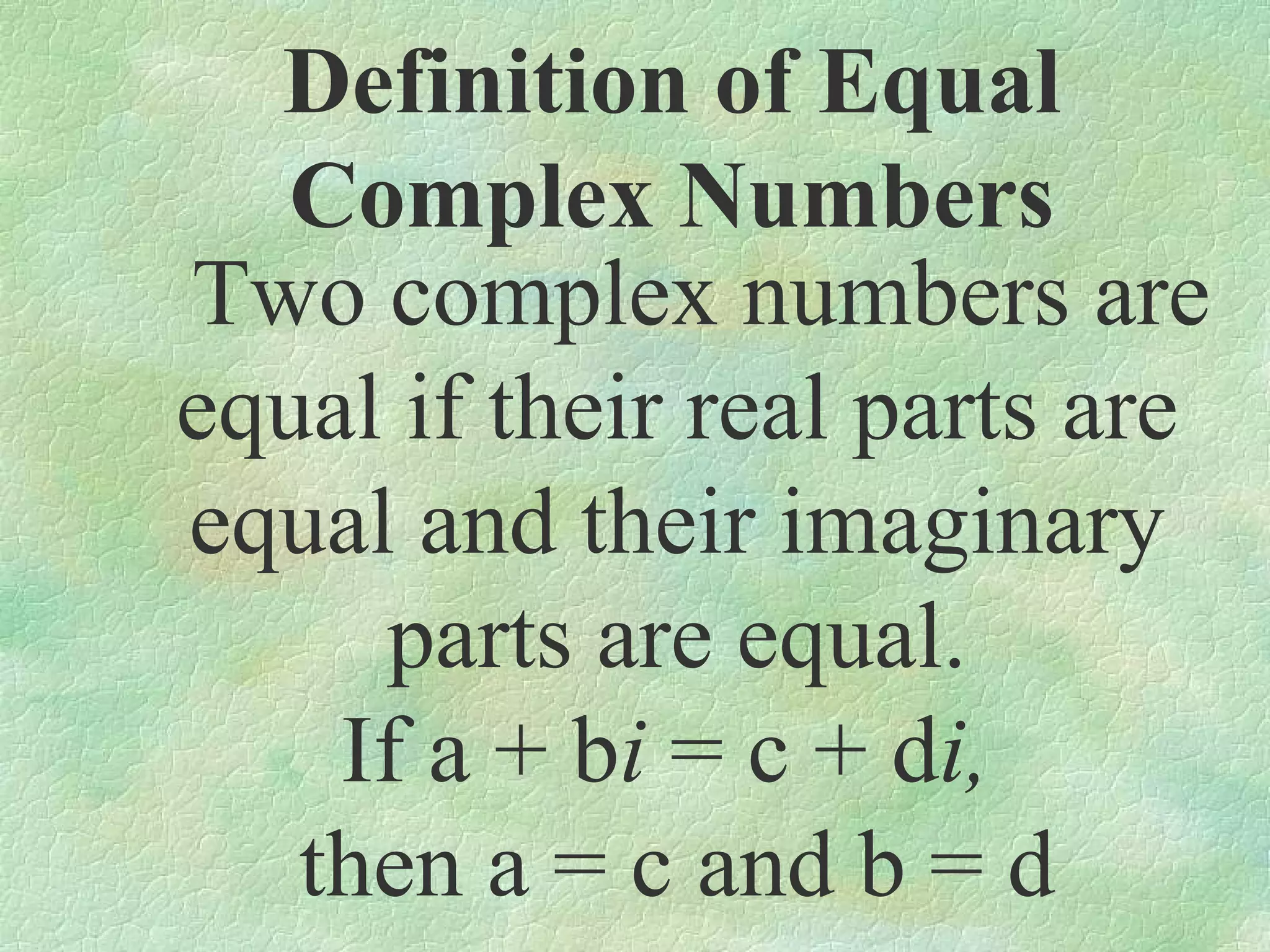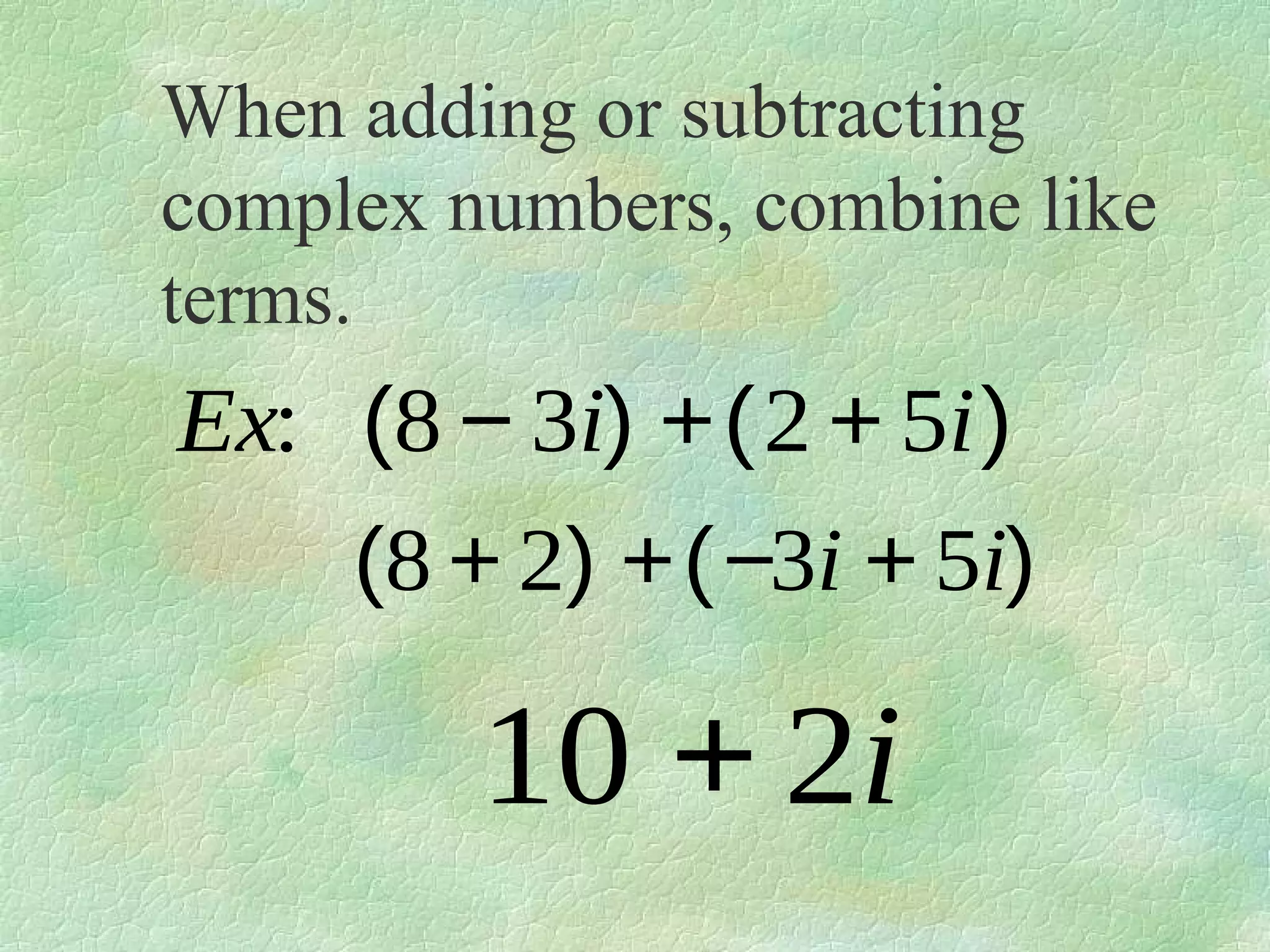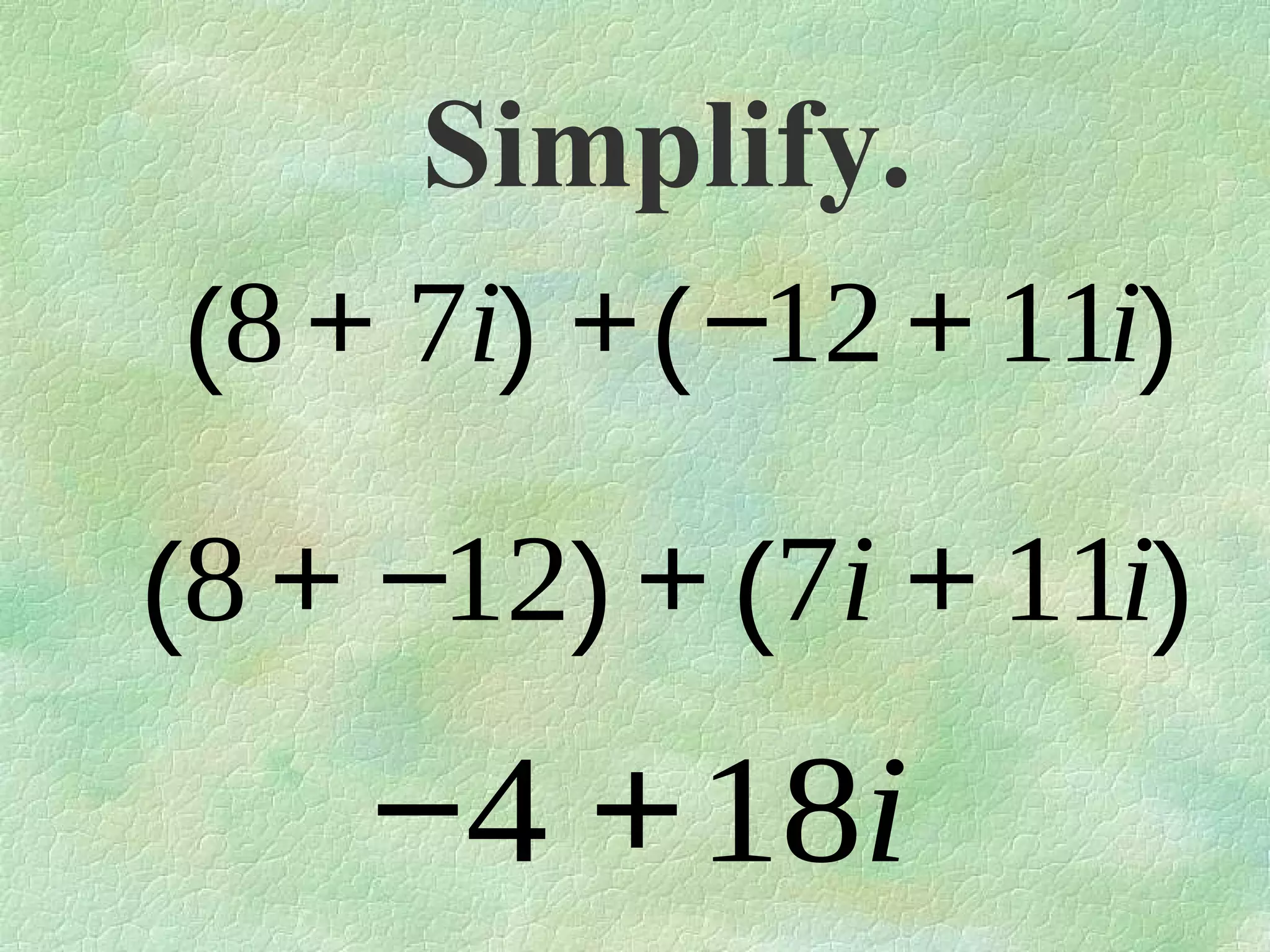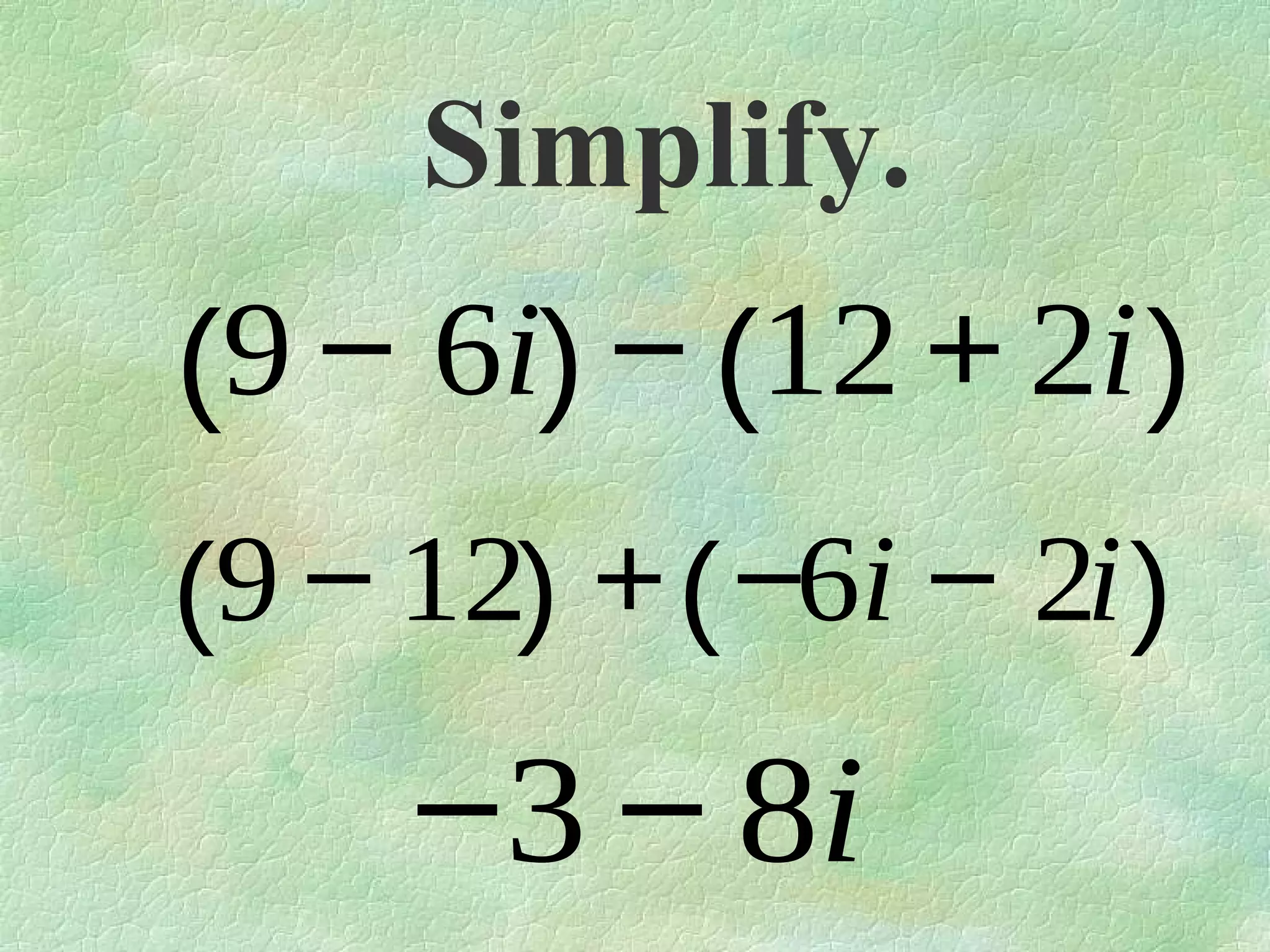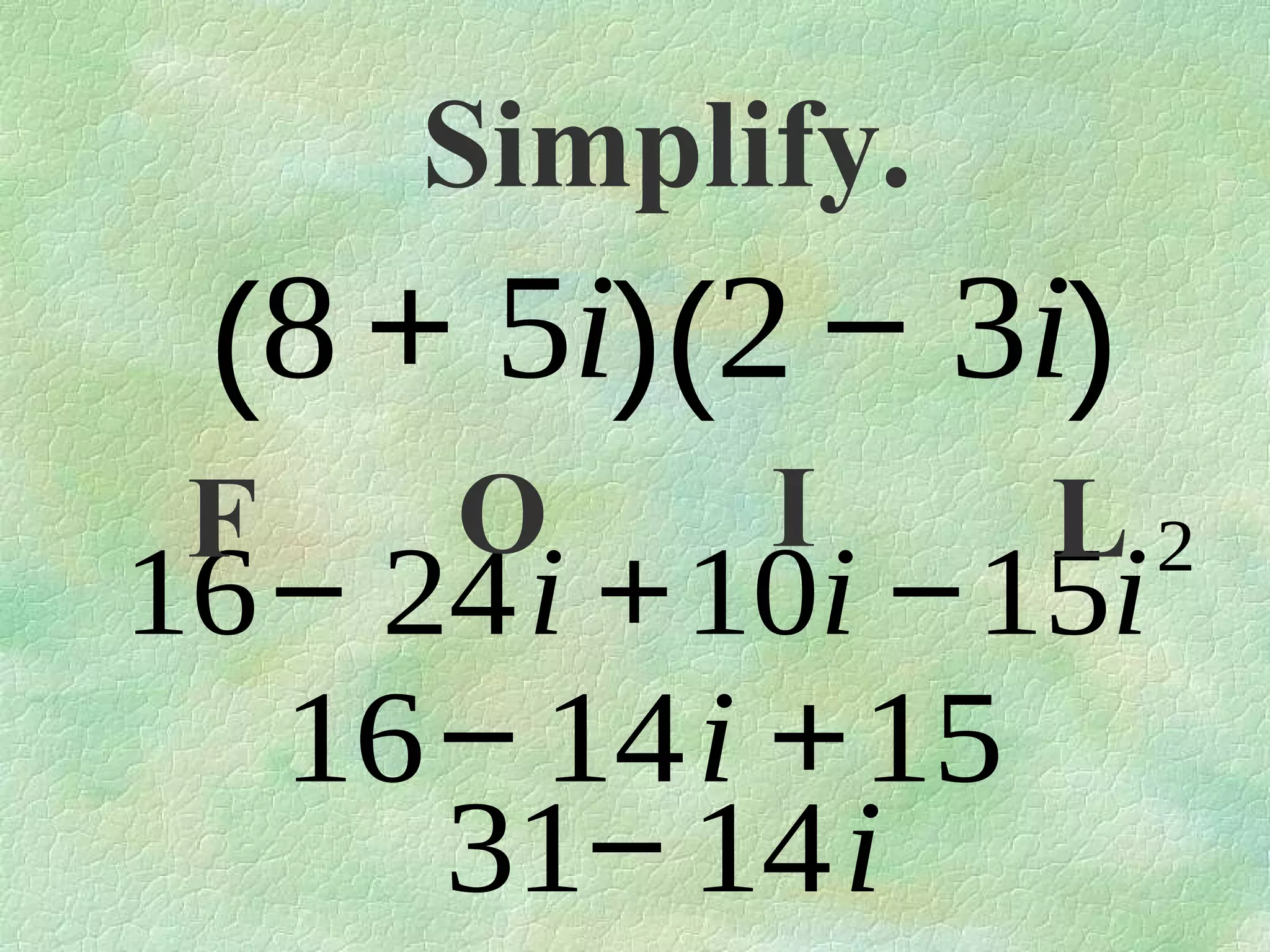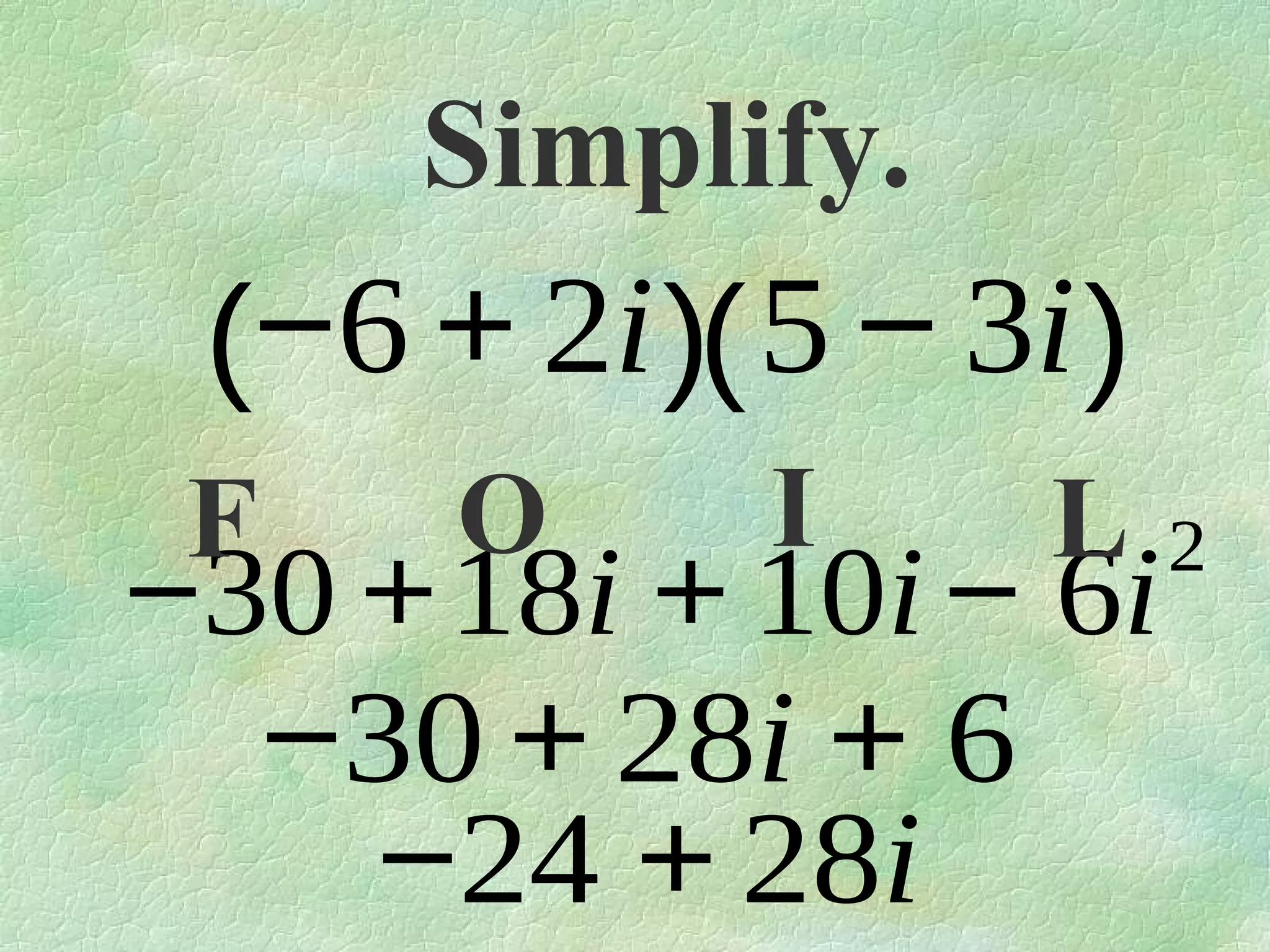The document discusses complex numbers. It begins by defining pure imaginary numbers as any positive real number b multiplied by the imaginary unit i, where i^2 = -1. It then defines i as the square root of -1. The document proceeds to simplify various expressions involving complex numbers. It introduces the concept of a cycle of i where the value repeats every 4 exponents. It defines complex numbers as numbers in the form a + bi, where a and b are real numbers. The document concludes by showing how to add, subtract, and multiply complex numbers by distributing like terms.

1. Complex Numbers

2. Definition of pure
imaginary numbers:
Any positive real number b,
−b = b ⋅ −1 = bi
2
2
where i is the imaginary unit
and bi is called the pure
imaginary number.

3. Definition of pure
imaginary numbers:
i = −1
2
i = −1
i is not a variable
it is a symbol for a specific
number

4. Simplify each expression.
81 −1 = 9i
1. −81 =
2. −121x =
5
4
121x −1 x
2
= 11x i x
3. −200x = 100 −1 2x
= 10i 2x

5. Simplify each expression.
4. 8i ⋅ 3i = 24i = 24 ⋅ −1
2
2
Remember i = −1
= −24
5. −5 ⋅ −20 = i 5 ⋅ i 20
Remember that
−1 = i
= i ⋅ 100 = −1⋅10 = −10
2
2
Remember i = −1

6. Cycle of "i"
0
i =1
1
i =i
2
i = −1
3
i = −i
4
i =1
5
i =i
6
i = −1
7
i = −i

7. Simplify.
12
i
To figure out where we
are in the cycle divide the
exponent by 4 and look at
the remainder.
12 ÷ 4 = 3 with remainder 0
12
So i
0
=i =1

8. Simplify.
17 Divide the exponent by 4
i
and look at the
remainder.
17 ÷ 4 = 4 with remainder 1
17
So i
1
=i =i

9. Simplify.
i
26 Divide the exponent by 4
and look at the
remainder.
26÷ 4 = 6 with remainder 2
So i
26
2
= i = −1

10. Simplify.
11 Divide the exponent by 4
i
and look at the
remainder.
11÷ 4 = 2 with remainder 3
11
3
So i = i = −i

11. Definition of Complex
Numbers
Any number in form
a+bi, where a and b are
real numbers and i is
imaginary unit.

12. Definition of Equal
Complex Numbers
Two complex numbers are
equal if their real parts are
equal and their imaginary
parts are equal.
If a + bi = c + di,
then a = c and b = d

13. When adding or subtracting
complex numbers, combine like
terms.
Ex: (8 − 3i) + ( 2 + 5i )
(8 + 2) + ( −3i + 5i)
10 + 2i

14. Simplify.
(8 + 7i) + ( −12 + 11i)
(8 + −12) + (7i + 11i)
−4 +18i

15. Simplify.
(9 − 6i) − (12 + 2i )
(9 − 12) + ( −6i − 2i )
−3 − 8i

16. Multiplying
complex numbers.
To multiply complex
numbers, you use the
same procedure as
multiplying polynomials.

17. Simplify.
(8 + 5i)(2 − 3i)
F
O
I
L2
16− 24i +10i −15i
16− 14i +15
31− 14i

18. Simplify.
(−6 + 2i )( 5 − 3i )
F
O
I
L
−30 +18i + 10i − 6i
−30 + 28i + 6
−24 + 28i
2

19. The Habitat for humanity project utilizes
volunteers to help build house for low – income
families who might not be able to afford the
purchase of a home. At a recent site, Habitat
workers built a small storage shed attached to
the house. The electrical blueprint for the shed
called for two AC circuits connected in series
with a total voltage of 220 volts. One of the
circuits must have an impedance of 7-10j ohms,
and the other needs to have an impedance of
9+5j ohms. According to the building codes,
the impedance cannot exceed 20-5j ohms. Will
the circuits, as designed, meet the code?