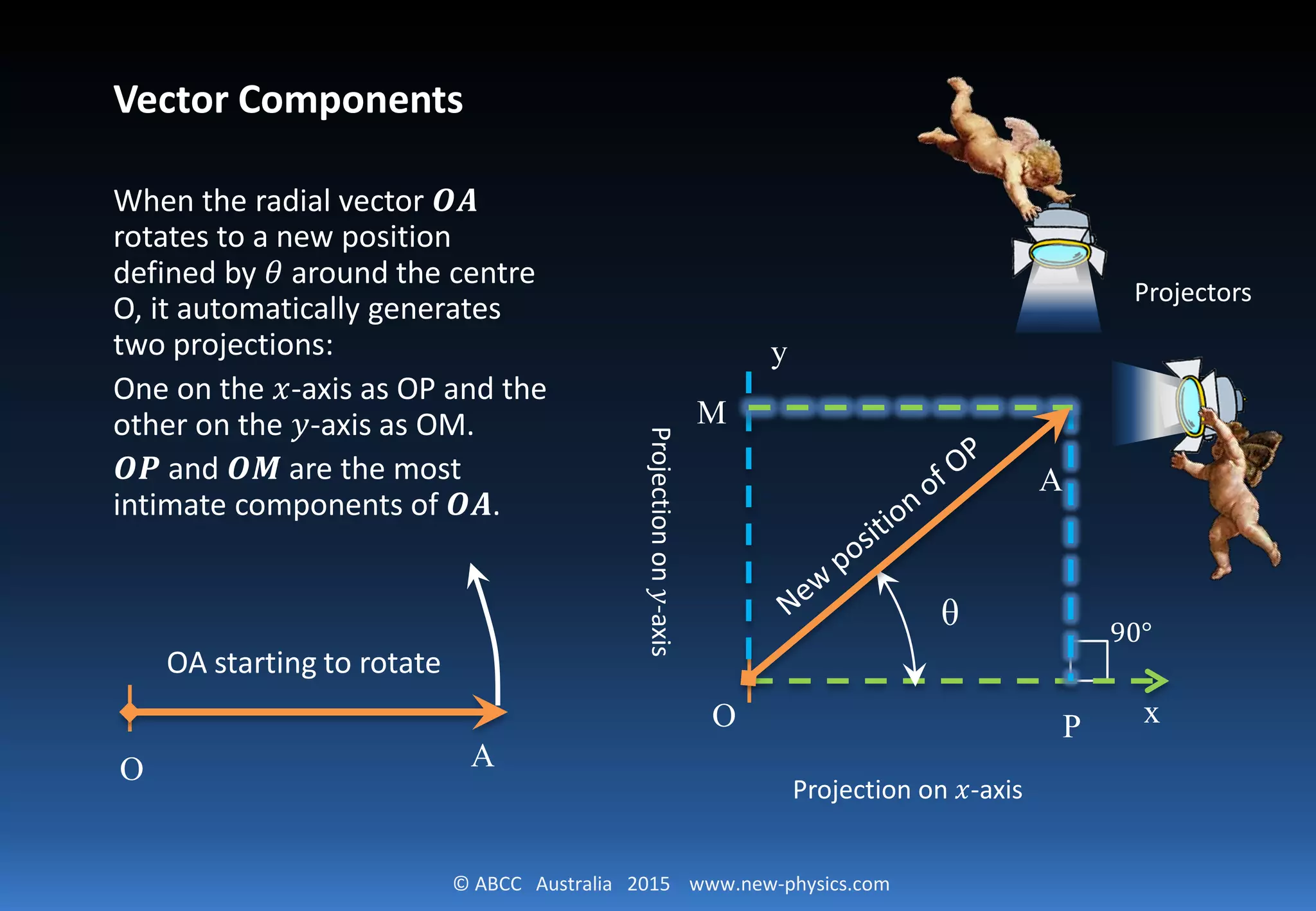
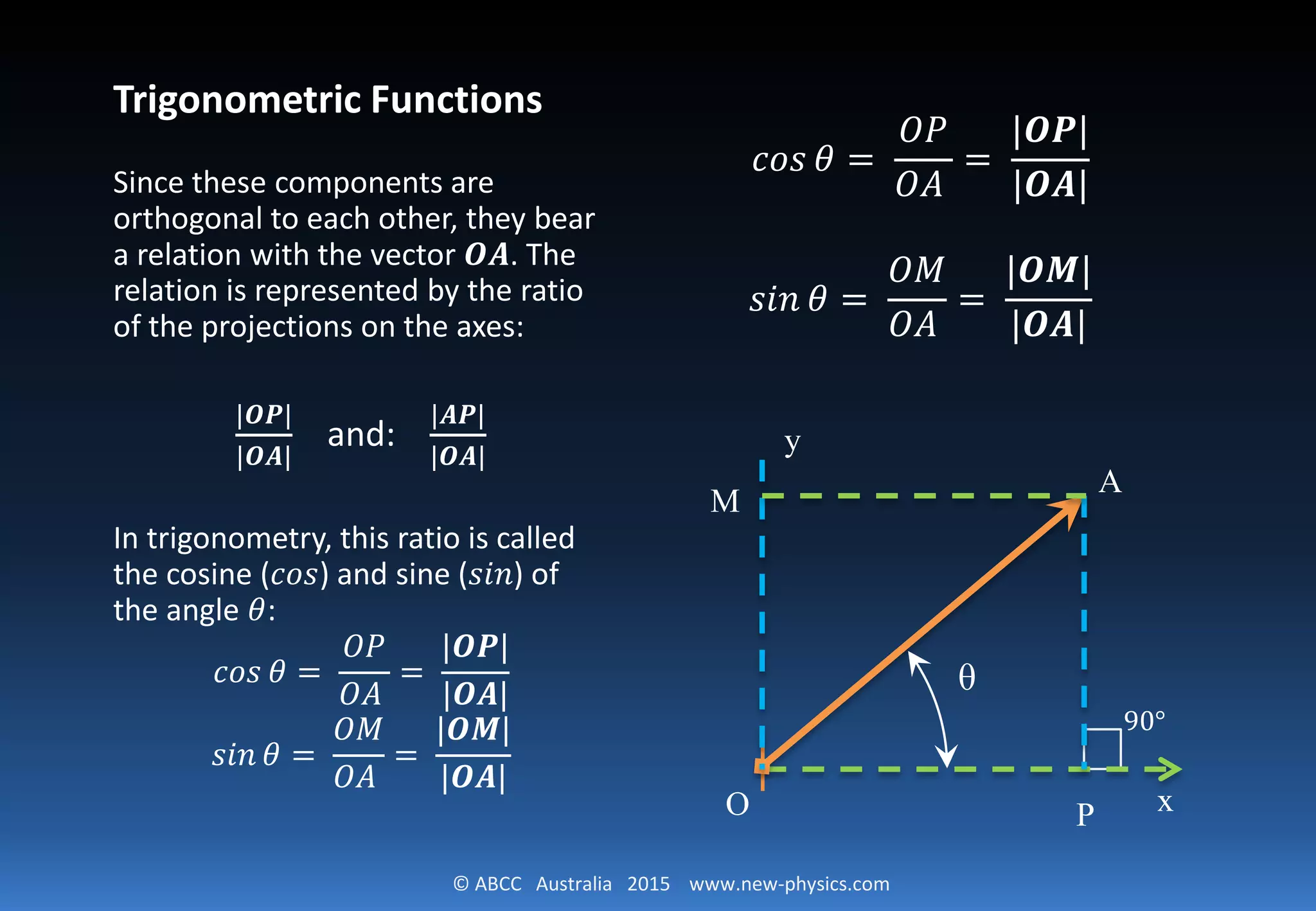
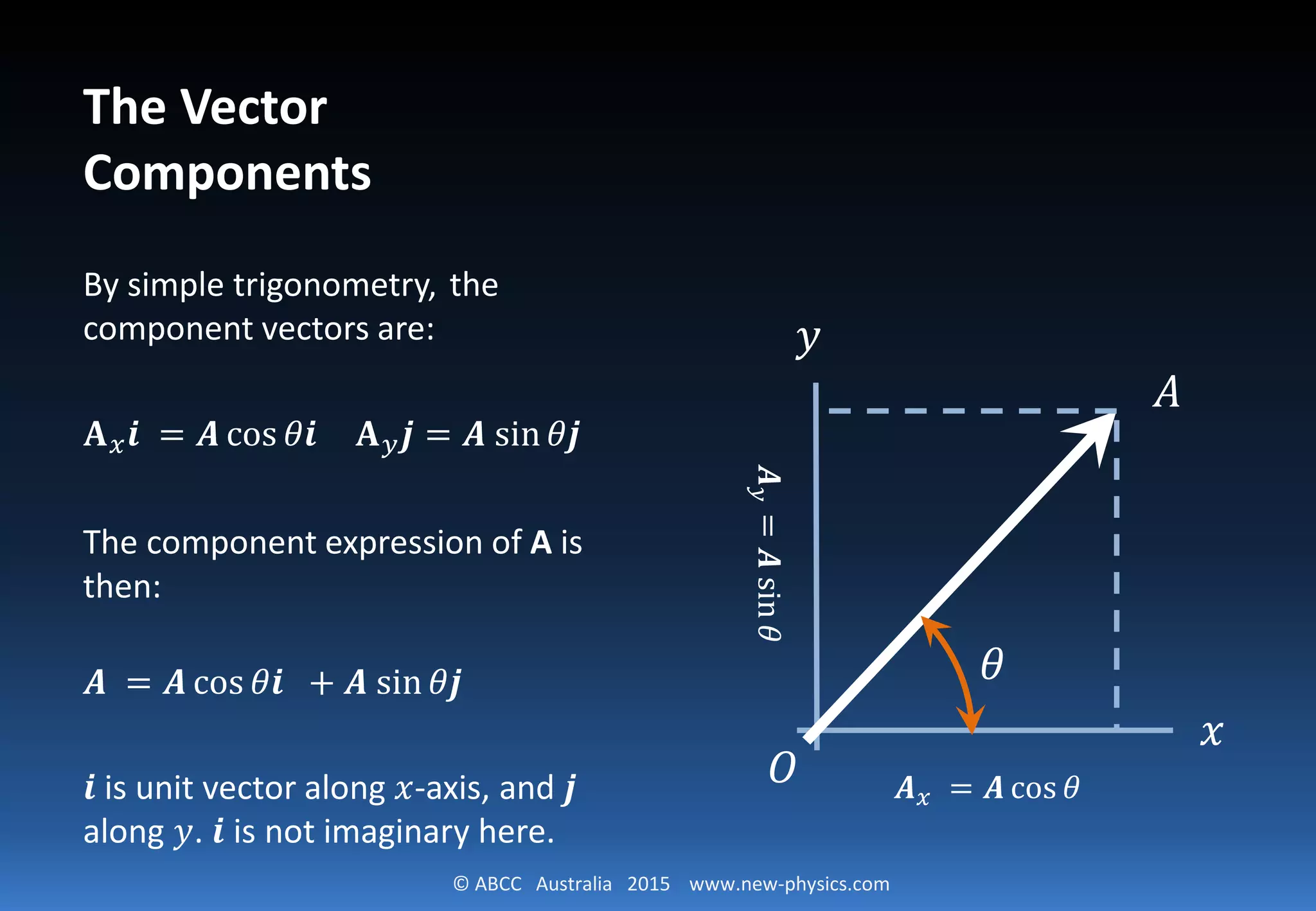
The document discusses the concept of plane polar coordinates, defining a vector using its length and polar angle, which offers advantages over Cartesian coordinates. It explains how the radial vector projects onto the x and y axes and introduces the trigonometric functions cosine and sine to relate these components. The document concludes by deriving the component expressions of a vector in a polar coordinate system.

1. © ABCC Australia 2015 www.new-physics.com
THE PLANE POLAR COORDINATES
PM [BO4]
90°
180° 0°

2. © ABCC Australia 2015 www.new-physics.com
PLANE POLAR
COORDINATES
Another way of specifying the
vector unequivocally is to make
use of the angle 𝜃𝜃 between the
vector and the 𝑥𝑥-axis.
The vector OA will be uniquely
defined by its length 𝑟𝑟 and its
angle 𝜃𝜃 as:
𝑶𝑶𝑶𝑶 ≡ 𝑂𝑂𝑂𝑂 𝒓𝒓, 𝜃𝜃
This is a system more effective
than the ordinary plane
Cartesian coordinate system in
many situations.
𝜃𝜃
𝑦𝑦
𝑥𝑥
𝑂𝑂
𝑂𝑂𝐴𝐴 𝒓𝒓, 𝜃𝜃
𝑟𝑟
Pole
Polar axis 𝜃𝜃 = 0

3. © ABCC Australia 2015 www.new-physics.com
PLANE POLAR CARTESIAN
COORDINATES
This angle 𝜃𝜃 is known as the
polar angle and the system is
therefore called the polar
Cartesian coordinates.
𝜃𝜃
𝑦𝑦
𝑥𝑥
𝑂𝑂
𝐴𝐴

4. © ABCC Australia 2015 www.new-physics.com
Vector Components
When the radial vector 𝑶𝑶𝑶𝑶
rotates to a new position
defined by 𝜃𝜃 around the centre
O, it automatically generates
two projections:
One on the 𝑥𝑥-axis as OP and the
other on the 𝑦𝑦-axis as OM.
𝑶𝑶𝑶𝑶 and 𝑶𝑶𝑶𝑶 are the most
intimate components of 𝑶𝑶𝑶𝑶.
O
A
x
θ 90°
P
O A
OA starting to rotate
y
Projectionon𝑦𝑦-axis
Projection on 𝑥𝑥-axis
Projectors
M

5. © ABCC Australia 2015 www.new-physics.com
Trigonometric Functions
Since these components are
orthogonal to each other, they bear
a relation with the vector 𝑶𝑶𝑨𝑨. The
relation is represented by the ratio
of the projections on the axes:
|𝑶𝑶𝑶𝑶|
|𝑶𝑶𝑶𝑶|
and:
|𝑨𝑨𝑷𝑷|
|𝑶𝑶𝑶𝑶|
In trigonometry, this ratio is called
the cosine (𝑐𝑐𝑐𝑐𝑐𝑐) and sine (𝑠𝑠𝑠𝑠𝑠𝑠) of
the angle 𝜃𝜃:
𝑐𝑐𝑐𝑐𝑐𝑐 𝜃𝜃 =
𝑂𝑂𝑂𝑂
𝑂𝑂𝑂𝑂
=
|𝑶𝑶𝑶𝑶|
|𝑶𝑶𝑶𝑶|
𝑠𝑠𝑠𝑠𝑠𝑠 𝜃𝜃 =
𝑂𝑂𝑀𝑀
𝑂𝑂𝑂𝑂
=
|𝑶𝑶𝑴𝑴|
|𝑶𝑶𝑶𝑶|
O
A
x
θ
90°
P
y
M
𝑐𝑐𝑐𝑐𝑐𝑐 𝜃𝜃 =
𝑂𝑂𝑂𝑂
𝑂𝑂𝑂𝑂
=
|𝑶𝑶𝑶𝑶|
|𝑶𝑶𝑶𝑶|
𝑠𝑠𝑠𝑠𝑠𝑠 𝜃𝜃 =
𝑂𝑂𝑀𝑀
𝑂𝑂𝑂𝑂
=
|𝑶𝑶𝑴𝑴|
|𝑶𝑶𝑶𝑶|

6. © ABCC Australia 2015 www.new-physics.com
The Vector
Components
By simple trigonometry, the
component vectors are:
𝐀𝐀𝑥𝑥 𝒊𝒊 = 𝑨𝑨 cos 𝜃𝜃𝒊𝒊 𝐀𝐀𝑦𝑦 𝒋𝒋 = 𝑨𝑨 sin 𝜃𝜃𝒋𝒋
The component expression of A is
then:
𝑨𝑨 = 𝑨𝑨 cos 𝜃𝜃𝒊𝒊 + 𝑨𝑨 sin 𝜃𝜃𝒋𝒋
𝒊𝒊 is unit vector along 𝑥𝑥-axis, and 𝒋𝒋
along 𝑦𝑦. 𝒊𝒊 is not imaginary here.
𝜃𝜃
𝑦𝑦
𝑥𝑥
𝑂𝑂
𝐴𝐴
𝑨𝑨𝑦𝑦=𝑨𝑨sin𝜃𝜃
𝑨𝑨𝑥𝑥 = 𝑨𝑨 cos 𝜃𝜃

7. © ABCC Australia 2015 www.new-physics.com
ANGLES & MEASUREMENT
PM [B05]