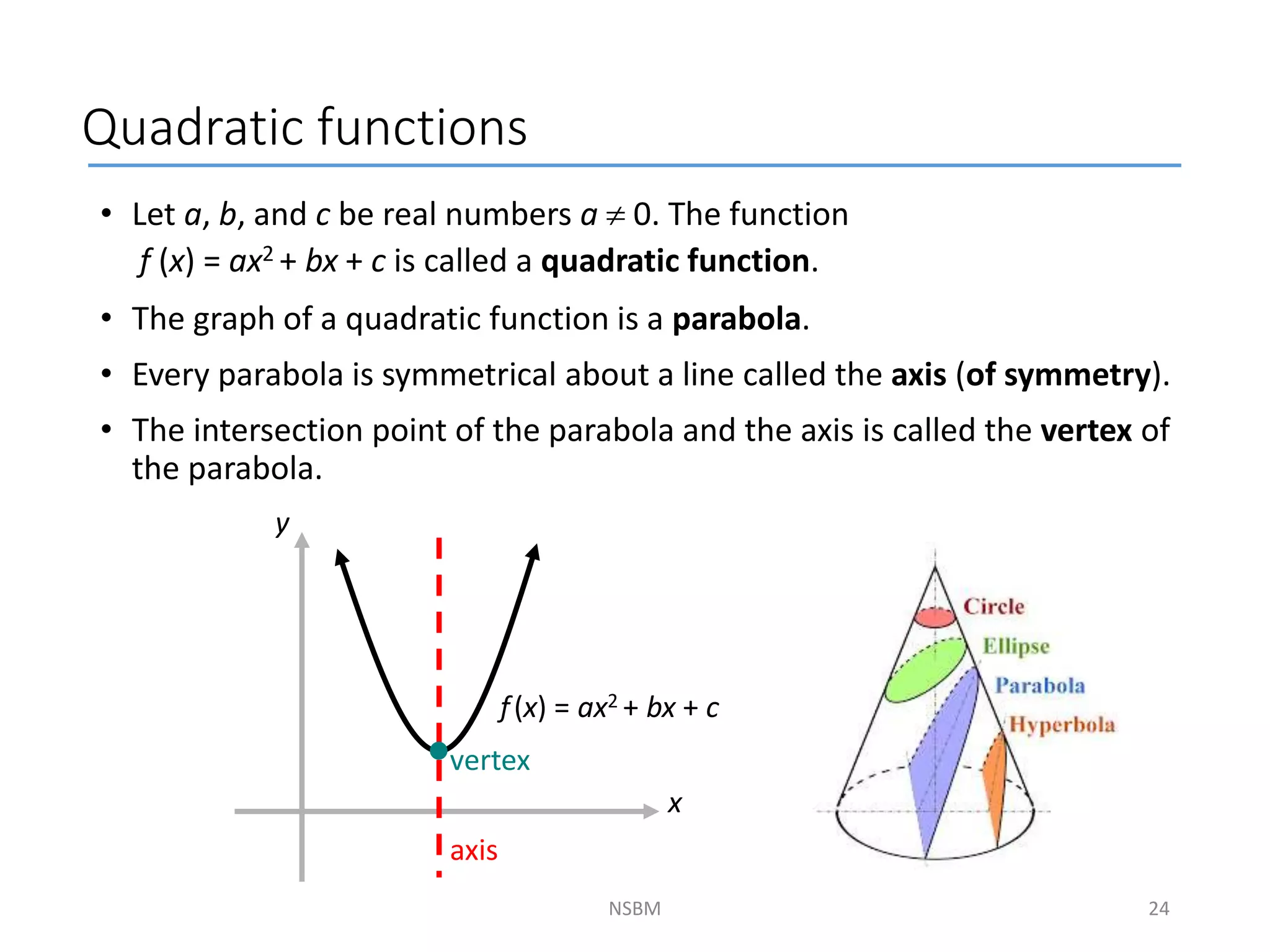
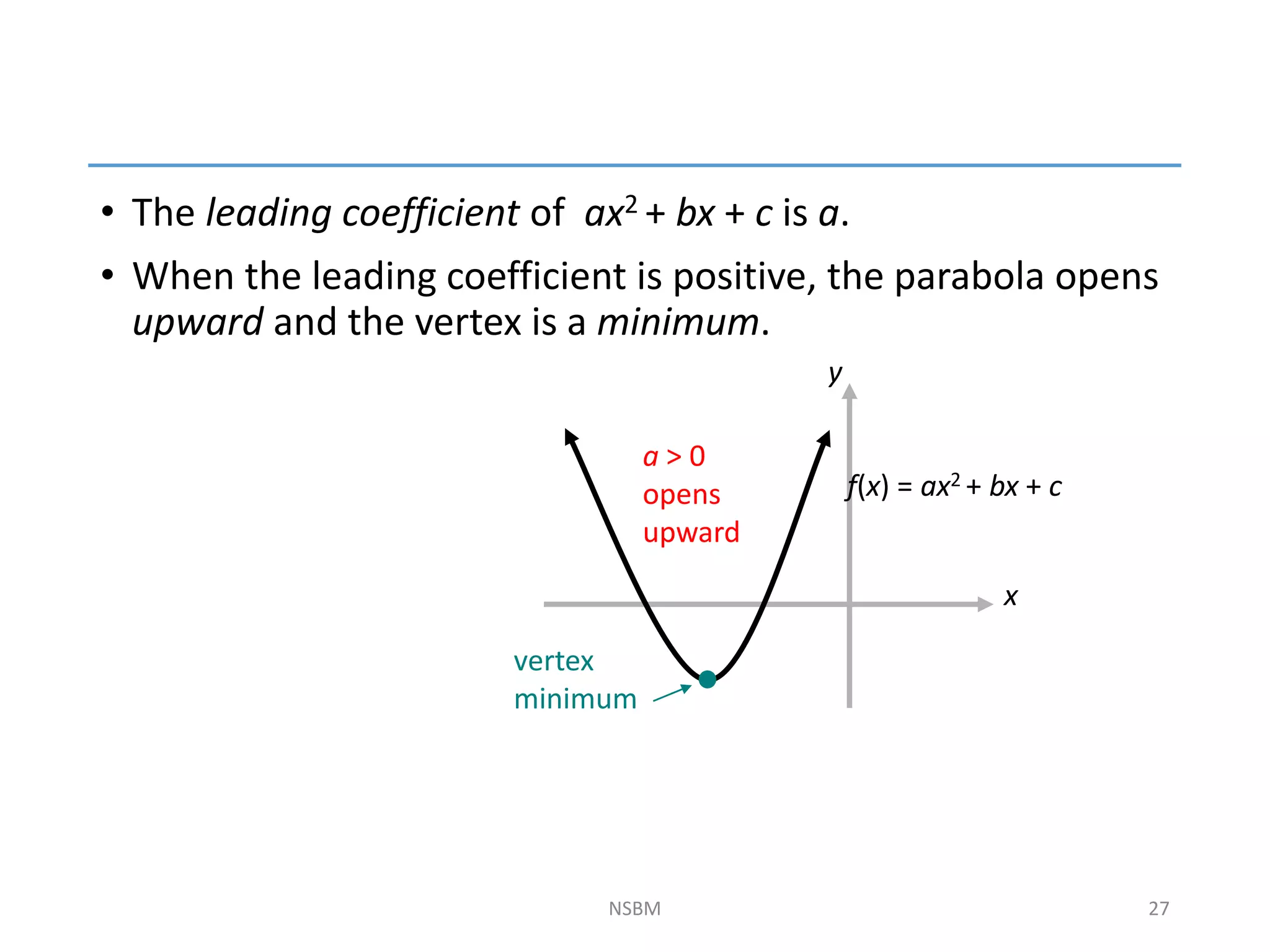
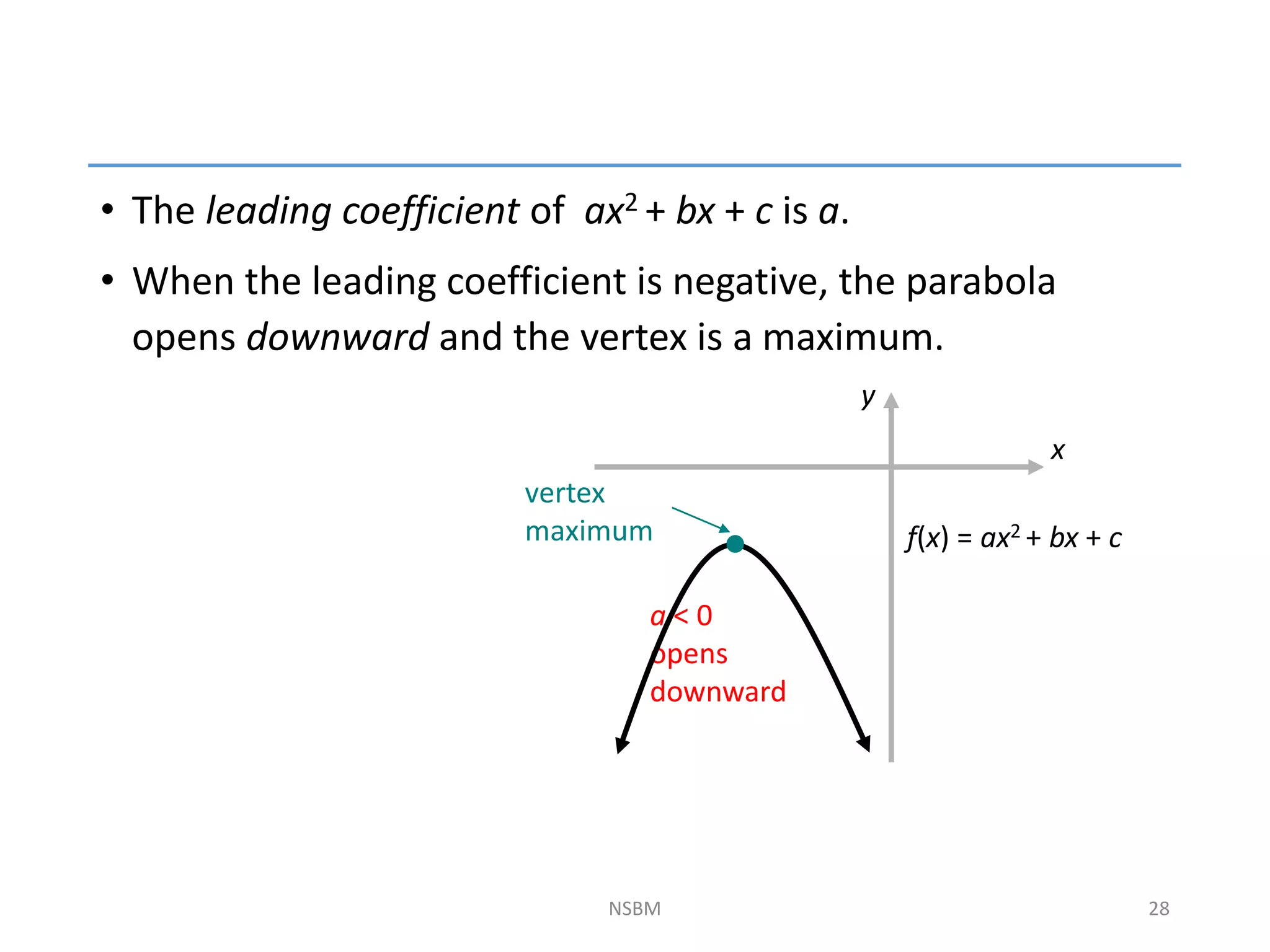
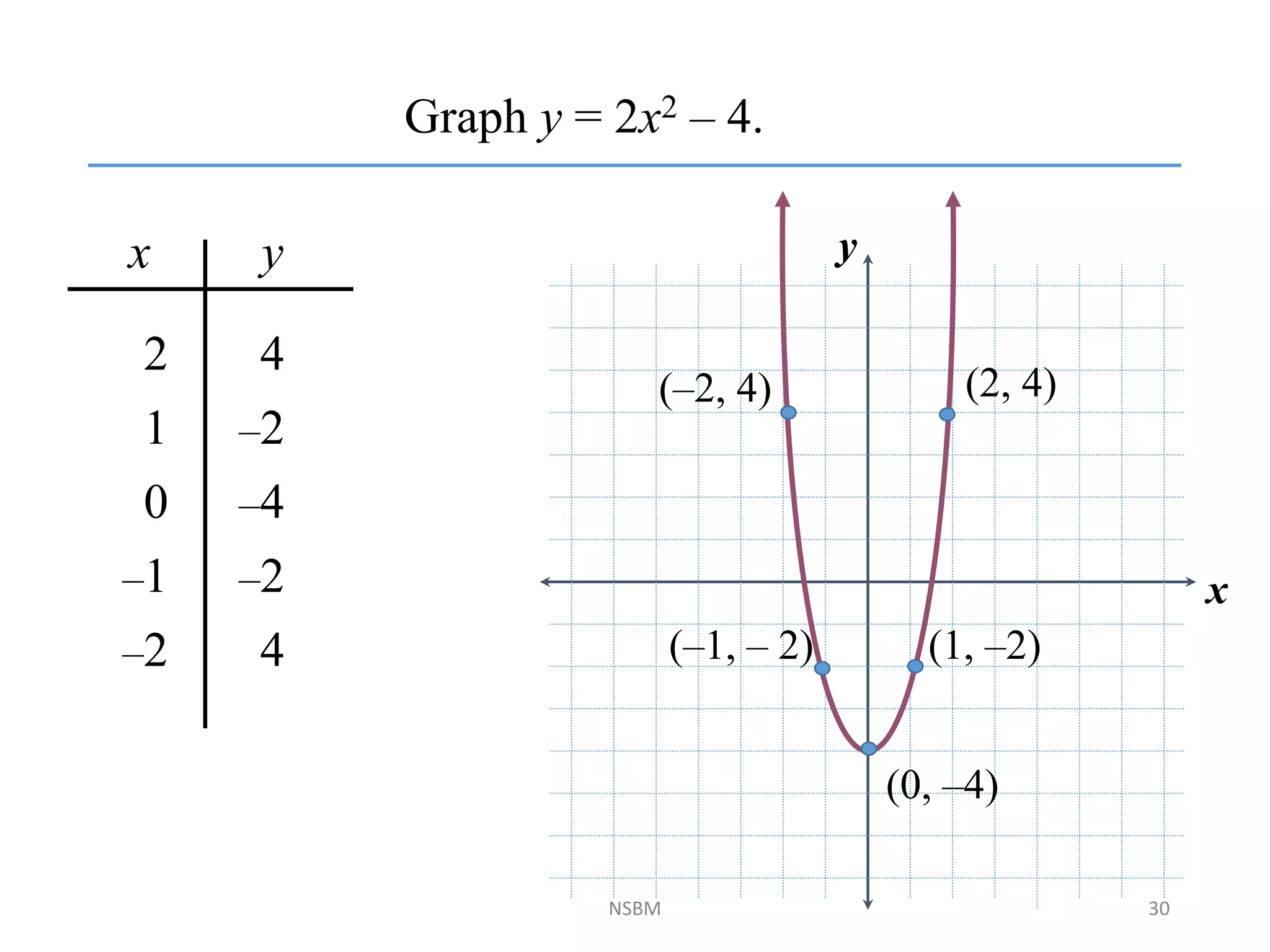
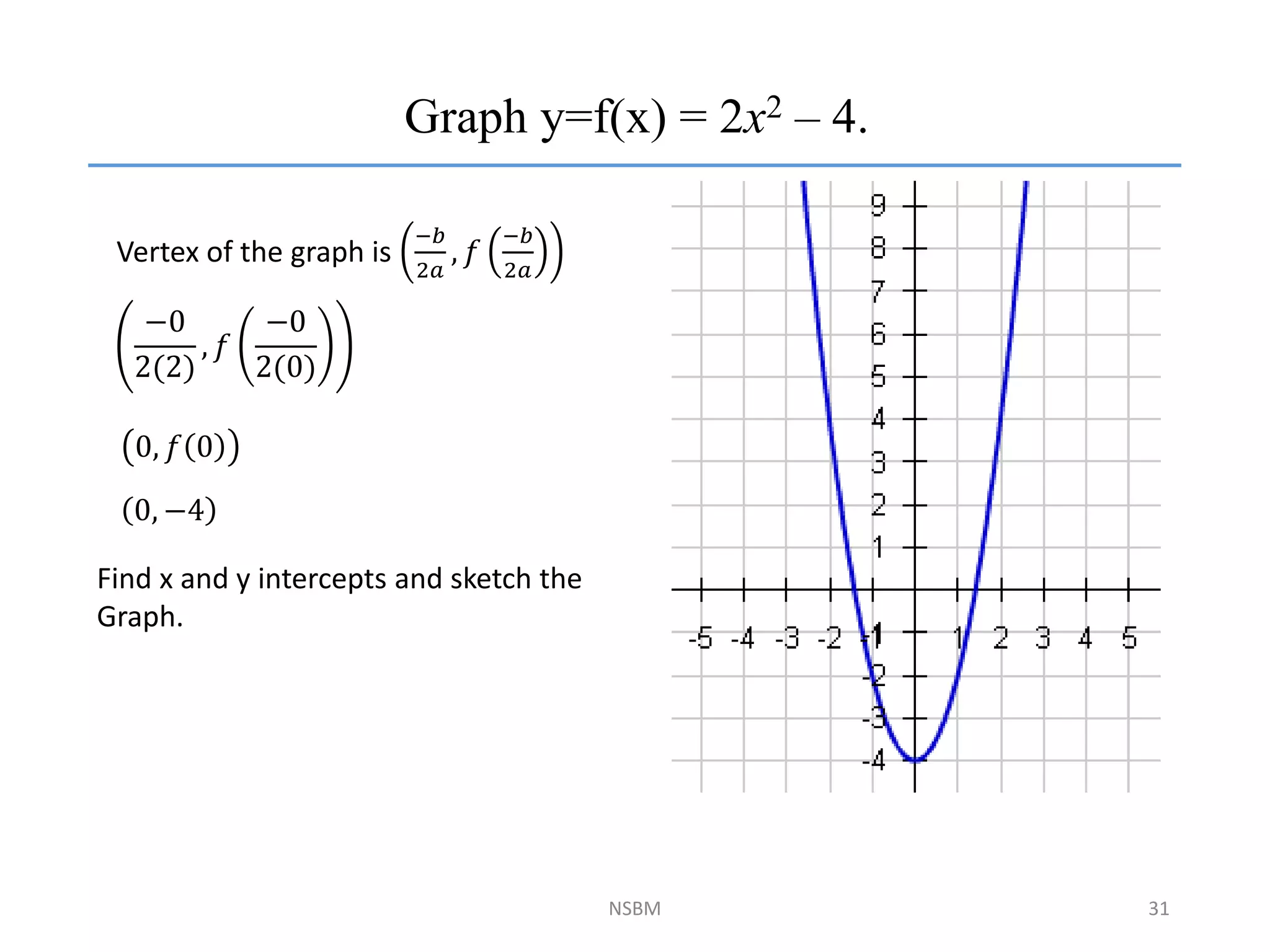
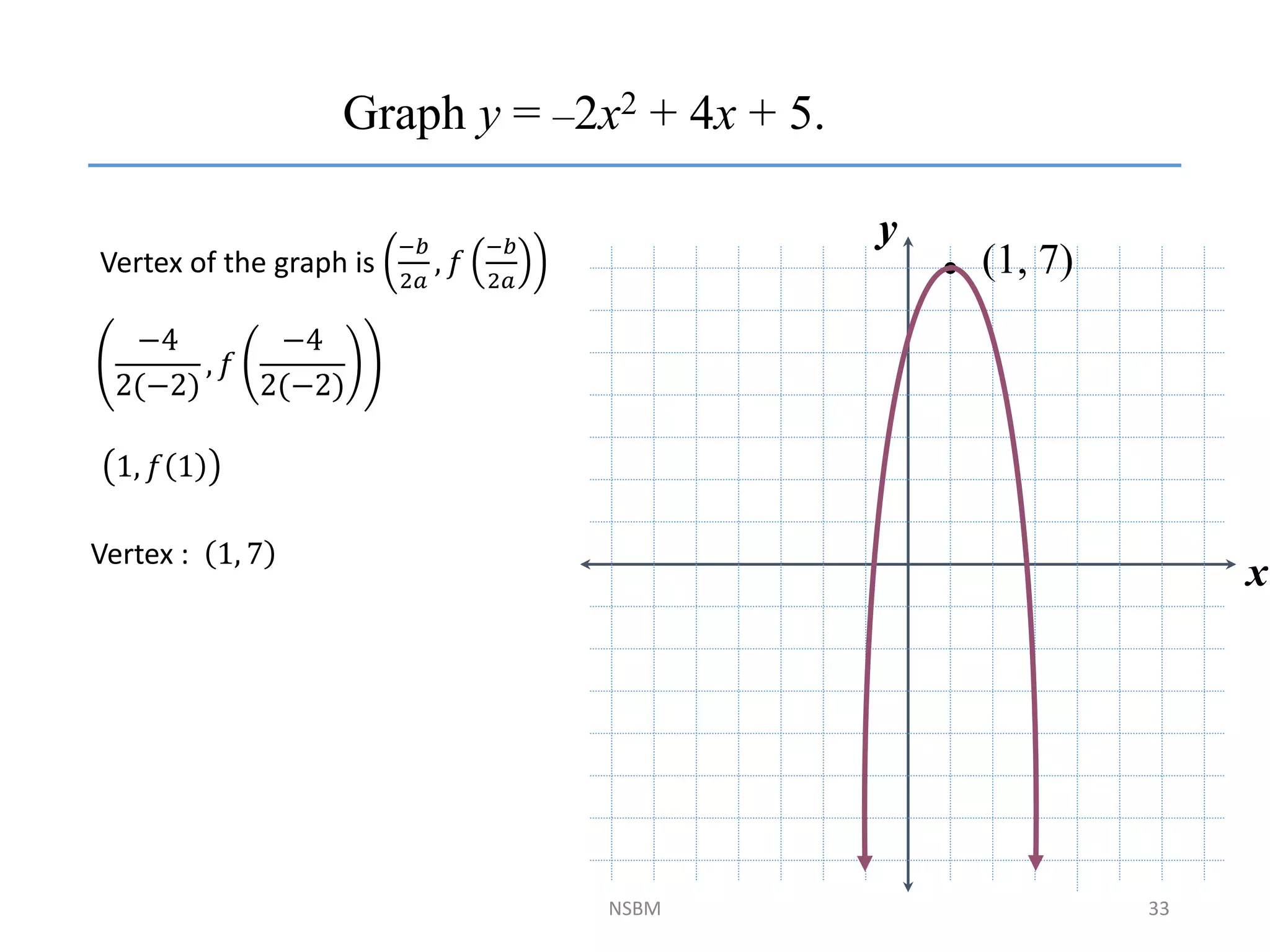
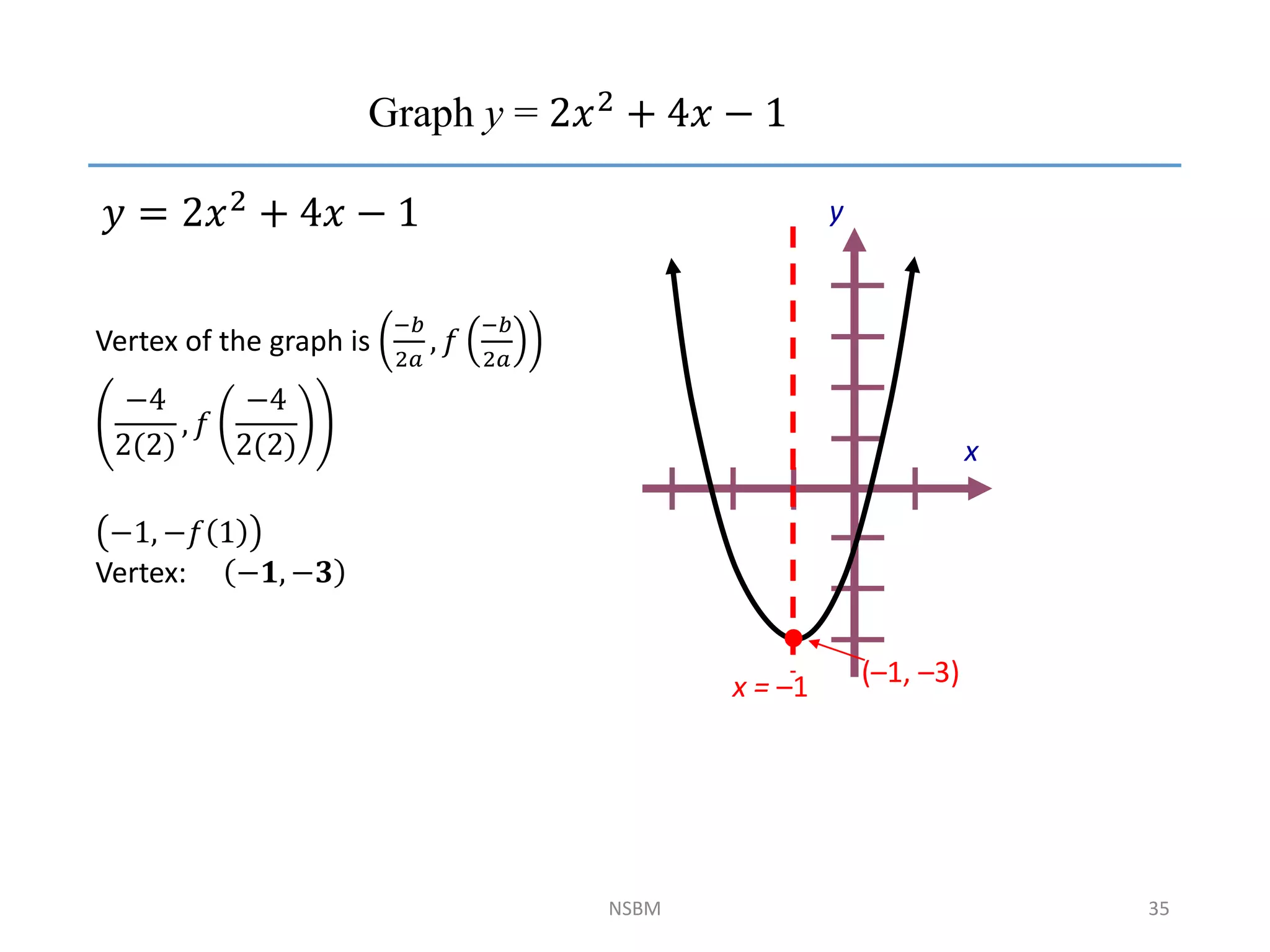
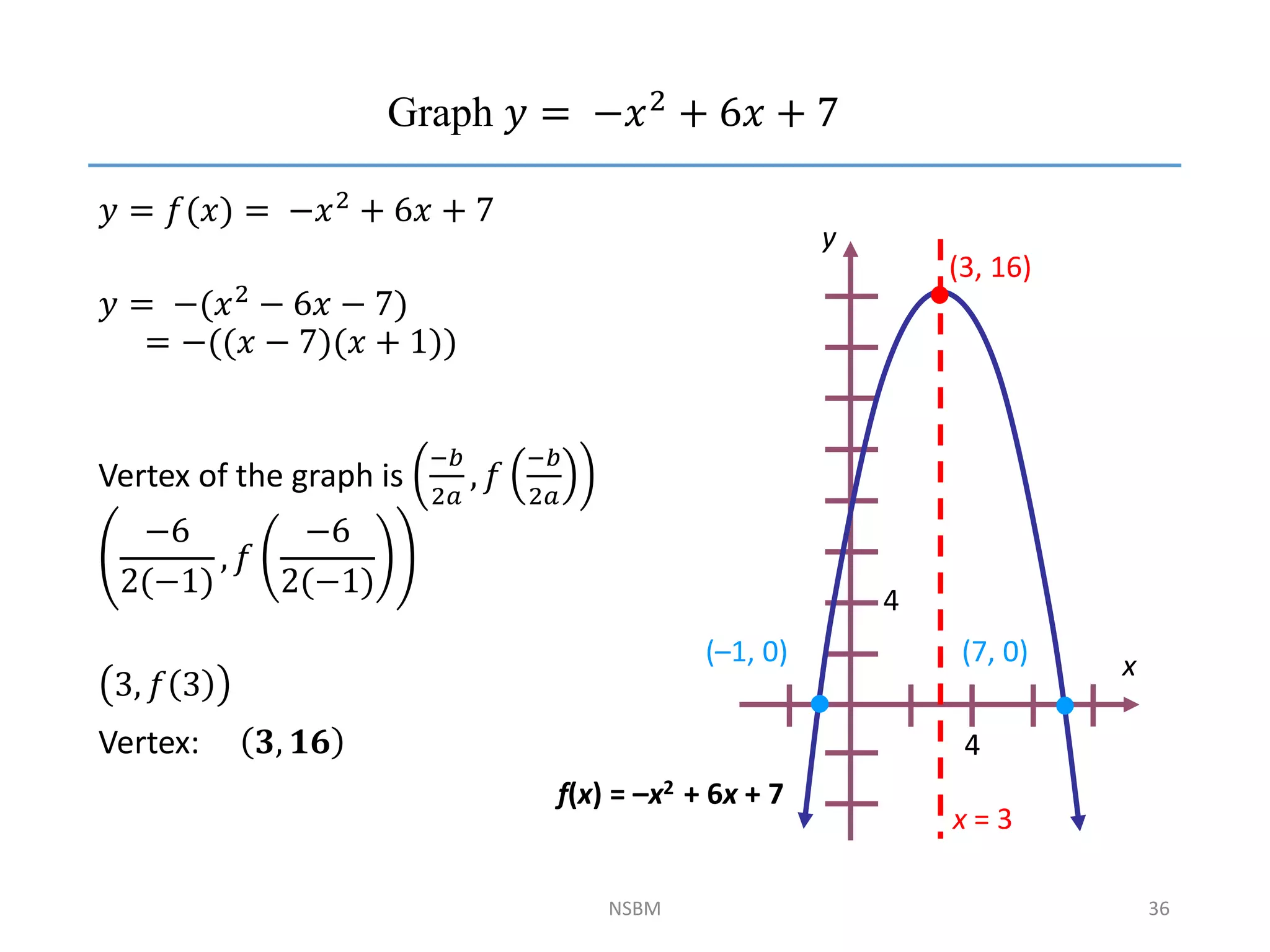
This document discusses factorizing algebraic expressions and quadratic functions. It provides examples of factorizing different types of algebraic expressions like binomials, trinomials and expressions with multiple terms. It also discusses key concepts related to quadratic functions like their standard form, graphing quadratics by finding the vertex, x-intercepts and y-intercepts. Methods to find the roots of a quadratic function include factoring, completing the square and using the quadratic formula.

1. Factorizing Algebraic Expressions
&
Quadratic Functions
D. J. Jayamanne
NSBM 1

2. • When we factorize an algebraic expression, we write it as a product of
factors. These factors may be numbers, algebraic variables or algebraic
expressions.
• Expressions like 3𝑥𝑦, 5𝑥2
𝑦 , 2𝑥 (𝑦 + 2), 5 (𝑦 + 1) (𝑥 + 2) are
already in factor form.
• On the other hand consider expressions like 2𝑥 + 4, 3𝑥 + 3𝑦, 𝑥2 +
5𝑥, 𝑥2 + 5𝑥 + 6.
• It is not obvious what their factors are. Therefore systematic methods
are required to factorize these expressions, i.e., to find their factors.
What is factorizing?
NSBM 2

3. • We can start by taking common factors out of every term in the sum.
1. 6𝑥 + 24
2. 8𝑥2 − 4𝑥
3. 6𝑥𝑦 + 10𝑥2
𝑦
4. 𝑚4
− 3𝑚2
5. 6𝑥2
+ 8𝑥 + 12𝑦𝑥
6. 3𝑥𝑦 + 9𝑥𝑦2 + 6𝑥2𝑦
Factorize the following algebraic expressions
NSBM 3

4. • For the following expressions, factorize the first pair, then the second
pair.
1. 8𝑚2 − 12𝑚 + 10𝑚 − 15
2. 𝑥2 + 5𝑥 + 2𝑥 + 10
3. 𝑚2 − 4𝑚 + 3𝑚 − 12
4. 2𝑡2 − 4𝑡 + 𝑡 − 2
5. 6𝑦2 − 15𝑦 + 4𝑦 − 10
6. 9𝑎2
𝑏 + 3𝑎2
+ 5𝑏 + 5 𝑏2
𝑎
7. 10𝑥2
+ 5𝑥 + 2𝑥𝑦 + 𝑦
8. 𝑥2 + 2𝑥𝑦 + 5𝑥3 + 10𝑥2𝑦
Factorizing algebraic expressions
NSBM 4

5. • For any real numbers a and b,
Factorizing formulae
NSBM 5

6. • Factorize the following:
Qs
NSBM 6

7. What is a Quadratic function
• A quadratic function is any function having the form
where x is the variable and a, b and c are known values.
a is the coefficient of the squared term
b is the coefficient of x and can be any number.
c is the called the constant term can be any number.
• Quadratics are algebraic expressions of one variable, and they have
degree two. Having degree two means that the highest power of the
variable that occurs is a squared term.
NSBM
c
bx
ax 

2
7

8. Q
• Which of the following algebraic expression is a quadratic?
NSBM 8

9. Factorizing quadratics
NSBM
• How to factor an expression like 𝑥2 + 4𝑥 + 3
• Requirement is to find two numbers that add to give 4 and multiply to
give 3, and the numbers that do this is 1 and 3.
9
𝑥2
+ 1𝑥 + 3𝑥 + 3
𝑥 𝑥 + 1 + 3 𝑥 + 1
𝑥 + 1 𝑥 + 3

10. NSBM
• How to factor an expression like 𝑥2 + 4𝑥 + 3
1. Identify the coefficient of x2 e.g. a=1
2. Identify the constant e.g. c=3
3. Multiply: a x c e.g. 1 x 3= 3
4. Form the coefficient of x using the factors of a x c. e.g. b=1 + 3= 4
5. Re-write the expression
c
bx
ax 

2
10
Factorizing quadratics
𝑥2
+ 1𝑥 + 3𝑥 + 3
𝑥 𝑥 + 1 + 3 𝑥 + 1
𝑥 + 1 𝑥 + 3

11. Factorize the following quadratic functions-1
NSBM 11

12. Factorize the following quadratic functions-2
NSBM 12

13. Finding Roots of a Quadratic function
• A roots of a function are the x-intercepts. A root exists where the
function equals zero.
Roots of a quadratic equation can be found by solving:
a𝑥2 + 𝑏𝑥 + 𝑐 = 0
Methods to find roots:
1. Factor the Quadratic
2. Complete the Square
3. Use the special Quadratic Formula
4. Graphing
NSBM 13

14. 1. Factoring the Quadratic function
NSBM
In order to find roots,
i) Factor the quadratic function
ii) Equate to zero to find roots
Q1) Factor the following quadratic functions and find roots
1. 𝑓(𝑥) = 𝑥2 + 2𝑥 − 3
2. 𝑓 𝑥 = 17𝑥2
+ 19𝑥 + 2
3. 𝑓 𝑥 = 𝑥2 − 6𝑥 − 16
4. 𝑓 𝑥 = 𝑥2
+ 6𝑥 + 8
5. 𝑓 𝑥 = 𝑥2 − 3𝑥 + 2
14

15. 1. Factoring the Quadratic function
NSBM
Q2) Factor the following quadratic functions and find roots
1. 𝑓 𝑥 = 𝑥2 − 9
2. 𝑓(𝑥) = 10𝑥2 + 𝑥 − 2
3. 𝑓 𝑥 = 4𝑥2 − 15𝑥 − 25
4. 𝑓 𝑥 = 4𝑥2
− 25
15

16. Square root property
NSBM
• If 𝑏 is a real number and 𝑎2 = 𝑏
• Suppose the equation is in the form
• Then, you may use the square root property to find roots.
b
a 

c
b
ax 
 2
)
(
c
b
ax 

 )
(
16

17. Qs
NSBM
• Find the roots of the following:
1. 𝑓 𝑥 = (𝑥 + 2)2−25
2. 𝑓 𝑥 = (3𝑥 − 17)2
−28
3. 𝑓 𝑥 = (2𝑥 − 3)2−49
4. 𝑓 𝑥 = 4𝑥2 + 25
17

18. 2. Find the roots by completing the square
NSBM
We now look at a method for solving quadratics that involves a technique
called completing the square.
It involves creating a trinomial that is a perfect square, setting the factored
trinomial equal to a constant, then using the square root property from
the previous section.
Note: A perfect square trinomial is the expansion of a binomials squared.
18

19. 2. Find the roots by completing the square
NSBM
1) If the coefficient of x2 is NOT 1, divide both sides of the equation
by the coefficient.
2) Isolate all variable terms on one side of the equation.
3) Complete the square (half the coefficient of the x term squared,
added to both sides of the equation).
4) Factor the resulting trinomial.
5) Use the square root property.
19

20. 2. Find the roots by completing the square
NSBM
Find the roots by completing the square.
𝑦 = 𝑥2 + 4𝑥 + 2
20
𝑥2
+ 4𝑥 + 2 = 0
𝑥2
+ 4𝑥 = −2
𝑥2
+ 4𝑥 + (2)2
= −2 + (2)2
(𝑥 + 2)2
= 2
𝑥 + 2 = ± 2
𝑥 = −2 ± 2

21. 2. Find the roots by completing the square
NSBM
Find the roots by completing the square.
1. 𝑥2 + 𝑥 − 7
2. 2𝑥2 + 14𝑥 − 1
3. 3𝑥2 + 12𝑥 − 1
4. −𝑥2
+ 𝑥 + 1
5. 𝑥2 + 𝑥 +
1
4
21

22. 3. Finding Roots of a Quadratic function by using the
special Quadratic Formula
NSBM
• A quadratic equation written in standard form
𝑎𝑥2 + 𝑏𝑥 + 𝑐 has the following solutions.
a
ac
b
b
x
2
4
2




22

23. • Use the quadratic formula to find roots of the following
NSBM
8
6x
x
y 2



16
-
6x
-
x
y 2

2
3x
-
x
y 2


3
2x
x
y 2


 7
–
x
x
y 2


1
–
14x
2x
y 2


1
–
12x
3x
y 2


1
x
-x
y 2



4
1
x
x
y 2



2
4x
x
y 2



23

24. Quadratic functions
• Let a, b, and c be real numbers a  0. The function
f (x) = ax2 + bx + c is called a quadratic function.
• The graph of a quadratic function is a parabola.
• Every parabola is symmetrical about a line called the axis (of symmetry).
• The intersection point of the parabola and the axis is called the vertex of
the parabola.
NSBM 24
x
y
axis
f(x) = ax2 + bx + c
vertex

25. Graphing quadratic functions
NSBM 25
• The graph of a quadratic equation is a parabola.
• The highest point or lowest point on the parabola is the
vertex.
• Axis of symmetry is the line that runs through the vertex
and through the middle of the parabola.

26. Intercepts of parabola
• Although we can simply plot points, it is helpful to know
some information about the parabola we will be graphing
prior to finding individual points.
• To find x-intercepts of the parabola, let y = 0 and solve for x.
• To find y-intercepts of the parabola, let x = 0 and solve for y.
NSBM 26

27. • The leading coefficient of ax2 + bx + c is a.
• When the leading coefficient is positive, the parabola opens
upward and the vertex is a minimum.
NSBM 27
x
y
f(x) = ax2 + bx + c
a > 0
opens
upward
vertex
minimum

28. • The leading coefficient of ax2 + bx + c is a.
• When the leading coefficient is negative, the parabola
opens downward and the vertex is a maximum.
NSBM 28
x
y
f(x) = ax2 + bx + c
a < 0
opens
downward
vertex
maximum

29. Characteristics of parabola
If the quadratic equation is written in standard form, y = ax2 + bx + c,
1) the parabola opens up when a > 0 and opens down when a < 0
2) the x-coordinate of the vertex is
• To find the corresponding y-coordinate, you substitute the x-coordinate into
the equation and evaluate for y.
3) the y-coordinate of the vertex is
Vertex of the graph is
−𝑏
2𝑎
, 𝑓
−𝑏
2𝑎
NSBM
a
b
2

a
b
c
4
2

29

30. NSBM
x
y
(2, 4)
(–2, 4)
(1, –2)
(–1, – 2)
(0, –4)
x y
0 –4
1 –2
–1 –2
2 4
–2 4
30
Graph y = 2x2 – 4.

31. NSBM 31
Graph y=f(x) = 2x2 – 4.
Vertex of the graph is
−𝑏
2𝑎
, 𝑓
−𝑏
2𝑎
−0
2(2)
, 𝑓
−0
2(0)
0, −4
Find x and y intercepts and sketch the
Graph.
0, 𝑓 0

32. • A quadratic function written in the form 𝑓(𝑥) = 𝑎(𝑥 − ℎ)2+ 𝑘
will have a vertex at the point (ℎ, 𝑘).
• The value of “a” will determine whether the parabola opens up or down
(positive or negative) and whether the parabola is narrow or wide.
NSBM 32

33. NSBM
x
y
Graph y = –2x2 + 4x + 5.
(1, 7)
33
Vertex of the graph is
−𝑏
2𝑎
, 𝑓
−𝑏
2𝑎
−4
2(−2)
, 𝑓
−4
2(−2)
Vertex : 1, 7
1, 𝑓 1

34. NSBM 34
Graph the following:
1. 𝑦 = 2𝑥2 + 4𝑥 − 1
2. 𝑦 = −𝑥2 + 6𝑥 + 7

35. 𝑦 = 2𝑥2 + 4𝑥 − 1
NSBM 35
x
y
x = –1 (–1, –3)
Graph y = 2𝑥2 + 4𝑥 − 1
Vertex of the graph is
−𝑏
2𝑎
, 𝑓
−𝑏
2𝑎
−4
2(2)
, 𝑓
−4
2(2)
−1, −𝑓 1
Vertex: −𝟏, −𝟑

36. 𝑦 = 𝑓(𝑥) = −𝑥2 + 6𝑥 + 7
𝑦 = −(𝑥2
− 6𝑥 − 7)
= −((𝑥 − 7)(𝑥 + 1))
Vertex of the graph is
−𝑏
2𝑎
, 𝑓
−𝑏
2𝑎
−6
2(−1)
, 𝑓
−6
2(−1)
3, 𝑓 3
Vertex: 𝟑, 𝟏𝟔
NSBM 36
x
y
4
4
x = 3
(7, 0)
(–1, 0)
(3, 16)
Graph 𝑦 = −𝑥2 + 6𝑥 + 7
f(x) = –x2 + 6x + 7