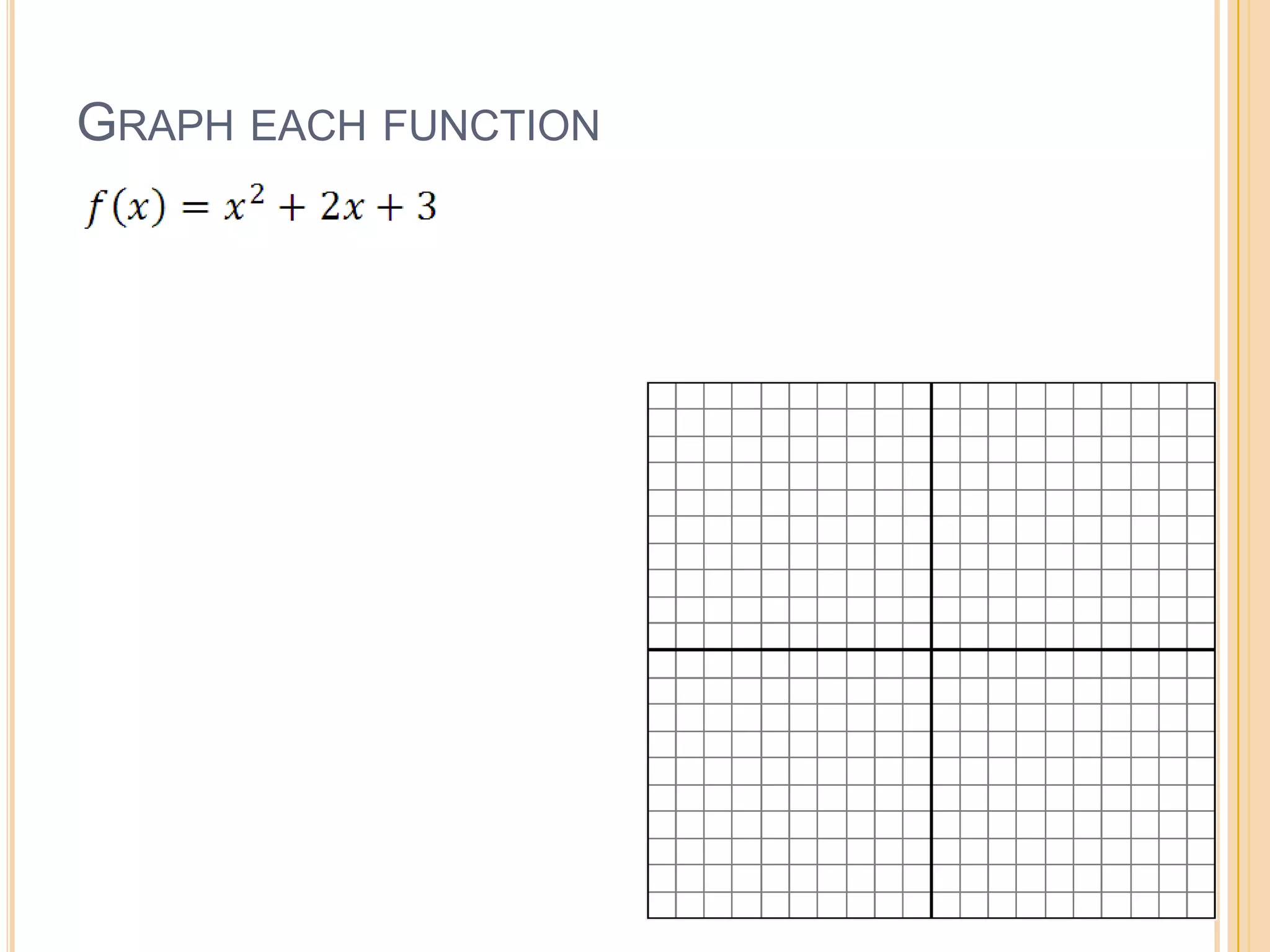
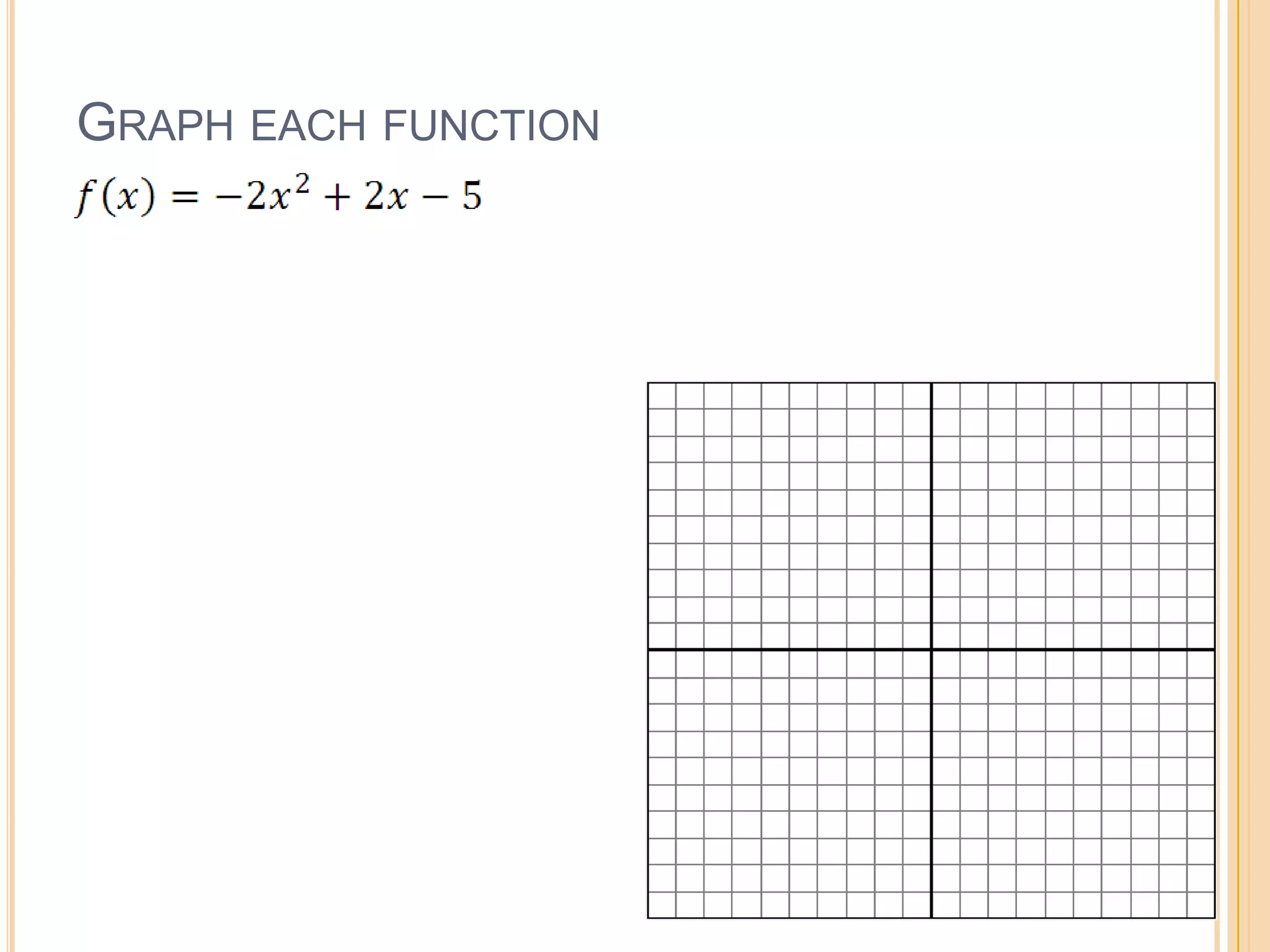
Standard form of a quadratic function is f(x) = ax^2 + bx + c. The graph is a parabola that opens up if a > 0 and opens down if a < 0. The axis of symmetry is the line x = -b/2a and the vertex is (-b/2a, f(-b/2a)). To graph in standard form, identify a, b, c, find the axis of symmetry and vertex, then plot the y-intercept and use reflection to sketch the parabola. The document provides an example of using standard form to identify the vertex, axis of symmetry, minimum/maximum value, and range of a parabola.

1. 4.2 STANDARD FORM OF A
QUADRATIC FUNCTION
Part 1: Properties of Standard Form and Graphing
using Standard Form

2. QUADRATIC FUNCTIONS
 Vertex Form:
 Standard Form is another way to write the
equation of a quadratic function.
Standard form is:
Both forms can represent the same function. Vertex
form makes it easy to identify the vertex and other
information about the graph. Standard form is easier
to put into a graphing calculator and is more “formal”.

3. PROPERTIES OF STANDARD FORM
 The graph of is a parabola.
 If a > 0, the graph opens up. If a < 0, the graph
opens down.
 The axis of symmetry is the line
 The x – value of the vertex is and the y –
value of the vertex is
 The y – intercept is (0, c)

4. EXAMPLE: IDENTIFY THE VERTEX, AXIS OF
SYMMETRY, THE MAXIMUM OR MINIMUM VALUE, AND
THE RANGE OF THE PARABOLA

5. EXAMPLE: IDENTIFY THE VERTEX, AXIS OF
SYMMETRY, THE MAXIMUM OR MINIMUM VALUE, AND
THE RANGE OF THE PARABOLA

6. GRAPHING A FUNCTION IN STANDARD FORM
1. Identify a, b, and c
2. Identify and sketch the axis of symmetry,
3. Identify and plot the vertex,
4. Identify and plot the y – intercept, (0, c)
5. Use the axis of symmetry and y – intercept to plot
the reflected point
6. Sketch the parabola

7. GRAPH EACH FUNCTION

8. GRAPH EACH FUNCTION