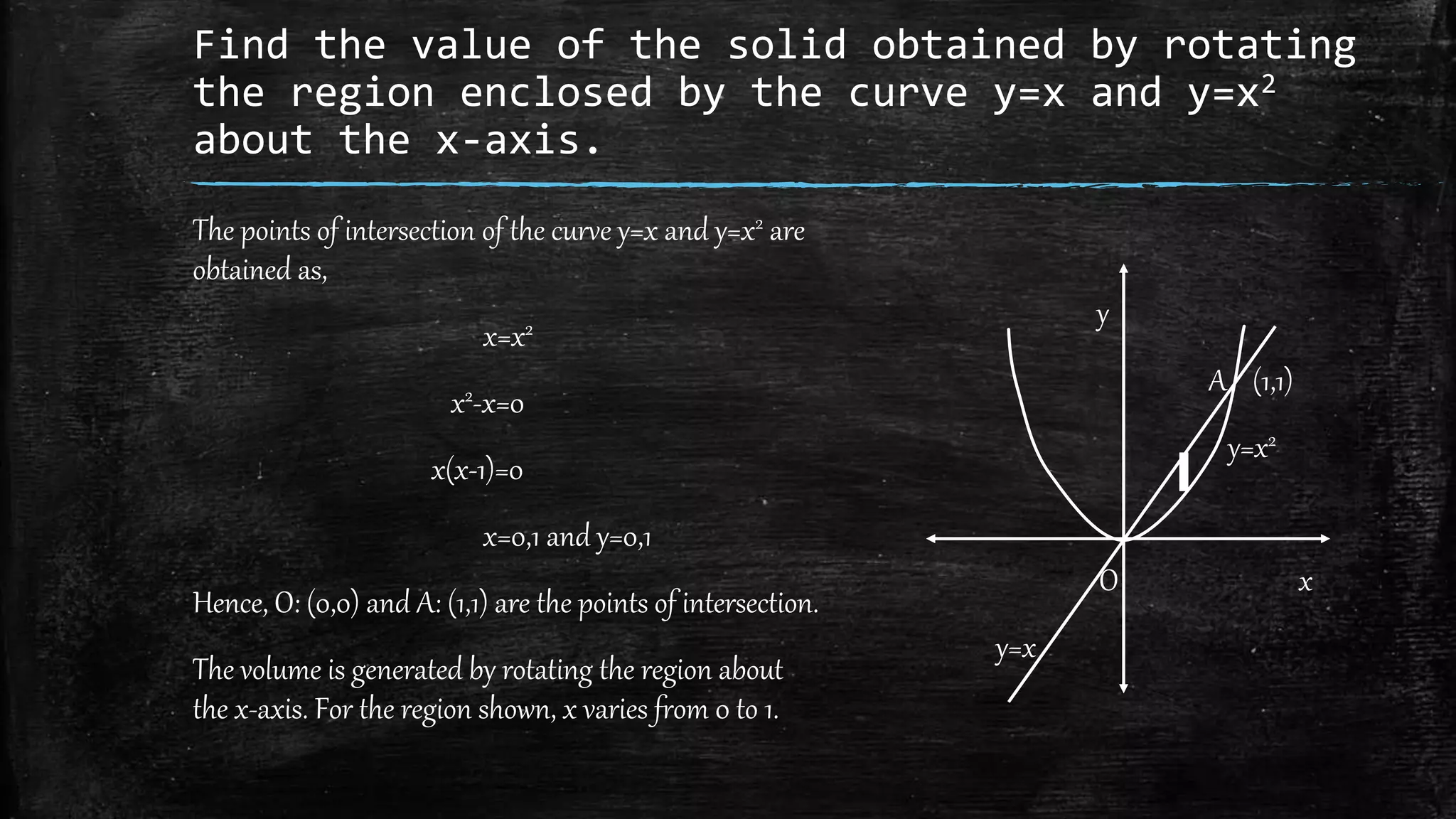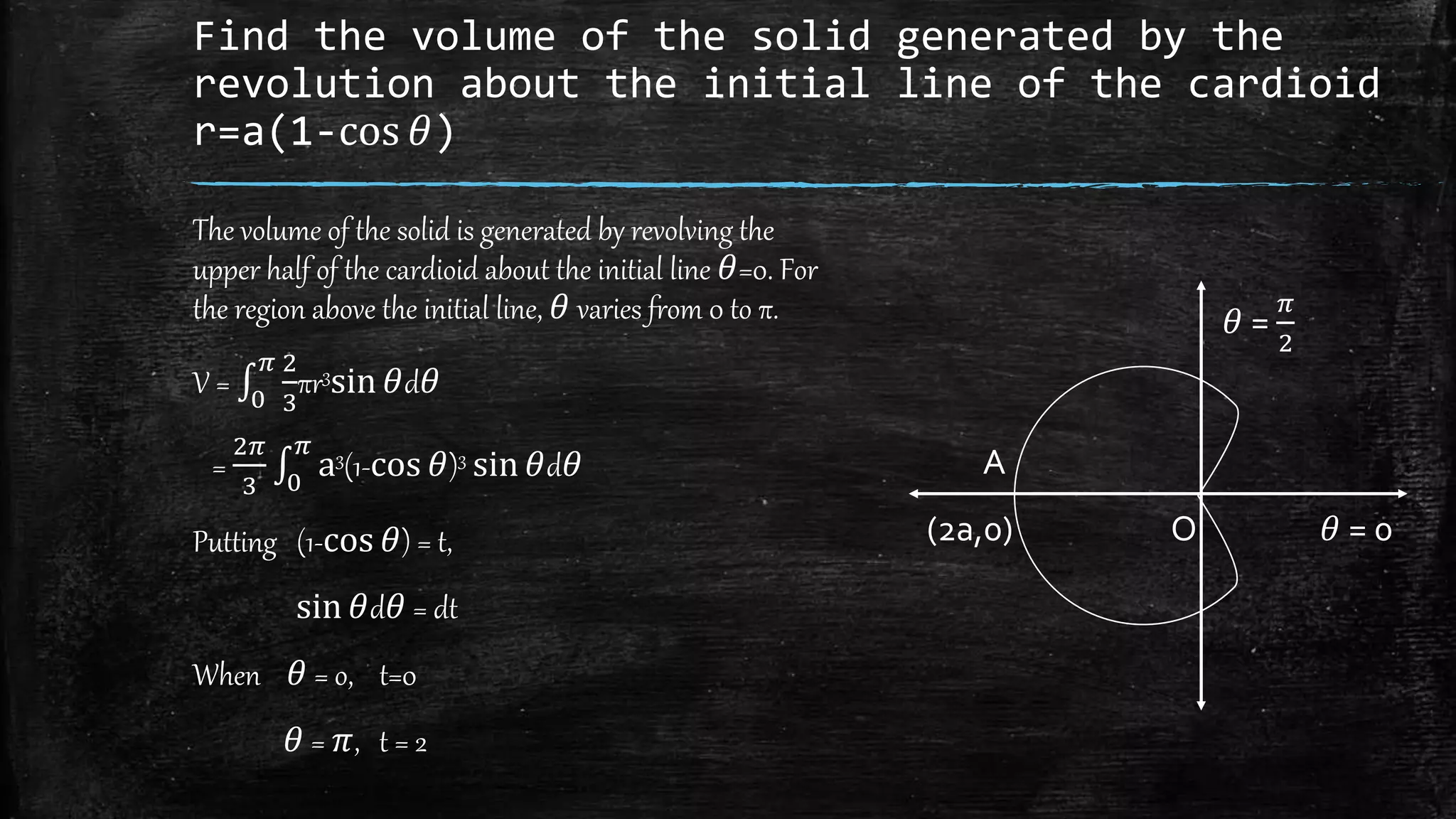This document discusses methods for calculating the volume of solids of revolution generated by rotating plane regions about lines. It covers the disk and washer methods for rotation about axes in the plane of the region. Formulas are provided for calculating volumes of revolution in Cartesian, parametric, and polar coordinate systems by integrating the area of thin cross-sectional disks/washers. Several examples demonstrate applying these formulas to find the volumes of solids generated by rotating curves like ellipses, lines, and cardioids.

1. Volume of solid of Revolution
By Disk andWasher Method

2. Disk and Washer Method
A solid generated by
revolving a plane area
about a line in the
plane is called a solid
of revolution.
 A side generated by revolving a plane area about a line
in the plane is called a solid of revolution and the
method is known as Disk Method.
 The method to find volume of solid generated by
revolving the region bounded between two curves is
known as Washer Method.

3. Volume of solid of Revolution in Cartesian Form
• Let the y=f(x) be the curve and the area
bounded by the curve, the x-axis and the two
lines x=a and x=b be revolved about the x-axis.
An elementary strip of width dx at point P(x,y)
of the curve, generates elementary solid of
volume 𝜋y2dx, when revolved about the x-axis.
• Summing up the volume of revolution of all
such strip from x=a to x=b, the volume of solid
of revolution is given by
V = 𝑎
𝑏
𝜋 𝑦2dx
y P(x,y) y=f(x)
O x=a x=b x

4. Continue
 Similarly, if the area bounded by the curve
x=f(y), the y-axis and the two lines, y=c and
y=d is revolved about the y-axis, then the
volume of solid of revolution is given by
V = 𝑐
𝑑
𝜋 𝑥2
dy
 The volume of the solid of revolution
about any axis can be obtain by
calculating the length of the
perpendicular from point P(x,y) on the
axis of revolution. If the area bounded by
the curve y=f(x) is resolved about the line
AB, then the volume of the solid of
revolution is given by
V = 𝜋 (𝑃𝑀)2d(AM)
y
y=d x=f(y)
P(x,y)
y=a
O x

5. Find the volume generated by revolving the ellipse
x2
a2 +
y2
b2 = 1 about the x-axis.
The volume is generated by revolving the upper-half
of the ellipse about the x-axis. For the upper-half of
the ellipse , x varies from -a to a. Due to symmetry
about y-axis, considering the region in the first
quadrant where x varies from 0 to a.
V=2 0
𝑎
𝜋 𝑦2dx
=2π b2
0
𝑎
1 −
x2
y2 dx
=2π b2 𝑥 −
x3
3𝑎2
=2π b2 𝑎 −
𝑎3
3𝑎2
=
4
3
π 𝑎 b2
y
(0,b)
(-a,0)B O A(a,0) x
(0.-b)

6. Volume of Solid of Revolution is Parametric Form
y B P(x,y)
M y=f(x)
A
O x
▪ When the equation of the curve is given in
parametric form x=f1(t), y=f2(t) with
t1<=t<=t2, the volume of the solid of
revolution about the x-axis is given by,
V= t1
t2
𝜋y2 𝑑𝑥
𝑑𝑡
dt
 Similarly, the volume of the solid of
revolution about the y-axis is given by,
V= t1
t2
𝜋 𝑥2 𝑑𝑦
𝑑𝑡
dt

7. Find the value of the solid obtained by rotating
the region enclosed by the curve y=x and y=x2
about the x-axis.
The points of intersection of the curve y=x and y=x2 are
obtained as,
x=x2
x2-x=0
x(x-1)=0
x=0,1 and y=0,1
Hence, O: (0,0) and A: (1,1) are the points of intersection.
The volume is generated by rotating the region about
the x-axis. For the region shown, x varies from 0 to 1.
y
A (1,1)
y=x2
O x
y=x

8. Continue
V = 0
1
𝜋( y2
1 – y2
2 )dx where y1 = x and y2 = x2
= π 0
1
(x2-x4)dx
= π
x3
3
−
x5
5
= π
1
3
−
1
5
=
2𝜋
15

9. Volume of Solid of Revolution in Polar Form
o For the curve r=f(𝜃), bounded between the radii
vectors Θ=Θ1 and Θ=Θ2, the volume of the solid of
revolution about the initial line Θ=0 is given by,
V= Θ1
Θ2 2
3
πr2. rsin 𝜃d𝜃
= Θ1
Θ2 2
3
πr3sin 𝜃d𝜃
o Similarly, the volume of the solid of revolution
about the line through the pole and perpendicular
to the initial line is given by,
V= Θ1
Θ2 2
3
πr2. rcos 𝜃d𝜃
Θ1
Θ2 2
3
πr3cos 𝜃d𝜃
𝜃=𝜋 B
P(r,𝜃)
r
A
O 𝜃=o

10. Find the volume of the solid generated by the
revolution about the initial line of the cardioid
r=a(1-cos 𝜃)
The volume of the solid is generated by revolving the
upper half of the cardioid about the initial line 𝜃=0. For
the region above the initial line, 𝜃 varies from 0 to π.
V = 0
𝜋 2
3
πr3sin 𝜃d𝜃
=
2𝜋
3 0
𝜋
a3(1-cos 𝜃)3 sin 𝜃d𝜃
Putting (1-cos 𝜃) = t,
sin 𝜃d𝜃 = dt
When 𝜃 = o, t=0
𝜃 = 𝜋, t = 2
𝜃 =
𝜋
2
A
(2a,0) O 𝜃 = 0

11. Continue
V =
2𝜋
3
a3
0
2
t3dt
=
2𝜋
3
a3 t4
4
=
8
3
𝜋a3

12. Created By
Calculus
Sem : 1
Branch : Computer
Jinesh Kamdar (160210107024)
Jasmin Makvana (160210107030)
Sagar Pandya (160210107036)
Kushal Gohel (160210107015)
Ishan Shah (160210107046)

13. Thank You
Government Engineering College
Bhavnagar