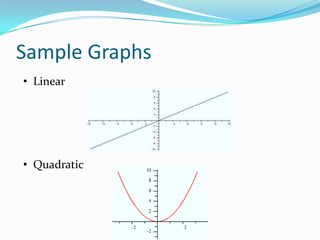
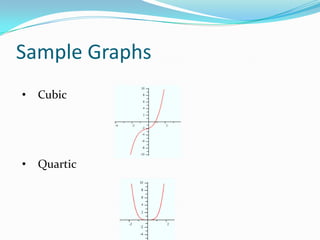
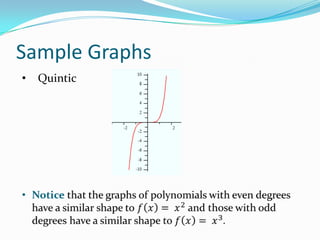
This document provides an introduction to polynomial functions including definitions of key terms like monomial, polynomial, standard form, degree of terms and polynomials, classifying polynomials by number of terms and degree, examples of graphs of low-degree polynomials, and how to combine like terms. It defines a monomial as an expression with variables and numbers, a polynomial as a sum of terms with whole number exponents. Standard form writes polynomials in descending order of exponents. Degree is determined by highest exponent of terms or polynomial. Polynomials are classified by number of terms (monomial, binomial, trinomial, etc.) or degree (linear, quadratic, cubic, etc.). Examples show graphs changing shape with increasing degree. Combining like terms adds coefficients of

1. Introduction to Polynomial FunctionsKaren Shoskey

2. DefinitionsMonomialAn expression that is either a real number, a variable, or a product of real numbers and variablesExamples3𝑐7𝑥22𝑥𝑦3

3. DefinitionsPolynomialAn algebraic expression that is a sum of termsEach term contains only variables with whole number exponents and real number coefficientsExamples3𝑐+77𝑥2−5𝑥+32𝑥4𝑦3+ 3𝑥𝑦2

4. Standard FormA polynomial is in standard form when its terms are written in descending order of exponents from left to rightExamples2𝑥+714𝑐3−5𝑐+84𝑎𝑏2−3𝑎𝑏+2

5. Standard FormParts of a polynomial2𝑥3− 5𝑥2−2𝑥+5 ConstantLeading CoefficientCubic TermLinear TermQuadraticTerm

6. Degree of the TermThe exponent of the variable in the term determines the degree of the termExampleThe degree of 12𝑑5 is 5 or fifth degreeWhat is the degree of 4𝑐3?

7. Degree of the TermThe exponent of the variable in the term determines the degree of the termExampleThe degree of 12𝑑5 is 5 or fifth degreeWhat is the degree of 4𝑐3?Answer: Since the exponent is 3, the term is of degree three or cubic.

8. Degree of the PolynomialThe degree of the polynomial is equal to the largest degree of any term of the polynomialExampleWhat is the degree of 6𝑝2−7𝑝+3?This is second degree, or quadratic, polynomial since the highest exponent is 2.What is the degree of 7𝑥4 −2?

9. Degree of the PolynomialThe degree of the polynomial is equal to the largest degree of any term of the polynomialExampleWhat is the degree of 6𝑝2−7𝑝+3?This is second degree, or quadratic, polynomial since the highest exponent is 2.What is the degree of 7𝑥4 −2?Answer: This polynomial is of degree 4, or quartic, since the largest exponent is 4.

10. Multiple Variable TermsPolynomials and terms can have more than one variable. Here is another example of a polynomial.𝑡4−6𝑠3𝑡2 −12𝑠𝑡+4𝑠4−5The positive integer exponents confirm this example is a polynomial. The polynomial has five terms.

11. Multiple Variable Terms𝑡4−6𝑠3𝑡2 −12𝑠𝑡+4𝑠4−5When a term has multiple variables, the degree of the term is the sum of the exponentswithin the term.t4 has a degree of 4, so it's a 4th order term,-6s3t2 has a degree of 5 (3+2), so it's a 5th order term, -12st has a degree of 2 (1+1), so it's a 2nd order term,4s4 has a degree of 4, so it's a 4th order term,-5 is a constant, so its degree is 0.Since the largest degree of a term in this polynomial is 5, then this is a polynomial of degree 5 or a 5th order polynomial.

12. Classifying Polynomialsby Number of Terms Number Name ExampleOf Terms 1 Monomial 4𝑥 2 Binomial 2𝑥−7 3 Trinomial 14𝑥2+8𝑥 −5 4 + Polynomial 5𝑥3+2𝑥2−𝑥+1

13. Classifying Polynomials by DegreeDegree Name Example 0 Constant 3 1 Linear 2𝑥−7 2 Quadratic 7𝑥2−18𝑥+15 3 Cubic 9𝑥3+16 4 Quartic 23𝑐4+7𝑐−2 5 Quintic−12h5−3h3

14. Classify the PolynomialWrite each polynomial in standard form and classify it by degree and number of terms.−7𝑥+5𝑥4𝑥2−4𝑥+3𝑥3+2

15. Classify the PolynomialWrite each polynomial in standard form and classify it by degree and number of terms.−7𝑥+5𝑥4Answer: 5𝑥4−7𝑥This is a fourth degree (quartic) binomial𝑥2−4𝑥+3𝑥3+2Answer: 3𝑥3+𝑥2−4𝑥+2This is a third degree (cubic) trinomial

16. Sample GraphsLinear

17. QuadraticSample GraphsCubic

18. QuarticSample GraphsQuintic

19. Notice that the graphs of polynomials with even degrees have a similar shape to 𝑓𝑥= 𝑥2 and those with odd degrees have a similar shape to 𝑓𝑥= 𝑥3.

20. Combining Like TermsA polynomial is in simplest form if all like terms have been combined (added). Like terms have the same variable(s) wit the same exponents, but can have different coefficients.2𝑥𝑦2 𝑎𝑛𝑑 15𝑥𝑦2 are like terms6𝑥2𝑦 𝑎𝑛𝑑 6𝑥𝑦2 are NOT like terms

21. Combining Like TermsIf a polynomial has like terms, we simplify it by combining (adding) them.𝑥2+6𝑥𝑦 −4𝑥𝑦+𝑦2This polynomial is simplified by combining the like terms of 𝟔𝒙𝒚 𝑎𝑛𝑑 −𝟒𝒙𝒚, giving us 𝟐𝒙𝒚.𝑥2+𝟐𝒙𝒚+𝑦2

22. Combining Like TermsSimplify the polynomials2𝑐2+9 − 3𝑐2+77𝑥2+8𝑥−5+9𝑥2−9𝑥

23. Combining Like TermsSimplify the polynomials2𝑐2+9 − 3𝑐2+72𝑐2−3𝑐2+ (9+7)−𝑐2+167𝑥2+8𝑥−5+9𝑥2−9𝑥7𝑥2+9𝑥2+8𝑥−9𝑥−516𝑥2−𝑥−5