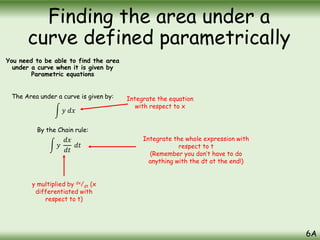
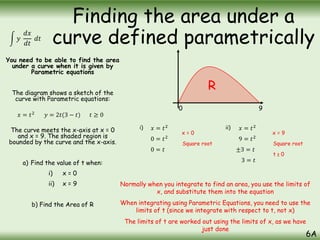
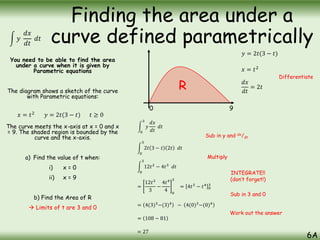
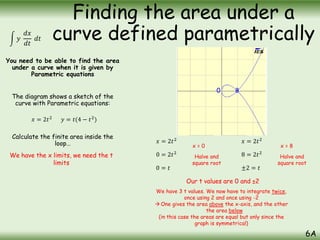
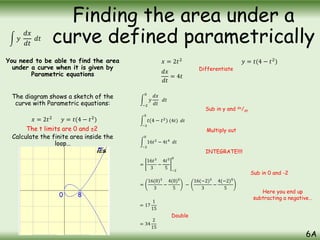
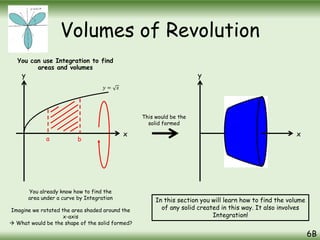
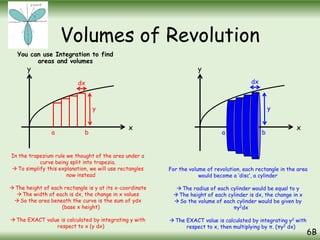
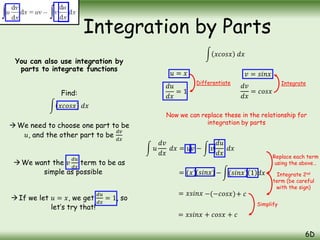
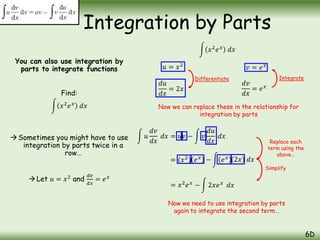
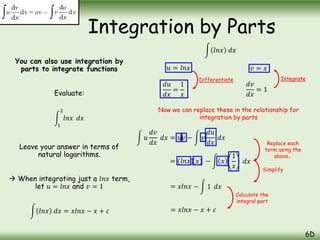
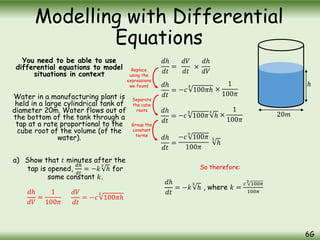
The document is a comprehensive guide on calculus concepts focusing on differentiation, integration, and parametric equations. It includes examples on finding areas and volumes using integration of functions in both Cartesian and parametric forms. Key topics covered are the areas under curves, volume of solids of revolution, and methods to solve these mathematical problems using various techniques.