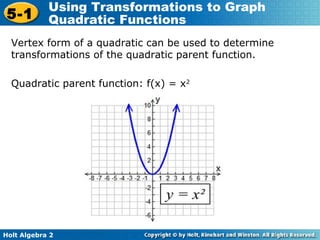
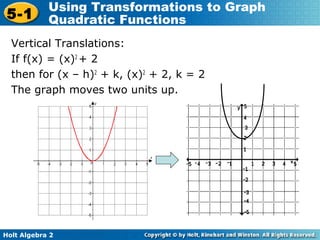
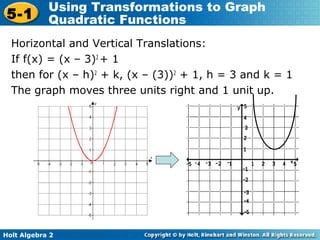
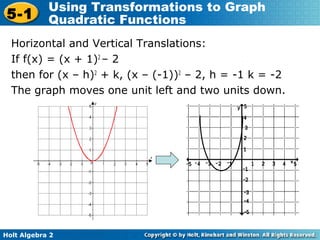
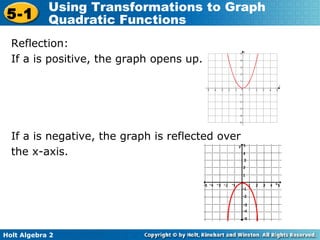
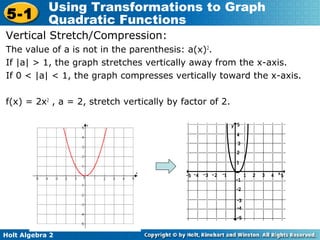
The document discusses transformations of quadratic functions, including horizontal and vertical translations, reflections, and stretches or compressions. Horizontal translations move the graph right or left, depending on the value of h in the function f(x) = (x - h)2. Vertical translations move the graph up or down depending on the value of k. The vertex of the parabola after any transformation is located at the point (h, k). Reflections occur when the value of a in the function f(x) = a(x)2 is negative, causing the graph to reflect over the x-axis. Stretches and compressions occur when the absolute value of a is greater or less than 1, respectively.

1. Holt Algebra 2
5-1
Using Transformations to Graph
Quadratic Functions
The vertex of the parabola is at (h, k).

2. Holt Algebra 2
5-1
Using Transformations to Graph
Quadratic Functions
Vertex form of a quadratic can be used to determine
transformations of the quadratic parent function.
Quadratic parent function: f(x) = x2

3. Holt Algebra 2
5-1
Using Transformations to Graph
Quadratic Functions
Horizontal Translations:
If f(x) = (x – 2)2
then for (x – h)2
,(x – (2))2
, h = 2.
The graph moves two units to the right.

4. Holt Algebra 2
5-1
Using Transformations to Graph
Quadratic Functions
Horizontal Translations:
If f(x) = (x + 3)2
then for (x – h)2
,(x – (-3))2
, h = -3
The graph moves three units to the left.

5. Holt Algebra 2
5-1
Using Transformations to Graph
Quadratic Functions
Vertical Translations:
If f(x) = (x)2
+ 2
then for (x – h)2
+ k, (x)2
+ 2, k = 2
The graph moves two units up.

6. Holt Algebra 2
5-1
Using Transformations to Graph
Quadratic Functions
Vertical Translations:
If f(x) = (x)2
– 1
then for (x – h)2
+ k, (x)2
– 1, k = -1
The graph moves one unit down.

7. Holt Algebra 2
5-1
Using Transformations to Graph
Quadratic Functions
Horizontal and Vertical Translations:
If f(x) = (x – 3)2
+ 1
then for (x – h)2
+ k, (x – (3))2
+ 1, h = 3 and k = 1
The graph moves three units right and 1 unit up.

8. Holt Algebra 2
5-1
Using Transformations to Graph
Quadratic Functions
Horizontal and Vertical Translations:
If f(x) = (x + 1)2
– 2
then for (x – h)2
+ k, (x – (-1))2
– 2, h = -1 k = -2
The graph moves one unit left and two units down.

9. Holt Algebra 2
5-1
Using Transformations to Graph
Quadratic Functions
Horizontal and Vertical Translations:
The vertex of a parabola after a translation is located
at the point (h, k).
If f(x) = (x + 7)2
+ 3
then for (x – h)2
+ k, (x – (-7))2
+ 3, h = -7 k = 3.
The translated vertex is located at the point (-7, 3).

10. Holt Algebra 2
5-1
Using Transformations to Graph
Quadratic Functions
Reflection:
If a is positive, the graph opens up.
If a is negative, the graph is reflected over
the x-axis.

11. Holt Algebra 2
5-1
Using Transformations to Graph
Quadratic Functions
Vertical Stretch/Compression:
The value of a is not in the parenthesis: a(x)2
.
If |a| > 1, the graph stretches vertically away from the x-axis.
If 0 < |a| < 1, the graph compresses vertically toward the x-axis.
f(x) = 2x2
, a = 2, stretch vertically by factor of 2.

12. Holt Algebra 2
5-1
Using Transformations to Graph
Quadratic Functions

13. Holt Algebra 2
5-1
Using Transformations to Graph
Quadratic Functions

14. Holt Algebra 2
5-1
Using Transformations to Graph
Quadratic Functions

15. Holt Algebra 2
5-1
Using Transformations to Graph
Quadratic Functions
Horizontal and Vertical Stretch/Compression:
Create a table of values of a horizontal and vertical stretch and
compression.

16. Holt Algebra 2
5-1
Using Transformations to Graph
Quadratic Functions
Vertical Stretch: f(x) = 2x2
x f(x)
1 2(1)2
= 2
2 2(2)2
= 8
3 2(3)2
= 18
Hor. Compress: f(x) = (2x)2
x f(x)
1 (2∙1)2
=4
2 (2∙2)2
= 16
3 (2∙3)2
=81
a = 2