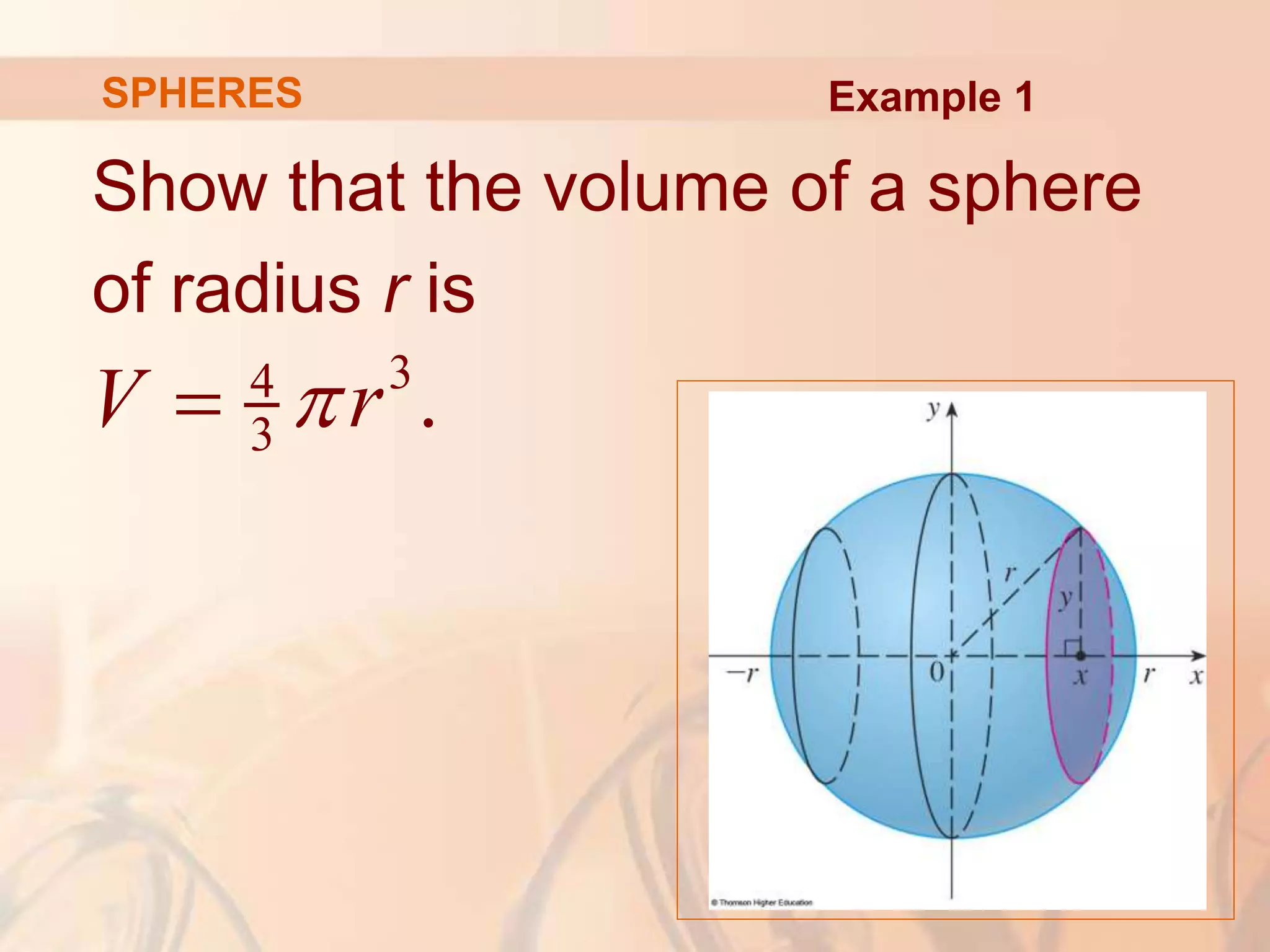
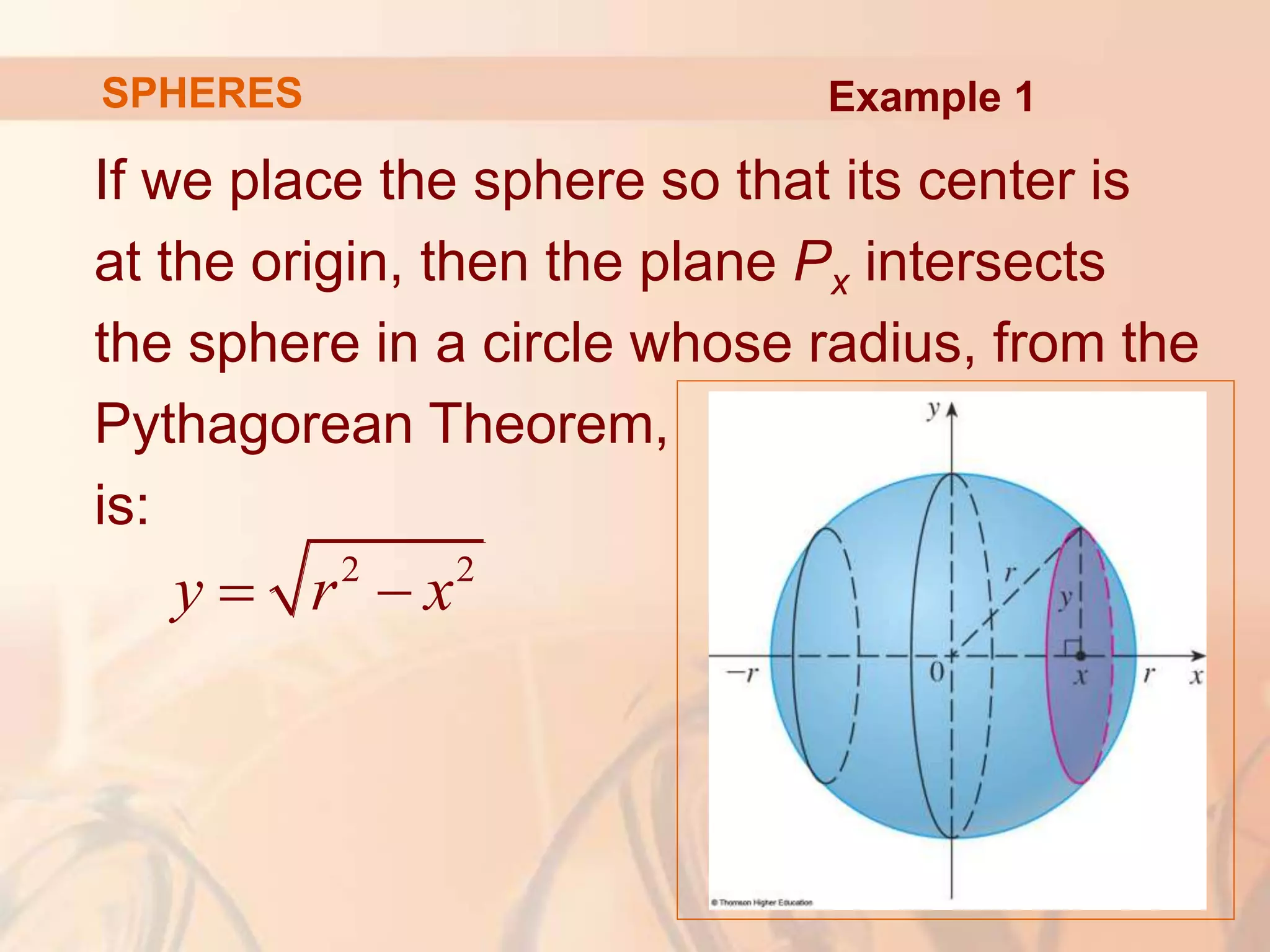
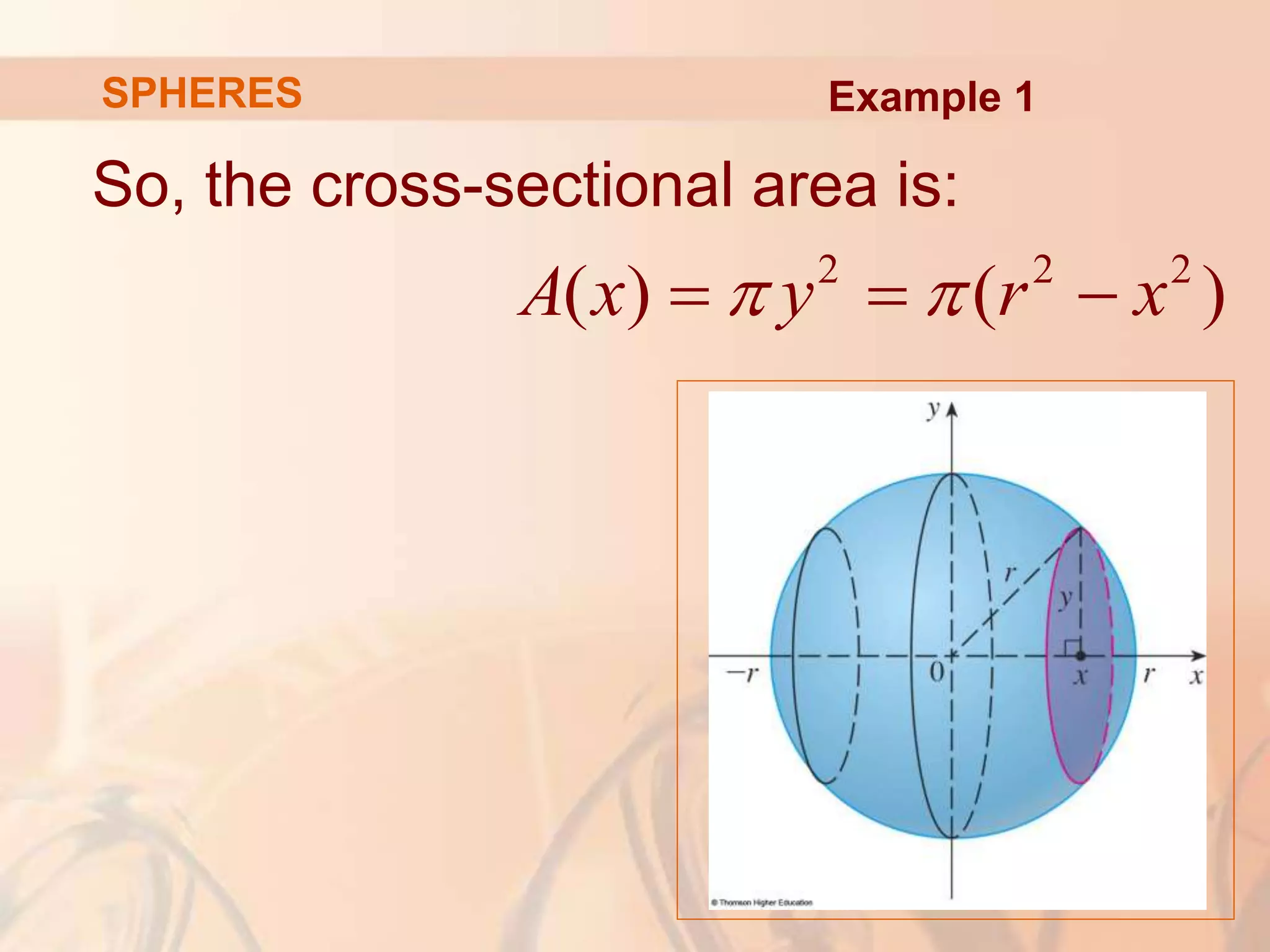
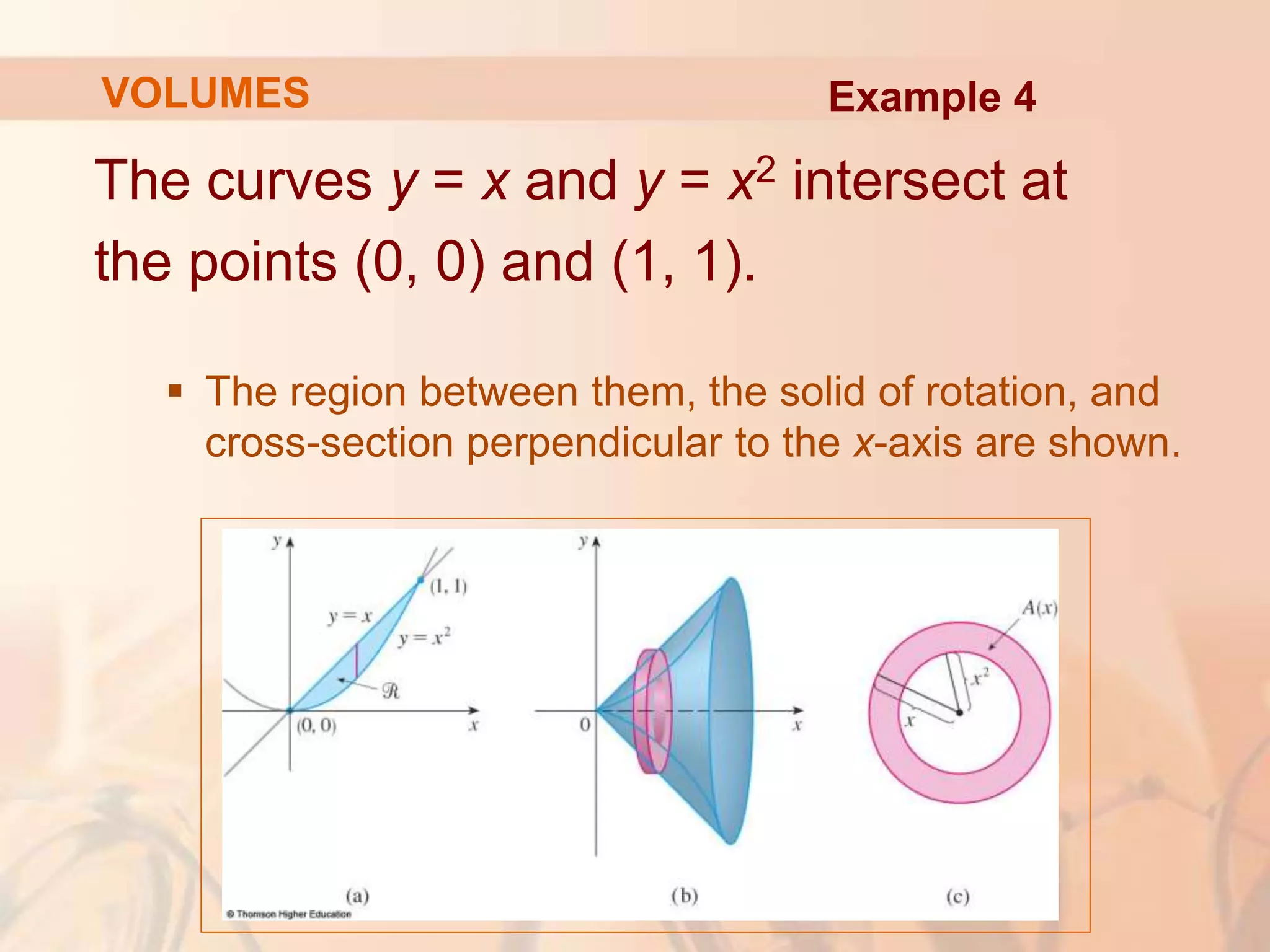
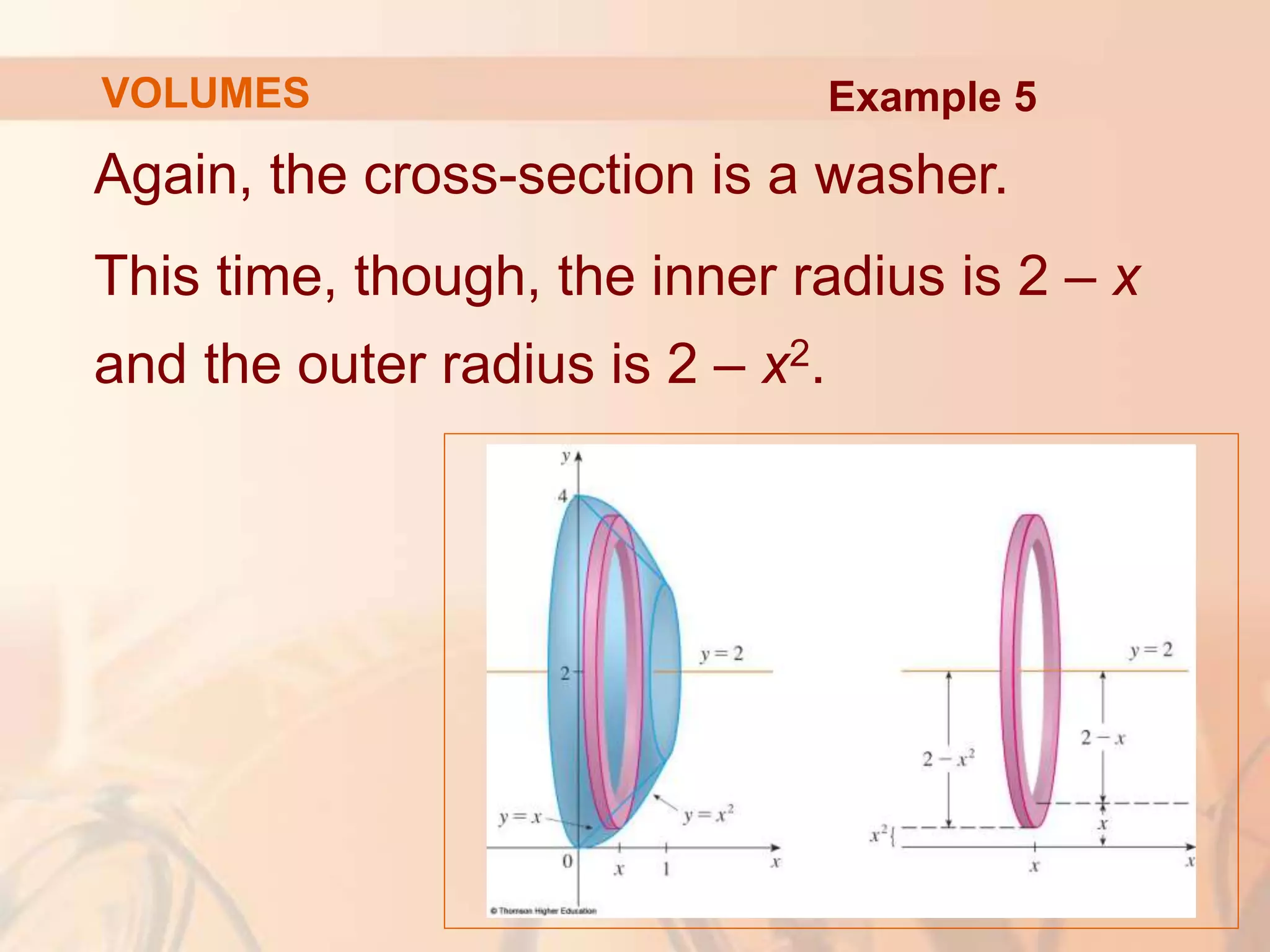
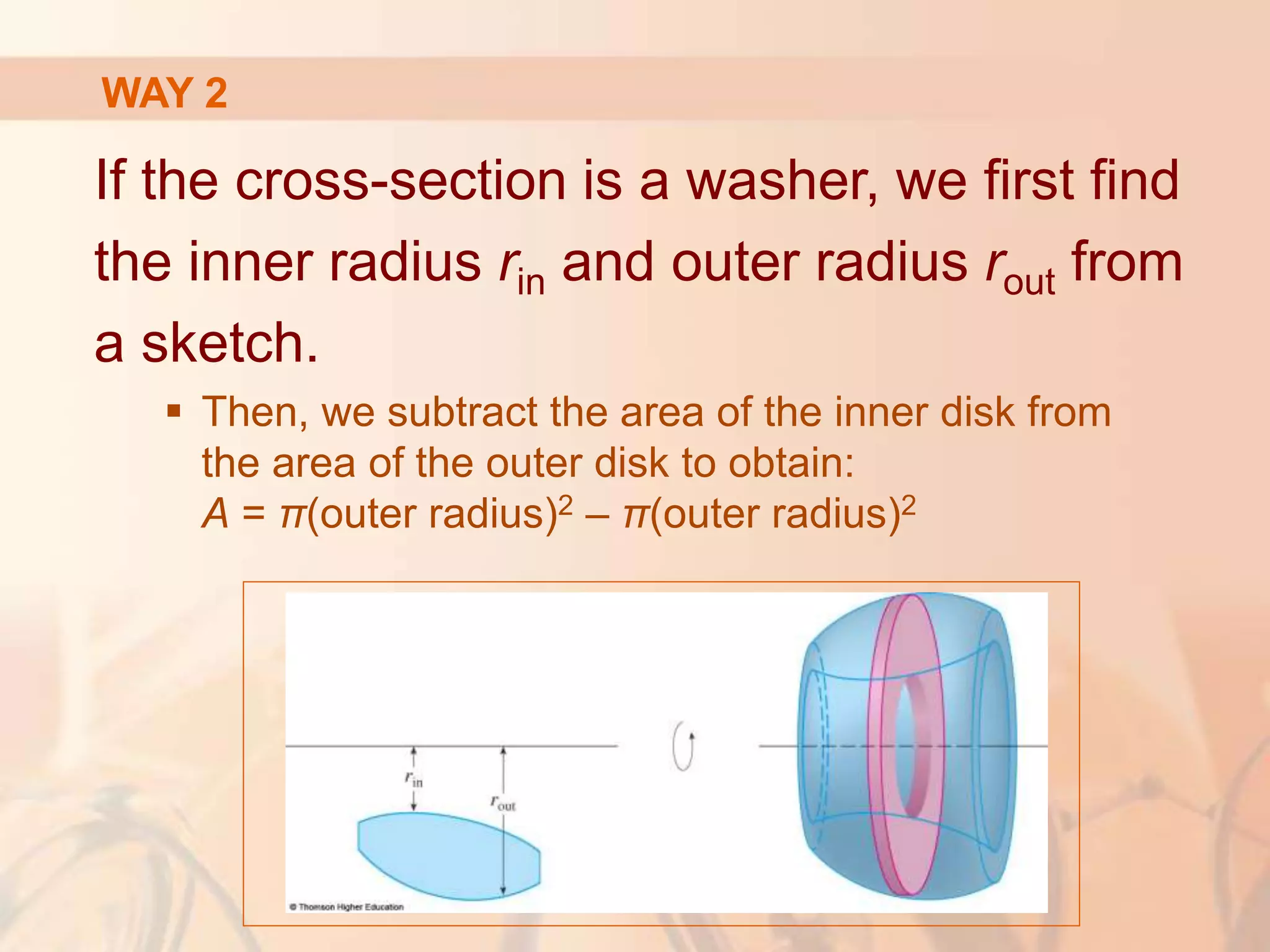
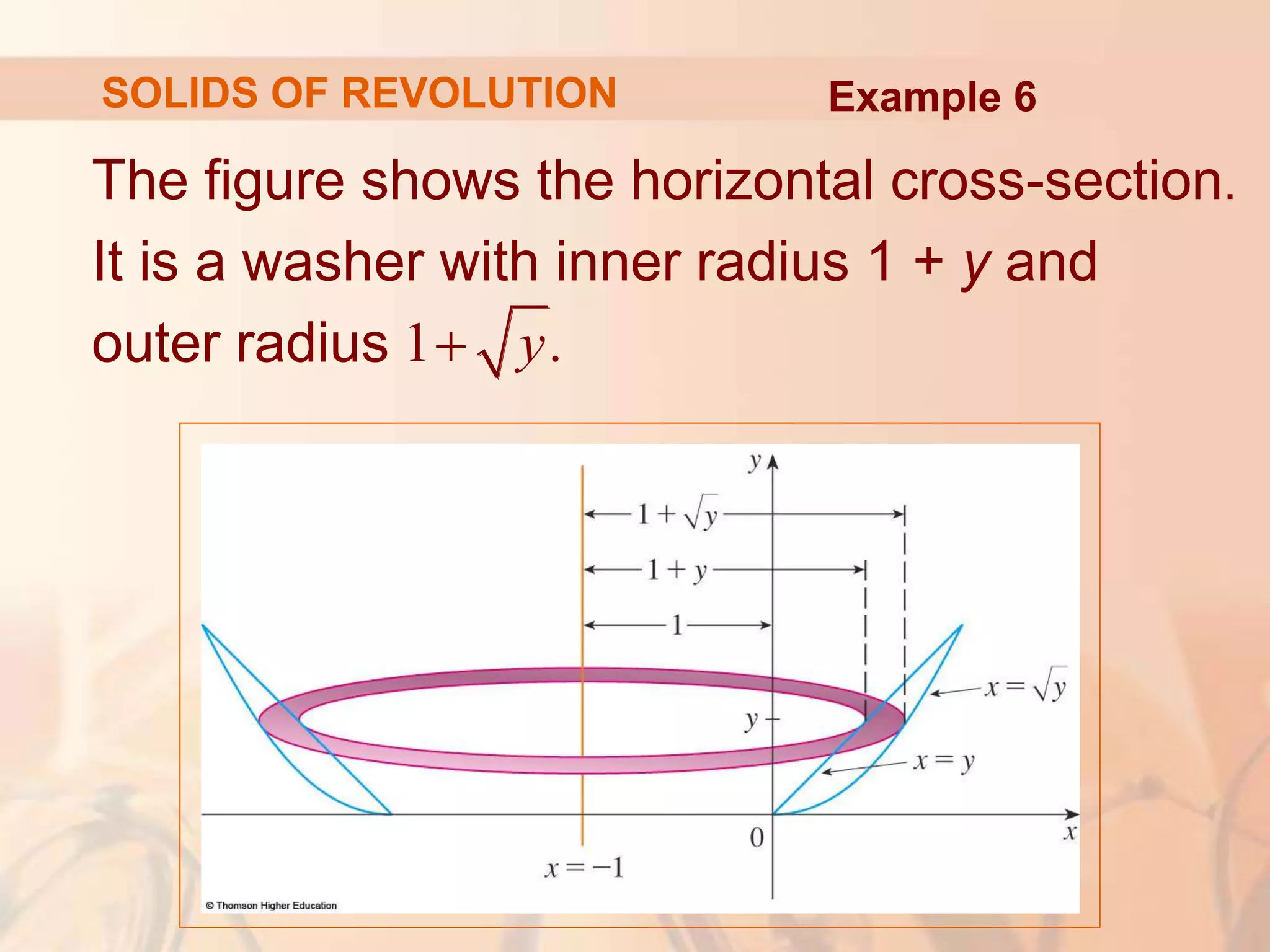
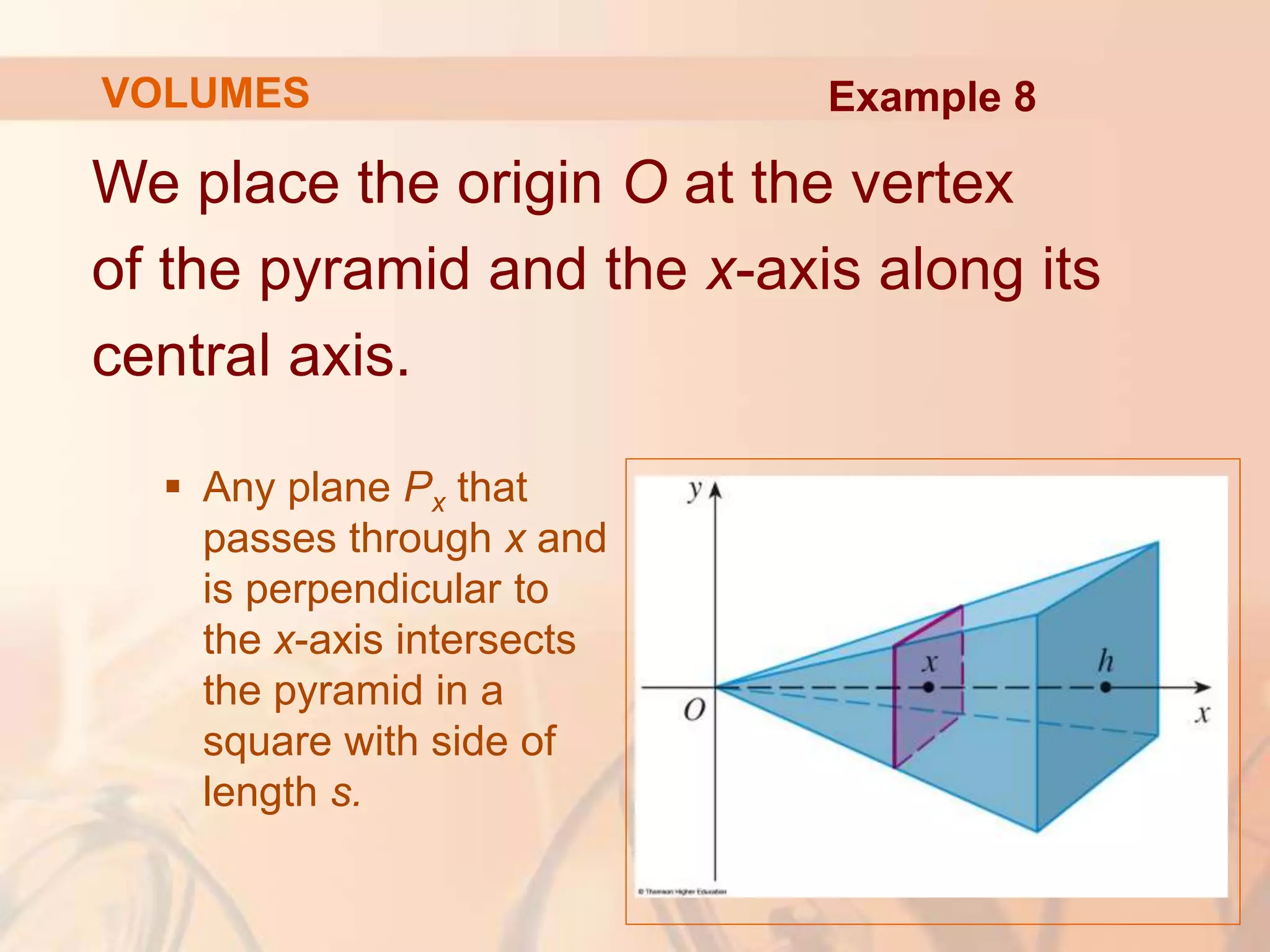
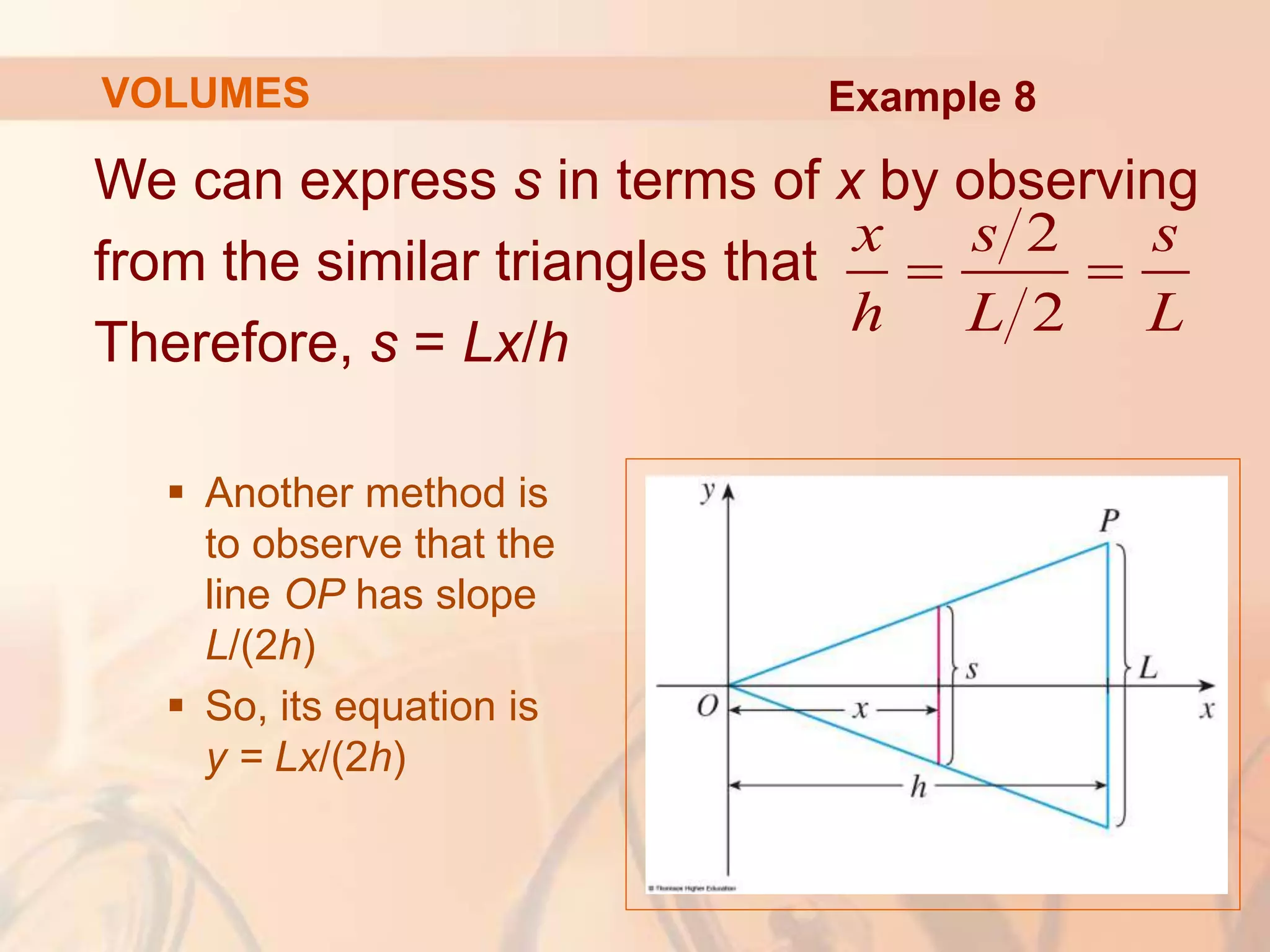
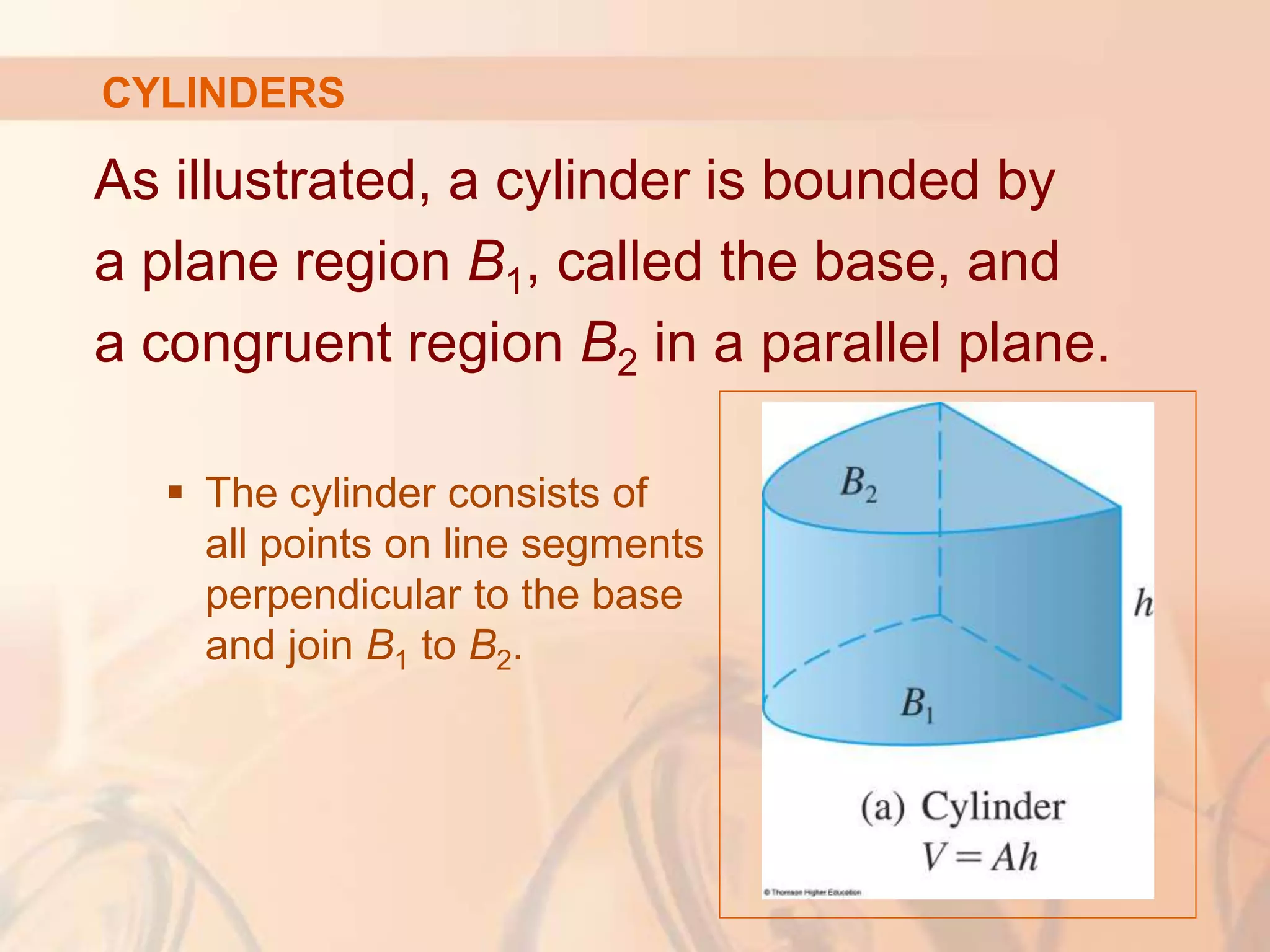
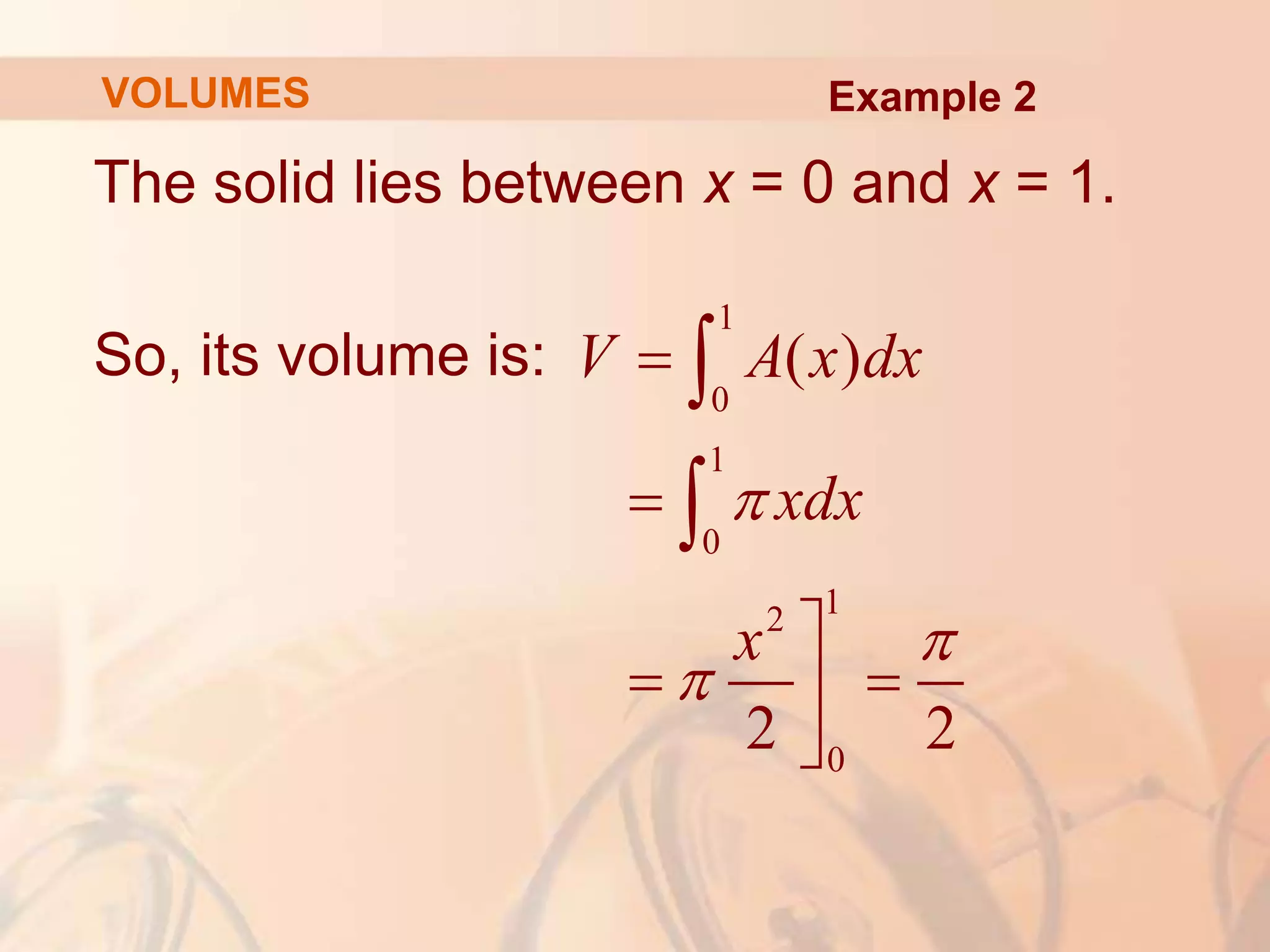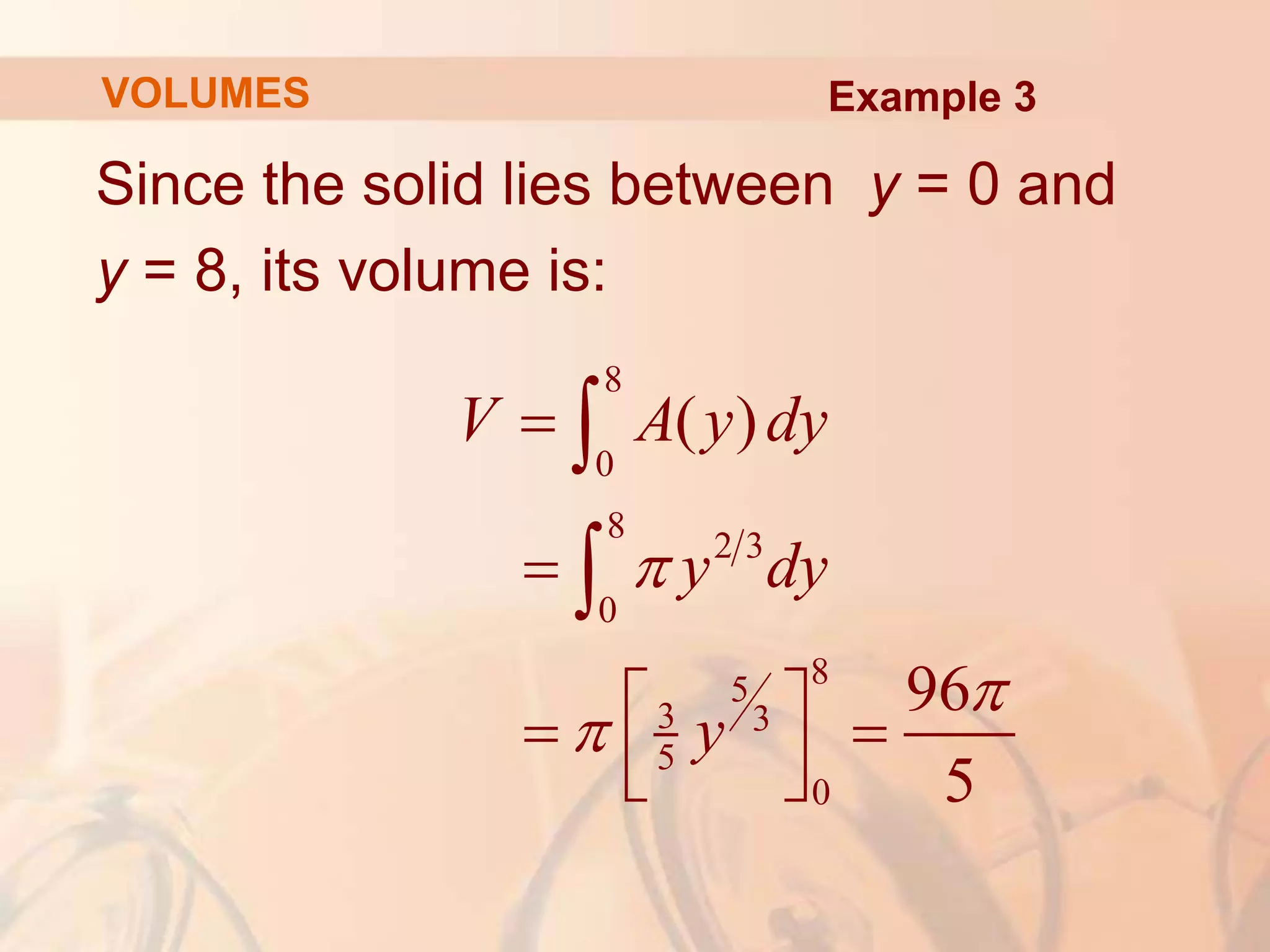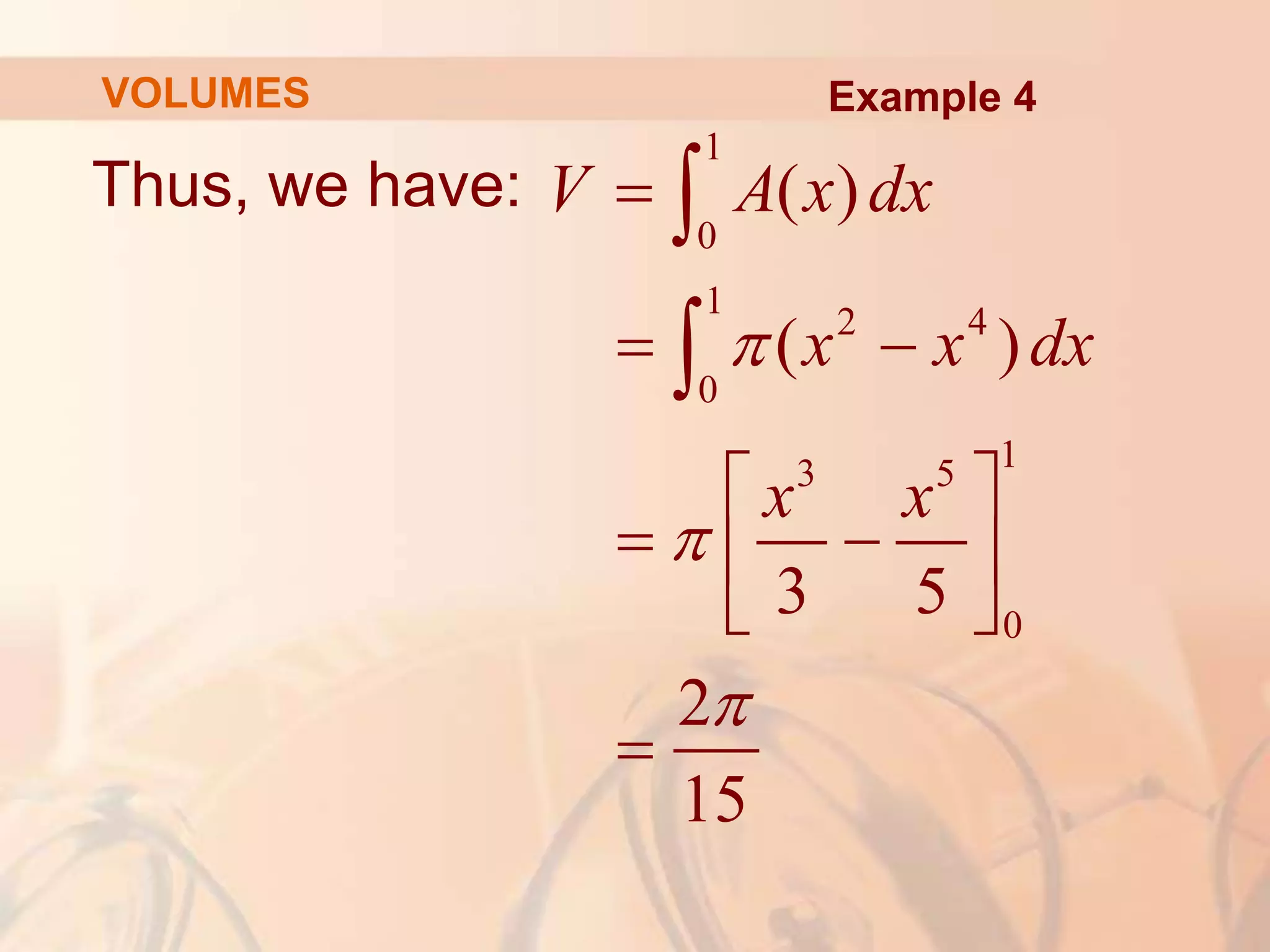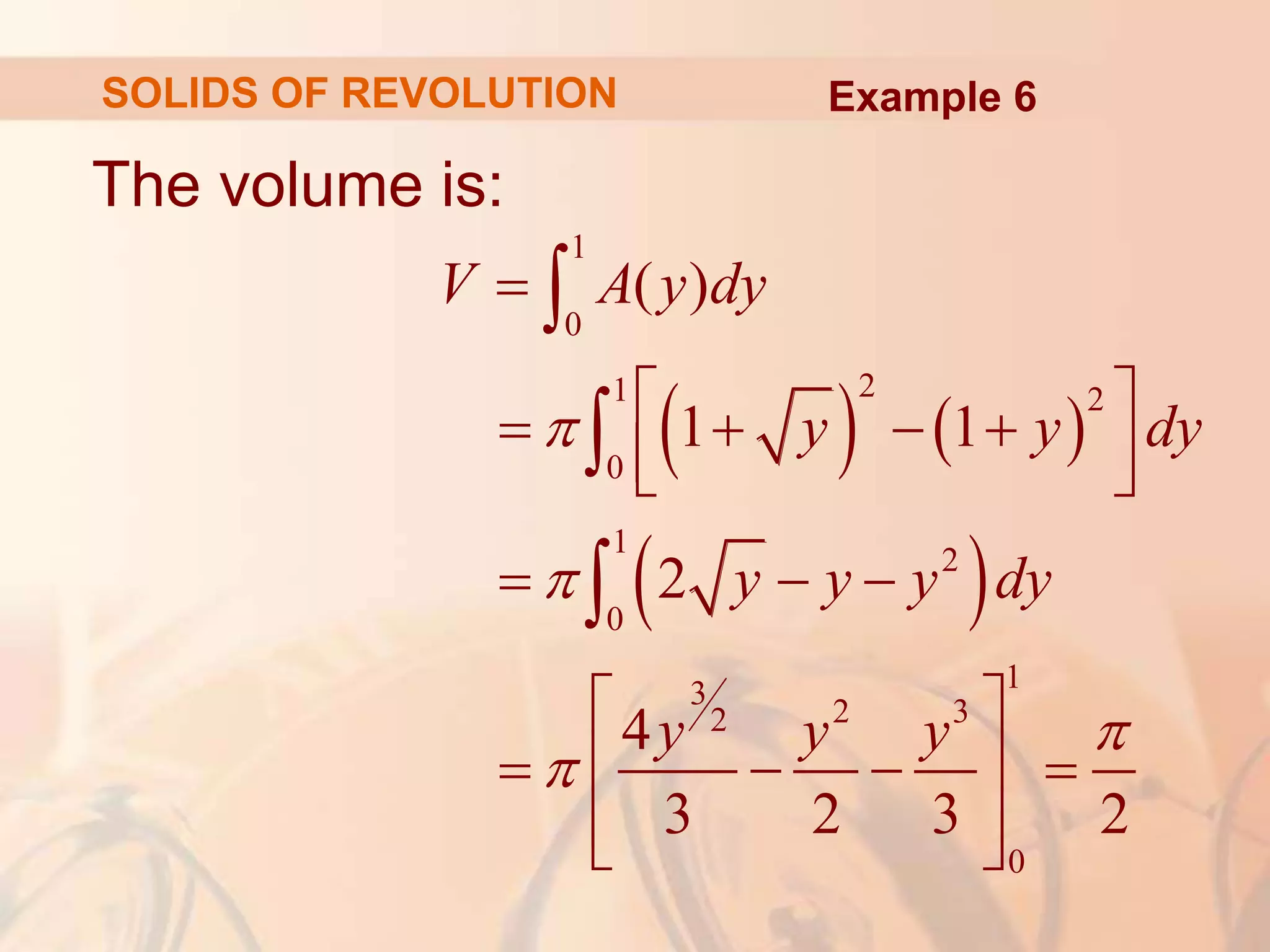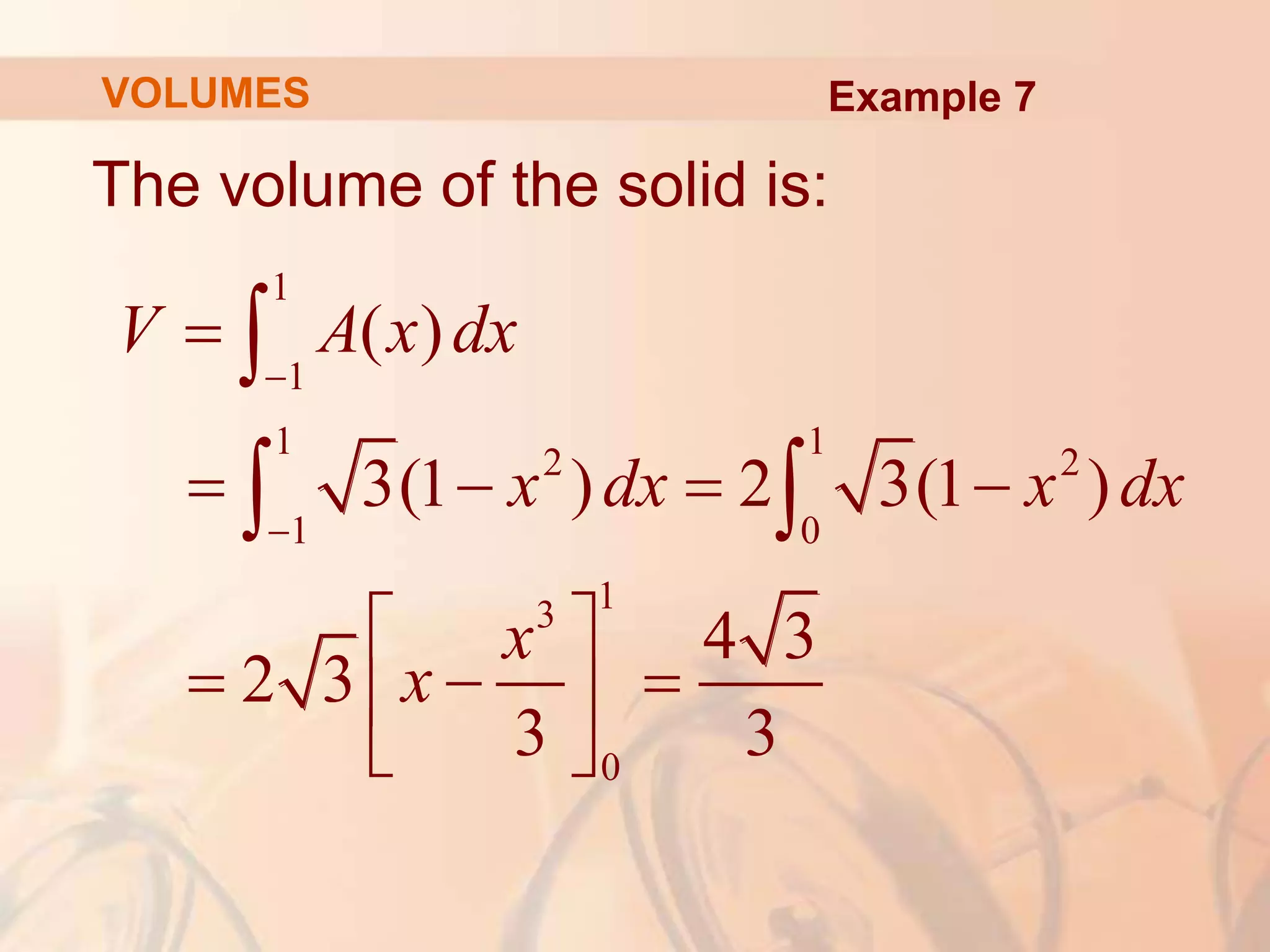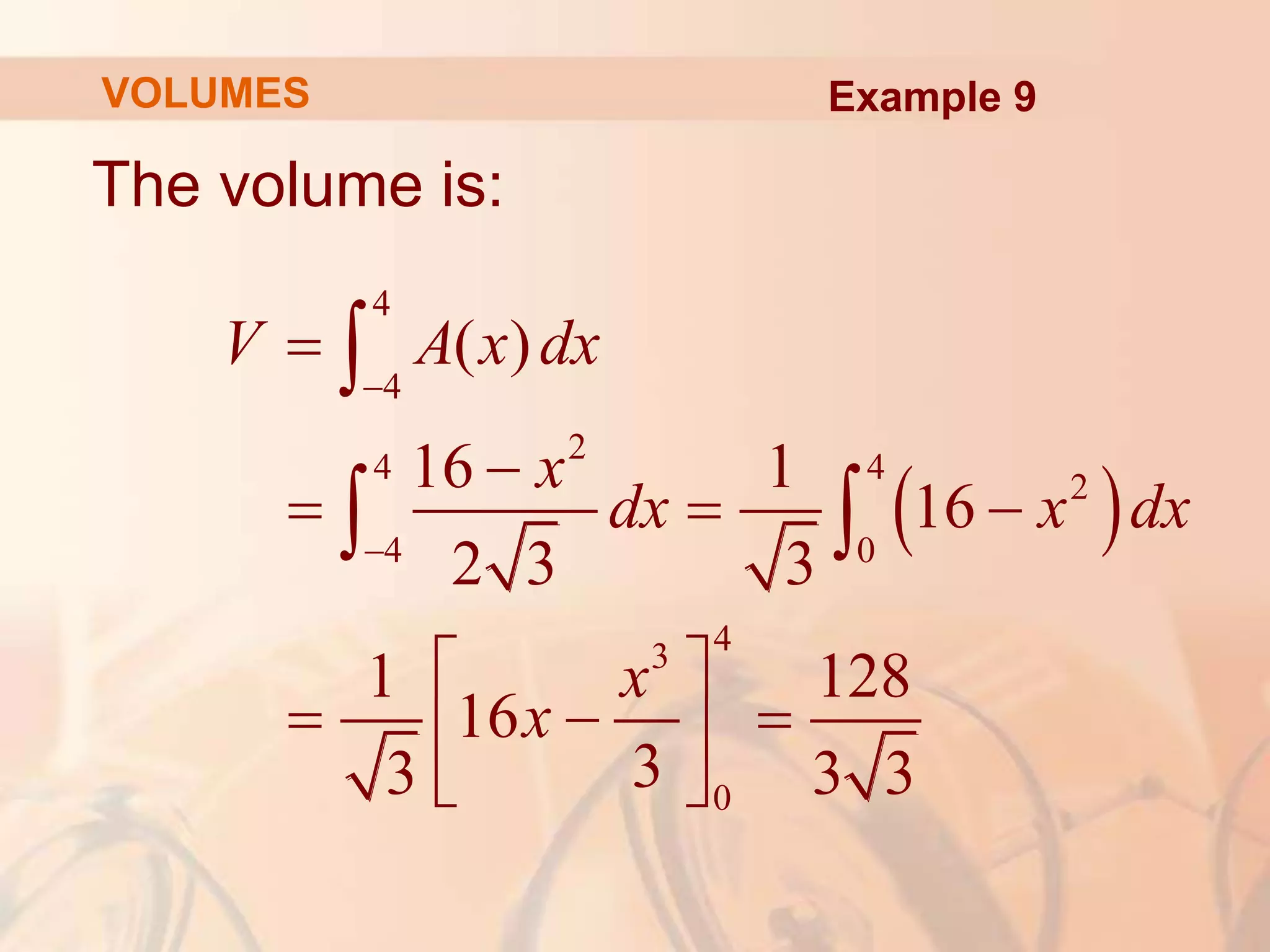This document discusses calculating volumes of solids using integration. It begins by defining volumes precisely using calculus and cross-sectional areas. Cylinders are used as simple examples, where volume equals the area of the base times the height. Irregular solids are approximated as cylinders of infinitesimal thickness to define their volumes through integration. Several examples calculate volumes of solids obtained by rotating regions about axes, with disks or washers as cross-sections. The final examples calculate volumes without revolution by other methods.

1. APPLICATIONS OF INTEGRATION
6

2. 6.2
Volumes
APPLICATIONS OF INTEGRATION
In this section, we will learn about:
Using integration to find out
the volume of a solid.

3. In trying to find the volume of a solid,
we face the same type of problem as
in finding areas.
VOLUMES

4. We have an intuitive idea of what volume
means.
However, we must make this idea precise
by using calculus to give an exact definition
of volume.
VOLUMES

5. We start with a simple type of solid
called a cylinder or, more precisely,
a right cylinder.
VOLUMES

6. As illustrated, a cylinder is bounded by
a plane region B1, called the base, and
a congruent region B2 in a parallel plane.
 The cylinder consists of
all points on line segments
perpendicular to the base
and join B1 to B2.
CYLINDERS

7. If the area of the base is A and the height of
the cylinder (the distance from B1 to B2) is h,
then the volume V of the cylinder is defined
as:
V = Ah
CYLINDERS

8. In particular, if the base is a circle with
radius r, then the cylinder is a circular
cylinder with volume V = πr2h.
CYLINDERS

9. If the base is a rectangle with length l and
width w, then the cylinder is a rectangular box
(also called a rectangular parallelepiped) with
volume V = lwh.
RECTANGULAR PARALLELEPIPEDS

10. For a solid S that isn’t a cylinder, we first
‘cut’ S into pieces and approximate each
piece by a cylinder.
 We estimate the volume of S by adding the volumes
of the cylinders.
 We arrive at the exact volume of S through a limiting
process in which the number of pieces becomes large.
IRREGULAR SOLIDS

11. We start by intersecting S with a plane
and obtaining a plane region that is called
a cross-section of S.
IRREGULAR SOLIDS

12. Let A(x) be the area of the cross-section of S
in a plane Px perpendicular to the x-axis and
passing through the point x, where a ≤ x ≤ b.
 Think of slicing S
with a knife
through x and
computing the
area of this slice.
IRREGULAR SOLIDS

13. The cross-sectional area A(x) will vary
as x increases from a to b.
IRREGULAR SOLIDS

14. We divide S into n ‘slabs’ of equal width ∆x
using the planes Px1, Px2, . . . to slice the solid.
 Think of slicing a loaf of bread.
IRREGULAR SOLIDS

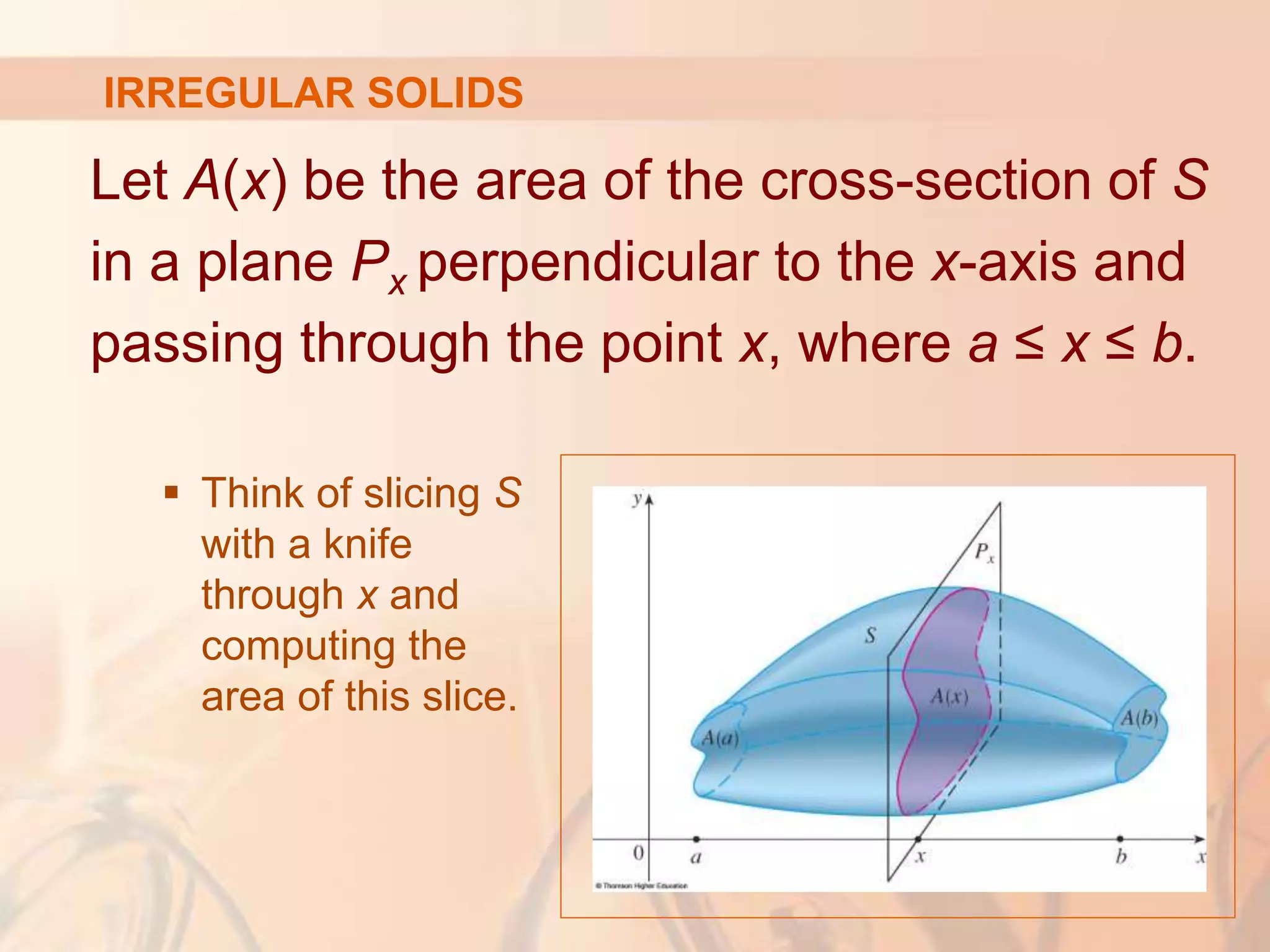
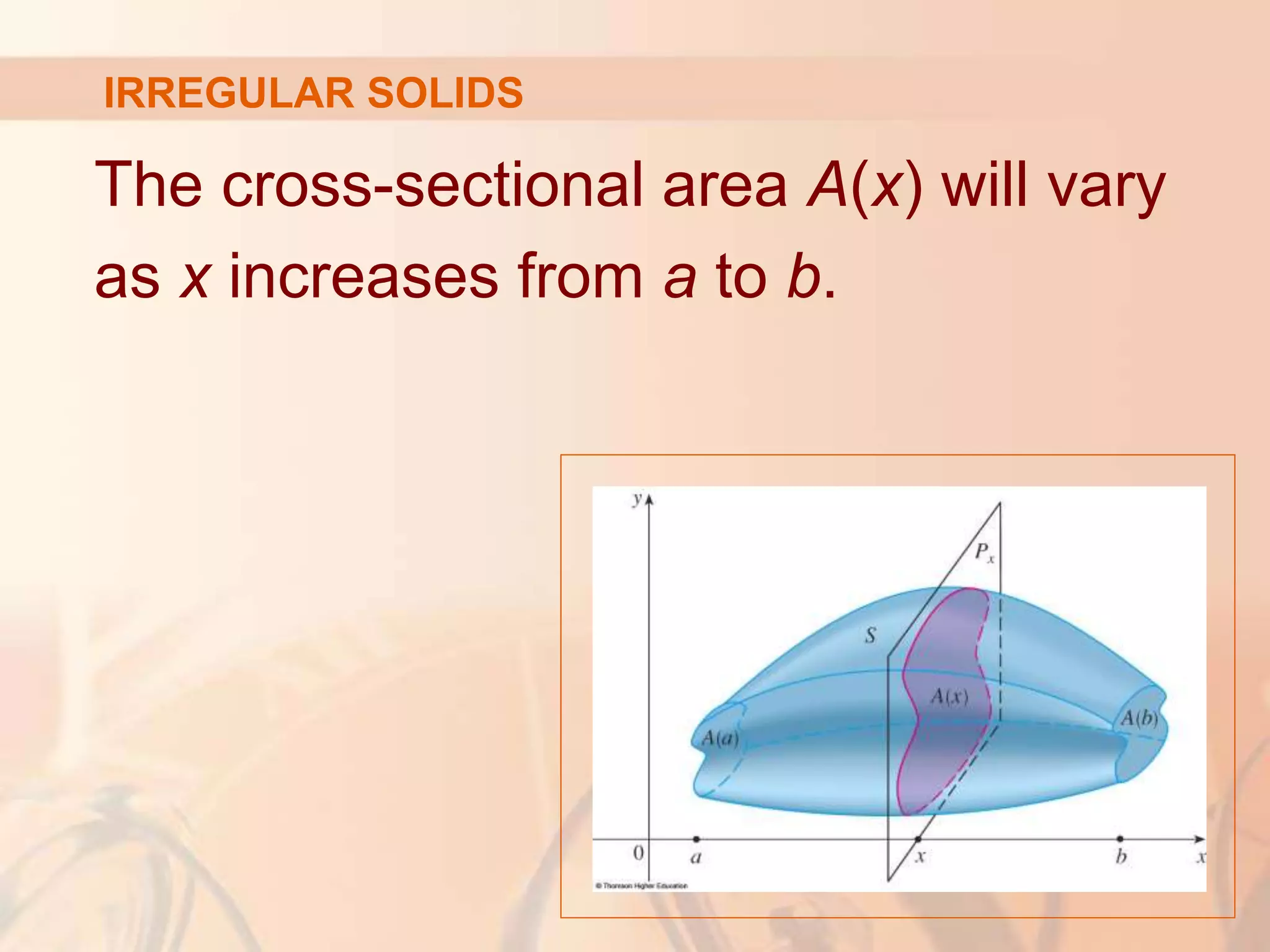
15. If we choose sample points xi* in [xi - 1, xi], we
can approximate the i th slab Si (the part of S
that lies between the planes and ) by a
cylinder with base area A(xi*) and ‘height’ ∆x.
1
i
x
P  i
x
P
IRREGULAR SOLIDS

16. The volume of this cylinder is A(xi*).
So, an approximation to our intuitive
conception of the volume of the i th slab Si
is:
( ) ( *)
 
i
V S A xi x
IRREGULAR SOLIDS

17. Adding the volumes of these slabs, we get an
approximation to the total volume (that is,
what we think of intuitively as the volume):
 This approximation appears to become
better and better as n → ∞.
 Think of the slices as becoming thinner and thinner.
1
( *)
n
i
i
V A x x

 

IRREGULAR SOLIDS

18. Therefore, we define the volume as the limit
of these sums as n → ∞).
However, we recognize the limit of Riemann
sums as a definite integral and so we have
the following definition.
IRREGULAR SOLIDS

19. Let S be a solid that lies between x = a
and x = b.
If the cross-sectional area of S in the plane Px,
through x and perpendicular to the x-axis,
is A(x), where A is a continuous function, then
the volume of S is:
1
lim ( *) ( )
n b
i a
x
i
V A x x A x dx


  
 
DEFINITION OF VOLUME

20. When we use the volume formula
, it is important to remember
that A(x) is the area of a moving
cross-section obtained by slicing through
x perpendicular to the x-axis.
VOLUMES
( )
b
a
V A x dx
 

21. Notice that, for a cylinder, the cross-sectional
area is constant: A(x) = A for all x.
 So, our definition of volume gives:
 This agrees with the formula V = Ah.
 
b
a
V Adx A b a
  

VOLUMES

22. Show that the volume of a sphere
of radius r is
3
4
3 .
V r


Example 1
SPHERES

23. If we place the sphere so that its center is
at the origin, then the plane Px intersects
the sphere in a circle whose radius, from the
Pythagorean Theorem,
is:
2 2
y r x
 
Example 1
SPHERES

24. So, the cross-sectional area is:
2 2 2
( ) ( )
A x y r x
 
  
Example 1
SPHERES

25. Using the definition of volume with a = -r and
b = r, we have:
(The integrand is even.)
 
2 2
2 2
0
3 3
2 3
0
3
4
3
( )
2 ( )
2 2
3 3
r r
r r
r
r
V A x dx r x dx
r x dx
x r
r x r
r


 

 
  
 
   
   
 
 
   

 

Example 1
SPHERES

26. The figure illustrates the definition of volume
when the solid is a sphere with radius r = 1.
 From the example, we know that the volume of
the sphere is
 The slabs are circular cylinders, or disks.
4
3 4.18879
 
SPHERES

27. The three parts show the geometric
interpretations of the Riemann sums
when n = 5, 10,
and 20 if we choose the sample points xi*
to be the midpoints .
2 2
1 1
( ) (1 )
n n
i i
i i
A x x x x

 
   
 
i
x
SPHERES

28. Notice that as we increase the number
of approximating cylinders, the corresponding
Riemann sums become closer to the true
volume.
SPHERES

29. Find the volume of the solid obtained by
rotating about the x-axis the region under
the curve from 0 to 1.
Illustrate the definition of volume by sketching
a typical approximating cylinder.
y x

Example 2
VOLUMES

30. The region is shown in the first figure.
If we rotate about the x-axis, we get the solid
shown in the next figure.
 When we slice through the point x, we get a disk
with radius .
VOLUMES
x
Example 2

31. The area of the cross-section is:
The volume of the approximating cylinder
(a disk with thickness ∆x) is:
2
( ) ( )
A x x x
 
 
( )
A x x x x

  
Example 2
VOLUMES

32. The solid lies between x = 0 and x = 1.
So, its volume is:
1
0
1
0
1
2
0
( )
2 2
V A x dx
xdx
x






 




VOLUMES Example 2

33. Find the volume of the solid obtained
by rotating the region bounded by y = x3,
Y = 8, and x = 0 about the y-axis.
Example 3
VOLUMES

34. As the region is rotated about the y-axis, it
makes sense to slice the solid perpendicular
to the y-axis and thus to integrate with
respect to y.
 Slicing at height y,
we get a circular
disk with radius x,
where
VOLUMES Example 3
3
x y


35. So, the area of a cross-section through y is:
The volume of the approximating
cylinder is:
2 2 2/3
3
( ) ( )
A y x y y
  
  
2/3
( )
A y y y y

  
Example 3
VOLUMES

36. Since the solid lies between y = 0 and
y = 8, its volume is:
8
0
8
2 3
0
8
5
3 3
5
0
( )
96
5
V A y dy
y dy
y





 
 
 
 


Example 3
VOLUMES

37. The region R enclosed by the curves y = x
and y = x2 is rotated about the x-axis.
Find the volume of the resulting solid.
Example 4
VOLUMES

38. The curves y = x and y = x2 intersect at
the points (0, 0) and (1, 1).
 The region between them, the solid of rotation, and
cross-section perpendicular to the x-axis are shown.
VOLUMES Example 4

39. A cross-section in the plane Px has the shape
of a washer (an annular ring) with inner
radius x2 and outer radius x.
Example 4
VOLUMES

40. Thus, we find the cross-sectional area by
subtracting the area of the inner circle from
the area of the outer circle:
2 2 2
2 4
( ) ( )
( )
A x x x
x x
 

 
 
VOLUMES Example 4

41. Thus, we have:
1
0
1
2 4
0
1
3 5
0
( )
( )
3 5
2
15
V A x dx
x x dx
x x




 
 
 
 
 



Example 4
VOLUMES

42. Find the volume of the solid obtained
by rotating the region in Example 4
about the line y = 2.
Example 5
VOLUMES

43. Again, the cross-section is a washer.
This time, though, the inner radius is 2 – x
and the outer radius is 2 – x2.
VOLUMES Example 5

44. The cross-sectional area is:
2 2 2
( ) (2 ) (2 )
A x x x
 
   
Example 5
VOLUMES

45. So, the volume is:
 
 
1
0
1 2
2 2
0
1
4 2
0
1
5 3 2
0
( )
2 (2 )
5 4
8
5 4
5 3 2 5





 
   
 
 
  
 
   
 
 



V A x dx
x x dx
x x x dx
x x x
VOLUMES Example 5

46. The solids in Examples 1–5 are all
called solids of revolution because
they are obtained by revolving a region
about a line.
SOLIDS OF REVOLUTION

47. In general, we calculate the volume of
a solid of revolution by using the basic
defining formula
 
( ) or
b d
a c
V A x dx V A y dy
 
 
SOLIDS OF REVOLUTION

48. We find the cross-sectional area
A(x) or A(y) in one of the following
two ways.
SOLIDS OF REVOLUTION

49. If the cross-section is a disk, we find
the radius of the disk (in terms of x or y)
and use:
A = π(radius)2
WAY 1

50. If the cross-section is a washer, we first find
the inner radius rin and outer radius rout from
a sketch.
 Then, we subtract the area of the inner disk from
the area of the outer disk to obtain:
A = π(outer radius)2 – π(outer radius)2
WAY 2

51. Find the volume of the solid obtained
by rotating the region in Example 4
about the line x = -1.
Example 6
SOLIDS OF REVOLUTION

52. The figure shows the horizontal cross-section.
It is a washer with inner radius 1 + y and
outer radius
Example 6
1 .
y

SOLIDS OF REVOLUTION

53. So, the cross-sectional area is:
   
2 2
2 2
( ) (outer radius) (inner radius)
1 1
A y
y y
 
 
 
   
Example 6
SOLIDS OF REVOLUTION

54. The volume is:
   
 
1
0
2
1 2
0
1
2
0
1
3
2 3
2
0
( )
1 1
2
4
3 2 3 2
V A y dy
y y dy
y y y dy
y y y





 
   
 
 
  
 
 
   
 
 



Example 6
SOLIDS OF REVOLUTION

55. In the following examples, we find
the volumes of three solids that are
not solids of revolution.
VOLUMES

56. The figure shows a solid with a circular base
of radius 1. Parallel cross-sections
perpendicular to the base are equilateral
triangles.
Find the volume of the solid.
Example 7
VOLUMES

57. Let’s take the circle to be x2 + y2 = 1.
The solid, its base, and a typical cross-section
at a distance x from the origin are shown.
Example 7
VOLUMES

58. As B lies on the circle, we have
So, the base of the triangle ABC is
|AB| =
2
1
y x
 
2
2 1 x

Example 7
VOLUMES

59. Since the triangle is equilateral, we see
that its height is 2
3 3 1
y x
 
VOLUMES Example 7

60. Thus, the cross-sectional area is :
VOLUMES Example 7
2 2
1
2
2
( ) 2 1 3 1
3(1 )
A x x x
x
    
 

61. The volume of the solid is:
1
1
1 1
2 2
1 0
1
3
0
( )
3(1 ) 2 3(1 )
4 3
2 3
3 3
V A x dx
x dx x dx
x
x



   
 
  
 
 

 
Example 7
VOLUMES

62. Find the volume of a pyramid
whose base is a square with side L
and whose height is h.
Example 8
VOLUMES

63. We place the origin O at the vertex
of the pyramid and the x-axis along its
central axis.
 Any plane Px that
passes through x and
is perpendicular to
the x-axis intersects
the pyramid in a
square with side of
length s.
VOLUMES Example 8

64. We can express s in terms of x by observing
from the similar triangles that
Therefore, s = Lx/h
 Another method is
to observe that the
line OP has slope
L/(2h)
 So, its equation is
y = Lx/(2h)
2
2
x s s
h L L
 
Example 8
VOLUMES

65. Thus, the cross-sectional area is:
VOLUMES Example 8
2
2 2
2
( )
L
A x s x
h
 

66. The pyramid lies between x = 0 and x = h.
So, its volume is:
0
2
2
2
0
2 3 2
2
0
( )
3 3
h
h
h
V A x dx
L
x dx
h
L x L h
h



 




Example 8
VOLUMES

67. In the example, we didn’t need to place
the vertex of the pyramid at the origin.
 We did so merely to make the equations
simple.
NOTE

68. Instead, if we had placed the center of
the base at the origin and the vertex on
the positive y-axis, as in the figure, you can
verify that we would have
obtained the integral:
2
2
2
0
2
( )
3
h L
V h y dy
h
L h
 


NOTE

69. A wedge is cut out of a circular cylinder of
radius 4 by two planes. One plane is
perpendicular to the axis of the cylinder.
The other intersects the first at an angle of 30°
along a diameter of the cylinder.
Find the volume of the wedge.
Example 9
VOLUMES

70. If we place the x-axis along the diameter
where the planes meet, then the base of
the solid is a semicircle
with equation
-4 ≤ x ≤ 4
2
16 ,
y x
 
VOLUMES Example 9

71. A cross-section perpendicular to the x-axis at
a distance x from the origin is a triangle ABC,
whose base is and whose height
is |BC| = y tan 30° =
2
16
y x
 
2
16 3.
x

Example 9
VOLUMES

72. Thus, the cross-sectional area is:
2 2
1
2
2
1
( ) 16 16
3
16
2 3
A x x x
x
   


VOLUMES Example 9

73. The volume is:
 
4
4
2
4 4
2
4 0
4
3
0
( )
16 1
16
2 3 3
1 128
16
3
3 3 3
V A x dx
x
dx x dx
x
x




  
 
  
 
 

 
Example 9
VOLUMES