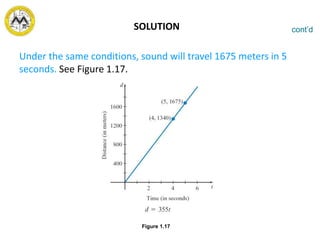
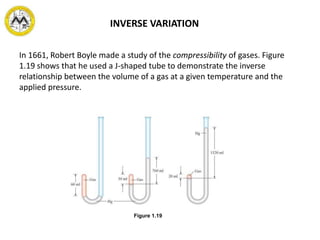
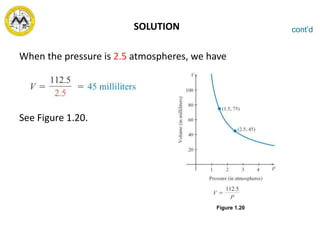
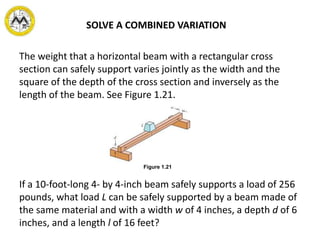
Ratio is an indicated quotient of two quantities that can be expressed as a fraction. A proportion is a statement that indicates the equality of two ratios. There are three main types of variation: direct variation, where y varies directly with x; inverse variation, where y varies inversely with x; and joint variation, where z varies jointly as two other variables.