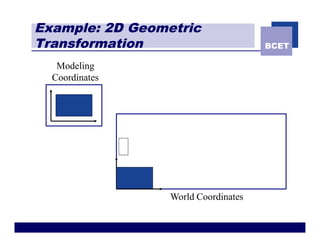
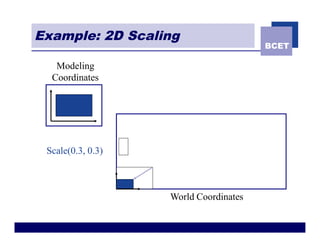
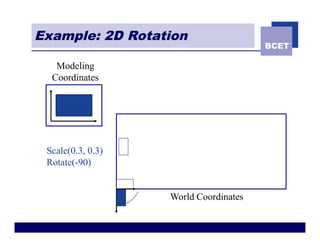
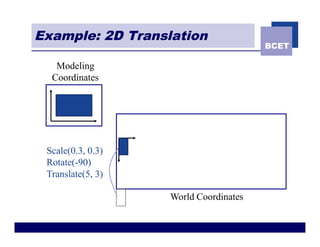
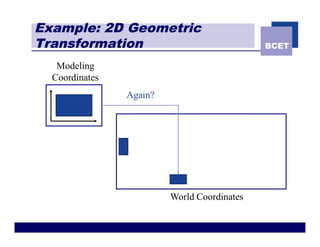
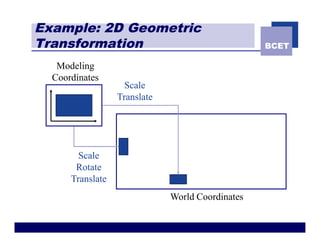
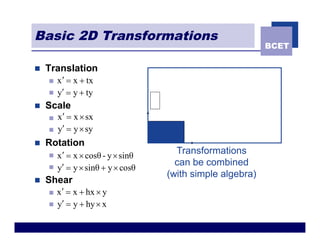
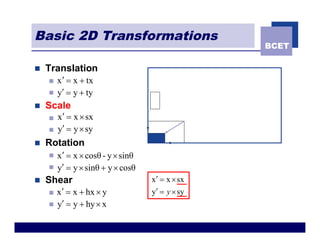
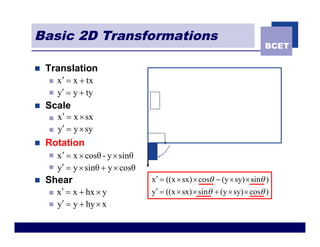
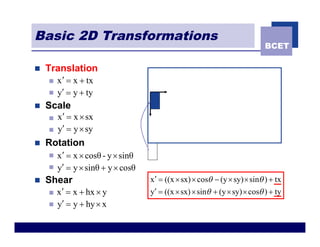
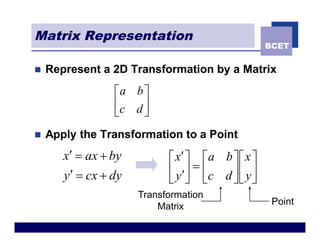
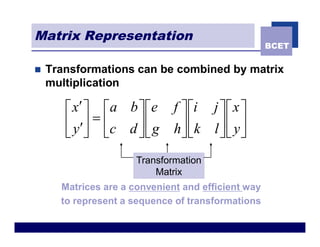
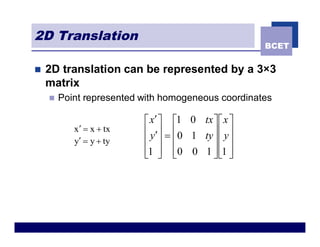
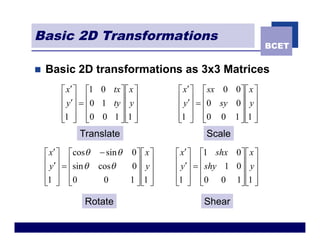
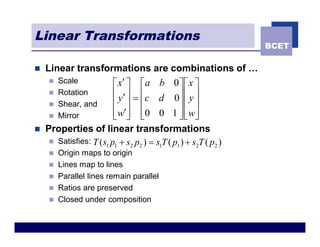
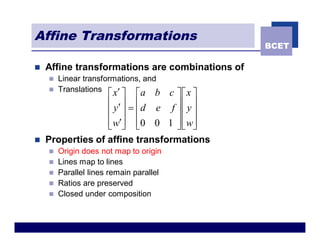
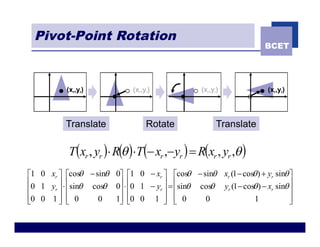
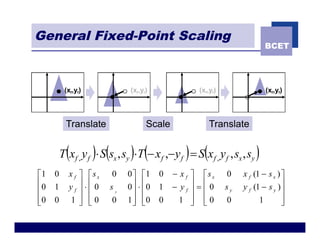
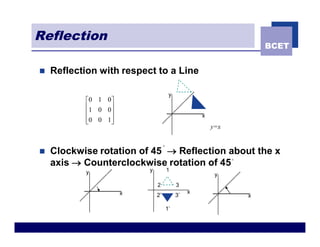
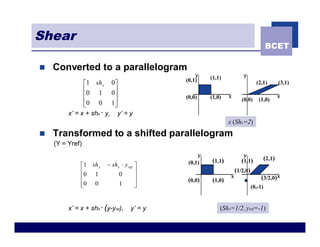
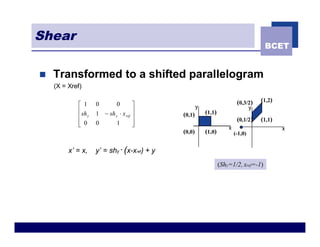
The document discusses 2D geometric transformations including translation, rotation, scaling, and shearing. It introduces representing transformations using 2x2 matrices and homogeneous coordinates using 3x3 matrices. Transformations can be combined by matrix multiplication, allowing multiple transformations to be applied sequentially in an efficient manner.

1. Graphics
2D Geometric
Transformations
Sudipta Mondal
sudipta.hit@gmail.com

2. Contents
BCET
n Definition & Motivation
n 2D Geometric Transformation
n Translation
n Rotation
n Scaling
n Matrix Representation
n Homogeneous Coordinates
n Matrix Composition
n Composite Transformations
n Pivot-Point Rotation
n General Fixed-Point Scaling
n Reflection and Shearing
n Transformations Between Coordinate Systems

3. Geometric Transformation
BCET
n Definition
n Translation, Rotation, Scaling.
n Motivation – Why do we need geometric
transformations in CG?
n As a viewing aid
n As a modeling tool
n As an image manipulation tool

4. Example: 2D Geometric
Transformation BCET
Modeling
Coordinates
World Coordinates

5. Example: 2D Scaling
BCET
Modeling
Coordinates
Scale(0.3, 0.3)
World Coordinates

6. Example: 2D Rotation
BCET
Modeling
Coordinates
Scale(0.3, 0.3)
Rotate(-90)
World Coordinates

7. Example: 2D Translation
BCET
Modeling
Coordinates
Scale(0.3, 0.3)
Rotate(-90)
Translate(5, 3)
World Coordinates

8. Example: 2D Geometric
Transformation BCET
Modeling
Coordinates
Again?
World Coordinates

9. Example: 2D Geometric
Transformation BCET
Modeling
Coordinates
Scale
Translate
Scale
Rotate
Translate
World Coordinates

10. Basic 2D Transformations
BCET
n Translation
n x ¢ = x + tx
n y¢ = y + ty
n Scale
n x¢ = x ´ sx
n y¢ = y ´ sy
n Rotation
n x ¢ = x ´ cosθ - y ´ sinθ
n y¢ = y ´ sinθ + y ´ cosθ
n Shear
n x ¢ = x + hx ´ y
n y¢ = y + hy ´ x

11. Basic 2D Transformations
BCET
n Translation
n x ¢ = x + tx
n y¢ = y + ty
n Scale
n x¢ = x ´ sx
n y¢ = y ´ sy
n Rotation
n x ¢ = x ´ cosθ - y ´ sinθ
Transformations
can be combined
n y¢ = y ´ sinθ + y ´ cosθ
(with simple algebra)
n Shear
n x ¢ = x + hx ´ y
n y¢ = y + hy ´ x

12. Basic 2D Transformations
BCET
n Translation
n x ¢ = x + tx
n y¢ = y + ty
n Scale
n x¢ = x ´ sx
n y¢ = y ´ sy
n Rotation
n x ¢ = x ´ cosθ - y ´ sinθ
n y¢ = y ´ sinθ + y ´ cosθ
n Shear x ¢ = x ´ sx
n x ¢ = x + hx ´ y y¢ = y ´ sy
n y¢ = y + hy ´ x

13. Basic 2D Transformations
BCET
n Translation
n x ¢ = x + tx
n y¢ = y + ty
n Scale
n x¢ = x ´ sx
n y¢ = y ´ sy
n Rotation
n x ¢ = x ´ cosθ - y ´ sinθ
n y¢ = y ´ sinθ + y ´ cosθ
n Shear x ¢ = ((x ´ sx) ´ cosq - (y ´ sy) ´ sinq )
n x ¢ = x + hx ´ y y¢ = ((x ´ sx) ´ sinq + (y ´ sy) ´ cosq )
n y¢ = y + hy ´ x

14. Basic 2D Transformations
BCET
n Translation
n x ¢ = x + tx
n y¢ = y + ty
n Scale
n x¢ = x ´ sx
n y¢ = y ´ sy
n Rotation
n x ¢ = x ´ cosθ - y ´ sinθ
n y¢ = y ´ sinθ + y ´ cosθ
n Shear x ¢ = ((x ´ sx) ´ cosq - (y ´ sy) ´ sinq ) + tx
n x ¢ = x + hx ´ y y¢ = ((x ´ sx) ´ sinq + (y ´ sy) ´ cosq ) + ty
n y¢ = y + hy ´ x

15. Basic 2D Transformations
BCET
n Translation
n x ¢ = x + tx
n y¢ = y + ty
n Scale
n x¢ = x ´ sx
n y¢ = y ´ sy
n Rotation
n x ¢ = x ´ cosθ - y ´ sinθ
n y¢ = y ´ sinθ + y ´ cosθ
n Shear x ¢ = ((x ´ sx) ´ cosq - (y ´ sy) ´ sinq ) + tx
n x ¢ = x + hx ´ y y¢ = ((x ´ sx) ´ sinq + (y ´ sy) ´ cosq ) + ty
n y¢ = y + hy ´ x

16. Matrix Representation
BCET
n Represent a 2D Transformation by a Matrix
éa b ù
êc d ú
ë û
n Apply the Transformation to a Point
x¢ = ax + by é x¢ ù é a b ù é x ù
y¢ = cx + dy ê y ¢ú = êc d ú ê y ú
ë û ë ûë û
Transformation
Point
Matrix

17. Matrix Representation
BCET
n Transformations can be combined by matrix
multiplication
é x¢ ù é a b ù ée f ù éi j ù é x ù
ê y ¢ú = ê c d ú ê g ú êk l ú ê y ú
hû ë
ë û ë ûë ûë û
Transformation
Matrix
Matrices are a convenient and efficient way
to represent a sequence of transformations

18. 2×2 Matrices
BCET
n What types of transformations can be
represented with a 2×2 matrix?
2D Identity
x¢ = x é x¢ ù é1 0ù é x ù
ê y¢ú = ê0 1ú ê y ú
y¢ = y ë û ë ûë û
2D Scaling
x¢ = sx ´ x é x¢ ù é sx 0 ù é x ù
y¢ = sy ´ y ê y¢ú = ê0 sy ú ê y ú
ë û ë ûë û

19. 2×2 Matrices
BCET
n What types of transformations can be
represented with a 2×2 matrix?
2D Rotation
x¢ = cos q ´ x - sin q ´ y é x¢ ù écosq - sin q ù é x ù
ê y¢ú = êsin q cosq ú ê y ú
y¢ = sin q ´ x + cosq ´ y ë û ë ûë û
2D Shearing
x¢ = x + shx ´ y é x¢ ù é1 shx ù é x ù
y¢ = shy ´ x + y ê y¢ú = ê shy 1ú ê y ú
ë û ë ûë û

20. 2×2 Matrices
BCET
n What types of transformations can be
represented with a 2×2 matrix?
2D Mirror over Y axis
x¢ = - x é x¢ ù é - 1 0ù é x ù
y¢ = y ê y ¢ú = ê 0 1 úê yú
ë û ë ûë û
2D Mirror over (0,0)
x¢ = - x é x¢ ù é - 1 0ù é x ù
y¢ = - y ê y ¢ú = ê 0 - 1ú ê y ú
ë û ë ûë û

21. 2×2 Matrices
BCET
n What types of transformations can be
represented with a 2×2 matrix?
2D Translation
x¢ = x + tx
y¢ = y + ty NO!!
Only linear 2D transformations
can be Represented with 2x2 matrix

22. Homogeneous Coordinates
BCET
nA point (x,
y) can be re-written in homogeneous
coordinates as (xh, yh, h).
nThe homogeneous parameter h is a non-
zero value such that:
xh yh
x= y=
h h
nWe can then write any point (x, y) as (hx, hy, h)
nWe can conveniently choose h = 1 so that
(x, y) becomes (x, y, 1)

23. Why Homogeneous
Coordinates? BCET
nMathematicians commonly use homogeneous
coordinates as they allow scaling factors to be
removed from equations.
nWe will see in a moment that all of the
transformations we discussed previously can be
represented as 3*3 matrices.
nUsing homogeneous coordinates allows us use
matrix multiplication to calculate transformations –
extremely efficient!

24. Homogeneous Translation
BCET
nThe translation of a point by (dx, dy) can be
written in matrix form as:
é1 0 dx ù
ê0 1 dy ú
ê ú
ê0
ë 0 1ú û
nRepresenting the point as a homogeneous
column vector we perform the calculation as:
é1 0 dxù éxù é1* x + 0* y + dx*1ù éx + dxù
ê0 1 dyú ´êyú = ê0* x +1* y + dy*1ú = êy + dyú
ê ú ê ú ê ú ê ú
ê0 0 1 ú ê1 ú ê 0* x + 0* y +1*1 ú ë 1 ú
ë û ë û ë û ê û

25. 2D Translation
BCET
n 2D translation can be represented by a 3×3
matrix
n Point represented with homogeneous coordinates
é x¢ ù é1 0 tx ù é x ù
x ¢ = x + tx ê y¢ú = ê0 1 ty ú ê y ú
y¢ = y + ty ê ú ê úê ú
ê1 ú ê0 0 1 ú ê1 ú
ë û ë ûë û

26. Basic 2D Transformations
BCET
n Basic 2D transformations as 3x3 Matrices
é x¢ ù é1 0 tx ù é x ù é x¢ ù ésx 0 0 ù é x ù
ê y¢ú = ê0 1 ty ú ê y ú ê y¢ú = ê0 sy 0ú ê y ú
ê ú ê úê ú ê ú ê úê ú
ê1 ú ê0 0 1 ú ê1 ú
ë û ë ûë û ê1 ú ê0 0 1 ú ê1 ú
ë û ë ûë û
Translate Scale
é x¢ ù écosq - sin q 0 ù é x ù é x¢ ù é1 shx 0 ù é x ù
ê y¢ú = êsin q cosq 0ú ê y ú ê y¢ú = ê shy 1 0ú ê y ú
ê ú ê úê ú ê ú ê úê ú
ê1 ú ê0
ë û ë 0 1 ú ë1 ú
ûê û ê1 ú ê0 0 1ú ê1 ú
ë û ë ûë û
Rotate Shear

27. Homogeneous Coordinates
BCET
n Add a 3rd coordinate to every 2D point
n (x, y, w) represents a point at location (x/w, y/w)
n (x, y, 0) represents a point at infinity
n (0, 0, 0) is not allowed
y
2
(2, 1, 1) or (4, 2, 2) or (6, 3, 3)
1
x
1 2
Convenient Coordinate System to
Represent Many Useful Transformations

28. Linear Transformations
BCET
n Linear transformations are combinations of …
n Scale
é x¢ ù é a b 0 ù é x ù
n Rotation ê y ¢ ú = êc d 0 ú ê y ú
n Shear, and ê ú ê úê ú
n Mirror ê w¢ú ê0 0 1 ú ê wû
ë û ë ûë ú
n Properties of linear transformations
n Satisfies: T ( s p + s p ) = s T ( p ) + s T ( p )
1 1 2 2 1 1 2 2
n Origin maps to origin
n Lines map to lines
n Parallel lines remain parallel
n Ratios are preserved
n Closed under composition

29. Affine Transformations
BCET
n Affine transformations are combinations of
n Linear transformations, and
n Translations
x¢
é ù é a bc ùéx ù
ê y¢ ú = êd e f ú ê y ú
ê ú ê úê ú
ê w¢ú ê0 0 1 ú ê wú
ë û ë ûë û
n Properties of affine transformations
n Origin does not map to origin
n Lines map to lines
n Parallel lines remain parallel
n Ratios are preserved
n Closed under composition

30. Matrix Composition
BCET
n Transformations can be combined by matrix
multiplication
é x¢ ù æ é1 0 tx ù écos θ - sinθ 0 ù ésx 0 0ù ö é x ù
ê y¢ ú = ç ê0 1 ty ú ê sinθ cosθ 0ú ê0 sy 0 ú ÷ ê y ú
ê ú çê úê úê ú ÷ê ú
ê w¢ú ç ê0 0 1 ú ê 0
ë û èë ûë 0 1 ú ê0 0 1 ú ÷ ê w ú
ûë û øë û
p¢ = T(tx, ty) R(q ) S(sx, sy) p
n Efficiency with premultiplication
n Matrix multiplication is associative
p¢ = (T ´ (R ´ (S ´ p))) p¢ = (T ´ R ´ S) ´ p

31. Matrix Composition
BCET
n Rotate by q around arbitrary point (a,b)
n M = T(a, b) ´ R(θ ) ´ T(-a,-b)
(a,b)
n Scale by sx, sy around arbitrary point (a,b)
n M = T(a, b) ´ S(sx, sy) ´ T(-a,-b)
(a,b)

32. Inverse Transformations
BCET
nTransformations can easily be reversed using
inverse transformations
é1 0 - dxù
-1 ê ú é1 ù
T = ê0 1 - dyú ês 0 0ú
ê0 0 1 ú
ë û êx ú
-1 ê 1 ú
S = 0 0
é cos sinq 0ù
q ê sy ú
-1 ê ú ê 0 0 1ú
R = ê-sinq cos 0ú
q ê ú
ê 0 ë û
ë 0 1úû

33. Pivot-Point Rotation
BCET
(xr,yr) (xr,yr) (xr,yr) (xr,yr)
Translate Rotate Translate
T (xr , yr ) × R(q ) ×T (- xr ,-yr ) = R(xr , yr ,q )
é1 0 xr ù écosq - sinq 0ù é1 0 - xr ù écosq - sinq xr (1 - cosq ) + yr sinq ù
ê0 1 y ú × êsinq cosq 0ú × ê0 1 - y ú = êsinq cosq y (1 - cosq ) - x sinq ú
ê rú ê ú ê rú ê r r ú
ê0 0 1 û ê 0
ë ú ë 0 1ú ê0 0 1 ú ê 0
û ë û ë 0 1 ú
û

34. General Fixed-Point Scaling
BCET
(xf,yf) (xf,yf) (xf,yf) (xf,yf)
Translate Scale Translate
T (xf , y f )× S(sx , sy )×T (- x f ,-y f ) = S(x f , y f , sx , sy )
é1 0 xf ù és x 0 0 ù é1 0 - x f ù és x 0 x f (1 - s x ) ù
ê0 1 yf ú×ê0 sy 0 ú × ê0 1 - yf ú = ê0 sy y f (1 - s y ) ú
ê ú ê ú ê ú ê ú
ê0
ë 0 1 ú ê0
û ë 0 1 ú ê0
û ë 0 1 ú ê0
û ë 0 1 ú
û

35. Reflection
BCET
n Reflection with respect to the axis
• x • y • xy
é1 0 0ù é- 1 0 0ù é - 1 0 0ù
ê0 - 1 0 ú ê 0 1 0ú ê 0 - 1 0ú
ê ú ê ú ê ú
ê0 0 1 ú
ë û ê 0 0 1ú
ë û ê0
ë 0 1ú
û
y 1 y y
1 1’ 1’
2 3 2 3 3’ 2 3’ 2
x x 3 x
2’ 3’ 1
1’ 2
X AXIS Y AXIS XY AXIS

36. Reflection
BCET
n Reflection with respect to a Line
y
é0 1 0 ù
ê1 0 0 ú
ê ú x
ê0 0 1 ú
ë û
y=x
°
n Clockwise rotation of 45 ® Reflection about the x
axis ® Counterclockwise rotation of 45 °
y y 1
y
2 3
x x
2’ 3’ x
1’

37. Shear
BCET
n Converted to a parallelogram
y (1,1) y
(0,1)
é1 sh x 0ù (2,1) (3,1)
ê0 1 0 ú
ê ú (0,0) (1,0) x
(0,0) (1,0)
x
ê0 0 1 ú
ë û
x’ = x + shx · y, y’ = y
x (Shx=2)
n Transformed to a shifted parallelogram
(Y = Yref)
y y
(1,1) (1,1) (2,1)
- sh x × y ref ù (0,1)
é1 sh x
ê0 1 ú (1/2,0)
ê 0 ú x
(0,0) (1,0) (3/2,0) x
ê0 0
ë 1 ú
û (0,-1)
x’ = x + shx · (y-yref), y’ = y (Shx=1/2, yref=-1)

38. Shear
BCET
n Transformed to a shifted parallelogram
(X = Xref)
(0,3/2) (1,2)
é 1 0 0 ù y y
ê sh 1 - sh y × x ref ú (1,1)
ê y ú (0,1)
ê 0 ú
(0,1/2) (1,1)
ë 0 1 û x x
(0,0) (1,0) (-1,0)
x’ = x, y’ = shy · (x-xref) + y
(Shy=1/2, xref=-1)