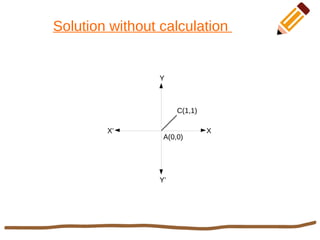
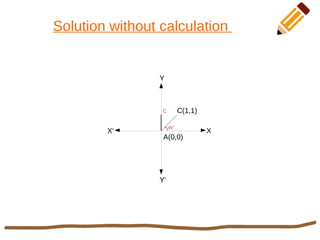
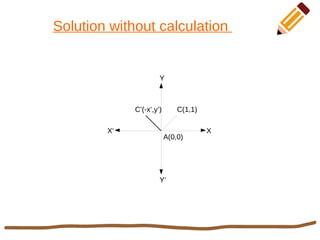
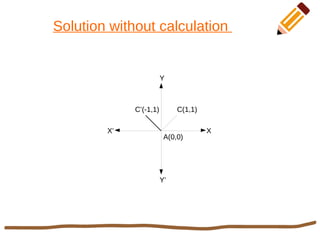
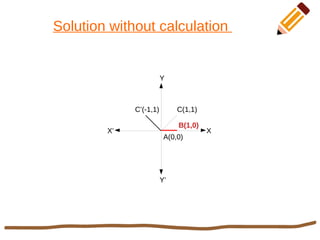
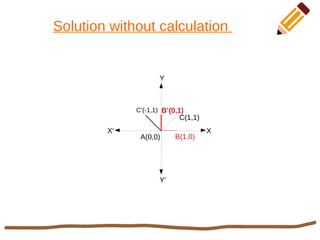
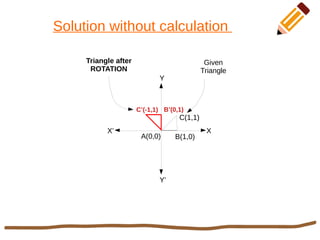
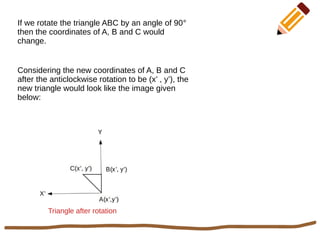
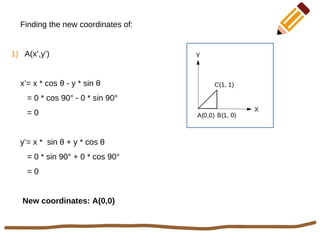
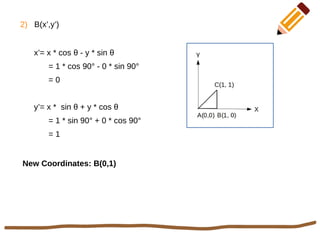
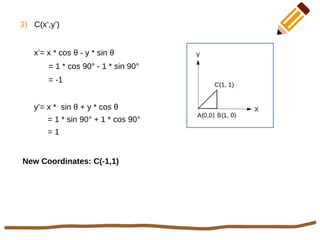
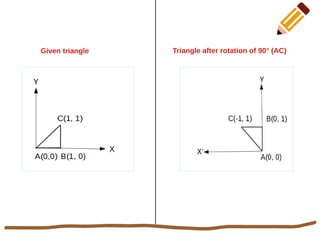
This document discusses 2D rotation in computer graphics. It provides the rotation equations to calculate new x- and y-coordinates when an object is rotated by an angle θ. As an example, it solves the problem of rotating a triangle with vertices at (0,0), (1,0), and (1,1) by 90 degrees counterclockwise. The new coordinates of the rotated triangle are found to be (0,0), (0,1), and (-1,1).

1. Computer Graphics
Transformation in Computer
Graphics
Guided by- Prof. Karthikeyan S

2. 2D- Rotation
2D Rotation is a process of rotating an object with
respect to an angle in a two dimensional plane.
This rotation is achieved by using the following
rotation equations-
1) Xnew = Xold*cos θ – Yold*sin θ
2) Ynew = Xold*sin θ + Yold*cos θ

3. Question: Given a triangle with corner coordinates (0, 0), (1, 0) and
(1, 1). Rotate the triangle by 90 degree anticlockwise direction and
find out the new coordinates.
Considering:
●
(0,0) to be the coordinates of point A.
●
(1,0) to be the coordinates of point B.
●
(1,1) to be the coordinates of point C.
Initial Triangle

4. Solution without calculation
C(1,1)
A(0,0)
Y
XX’
Y’

5. Solution without calculation
C(1,1)
A(0,0)
Y
XX’
Y’
45°
P
Q

6. Solution without calculation
C(1,1)
A(0,0)
Y
XX’
Y’
45°
C

7. C’(-x’,y’)
A(0,0)
C(1,1)
Solution without calculation
Y
XX’
Y’

8. C’(-x’,y’)
A(0,0)
C(1,1)
Solution without calculation
Y
XX’
Y’
P

9. C’(-1,1)
A(0,0)
C(1,1)
Solution without calculation
Y
XX’
Y’

10. C’(-1,1)
A(0,0)
C(1,1)
B(1,0)
Solution without calculation
Y
XX’
Y’

11. C’(-1,1)
A(0,0)
C(1,1)
B(1,0)
B’(0,1)
Y
XX’
Y’
Solution without calculation

12. C’(-1,1)
A(0,0)
C(1,1)
B(1,0)
B’(0,1)
Solution without calculation
Y
XX’
Y’
Triangle after
ROTATION
Given
Triangle

13. If we rotate the triangle ABC by an angle of 90°
then the coordinates of A, B and C would
change.
Considering the new coordinates of A, B and C
after the anticlockwise rotation to be (x’ , y’), the
new triangle would look like the image given
below:
Triangle after rotation

14. Finding the new coordinates of:
1) A(x’,y’)
x’= x * cos θ - y * sin θ
= 0 * cos 90° - 0 * sin 90°
= 0
y’= x * sin θ + y * cos θ
= 0 * sin 90° + 0 * cos 90°
= 0
New coordinates: A(0,0)

15. 2) B(x’,y’)
x’= x * cos θ - y * sin θ
= 1 * cos 90° - 0 * sin 90°
= 0
y’= x * sin θ + y * cos θ
= 1 * sin 90° + 0 * cos 90°
= 1
New Coordinates: B(0,1)

16. 3) C(x’,y’)
x’= x * cos θ - y * sin θ
= 1 * cos 90° - 1 * sin 90°
= -1
y’= x * sin θ + y * cos θ
= 1 * sin 90° + 1 * cos 90°
= 1
New Coordinates: C(-1,1)

17. Triangle after rotation of 90° (AC)Given triangle

18. Thank You