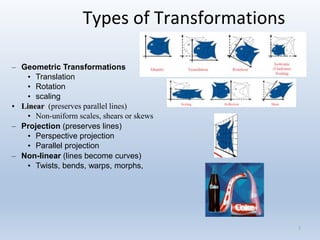
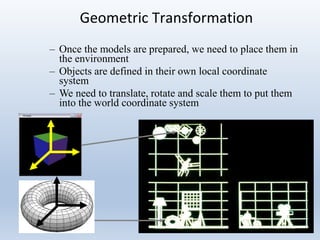
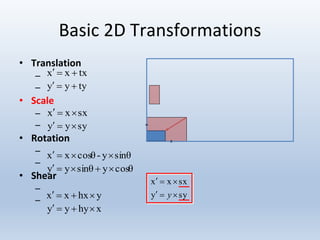
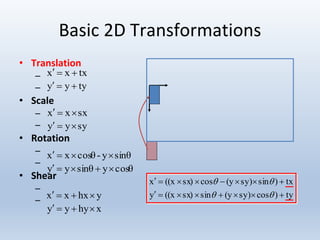
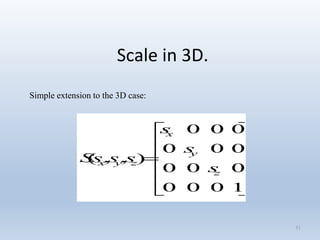
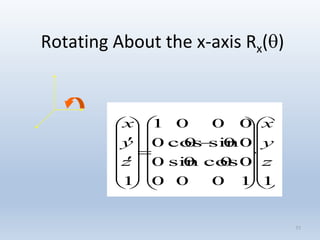
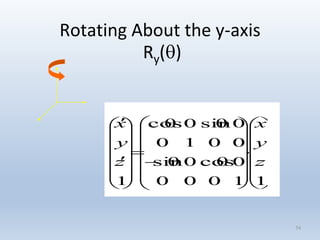
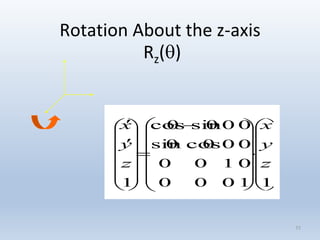
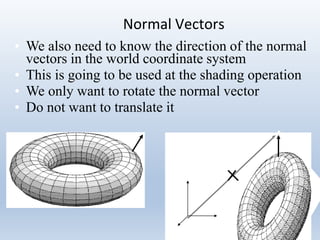
Transformations are used to move and manipulate 3D objects in computer graphics. The key types of 2D transformations are:
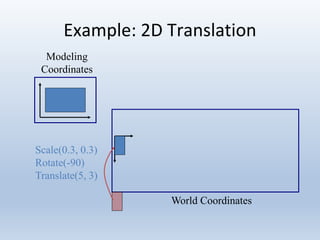
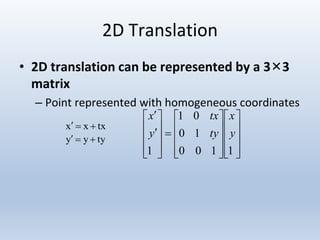
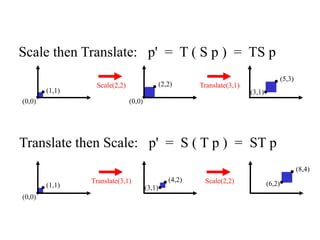
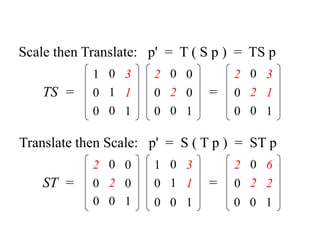
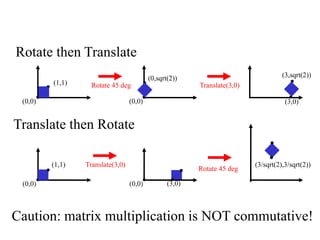
1. Translation moves objects by adding offsets to the x and y coordinates.
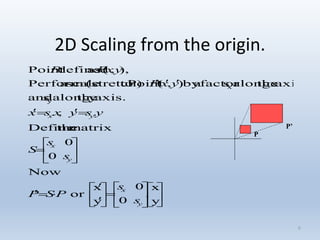
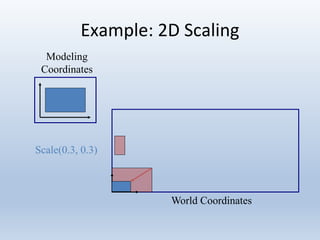
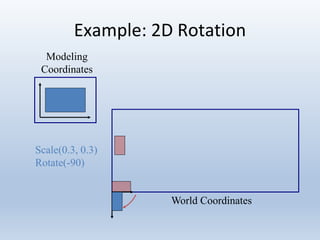
2. Scaling enlarges or shrinks objects by multiplying the x and y coordinates by scale factors.
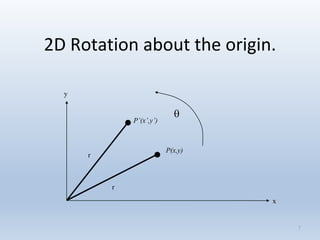
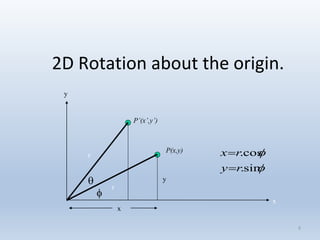
3. Rotation spins objects around the origin by applying trigonometric functions to the coordinates.
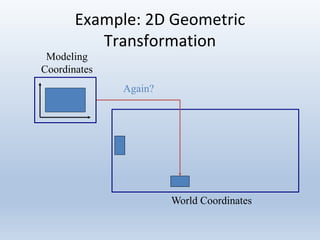
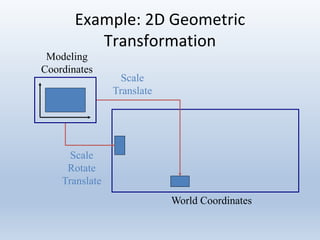
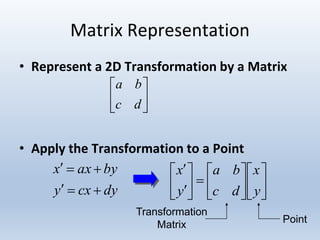
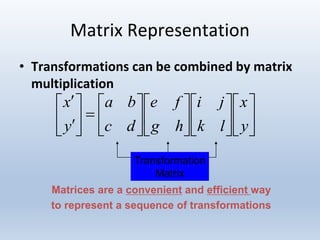
Transformations can be represented using matrices, allowing multiple transformations to be combined through matrix multiplication. Common 2D transformations like translation, scaling, rotation, and shearing can be encoded concisely using 2×2 transformation matrices.
Divide and Conquer Algorithms - D&C forms a distinct algorithm design technique in computer science, wherein a problem is solved by repeatedly invoking the algorithm on smaller occurrences of the same problem. Binary search, merge sort, Euclid's algorithm can all be formulated as examples of divide and conquer algorithms. Strassen's algorithm and Nearest Neighbor algorithm are two other examples.
Divide and Conquer Algorithms - D&C forms a distinct algorithm design technique in computer science, wherein a problem is solved by repeatedly invoking the algorithm on smaller occurrences of the same problem. Binary search, merge sort, Euclid's algorithm can all be formulated as examples of divide and conquer algorithms. Strassen's algorithm and Nearest Neighbor algorithm are two other examples.
its very useful for students.
Sharpening process in spatial domain
Direct Manipulation of image Pixels.
The objective of Sharpening is to highlight transitions in intensity
The image blurring is accomplished by pixel averaging in a neighborhood.
Since averaging is analogous to integration.
Prepared by
M. Sahaya Pretha
Department of Computer Science and Engineering,
MS University, Tirunelveli Dist, Tamilnadu.
with today's advanced technology like photoshop, paint etc. we need to understand some basic concepts like how they are cropping the image , tilt the image etc.
In our presentation you will find basic introduction of 2D transformation.
Commonly a fixed area of the system memory is reserved for the frame buffer,
Video controller can direct access to the frame-buffer
Frame-buffer locations, and the corresponding screen positions, are referenced in Cartesian coordinates.
Some system employ lower-left corner as origin
But most common system employ upper-left corner as origin.
Scan lines are labeled from ymax, at the top of the screen to 0 at the bottom.
Along each scan line, screen pixel positions are labeled from 0 to xmax
Cohen-Sutherland Line Clipping Algorithm:
When drawing a 2D line on screen, it might happen that one or both of the endpoints are outside the screen while a part of the line should still be visible. In that case, an efficient algorithm is needed to find two new endpoints that are on the edges on the screen, so that the part of the line that's visible can now be drawn. This way, all those points of the line outside the screen are clipped away and you don't need to waste any execution time on them.
A good clipping algorithm is the Cohen-Sutherland algorithm for this solution.
By,
Maruf Abdullah Rion
its very useful for students.
Sharpening process in spatial domain
Direct Manipulation of image Pixels.
The objective of Sharpening is to highlight transitions in intensity
The image blurring is accomplished by pixel averaging in a neighborhood.
Since averaging is analogous to integration.
Prepared by
M. Sahaya Pretha
Department of Computer Science and Engineering,
MS University, Tirunelveli Dist, Tamilnadu.
with today's advanced technology like photoshop, paint etc. we need to understand some basic concepts like how they are cropping the image , tilt the image etc.
In our presentation you will find basic introduction of 2D transformation.
Commonly a fixed area of the system memory is reserved for the frame buffer,
Video controller can direct access to the frame-buffer
Frame-buffer locations, and the corresponding screen positions, are referenced in Cartesian coordinates.
Some system employ lower-left corner as origin
But most common system employ upper-left corner as origin.
Scan lines are labeled from ymax, at the top of the screen to 0 at the bottom.
Along each scan line, screen pixel positions are labeled from 0 to xmax
Cohen-Sutherland Line Clipping Algorithm:
When drawing a 2D line on screen, it might happen that one or both of the endpoints are outside the screen while a part of the line should still be visible. In that case, an efficient algorithm is needed to find two new endpoints that are on the edges on the screen, so that the part of the line that's visible can now be drawn. This way, all those points of the line outside the screen are clipped away and you don't need to waste any execution time on them.
A good clipping algorithm is the Cohen-Sutherland algorithm for this solution.
By,
Maruf Abdullah Rion
2. 2
Transformations.
What is a transformation?
• P=T(P)
What does it do?
Transform the coordinates / normal vectors of objects
Why use them?
• Modelling
-Moving the objects to the desired location in the environment
-Multiple instances of a prototype shape
-Kinematics of linkages/skeletons – character animation
• Viewing
– Virtual camera: parallel and perspective projections
4. 12/12/2019 Lecture 1 4
Geometric Transformation
– Once the models are prepared, we need to place them in
the environment
– Objects are defined in their own local coordinate
system
– We need to translate, rotate and scale them to put them
into the world coordinate system
6. 6
2D Scaling from the origin.
y
x
.
0
0
y
x
or
Now
0
0
matrixtheDefine
.,.
axis.ythealongsand
axis,xthealongsfactoraby),(Pointto(stretch)scaleaPerform
),,(asdefinedPoint
y
x
y
x
y
x
yx
s
s
PSP
s
s
S
ysyxsx
yxP
yxPP
P
P’
8. 8
2D Rotation about the origin.
y
x
r
r
P’(x’,y’)
P(x,y)
y
sin.
cos.
ry
rx
x
9. 9
2D Rotation about the origin.
y
x
r
r
P’(x’,y’)
P(x,y)
y
sin.
cos.
ry
rx
x
co.sin.sin.cos.)sin(.
sin.sin.cos.cos.)cos(.
rrry
rrrx
10. 10
2D Rotation about the origin.
sin.
cos.
ry
rx
cos.sin.sin.cos.)sin(.
sin.sin.cos.cos.)cos(.
rrry
rrrx
Substituting for r :
Gives us :
cos.sin.
sin.cos.
yxy
yxx
11. 11
2D Rotation about the origin.
cos.sin.
sin.cos.
yxy
yxx
Rewriting in matrix form gives us :
y
x
y
x
.
cossin
sincos
PRPR
,
cossin
sincos
matrixtheDefine
12. Transformations.
• Translation.
– P=T + P
• Scale
– P=S P
• Rotation
– P=R P
• We would like all transformations to be multiplications so
we can concatenate them
• express points in homogenous coordinates.
12
y
x
y
x
.
cossin
sincos
25. Matrix Representation
• Represent a 2D Transformation by a Matrix
• Apply the Transformation to a Point
y
x
dc
ba
y
x
dycxy
byaxx
dc
ba
Transformation
Matrix
Point
26. Matrix Representation
• Transformations can be combined by matrix
multiplication
y
x
lk
ji
hg
fe
dc
ba
y
x
Matrices are a convenient and efficient way
to represent a sequence of transformations
Transformation
Matrix
27. 2×2 Matrices
• What types of transformations can be
represented with a 2×2 matrix?
2D Identity
2D Scaling
yy
xx
ysyy
xsxx
y
x
y
x
10
01
y
x
sy
sx
y
x
0
0
28. 2×2 Matrices
• What types of transformations can be
represented with a 2×2 matrix?
2D Rotation
2D Shearing
y
x
y
x
cossin
sincos
y
x
shy
shx
y
x
1
1
yxy
yxx
cossin
sincos
yxshyy
yshxxx
29. 2×2 Matrices
• What types of transformations can be
represented with a 2×2 matrix?
2D Mirror over Y axis
2D Mirror over (0,0)
yy
xx
yy
xx
y
x
y
x
10
01
y
x
y
x
10
01
30. 2×2 Matrices
• What types of transformations can be
represented with a 2×2 matrix?
2D Translation
txxx
tyyy NO!!
Only linear 2D transformations
can be Represented with 2x2 matrix
31. 2D Translation
• 2D translation can be represented by a 3×3
matrix
– Point represented with homogeneous coordinates
txxx
tyyy
1100
10
01
1
y
x
ty
tx
y
x
32. Homogeneous coordinates
• Add an extra coordinate, W, to a point.
– P(x,y,W).
• Two sets of homogeneous coordinates represent the
same point if they are a multiple of each other.
– (2,5,3) and (4,10,6) represent the same point.
• If W 0 , divide by it to get Cartesian coordinates of point
(x/W,y/W,1).
• If W=0, point is said to be at infinity.
32
33. Translations in homogenised
coordinates
• Transformation matrices for 2D translation
are now 3x3.
33
1
.
100
10
01
1
y
x
d
d
y
x
y
x
11
y
x
dyy
dxx
34. Concatenation.
• When we perform 2 translations on the same point
34
),(),(),(
:expectweSo
),(),(),(
),(
),(
21212211
21212211
22
11
yyxxyxyx
yyxxyxyx
yx
yx
ddddTddTddT
PddddTPddTddTP
PddTP
PddTP
38. Homogeneous form of scale.
38
y
x
yx
s
s
ssS
0
0
),(
Recall the (x,y) form of Scale :
100
00
00
),( y
x
yx s
s
ssS
In homogeneous coordinates :
42. Other properties of rotation.
42
carefulmorebetoneed,rotations3DFor
sametheis
rotationofaxisthebecauseonlyisBut this
)()()()(
and
)()()(
)0(
RRRR
RRR
IR
43. How are transforms combined?
02/10/09 Lecture 4 43
(0,0)
(1,1)
(2,2)
(0,0)
(5,3)
(3,1)
Scale(2,2) Translate(3,1)
TS =
2
0
0
2
0
0
1
0
0
1
3
1
2
0
0
2
3
1=
Scale then Translate
Use matrix multiplication: p' = T ( S p ) = TS p
Caution: matrix multiplication is NOT commutative!
0 0 1 0 0 1 0 0 1
44. Non-commutative Composition
02/10/09 Lecture 4 44
Scale then Translate: p' = T ( S p ) = TS p
Translate then Scale: p' = S ( T p ) = ST p
(0,0)
(1,1)
(4,2)
(3,1)
(8,4)
(6,2)
(0,0)
(1,1)
(2,2)
(0,0)
(5,3)
(3,1)
Scale(2,2) Translate(3,1)
Translate(3,1) Scale(2,2)
45. Non-commutative Composition
02/10/09 Lecture 4 45
TS =
2
0
0
0
2
0
0
0
1
1
0
0
0
1
0
3
1
1
ST =
2
0
0
2
0
0
1
0
0
1
3
1
Scale then Translate: p' = T ( S p ) = TS p
2
0
0
0
2
0
3
1
1
2
0
0
2
6
2
=
=
Translate then Scale: p' = S ( T p ) = ST p
0 0 1 0 0 1 0 0 1
46. How are transforms combined?
02/10/09 Lecture 4 46
(0,0)
(1,1)
(0,sqrt(2))
(0,0)
(3,sqrt(2))
(3,0)
Rotate 45 deg Translate(3,0)
Rotate then Translate
Caution: matrix multiplication is NOT commutative!
Translate then Rotate
(0,0)
(1,1)
(0,0) (3,0)
Rotate 45 deg
Translate(3,0) (3/sqrt(2),3/sqrt(2))
48. Types of transformations.
• Rotation and translation
– Angles and distances are preserved
– Unit cube is always unit cube
– Rigid-Body transformations.
• Rotation, translation and scale.
– Angles & distances not preserved.
– But parallel lines are.
48
49. 3D Transformations.
• Use homogeneous coordinates, just as in 2D case.
• Transformations are now 4x4 matrices.
• We will use a right-handed (world) coordinate
system - ( z out of page ).
Lecture 4 49
52. Rotation in 3D
• Need to specify which axis the rotation is about.
• z-axis rotation is the same as the 2D case.
52
1000
0100
00cossin
00sincos
)(
zR
53. Rotating About the x-axis Rx()
53
11000
0θcosθsin0
0θsinθcos0
0001
1
z
y
x
z
y
x
54. Rotating About the y-axis
Ry()
54
11000
0θcos0θsin
0010
0θsin0θcos
1
z
y
x
z
y
x
55. Rotation About the z-axis
Rz()
55
11000
0100
00θcosθsin
00θsinθcos
1
z
y
x
z
y
x
57. Calculating the world
coordinates of all vertices
• For each object, there is a local-to-global
transformation matrix
• So we apply the transformations to all the
vertices of each object
• We now know the world coordinates of all
the points in the scene
57
58. Normal Vectors
58
• We also need to know the direction of the normal
vectors in the world coordinate system
• This is going to be used at the shading operation
• We only want to rotate the normal vector
• Do not want to translate it
59. Normal Vectors - (2)
59
• We need to set elements of the translation
part to zero
1000
0
0
0
1000
111111
111111
111111
111111
111111
111111
rrr
rrr
rrr
trrr
trrr
trrr
z
y
x
60. Summary.
• Transformations: translation, rotation and scaling
• Using homogeneous transformation, 2D (3D)
transformations can be represented by multiplication of a
3x3 (4x4) matrix.
• Multiplication from left-to-right can be considered as the
transformation of the coordinate system
60
