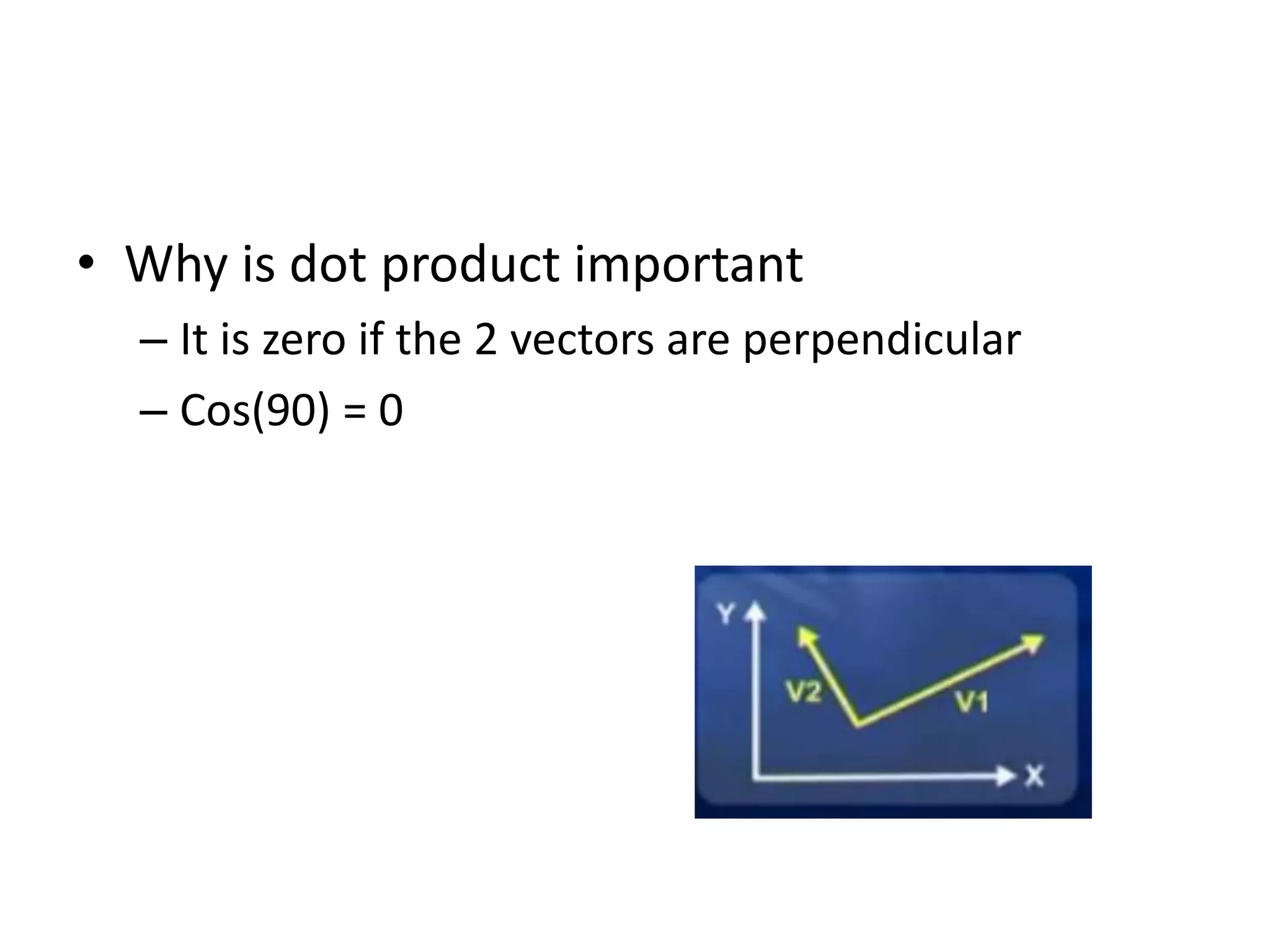
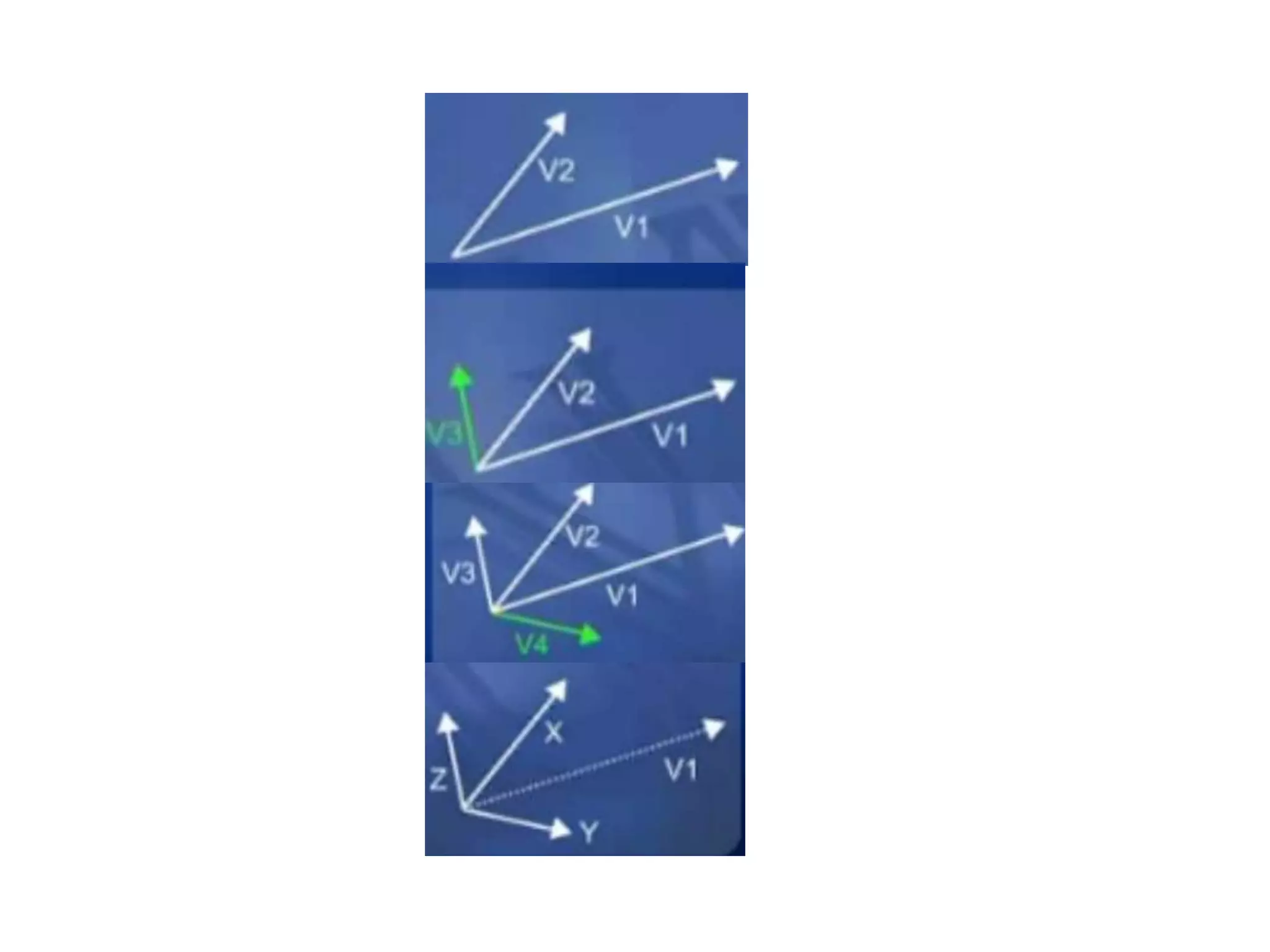
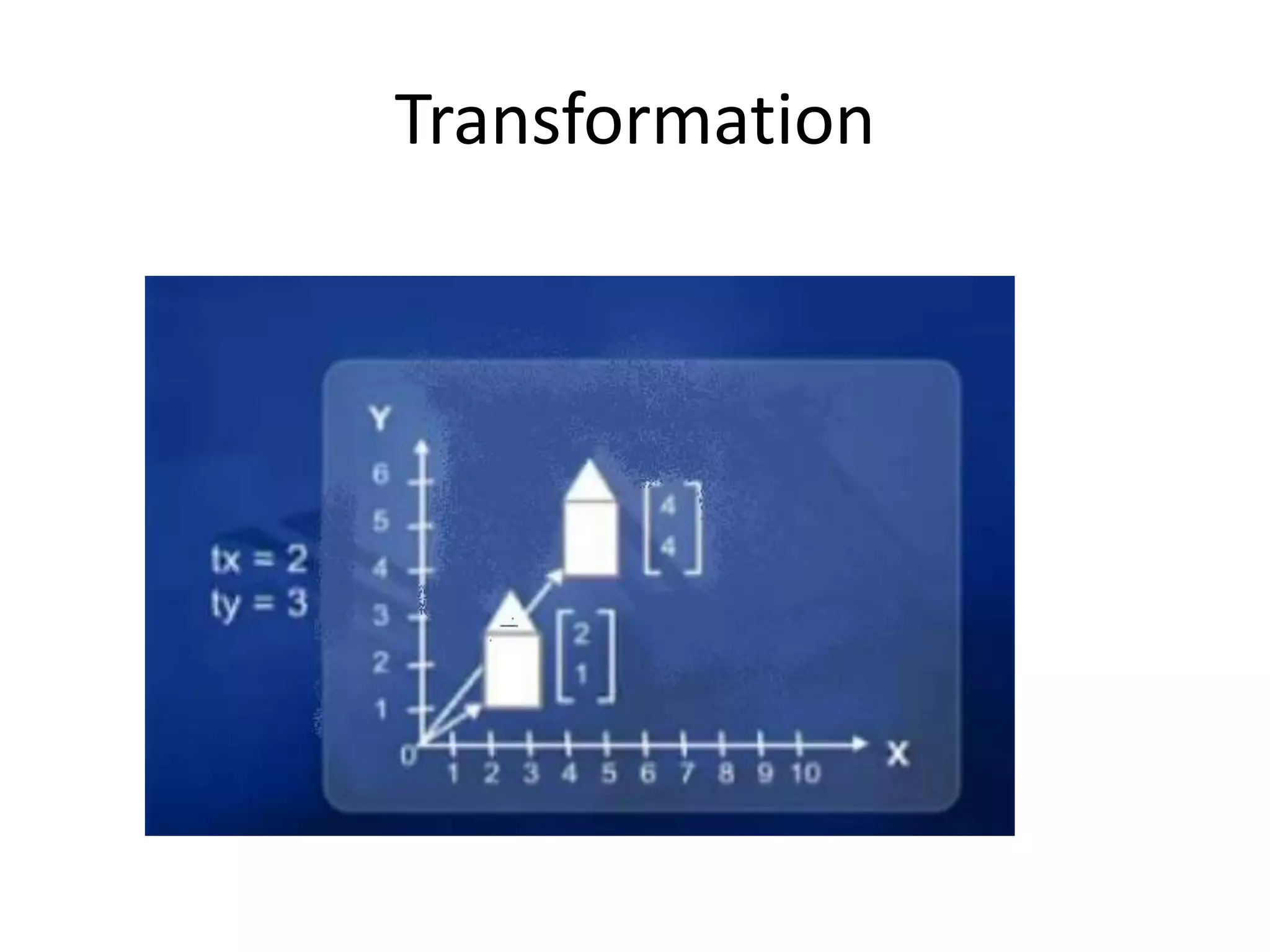
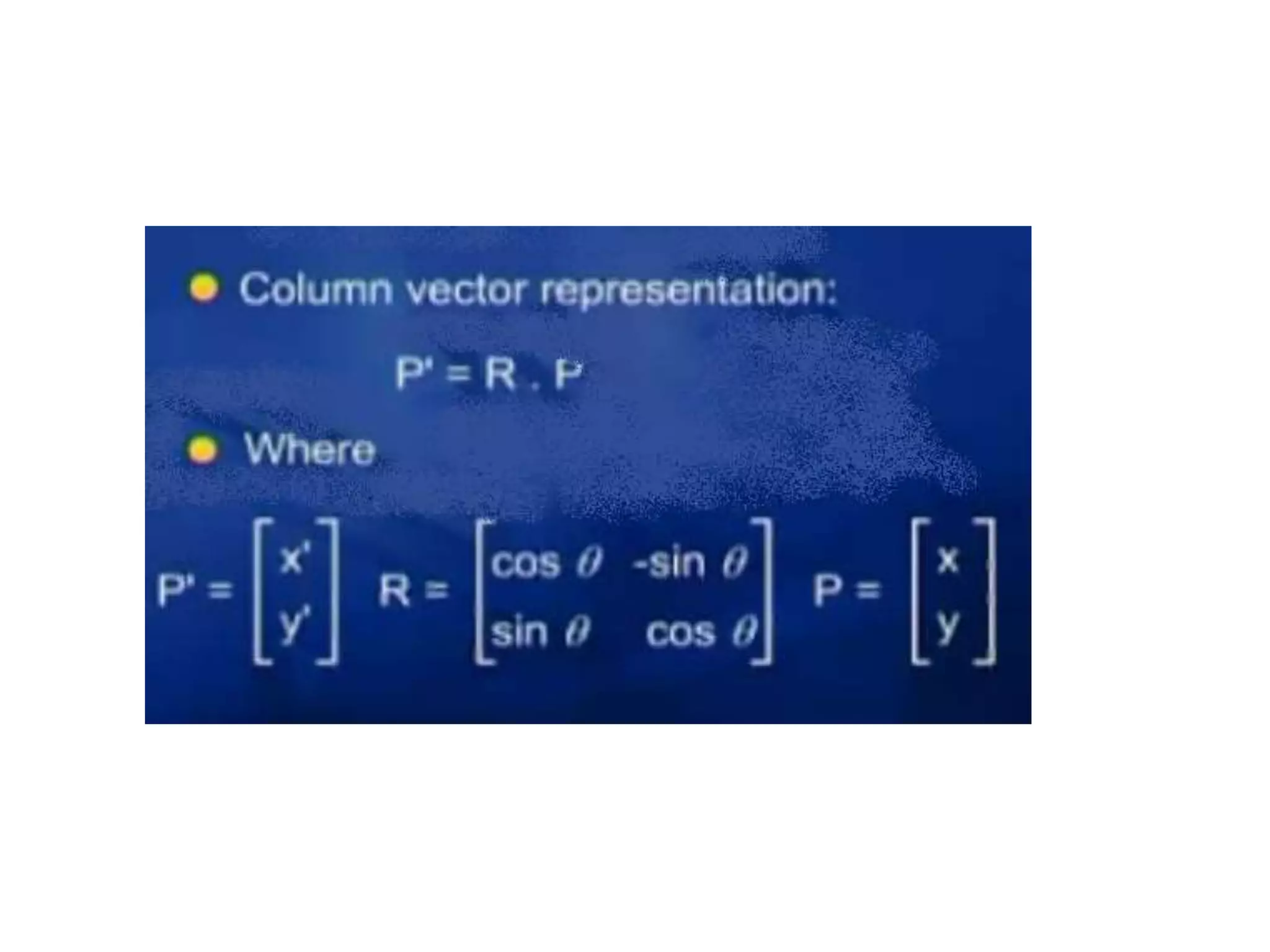
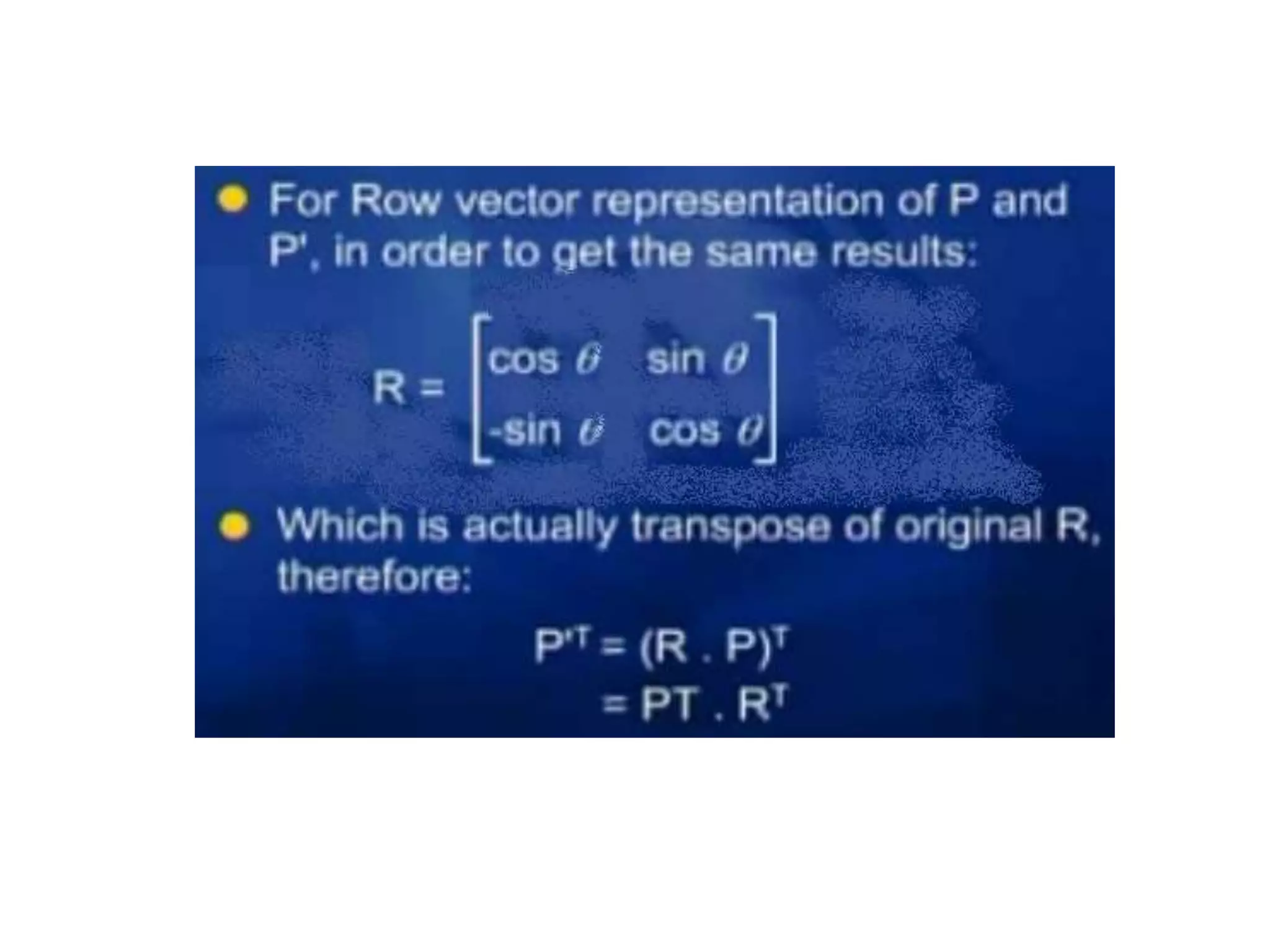
This document discusses 2D transformations including vector addition, dot products, cross products, translation, rotation, and scaling. Vector addition involves adding the x and y components of two vectors. The dot product of two vectors produces a scalar value based on the cosine of the angle between the vectors and can be used to determine if they are perpendicular. The cross product of two vectors produces a new vector perpendicular to both input vectors, determined by the right hand rule. Translation moves every point of an object by the same displacement amounts. Rotation rotates every point of an object by the same angle. Scaling enlarges or shrinks an object by a uniform scaling factor.

1. 2D Transformations

2. • Vector Addition

4. Dot product
• The dot product is the magnitude of 2 vectors
which is scalar value
• Or perhaps more importantly for graphics
•
• Where o is the angle between
• The two vectors

5. • Why is dot product important
– It is zero if the 2 vectors are perpendicular
– Cos(90) = 0

6. • The dot product can be simplified when it is
known that the vector are unit vector
• V1. V2 = cos(ø)
• Because |V1| and |V2| are both 1 then its
resulting value will be only based on the cos()
of the angle of both
• Saves 6 squares 4 additions and 2 square roots

7. cross product
• The cross product of 2 vectors is a vector
• When we are calculating x of resultant vector
then we use y,z only …. So on

8. cross product
• By other way cross product
• U is the unit vector which brings the direction
and it is perpendicular to both vectors
• Why u?
– |V1| and |V2| and sin(o) produces a scalar and
the result needs to be vector

9. • The direction of u is determined by right hand
rule
• Note that you can’t take the cross product of 2
vectors that are parallel to each other
• Sine(0) = sin(180) = 0 produces the
vector(0,0,0)
– As the magnitude is 0 then
What ever the angle is it will
Become 0

12. Transformation

13. • T(x,y) the translation values
• If P(x,y) after translation P(x’, y’)
• Where
x’ = x + Tx
y‘ = y + Ty
Take it as matrix addition
P’ = P + T
When know that both matrices should be equale

14. • Rigid boy transformation
• Objects are moved without deformation
• Every point on the object is translated by the
same amount
• Typically all endpoints are translated and
object is redrawn using new endpoint
positions

15. Rotation
• We need angle to rotate

22. • Rigid body transformation
• Objects are rotated without deformation
• Same angle for each point
• The end points are rotated and redrawn the
object

26. If Scaling factor
• More then 1 scale up
• Less then 1 scale down
• Equal to 1 nothing
• sx and sy are with same values then uniform