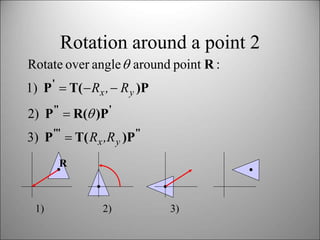
This document discusses 2D transformations in computer graphics including translation, rotation, scaling, and combining transformations using homogeneous coordinates and transformation matrices. It provides examples of translating, rotating, and scaling polygons and explains that the order of transformations matters as matrix multiplication does not commute, so the final result depends on the order the transformations are applied.

1. Computer Graphics
2D transformations

2. Overview
• Why transformations?
• Basic transformations:
– translation, rotation, scaling
• Combining transformations
– homogenous coordinates, transform. Matrices

3. Why transformation?
• Model of objects
world coordinates: km, mm, etc.
Hierarchical models::
human = torso + arm + arm + head + leg + leg
arm = upperarm + lowerarm + hand …
• Viewing
zoom in, move drawing, etc.
• Animation

4. Translation
Translate over vector (tx, ty)
x’=x+ tx, y’=y+ ty
or
x
y
P
P+T
T





























y
x
t
t
y
x
y
x
T
P
P
T
P
P'
and
,
'
'
'
with
,

5. Translation polygon
Translate polygon:
Apply the same operation
on all points.
Works always, for all
transformations of
objects defined as a set
of points.
x
y
T

6. Rotation
x
y
P
x
y
P’
a
















 















y
x
y
x
y
x
y
y
x
x
P
R
P
RP
P'
and
cos
sin
sin
cos
,
'
'
'
with
,
Or
cos
sin
'
sin
cos
'
:
angle
an
over
Rotate
a
a
a
a
a
a
a
a
a

7. Rotation around a point Q
x
y
P
x
y
P’
a
Q
PQ
a
a
a
a
cos
sin
'
sin
cos
'
:
origin
around
Rotate
y
x
y
y
x
x
P
P
P
P
P
P




a
a
a
a
a
cos
)
(
sin
)
(
'
sin
)
(
cos
)
(
'
:
angle
an
over
around
Rotate
y
y
x
x
y
y
y
y
x
x
x
x
Q
P
Q
P
Q
P
Q
P
Q
P
Q
P










Q

8. Scale with factor sx and sy:
x’= sx x, y’= sy y
or
and
0
0
,
'
'
'
with
,




























y
x
s
s
y
x
y
x
P
S
P
SP
P'
Scaling
x
y
P
x
P’
Q’
Q

9. Scaling with respect to a point F
Scale with factors sx and sy:
Px’= sx Px, Py’= syPy
With respect to F:
Px’  Fx = sx (Px  Fx),
Py’  Fy = sy (Py  Fy)
or
Px’= Fx + sx (Px  Fx),
Py’= Fy + sy (Py  Fy)
x
y
P
x
P’
Q’
Q
F
PF

10. Transformations
• Translate with V:
T = P + V
• Scale with factor sx = sy =s:
S = sP
• Rotate over angle a:
R’x = cos a Px  sin a Py
R’y = sin a Px + cos a Py
x
y
P
T
S
R

11. Transformations…
• Messy!
• Transformations with respect to points:
even more messy!
• How to combine transformations?

12. Homogeneous coordinates 1
• Uniform representation of translation,
rotation, scaling
• Uniforme representation of points and
vectors
• Compact representation of sequence of
transformations

13. Homogeneous coordinates 2
• Add extra coordinate:
P = (px , py , ph) or
x = (x, y, h)
• Cartesian coordinates: divide by h
x = (x/h, y/h)
• Points: h = 1 (for the time being…),
vectors: h = 0

14. )
,
(
'
or
1
1
0
0
1
0
0
1
1
'
'
:
n
Translatio
P
T
P y
x
y
x
t
t
y
x
t
t
y
x
































Translation matrix

15. )
(
'
or
1
1
0
0
0
cos
sin
0
sin
cos
1
'
'
:
Rotation
P
R
P 
























 











y
x
y
x
Rotation matrix

16. Scaling matrix
)
,
(
'
or
1
1
0
0
0
0
0
0
1
'
'
:
Scaling
P
S
P y
x
y
x
s
s
y
x
s
s
y
x

































17. Inverse transformations
)
1
,
1
(
)
,
(
:
Scaling
)
(
)
(
:
Rotation
)
,
(
)
,
(
:
n
Translatio
1
1
-
1
-
y
x
y
x
y
x
y
x
s
s
s
s
t
t
t
t
S
S
R
R
T
T










18. 1
2
1
2
1
2
'
'
'
2
'
'
1
'
M
M
M
MP
P
M
M
P)
(M
M
P
P
M
P
P
M
P






with
:
Combined
ation...
transform
second
...
sformation
first tran
Combining transformations 1

19. P
T
P
P
P
T
T
P
P
T
P
P
T
P
'
'
'
'
'
'
)
,
(
1
0
0
1
0
0
1
1
0
0
1
0
0
1
1
0
0
1
0
0
1
)
,
(
)
,
(
:
Combined
on
translati
second
)
,
(
slation
first tran
)
,
(
2
1
2
1
2
1
2
1
1
1
2
2
1
1
2
2
2
2
1
1
y
x
x
x
y
y
x
x
y
x
y
x
y
x
y
x
y
x
y
x
t
t
t
t
t
t
t
t
t
t
t
t
t
t
t
t
t
t
t
t








































Combining transformations 2

20. )
,
(
)
,
(
)
,
(
:
scaling
Composite
)
(
)
(
)
(
:
rotations
Composite
)
,
(
)
,
(
)
,
(
:
ons
translati
Composite
2
1
2
1
1
1
2
2
2
1
1
2
2
1
2
1
1
1
2
2
y
y
x
x
y
x
y
x
y
x
x
x
y
x
y
x
s
s
s
s
s
s
s
s
R
t
t
t
t
t
t
t
t
S
S
S
R
R
T
T
T










Combining transformations 3

21. back.
Translate
3)
origin;
around
angle
over
Rotate
2)
origin;
with
coincides
such that
Translate
1)
:
point
around
angle
over
Rotate


R
R
Rotation around a point 1
R
1) 2) 3)

22. '
'
'
'
'
'
'
'
'
)P
T(
P
)P
R(
P
)P
T(
P
R
y
x
y
x
,R
R
R
,
R





3)
2)
1)
:
point
around
angle
over
Rotate


Rotation around a point 2
R
1) 2) 3)

23. )P
)T(
)R(
T(
)P
)R(
T(
)P
T(
P
)P
)T(
R(
)P
R(
P
)P
T(
P
'
'
'
'
'
'
'
'
'
'
y
x
y
x
y
x
y
x
y
x
y
x
R
,
R
,R
R
,R
R
,R
R
R
,
R
R
,
R
















3)
2)
1)
Rotation around point 3
R
1) 2) 3)

24. P
P
)P
)T(
)R(
T(
P
'
'
'
'
'
'



















1
0
0
sin
)
cos
1
(
cos
sin
sin
)
cos
1
(
sin
cos
or
3)
-
1









x
y
y
x
y
x
y
x
R
R
R
R
R
,
R
,R
R
Rotation around point 4
R
1) 2) 3)

25. again.
back
Translate
3)
origin;
w.r.t.
Schale
2)
origin;
with
coincides
such that
Translate
1)
:
point
w.r.t.
and
factors
with
Scale
F
F
x
x s
s
Scaling w.r.t. point 1
F
1) 2) 3)

26. '
'
'
'
'
'
'
'
'
)P
T(
P
)P
S(
P
)P
T(
P
F
y
x
y
x
y
x
,F
F
s
s
F
,
F





3)
,
2)
1)
:
point
w.r.t.
Schale
Scaling w.r.t.point 2
F
1) 2) 3)

27. P
P
)P
T(
)S
T(
P
'
'
'
'
'
'
















1
0
0
)
1
(
0
)
1
(
0
or
)
,
(
3)
-
1
y
y
y
x
x
x
y
x
y
x
y
x
s
F
s
s
F
s
F
,
F
s
s
,F
F
Scaling w.r.t.point 3
F
1) 2) 3)

28. Order of transformations 1
x
y
x
y
x’
y’
x
x )
T(2,3)R(30
'
'  x
x )
R(30)T(2,3
'
' 
Matrix multiplication does not commute.
The order of transformations makes a difference!
Rotation, translation… Translation, rotation…

29. Order of transformations 2
• Pre-multiplication:
P’ = M n M n-1…M 2 M 1 P
Transformation M n in global coordinates
• Post-multiplication:
P’ = M 1 M 2…M n-1 M n P
Transformation M n in local coordinates: the
coordinate system after application of
M 1 M 2…M n-1

30. Order of transformations 3
OpenGL: glRotate, glScale, etc.:
• Post-multiplication of current
transformation matrix
• Always transformation in local coordinates
• Global coordinate version: read in reverse
order

31. Order of transformations 4
x
x )
R(30)T(2,3
'
'  glTranslate(…);
glRotate(…);
x
y
Local trafo
interpretation
Local transformations:
x
y
Global transformations:
Global trafo
interpretation

32. Matrices in general
rotation and scaling
translation

33. Direct construction of matrix
x
y
A
B
T
If you know the target frame:
Construct matrix directly.
Define shape in nice local
u,v coordinates, use matrix
transformation to put it
in x,y space.

34.  
1
1
0
0
1
or
,
1
1
or
,
'























































v
u
T
B
A
T
B
A
y
x
v
u
y
x
v
u
y
y
y
x
x
x
T
B
A
T
B
A
P
Direct construction of matrix
x
y
A
B
T
If you know the target frame:
Construct matrix directly.

35. Other 2D transformations
• Reflection
• Shear
Can also be combined

36. P
P'












1
0
0
0
1
0
0
0
1
Reflection over axis
Reflext over x-axis:
x’= x, y’= y
or
x
y

37. P
R
P'
P
P'
)
180
(
as
Same
1
0
0
0
1
0
0
0
1














Reflect over origin
Reflect over origin:
x’= x, y’=  y
or
x
y

38. 
tan
with
1
0
0
0
1
0
0
1












f
f
P
P'
Shear
Shear the y-as:
x’=x+f, y’=y
or
x
y


39. 2D transformations summarized
- Transformations: modelling, viewing,
animation;
- Several kinds of transformations;
- Homogeneous coordinates;
- Combine transformations using matrix
multiplication.