2 d transformation
•Download as PPT, PDF•
6 likes•22,148 views
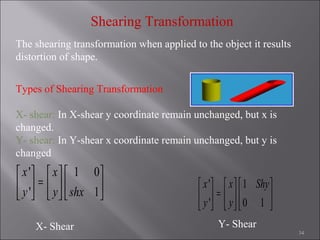
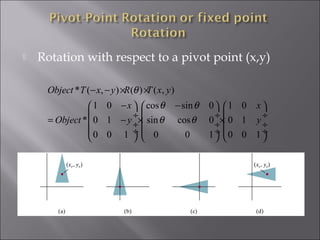
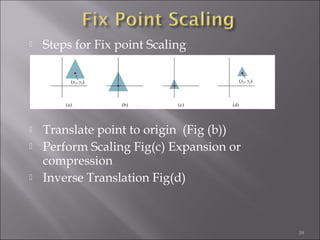
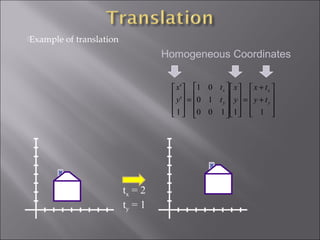
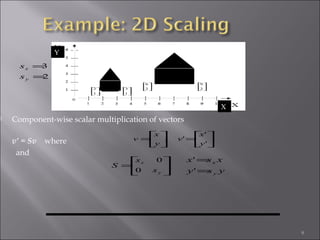
1) 2D geometric transformations include translations, scaling, and rotations. They can be represented by transformation matrices. 2) Translation moves an object by adding offsets to x and y coordinates. It can be represented by a 3x3 matrix with 1s on the diagonal and offsets as the last column. 3) Scaling enlarges or shrinks an object by multiplying x and y coordinates by scaling factors. It can be represented by a 2x2 diagonal matrix with scaling factors. 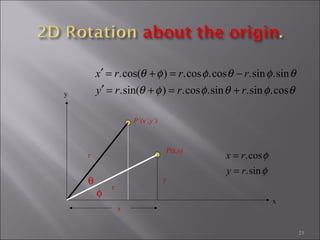4) Rotation rotates an object by applying a trigonometric transformation to x and y coordinates. It can be represented by a 2x2 rotation matrix containing cosine and sine of the rotation angle.
Recommended
More Related Content
What's hot
What's hot (20)
Similar to 2 d transformation
Similar to 2 d transformation (20)
More from Ankit Garg
More from Ankit Garg (19)
Recently uploaded
Recently uploaded (20)
2 d transformation
- 1. 2D Geometric Transformations Total Slide (51) 1
- 2. Geometric transformation means change in Place orientation Size Shape. 2
- 3. 2D Translations. 2D Scaling 2D Rotation 2D shearing Matrix Representation of 2D transformation Formula for Transformation Matrix of Transformed object= Matrix of object in 2D * Matrix of transformation 3
- 4. 4 x y x y Point defined as ( , ), translate to Point ( , ) a distance d parallel to x axis, d parallel to y axis. , , Now x y P P x y P x y x x d y y d dx x P P T dy y P P T ′ ′ ′ ′ ′= + = + ′ ′= = = ′ ′ = + P P’ Original Point, Transformed point and Displacement in X and Y can be written in the form of matrix
- 5. 5 Component-wise addition v’ = v + t where and x’ = x + dx y’ = y + dy To move polygons: translate vertices of polygon after adding translation factors and redraw lines between them. Translation always Preserves lengths and shape of object (Distortion in object shape will not occur). dx = 2 dy = 3 Y X 0 1 1 2 2 3 4 5 6 7 8 9 10 3 4 5 6 = = = dy dx t y x v y x v , ' ' ', 3 3 6 5
- 7. After applying Scaling factor coordinates of object is either increase or decrease. Expansion and compression of object is depend upon the scaling factor Sx and Sy. Uniform Scaling If Sx = Sy < 1 Uniform compression occurs. If Sx = Sy > 1 Uniform Expansion Will occur. If Sx=Sy=1 No Change will occur. Non uniform scaling If Sx ≠ Sy < 1 Non uniform compression occurs. If Sx ≠ Sy > 1 Non uniform expansion Will occur. 7
- 8. Uniform Scaling Non Uniform scaling 8
- 9. 9 Component-wise scalar multiplication of vectors v’ = Sv where and = = ' ' ', y x v y x v = y x s s S 0 0 ysy xsx y x = = ' ' Y X 0 1 1 2 2 3 4 5 6 7 8 9 10 3 4 5 6 2 3 = = y x s s 1 2 1 3 2 6 2 9
- 10. Add a 3rd coordinate to every 2D point. A point (a, b) in 2D can be represented as (a,b,1) in homogeneous coordinate system. Any point (x, y, w) where w!=0 represents a point at location (x/w, y/w) in this coordinate system. Point (2/3,4/3) can be represented in homogeneous coordinate system (6,12,9) 2D case 3D Case • Add a 4th coordinate to every 3D point. A point (a, b, c) in 3D can be represented as (a,b,c,1) in homogeneous coordinate system. Any point (x, y, z, w) in 3D where w!=0 represents a point at location (x/w, y/w, z/w) in this coordinate system.
- 12. Object coordinates are (00,10,11,01) Perform uniform expansion of this object. Take scaling factor from your side.Draw final Figure also. 12
- 13. Q1. Write a 2X2 transformation matrix for each of the following scaling transformation. (1)The entire picture is 3 times as large. (2)The entire picture is 1/3 as large. (3)The X direction is 4 times as large and the y direction unchanged. (4) The x direction reduced to ¾ the original and y direction increased by 7/5 times. 13
- 14. Translate the square ABCD whose coordinates are A(0,0), B(3,0),c(3,3), D(0,3). Translate this square 1.5 unit in x direction and 0.5 unit in y direction. After translation performing scaling with scaling factor sx=1.5 and sy=0.5 14
- 15. Find the transformation matrix that transforms the square ABCD whose center is at (2,2) is reduced to half of its size, with center still remaining at (2,2). The coordinate of square ABCD are A(0,0), B(0,4), C(4,4),D(4,0). Find the coordinates of new square. 15
- 16. Q: How can we represent translation as a 3x3 matrix? y x tyy txx += += ' ' = 1 010 001 tytx ranslationT
- 17. Example of translation + + = = 11100 10 01 1 ' ' y x y x ty tx y x t t y x tx = 2 ty = 1 Homogeneous Coordinates
- 18. Prove that two scaling transformation is commutative Commutative property is S1.s2=s2.s1 Prove that two successive translation are additive. Prove that two successive scaling is multiplicative 18
- 19. Composite 2D Translation (Two successive Translation) ),( ),(),( 2121 2211 yyxx yxyx tttt ttttT ++= ⋅= T TT + + = ⋅ 100 10 01 100 10 01 100 10 01 21 21 1 1 2 2 yy xx y x y x tt tt t t t t Two Successive Translation is Additive
- 20. Composite 2D Scaling (two successive Scaling) ),( ),(),( 2121 2211 yyxx yxyx ssss ssssT S SS = ⋅= ⋅ ⋅ = ⋅ 100 00 00 100 00 00 100 00 00 21 21 1 1 2 2 yy xx y x y x ss ss s s s s Two Successive Scaling is Multiplicative
- 21. 21 2D Rotation
- 24. 24 φ φ sin. cos. ry rx = = θφθφφθ θφθφφθ cos.sin.sin.cos.)sin(. sin.sin.cos.cos.)cos(. rrry rrrx +=+=′ −=+=′ Substituting for r : Gives us : θθ θθ cos.sin. sin.cos. yxy yxx +=′ −=′ − = ′ ′ y x y x . cossin sincos θθ θθ Rotation (Anticlockwise) − = ′ ′ y x y x . cossin sincos θθ θθ Rotation (Clockwise)
- 25. Rotate a point (10,0) in anticlockwise direction Angle is 90 degree. After rotating this point rotate this point in clockwise direction. 25 − = ′ ′ θθ θθ cossin sincos y x y x − = ′ ′ θθ θθ cossin sincos y x y x Rotation (Clockwise)Rotation (Anti-Clockwise)
- 26. Example Find the transformed point, P’, caused by rotating P= (5, 1) about the origin through an angle of 90°. ⋅+⋅ ⋅−⋅ = • − θθ θθ θθ θθ cossin sincos cossin sincos yx yx y x ⋅+⋅ ⋅−⋅ = 90cos190sin5 90sin190cos5 ⋅+⋅ ⋅−⋅ = 0115 1105 − = 5 1
- 27. 27
- 28. What happens when you apply a rotation transformation to an object that is not at the origin? Solution: Translate the center of rotation to the origin Rotate the object Translate back to the original location
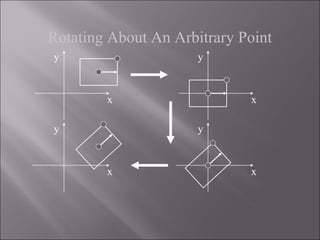
- 29. In matrix form, it can be shown as Here TR is Translation Matrix (Translation towards Origin) RƟ is Rotation Matrix (Rotation Matrix can be clockwise and anticlockwise Rotation) TR -1 is Translation matrix (Away from origin) 29 [ ] [ ][ ][ ] 1 R RT T R Tθ − =
- 30. Rotating About An Arbitrary Point x y x y x y x y
- 31. Consider the square A(1,0) B(0,0) C(0,1) D(1,1). Rotate the square ABCD by 90 degree clockwise about A(1,0). Apply rotation about arbitrary point to solve this question. 31
- 32. Translation. P′=T + P Scale P′=S ⋅ P Rotation P′=R ⋅ P We would like all transformations to be multiplications 32
- 33. 33 Translate [1,3] by [7,9] Scale [2,3] by 5 in the X direction and 10 in the Y direction Rotate [2,2] by 90° (π/2) = ⋅ 1 12 8 1 3 1 100 910 701 = ⋅ 1 30 10 1 3 2 100 0100 005 − = ⋅ − = ⋅ − 1 2 2 1 2 2 100 001 010 1 2 2 100 0)2/cos()2/sin( 0)2/sin()2/cos( ππ ππ
- 34. 34 Shearing Transformation The shearing transformation when applied to the object it results distortion of shape. Types of Shearing Transformation X- shear: In X-shear y coordinate remain unchanged, but x is changed. Y- shear: In Y-shear x coordinate remain unchanged, but y is changed ' 1 ' 0 1 x x Shy y y = X- Shear Y- Shear ' 1 0 ' 1 x x y y shx =
- 35. Shear following object 2 unit in x direction and 2 unit in y direction. Object coordinates are (00,10,11,01). 35
- 36. Basic 2D transformations as 3x3 matrices ΘΘ Θ−Θ = 1100 0cossin 0sincos 1 ' ' y x y x = 1100 10 01 1 ' ' y x t t y x y x = 1100 01 01 1 ' ' y x sh sh y x x y Translate Rotate Shear = 1100 00 00 1 ' ' y x s s y x y x Scale
- 37. Transformations can be combined by matrix multiplication ΘΘ Θ−Θ = w y x sy sx ty tx w y x 100 00 00 100 0cossin 0sincos 100 10 01 ' ' ' p’ = T(tx,ty) R(Θ) S(sx,sy) p
- 38. Rotation with respect to a pivot point (x,y) * ( , ) ( ) ( , ) 1 0 cos sin 0 1 0 * 0 1 sin cos 0 0 1 0 0 1 0 0 1 0 0 1 Object T x y R T x y x x Object y y θ θ θ θ θ − − × × − − ÷ ÷ ÷ = − × × ÷ ÷ ÷ ÷ ÷ ÷
- 39. Steps for Fix point Scaling Translate point to origin (Fig (b)) Perform Scaling Fig(c) Expansion or compression Inverse Translation Fig(d) 39
- 40. Scaling with respect to a fixed point (x,y) * ( , ) ( , ) ( , ) 1 0 0 0 0 1 0 0 * 0 1 0 0 0 0 1 0 1 0 0 1 1 x y x y Object T x y S s s T x y s Object s x y x y − − × × ÷ ÷ ÷ = × × ÷ ÷ ÷ ÷ ÷ ÷− −
- 41. Q1. Magnify the triangle with vertices A(0,0), B(1,1), C(5,2) to twice its size while keeping c(5,2) fixed. 41
- 42. Composite 2D Rotation (Two Successive Rotation) )( )()( 12 12 θθ θθ += ⋅= R RRT ++ +−+ = − ⋅ − 100 0)cos()sin( 0)sin()cos( 100 0cossin 0sincos 100 0cossin 0sincos 1212 1212 11 11 22 22 θθθθ θθθθ θθ θθ θθ θθ Two Successive Rotation is Additive
- 43. 43 Thanks !!