PG
Uploaded byPrasanth George
955 views

Linear Combination, Matrix Equations

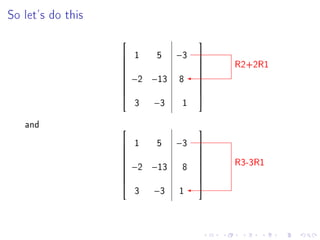
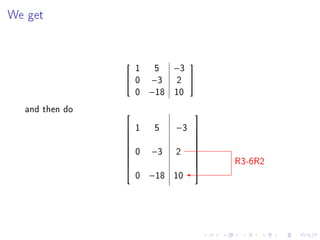
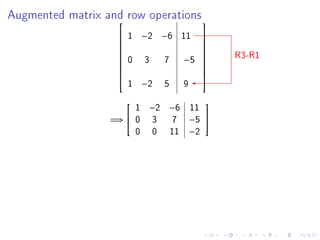
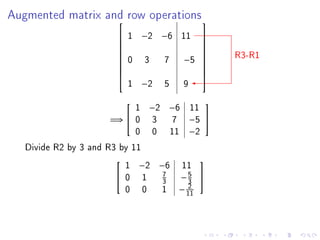
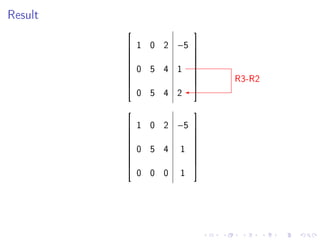
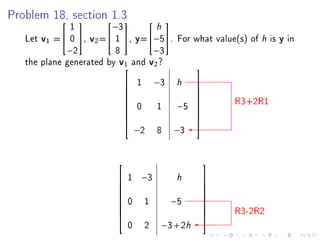
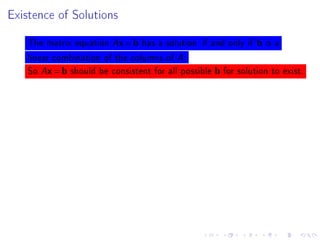
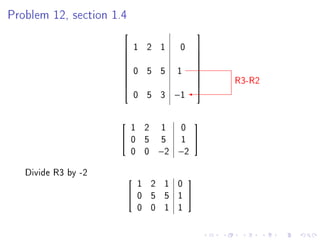
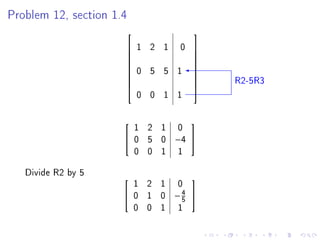
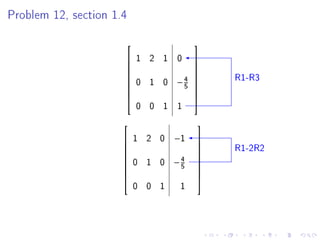
- There will be no class on Monday for Martin Luther King Day. - Quiz 1 will be held in class on Wednesday and will cover sections 1.1, 1.2, and 1.3. - Students should know all definitions clearly for the quiz, which will focus on conceptual understanding rather than lengthy calculations.

Embed presentation

Downloaded 40 times
Announcements If anyone has not been able to access the class website please email me at pgeorge@mtu.edu No class on Monday (Martin Luther King day) Quiz 1 in class on Wednesday Jan 20 on sections 1.1, 1.2 and 1.3 Please know all denitions clearly for the quiz. The quiz will not be about doing lengthy and tiresome row operations but smaller problems to see whether you know the concepts.
Sec 1.3 Contd: Vector Equations Vectors in n-dimensions, Rn Just like we had an ordered pair for x − y (or R2 ) and ordered triplet for x − y − z (or R3 ), we have ordered n−tuples for n-dimensions (or Rn ) Obviously not possible to draw or visualize u1   u   2 Vectors in Rn is a n × 1 column matrix of the form u= u3    . .   . un
Basic Algebraic Properties For all u, v and w in Rn and all scalars c and d u+v=v+u (u+v)+w=u+(v+w) u+0=0+u=u u+(-u)=-u+u=0 c (u+v)=c u+c v (c + d )u=c u+d u c (d u)=(cd )(u) 1u=u
Linear Combinations Let v1 , v2 , v3 , . . ., vp be vectors in Rn and let c1, c2, c3, . . ., cp be scalars.
Linear Combinations Let v1 , v2 , v3 , . . ., vp be vectors in Rn and let c1, c2, c3, . . ., cp be scalars. We can dene a new vector y as follows y = c1 v1 + c2 v2 + c3 v3 + . . . + cp vp
Linear Combinations Let v1 , v2 , v3 , . . ., vp be vectors in Rn and let c1, c2, c3, . . ., cp be scalars. We can dene a new vector y as follows y = c1 v1 + c2 v2 + c3 v3 + . . . + cp vp This new vector y is called a LINEAR COMBINATION of v1 , v2 , v3 , . . ., vp with WEIGHTS c1 , c2 , c3 , . . ., cp
Simple Examples Let v1 and v2 be vectors in R2 The following are examples of linear combinations of v1 and v2 5v 1 + v 2 , v 1 + 13v2 , πv1 - 0.5v2 , 3v2 (=0v1 + 3v2 )
Vector Equation An equation with vectors on both sides!!
Vector Equation An equation with vectors on both sides!! For vectors a1 and a2 and b in R2 , the equation x1 a1 + x2 a2 = b is a vector equation. Here x1 and x2 are weights. This extends to R3 and Rn
Vector Equation An equation with vectors on both sides!! For vectors a1 and a2 and b in R2 , the equation x1 a1 + x2 a2 = b is a vector equation. Here x1 and x2 are weights. This extends to R3 and Rn The solution set of a vector equation (we want to solve for the weights) is the same as the solution of the linear system whose augmented matrix is formed by the vectors written as columns.
Meaning... 1 5 −3       Suppose we are given a1 =−2, a2 =−13 and b= 8 . Can we 3 −3 1 nd two scalars (weights) x1 and x2 such that we can write x1a1 + x1a2 = b? What I said earlier was.. To do this, you write the 3 vectors as the 3 columns of a matrix, the last column corresponding to b being the augmented column.
Meaning... 1 5 −3       Suppose we are given a1 =−2, a2 =−13 and b= 8 . Can we 3 −3 1 nd two scalars (weights) x1 and x2 such that we can write x1a1 + x1a2 = b? What I said earlier was.. To do this, you write the 3 vectors as the 3 columns of a matrix, the last column corresponding to b being the augmented column. Do row reductions to solve for x1 and x2 .
Meaning... 1 5 −3       Suppose we are given a1 =−2, a2 =−13 and b= 8 . Can we 3 −3 1 nd two scalars (weights) x1 and x2 such that we can write x1a1 + x1a2 = b? What I said earlier was.. To do this, you write the 3 vectors as the 3 columns of a matrix, the last column corresponding to b being the augmented column. Do row reductions to solve for x1 and x2 . If the system is inconsistent (remember that 0=nonzero?), that means we cannot nd such weights.
Meaning... 1 5 −3       Suppose we are given a1 =−2, a2 =−13 and b= 8 . Can we 3 −3 1 nd two scalars (weights) x1 and x2 such that we can write x1a1 + x1a2 = b? What I said earlier was.. To do this, you write the 3 vectors as the 3 columns of a matrix, the last column corresponding to b being the augmented column. Do row reductions to solve for x1 and x2 . If the system is inconsistent (remember that 0=nonzero?), that means we cannot nd such weights. If the system is inconsistent, b CANNOT be written as a linear combination of a1 and a2 .
So let's do this    1 5 −3 R2+2R1       −2 −13 8          3 −3 1 and    1 5 −3    R3-3R1    −2 −13 8          3 −3 1
We get 1 5 −3    0 −3 2  0 −18 10 and then do    1 5 −3       0 −3 2    R3-6R2       0 −18 10
Result 1 5 −3    0 −3 2  0 0 −2
Result 1 5 −3    0 −3 2  0 0 −2 So the last row says 0=-2. This means the system is inconsistent. So we CANNOT write b as a linear combination of a1 and a2 .
Result 1 5 −3    0 −3 2  0 0 −2 So the last row says 0=-2. This means the system is inconsistent. So we CANNOT write b as a linear combination of a1 and a2 . So testing whether a vector can be written as a linear combination of 2 or more vectors involve writing the augmented matrix and solving for the weights.
Problem 14, sec 1.3 Determine if b is a linear combination of the vectors formed from the columns of the matrix A. 1 −2 −6 11     A = 0 3 7 , b=−5 1 −2 5 9 Before we start, this problem is same as
Problem 14, sec 1.3 Determine if b is a linear combination of the vectors formed from the columns of the matrix A. 1 −2 −6 11     A = 0 3 7 , b=−5 1 −2 5 9 Before we start, this problem is same as Determine if b a  is linear combination of  1 , a2 and a3 where a 1 −2 −6 11      a1 =0, a2 = 3 , a3 = 7 , b=−5 1 −2 5 9
Augmented matrix and row operations    1 −2 −6 11    R3-R1    0 3 7 −5          1 −2 5 9 1 −2 −6 11   =⇒  0 3 7 −5  0 0 11 −2
Augmented matrix and row operations    1 −2 −6 11    R3-R1    0 3 7 −5          1 −2 5 9 1 −2 −6 11   =⇒  0 3 7 −5  0 0 11 −2 Divide R2 by 3 and R3 by 11 1 −2 −6 11   7  0 1 3 −5  3 2 0 0 1 − 11
Augmented matrix and row operations    1 −2 −6 11    R3-R1    0 3 7 −5          1 −2 5 9 1 −2 −6 11   =⇒  0 3 7 −5  0 0 11 −2 Divide R2 by 3 and R3 by 11 1 −2 −6 11   7  0 1 3 −5  3 2 0 0 1 − 11 This matrix tells you that the system is consistent. That is all what you want to know to decide whether the linear combination is possible. Finding the complete solution here is not necessary.
Span Span is a fancy term for a collection of linear combinations of vectors. Here is the formal denition
Span Span is a fancy term for a collection of linear combinations of vectors. Here is the formal denition Let v1 , v2 , v3 , . . ., vp be vectors in Rn . The set of all linear combinations of v1 , v2 , v3 , . . ., vp is denoted by Span v1 , v2 , . . . vp
Span Span is a fancy term for a collection of linear combinations of vectors. Here is the formal denition Let v1 , v2 , v3 , . . ., vp be vectors in Rn . The set of all linear combinations of v1 , v2 , v3 , . . ., vp is denoted by Span v1 , v2 , . . . vp This is called the subset of Rn spanned (or generated) by v1 , v2 , v 3 , . . ., v p .
Span Span v1 , v2 , . . . vp is a collection of all vectors that can be written as c1 v1 + c2 v2 + c3 v3 + . . . + cp vp If someone asks you whether a vector b is in Span {v1 , v2 , v3 } what should you do?
Span Span v1 , v2 , . . . vp is a collection of all vectors that can be written as c1 v1 + c2 v2 + c3 v3 + . . . + cp vp If someone asks you whether a vector b is in Span {v1 , v2 , v3 } what should you do? Just do the same thing you do to check whether b is a linear combination of v1 , v2 , and v3 .
Span Span v1 , v2 , . . . vp is a collection of all vectors that can be written as c1 v1 + c2 v2 + c3 v3 + . . . + cp vp If someone asks you whether a vector b is in Span {v1 , v2 , v3 } what should you do? Just do the same thing you do to check whether b is a linear combination of v1 , v2 , and v3 . Or whether the linear system with augmented matrix formed by v1 , v2 , v3 and b has a solution (consistent)
Problem 12 section 1.3 (Re-worded) Determine if b is in Span {a1a2 , a3 where , } 1 0 2 −5       a1 =−2, a2 =5, a3 =0, b= 11  2 5 8 −7    1 0 2 −5       −2 5 0 11    R3+R2       2 5 8 −7    1 0 2 −5 R2+2R1       −2 5 0 11          0 5 4 2
Result    1 0 2 −5       0 5 4 1    R3-R2       0 5 4 2    1 0 2 −5       0 5 4 1          0 0 0 1
Result    1 0 2 −5       0 5 4 1    R3-R2       0 5 4 2    1 0 2 −5       0 5 4 1          0 0 0 1 There we have it again, 0=1!!! The system is inconsistent, no solution which means no linear combination of b possible in terms of the 3 given vectors or b IS NOT in Span {v1 , v2 , v3 }
Problem 18, section 1.3  1   −3   h  Let v1 = 0 , v2 = 1 , y=−5. For what value(s) of h is y in −2 8 −3 the plane generated by v1 and v2 ?    1 −3  h   R3+2R1    0 1 −5          −2 8 −3    1 −3  h      0 1 −5    R3-2R2     h   0 2 −3 + 2
Problem 18, section 1.3 Remember, the problem is just asking you the value(s) of h that will make the linear system represented by this augmented matrix consistent.    1 −3  h      0 1 −5        0 0 7 + 2h   To have a consistent system, just make sure that 7 + 2h = 0 or h = −2. 7
Section 1.4 The Matrix Equation Ax = b A linear combination of vectors is the product of a matrix and a vector. Denition If A is an m × n matrix with columns formed by the vectors a1 , a2 , . . . an and if x is in Rn , then the product of A and x denoted A by x is the linear combination of the columns of A using the corresponding entries in x as weights.
Section 1.4 The Matrix Equation Ax = b A linear combination of vectors is the product of a matrix and a vector. Denition If A is an m × n matrix with columns formed by the vectors a1 , a2 , . . . an and if x is in Rn , then the product of A and x denoted A by x is the linear combination of the columns of A using the corresponding entries in x as weights. x1    x2  Ax = .  = x1 a1 + x2 a2 + . . . + xn an  . . . an  a1 a2 .   .  xn 
Section 1.4 The Matrix Equation Ax = b For this product to be possible, the number of columns in A must be same as the number of entries in x
Section 1.4 The Matrix Equation Ax = b For this product to be possible, the number of columns in A must be same as the number of entries in x Example  1   1 −3 7 1   1 −3 7 1          2  2 1 −5 2    = 1 2 + 2  1  + 3 −5 + 4 2 3 5 2 −3 3 5 2 −3 3 4
Section 1.4 The Matrix Equation Ax = b For this product to be possible, the number of columns in A must be same as the number of entries in x Example  1   1 −3 7 1   1 −3 7 1          2  2 1 −5 2    = 1 2 + 2  1  + 3 −5 + 4 2 3 5 2 −3 3 5 2 −3 3 4 1 −6 21 4 20           = 2 +  2  + −15 +  8  = −3 5 4 −9 12 12
Matrix Equation and Vector Equation Consider the following system  x − 6 2 x x + 7 3 5    1  = x2 x + 2 3 = −3    
Matrix Equation and Vector Equation Consider the following system  x x − 6 2 x + 7 3 5    1  = x2 x + 2 3 = −3     This is the same as 1 −6 7 5 x1 0 + x2 1 + x3 2 = −3
Matrix Equation and Vector Equation Consider the following system  x x − 6 2 x + 7 3 5    1  = x2 x + 2 3 = −3     This is the same as 1 −6 7 5 x1 0 + x2 1 + x3 2 = −3 This is the Vector Equation.
Matrix Equation and Vector Equation Consider the following system  x − 6 2 x x + 7 3 5    1  = x2 x + 2 3 = −3    
Matrix Equation and Vector Equation Consider the following system  x − 6 2x + 7 3 x 5    1  = x2 + 2 3 x = −3     This is the same as x   1 −6 7  1  5 0 1 2 x2 = −3 x3
Matrix Equation and Vector Equation Consider the following system  x − 6 2x + 7 3 x 5    1  = x2 + 2 3 x = −3     This is the same as x   1 −6 7  1  5 0 1 2 x2 = −3 x3 This is the Matrix Equation.
Everything is the same Theorem If A is an m × n matrix with columns formed by the vectors a1 , a2 , . . . an and if b is in Rm , then the matrix equation Ax = b has the same solution as the following:
Everything is the same Theorem If A is an m × n matrix with columns formed by the vectors a1 , a2 , . . . an and if b is in Rm , then the matrix equation Ax = b has the same solution as the following: The vector equation x1a1 + x2a2 + . . . + xn an = b
Everything is the same Theorem If A is an m × n matrix with columns formed by the vectors a1 , a2 , . . . an and if b is in Rm , then the matrix equation Ax = b has the same solution as the following: The vector equation x1a1 + x2a2 + . . . + xn an = b The system of linear equations whose augmented matrix is a1 a2 . . . an (which you have been all these days)
Everything is the same Theorem If A is an m × n matrix with columns formed by the vectors a1 , a2 , . . . an and if b is in Rm , then the matrix equation Ax = b has the same solution as the following: The vector equation x1a1 + x2a2 + . . . + xn an = b The system of linear equations whose augmented matrix is a1 a2 . . . an (which you have been all these days) That is, solving a matrix equation is the same as solving the corresponding vector equation which is the same as solving the corresponding system of linear equations by row-reducing the augmented matrix.
Existence of Solutions The matrix equation Ax = b has a solution if and only if b is a linear combination of the columns of A. So Ax = b should be consistent for all possible b for solution to exist.
Existence of Solutions The matrix equation Ax = b has a solution if and only if b is a linear combination of the columns of A. So Ax = b should be consistent for all possible b for solution to exist. Theorem If A is an m × n matrix and if the matrix equation Ax = b has a solution then Each b is a linear combination of the columns of A The columns of A span Rm (very important) A has pivot position in every row (not necessarily every column). Please note that A is the coecient matrix (and not the augmented matrix)
Problem 12, section 1.4 Write the augmented matrix for the linear system corresponding to the matrix equation Ax = b, solve the system and write the answer as avector. 1 2 1 0    A= −3 −1 2, b= 1  0 5 3 −1 The augmented matrix is    1 2 1 0 R2+3R1       −3 −1 2 1          0 5 3 −1
Problem 12, section 1.4    1 2 1 0       0 5 5 1    R3-R2       0 5 3 −1 1 2 1 0    0 5 5 1  0 0 −2 −2 Divide R3 by -2 1 2 1 0    0 5 5 1  0 0 1 1
Problem 12, section 1.4    1 2 1 0       0 5 5 1    R2-5R3       0 0 1 1 1 2 1 0    0 5 0 −4  0 0 1 1 Divide R2 by 5 1 2 1 0    0 1 0 −4  5 0 0 1 1
Problem 12, section 1.4    1 2 1 0    R1-R3    0 1 0 −4     5      0 0 1 1    1 2 0 −1 R1-2R2       0 1 0 −4   5        0 0 1 1
1 0 0 3   5  0 1 0 −4  5 0 0 1 1 The augmented column in the above matrix is the solution vector x1  5    3 x= x2  = − 4  5 x3 1 Problem 22, section 1.4 0 0 4       Let v1 = 0 , v2 =−3, v3 =−1. Does {a1 , a2 , a3 } span R3 ? −2 8 −5 Why or why not?
Problem 22, section 1.4 OutlineThis problem is a direct application of the theorem we saw just now. We need to see the connection between pivots, existence of solution and span. If we show that this matrix has pivot in each row, we have a solution and that means these vectors span R3    0 0 4    Swap    0 −3 −1          −2 8 5    −2 8 5       0 −3 −1          0 0 4
Problem 22, section 1.4 Divide rst row by -2, second row by -3 and third row by 4 5 1 −4 2    0 1 1  3 0 0 1 We have pivot position in each row which means that by our theorem, {a1 , a2 , a3 } span R3 .
Row-Vector Rule for Computing Ax = b If the product Ax = b is dened, the entry in the i th position of Ax is the sum of the products of the entries from row i of A and from the vector x (very important for matrix multiplication in chapter 2) Example 1.  1   1 −3 7 1   1.1 + (−3).2 + 7.3 + 1.4 20      2   2 1 −5 2    = 2.1 + 1.2 + (−5).3 + 2.4  = −3 3 5 2 −3 3 5.1 + 2.2 + (−3).3 + 3.4 12 4 2. 1 0 0 5 1. 5 + 0. 6 + 0. 7 5         0 1 0  6 =  0.5 + 1.6 + 0.7  = 6 0 0 1 7 0.5 + 0.2 + 1.7 7

More Related Content

ODP
Simplifying exponents
byswartzje
 
PPT
systems of equations.ppt
byJennilynBalusdan3
 
PPTX
Lesson 19: Exponential and Logarithmic Functions
byKevin Johnson
 
PPTX
Volume of revolution
byChristopher Chibangu
 
PPTX
Matrices and System of Linear Equations ppt
byDrazzer_Dhruv
 
PDF
Chapter 3: Linear Systems and Matrices - Part 1/Slides
byChaimae Baroudi
 
DOCX
Binomial theorem
byindu psthakur
 
PPTX
1.1 exponents t
bymath260
 
Simplifying exponents
byswartzje
 
systems of equations.ppt
byJennilynBalusdan3
 
Lesson 19: Exponential and Logarithmic Functions
byKevin Johnson
 
Volume of revolution
byChristopher Chibangu
 
Matrices and System of Linear Equations ppt
byDrazzer_Dhruv
 
Chapter 3: Linear Systems and Matrices - Part 1/Slides
byChaimae Baroudi
 
Binomial theorem
byindu psthakur
 
1.1 exponents t
bymath260
 

What's hot

KEY
Compound Inequalities Notes
byLori Rapp
 
PDF
Trig substitution
bydynx24
 
PPTX
Solve linear equations in one unknown
byAlona Hall
 
PPTX
Lilliefors test
byIslamia College University Peshawar
 
PPT
Parent Functions
byVLB10525
 
PPT
Introduction to differentiation
byShaun Wilson
 
PPTX
Factorial Notations.pptx
byCHIRANTANMONDAL2
 
DOCX
BSC_COMPUTER _SCIENCE_UNIT-4_DISCRETE MATHEMATICS
byRai University
 
PPTX
Course Orientation for Probability and Statistics.pptx
byMarjorie Malveda
 
PPT
Exponential functions
bycarljeffmorris
 
PPTX
Rational expressions
byLeslie Amoguis
 
PPT
QUADRATIC EQUATIONS
byhiratufail
 
PPTX
Gamma, Expoential, Poisson And Chi Squared Distributions
byDataminingTools Inc
 
PPT
Equation Of A Line
byGillian Guiang
 
PPTX
complex numbers
bySamra Kanwal
 
PPTX
Integration of Trigonometric Functions
byRaymundo Raymund
 
PPT
matrices and algbra
bygandhinagar
 
PDF
Gauss elimination & Gauss Jordan method
byNaimesh Bhavsar
 
PPTX
Remainder and Factor Theorem
byTrish Hammond
 
PPTX
1.2 algebraic expressions t
bymath260
 
Compound Inequalities Notes
byLori Rapp
 
Trig substitution
bydynx24
 
Solve linear equations in one unknown
byAlona Hall
 
Lilliefors test
byIslamia College University Peshawar
 
Parent Functions
byVLB10525
 
Introduction to differentiation
byShaun Wilson
 
Factorial Notations.pptx
byCHIRANTANMONDAL2
 
BSC_COMPUTER _SCIENCE_UNIT-4_DISCRETE MATHEMATICS
byRai University
 
Course Orientation for Probability and Statistics.pptx
byMarjorie Malveda
 
Exponential functions
bycarljeffmorris
 
Rational expressions
byLeslie Amoguis
 
QUADRATIC EQUATIONS
byhiratufail
 
Gamma, Expoential, Poisson And Chi Squared Distributions
byDataminingTools Inc
 
Equation Of A Line
byGillian Guiang
 
complex numbers
bySamra Kanwal
 
Integration of Trigonometric Functions
byRaymundo Raymund
 
matrices and algbra
bygandhinagar
 
Gauss elimination & Gauss Jordan method
byNaimesh Bhavsar
 
Remainder and Factor Theorem
byTrish Hammond
 
1.2 algebraic expressions t
bymath260
 

Viewers also liked

PPTX
Linear Combination, Span And Linearly Independent, Dependent Set
byDhaval Shukla
 
PDF
Complex Eigenvalues
byPrasanth George
 
PDF
Orthogonal Projection
byPrasanth George
 
PDF
Systems of Linear Equations
byPrasanth George
 
PDF
Orthogonal Decomp. Thm
byPrasanth George
 
PDF
Determinants, Properties and IMT
byPrasanth George
 
PDF
Systems of Linear Equations, RREF
byPrasanth George
 
PDF
Orthogonal sets and basis
byPrasanth George
 
PDF
Linear (in)dependence
byPrasanth George
 
PDF
Diagonalization
byPrasanth George
 
PDF
Linear Transformations, Matrix Algebra
byPrasanth George
 
PDF
Alg1 8.3 Linear Combination
byJaqueline Vallejo
 
PPTX
Vector Spaces,subspaces,Span,Basis
byRavi Gelani
 
PDF
Lesson 12: Linear Independence
byMatthew Leingang
 
PPTX
Digital bangladesh
byMD MAJHARUL ISLAM
 
PPTX
Digital Bangladesh
byJashim Uddin
 
PPTX
Alternating Current
byamckaytghs
 
PDF
Linear Transformations
byPrasanth George
 
PPTX
Alternating current
byAlper GÜNEREN
 
PPT
Alternating current circuits
bycse1014
 
Linear Combination, Span And Linearly Independent, Dependent Set
byDhaval Shukla
 
Complex Eigenvalues
byPrasanth George
 
Orthogonal Projection
byPrasanth George
 
Systems of Linear Equations
byPrasanth George
 
Orthogonal Decomp. Thm
byPrasanth George
 
Determinants, Properties and IMT
byPrasanth George
 
Systems of Linear Equations, RREF
byPrasanth George
 
Orthogonal sets and basis
byPrasanth George
 
Linear (in)dependence
byPrasanth George
 
Diagonalization
byPrasanth George
 
Linear Transformations, Matrix Algebra
byPrasanth George
 
Alg1 8.3 Linear Combination
byJaqueline Vallejo
 
Vector Spaces,subspaces,Span,Basis
byRavi Gelani
 
Lesson 12: Linear Independence
byMatthew Leingang
 
Digital bangladesh
byMD MAJHARUL ISLAM
 
Digital Bangladesh
byJashim Uddin
 
Alternating Current
byamckaytghs
 
Linear Transformations
byPrasanth George
 
Alternating current
byAlper GÜNEREN
 
Alternating current circuits
bycse1014
 

Similar to Linear Combination, Matrix Equations

PDF
Subspace, Col Space, basis
byPrasanth George
 
PDF
Summary (chapter 1 chapter6)
byNizam Mustapha
 
PDF
Lesson 9: Gaussian Elimination
byMatthew Leingang
 
KEY
0908 ch 9 day 8
byfestivalelmo
 
PDF
IMT, col space again
byPrasanth George
 
PDF
Notes
byguest151806
 
PDF
mth3201 Tutorials
byDrradz Maths
 
PDF
Tutorials Question
byDrradz Maths
 
KEY
0911 ch 9 day 11
byfestivalelmo
 
PDF
Sect4 1
byinKFUPM
 
PPTX
Lecture # 3.pptx the edge oc homu yay nn
by241579
 
PPTX
linear algebra.pptx
byMaths Assignment Help
 
PDF
linear algebra sides 5th edition chapter 1
byAhsanKhan837024
 
PDF
Jacobi and gauss-seidel
byarunsmm
 
PDF
Tutorial 6 mth 3201
byDrradz Maths
 
DOC
Tutorial 2 -_sem_a102
bynurulhanim
 
PPTX
Linear Algebra.pptx
byMaths Assignment Help
 
PDF
Cofactors, Applications
byPrasanth George
 
PDF
P2 Matrices Modul
byguestcc333c
 
PPTX
V2.0
byManmeet Singh
 
Subspace, Col Space, basis
byPrasanth George
 
Summary (chapter 1 chapter6)
byNizam Mustapha
 
Lesson 9: Gaussian Elimination
byMatthew Leingang
 
0908 ch 9 day 8
byfestivalelmo
 
IMT, col space again
byPrasanth George
 
Notes
byguest151806
 
mth3201 Tutorials
byDrradz Maths
 
Tutorials Question
byDrradz Maths
 
0911 ch 9 day 11
byfestivalelmo
 
Sect4 1
byinKFUPM
 
Lecture # 3.pptx the edge oc homu yay nn
by241579
 
linear algebra.pptx
byMaths Assignment Help
 
linear algebra sides 5th edition chapter 1
byAhsanKhan837024
 
Jacobi and gauss-seidel
byarunsmm
 
Tutorial 6 mth 3201
byDrradz Maths
 
Tutorial 2 -_sem_a102
bynurulhanim
 
Linear Algebra.pptx
byMaths Assignment Help
 
Cofactors, Applications
byPrasanth George
 
P2 Matrices Modul
byguestcc333c
 
V2.0
byManmeet Singh
 

More from Prasanth George

PDF
Finding eigenvalues, char poly
byPrasanth George
 
PDF
Eigenvalues - Contd
byPrasanth George
 
PDF
Eigenvalues and Eigenvectors (Tacoma Narrows Bridge video included)
byPrasanth George
 
PDF
Determinants
byPrasanth George
 
PDF
Matrix Inverse, IMT
byPrasanth George
 
PDF
Matrix multiplication, inverse
byPrasanth George
 
Finding eigenvalues, char poly
byPrasanth George
 
Eigenvalues - Contd
byPrasanth George
 
Eigenvalues and Eigenvectors (Tacoma Narrows Bridge video included)
byPrasanth George
 
Determinants
byPrasanth George
 
Matrix Inverse, IMT
byPrasanth George
 
Matrix multiplication, inverse
byPrasanth George
 

Recently uploaded

PPTX
Renal Physiology- Juxtaglomerular Apparatus.pptx
byDisha Soriya
 
PPTX
How to Create_Generate Engineering Change Orders ECOs in Odoo 18
byCeline George
 
PDF
Artificial Intelligence in Research and Academic Writing, Workshop on Researc...
byProf. Vinod Kumar Kanvaria
 
PDF
Workshop 29 Crystal Review All Students by YogiGoddess
by©LDMMIA, ©Reiki Yoga
 
PPTX
WEEK 2 (2).pptx TLE COOKERY 10 QUARTER 4
byResynFayeCortez2
 
PPTX
Greengnorance Toolkit Module1 Climate Change
byKarl Donert
 
PDF
Pratishta Educational Society., Courses & Opportunities
byGanapathiVankudoth
 
PDF
Nursing care plan for Vomiting /B.Sc nsg
byDr. Sudhadevi Sadanandan
 
PDF
java full stack programming and interview questions
byrajuashokit
 
PPTX
MEMORY &FORGETTING. Shilpa Hotakar.Psychology pptx
bySHILPA HOTAKAR
 
PPTX
Overview of How to set priority in Odoo 19 Todo
byCeline George
 
PDF
Family and Marriage __ Sociology __ Jhasketan Kuanar __ NURSING VIBE ONLY .pdf
byJK NURSING VIBES ONLY JHASKETAN KUANAR
 
PDF
Beyond the Absurd: A Comparative Reading of Waiting for Godot and the Bhagava...
byKruti Vyas
 
PDF
Judgement Regarding Land Acquisition Act not Applicable to Encroachers.pdf
byssuser9d8e4e
 
PDF
Holm Community Heritage at St Nicholas Kirk - 2025 AGM Minutes (30.04.2025)
byAntoine Pietri
 
PPTX
How to Track & Manage My Time Section in Odoo 18 Time Off
byCeline George
 
PDF
AI Is a Tool, Not a Voice: Radio, Trust, and the Human Factor
byN.A. Shah Ansari
 
PDF
BP502T Industrial Pharmacy I (Theory) UNIT– I (Part 1)
byRushi Mandali
 
PPTX
How to Manage Reservation Method in Odoo 18 Inventory
byCeline George
 
PPTX
Greengnorance Toolkit Module 6 Water Resources
byKarl Donert
 
Renal Physiology- Juxtaglomerular Apparatus.pptx
byDisha Soriya
 
How to Create_Generate Engineering Change Orders ECOs in Odoo 18
byCeline George
 
Artificial Intelligence in Research and Academic Writing, Workshop on Researc...
byProf. Vinod Kumar Kanvaria
 
Workshop 29 Crystal Review All Students by YogiGoddess
by©LDMMIA, ©Reiki Yoga
 
WEEK 2 (2).pptx TLE COOKERY 10 QUARTER 4
byResynFayeCortez2
 
Greengnorance Toolkit Module1 Climate Change
byKarl Donert
 
Pratishta Educational Society., Courses & Opportunities
byGanapathiVankudoth
 
Nursing care plan for Vomiting /B.Sc nsg
byDr. Sudhadevi Sadanandan
 
java full stack programming and interview questions
byrajuashokit
 
MEMORY &FORGETTING. Shilpa Hotakar.Psychology pptx
bySHILPA HOTAKAR
 
Overview of How to set priority in Odoo 19 Todo
byCeline George
 
Family and Marriage __ Sociology __ Jhasketan Kuanar __ NURSING VIBE ONLY .pdf
byJK NURSING VIBES ONLY JHASKETAN KUANAR
 
Beyond the Absurd: A Comparative Reading of Waiting for Godot and the Bhagava...
byKruti Vyas
 
Judgement Regarding Land Acquisition Act not Applicable to Encroachers.pdf
byssuser9d8e4e
 
Holm Community Heritage at St Nicholas Kirk - 2025 AGM Minutes (30.04.2025)
byAntoine Pietri
 
How to Track & Manage My Time Section in Odoo 18 Time Off
byCeline George
 
AI Is a Tool, Not a Voice: Radio, Trust, and the Human Factor
byN.A. Shah Ansari
 
BP502T Industrial Pharmacy I (Theory) UNIT– I (Part 1)
byRushi Mandali
 
How to Manage Reservation Method in Odoo 18 Inventory
byCeline George
 
Greengnorance Toolkit Module 6 Water Resources
byKarl Donert
 

Linear Combination, Matrix Equations

  • 1.
    Announcements If anyone has not been able to access the class website please email me at pgeorge@mtu.edu No class on Monday (Martin Luther King day) Quiz 1 in class on Wednesday Jan 20 on sections 1.1, 1.2 and 1.3 Please know all denitions clearly for the quiz. The quiz will not be about doing lengthy and tiresome row operations but smaller problems to see whether you know the concepts.
  • 2.
    Sec 1.3 Contd:Vector Equations Vectors in n-dimensions, Rn Just like we had an ordered pair for x − y (or R2 ) and ordered triplet for x − y − z (or R3 ), we have ordered n−tuples for n-dimensions (or Rn ) Obviously not possible to draw or visualize u1   u   2 Vectors in Rn is a n × 1 column matrix of the form u= u3    . .   . un
  • 3.
    Basic Algebraic Properties For all u, v and w in Rn and all scalars c and d u+v=v+u (u+v)+w=u+(v+w) u+0=0+u=u u+(-u)=-u+u=0 c (u+v)=c u+c v (c + d )u=c u+d u c (d u)=(cd )(u) 1u=u
  • 4.
    Linear Combinations Let v1 , v2 , v3 , . . ., vp be vectors in Rn and let c1, c2, c3, . . ., cp be scalars.
  • 5.
    Linear Combinations Let v1 , v2 , v3 , . . ., vp be vectors in Rn and let c1, c2, c3, . . ., cp be scalars. We can dene a new vector y as follows y = c1 v1 + c2 v2 + c3 v3 + . . . + cp vp
  • 6.
    Linear Combinations Let v1 , v2 , v3 , . . ., vp be vectors in Rn and let c1, c2, c3, . . ., cp be scalars. We can dene a new vector y as follows y = c1 v1 + c2 v2 + c3 v3 + . . . + cp vp This new vector y is called a LINEAR COMBINATION of v1 , v2 , v3 , . . ., vp with WEIGHTS c1 , c2 , c3 , . . ., cp
  • 7.
    Simple Examples Let v1 and v2 be vectors in R2 The following are examples of linear combinations of v1 and v2 5v 1 + v 2 , v 1 + 13v2 , πv1 - 0.5v2 , 3v2 (=0v1 + 3v2 )
  • 8.
    Vector Equation An equation with vectors on both sides!!
  • 9.
    Vector Equation An equation with vectors on both sides!! For vectors a1 and a2 and b in R2 , the equation x1 a1 + x2 a2 = b is a vector equation. Here x1 and x2 are weights. This extends to R3 and Rn
  • 10.
    Vector Equation An equation with vectors on both sides!! For vectors a1 and a2 and b in R2 , the equation x1 a1 + x2 a2 = b is a vector equation. Here x1 and x2 are weights. This extends to R3 and Rn The solution set of a vector equation (we want to solve for the weights) is the same as the solution of the linear system whose augmented matrix is formed by the vectors written as columns.
  • 11.
    Meaning... 1 5 −3       Suppose we are given a1 =−2, a2 =−13 and b= 8 . Can we 3 −3 1 nd two scalars (weights) x1 and x2 such that we can write x1a1 + x1a2 = b? What I said earlier was.. To do this, you write the 3 vectors as the 3 columns of a matrix, the last column corresponding to b being the augmented column.
  • 12.
    Meaning... 1 5 −3       Suppose we are given a1 =−2, a2 =−13 and b= 8 . Can we 3 −3 1 nd two scalars (weights) x1 and x2 such that we can write x1a1 + x1a2 = b? What I said earlier was.. To do this, you write the 3 vectors as the 3 columns of a matrix, the last column corresponding to b being the augmented column. Do row reductions to solve for x1 and x2 .
  • 13.
    Meaning... 1 5 −3       Suppose we are given a1 =−2, a2 =−13 and b= 8 . Can we 3 −3 1 nd two scalars (weights) x1 and x2 such that we can write x1a1 + x1a2 = b? What I said earlier was.. To do this, you write the 3 vectors as the 3 columns of a matrix, the last column corresponding to b being the augmented column. Do row reductions to solve for x1 and x2 . If the system is inconsistent (remember that 0=nonzero?), that means we cannot nd such weights.
  • 14.
    Meaning... 1 5 −3       Suppose we are given a1 =−2, a2 =−13 and b= 8 . Can we 3 −3 1 nd two scalars (weights) x1 and x2 such that we can write x1a1 + x1a2 = b? What I said earlier was.. To do this, you write the 3 vectors as the 3 columns of a matrix, the last column corresponding to b being the augmented column. Do row reductions to solve for x1 and x2 . If the system is inconsistent (remember that 0=nonzero?), that means we cannot nd such weights. If the system is inconsistent, b CANNOT be written as a linear combination of a1 and a2 .
  • 15.
    So let's dothis    1 5 −3 R2+2R1       −2 −13 8          3 −3 1 and    1 5 −3    R3-3R1    −2 −13 8          3 −3 1
  • 16.
    We get 1 5 −3    0 −3 2  0 −18 10 and then do    1 5 −3       0 −3 2    R3-6R2       0 −18 10
  • 17.
    Result 1 5 −3    0 −3 2  0 0 −2
  • 18.
    Result 1 5 −3    0 −3 2  0 0 −2 So the last row says 0=-2. This means the system is inconsistent. So we CANNOT write b as a linear combination of a1 and a2 .
  • 19.
    Result 1 5 −3    0 −3 2  0 0 −2 So the last row says 0=-2. This means the system is inconsistent. So we CANNOT write b as a linear combination of a1 and a2 . So testing whether a vector can be written as a linear combination of 2 or more vectors involve writing the augmented matrix and solving for the weights.
  • 20.
    Problem 14, sec1.3 Determine if b is a linear combination of the vectors formed from the columns of the matrix A. 1 −2 −6 11     A = 0 3 7 , b=−5 1 −2 5 9 Before we start, this problem is same as
  • 21.
    Problem 14, sec1.3 Determine if b is a linear combination of the vectors formed from the columns of the matrix A. 1 −2 −6 11     A = 0 3 7 , b=−5 1 −2 5 9 Before we start, this problem is same as Determine if b a  is linear combination of  1 , a2 and a3 where a 1 −2 −6 11      a1 =0, a2 = 3 , a3 = 7 , b=−5 1 −2 5 9
  • 22.
    Augmented matrix androw operations    1 −2 −6 11    R3-R1    0 3 7 −5          1 −2 5 9 1 −2 −6 11   =⇒  0 3 7 −5  0 0 11 −2
  • 23.
    Augmented matrix androw operations    1 −2 −6 11    R3-R1    0 3 7 −5          1 −2 5 9 1 −2 −6 11   =⇒  0 3 7 −5  0 0 11 −2 Divide R2 by 3 and R3 by 11 1 −2 −6 11   7  0 1 3 −5  3 2 0 0 1 − 11
  • 24.
    Augmented matrix androw operations    1 −2 −6 11    R3-R1    0 3 7 −5          1 −2 5 9 1 −2 −6 11   =⇒  0 3 7 −5  0 0 11 −2 Divide R2 by 3 and R3 by 11 1 −2 −6 11   7  0 1 3 −5  3 2 0 0 1 − 11 This matrix tells you that the system is consistent. That is all what you want to know to decide whether the linear combination is possible. Finding the complete solution here is not necessary.
  • 25.
    Span Spanis a fancy term for a collection of linear combinations of vectors. Here is the formal denition
  • 26.
    Span Spanis a fancy term for a collection of linear combinations of vectors. Here is the formal denition Let v1 , v2 , v3 , . . ., vp be vectors in Rn . The set of all linear combinations of v1 , v2 , v3 , . . ., vp is denoted by Span v1 , v2 , . . . vp
  • 27.
    Span Spanis a fancy term for a collection of linear combinations of vectors. Here is the formal denition Let v1 , v2 , v3 , . . ., vp be vectors in Rn . The set of all linear combinations of v1 , v2 , v3 , . . ., vp is denoted by Span v1 , v2 , . . . vp This is called the subset of Rn spanned (or generated) by v1 , v2 , v 3 , . . ., v p .
  • 28.
    Span Spanv1 , v2 , . . . vp is a collection of all vectors that can be written as c1 v1 + c2 v2 + c3 v3 + . . . + cp vp If someone asks you whether a vector b is in Span {v1 , v2 , v3 } what should you do?
  • 29.
    Span Spanv1 , v2 , . . . vp is a collection of all vectors that can be written as c1 v1 + c2 v2 + c3 v3 + . . . + cp vp If someone asks you whether a vector b is in Span {v1 , v2 , v3 } what should you do? Just do the same thing you do to check whether b is a linear combination of v1 , v2 , and v3 .
  • 30.
    Span Spanv1 , v2 , . . . vp is a collection of all vectors that can be written as c1 v1 + c2 v2 + c3 v3 + . . . + cp vp If someone asks you whether a vector b is in Span {v1 , v2 , v3 } what should you do? Just do the same thing you do to check whether b is a linear combination of v1 , v2 , and v3 . Or whether the linear system with augmented matrix formed by v1 , v2 , v3 and b has a solution (consistent)
  • 31.
    Problem 12 section1.3 (Re-worded) Determine if b is in Span {a1a2 , a3 where , } 1 0 2 −5       a1 =−2, a2 =5, a3 =0, b= 11  2 5 8 −7    1 0 2 −5       −2 5 0 11    R3+R2       2 5 8 −7    1 0 2 −5 R2+2R1       −2 5 0 11          0 5 4 2
  • 32.
    Result    1 0 2 −5       0 5 4 1    R3-R2       0 5 4 2    1 0 2 −5       0 5 4 1          0 0 0 1
  • 33.
    Result    1 0 2 −5       0 5 4 1    R3-R2       0 5 4 2    1 0 2 −5       0 5 4 1          0 0 0 1 There we have it again, 0=1!!! The system is inconsistent, no solution which means no linear combination of b possible in terms of the 3 given vectors or b IS NOT in Span {v1 , v2 , v3 }
  • 34.
    Problem 18, section1.3  1   −3   h  Let v1 = 0 , v2 = 1 , y=−5. For what value(s) of h is y in −2 8 −3 the plane generated by v1 and v2 ?    1 −3  h   R3+2R1    0 1 −5          −2 8 −3    1 −3  h      0 1 −5    R3-2R2     h   0 2 −3 + 2
  • 35.
    Problem 18, section1.3 Remember, the problem is just asking you the value(s) of h that will make the linear system represented by this augmented matrix consistent.    1 −3  h      0 1 −5        0 0 7 + 2h   To have a consistent system, just make sure that 7 + 2h = 0 or h = −2. 7
  • 36.
    Section 1.4 TheMatrix Equation Ax = b A linear combination of vectors is the product of a matrix and a vector. Denition If A is an m × n matrix with columns formed by the vectors a1 , a2 , . . . an and if x is in Rn , then the product of A and x denoted A by x is the linear combination of the columns of A using the corresponding entries in x as weights.
  • 37.
    Section 1.4 TheMatrix Equation Ax = b A linear combination of vectors is the product of a matrix and a vector. Denition If A is an m × n matrix with columns formed by the vectors a1 , a2 , . . . an and if x is in Rn , then the product of A and x denoted A by x is the linear combination of the columns of A using the corresponding entries in x as weights. x1    x2  Ax = .  = x1 a1 + x2 a2 + . . . + xn an  . . . an  a1 a2 .   .  xn 
  • 38.
    Section 1.4 TheMatrix Equation Ax = b For this product to be possible, the number of columns in A must be same as the number of entries in x
  • 39.
    Section 1.4 TheMatrix Equation Ax = b For this product to be possible, the number of columns in A must be same as the number of entries in x Example  1   1 −3 7 1   1 −3 7 1          2  2 1 −5 2    = 1 2 + 2  1  + 3 −5 + 4 2 3 5 2 −3 3 5 2 −3 3 4
  • 40.
    Section 1.4 TheMatrix Equation Ax = b For this product to be possible, the number of columns in A must be same as the number of entries in x Example  1   1 −3 7 1   1 −3 7 1          2  2 1 −5 2    = 1 2 + 2  1  + 3 −5 + 4 2 3 5 2 −3 3 5 2 −3 3 4 1 −6 21 4 20           = 2 +  2  + −15 +  8  = −3 5 4 −9 12 12
  • 41.
    Matrix Equation andVector Equation Consider the following system  x − 6 2 x x + 7 3 5    1  = x2 x + 2 3 = −3    
  • 42.
    Matrix Equation andVector Equation Consider the following system  x x − 6 2 x + 7 3 5    1  = x2 x + 2 3 = −3     This is the same as 1 −6 7 5 x1 0 + x2 1 + x3 2 = −3
  • 43.
    Matrix Equation andVector Equation Consider the following system  x x − 6 2 x + 7 3 5    1  = x2 x + 2 3 = −3     This is the same as 1 −6 7 5 x1 0 + x2 1 + x3 2 = −3 This is the Vector Equation.
  • 44.
    Matrix Equation andVector Equation Consider the following system  x − 6 2 x x + 7 3 5    1  = x2 x + 2 3 = −3    
  • 45.
    Matrix Equation andVector Equation Consider the following system  x − 6 2x + 7 3 x 5    1  = x2 + 2 3 x = −3     This is the same as x   1 −6 7  1  5 0 1 2 x2 = −3 x3
  • 46.
    Matrix Equation andVector Equation Consider the following system  x − 6 2x + 7 3 x 5    1  = x2 + 2 3 x = −3     This is the same as x   1 −6 7  1  5 0 1 2 x2 = −3 x3 This is the Matrix Equation.
  • 47.
    Everything is thesame Theorem If A is an m × n matrix with columns formed by the vectors a1 , a2 , . . . an and if b is in Rm , then the matrix equation Ax = b has the same solution as the following:
  • 48.
    Everything is thesame Theorem If A is an m × n matrix with columns formed by the vectors a1 , a2 , . . . an and if b is in Rm , then the matrix equation Ax = b has the same solution as the following: The vector equation x1a1 + x2a2 + . . . + xn an = b
  • 49.
    Everything is thesame Theorem If A is an m × n matrix with columns formed by the vectors a1 , a2 , . . . an and if b is in Rm , then the matrix equation Ax = b has the same solution as the following: The vector equation x1a1 + x2a2 + . . . + xn an = b The system of linear equations whose augmented matrix is a1 a2 . . . an (which you have been all these days)
  • 50.
    Everything is thesame Theorem If A is an m × n matrix with columns formed by the vectors a1 , a2 , . . . an and if b is in Rm , then the matrix equation Ax = b has the same solution as the following: The vector equation x1a1 + x2a2 + . . . + xn an = b The system of linear equations whose augmented matrix is a1 a2 . . . an (which you have been all these days) That is, solving a matrix equation is the same as solving the corresponding vector equation which is the same as solving the corresponding system of linear equations by row-reducing the augmented matrix.
  • 51.
    Existence of Solutions The matrix equation Ax = b has a solution if and only if b is a linear combination of the columns of A. So Ax = b should be consistent for all possible b for solution to exist.
  • 52.
    Existence of Solutions The matrix equation Ax = b has a solution if and only if b is a linear combination of the columns of A. So Ax = b should be consistent for all possible b for solution to exist. Theorem If A is an m × n matrix and if the matrix equation Ax = b has a solution then Each b is a linear combination of the columns of A The columns of A span Rm (very important) A has pivot position in every row (not necessarily every column). Please note that A is the coecient matrix (and not the augmented matrix)
  • 53.
    Problem 12, section1.4 Write the augmented matrix for the linear system corresponding to the matrix equation Ax = b, solve the system and write the answer as avector. 1 2 1 0    A= −3 −1 2, b= 1  0 5 3 −1 The augmented matrix is    1 2 1 0 R2+3R1       −3 −1 2 1          0 5 3 −1
  • 54.
    Problem 12, section1.4    1 2 1 0       0 5 5 1    R3-R2       0 5 3 −1 1 2 1 0    0 5 5 1  0 0 −2 −2 Divide R3 by -2 1 2 1 0    0 5 5 1  0 0 1 1
  • 55.
    Problem 12, section1.4    1 2 1 0       0 5 5 1    R2-5R3       0 0 1 1 1 2 1 0    0 5 0 −4  0 0 1 1 Divide R2 by 5 1 2 1 0    0 1 0 −4  5 0 0 1 1
  • 56.
    Problem 12, section1.4    1 2 1 0    R1-R3    0 1 0 −4     5      0 0 1 1    1 2 0 −1 R1-2R2       0 1 0 −4   5        0 0 1 1
  • 57.
    1 0 03   5  0 1 0 −4  5 0 0 1 1 The augmented column in the above matrix is the solution vector x1  5    3 x= x2  = − 4  5 x3 1 Problem 22, section 1.4 0 0 4       Let v1 = 0 , v2 =−3, v3 =−1. Does {a1 , a2 , a3 } span R3 ? −2 8 −5 Why or why not?
  • 58.
    Problem 22, section1.4 OutlineThis problem is a direct application of the theorem we saw just now. We need to see the connection between pivots, existence of solution and span. If we show that this matrix has pivot in each row, we have a solution and that means these vectors span R3    0 0 4    Swap    0 −3 −1          −2 8 5    −2 8 5       0 −3 −1          0 0 4
  • 59.
    Problem 22, section1.4 Divide rst row by -2, second row by -3 and third row by 4 5 1 −4 2    0 1 1  3 0 0 1 We have pivot position in each row which means that by our theorem, {a1 , a2 , a3 } span R3 .
  • 60.
    Row-Vector Rule forComputing Ax = b If the product Ax = b is dened, the entry in the i th position of Ax is the sum of the products of the entries from row i of A and from the vector x (very important for matrix multiplication in chapter 2) Example 1.  1   1 −3 7 1   1.1 + (−3).2 + 7.3 + 1.4 20      2   2 1 −5 2    = 2.1 + 1.2 + (−5).3 + 2.4  = −3 3 5 2 −3 3 5.1 + 2.2 + (−3).3 + 3.4 12 4 2. 1 0 0 5 1. 5 + 0. 6 + 0. 7 5         0 1 0  6 =  0.5 + 1.6 + 0.7  = 6 0 0 1 7 0.5 + 0.2 + 1.7 7