This document discusses different methods for finding the equation of a line, including:
1) Given the slope and y-intercept
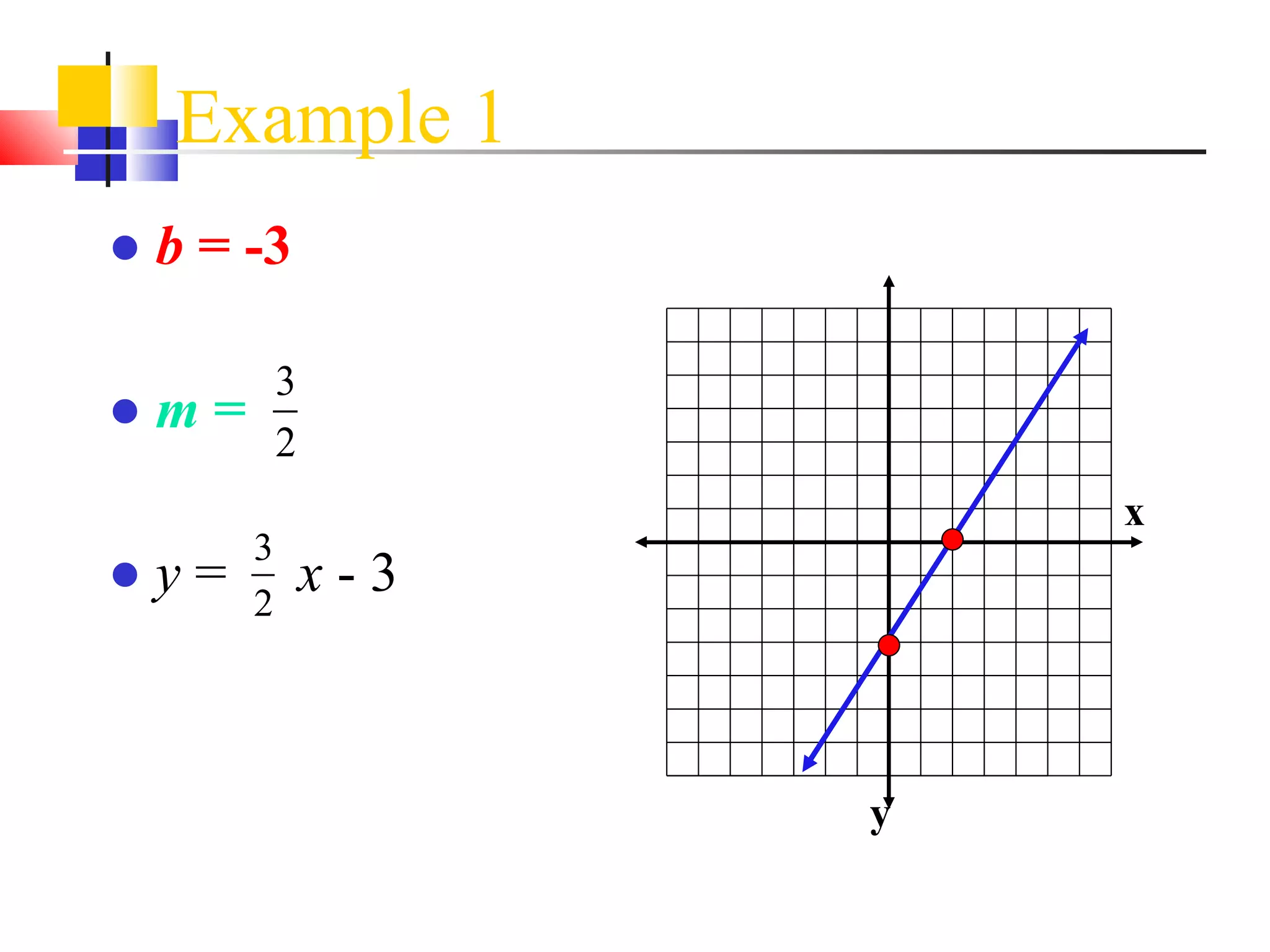
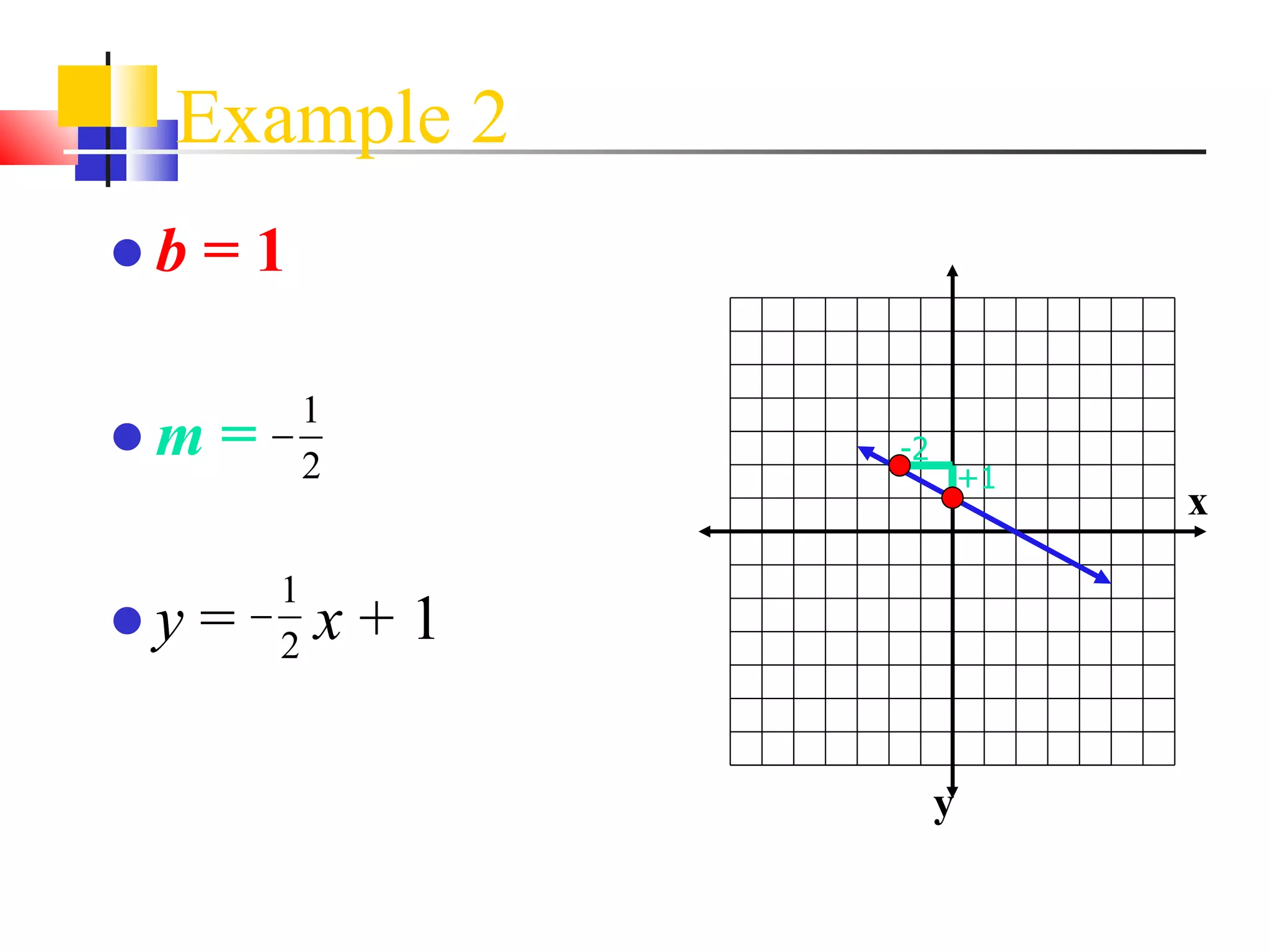
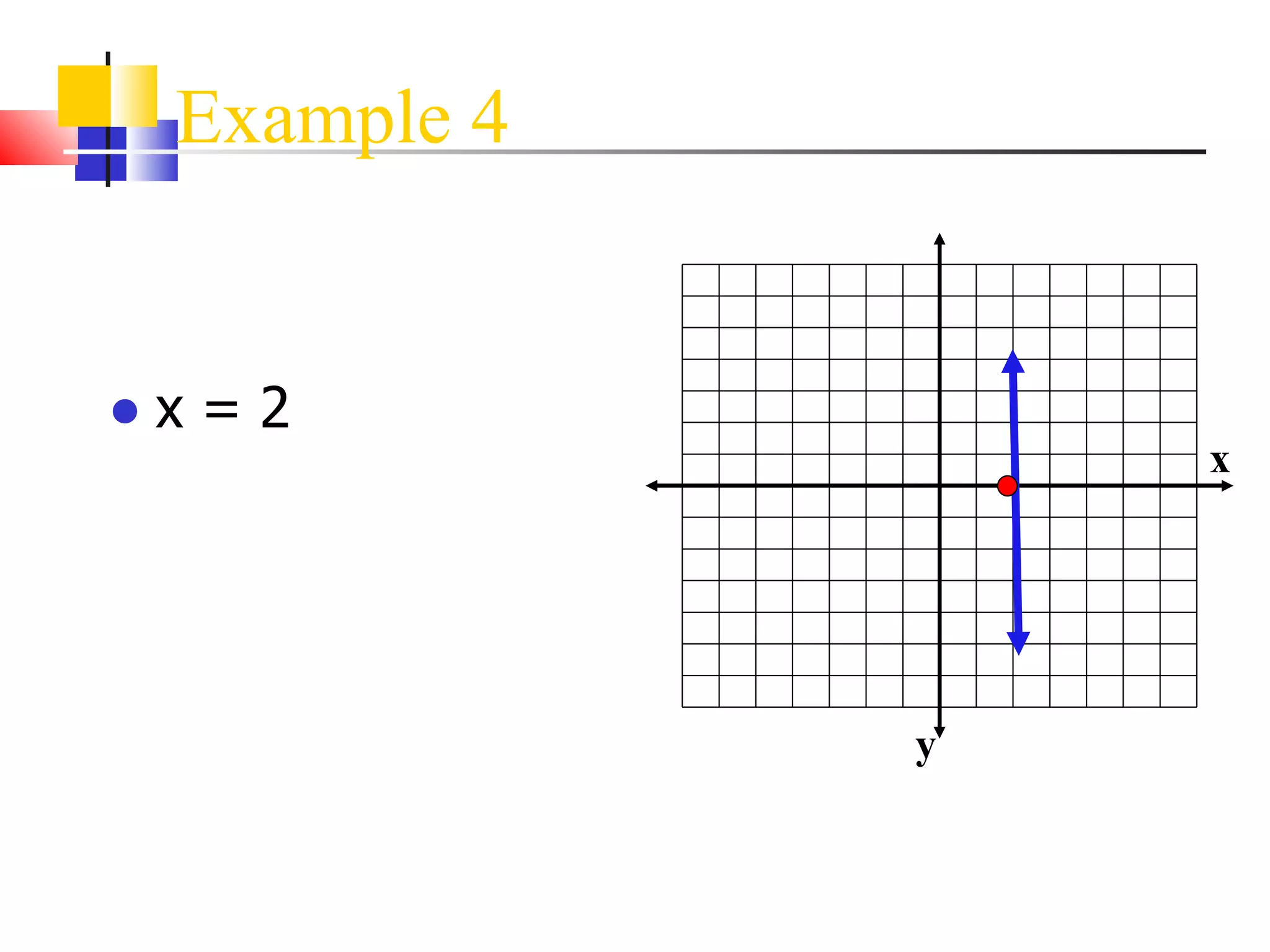
2) Using a graph
3) Given a point and the slope
4) Given two points
It provides examples of how to write the line equation using each method.