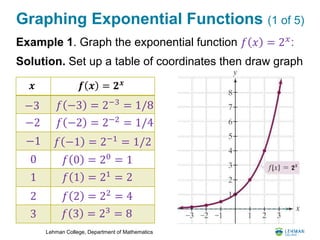
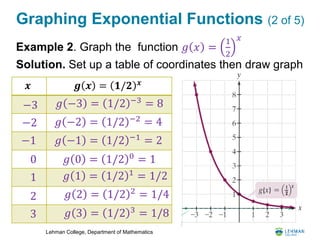
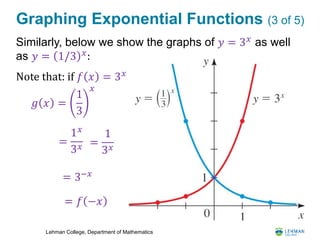
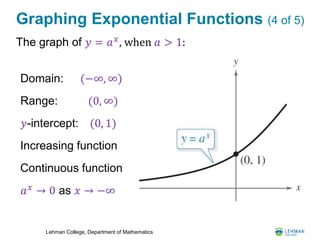
- The document is a lesson on exponential and logarithmic functions from a Bridge to Calculus workshop.
- It reviews rational exponents, defines exponential and logarithmic functions, and covers graphing and solving equations involving exponential and logarithmic functions.
- Key topics include the definitions and properties of exponential and logarithmic functions, as well as how to convert between exponential and logarithmic form.