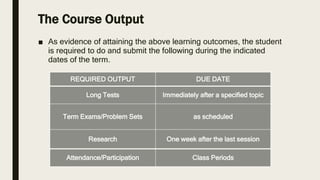
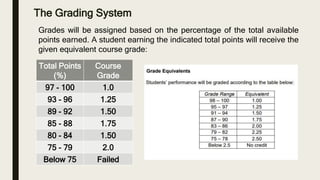
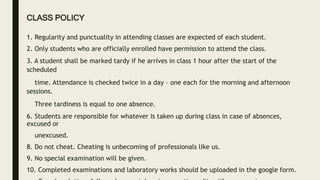
This document provides an orientation for a Probability and Statistics course. It outlines the course schedule, instructor information, learning outcomes, assignments, assessments, grading system, and policies. The course introduces concepts of probability, random variables, probability distributions, and mathematical expectations. It will be taught on Saturdays in May and June 2021 and will include exams, problem sets, and a research paper. Students will learn counting techniques, probability laws, discrete and continuous distributions, and their applications. Attendance and participation are required.

1. COURSE ORIENTATION FOR
PROBABILITY AND STATISTICS
MATH 516

2. SCHEDULE C - Second Trimester, School Year 2021 - 2022
PROGRAM: Master of Arts in Education major in MATHEMATICS
COURSE CODE: Math 516
COURSE TITLE: Probability amd Statistics
SCHEDULE: May 28, June 4, 11, 18, 25, 2021
TIME: Saturdays 8:00 am - 4:00 pm
Written Examinations: Thursdays 4: 00 – 11:00
PROFESSOR: EDGARDO M. SANTOS, Ph. D.
Vice President for Academic Affairs
OIC – Dean, College of Science
edgardo.santos@bulsu.edu.ph

3. The Course Syllabus
COURSE DESCRIPTION:
The course introduces students to the mathematics of
chance that includes counting techniques, probability
distribution and mathematical expectations. It exemplifies
the usefulness of mathematical probability in decision
making. It also discusses the basic concepts of probability
and the different probability distribution and their actual
applications in different fields.

4. The Course Output
■ As evidence of attaining the above learning outcomes, the student
is required to do and submit the following during the indicated
dates of the term.
REQUIRED OUTPUT DUE DATE
Long Tests Immediately after a specified topic
Term Exams/Problem Sets as scheduled
Research One week after the last session
Attendance/Participation Class Periods

5. REQUIREMENTS AND ASSESSMENTS:
Students are expected to keep up with the discussions, written /laboratory works, readings, and
research papers.
There will be TWO required research outputs on topics related to the course.
- The first research output allows you to analyze /critique one related study / paper published in
educational journals or any journals related to your specialization used as reference in your
collaborative research output. It must be recent and was published during the past five (5) years.
- The second research output allows you the chance to do research on some aspects of
mathematics and to apply your writing skills. The study must consider the post pandemic setting.
The paper must be at least 20 pages plus a complete bibliography, including explicit web sites
and sources of quotes. A video presentation of at most 30 minutes must be submitted together
with the write up.
The content of the second paper will be synthesized in terms of the following domains Introduction
/ Objective of the study, Research Methodology, and Results and Discussions.
 Submit papers on time. The critique papers are due at the end of the course subject (June 25,
2022), the second paper on June 30, 2022.

6. Title of the Research Authors
Paper No.___
Abstract
Statement of the Problem/
Objectives of the Study
Brief Discussion of the Conceptual
Framework
Research Methodology Design
Used in the Study
Results and Discussions
Learning/Ideas from the Paper that
contributed in the Development of
the Collaborative Research Papers

7. REQUIREMENTS AND ASSESSMENTS
Sample of Research Titles:
o Flexibility in the Teaching of Mathematics During the Post Pandemic:
On – line Learning vs. Hybrid Learning
o Restructuring On-line Learning with consideration of Students’
Learning Styles
Note:
1. In the essence of time, use descriptive research or meta-analysis/
meta-synthesis.
2. Research is collaborative. Form a group of 2.

8.  Written Examinations will be given. The activities will test your
knowledge on the various sections of the course. When a student
misses an activity, no makeup activity may be arranged.
 Attendance will be taken, and anyone with one Saturday of absence
may be dropped from the course. Students are expected to attend
each class meeting and pay attention to the discussion. A student who
misses class with valid reason (excused) is responsible to find out
what was discussed and learn the material that was covered on the
missed day.
 Participation is measured by your inputs and engagements at each
session.
 Any student who exhibits academic dishonesty in any form will receive
a failing grade (F) for the entire course. Intellectual integrity is a
course expectation and requirement.

9. Sample Research and Proforma
 A Look into the Students' Conceptual Understanding of the Definite
Integral via the APOS Model
 Moving from Concrete to Abstract
 Students' Mathematical Communication and Conceptual Understanding
 Exploring the Use of CRA
 STUDENTS’ MOTIVATIONAL BELIEFS, VALUES AND GOALS AS RELATED TO
ACADEMIC HARDINESS:
 Students' Motivation, Learning Strategies and Proof Construction Skills
 Using the APOS Perspective in Analyzing Students' Responses to Talk - Aloud Test
on the Definite Integral

10. The Grading System
Total Points
(%)
Course
Grade
97 - 100 1.0
93 - 96 1.25
89 - 92 1.50
85 - 88 1.75
80 - 84 1.50
75 - 79 2.0
Below 75 Failed
Grades will be assigned based on the percentage of the total available
points earned. A student earning the indicated total points will receive the
given equivalent course grade:

11. Components in the Grading System
Note: Research will require a recorded video presentation of at most 30 minutes.

12. Components in the Grading System

13. The Course Content
Specific Learning Outcomes Topics Learning Activities
Orientation of the vision, mission goals, and
objectives of the university and institution
1. Define the various counting
techniques.
2. Solve Problems involving FCP,
CPAC, permutations, and
combinations.
Counting Techniques
 Fundamental Principles of Counting
 Permutations
 Combination
Lecture/Interactive Class
Discussion
3. Define the basic probability concepts.
4. Discuss and apply the properties,
laws of probability, conditional
probability and Baye’s Rule.
5. Define and give examples of mutually
exclusive and independent events.
6. Compute probabilities of events.
Concepts of Probability
 Probability of Events
 Laws of Probability
 Additive Rules
 Conditional Probability
 Dependent and Independent Event
 Multiplicative Rules
 Baye’s Rule
Lecture/Interactive Class
Discussion/Seat works

14. The Course Content
Specific Learning Outcomes Topics Learning Activities
7. Explain the relevance of random
variables in the determination of
probabilities.
8. Distinguish between discrete and
continuous probability distributions.
9. Enumerate the properties of
probability and cumulative
distributions, joint probability
distributions.
10. Explain and show independence of
random variables.
11. Derive conditional and marginal
distributions.
12. Solve problems involving discrete
and continuous probability
distributions.
Random Variables and Probability
Distribution
 Concepts of Random Variables
 Probability Distribution
 Discrete and Continuous Distribution
 Joint Probability Distribution
Lecture/Interactive
Class
Discussion/Seat
works

15. The Course Content
Specific Learning Outcomes Topics Learning Activities
13. Define expected value of a
discrete and continuous random
variables; variance of random
variables.
14. Compute mathematical
expectations involving functions
of random variables.
Mathematical Expectations
 Expected Value of Discrete Random Variable
 Expected Value of One Variable Function
 Expected Value of Two Variable Function
 Variance of Random Variables
 Variance of One Variable Function
 Properties of Mean and Variance
 Chebyshev’s Theorem
Lecture/Interactive Class
Discussion/
Seat works
15. Name some commonly used
special discrete and continuous
distributions. Give their
properties.
16. Solve problems involving
practical application of discrete
and continuous probability
distribution
Discrete Probability Distribution
 Uniform Distribution
 Binomial Distribution
 Multinomial Distribution
 Hypergeometric Distribution
 Negative Binomial Distribution
 Geometric Distribution
 Poisson Distribution
Continuous Probability Distribution
 Normal Distribution
 Application of the Normal Distribution
 Normal Approximation to the Binomial

16. REFERENCES:
Mendenhall, William, Robert j. Beaver and Barbara M. Beaver
Introduction to Probability and Statistics, 10th edition, Duxbury Press,
Massachusetts, 1999.
Richard J. Larsen and Morris L. Marx (2006), Mathematical Statistics and
Its Application 4th Edition, (Singapore: Pearson Prentice Hall).
Walpole, R. and Myers, R. Probability and Statistics for Engineers and
Scientists, 6th edition. MacMillan Publishing Co., Inc., New York,
1998.
Basic Statistical Methods (5th ed.) , 1984, by Downie & Heath
Walpole, Ronald E.,Introduction to Statistics , 3rd edition, 1997

17. ONLINE RESOURCES:
Devore, J. L. (2012). Probability and Statistics for Engineering and the Sciences, 8th
edition, funnel.sfsu.edu/.../%255bJay_L._Devore%...
Kerns, J. (2010). Introduction to Probability and Statistics Using R cran.r
project.org/web/packages/IPSUR/vignettes/IPSUR.pdf
Larsen,J. (2006). Probability Theory & Statistics
ads.harvard.edu/books/1990fnmd.book/chapt7.pdf
Walpole, R. E., Myers, R.H., Myers, S. L.& Ye, k. Probability & Statistics for
Engineers & Scientists, 9th Ed. (2012). folk.ntnu.no/jenswerg/40CEFd01.pdf
Soong, T. T. (2004). Fundamentals of of Probability and Statistics for Engineer.
vfu.bg/.../Math-- Soong_Fundamentals_of_probabi...

18. CLASS POLICY
1. Regularity and punctuality in attending classes are expected of each student.
2. Only students who are officially enrolled have permission to attend the class.
3. A student shall be marked tardy if he arrives in class 1 hour after the start of the
scheduled
time. Attendance is checked twice in a day – one each for the morning and afternoon
sessions.
Three tardiness is equal to one absence.
6. Students are responsible for whatever is taken up during class in case of absences,
excused or
unexcused.
8. Do not cheat. Cheating is unbecoming of professionals like us.
9. No special examination will be given.
10. Completed examinations and laboratory works should be uploaded in the google form.