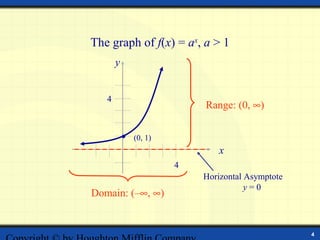
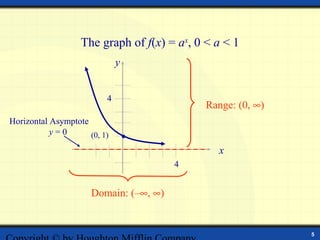
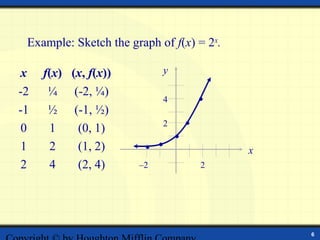
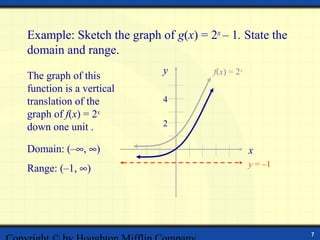
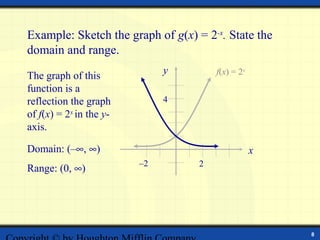
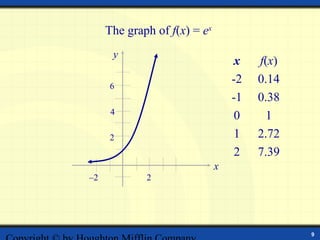
The document discusses exponential functions of the form f(x) = ax, where a is the base. It defines exponential functions and provides examples of evaluating them. The key aspects of exponential graphs are that they increase rapidly as x increases and have a horizontal asymptote of y = 0 if a > 1 or y = 0 if 0 < a < 1. Examples are given of sketching graphs of exponential functions and stating their domains and ranges. The graph of the natural exponential function f(x) = ex is also discussed.

1. Digital Lesson
Exponential Functions and
Their Graphs

2. The exponential function f with base a is
defined by
f(x) = ax
where a > 0, a ≠ 1, and x is any real number.
For instance,
f(x) = 3x and g(x) = 0.5x
are exponential functions.
2

3. The value of f(x) = 3x when x = 2 is
f(2) = 32 = 9
The value of f(x) = 3x when x = –2 is
1
f(–2) = 3 –2
=
9
The value of g(x) = 0.5x when x = 4 is
g(4) = 0.54 = 0.0625
3

4. The graph of f(x) = ax, a > 1
y
4
Range: (0, ∞)
(0, 1)
x
4
Horizontal Asymptote
y=0
Domain: (–∞, ∞)
4

5. The graph of f(x) = ax, 0 < a < 1
y
4
Range: (0, ∞)
Horizontal Asymptote
y=0 (0, 1)
x
4
Domain: (–∞, ∞)
5

6. Example: Sketch the graph of f(x) = 2x.
x f(x) (x, f(x)) y
-2 ¼ (-2, ¼)
4
-1 ½ (-1, ½)
2
0 1 (0, 1)
1 2 (1, 2) x
2 4 (2, 4) –2 2
6

7. Example: Sketch the graph of g(x) = 2x – 1. State the
domain and range.
y f(x) = 2x
The graph of this
function is a vertical
translation of the 4
graph of f(x) = 2x
down one unit . 2
Domain: (–∞, ∞) x
y = –1
Range: (–1, ∞)
7

8. Example: Sketch the graph of g(x) = 2-x. State the
domain and range.
y f(x) = 2x
The graph of this
function is a
reflection the graph 4
of f(x) = 2x in the y-
axis.
Domain: (–∞, ∞) x
–2 2
Range: (0, ∞)
8

9. The graph of f(x) = ex
y
x f(x)
6
-2 0.14
-1 0.38
4
0 1
2 1 2.72
2 7.39
x
–2 2
9

10. The irrational number e, where
e ≈ 2.718281828…
is used in applications involving growth and
decay.
Using techniques of calculus, it can be shown
that
n
 1
 1 +  → e as n → ∞
 n
10