1. The document announces that students should bring any exam 1 grade questions without delay, and that the homework for exam 2 has been uploaded and may be updated. It also notes that the last day to drop the class is February 4th and there is no class on that date. 2. The document covers topics from the last class including computing 3x3 determinants, determinants of triangular matrices, and techniques for larger matrices. 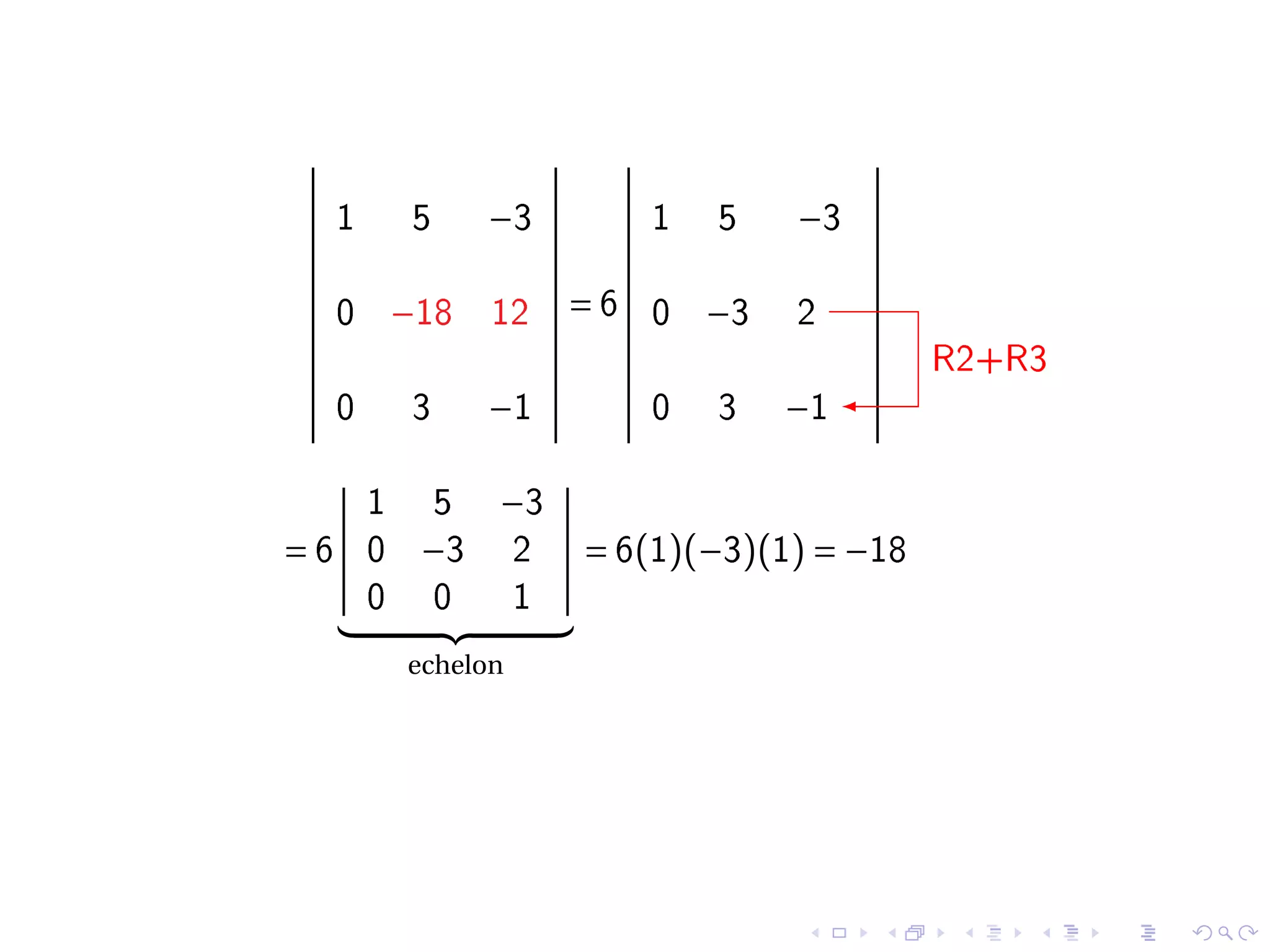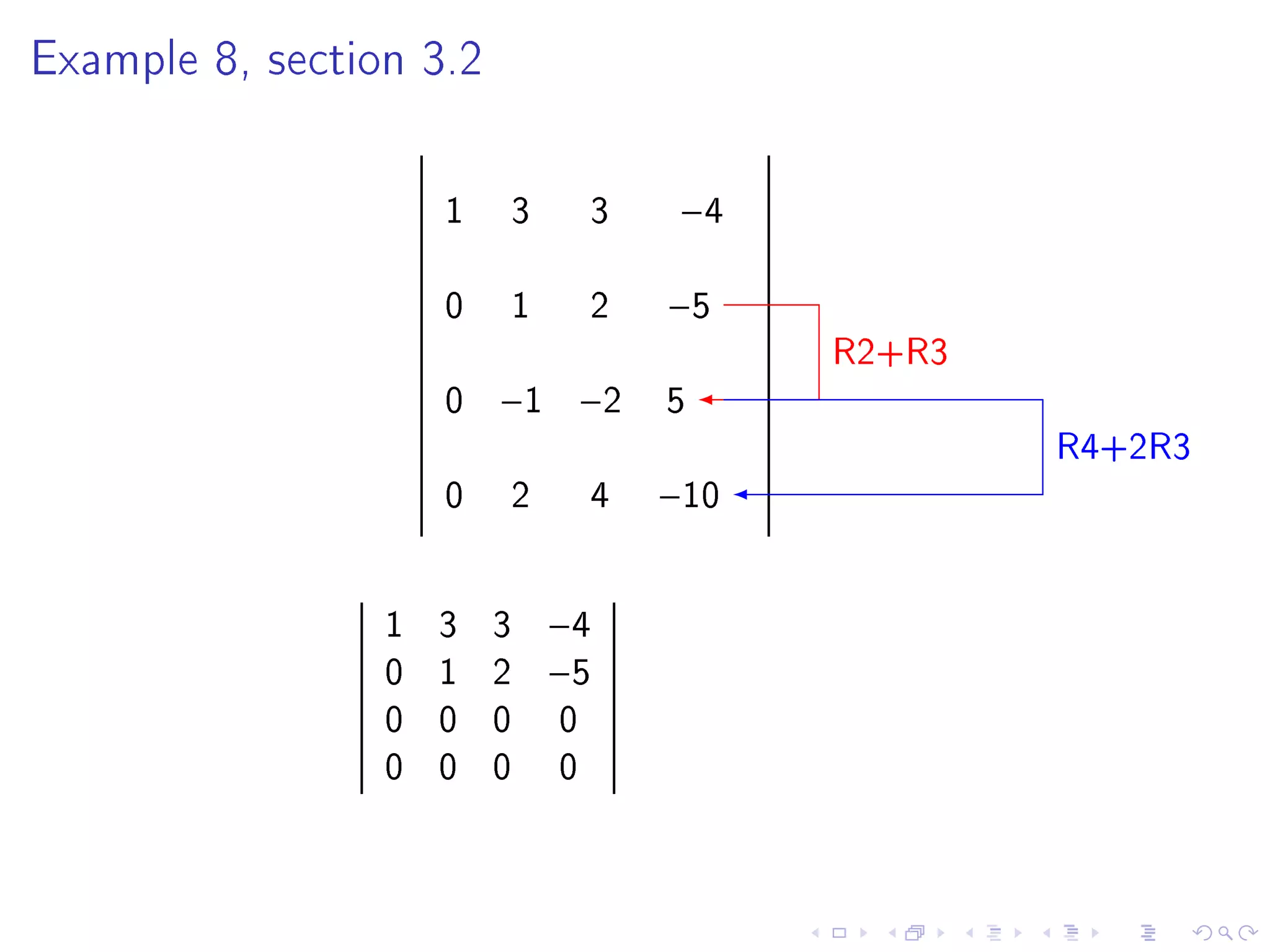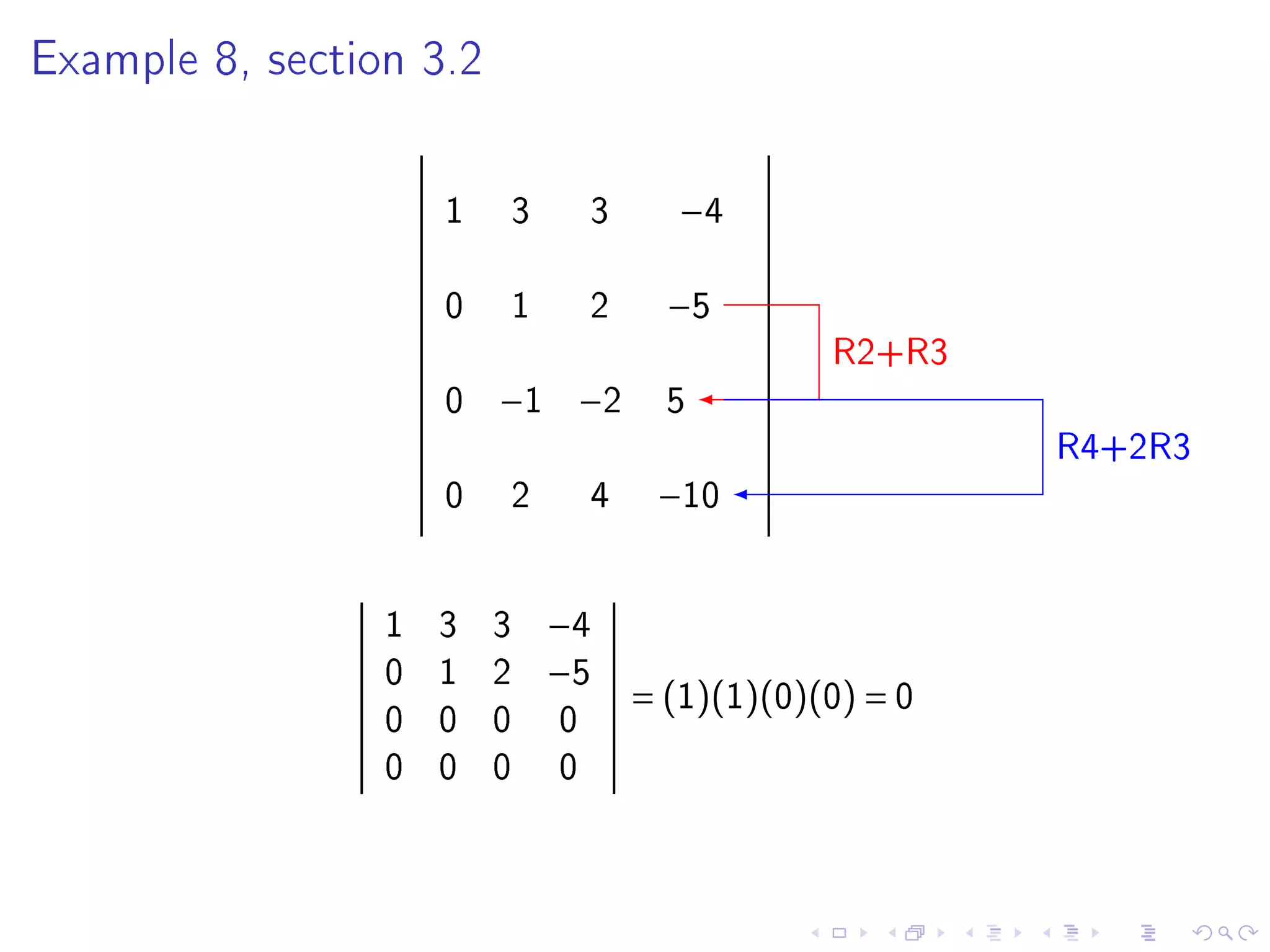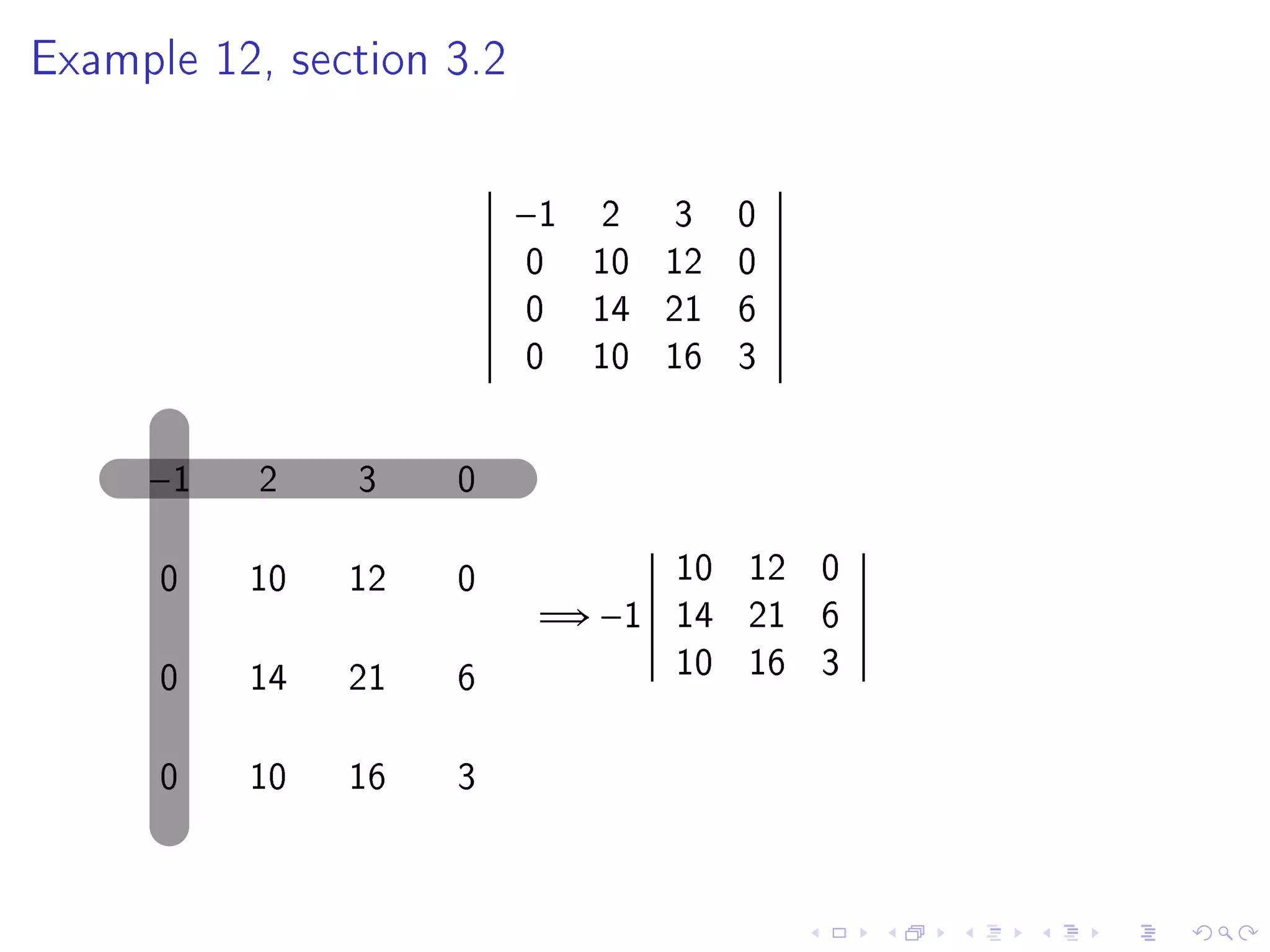3. The document then provides examples of computing determinants and discusses important properties including that row operations do not change the determinant value while row interchanges flip the sign, and multiplying a row scales the determinant.

1. Announcements
Please bring any grade related questions regarding exam 1
without delay.
Homework set for exam 2 has been uploaded. Please check it
often, I may make small inclusions/exclusions.
Last day to drop this class with grade "W" is Feb 4.
No class tomorrow (Thurs, Feb 4).

2. Last Class
1. Saw how to compute 3 × 3 determinants.

3. Last Class
1. Saw how to compute 3 × 3 determinants.
2. Determinants of triangular matrices (just the product of the
numbers along the main diagonal)

4. Last Class
1. Saw how to compute 3 × 3 determinants.
2. Determinants of triangular matrices (just the product of the
numbers along the main diagonal)
3. Determinants of nice larger matrices:- Take advantage of
rows/columns which are predominantly zeros

5. Important Facts about Determinants
What is
1 2
A = ?
3 4
It is (1)(4) − (3)(2) = −2.
What about
3 4
A = ?
1 2
It is (3)(2) − (1)(4) = 2

6. Important Facts about Determinants
What is
1 2
A = ?
3 4
It is (1)(4) − (3)(2) = −2.
What about
3 4
A = ?
1 2
It is (3)(2) − (1)(4) = 2
Interchanged the rows and we have the same value but opposite
sign

7. Important Facts about Determinants
What about
12 16
A = ?
1 2
It is (12)(2) − (1)(16) = 24 − 16 = 8.

8. Important Facts about Determinants
What about
12 16
A = ?
1 2
It is (12)(2) − (1)(16) = 24 − 16 = 8.
Multiplied ONE row by 4 and the answer gets multiplied by 4

9. Important Facts about Determinants
What about
12 16
A = ?
1 2
It is (12)(2) − (1)(16) = 24 − 16 = 8.
Multiplied ONE row by 4 and the answer gets multiplied by 4
Note: If you multiply the entire determinant by 4, then the answer
gets multiplied by 4.4=16 not just by 4. Try it yourself.

10. Important Facts about Determinants
3 4 3 4
Let A = and B =
1 2 4 6

11. Important Facts about Determinants
3 4 3 4
Let A = and B =
1 2 4 6
Here B is obtained by adding row 1 to row 2 of A.

12. Important Facts about Determinants
3 4 3 4
Let A = and B =
1 2 4 6
Here B is obtained by adding row 1 to row 2 of A.
What is B ? It is (3)(6) − (4)(4) = 18 − 16 = 2. The same!!

13. Important Facts about Determinants
3 4 3 4
Let A = and B =
1 2 7 10

14. Important Facts about Determinants
3 4 3 4
Let A = and B =
1 2 7 10
Here B is obtained by adding 2R1 to R2 of A.

15. Important Facts about Determinants
3 4 3 4
Let A = and B =
1 2 7 10
Here B is obtained by adding 2R1 to R2 of A.
What is B ? It is (3)(10) − (7)(4) = 30 − 28 = 2. The same!!

16. Theorem
Theorem
1. The value of determinant DOES NOT change if you add a
multiple of a row to another row.

17. Theorem
Theorem
1. The value of determinant DOES NOT change if you add a
multiple of a row to another row.
2. The value of determinant only changes sign if you interchange
any 2 rows.

18. Theorem
Theorem
1. The value of determinant DOES NOT change if you add a
multiple of a row to another row.
2. The value of determinant only changes sign if you interchange
any 2 rows.
3. If you multiply any row of a determinant by a number k , the
value of the determinant gets multiplied by k .

19. Any uses?
1. Use these properties eectively and appropriately to reduce a
determinant to echelon form.

20. Any uses?
1. Use these properties eectively and appropriately to reduce a
determinant to echelon form.
2. Then the determinant is just the product of the main diagonal
entries. (It is a triangular matrix)

21. Any uses?
1. Use these properties eectively and appropriately to reduce a
determinant to echelon form.
2. Then the determinant is just the product of the main diagonal
entries. (It is a triangular matrix)
3. Do not forget to change sign if you interchange rows.

22. Any uses?
1. Use these properties eectively and appropriately to reduce a
determinant to echelon form.
2. Then the determinant is just the product of the main diagonal
entries. (It is a triangular matrix)
3. Do not forget to change sign if you interchange rows.
4. You can factor out any number common to all entries in a row
to make your determinant easier to work with.

23. Example 6, section 3.2
Find the determinant by row reduction to the echelon form.
1 5 −3
3 −3 3
2 13 −7

24. Example 6, section 3.2
Find the determinant by row reduction to the echelon form.
1 5 −3
3 −3 3
2 13 −7
Solution: Basic row operations
1 5 −3
R2-3R1
3 −3 3 R3-2R1
2 13 −7

25. 1 5 −3 1 5 −3
0 −18 12 =6 0 −3 2
R2+R3
0 3 −1 0 3 −1
1 5 −3
=6 0 −3 2
0 0 1
echelon

26. 1 5 −3 1 5 −3
0 −18 12 =6 0 −3 2
R2+R3
0 3 −1 0 3 −1
1 5 −3
=6 0 −3 2 = 6(1)(−3)(1) = −18
0 0 1
echelon

27. Example 8, section 3.2
Find the determinant by row reduction to the echelon form.
1 3 3 −4
0 1 2 −5
2 5 4 −3
−3 −7 −5 2

28. Example 8, section 3.2
Find the determinant by row reduction to the echelon form.
1 3 3 −4
0 1 2 −5
2 5 4 −3
−3 −7 −5 2
Solution: Basic row operations
1 3 3 −4
0 1 2 −5 R3-2R1
R4+3R1
2 5 4 −3
−3 −7 −5 2

29. Example 8, section 3.2
1 3 3 −4
0 1 2 −5
R2+R3
0 −1 −2 5
R4+2R3
0 2 4 −10
1 3 3 −4
0 1 2 −5
0 0 0 0
0 0 0 0

30. Example 8, section 3.2
1 3 3 −4
0 1 2 −5
R2+R3
0 −1 −2 5
R4+2R3
0 2 4 −10
1 3 3 −4
0 1 2 −5
= (1)(1)(0)(0) = 0
0 0 0 0
0 0 0 0

31. Important
1. If a determinant has a row (or column) full of zeros, then it is
equal to 0. ALWAYS!

32. Important
1. If a determinant has a row (or column) full of zeros, then it is
equal to 0. ALWAYS!
2. Even before reaching the all-zero stage if you see two (or
more) rows (or columns) being exactly the same, then the
determinant is 0.

33. Important
1. If a determinant has a row (or column) full of zeros, then it is
equal to 0. ALWAYS!
2. Even before reaching the all-zero stage if you see two (or
more) rows (or columns) being exactly the same, then the
determinant is 0.
3. Same when any row (or respectively column) is a multiple of
any other row (or respectively column). The determinant is 0.

34. Important
1. If a determinant has a row (or column) full of zeros, then it is
equal to 0. ALWAYS!
2. Even before reaching the all-zero stage if you see two (or
more) rows (or columns) being exactly the same, then the
determinant is 0.
3. Same when any row (or respectively column) is a multiple of
any other row (or respectively column). The determinant is 0.
4. Sometimes you may have to do row reductions rst and then
do co-factor expansion. (An echelon form may not happen
always)

35. Example 12, section 3.2
Combine row reduction and cofactor expansion
−1 2 3 0
3 4 3 0
5 4 6 6
4 2 4 3

36. Example 12, section 3.2
Combine row reduction and cofactor expansion
−1 2 3 0
3 4 3 0
5 4 6 6
4 2 4 3
Solution: Basic row operations
−1 2 3 0
R2+3R1
3 4 3 0 R3+5R1
R4+4R1
5 4 6 6
4 2 4 3

37. Example 12, section 3.2
−1 2 3 0
0 10 12 0
0 14 21 6
0 10 16 3
−1 2 3 0
0 10 12 0
0 14 21 6
0 10 16 3

38. Example 12, section 3.2
−1 2 3 0
0 10 12 0
0 14 21 6
0 10 16 3
−1 2 3 0
0 10 12 0 10 12 0
=⇒ −1 14 21 6
0 14 21 6 10 16 3
0 10 16 3

39. Example 12, section 3.2
5 6 0
Factor 2 from rst row, =⇒ −1(2) 14 21 6 .
10 16 3
Do cofactor expansion along the rst row

40. 5 6 0
14 21 6
10 16 3
21 6
det A = 5
16 3
63−96=−33

41. 5 6 0 5 6 0
14 21 6 14 21 6
10 16 3 10 16 3
21 6 14 6
det A = 5 −6
16 3 10 3
63−96=−33 42−60=−18

42. 5 6 0 5 6 0 5 6 0
14 21 6 14 21 6 14 21 6
10 16 3 10 16 3 10 16 3
21 6 14 6 14 21
det A = 5 −6 +0
16 3 10 3 10 16
63−96=−33 42−60=−18 14
= −165 + 108 + 0 = −57
Don't forget to multiply the -2 we had. So the answer is 114.

43. Example 16, 18, 20 section 3.2
a b c
If d e f = 7, nd the following.
g h i

44. Example 16, 18, 20 section 3.2
a b c
If d e f = 7, nd the following.
g h i
a b c
1. 3d 3e 3f
g h i

45. Example 16, 18, 20 section 3.2
a b c
If d e f = 7, nd the following.
g h i
a b c
1. 3d 3e 3f = 21
g h i

46. Example 16, 18, 20 section 3.2
a b c
If d e f = 7, nd the following.
g h i
a b c
1. 3d 3e 3f = 21
g h i
g h i
2. a b c
d e f

47. Example 16, 18, 20 section 3.2
a b c
If d e f = 7, nd the following.
g h i
a b c
1. 3d 3e 3f = 21
g h i
g h i
2. a b c =7
d e f

48. Example 16, 18, 20 section 3.2
a b c
If d e f = 7, nd the following.
g h i
a b c
1. 3d 3e 3f = 21
g h i
g h i
2. a b c =7 (Two row interchanges, rst between R1 and
d e f
R3 making it -7 and then between R2 and new R3 making it
-(-7)=7)

49. Example 16, 18, 20 section 3.2
a b c
If d e f = 7, nd the following.
g h i
a b c
1. 3d 3e 3f = 21
g h i
g h i
2. a b c =7 (Two row interchanges, rst between R1 and
d e f
R3 making it -7 and then between R2 and new R3 making it
-(-7)=7)
a +d b +e c +f
3. d e f
g h i

50. Example 16, 18, 20 section 3.2
a b c
If d e f = 7, nd the following.
g h i
a b c
1. 3d 3e 3f = 21
g h i
g h i
2. a b c =7 (Two row interchanges, rst between R1 and
d e f
R3 making it -7 and then between R2 and new R3 making it
-(-7)=7)
a +d b +e c +f
3. d e f =7 (Adding 2 rows gives same value)
g h i

51. Back to Matrix Inverses
Theorem
A square matrix A is invertible if and only if detA= 0

52. Invertible Matrix Theorem.. Again
Remember the following from the invertible matrix theorem?
1. If the columns of the matrix are linearly dependent which
means
2. There are non-pivot columns (or free variables)
3. The matrix IS NOT invertible

53. Invertible Matrix Theorem.. Again
Remember the following from the invertible matrix theorem?
1. If the columns of the matrix are linearly dependent which
means
2. There are non-pivot columns (or free variables)
3. The matrix IS NOT invertible
This just means that the determinant of the matrix is 0.

54. Invertible Matrix Theorem.. Again
If the determinant of a matrix is 0 then one of the following could
be true.
1. The columns of the matrix are linearly dependent. (same
columns or one column being multiple of another)

55. Invertible Matrix Theorem.. Again
If the determinant of a matrix is 0 then one of the following could
be true.
1. The columns of the matrix are linearly dependent. (same
columns or one column being multiple of another)
2. The rows of the matrix are linearly dependent. (same rows or
one row being multiple of another)

56. Invertible Matrix Theorem.. Again
If the determinant of a matrix is 0 then one of the following could
be true.
1. The columns of the matrix are linearly dependent. (same
columns or one column being multiple of another)
2. The rows of the matrix are linearly dependent. (same rows or
one row being multiple of another)
3. Row or column full of zeros

57. Example 22, section 3.2
Use determinant to nd out if the matrix is invertible.
5 0 −1
 
 1 −3 −2 
0 5 3

58. Example 22, section 3.2
Use determinant to nd out if the matrix is invertible.
5 0 −1
 
 1 −3 −2 
0 5 3
5 0 −1
1 −3 −2
0 5 3
−3 −2
det A = 5
5 3
1

59. Example 22, section 3.2
Use determinant to nd out if the matrix is invertible.
5 0 −1
 
 1 −3 −2 
0 5 3
5 0 −1 5 0 −1
1 −3 −2 1 −3 −2
0 5 3 0 5 3
−3 −2 1 −2
det A = 5 −0
5 3 0 3
1 3

60. Example 22, section 3.2
Use determinant to nd out if the matrix is invertible.
5 0 −1
 
 1 −3 −2 
0 5 3
5 0 −1 5 0 −1 5 0 −1
1 −3 −2 1 −3 −2 1 −3 −2
0 5 3 0 5 3 0 5 3
−3 −2 1 −2 1 −3
det A = 5 −0 −1
5 3 0 3 0 5
1 3 5
= 5−0−5 = 0

61. Example 22, section 3.2
Use determinant to nd out if the matrix is invertible.
5 0 −1
 
 1 −3 −2 
0 5 3
5 0 −1 5 0 −1 5 0 −1
1 −3 −2 1 −3 −2 1 −3 −2
0 5 3 0 5 3 0 5 3
−3 −2 1 −2 1 −3
det A = 5 −0 −1
5 3 0 3 0 5
1 3 5
= 5−0−5 = 0
The matrix is not invertible.

62. Column Operations
1. You could do the same operations you do with the rows to the
columns as well
2. Not usually done, just to avoid confusion.
Theorem
If A is an n ×n matrix, then det A = det AT

63. Determinants and Matrix Products
Theorem
If A and B are n ×n matrices, then det AB = (det A)(det B )

64. Determinants and Matrix Products
Theorem
If A and B are n ×n matrices, then det AB = (det A)(det B )
Also,
If A is an n × n matrix, then det Ak = (det A)k for any number k .
(Use this in problem 29 in your homework)

65. Determinants and Matrix Products
Theorem
If A and B are n ×n matrices, then det AB = (det A)(det B )
Also,
If A is an n × n matrix, then det Ak = (det A)k for any number k .
(Use this in problem 29 in your homework)
However in general,
If A and B are n × n matrices, then det(A + B ) = det A + det B

66. Example 40 section 3.2
Let A and B be 4 × 4 matrices with det A =-1 and det B =2.
Compute

67. Example 40 section 3.2
Let A and B be 4 × 4 matrices with det A =-1 and det B =2.
Compute
1. det AB

68. Example 40 section 3.2
Let A and B be 4 × 4 matrices with det A =-1 and det B =2.
Compute
1. det AB = −2

69. Example 40 section 3.2
Let A and B be 4 × 4 matrices with det A =-1 and det B =2.
Compute
1. det AB = −2
2. det B 5

70. Example 40 section 3.2
Let A and B be 4 × 4 matrices with det A =-1 and det B =2.
Compute
1. det AB = −2
2. det B 5 = 25 = 32

71. Example 40 section 3.2
Let A and B be 4 × 4 matrices with det A =-1 and det B =2.
Compute
1. det AB = −2
2. det B 5 = 25 = 32
3. det2A

72. Example 40 section 3.2
Let A and B be 4 × 4 matrices with det A =-1 and det B =2.
Compute
1. det AB = −2
2. det B 5 = 25 = 32
3. det2A = −16

73. Example 40 section 3.2
Let A and B be 4 × 4 matrices with det A =-1 and det B =2.
Compute
1. det AB = −2
2. det B 5 = 25 = 32
3. det2A = −16
4. det AT A

74. Example 40 section 3.2
Let A and B be 4 × 4 matrices with det A =-1 and det B =2.
Compute
1. det AB = −2
2. det B 5 = 25 = 32
3. det2A = −16
4. det AT A = (det A)(det A) = 1

75. Example 40 section 3.2
Let A and B be 4 × 4 matrices with det A =-1 and det B =2.
Compute
1. det AB = −2
2. det B 5 = 25 = 32
3. det2A = −16
4. det AT A = (det A)(det A) = 1
5. det B −1 AB

76. Example 40 section 3.2
Let A and B be 4 × 4 matrices with det A =-1 and det B =2.
Compute
1. det AB = −2
2. det B 5 = 25 = 32
3. det2A = −16
4. det AT A = (det A)(det A) = 1
5. det B −1 AB = (det B −1 )(det A)(det B ) = 1 (−1)(2) = −1
2

77. Example 40 section 3.2
Let A and B be 4 × 4 matrices with det A =-1 and det B =2.
Compute
1. det AB = −2
2. det B 5 = 25 = 32
3. det2A = −16
4. det AT A = (det A)(det A) = 1
5. det B −1 AB = (det B −1 )(det A)(det B ) = 1 (−1)(2) = −1
2
Do you really believe here that det B −1 = 1 ?
2

78. Example 40 section 3.2
Let A and B be 4 × 4 matrices with det A =-1 and det B =2.
Compute
1. det AB = −2
2. det B 5 = 25 = 32
3. det2A = −16
4. det AT A = (det A)(det A) = 1
5. det B −1 AB = (det B −1 )(det A)(det B ) = 1 (−1)(2) = −1
2
Do you really believe here that det B −1 = 1 ?Yes! Think why and do
2
homework problem 31. It is simple.

79. Example
9 2
Let A = . Find det A9 .
4 1
Should you multiply the matrix A 9 times?

80. Example
9 2
Let A = . Find det A9 .
4 1
Should you multiply the matrix A 9 times? NO!!!!!!! Just remember
that det A9 = (det A)9 . Here det A = 9 − 8 = 1. So (det A)9 = 19 = 1