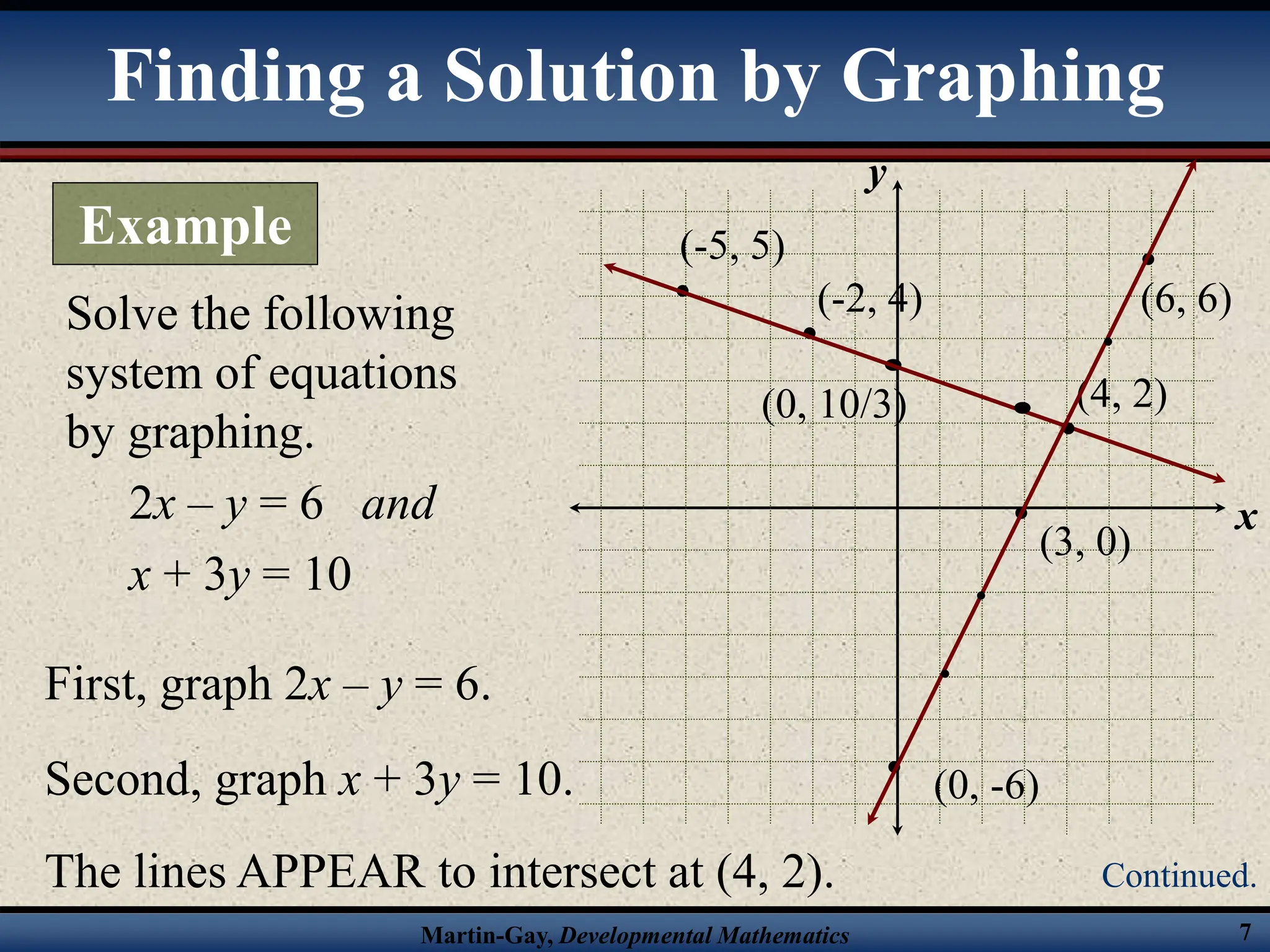
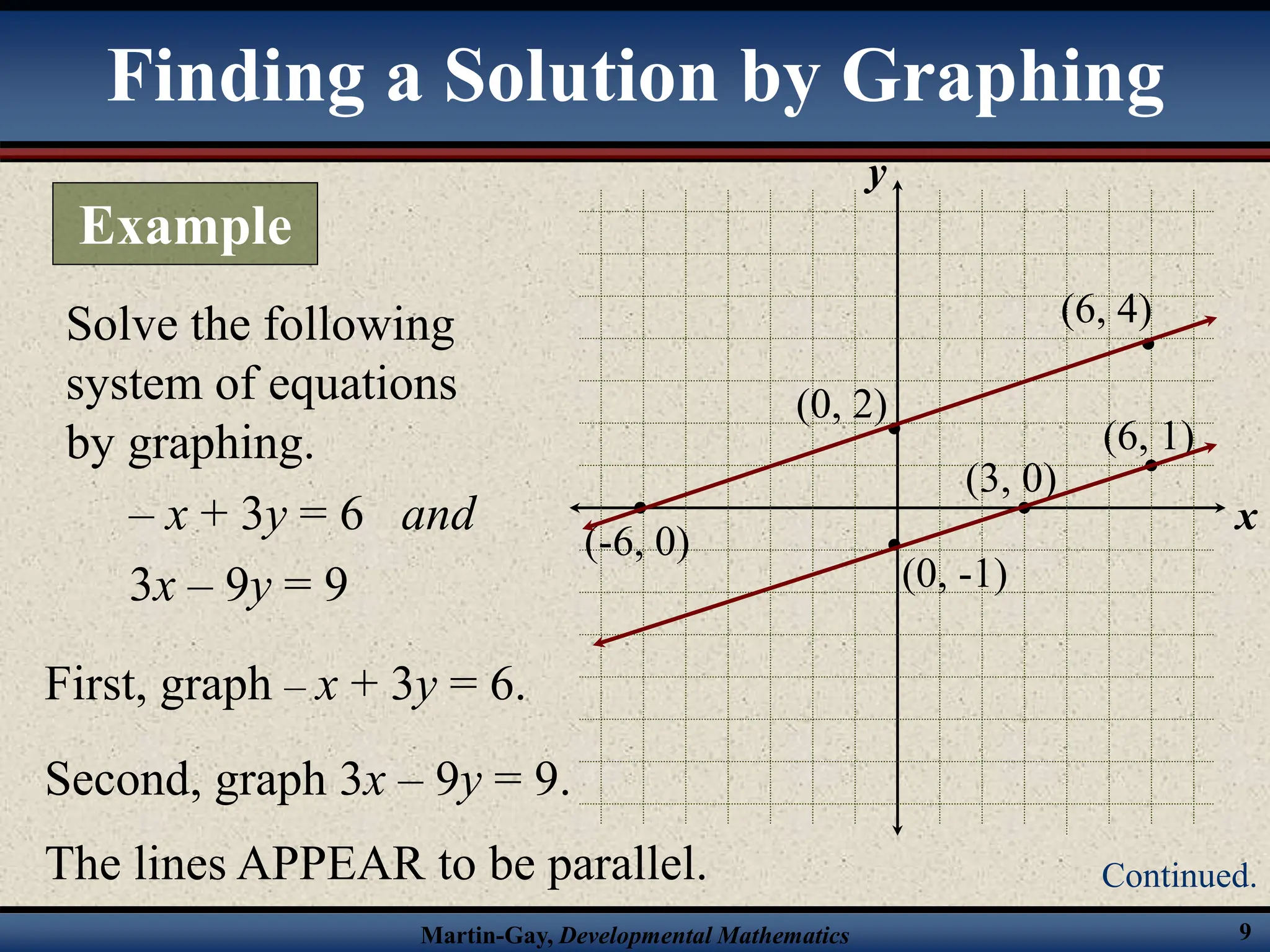
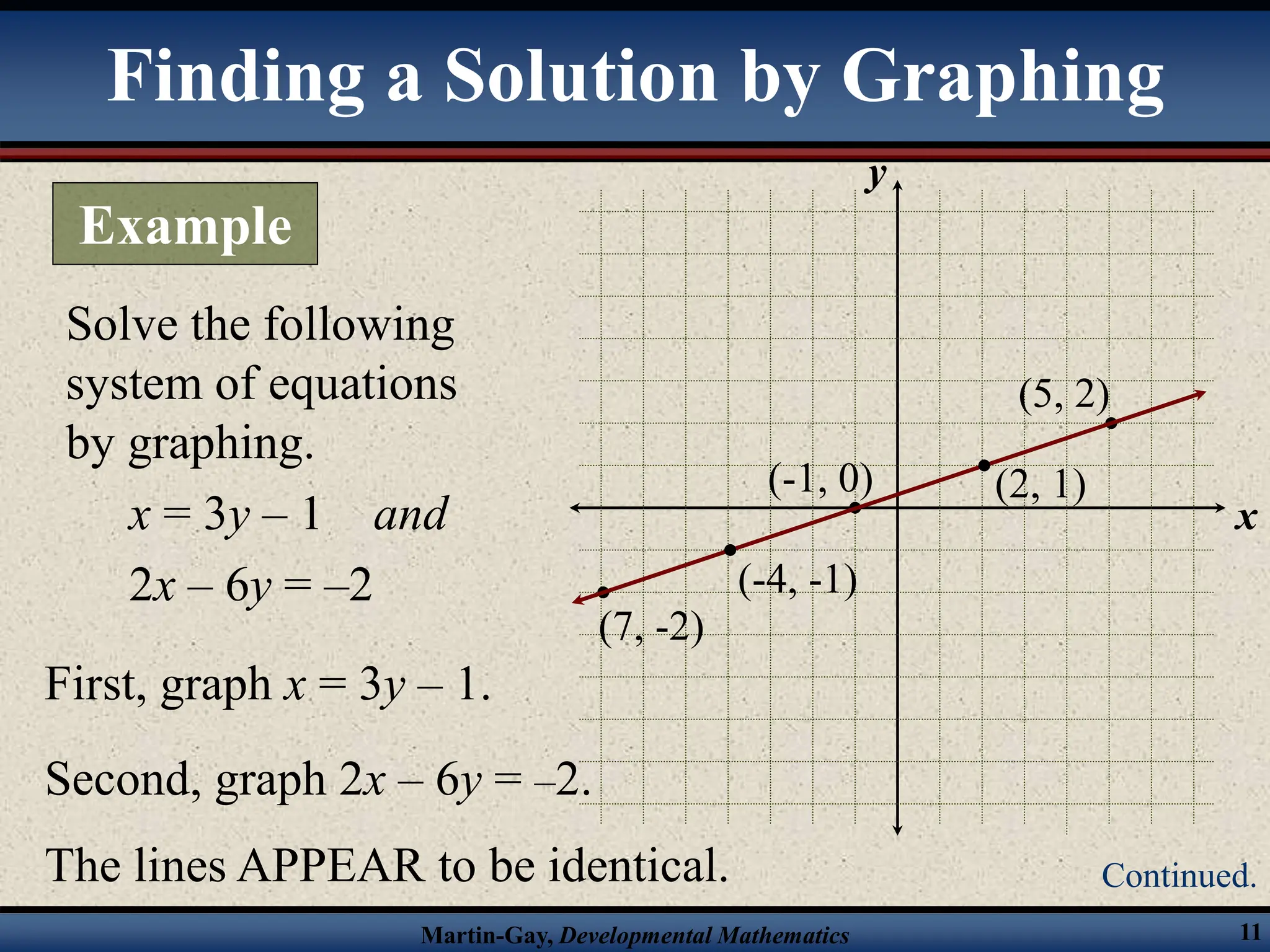
The document provides an overview of solving systems of linear equations by graphing and algebraically through substitution and elimination. It includes examples of using each method to solve systems. Key points covered include the three possible outcomes when graphing systems, the steps for the substitution and elimination methods, and checking solutions in the original equations.